ZADANIA Z PODSTAW DYNAMIKI BUDOWLI – cz. 2
1.
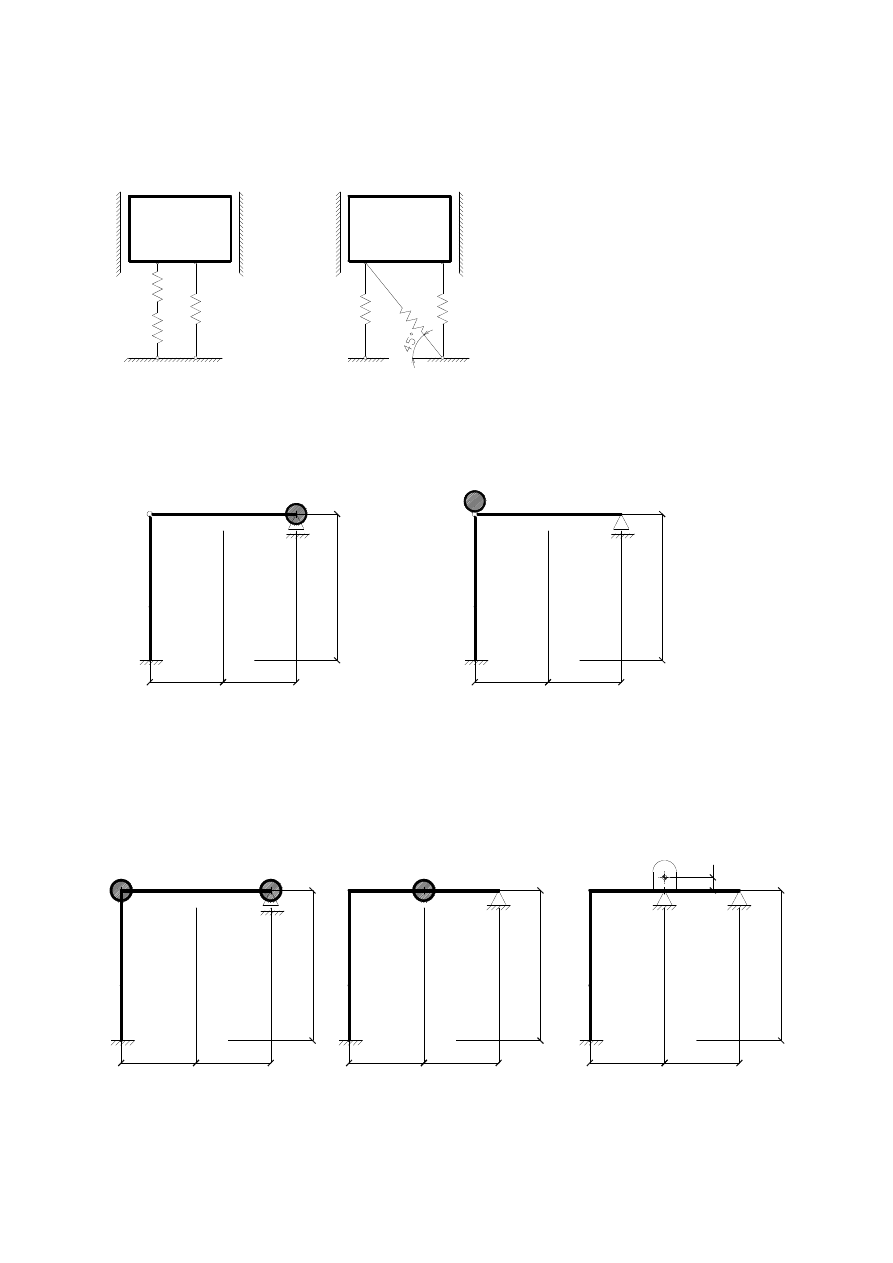
Oblicz sztywność zastępczą układów pokazanych na Rys. 1, dane: k.
k
m
k
k
m
k
k
k
Rys. 1a Rys. 1b
2.
Oblicz sztywność zastępczą układów pokazanych na Rys. 2, dane: EJ, EA, a.
a
2
a
a
EJ
m
A
B
B
EA
a
2
a
a
EJ
m
A
B
B
EA
Rys. 2a Rys. 2b
3.
Oblicz sztywność zastępczą i częstość drgań własnych układów pokazanych na Rys. 3, dane:
EJ, EA=
∞
, a, m, J
0
, h
0
.
4.
Rozwiąż poprzednie zadanie w wariancie podpór przegubowych w p. A.
m
3m
A
B
A
B
a
2
a
a
EJ =const
A
C
h
o
m,J
o
D
B
a
2
a
a
EJ =const
m
a
2
a
a
EJ =const
Rys. 3a Rys. 3b Rys. 3c
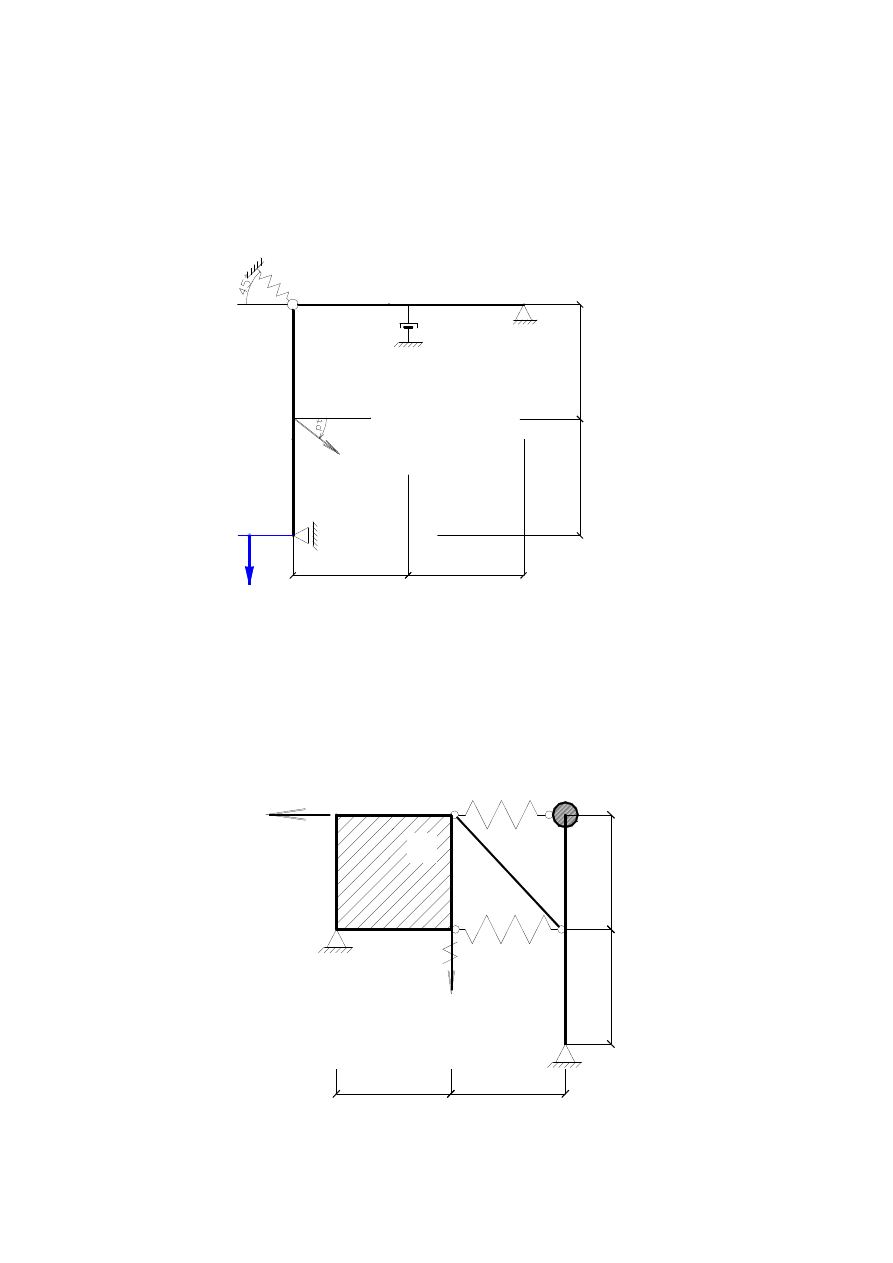
5.
Oblicz parametry układu o jednym dynamicznym stopniu swobody pokazanych na Rys.4:
częstość, częstotliwość, okres drgań własnych;
ułamek tłumienia krytycznego;
częstość, częstotliwość, okres drgań własnych.
Oblicz odpowiedź układu na wymuszenie harmoniczne : amplitudę drgań, opóźnienie fazowe.
Dane: µ= 200 kg/m, k=10
6
N/m , c=10
4
Ns/m, P
0
= 10 kN, p=20 rad/s, EJ=EA=
∞
.
k
µ
µ
c
3 m
3 m
3
m
3
m
P
o
q
A
C
D
E
B
Rys. 4
6.
Oblicz parametry układu o jednym dynamicznym stopniu swobody pokazanych na Rys.5:
częstość, częstotliwość, okres drgań własnych;
ułamek tłumienia krytycznego;
częstość, częstotliwość, okres drgań własnych.
Oblicz odpowiedź układu na wymuszenie harmoniczne : amplitudę drgań, opóźnienie fazowe.
Dane: a=3 m, ρ= 200 kg/m
2
, k=10
6
N/m, m=500 kg , P
o
= 10 kN, p=20 rad/s, EJ=EA=
∞
.
ρ
m
k
2k
a
a
a
a
q
P sinpt
o
Rys. 5
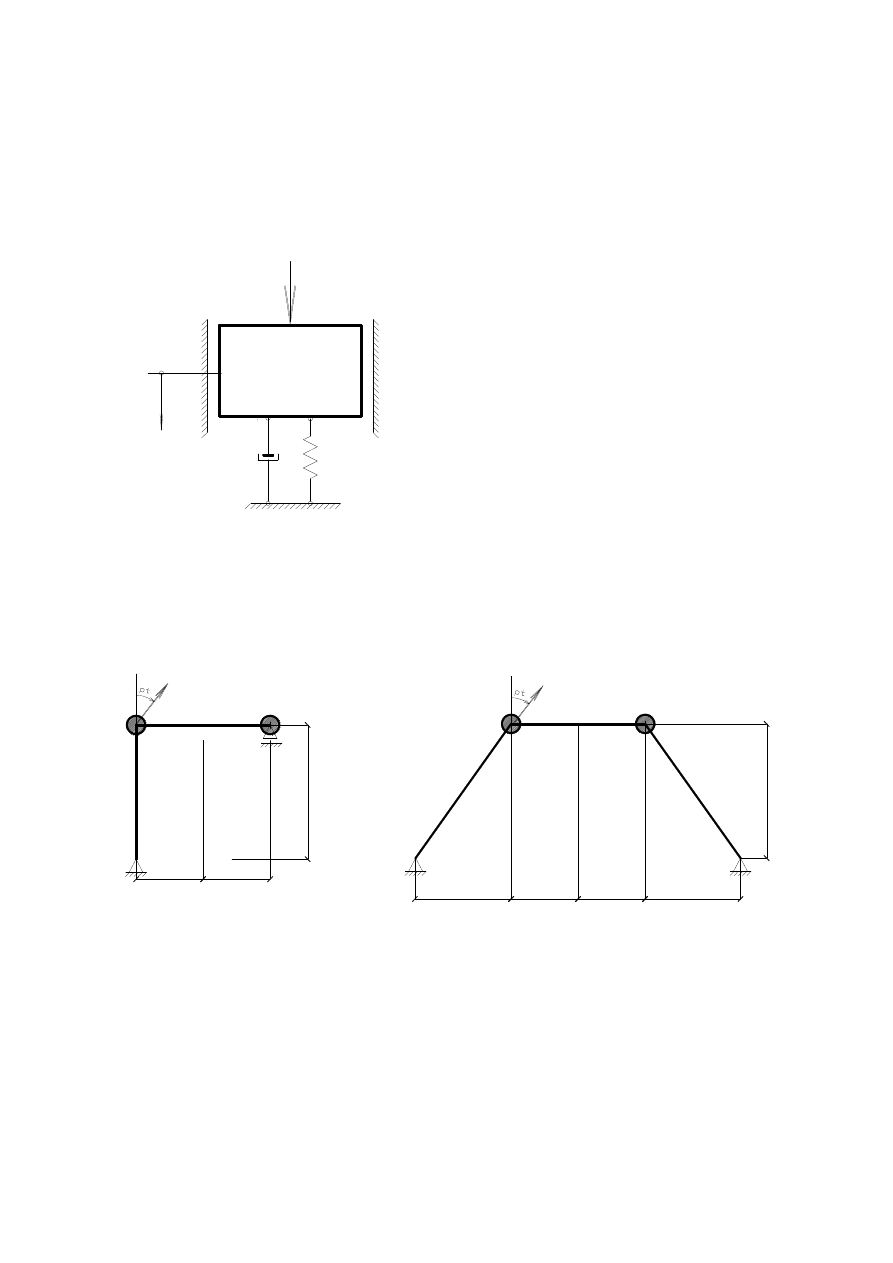
7.
Oblicz ile powinien wynosić parametr tłumienia c, aby w układzie pokazanym na Rys. 6 okres
drgań własnych tłumionych (T’) był dwa razy większy od okresu drgań własnych
nietłumionych (T). (m=50 kg, k=10 kN/m).
8.
Oblicz amplitudę przemieszczeń układu pokazanego na Rys. 6 (c=500 Ns/m, k=100 kN/m,
m=40 kg, F(t)=P
1
sin pt + P
2
cos pt, P
1
= 30 kN, P
2
=40 kN, p=40 rad/s). Wynik podaj w mm.
9.
Oblicz ile powinna wynosić sztywność więzi sprężystej k, aby kąt opóźnienia fazowego
w układzie pokazanym na Rys.6 wynosił 90˚. (m=50 kg, c=400 Ns/m, F(t) = P
0
sin 2πft,
P
0
=10 kN, f=10 Hz).
Rys. 6
10.
Oblicz amplitudę drgań punktu C, układów przedstawionych na Rys. 7. Dane: a=2 m,
m=500 kg, P
o
= 10 kN, p=20 rad/s, EJ=EA=
∞
1,5 a
2
a
EJ =const
A
B
m
2m
a
1,5 a
C
D
a
2
a
a
EJ =const
m
3m
A
B
E
a
P
o
P
o
C
Jacek Grosel
m
k
c
F(t)
q(t)