PROGRAMOWALNE FILTRY AKTYWNE, WARUNKI GENERACJI DRGAŃ

1.

Zaprojektować filtr bikwadratowy. Przeprowadzić obliczenia dla f

0

= 71kHz; Q = 2,5; wzmDC = -2.

Na-

rysować połączenia na schemacie oraz zaznaczyć wejście i wyjście filtru.

Naszkicować charakterystykę

amplitudową filtru. W obliczeniach przyjąć wartości rezystancji na schemacie R=250k

Ω.

Wyznaczyć analitycznie charakterystyki amplitudową i fazową filtru.

2.

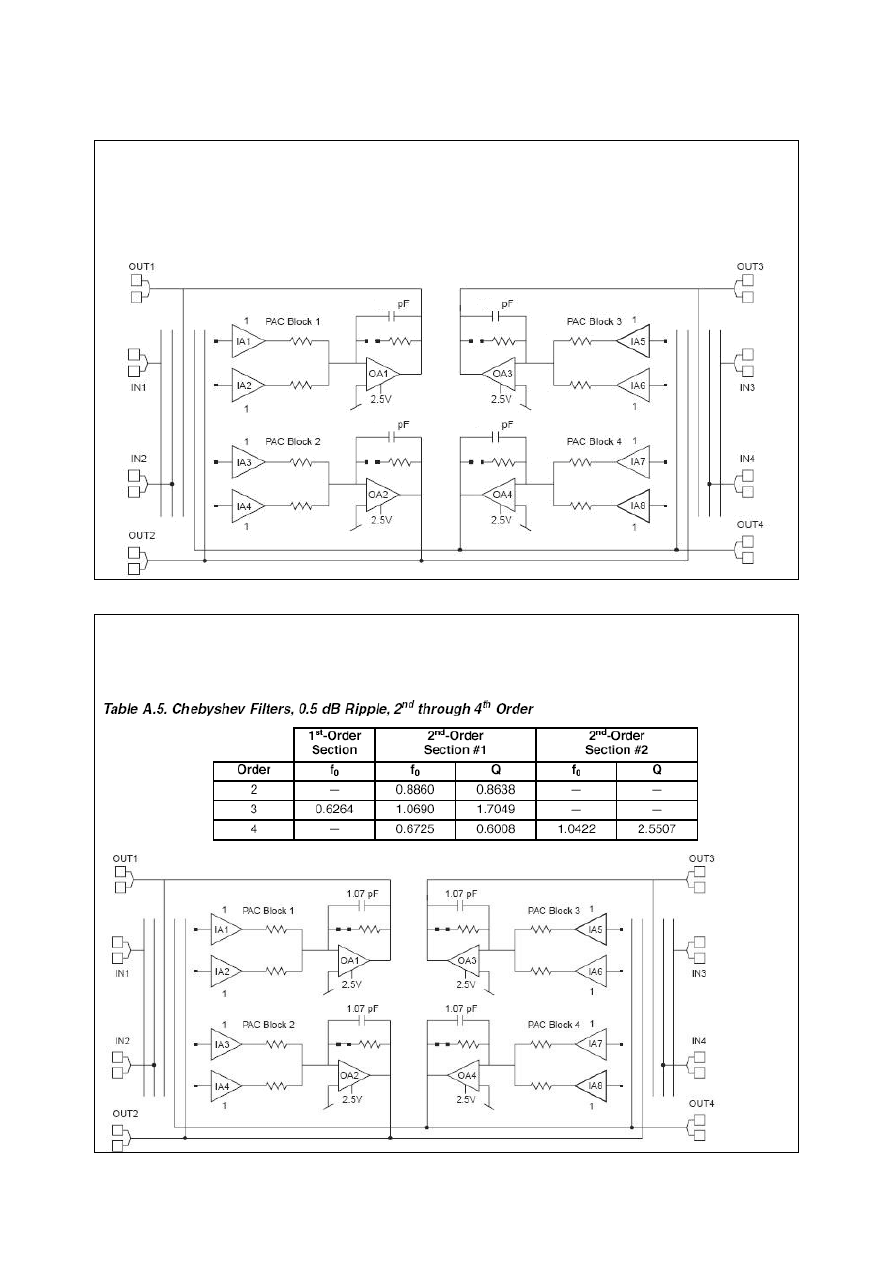
Zaprojektować filtr Czebyszewa 4. rzędu – przeprowadzić obliczenia dla f

0

= 35,5kHz; Q = 2,5;

wzmDC = 2.

Narysować połączenia na schemacie.

Naszkicować charakterystykę filtru. Jakie są jego

właściwości?

3.

Filtr Sallen-Key’a ma transmitancję operatorową daną wzorem

1

2

/

1

)

(

2

2

2

+

+

=

sRC

C

R

s

s

T

.

Naszkicować charakterystykę amplitudowo-fazową (wykres Nyquista) filtru. Obliczyć dobroć i
narysować logarytmiczną charakterystykę amplitudową. Jaki to filtr?

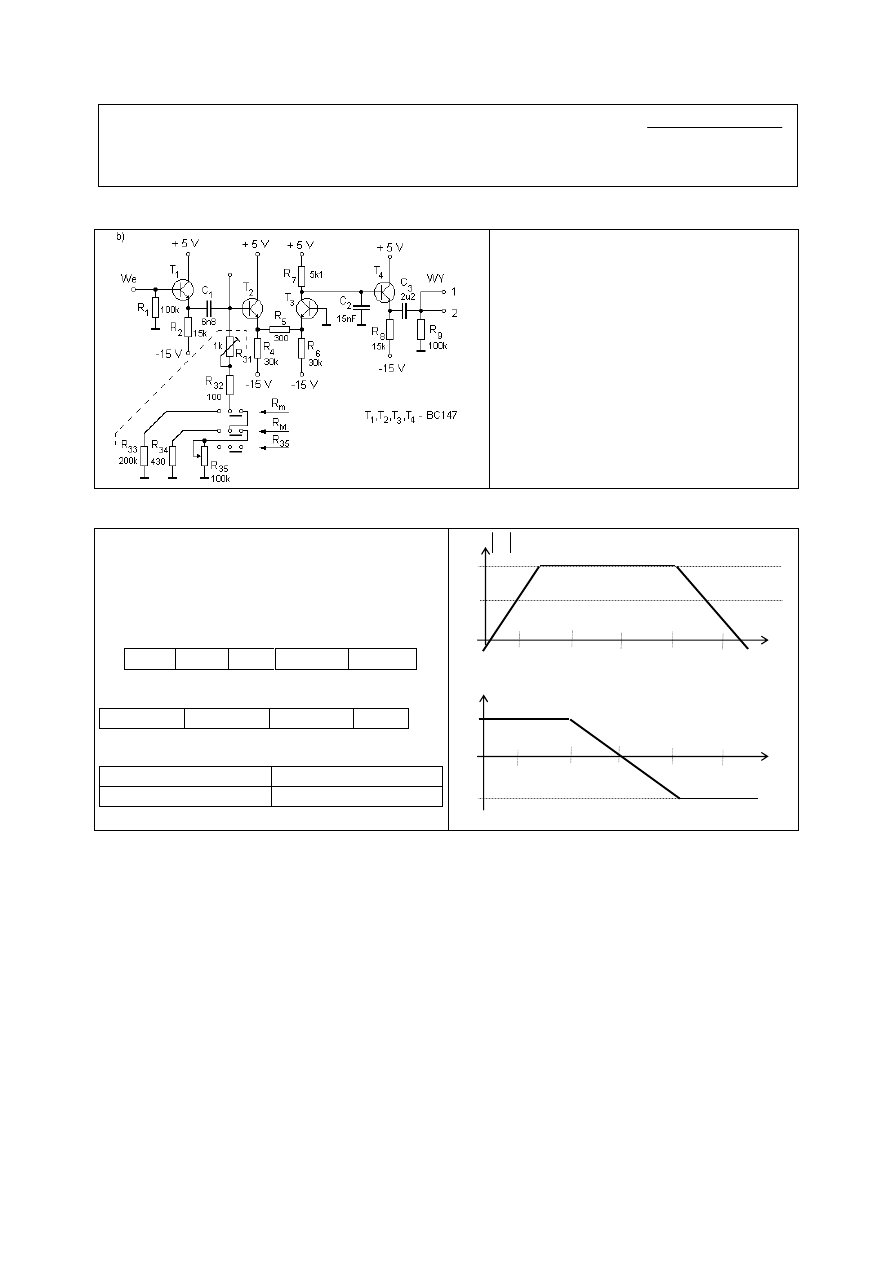
4.

Naszkicować charakterystykę amplitudową
wzmacniacza uwzględniając różne wartości
rezystancji R

3

. Wyznaczyć wzmocnienie

układu dla średnich częstotliwości oraz czę-
stotliwości graniczne. Górną częstotliwość
graniczną badanego wzmacniacza określa
filtr dolnoprzepustowy R

7

C

2

. Od dołu pasmo

ograniczane jest przez filtr górnoprzepusto-
wy R

3

C

1

.

5.

Zmierzono

charakterystyki

częstotliwościowe

wzmacniacza.
a) Która z podanych niżej transmitancji członu
sprzężenia zwrotnego

β

zapewni, że układ stanie

się generatorem po zamknięciu pętli s.z.?

β

= 0

β

=-1

β

=1

β

=-1/20

β

=1/20

b) Który z poniższych warunków będzie spełniać
częstotliwość f

g

powstałego generatora

f

g

< 10

4

Hz f

g

> 10

4

Hz f

g

> 10

5

Hz żaden

c) Jaki w przybliżeniu będzie kształt generowanego
sygnału

wykładniczy

logarytmiczny

sinusoidalny

prostokątny

dB

u

k

20

10
f
0
0,1 1 10 100 10

3

kHz

rad

ϕ

= arg(k

u

)

π/2
f
0
0,1 1 10 100 10

3

kHz

π/2