UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
1
EGZAMIN PISEMNY - przykładowy zestaw, rozwiązania zadań
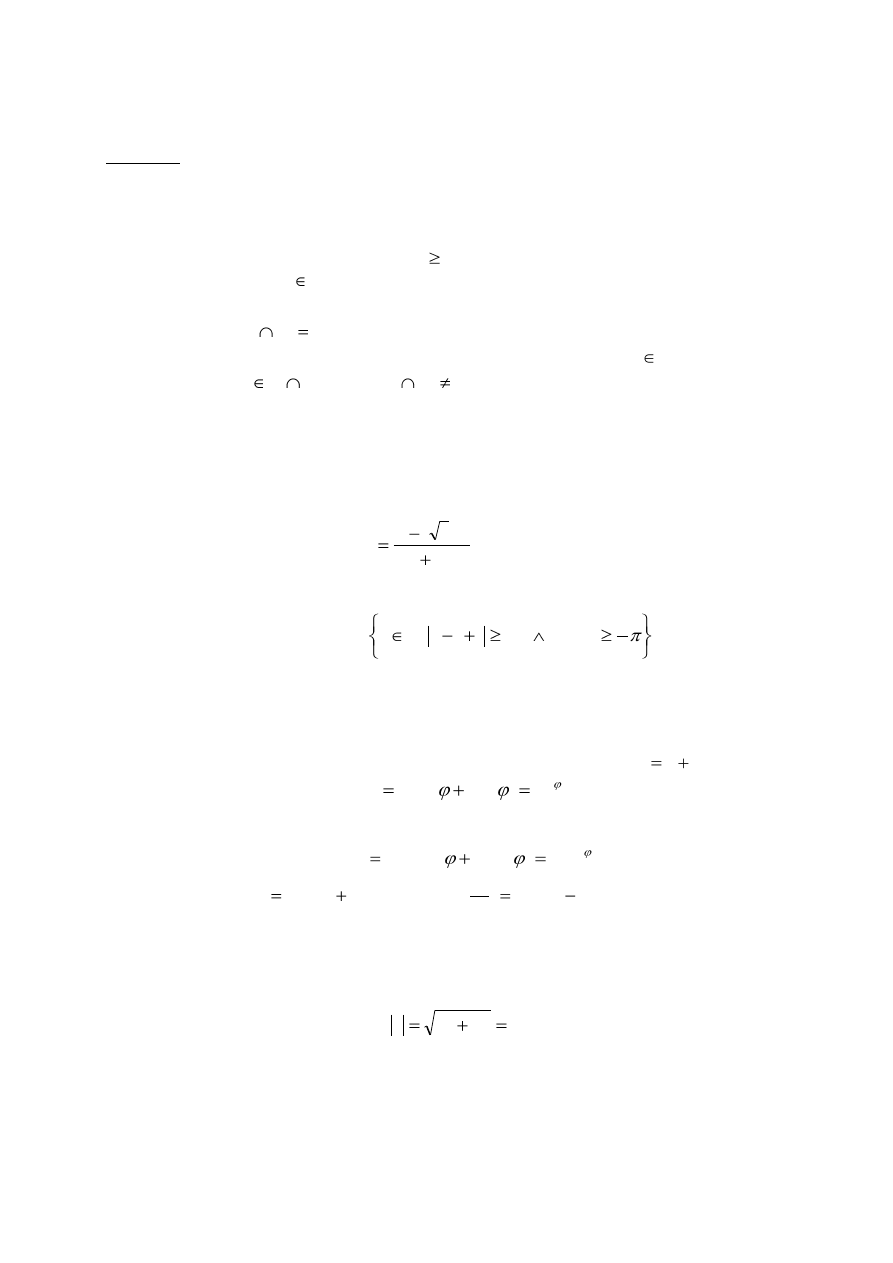
1. W przestrzeni liniowej V o wymiarze
2
dimV
, określona jest następująca relacja:
Wektor
u
jest w relacji z wektorem
v
(
u
~
v
) jeśli
u
jest liniowo zależny z
v
.
Określić zbiór wektorów
0
V będących w relacji z ustalonym wektorem
0
0
v
.
Czy zbiór
0
V jest podprzestrzenią liniową? Jeśli tak to podać bazę i wymiar.
Czy relacja ta jest relacją równoważności?
Rozwiązanie:
Wskazówka: Istota problemu sprowadza się do obserwacji, że wektor zerowy jest liniowo
zależny z każdym wektorem.
Liniowa zależność dwóch wektorów: Definicję liniowej zależności wektorów, przestrzeni
liniowej V nad ciałem K , zapisujemy w postaci symetrycznej.
Wektory
V
v
v
2
1
,
są liniowo zależne, jeśli istnieją
K
2
1
,
, z których
przynajmniej jeden jest różny od zera, takie, że
0
2
2
1
1
v
v
.
Zbiór wektorów
0
V liniowo zależnych z wektorem
0
0
v
:
Niech
0
1
v
v
. Występują dwa przypadki:
a)
0
2
v
. Wtedy
0
0
2
1
i
. Stąd
0
0
2
1
2
v
v
v
dla pewnego
K .
b)
0
2
v
. Wtedy
0
,
0
2
1
. Stąd
0
0
2
0
0
v
v
v
dla
0 .
W obu przypadkach wektor
2
v
liniowo zależny z wektorem
0
0
v
przyjmuje postać
0
2
v
v
, gdzie
K . Dlatego
K
v
v
V
v
V
,
:
0
0
Zbiór wektorów
0
V jako podprzestrzeń liniowa:
Zbiór
0
V jest domknięty ze względu na dodawanie wektorów i mnożenie przez liczbę ( dowód
wynika wprost z własności tych działań ):
0
2
1
0
2
0
1
)
(
v
v
v
,
0
1
2
0
1
2
)
(
)
(
v
v
W szczególności
0
V zawiera wektor zerowy
0
0
V . Zbiór
0
V jest więc podprzestrzenią
liniową. Co więcej, zbiór
0
V stanowi powłokę liniową rozpiętą przez jeden wektor
0
v .
Zatem
1
dim
0
V
, a dowolna baza składa się z jednego wektora postaci
0
0
1
v
e
,
0
0
.
Relacja równoważności ?:
Sposób I. - Relacja równoważności jest zwrotna, symetryczna i przechodnia.
Z powyższej definicji liniowej zależności wektorów wynika, że relacja:
Wektor
u
jest w relacji z wektorem
v
(
u
~
v
) jeśli
u
jest liniowo zależny z
v
.
jest oczywiście symetryczna, a także zwrotna (
0
u
u
).
Jeśli jednak
2
dimV
, to relacja ta nie jest przechodnia. Istnieją bowiem wtedy
przynajmniej dwa ( różne od zera ) wektory liniowo niezależne
V
u
u
2
1
,
, nie będące ze
sobą w relacji. Ale każdy z nich jest liniowo zależny z wektorem zerowym
V
0
.
Mamy więc:
1
u
~ 0 i 0 ~
2
u
podczas gdy
1
u
nie jest w relacji z
2
u
.
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
2
Sposób II. - Relacja równoważności dzieli zbiór na rozłączne podzbiory ( klasy
równoważności ).
Dowód nie wprost. Załóżmy, że relacja:
Wektor
u
jest w relacji z wektorem
v
(
u
~
v
) jeśli
u
jest liniowo zależny z
v
.
jest relacją równoważności. Ponieważ
2
dimV
, to istnieją dwa ( różne od zera ) wektory
liniowo niezależne
V
u
u
2
1
,
, nie będące ze sobą w relacji. Wtedy zbiór wektorów
1
V
będących w relacji z wektorem
1
u
jest rozłączny ze zbiorem wektorów
2
V
będących w relacji
z wektorem
2
u
,
2
1
V
V
Ø .
Ale każdy z wektorów
2
1
, u
u
jest liniowo zależny z wektorem zerowym
V
0
, co oznacza,
że wektor zerowy
2
1
0
V
V
, czyli
2
1
V
V
Ø . Doprowadzając do sprzeczności
wykazaliśmy, że nie jest to relacja równoważności.
......................................................................................................................................................
2. Znaleźć część rzeczywistą, urojoną oraz moduł liczby zespolonej
z
postaci:
12
12
)
1
(
)
3
1
(
i
i
z
Czy liczba
z
należy do zbioru
4
7
1
1
:
Argz
i
z
C
z
Wynik uzasadnić oraz naszkicować na płaszczyźnie zespolonej.
Rozwiązanie:
Wskazówka 1: Liczbę zespoloną można zapisać w postaci algebraicznej
iy
x
z
lub
trygonometrycznej ( wykładniczej )
i
re
i
r
z
)
sin
(cos
. Mnożenie, potęgowanie i
pierwiastkowanie wygodniej jest wykonywać korzystając z postaci trygonometrycznej,
w oparciu o wzór de Moivre’a:
in
n
n
n
e
r
n
i
n
r
z
)
sin
(cos
przy czym
2
1
2
1
)
(
z
Arg
z
Arg
z
z
Arg
,
2
1
2
1
)
(
z
Arg
z
Arg
z
z
Arg
.
Wskazówka 2: Wyrażenia z wysokimi potęgami można czasami uprościć, jeśli któraś
z kolejnych potęg przyjmuje prostą postać (
k
z
jest rzeczywiste lub urojone ).
Korzystanie ze wzoru na dwumian Newtona jest ostatecznością.
Wskazówka 3: Przy obliczaniu modułu
r
y
x
z
2
2
można korzystać z faktu:
- moduł iloczynu( ilorazu, potęgi) równy jest iloczynowi(ilorazowi, potędze) modułów.
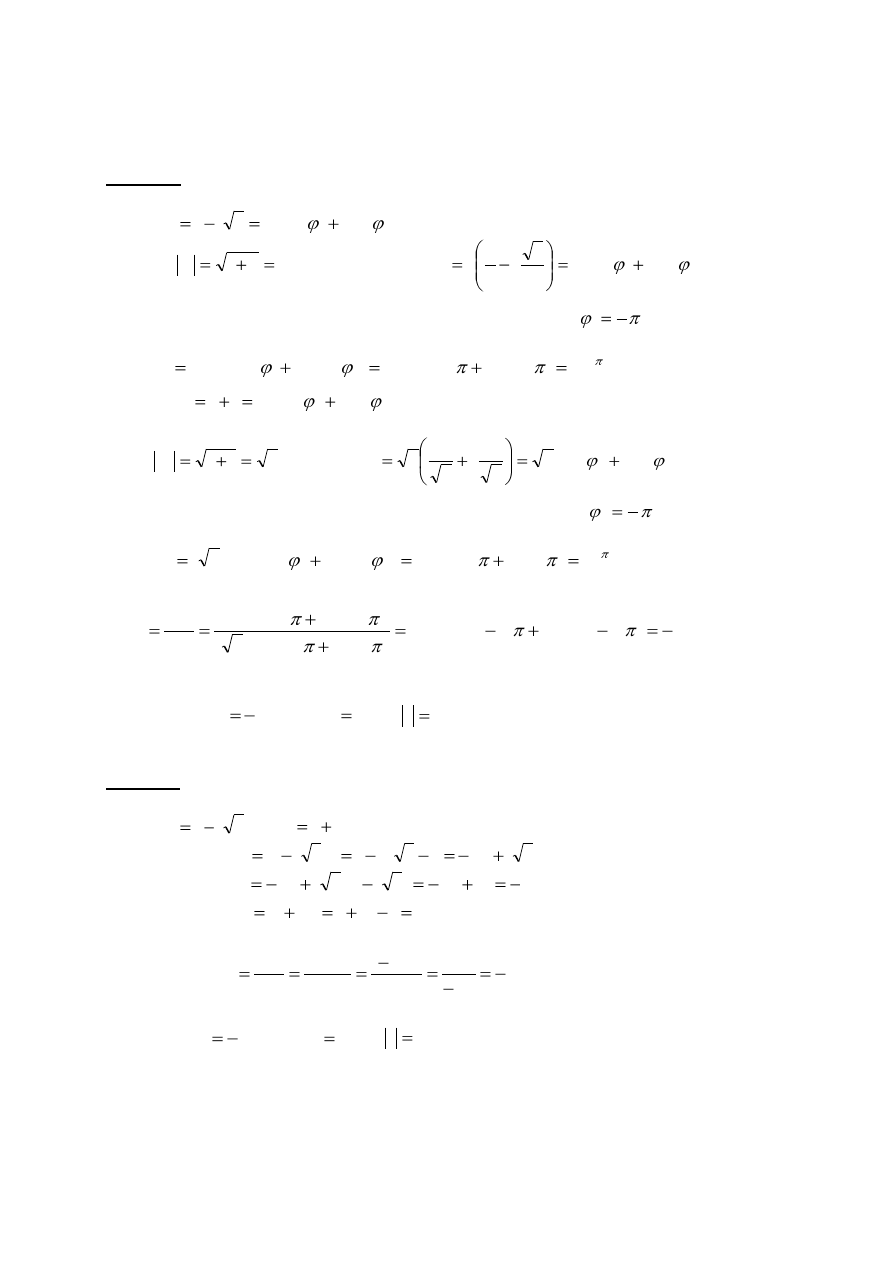
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
3
A. Postać liczby
z
Sposób 1: Postać trygonometryczna
Niech
)
sin
(cos
3
1
1
1
1
1
i
r
i
z
. Wtedy
2
3
1
1
z
,
)
sin
(cos
2
2
3
2
1
2
1
1
1
i
i
z
Stąd (
1
z
leży w czwartej ćwiartce na płaszczyźnie zespolonej )
3
5
1
,
20
12
1
1
12
12
1
)
20
sin
20
(cos
2
)
12
sin
12
(cos
2
i
e
i
i
z
Niech
)
sin
(cos
1
2
2
2
2
i
r
i
z
.
Wtedy
2
1
1
2
z
,
)
sin
(cos
2
2
1
2
1
2
2
2
2
i
i
z
Stąd (
2
z
leży w pierwszej ćwiartce na płaszczyźnie zespolonej )
4
1
2
,
3
12
2
2
12
12
2
)
3
sin
3
(cos
2
)
12
sin
12
(cos
)
2
(
i
e
i
i
z
Ostatecznie
6
6
12
12
12
2
12
1
2
)
)
3
20
sin(
)
3
20
(cos(
2
)
3
sin
3
(cos
)
2
(
)
20
sin
20
(cos
2
i
i
i
z
z
z
Zatem
64
Re z
,
0
Im z
,
64
z
.
Sposób 2: Postać arytmetyczna.
Niech
3
1
1
i
z
,
i
z
1
2
. Obliczamy kolejne potęgi liczb
2
1
, z
z
.
)
3
1
(
2
3
3
2
1
)
3
1
(
2
2
1
i
i
i
z
3
3
1
2
)
3
1
(
2
)
3
1
)(
3
1
(
2
i
i
z
i
i
i
z
2
1
2
1
)
1
(
2
2
2
Ostatecznie
6
6
12
6
4
3
6
2
2
4
3
1
12
2
12
1
2
2
2
)
2
(
)
2
(
)
(
)
(
i
z
z
z
z
z
Zatem
64
Re z
,
0
Im z
,
64
z
.
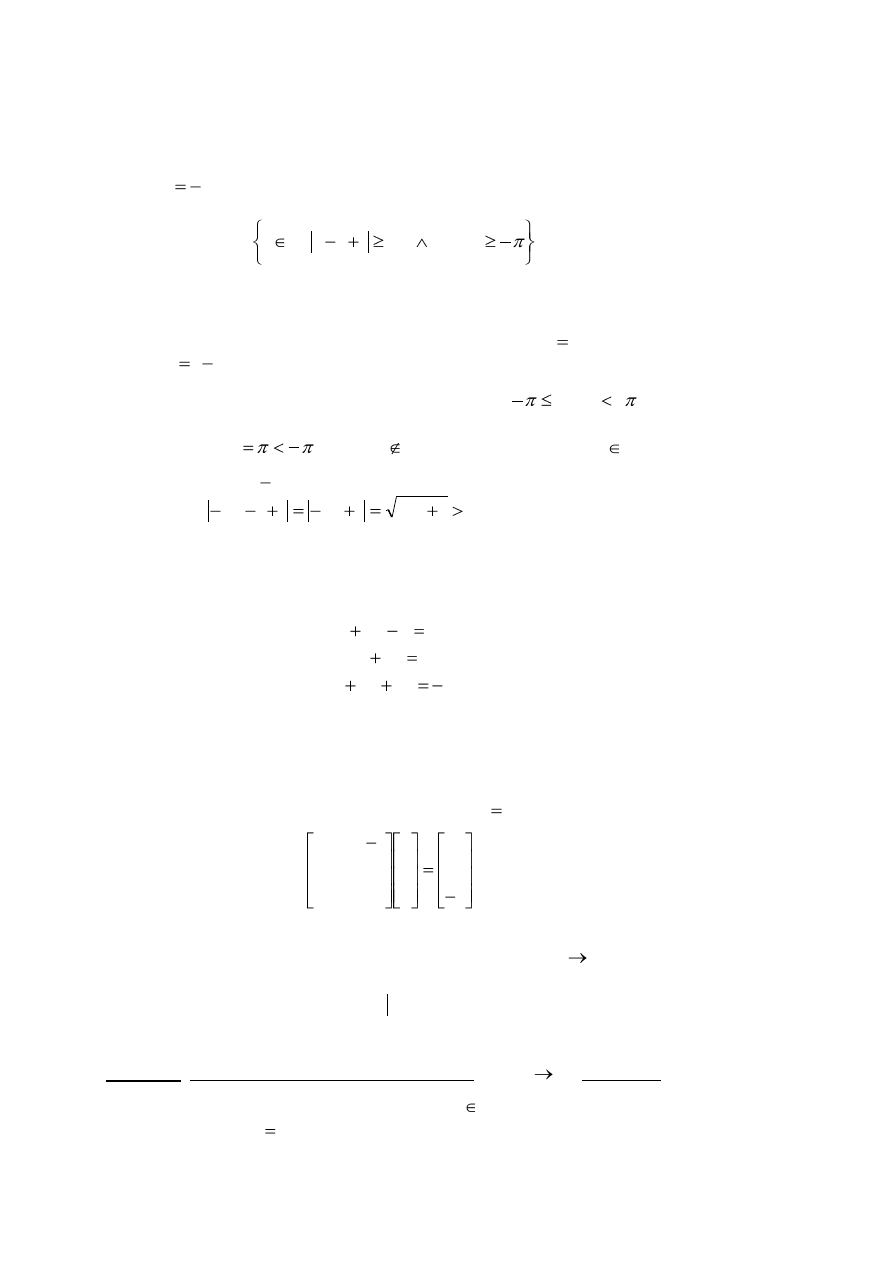
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
4
B. Położenie liczby
z
na płaszczyźnie zespolonej
Liczba
64
z
nie należy do podanego zbioru
4
7
1
1
:
Argz
i
z
C
z
który jest częścią wspólną zbiorów A i B , gdzie
-
A to zewnętrze koła ( wraz z okręgiem) o promieniu
1
r
i środku w punkcie
i
z
1
0
,
-
B to obszar ograniczony dwiema półprostymi:
2
4
7
z
Arg
.
bowiem
4
7
z
Arg
czyli
B
z
. Należy zauważyć, że
A
z
, ponieważ
odległość
z
od
i
1
( jako moduł różnicy liczb ) jest większa od 1
1
1
65
65
1
64
2
i
i
.
......................................................................................................................................................
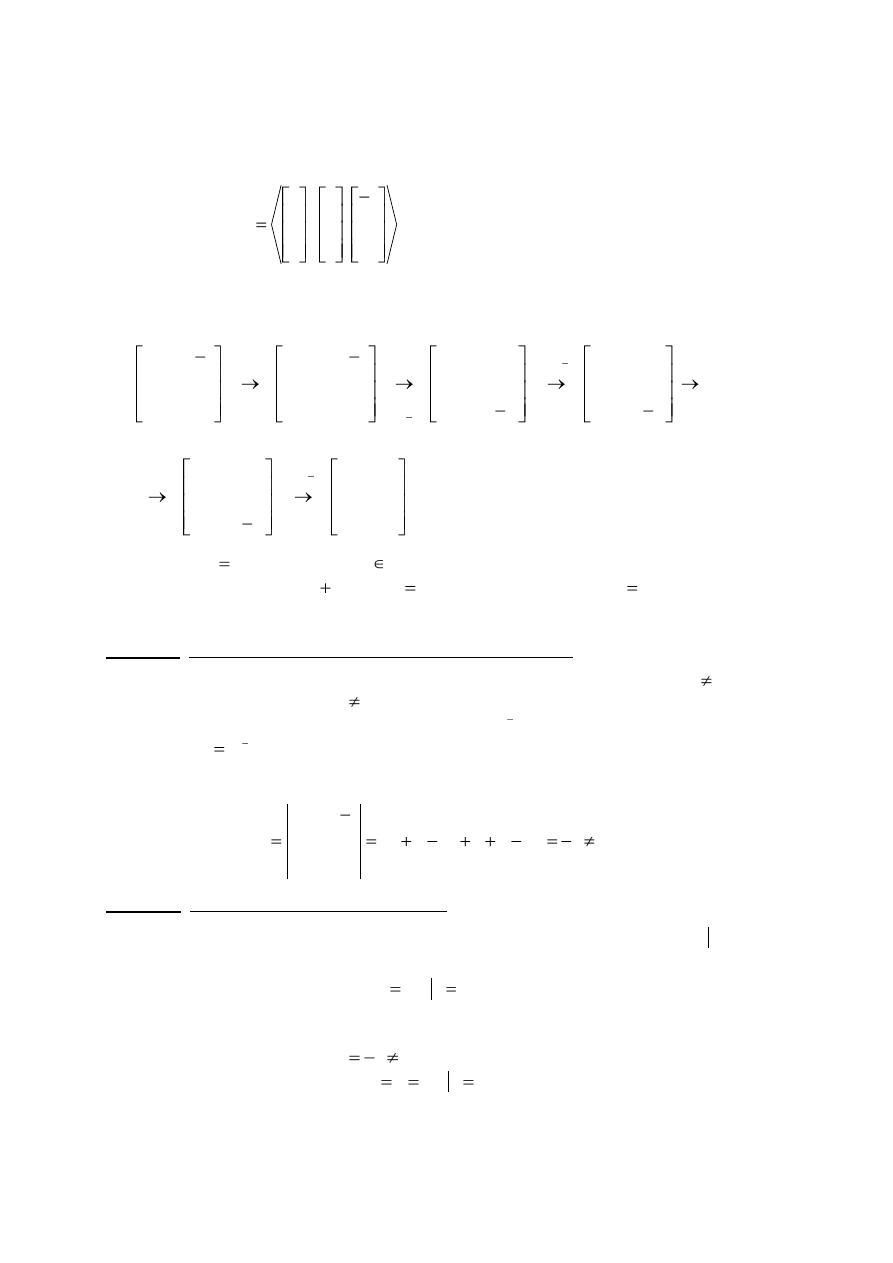
3. Wykazać ( dwoma sposobami ) bez rozwiązywania, że układ równań
1
7
5
3
1
3
2
2
2
z
y
x
y
x
z
y
x
posiada jedno rozwiązanie? Rozwiązać układ równań dwoma z trzech podanych metod:
metoda operacji elementarnych, metoda macierzy odwrotnej, wzory Cramera.
Rozwiązanie
Wskazówka: Postać macierzowa układu równań
b
Ax
1
1
2
7
5
3
0
3
2
1
2
1
z
y
x
pozwala wyjaśnić problem istnienia rozwiązań układu trzech równań z trzema niewiadomymi,
poprzez badanie właściwości przekształcenia liniowego
3
3
:
R
R
f
posiadającego w bazie
standardowej macierz A , sprawdzenie czy jest to układ typu Cramera lub badanie rzędów
macierzy A i macierzy rozszerzonej
b
A .
A. Istnienie rozwiązań
Sposób 1: Właściwości przekształcenia liniowego
3
3
:
R
R
f
o macierzy A .
Układ niejednorodny posiada rozwiązanie gdy
f
b
Im
. Rozwiązanie jest jedno jeśli
dodatkowo
Kerf
dim
0 .
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
5
Kolumny macierzy A , jako obrazy wektorów bazy rozpinają obraz
f
Im
7
0
1
,
5
3
2
,
3
2
1
Im f
Wykonując operacje elementarne na kolumnach macierzy A wykazujemy, że wszystkie trzy
są liniowo niezależne ( tworzą bazę w
3
R
)
0
1
0
0
0
1
1
0
0
7
1
5
0
0
1
1
0
0
7
4
5
0
0
1
1
0
0
7
19
5
0
3
1
1
0
0
7
19
10
0
3
2
1
0
0
7
5
3
0
3
2
1
2
1
)
7
(
2
,
3
)
5
(
2
,
1
)
4
/
1
(
2
)
3
(
1
,
2
)
1
(
3
)
2
/
1
(
1
)
2
(
3
,
2
)
1
(
3
,
1
K
K
K
K
K
K
K
K
F
F
F
F
F
F
F
F
Tak więc
3
Im
R
f
i oczywiście
f
b
Im
.
Ponadto z faktu, że
3
dim
Im
dim
Kerf
f
otrzymujemy
0
dim Kerf
.
Układ posiada więc jedno rozwiązanie.
Sposób 2: Układ typu Cramera lub metoda macierzy odwrotnej.
Macierz A jest macierzą kwadratową . Wystarczy wykazać, że wyznacznik
0
det A
.
Jeżeli bowiem wyznacznik
0
det A
to:
- po pierwsze, istnieje wówczas macierz odwrotna
1
A
i układ posiada jedyne rozwiązanie
postaci
b
A
x
1
,
- po drugie, układ posiada jedyne rozwiązanie opisane wzorami Cramera.
Rzeczywiście
0
8
28
0
9
10
0
21
7
5
3
0
3
2
1
2
1
det A
Sposób 3: Twierdzenie Kroneckera-Capellego
Układ posiada jedno rozwiązanie jeśli rzędy macierzy A i macierzy rozszerzonej
b
A
są
równe liczbie niewiadomych
n
:
n
b
rzA
rzA
Metoda wyznacznikowa: Rząd macierzy równy jest najwyższemu ze stopni jej minorów
różnych od zera.
Wykazując ( sposób 2 ), że
0
8
det A
otrzymujemy
n
b
rzA
rzA
3
Metoda operacji elementarnych: Rząd macierzy równy jest maksymalnej liczbie liniowo
niezależnych wektorów kolumnowych ( wierszowych ) macierzy.
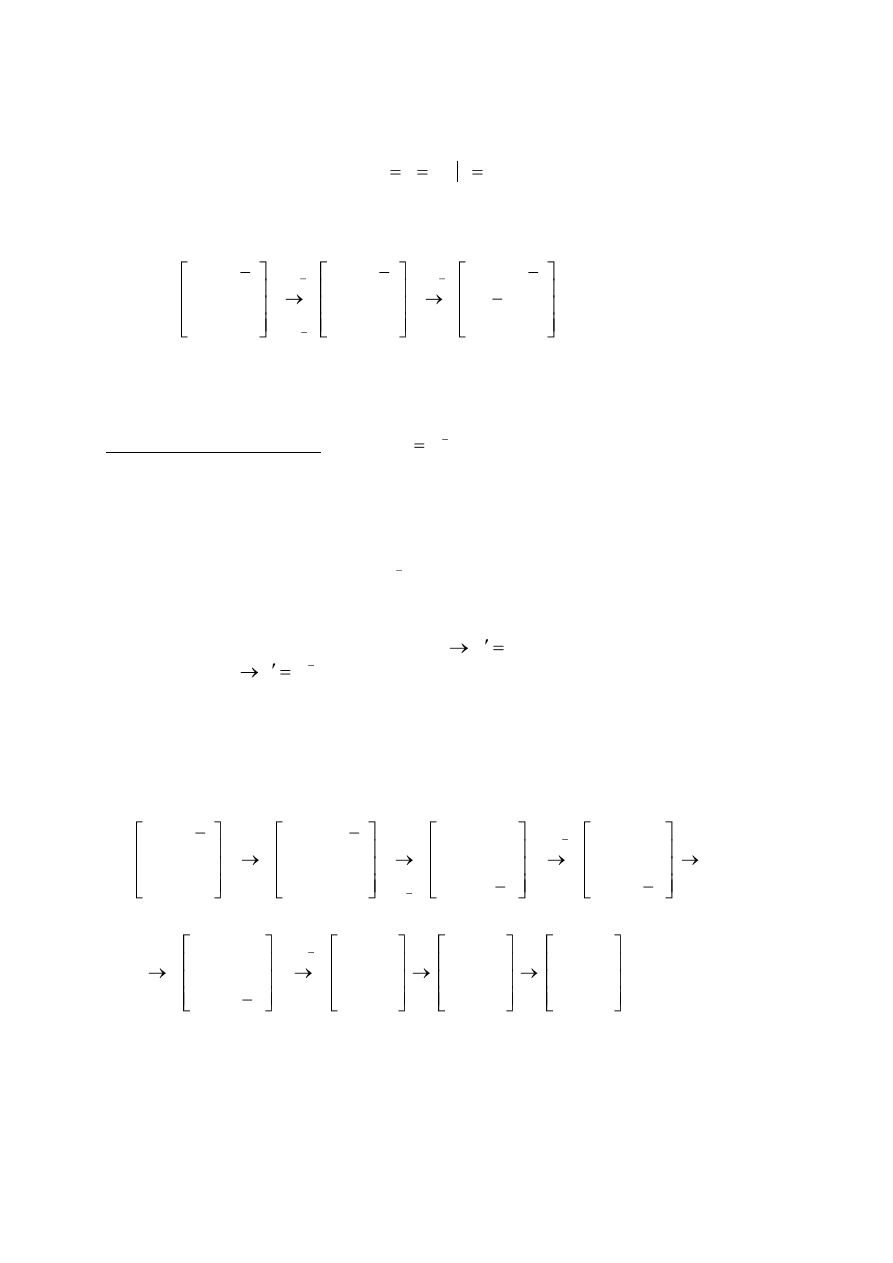
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
6
Wykonując operacje elementarne na kolumnach ( sposób 1 ) wykazaliśmy, że
n
b
rzA
rzA
3
Sprowadzając macierz do najprostszej postaci można w tym przypadku wykonywać operacje
elementarne zarówno na kolumnach jak i na wierszach. Wystarczy przy tym wyzerować
elementy pod (nad ) diagonalą ( operacjami na wierszach )
8
0
0
2
1
0
1
2
1
8
0
0
0
3
2
1
2
1
7
5
3
0
3
2
1
2
1
)
2
(
1
,
2
)
1
(
2
,
3
)
1
(
1
,
3
w
w
w
F
F
F
aby zauważyć, że trzy wektory kolumnowe ( wierszowe ) są liniowo niezależne.
B. Rozwiązanie układu równań
Sposób 1: Macierz odwrotna.
b
A
x
1
Macierz odwrotną można wyznaczyć dwoma metodami:
i)
przy pomocy operacji elementarnych,
ii)
przy pomocy wyznaczników ( dopełnienie algebraiczne, macierz dołączona )
i) Aby wyznaczyć macierz odwrotną
1
A
do macierzy A ( metodą operacji elementarnych )
należy skorzystać z następującego faktu:
Jeśli wykonamy równocześnie ciąg takich samych operacji elementarnych na macierzy
A i macierzy jednostkowej I, taki że
I
A
A
,
to wtedy
1
A
I
I
.
Uwaga! Wszystkie operacje wyłącznie na kolumnach lub wszystkie wyłącznie na wierszach.
Można wykorzystać ciąg operacji na kolumnach (
1
. Sposób
A
), uzupełniając go o zamiany
miejscami odpowiednich kolumn.
1
0
0
0
1
0
0
0
1
0
0
1
0
1
0
1
0
0
0
1
0
0
0
1
1
0
0
7
1
5
0
0
1
1
0
0
7
4
5
0
0
1
1
0
0
7
19
5
0
3
1
1
0
0
7
19
10
0
3
2
1
0
0
7
5
3
0
3
2
1
2
1
3
,
1
2
,
1
)
7
(
2
,
3
)
5
(
2
,
1
)
4
/
1
(
2
)
3
(
1
,
2
)
1
(
3
)
2
/
1
(
1
)
2
(
3
,
2
)
1
(
3
,
1
K
K
K
K
K
K
K
K
K
K
F
F
F
F
F
F
F
F
F
F
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
7
1
1
1
2
10
14
3
19
21
8
1
1
1
1
14
10
2
21
19
3
8
1
1
1
1
14
2
10
21
3
19
8
1
8
1
4
0
2
0
0
3
4
8
1
1
2
/
1
2
/
1
0
1
0
0
2
/
3
2
/
1
1
2
2
/
1
0
1
0
0
0
2
/
1
1
2
1
0
1
0
0
0
1
1
0
0
0
1
0
0
0
1
3
,
1
2
,
1
)
7
(
2
,
3
)
5
(
2
,
1
)
4
/
1
(
2
)
3
(
1
,
2
)
1
(
3
)
2
/
1
(
1
)
2
(
3
,
2
)
1
(
3
,
1
K
K
K
K
K
K
K
K
K
K
F
F
F
F
F
F
F
F
F
F
Stąd
1
1
1
2
10
14
3
19
21
8
1
1
A
,
2
/
1
2
2
/
5
1
1
2
1
1
1
2
10
14
3
19
21
8
1
z
y
x
ii) Korzystamy ze wzoru
D
A
A
A
det
1
1
, gdzie
D
A
oznacza macierz dołączoną, która jest
transpozycją macierzy dopełnień algebraicznych elementów macierzy
A
.
Niech
ij
A
~
oznacza
macierz utworzoną z macierzy A przez skreślenie i-tego wiersza oraz j-tej kolumny.
Dopełnienie algebraiczne
ij
d elementu
ij
a wynosi
ij
j
i
ij
A
d
~
det
)
1
(
natomiast elementy macierzy dołączonej mają postać:
ji
ij
D
d
A
nn
n
n
d
d
d
d
A
A
...
...
det
1
1
1
11
1
W tym przypadku ( A. Sposób 2 )
8
det A
.
21
7
5
0
3
11
d
,
19
7
5
1
2
21
d
,
3
0
3
1
2
31
d
,
14
7
3
0
2
12
d
,
10
7
3
1
1
22
d
,
2
0
2
1
1
32
d
,
1
5
3
3
2
13
d
,
1
5
3
2
1
23
d
,
1
3
2
2
1
33
d
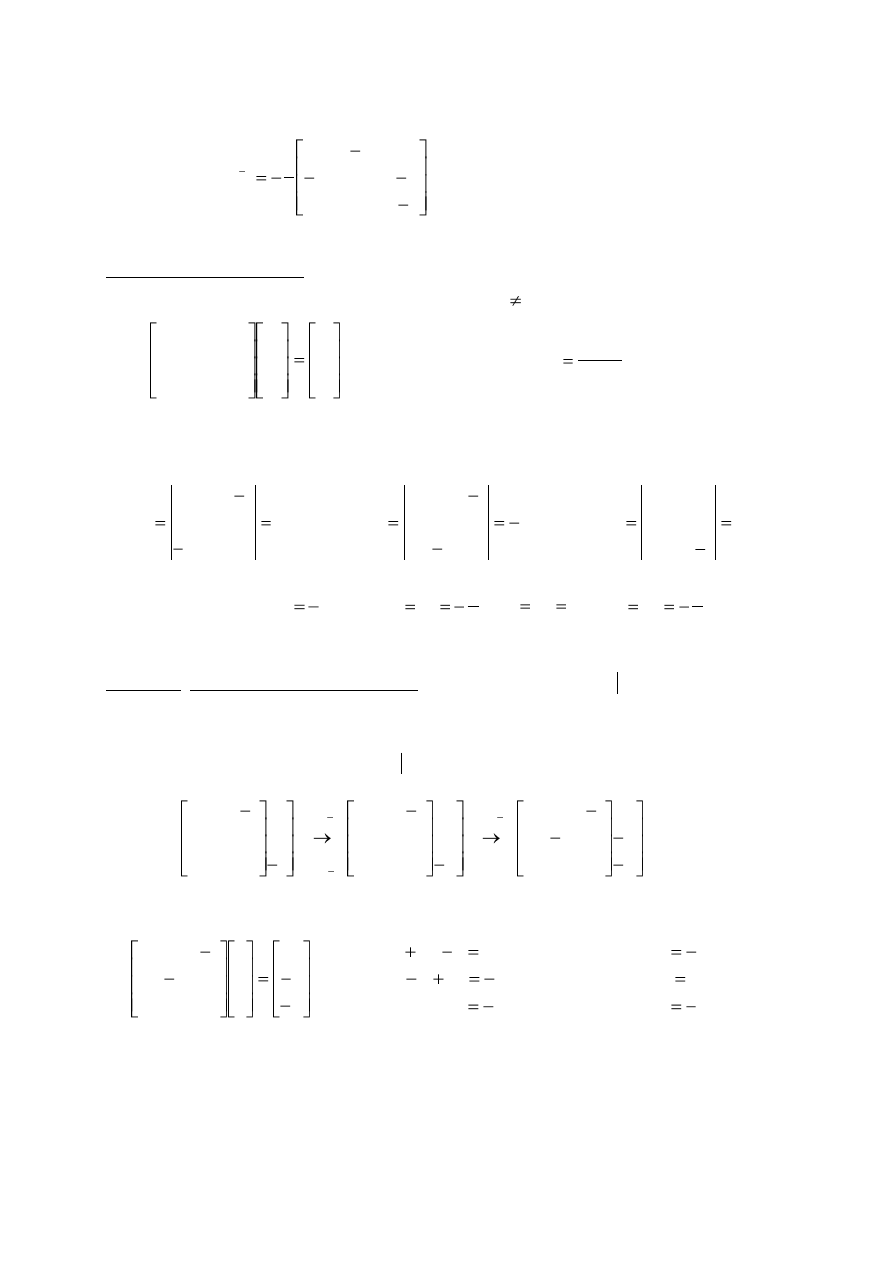
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
8
Stąd
1
1
1
2
10
14
3
19
21
8
1
1
A
Sposób 2. Wzory Cramera
Jeśli A jest macierzą kwadratową, nieosobliwą (
0
det A
) to rozwiązania układu równań
n
n
nn
n
n
b
b
x
x
a
a
a
a
1
1
1
1
11
...
...
są postaci
A
A
x
i
i
det
det
gdzie macierz
i
A
została utworzona z macierzy A poprzez zastąpienie i-tej kolumny,
kolumną wyrazów wolnych b .
20
7
5
1
0
3
1
1
2
2
det
1
A
,
16
7
1
3
0
1
2
1
2
1
det
2
A
,
4
1
5
3
1
3
2
2
2
1
det
3
A
Ale
( A. Sposób 2 )
8
det A
. Więc
2
5
1
x
x
,
2
2
x
y
,
2
1
3
x
z
.
Sposób 3: Metoda operacji elementarnych ( na wierszach macierzy b
A )
Aby wyzerować w macierzy A elementy pod diagonalą, wykonujemy ciąg operacji
elementarnych na wierszach macierzy
b
A ( taki sam jak w A. Sposób 3 )
4
3
2
8
0
0
2
1
0
1
2
1
4
1
2
8
0
0
0
3
2
1
2
1
1
1
2
7
5
3
0
3
2
1
2
1
)
2
(
1
,
2
)
1
(
2
,
3
)
1
(
1
,
3
w
w
w
F
F
F
Układ równań przyjmuje równoważną, prostą postać:
4
3
2
8
0
0
2
1
0
1
2
1
z
y
x
czyli
4
8
3
2
2
2
z
z
y
z
y
x
. Stąd kolejno
2
/
5
2
2
/
1
x
y
z
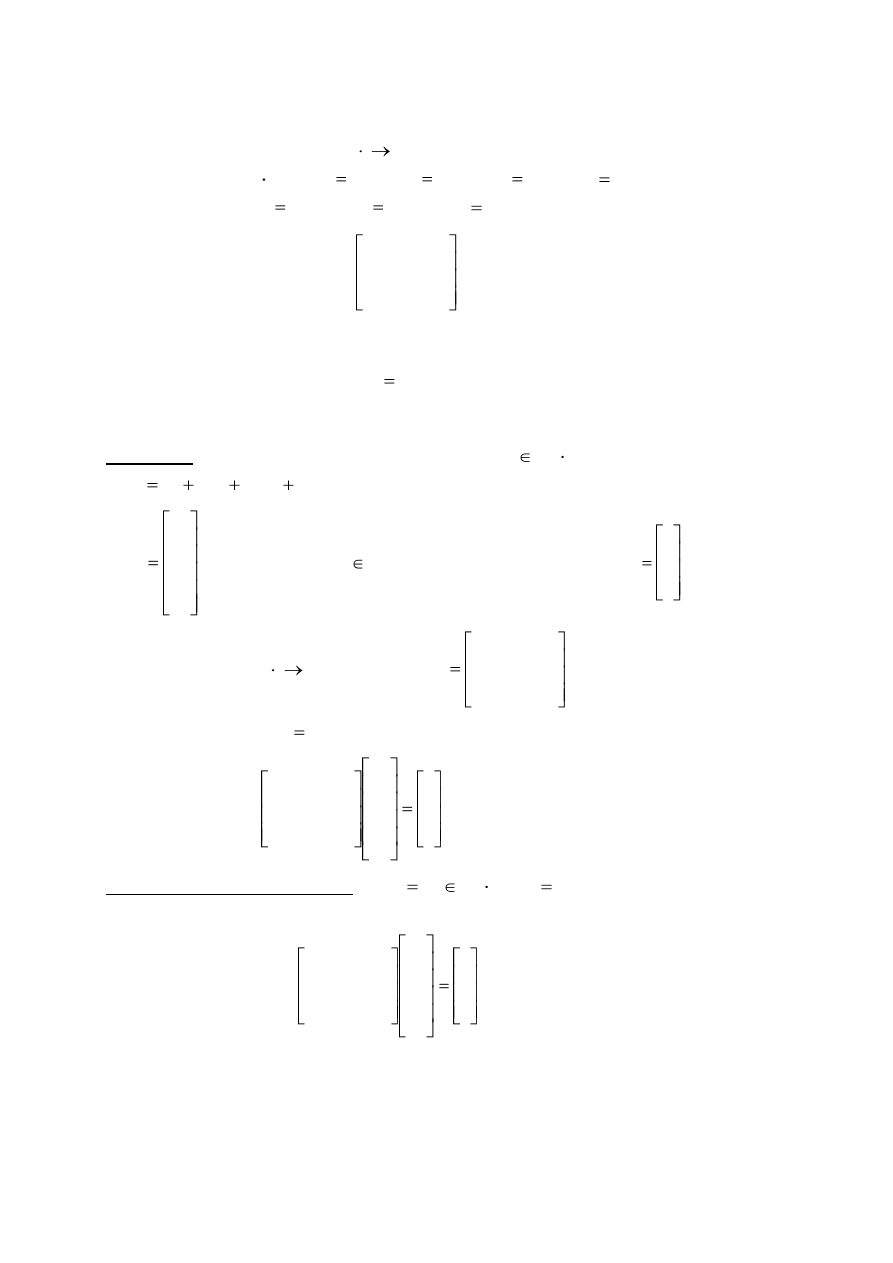
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
9
4. Przekształcenie liniowe
3
3
]
[
:
R
R
f
posiada ( w bazach standardowych: w przestrzeni
wielomianów
]
[
3
R
;
1
)
(
1
x
e
,
x
x
e
)
(
2
,
2
3
)
(
x
x
e
,
3
4
)
(
x
x
e
, natomiast w
przestrzeni
3
R
;
)
0
,
0
,
1
(
1
e
,
)
0
,
1
,
0
(
2
e
,
)
1
,
0
,
0
(
3
e
) macierz postaci:
3
2
3
2
2
2
3
1
1
1
1
1
Określić Ker f , Imf ( podając bazy i wymiar ) oraz postać wielomianu
)
(x
w
, dla
którego
)
2
,
0
,
1
(
)
(w
f
.
Rozwiązanie
Wskazówka. W podanych bazach, dowolny wielomian
]
[
3
R
w
postaci
3
4
2
3
2
1
)
(
x
w
x
w
x
w
w
x
w
reprezentowany jest przez wektor kolumnowy
w
w
w
w
w
3
2
1
, wektor
3
)
(
R
w
f
przez wektor kolumnowy
2
0
1
)
(w
f
,
przekształcenie
3
3
]
[
:
R
R
f
przez macierz
3
2
3
2
2
2
3
1
1
1
1
1
A
,
natomiast równanie
)
2
,
0
,
1
(
)
(w
f
w zapisie macierzowym przyjmuje postać
2
0
1
3
2
3
2
2
2
3
1
1
1
1
1
4
3
2
1
w
w
w
w
Jądro przekształcenia liniowego
}
0
:
]
[
{
3
Aw
R
w
f
Ker
Równanie jednorodne
0
0
0
3
2
3
2
2
2
3
1
1
1
1
1
4
3
2
1
w
w
w
w
sprowadzamy metodą operacji elementarnych na wierszach macierzy A
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
10
1
0
1
0
0
1
1
0
0
1
0
1
1
0
1
0
1
1
2
0
1
1
1
1
3
2
3
2
2
2
3
1
1
1
1
1
)
1
(
3
,
2
)
1
(
3
,
1
)
2
(
1
,
3
)
1
(
1
,
2
W
W
W
W
F
F
F
F
do prostej postaci
0
0
0
1
0
1
0
0
1
1
0
0
1
0
1
4
3
2
1
w
w
w
w
czyli
0
0
0
4
2
3
2
3
1
w
w
w
w
w
w
. Stąd kolejno
t
w
t
w
t
w
t
w
4
2
3
1
Jądro tworzą więc wektory
1
1
1
1
t
w
, to znaczy, że
1
ker
dim
f
, a baza składa się z jednego wektora np.
1
1
1
1
1
e
.
Obraz przekształcenia liniowego
f
Im
Kolumny macierzy A , jako obrazy wektorów bazy rozpinają obraz
f
Im
3
2
1
,
2
2
1
,
3
3
1
,
2
1
1
Im f
Wykonując operacje elementarne na kolumnach macierzy A wykazujemy, że trzy z nich są
liniowo niezależne ( tworzą bazę w
3
R
)
1
0
1
0
0
1
0
0
0
0
0
1
1
0
1
2
0
1
2
0
0
0
0
1
4
,
1
1
0
1
2
1
1
2
1
0
0
0
1
4
,
3
,
2
3
2
3
2
2
2
3
1
1
1
1
1
)
2
(
4
,
1
)
2
(
3
,
2
)
1
(
3
,
)
1
(
1
,
K
K
K
i
K
i
F
F
i
F
i
F
Tak więc
3
Im
R
f
,
3
Im
dim
f
, baza np. standardowa, zero-jedynkowa.
Uwaga. W tym przypadku
4
dim
Im
dim
Kerf
f
.
Przeciwobraz wektora
)
2
,
0
,
1
(
)
(w
f
Szukając wielomianów
)
(x
w
takich, że
)
2
,
0
,
1
(
)
(w
f
rozwiązujemy układ równań
niejednorodnych
2
0
1
3
2
3
2
2
2
3
1
1
1
1
1
4
3
2
1
w
w
w
w
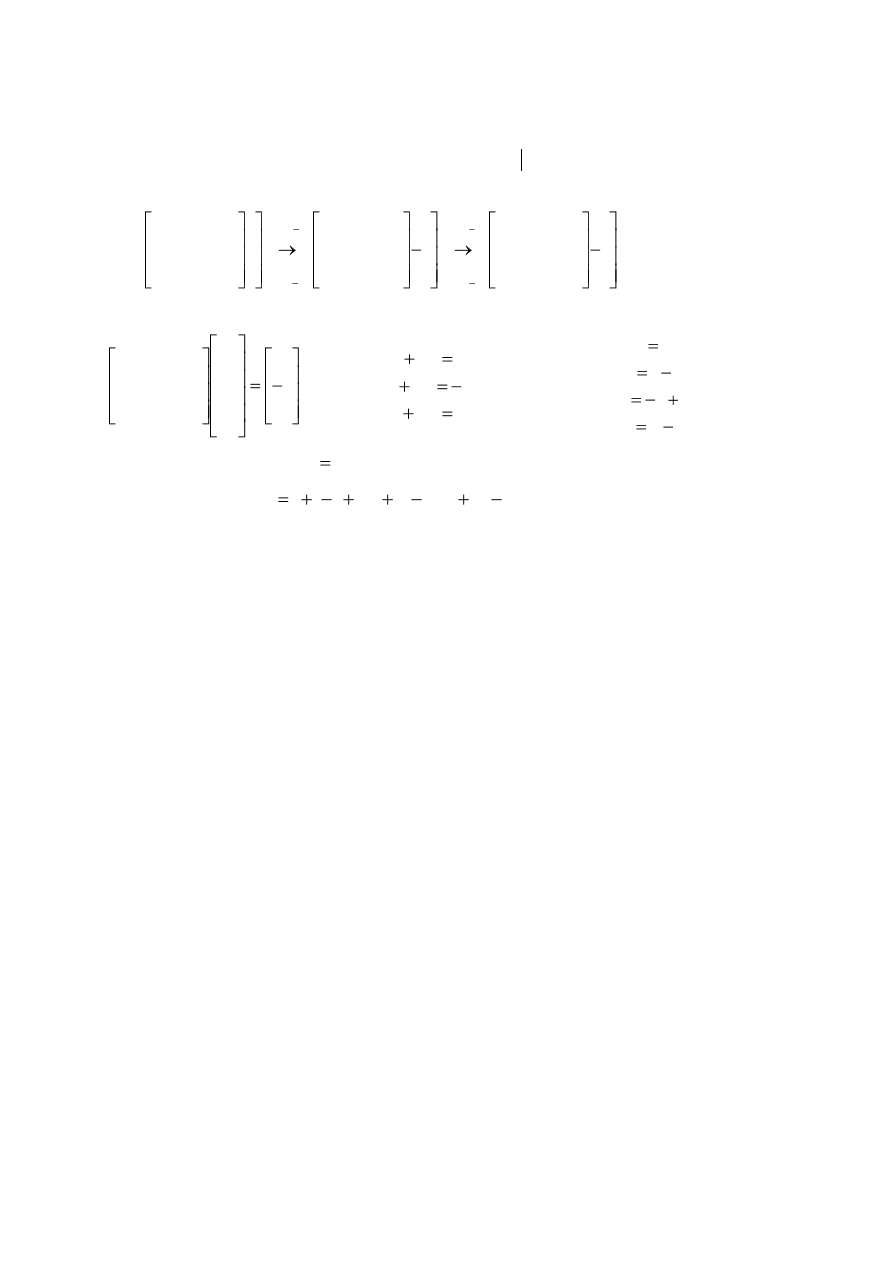
UKSW ALGEBRA LINIOWA
Matematyka – semestr I Kazimierz Jezuita
2008/2009
11
metodą operacji elementarnych na wierszach macierzy
b
A
postępując tak samo jak powyżej,
dla równania jednorodnego (
Kerf
)
0
1
1
1
0
1
0
0
1
1
0
0
1
0
1
0
1
1
1
0
1
0
1
1
2
0
1
1
1
1
2
0
1
3
2
3
2
2
2
3
1
1
1
1
1
)
1
(
3
,
2
)
1
(
3
,
1
)
2
(
1
,
3
)
1
(
1
,
2
W
W
W
W
F
F
F
F
sprowadzając układ równań do postaci:
0
1
1
1
0
1
0
0
1
1
0
0
1
0
1
4
3
2
1
w
w
w
w
czyli
0
1
1
4
2
3
2
3
1
w
w
w
w
w
w
. Stąd kolejno
t
w
t
w
t
w
t
w
2
2
1
4
2
3
1
Przeciwobraz wektora
)
2
,
0
,
1
(
)
(w
f
tworzą więc wielomiany
3
2
)
2
(
)
1
(
)
2
(
)
(
x
t
x
t
x
t
t
x
w