Z. Kąkol-Notatki do Wykładu z Fizyki

18-1

Wykład 18

18.

Siła elektrostatyczna

18.1

Wstęp

Oddziaływanie elektromagnetyczne - chyba najważniejsze w fizyce. Pozwala wyja-

ś

nić nie tylko zjawiska elektryczne ale też siły zespalające materię na poziomie atomów,

cząsteczek. Przewodniki i izolatory. Doświadczenie z naładowaniem pręta metalowego
i pręta szklanego. Zdolność izolacyjna stopionego kwarcu jest 10

25

razy większa niż

miedzi.

18.2

Ładunek elektryczny

Porównajmy siłę grawitacyjną pomiędzy elektronem i protonem w atomie wodoru

F = 3.61·10

-47

N z siła elektryczną pomiędzy nimi w tym samym atomie F = 2.27·10

-8

N.
To, że siły grawitacyjne dla "dużych" ciał dominują wynika stąd, że liczby protonów i
elektronów są równe.
Nie istnieje, żaden związek między masą i ładunkiem.
W przeciwieństwie do masy ładunki "+" lub "-".

18.2.1

Kwantyzacja ładunku

Ładunek elementarny e = 1.6·10

-19

C.

Wszystkie ładunki są wielokrotnością e.

18.2.2

Zachowanie ładunku

Zasada zachowania ładunku - B. Franklin.

Wypadkowy ładunek w układzie zamknię-

tym jest stały.

18.3

Prawo Coulomba

Siła oddziaływania dwóch ładunków q

1

i q

2

2

2

1

r

q

q

k

F

=

(18.1)

gdzie stała

0

4

1

πε

=

k

. Współczynnik

ε

0

= 8.854·10

-12

C

2

/(Nm

2

) nosi

nazwę przenikalno-

ś

ci elektrycznej próżni.

W układzie cgs k = 1.

18.3.1

Zasada superpozycji

Siłę wypadkową

(tak jak w grawitacji)

obliczamy dodając wektorowo siły dwuciało-

we

.

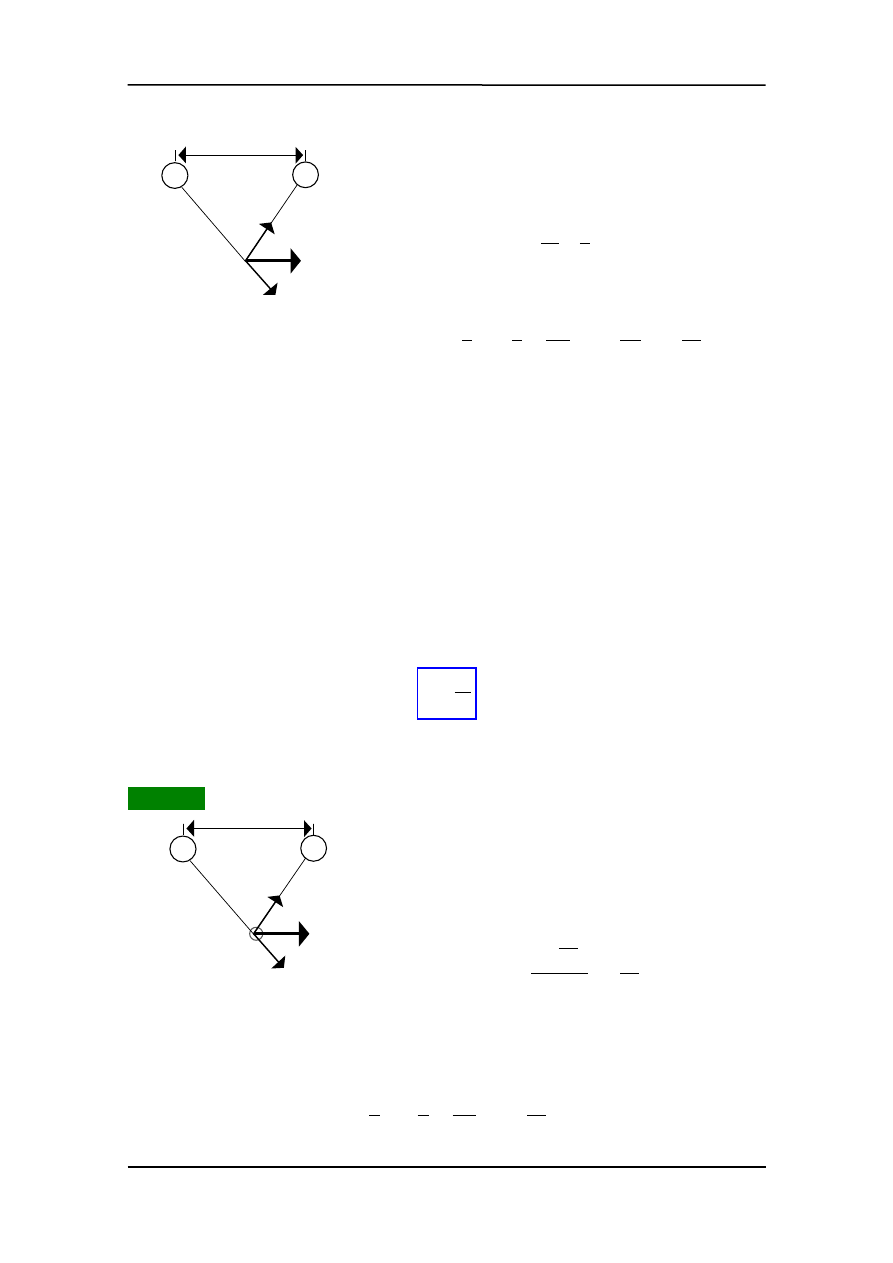
Przykład 1

Z. Kąkol-Notatki do Wykładu z Fizyki

18-2

Dipol elektryczny składa się z dwóch ładunków

oddalonych od siebie l. Jaka siła jest wywierana na ła-
dunek q umieszczony tak jak na rysunku?
Z podobieństwa trójkątów

r

l

F

F

=

1

Stąd

3

3

2

1

r

p

qk

r

Ql

qk

r

Qq

k

r

l

F

r

l

F

=

=













=

=

gdzie p = Ql jest

momentem dipolowym

.

18.4

Pole elektryczne

W wykładzie 6 zdefiniowaliśmy natężenie pola grawitacyjnego w dowolnym punk-

cie przestrzeni jako siłę grawitacyjną działająca na masę m umieszczoną w tym punkcie
przestrzeni podzieloną przez tę masę.
Analogicznie

definiujemy natężenie pola elektrycznego jako siłę działającą na ładunek

próbny q (umieszczony w danym punkcie przestrzeni) podzieloną przez ten ładunek

.

Aby zmierzyć natężenie pola elektrycznego E w dowolnym punkcie P, należy w tym
punkcie umieścić ładunek próbny i zmierzyć wypadkową siłę elektryczną F działającą
na ten ładunek. Należy upewnić się czy obecność ładunku q nie zmienia położeń innych
ładunków. Wtedy

q

F

E

=

(18.2)

Ładunek próbny jest dodatni

(umowa). Kierunek E jest taki sam jak F (na ładunek do-

datni).

Przykład 2

Ten sam układ co poprzednio tylko w punkcie P nie
ma "jakiegoś" ładunku tylko tam umieścimy ładunek
próbny. Korzystając z otrzymanej zależności obli-
czamy E

3

3

r

p

k

q

r

p

kq

E

=













=

Pole E w punkcie P jest skierowane w prawo.
Pole E w odległości r od ładunku punktowego Q jest równe

r

r

Q

k

r

r

Qq

k

q

q

ˆ

ˆ

1

1

2

2

=













=

=

F

E

+Q

-Q

l

q

F

F

2

F

1

r

r

+Q

-Q

l

F

F

2

F

1

r

r

P

Z. Kąkol-Notatki do Wykładu z Fizyki

18-3

Pole elektryczne od n ładunków punktowych jest równe sumie wektorowej pól elek-
trycznych

∑

=

=

n

i

i

i

i

r

r

Q

k

1

2

ˆ

E

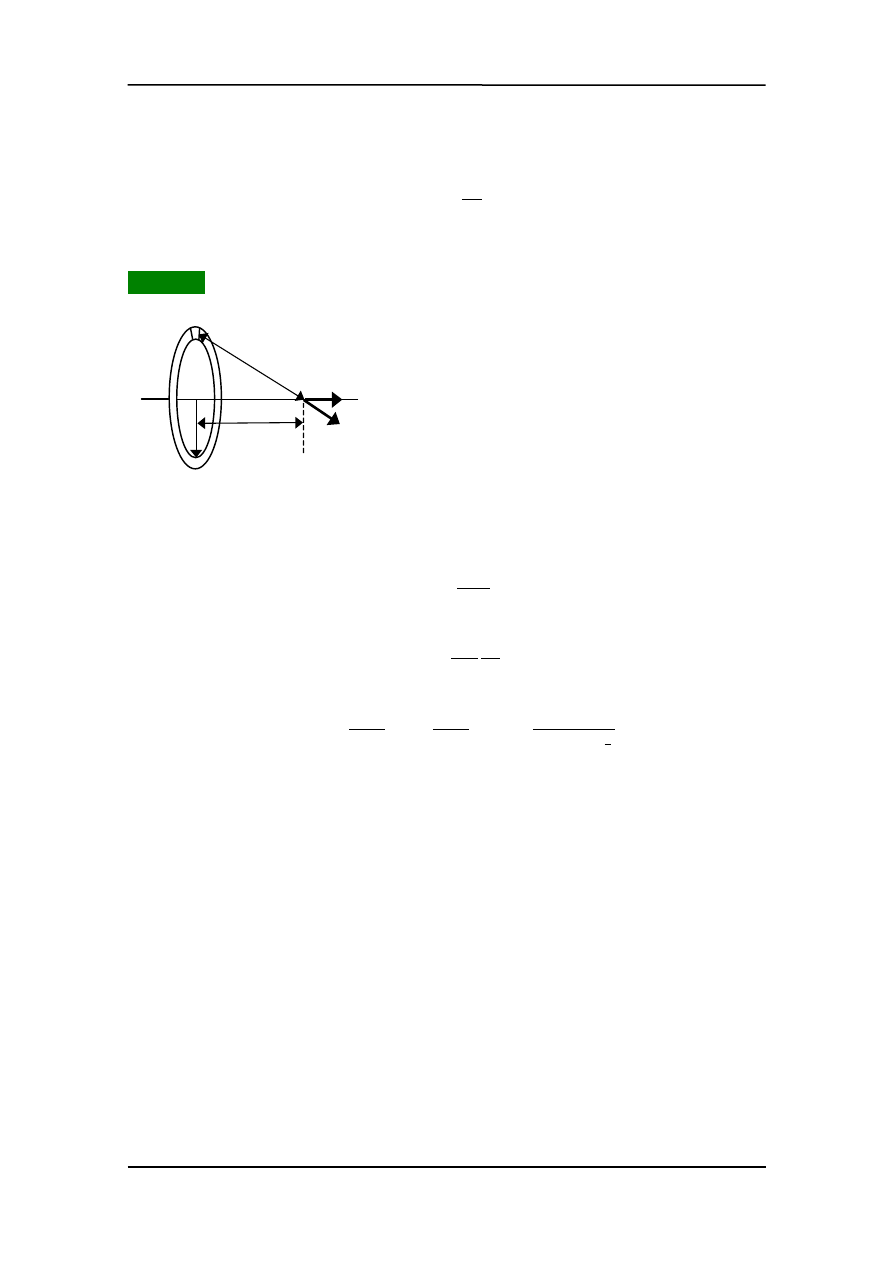
Przykład 3

Całkowity ładunek naładowanego pierście-

nia o promieniu R wynosi Q. Jakie jest pole elek-
tryczne na osi pierścienia w odległości x

0

od środ-

ka ? Pole wytwarzane przez element dl pierścienia
jest równe

dE

x

= dE(cos

α

)

cos

α

= x

0

/r

Jeżeli

λ

= Q/2

π

R jest liniową gęstością ładunku to

2

d

d

r

l

k

E

λ

=

oraz

r

x

r

l

k

E

x

0

2

d

d

λ

=

Stąd

2

3

2

2

0

0

3

0

3

0

)

(

)

2

(

d

R

x

Q

kx

R

r

x

k

l

r

x

k

E

E

x

+

=

=

=

=

∫

π

λ

λ

Zwróćmy uwagę, że w środku pierścienia (x

0

= 0) E = 0, a dla x

0

>> R pole E

→

kQ/x

0

2

i jest takie samo jak pole ładunku punktowego w tej odległości.

Jedną z zalet posługiwania się pojęciem pola elektrycznego jest to, że nie musimy

zajmować się szczegółami źródła pola. Np. pole E = kQ/r

2

może pochodzić od wielu

ź

ródeł.

18.4.1

Linie sił

Kierunek pola E w przestrzeni można przedstawić za pomocą tzw.

linii sił

. Linie nie

tylko pokazują kierunek

E ale też jego wartość (liczba linii na jednostkę powierzchni).

Jeżeli liczbę linii przechodzących przez powierzchnię

∆

S oznaczymy

∆

φ

to wówczas

∆

φ

=

E

∆

S = E

∆

S cos

α

gdzie

α

jest kątem pomiędzy wektorem powierzchni

∆

S i wektorem E.

W ogólności więc

R

x

0

r

P

dE

dE

x

α

Z. Kąkol-Notatki do Wykładu z Fizyki

18-4

d

φ

= d

E ds

(18.3)

i jest to definicja

strumienia elektrycznego

.

Całkowity strumień przechodzący przez powierzchnię S można obliczyć jako sumę
przyczynków od elementów powierzchni

∑

∆

=

ia

powierzchn

S

E

φ

Suma ta przedstawia całkę powierzchniową

∫

=

S

S

E d

φ

(18.4)

Obliczmy teraz strumień dla ładunku punktowego w odległości r od niego.
W tym celu rysujemy kulę o promieniu r wokół ładunku Q i liczymy strumień (liczbę
linii przez powierzchnię).

0

2

2

2

4

)

4

(

)

4

(

ε

π

π

π

φ

Q

kQ

r

r

Q

k

r

E

=

=













=

=

(18.5)

Otrzymany strumień nie zależy od r, a zatem strumień jest

jednakowy dla wszystkich r

.

Całkowita liczba linii wychodzących od ładunku jest równa Q/

ε

0

i linie te ciągną się do

nieskończoności.
Ponieważ pokazaliśmy, że strumień jest taki sam przez każdą powierzchnię niezależnie
od r więc jest to prawdą dla zamkniętej powierzchni o dowolnym kształcie (która otacza
ładunek Q).
Taka powierzchnia nazywa się

powierzchnią Gaussa

.

18.5

Prawo Gaussa.

Niech zamknięta powierzchnia obejmuje dwa ładunki Q

1

i Q

2

. Całkowita liczba linii

sił przecinająca powierzchnię zamkniętą wokół ładunków Q

1

i Q

2

jest równa

∫

∫

∫

∫

+

=

+

=

=

S

E

S

E

S

E

E

S

E

d

d

d

)

(

d

1

1

2

1

µ k

ca

φ

gdzie E

1

jest wytwarzane przez Q

1

, a E

2

przez Q

2

. Powołując się na wcześniejszy wynik

otrzymujemy

φ

całk

= (Q

1

/

ε

0

) + (Q

2

/

ε

0

) = (Q

1

+ Q

2

)/

ε

0

Całkowita liczba linii sił jest równa

całkowitemu ładunkowi

podzielonemu przez

ε

0

. Po-

dobnie można pokazać dla dowolnej liczby n ładunków.
Otrzymujemy więc

prawo Gaussa

Z. Kąkol-Notatki do Wykładu z Fizyki

18-5

0

.

.

4

d

ε

π

wewn

wewn

Q

kQ

=

=

∫

S

E

(18.6)

Strumień pola wychodzący z naładowanego ciała jest równa wypadkowemu ładunkowi
podzielonemu przez

ε

0

. Jeżeli Q jest ujemne strumień wpływa do ciała.

Linie mogą zaczynać się i kończyć tylko na ładunkach a wszędzie indziej są ciągłe.
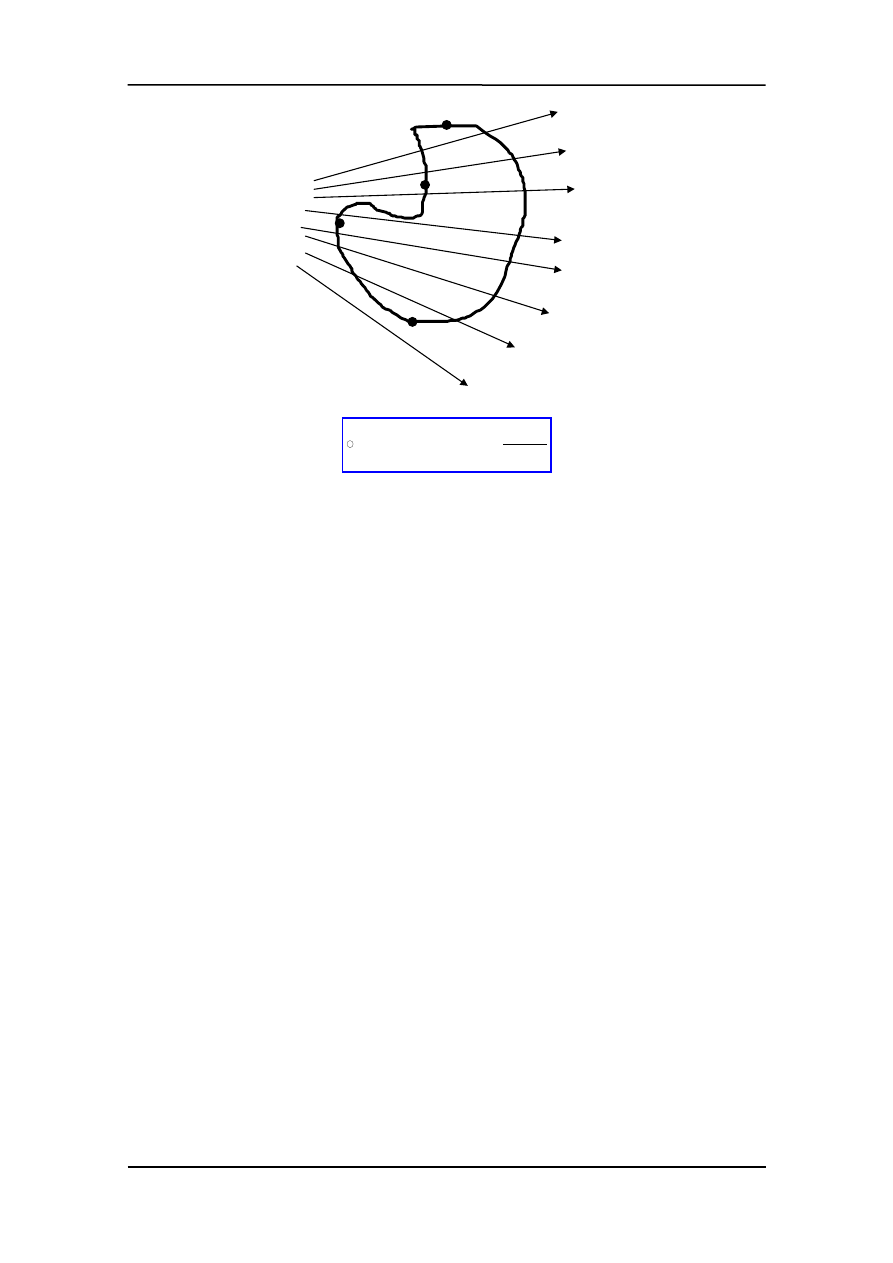
A co w sytuacji gdy na zewnątrz zamkniętej powierzchni są ładunki?
Rozważmy zamkniętą powierzchnię (rysunek) wewnątrz której Q

wewn.

= 0, a linie sił po-

chodzą od ładunku na zewnątrz.
Całkowity strumień dzielimy na części

φ

całk

=

φ

ab

+

φ

bc

+

φ

cd

+

φ

da

Z rysunku widać, że

φ

ab

= +2,

φ

bc

= +3,

φ

cd

= -7,

φ

da

= +2. Tak więc

φ

całk

= +2 + 3 - 7 + 2 = 0

Na następnym wykładzie zastosujemy prawo Gaussa do obliczania

E dla różnych nała-

dowanych ciał.

c

b

a

d