Efektywność i wymiana

Zastosowanie teorii popytu konsumpcyjnego

1. Efektywność
2. Wymiana w Skrzynce Edgeworth’a
3. Równowaga doskonale konkurencyjna w

gospodarce z dwoma osobami i dwoma dobrami

4. Problem dystrybucyjny
5. Inny proces alokacji zasobów i optymalność w

sensie Pareta

Efektywność

Efektywna alokacja = alokacja optymalna w sensie Pareta: nie
można polepszyć sytuacji jednej osoby bez pogorszenia
położenia co najmniej jednej, innej osoby.

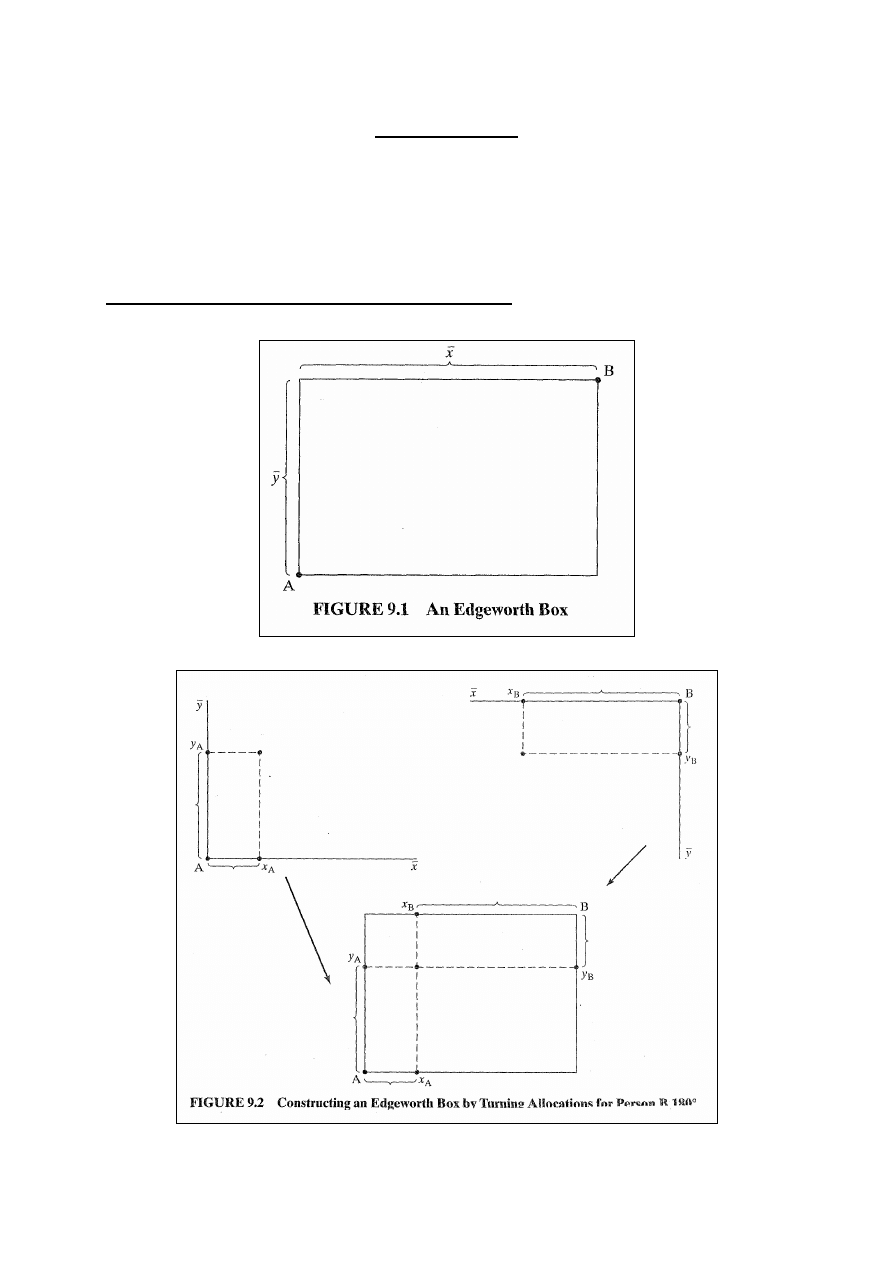
Konstruowanie skrzynki Edgeworth’a
Rysunki: 9.1, 9.2 i 9.3.

Wyznaczanie optymalności Pareto w Skrzynce Edgeworth’a
Zaczynamy od punktu (x

A

, y

A

), (x

B

, y

B

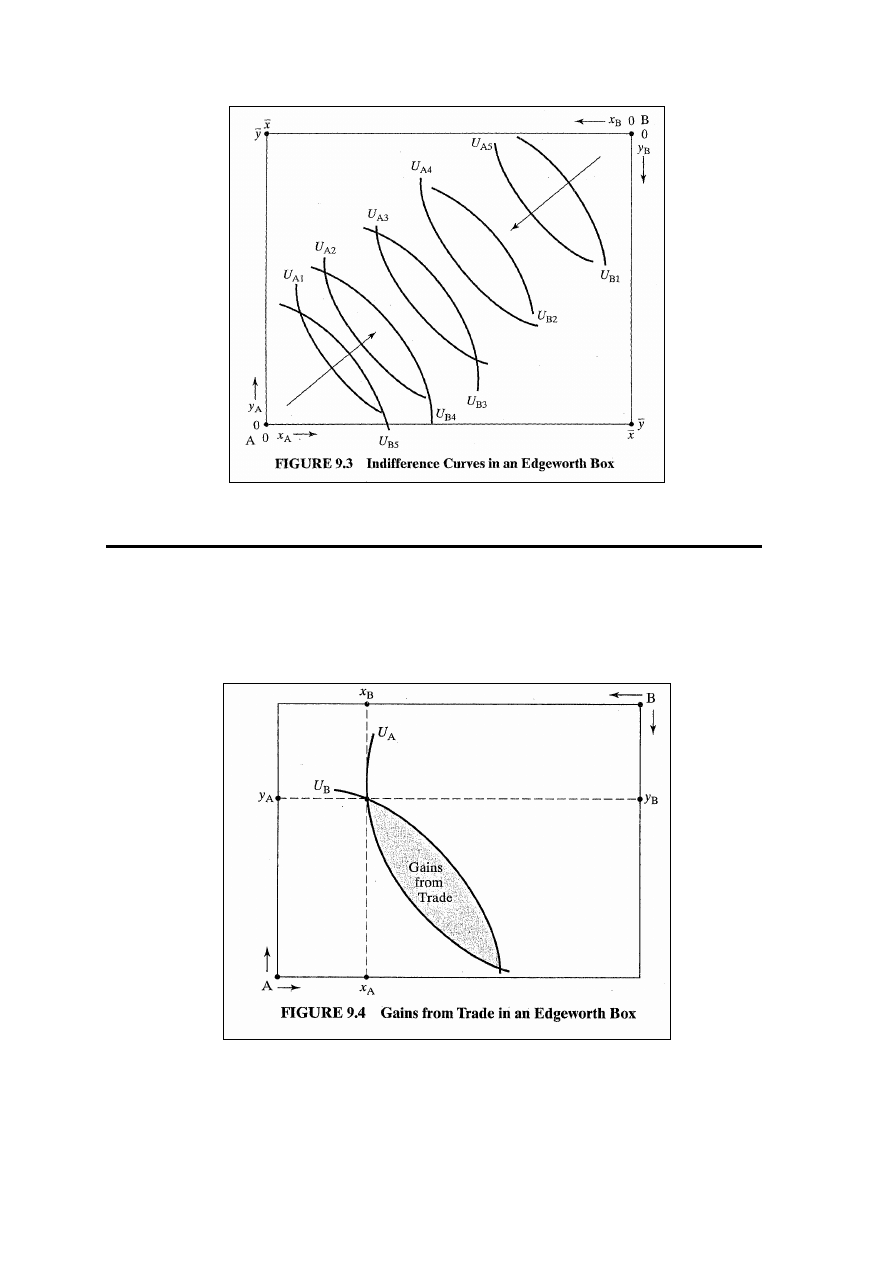
) na rys. 9.4. Obszar

zacieniowany zawiera punkty należące do wyższych krzywych
obojętności obu osób – pokazuje więc potencjalne korzyści z
wymiany.

Wyznaczenie punktu styczności – rys. 9.5: Najwyższy poziom
użyteczności konsumenta A bez obniżania użyteczności

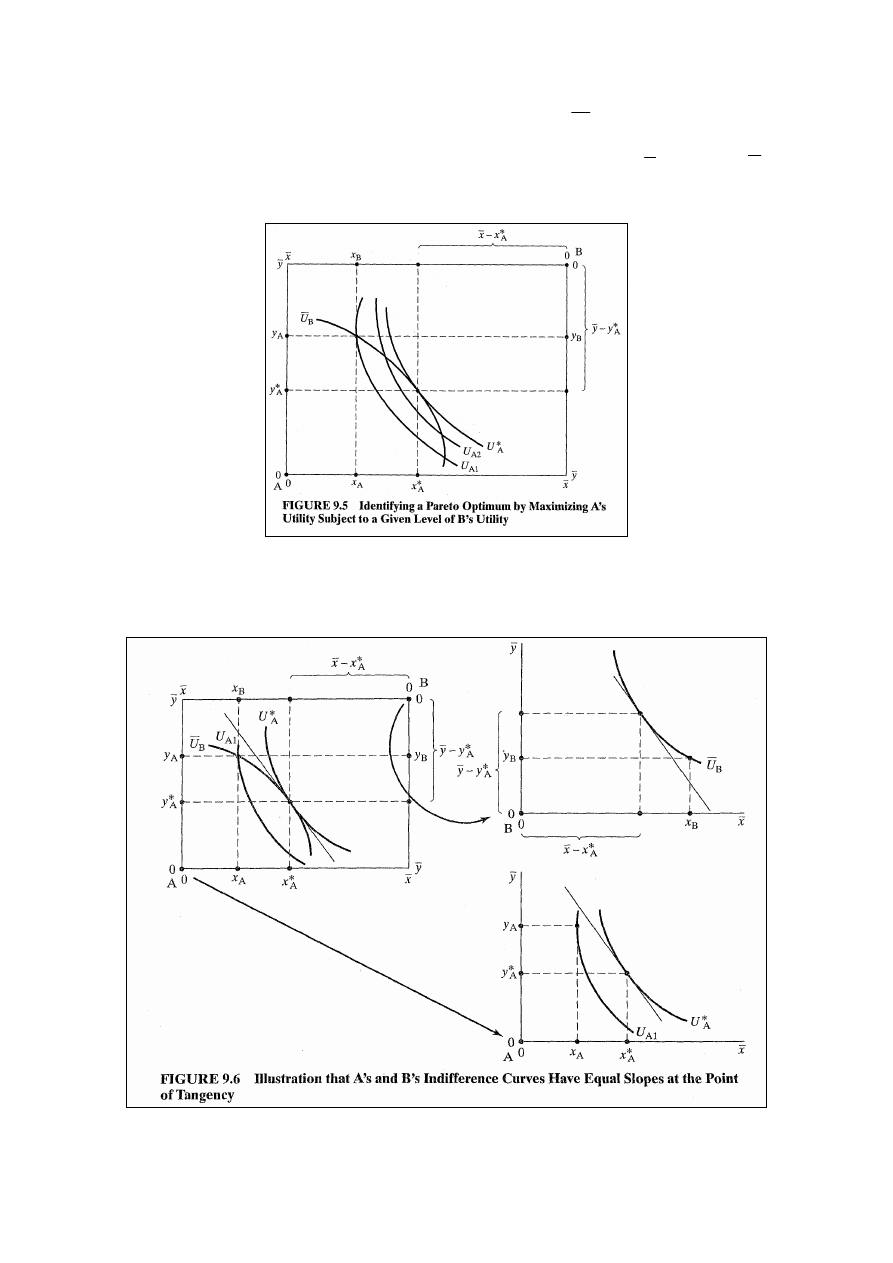
konsumenta B poniżej zadanego poziomu

B

U

wynosi: U*

A

, co

określa alokację: (x*

A

, y*

A

) dla osoby A oraz (

x

- x*

A

,

y

-

y*

A

) dla osoby B.

Rys. 9.6: jednakowe nachylenie krzywych obojętności obu
konsumentów w punkcje styczności.

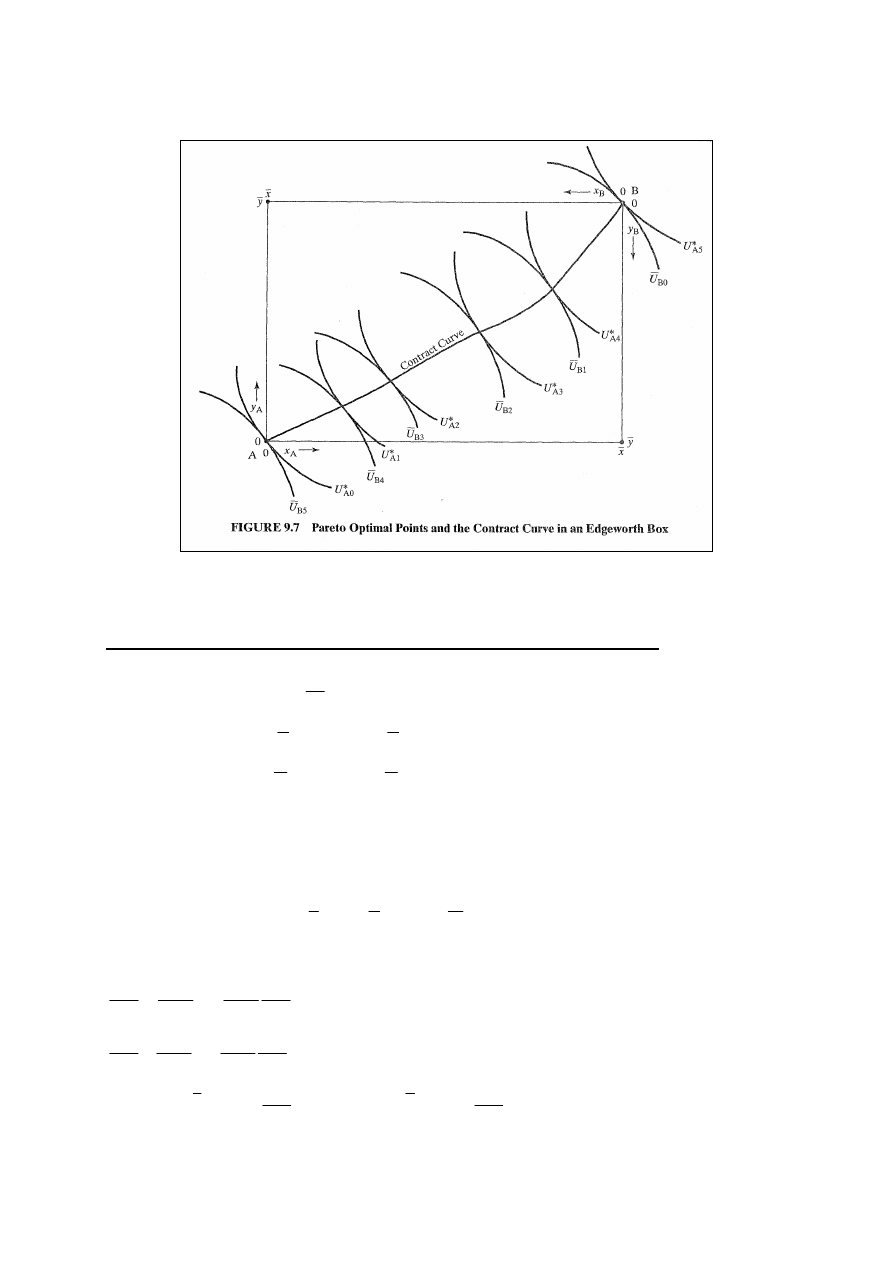
Rys. 9.7: wyznaczenie krzywej kontraktowej.

Matematyczne własności optimum w sensie Pareta
max U

A

(x

A

, y

A

)

p. w.: U

B

(x

B

, y

B

) =

B

U

x

A

+ x

B

=

x

⇒ x

B

=

x

- x

A

y

A

+ y

B

=

y

⇒ y

B

=

y

- y

A

Po wstawieniu dwóch ostatnich warunków ograniczających do
funkcji użyteczności osoby B konstruujemy funkcję
Lagrange’a:

(

)

(

)

[

]

B

A

A

B

A

A

A

U

y

y

x

x

U

y

x

U

−

−

−

+

=

ℜ

,

,

λ

Warunki konieczne:

0

=

∂

∂

∂

∂

+

∂

∂

=

∂

∂ℜ

A

B

B

B

A

A

A

x

x

x

U

x

U

x

λ

0

=

∂

∂

∂

∂

+

∂

∂

=

∂

∂ℜ

A

B

B

B

A

A

A

y

y

y

U

y

U

y

λ

ale:

1

−

=

∂

∂

⇒

−

=

A

B

A

B

x

x

x

x

x

i:

1

−

=

∂

∂

⇒

−

=

A

B

A

B

y

y

y

y

y

Po dokonaniu podstawień:

0

=

∂

∂

−

∂

∂

=

∂

∂ℜ

B

B

A

A

A

x

U

x

U

x

λ

0

=

∂

∂

−

∂

∂

=

∂

∂ℜ

B

B

A

A

A

y

U

y

U

y

λ

Rozwiązanie dla λ:

B

B

A

A

B

B

A

A

y

U

y

U

x

U

x

U

∂

∂

∂

∂

=

∂

∂

∂

∂

=

/

/

/

/

λ

Dlatego:

B

A

By

Bx

Ay

Ax

MRS

MRS

MU

MU

MU

MU

=

⇒

=

.

Warunek zrównania MRS osoby A z MRS osoby B
charakteryzuje alokację optymalną w sensie Paret’a dóbr X i
Y w dwuosobowej gospodarce.
Uogólnienie dla

n

konsumentów i

m

dóbr: max użyteczności

jednej osoby przy ograniczeniu użyteczności wszystkich
pozostałych osób. Rozwiązanie warunków pierwszego rzędu
głosi, że MRSy równają się sobie dla wszystkich osób dla
wszystkich par dóbr:
MRS

1,ij

= ... = MRS n,ij i, j = 1, ... , m, i ≠ j.

Wymiana w Skrzynce Edgeworth’a

Każdy konsument zaczyna od swojego wyposażenia
początkowego w każde z dwóch dóbr. Obaj konsumenci mogą
dokonywać wymiany.
Zał.: obaj konsumenci zachowują się konkurencyjnie, czyli są
cenobiorcami.
Oznaczenia: X i Y = dobra w gospodarce
A i B = konsumenci
(

A

x

,

A

y

) = wyposażenie początkowe A w dobro

X i Y
(

B

x

,

B

y

) = wyposażenie początkowe B w dobro

X i Y

A

x

+

B

x

=

x

= dostępna wielkość X

A

y

+

B

y

=

y

= dostępna wielkość Y

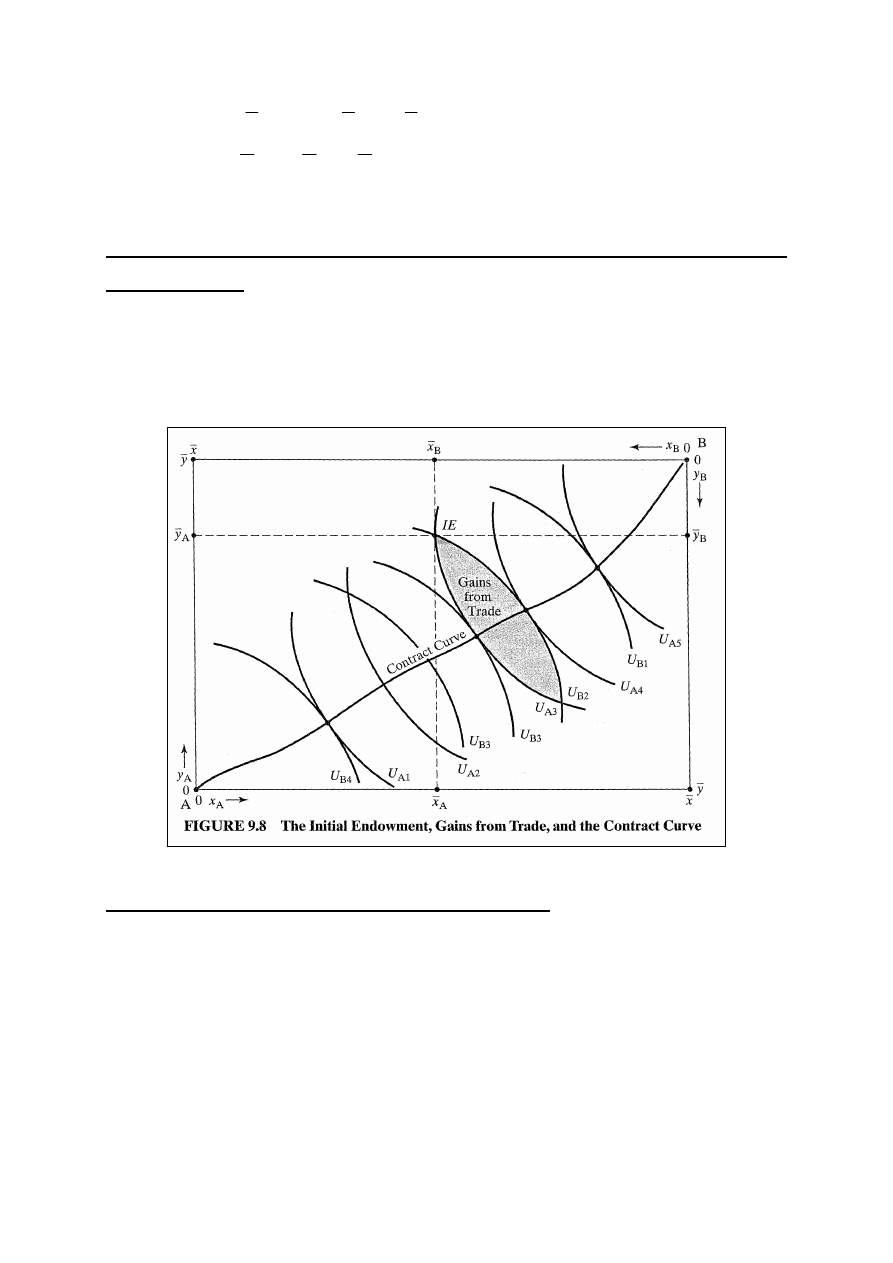
Wyposażenia początkowe i korzyści z wymiany w Skrzynce
Edgeworth’a
Rys. 9.8: punkt wyposażenia początkowego IE, poza krzywą
kontraktową, czyli konsumenci mogą dokonać wymiany i wejść
na wyższe krzywe obojętności realizując potencjalne
korzyści z wymiany.

Handel i określanie cen przez licytatora
Licytator ogłasza konsumentom ceny obu dóbr. Przyjmując
te ceny jako parametry konsumenci mogą obliczyć swoje
dochody dzięki obliczeniu wartości wyposażeń początkowych.
Następnie mogą oni max ich użyteczności przy
ograniczeniach budżetowych zdefiniowanych przy
wykorzystaniu obliczonych dochodów i podanych cen. (Np.
konsumenci sprzedają swoje wyposażenia początkowe po

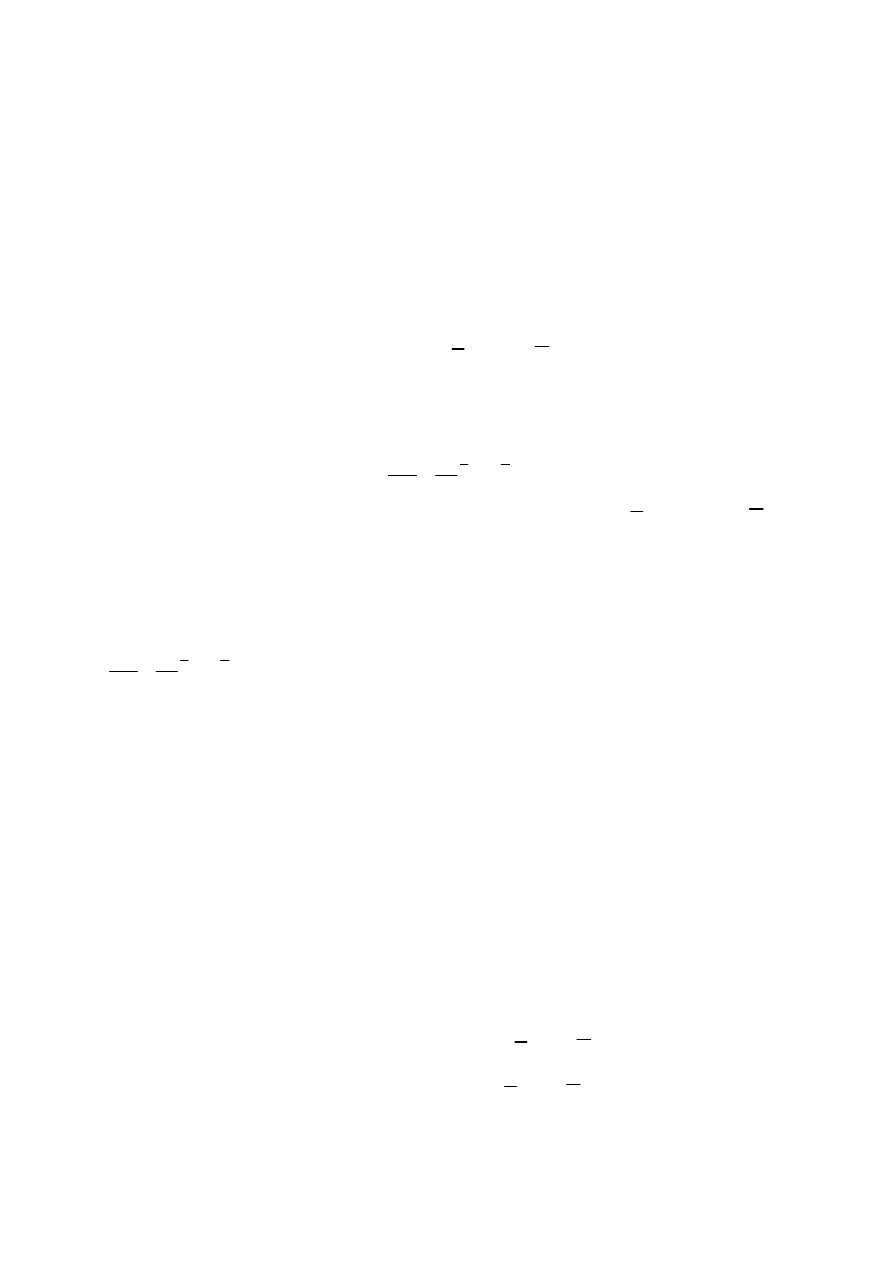
cenach rynkowych i następnie za uzyskane dochody kupują
koszyki dóbr max ich użyteczność przy tych samych cenach.)
Ponieważ funkcje popytu są homogeniczne stopnia 0
względem cen i dochodu, to wszystkie zbiory cen
zachowujące relacje cen podanych przez licytatora są
równoważne przy określaniu zachowania konsumenta w tym
modelu. Np.: licytator ogłosił ceny: p

x

i p

y

.

Dochód konsumenta A: M

A

= p

x

A

x

+ p

y

A

y

.

Wiadomo, że pomnożenie wszystkich cen i dochodu przez
dowolną dodatnią stałą np. 1/p

y

, nie zmienia linii ograniczenia

budżetowego, czyli:

A

A

y

x

y

A

y

x

p

p

p

M

1

+

=

jest tym samym

ograniczeniem budżetowym, co M

A

= p

x

A

x

+ p

y

A

y

.

Pomnożenie obu cen przez 1/p

y

oznacza pomnożenie dochodu

przez 1/p

y

.

Dochód konsumenta B jest wyznaczany w ten sam sposób:

B

B

y

x

y

B

y

x

p

p

p

M

1

+

=

.

Ponieważ możemy podzielić każde wyrażenie w równaniu
budżetowym przez p

y

i nie zmienimy położenia linii

ograniczenia, to oznacza, że liczą się tylko ceny względne.
Ceny p

x

i p

y

i dochód M są równoważne cenom p

x

/p

y

, 1 i

dochodowi M/p

y

. Obydwa zbiory cen i dochodu prowadzą do

tego samego zbioru dostępnego i dlatego do tych samych
wyborów.
Normalizacja – wyrażenie dochodu i cen jako stosunków
względem jednej ceny równej dodatniej stałej np. dla p

y

= 1:

problemy przyjmują postać:
A : maxU

A

(x

A

, y

A

) p.w.: p

x

x

A

+ y

A

= p

x

A

x

+

A

y

B : maxU

B

(x

B

, y

B

) p.w.: p

x

x

B

+ y

B

= p

x B

x

+

B

y

.

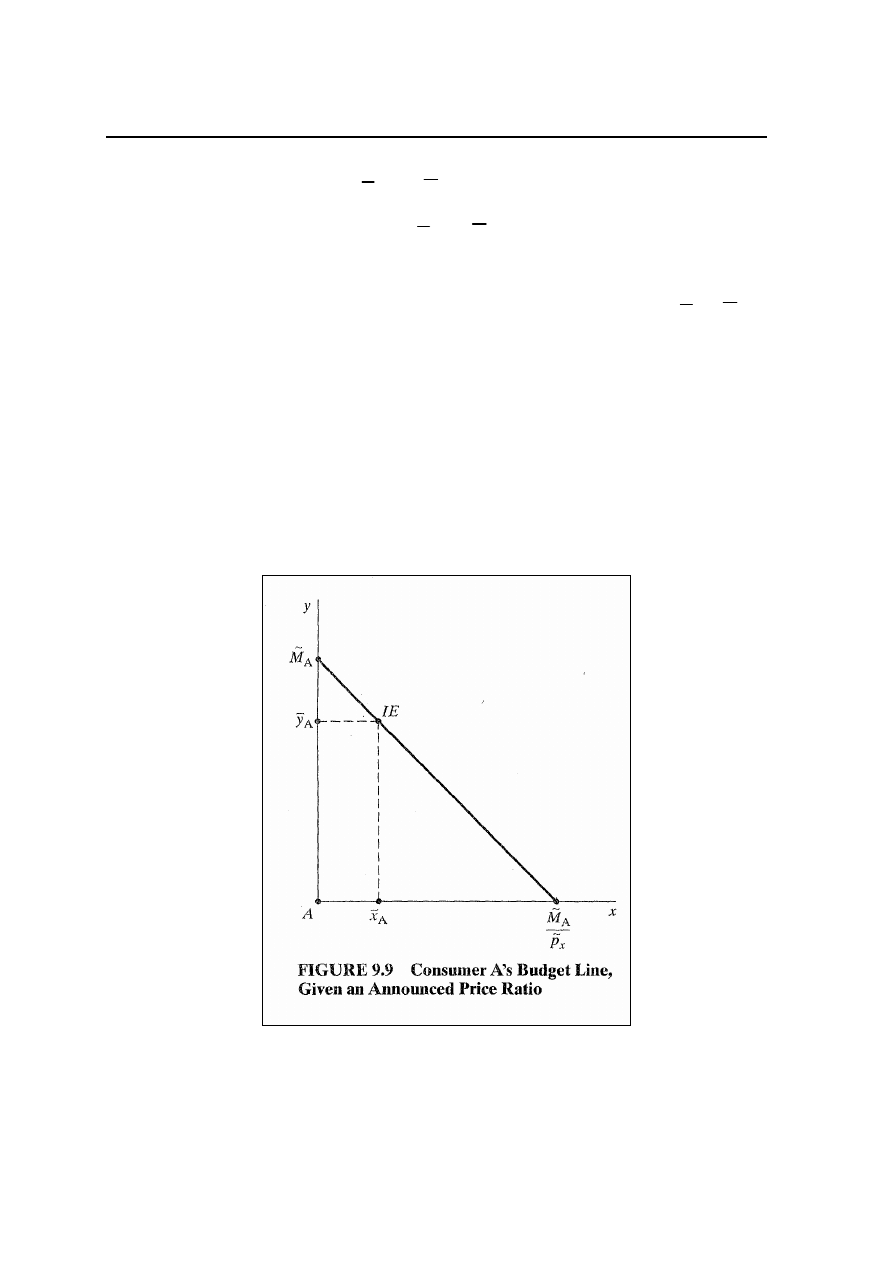
Znormalizowany budżet konsumenta i proponowana wymiana
Po normalizacji równanie ograniczenia budżetowego
konsumenta A: M

A

= p

x

A

x

+

A

y

= p

x

x

A

+ y

A

,

a dla konsumenta B: M

B

= p

x B

x

+

B

y

= p

x

x

B

+ y

B

.

Przy cenach i dochodach przedstawionych w ten sposób dla
każdego konsumenta, wyposażenie początkowe (

A

x

,

A

y

) i

każdy punkt satysfakcjonujący równanie budżetowe należą
do linii ograniczenia budżetowego. Dlatego dla każdego
konsumenta dokonującego wymiany w skrzynce Edgeworth’a
przyjmujemy, że linia ograniczenia budżetowego przechodzi
przez punkt wyposażenia początkowego i ma nachylenie
równe stosunkowi cen. (rys. 9.9: A; rys. 9.10: B)

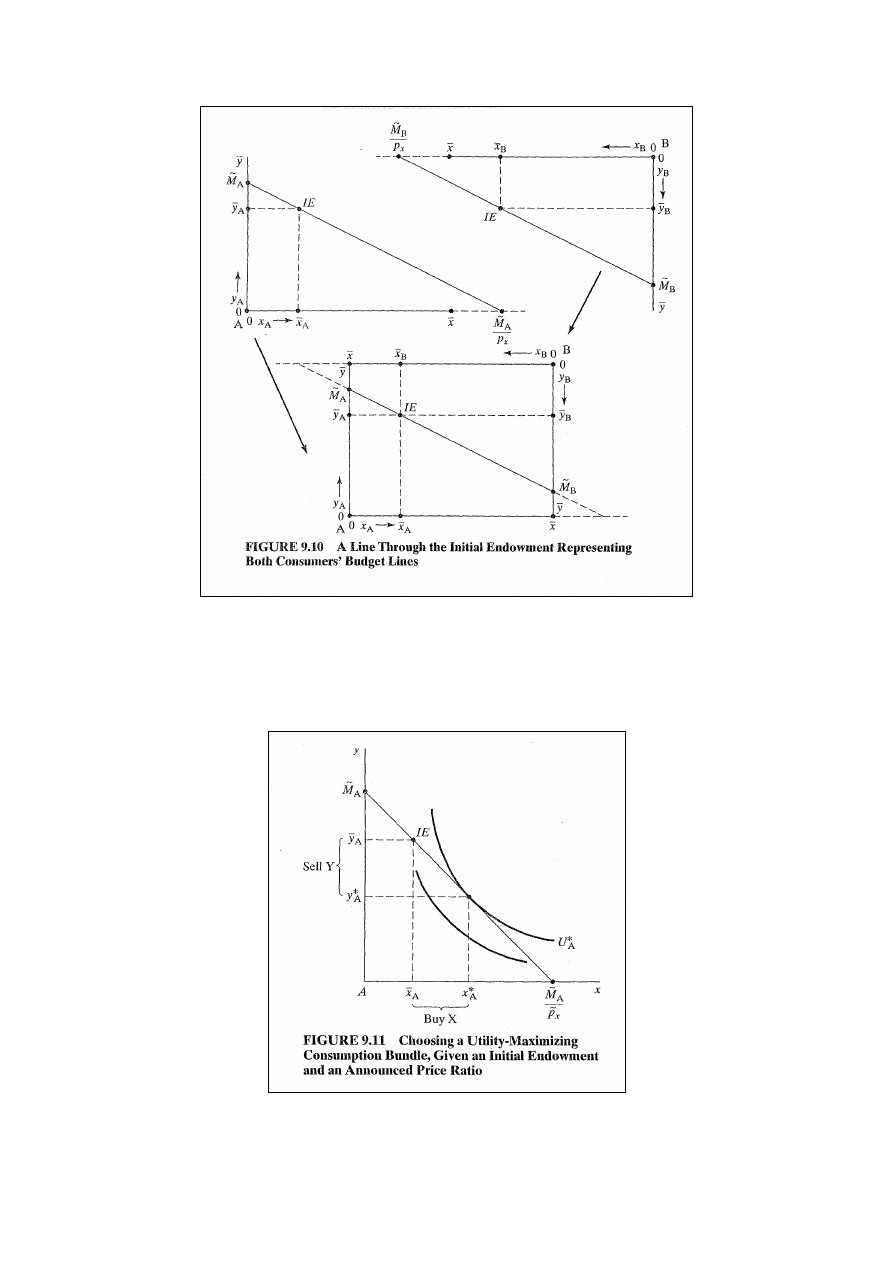
Każdy konsument dąży do maxU przy ograniczeniu w postaci
własnego ograniczenia budżetowego i anonsuje alokację, jaką
chciałby nabyć. Rys. 9.11: różnica między wyposażeniem
początkowym i koszykiem maxU osoby A.

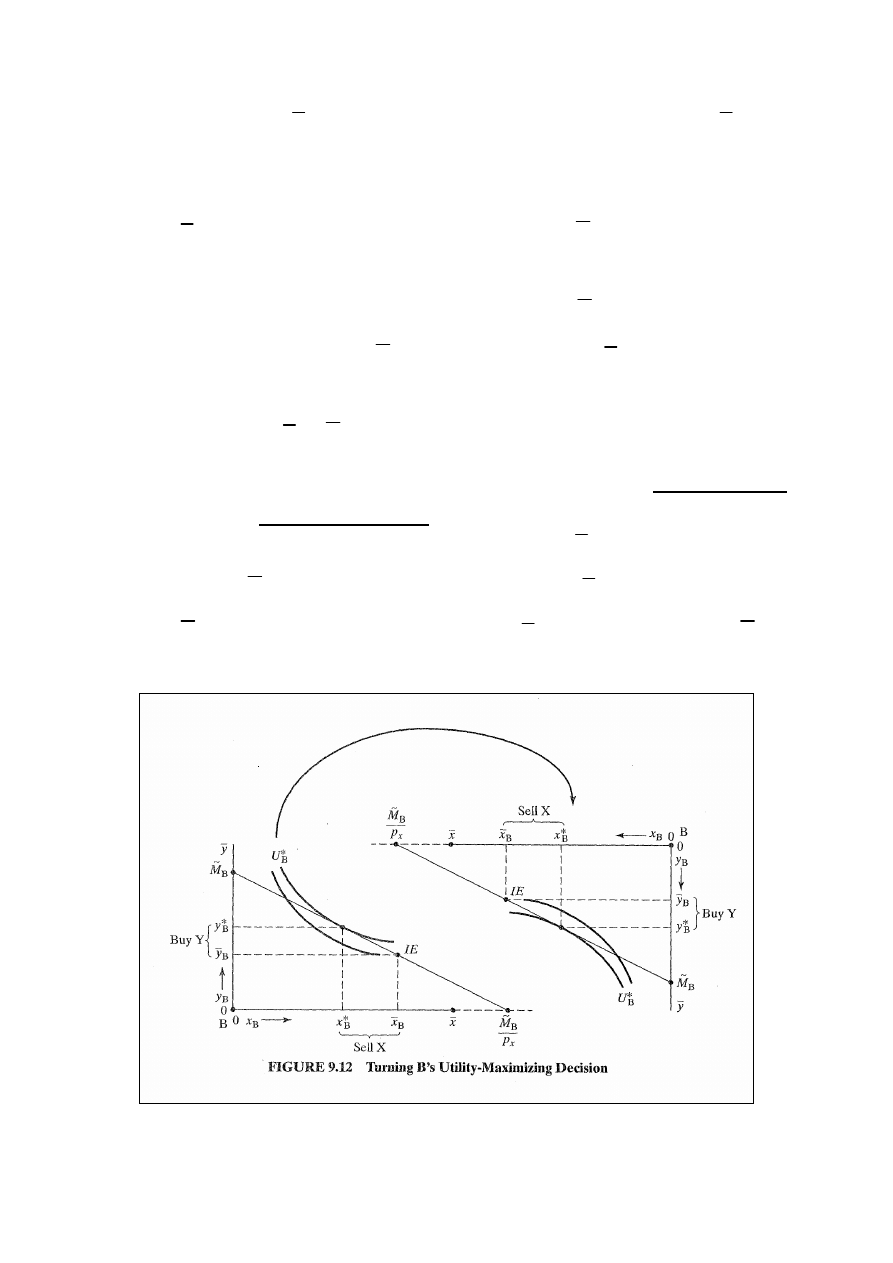
Wielkość x*

A

>

A

x

, czyli osoba A chce dokupić x*

A

-

A

x

do

wyposażenia początkowego. Przy dodatnich cenach linia
nachylenia budżetowego ma nachylenie ujemne. Jeżeli więc
x*

A

>

A

x

, to y*

A

musi być mniejsze od

A

y

aby konsument

pozostał na swej linii ograniczenia budżetowego. Oznacza to,
że osoba A chce dla równowagi sprzedać:

A

y

- y*

A

. Mówimy,

że proponuje wymianę (

A

y

- y*

A

) za (x*

A

-

A

x

). Ten sposób

wymiany jest równoważny sprzedaży całego wyposażenia
początkowego (

A

x

,

A

y

) i zakupowi koszyka maxU: (x*

A

, y*

A

).

Z punktu widzenia konsumenta A ta wymiana to kupno netto
dobra X oraz sprzedaż netto dobra Y.
Dla osoby B x*

B

musi być mniejsze od

B

x

i y*

B

musi być

większe od

B

y

, czyli B chce sprzedać: (

B

x

- x*

B

) i kupić:

(y*

B

-

B

y

), a więc chce on zamienić (

B

x

- x*

B

) za (y*

B

-

B

y

).

Rys. 9.12.

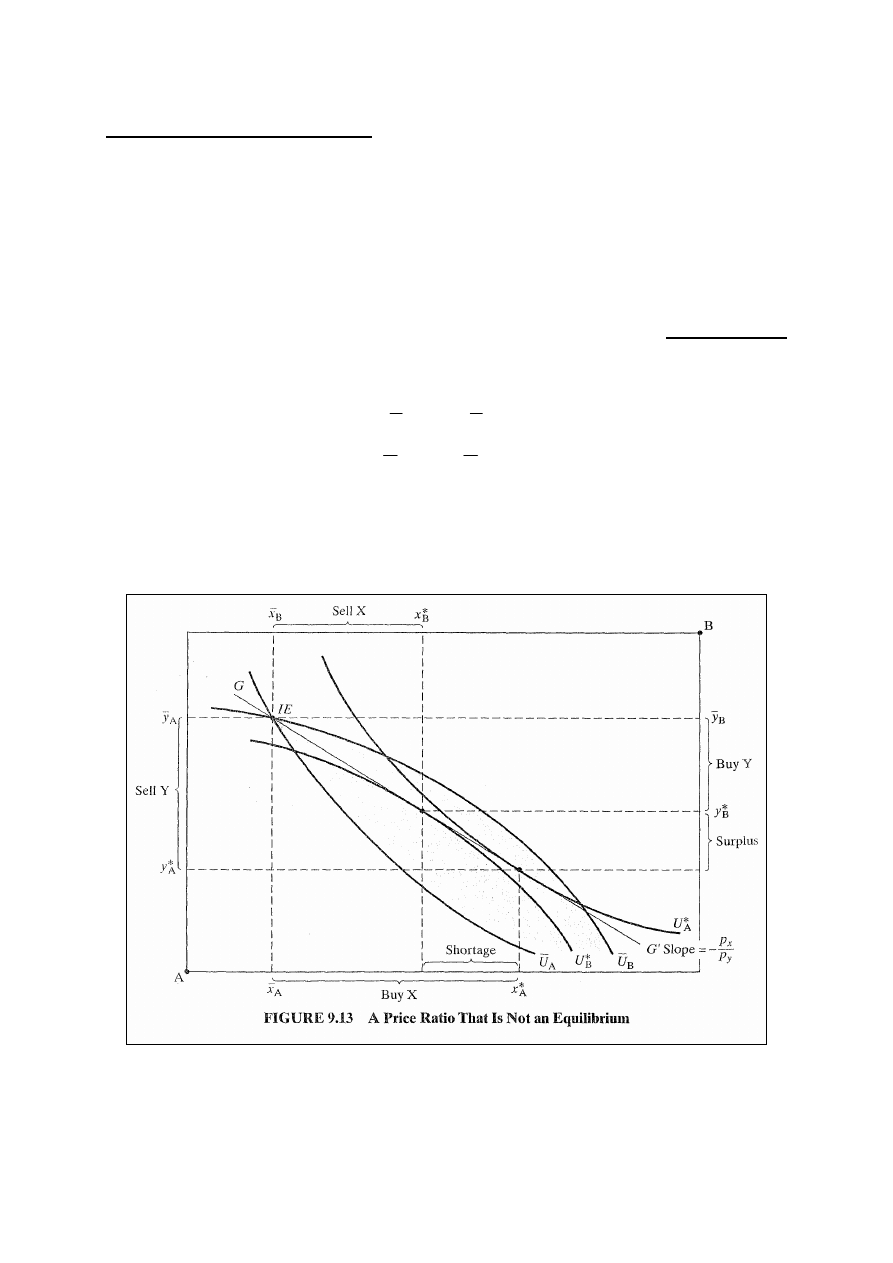
Wyznaczanie równowagi
Przy danych, ogłoszonych cenach osoba A chce kupić X i
sprzedać Y, a osoba B chce kupić Y i sprzedać X. Nie ma
powodu aby uważać, że przy podanych przez licytatora
cenach A będzie chciał kupić X dokładnie tyle, co B będzie
chciał sprzedać oraz, że B będzie chciał kupić Y dokładnie
tyle, co A będzie chciał sprzedać. Aby osiągnąć równowagę
podaż netto i popyt netto muszą być sobie równe na obu
rynkach:
popyt netto (x

A

) = (x*

A

-

A

x

) = (

B

x

- x*

B

) = podaż netto (x

B

)

popyt netto (y

B

) = (y*

B

-

B

y

) = (

A

y

- y*

A

) = podaż netto (y

A

).

Jeżeli podaż netto nie równa się popytowi netto, to licytator
musi zaproponować inny stosunek cen. Rys. 9.13: stosunek
cen prowadzi do nadwyżki Y i niedoboru X.

Przy tych znormalizowanych cenach osoba A chce sprzedać
więcej Y niż osoba B chce kupić. Natomiast B nie chce
sprzedać dostatecznie dużo X aby wystarczyło dla A. Linia

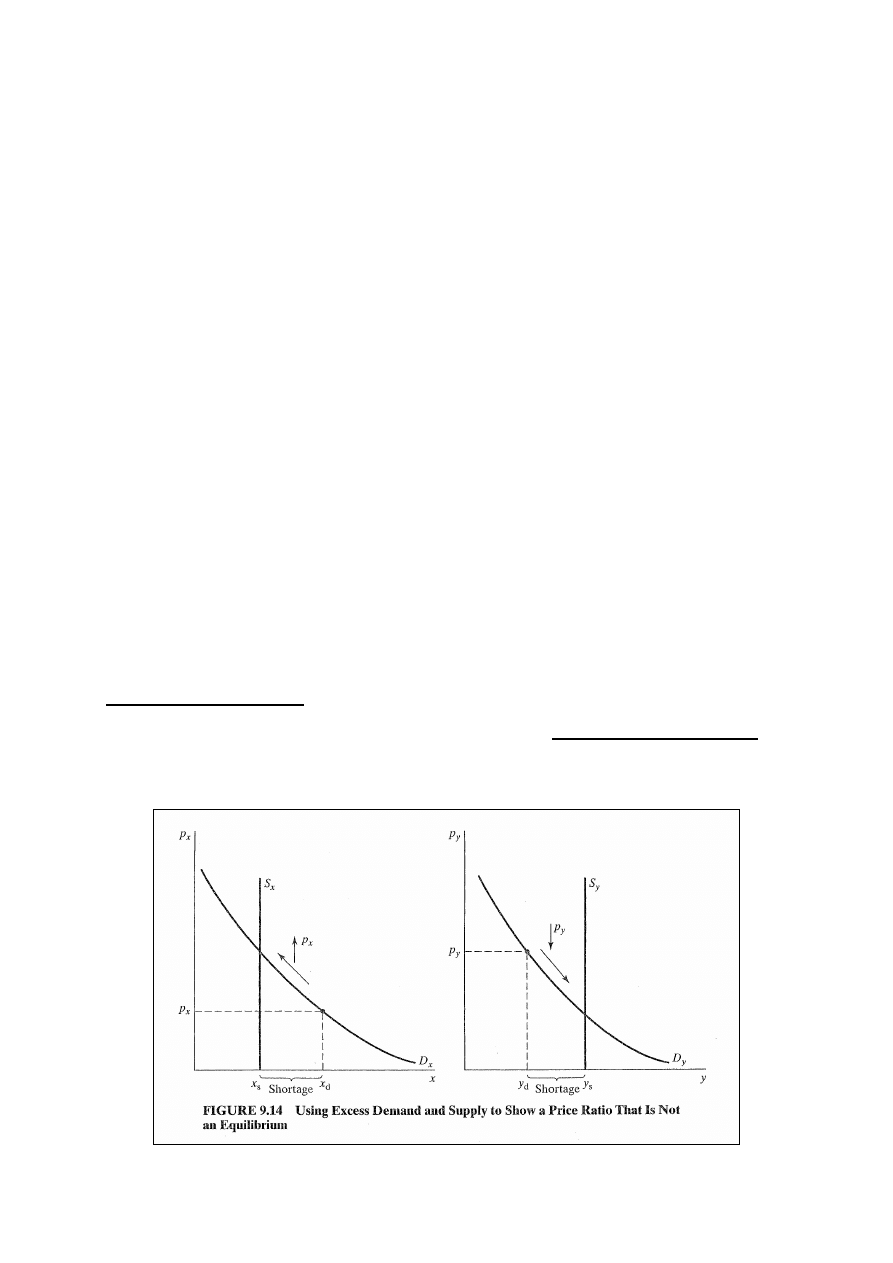
GG’ przedstawia ograniczenie budżetowe o nachyleniu (-
p

x

/p

y

) przechodzące przez punkt wyposażenia początkowego.

Osoba A maxU w punkcie (x*

A

, y*

A

), a osoba B: (x*

B

, y*

B

). Ta

alokacja nie jest osiągalna, gdyż popyt na X jest większy niż
dostępna podaż oraz jest nadwyżka podaży Y przy bieżących
cenach.

Jeśli przyjmiemy, że konsumenci sprzedają swoje
wyposażenia początkowe i następnie wyrażają popyty
wyznaczone przez budżety, to możemy sprawdzić czy
alokacja jest w równowadze dzięki porównaniu całkowitej
podaży i całkowitego popytu na obu rynkach. Na każdym
rynku popyt jest sumą popytów indywidualnych i podaż
rynkowa jest sumą podaży zgłaszanych przez wszystkie
jednostki. Równowaga na każdym rynku wyznaczona jest w
punkcie przecięcia opadającej krzywej popytu z pionową
krzywą podaży. Jeżeli popyt przewyższa podaż, to mamy
nadwyżkę popytu i licytator powinien obniżyć cenę. Przy
większej podaży od popytu mamy nadwyżkę podaży i
licytator powinien obniżyć cenę. Rys. 9.14 przedstawia
sytuację z rysunku 9.13.

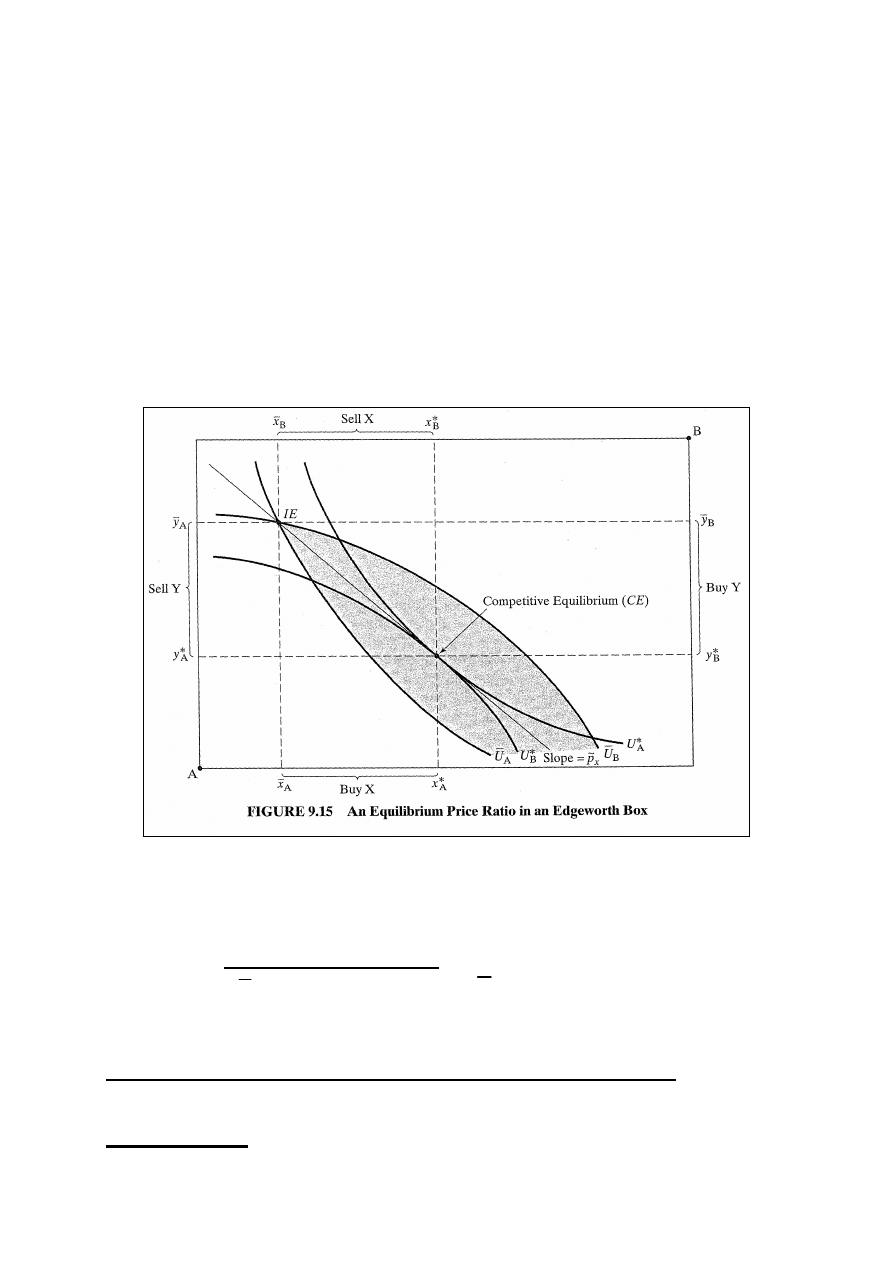
Lewy wykres: p

x

jest zbyt niska powodując nadwyżkowy

popyt i niedobór X; Prawy wykres: p

y

jest zbyt wysoka

powodując nadwyżkową podaż i nadwyżkę Y. Aby ceny
osiągnęły poziom równowagowy licytator musi podnieść cenę
X względem ceny Y, czyli podnieść p

x

.

Zaanonsowana zostaje wyższa cena X i popyt zrównuje się z
podażą na rynku X. Rys. 9.15: bardzo ważny wynik: przy
dwóch dobrach równowaga na rynku X automatycznie określa
równowagę na rynku Y.

Dzieje się tak, gdyż równowaga na rynku X wymaga aby
krzywe obojętności konsumentów były styczne. W punkcie
styczności rynek Y musi osiągnąć równowagę (prawo
Walras’a). Warunki równowagi można przedstawić w postaci:
x*

A

+ x*

B

=

A

x

oraz y*

A

+ y*

B

=

B

y

.

Tâtonnement i równowaga doskonale konkurencyjna
Proces dochodzenia do równowagi (opisany) nosi nazwę
tâtonnement (próby i błędy). Licytator próbuje dostosować

ceny na podstawie nadwyżek popytu i podaży. Przy nadwyżce
popytu cena względna musi być zwiększona, a przy nadwyżce
podaży – obniżona. Proces kończy się gdy popyt równa się
podaży na wszystkich rynkach. Tak osiągniętą równowagę
nazywamy równowagą ogólną. W równowadze ogólnej
istniejący zbiór cen względnych i alokację dóbr między
konsumentami charakteryzuje:

1. Zrównanie popytu i podaży na wszystkich rynkach;
2. Maksymalizacja użyteczności przy ograniczeniach

budżetowych wyznaczonych przy tych stosunkach
cen.

Z drugiej cechy wynika, że MRSy są równe dla wszystkich
konsumentów i jednocześnie są one równe stosunkowi cen,
gdyż wszyscy konsumenci napotykają ten sam stosunek cen:
MRS

A

= MRS

B

= p

x

/p

y

.

Pierwsze Twierdzenie Teorii Dobrobytu
Z równań:
MRS

1,ij

= ... = MRS n,ij i, j = 1, ... , m, i ≠ j oraz:

MRS

A

= MRS

B

= p

x

/p

y

wynika, że zarówno optimum Pareta,

jak i równowaga doskonale konkurencyjna posiadają cechę
polegającą na tym, że MRS równają się dla wszystkich
konsumentów. Wynika z tego, że równowaga doskonale
konkurencyjna jest optymalna w sensie Pareta. Jest to
prawda zawsze, gdy preferencje konsumentów spełniają
warunki 1-6 oraz gdy preferencje lub konsumpcja żadnego
konsumenta nie wchodzą do funkcji użyteczności
jakiegokolwiek innego konsumenta. Nie ma wtedy efektów
zewnętrznych w konsumpcji: nie żadnego altruizmu, żadnych
fizycznych efektów zewnętrznych jak np. oddziaływanie
palenia papierosów na niepalących. Ten wynik określany jest

mianem pierwszego fundamentalnego twierdzenia ekonomii
dobrobytu. W sytuacji czystej wymiany, jeżeli preferencje
konsumentów są

complete, refexiv, transitive, continuous

,

charakteryzują się nienasyceniem malejącymi MRSami i nie
ma efektów zewnętrznych w konsumpcji, to każda
równowaga czystej wymiany jest optymalna w sensie Pareta.
Przy tych warunkach rezultat ten jest prawdziwy dla wielu
konsumentów i wielu dóbr.

Równowaga doskonale konkurencyjna w gospodarce z

dwoma osobami i dwoma dobrami

Użyteczność konsumentów opisują funkcje:
U

A

= x

A

y

A

i U

B

= x

B

y

B

.

Wyposażenia początkowe wynoszą:

A

x

= 90;

A

y

= 35;

B

x

= 30;

B

y

= 25.

Całkowite ilości dostępne w gospodarce:

A

x

+

B

x

= 120 = podaż X

A

y

+

B

y

= 60 = podaż Y.

W równowadze wielkość popytu musi równać się wielkości
podaży, czyli popyt równa się podaży:
x*

A

+ x*

B

=

A

x

=

A

x

+

B

x

y*

A

+ y*

B

=

B

y

=

A

y

+

B

y

.

Powyższe warunki oczyszczania rynku określamy mianem
warunków równowagi doskonale konkurencyjnej. Po
normalizacji, czyli dla p

y

= 1, równania budżetowe można

zapisać:
A: p

x

x

A

+ y

A

= 90p

x

+ 35

B: p

x

x

B

+ y

B

= 30p

x

+ 25.

Wyznaczanie cen względnych w równowadze
Problem konsumenta A:
maxU

A

= x

A

y

A

p.w. p

x

x

A

+ y

A

= 90p

x

+ 35

Lagrancgian:

(

)

A

A

x

x

A

A

A

A

y

x

p

p

y

x

−

−

+

−

=

ℜ

35

90

λ

Warunki pierwszego rzędu:

x

A

A

x

A

A

A

p

y

p

y

x

1

0

=

⇒

=

−

=

∂

∂ℜ

λ

λ

A

A

A

A

A

x

x

y

=

⇒

=

−

=

∂

∂ℜ

λ

λ

0

0

35

90

=

−

−

+

=

∂

∂ℜ

A

A

x

x

A

y

x

p

p

λ

Rozwiązanie dla λ

A

:

λ

A

= x

A

= y

A

(1/p

x

).

Po wstawieniu rozwiązania dla λ

A

do ostatniego warunku

koniecznego:
90p

x

+ 35 – p

x

y

A

(1/p

x

) – y

A

= 0

⇒

y

A

= 45p

x

+ 17,5 : funkcja popytu na Y.

Po wstawieniu wzoru funkcji popytu na Y do rozwiązania dla
λ

A

:

X

A

= (1/p

x

)(45p

x

+ 17,5)

⇒

x

A

= 45 + 17,5(1/p

x

) : funkcja popytu na X.

Problem konsumenta B:
MaxU

B

= x

B

y

B

p.w. p

x

x

B

+ y

B

= 30p

x

+ 25

Lagrancgian:

(

)

B

B

x

x

B

B

B

B

y

x

p

p

y

x

−

−

+

−

=

ℜ

25

30

λ

Warunki pierwszego rzędu:

x

B

B

x

B

B

B

p

y

p

y

x

1

0

=

⇒

=

−

=

∂

∂ℜ

λ

λ

B

B

B

B

B

x

x

y

=

⇒

=

−

=

∂

∂ℜ

λ

λ

0

0

25

30

=

−

−

+

=

∂

∂ℜ

B

B

x

x

B

y

x

p

p

λ

Rozwiązanie dla λ

B

:

λ

B

= x

B

= y

B

(1/p

x

).

Po wstawieniu rozwiązania dla λ

B

do ostatniego warunku

koniecznego:
30p

x

+ 25 – p

x

y

B

(1/p

x

) – y

B

= 0

⇒

y

B

= 15p

x

+ 12,5 : funkcja popytu na Y.

Po wstawieniu wzoru funkcji popytu na Y do rozwiązania dla
λ

B

:

x

B

= (1/p

x

)(15p

x

+ 12,5)

⇒

x

B

= 15 + 12,5(1/p

x

) : funkcja popytu na X.

Aby wyznaczyć wielkości w równowadze i znormalizowaną
cenę X możemy zsumować oba równania popytu na Y i
zrównać tę sumę z całkowitą ilością Y dostępną w
gospodarce. Otrzymane równanie opisuje równowagę na
rynku Y: popyt konsumentów = dostępnej podaży.
y

A

= 45p

x

+ 17,5

y

B

= 15p

x

+ 12,5

y

A

+ y

B

= 45p

x

+ 17,5 + 15p

x

+ 12,5 =

A

y

+

B

y

.

Dlatego: 60p

x

+ 30 = 60 ⇒ p

x

= ½ .

Alokacja w równowadze doskonale konkurencyjnej
Cenę p

x

= ½ wstawiamy do czterech funkcji popytu:

y

A

= 45 ½ + 17,5 = 40

y

B

= 15 ½ + 12,5 = 20

x

A

= 45 + 17,5 (2) = 80

x

B

= 15 + 12,5 (2) = 40.

Możemy sprawdzić uzyskane odpowiedzi aby przekonać się,
czy spełniają one warunki równowagi:
x

A

+ x

B

= 80 + 40 = 120

y

A

+ y

B

= 40 + 20 = 60.

Sprawdzamy zrównanie się MRSów ze stosunkiem cen:
MRS = MU

x

/MU

y

= y/x

MRS

A

= y

A

/x

A

= 40/80 = ½

MRS

B

= y

B

/x

B

= 20/40 = ½

Dlatego: MRS

A

= MRS

B

= p

x

/p

y

= ½ .

Problem dystrybucyjny

Prawdą jest, że każda równowaga doskonale konkurencyjna
jest optymalna w sensie Pareta. Istnieje wiele optimów w
sensie Pareta, z których tylko niektóre polepszają sytuację
obu konsumentów w porównaniu do ich punktów wyposażenia
początkowego. W Skrzynce Edgeworth’a krzywą
kontraktową tworzą punkty, w których zrównują się MRSy
obu konsumentów, czyli są one efektywne w sensie Pareta.
Intuicyjnie możemy stwierdzić, że konsumenci będą
handlować aby skonsumować korzyści z wymiany dochodząc
do porozumienia na krzywej kontraktowej.

Optymalność Pareta i rozwiązania korzystniejsze w sensie
Pareta (Pareto superiority)
Rys. 9.16: wszystkie punkty krzywej kontraktowej między

A

U

i

B

U

reprezentują alokacje optymalne w sensie Pareta.

Jednocześnie sytuacja obu konsumentów poprawi się jeśli
znajdą się w którymś z nich w porównaniu do punktu
wyposażenia początkowego.

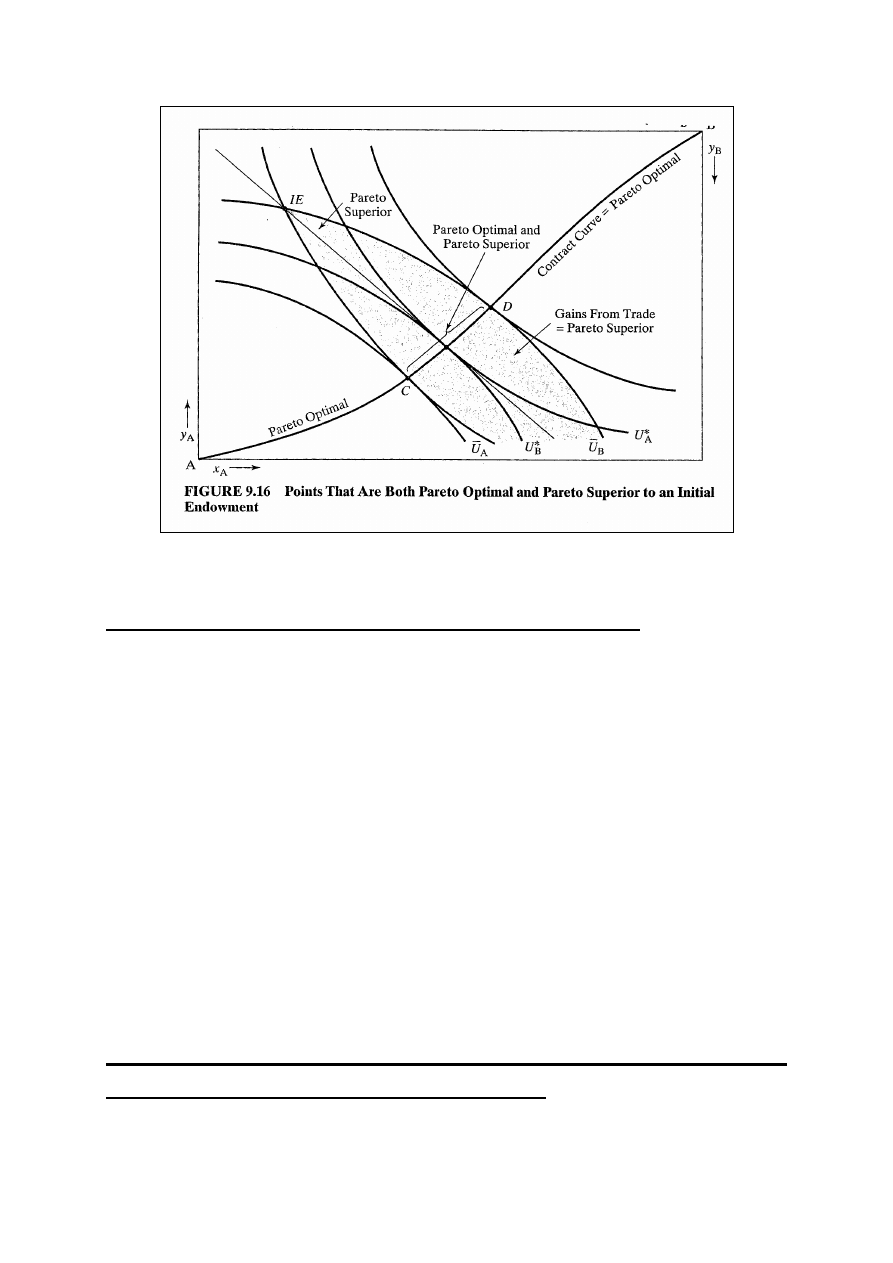
Punkty, w których sytuacja co najmniej jednej osoby
polepszy się i niczyja się nie pogorszy, określamy mianem
punktów korzystniejszych w sensie Pareta (zacieniony
obszar). Po dokonaniu alokacji początkowej każdy punkt na
krzywej kontraktowej z obszaru zacienionego (np.
równowaga doskonale konkurencyjna) jest jednocześnie
optymalny w sensie Pareta i korzystniejszy w sensie Pareta.
Alokacje są efektywne i niczyja sytuacja nie pogorszyła się
po wymianie. Punkty z krzywej kontraktowej poza obszarem
zacieniowanym są optymalne w sensie Pareta, a le nie są
korzystniejsze w sensie Pareta. W takim punkcie –
optymalnym w sensie Pareta – co najmniej jeden uczestnik
wymiany pogorszy swoje położenie w stosunku do punktu
wyposażenia początkowego.

Dochodzenie do równowagi doskonale konkurencyjnej i
dystrybucja wyposażenia początkowego
Rys. 9.17: punkty C i D są optymalne w sensie Pareta.

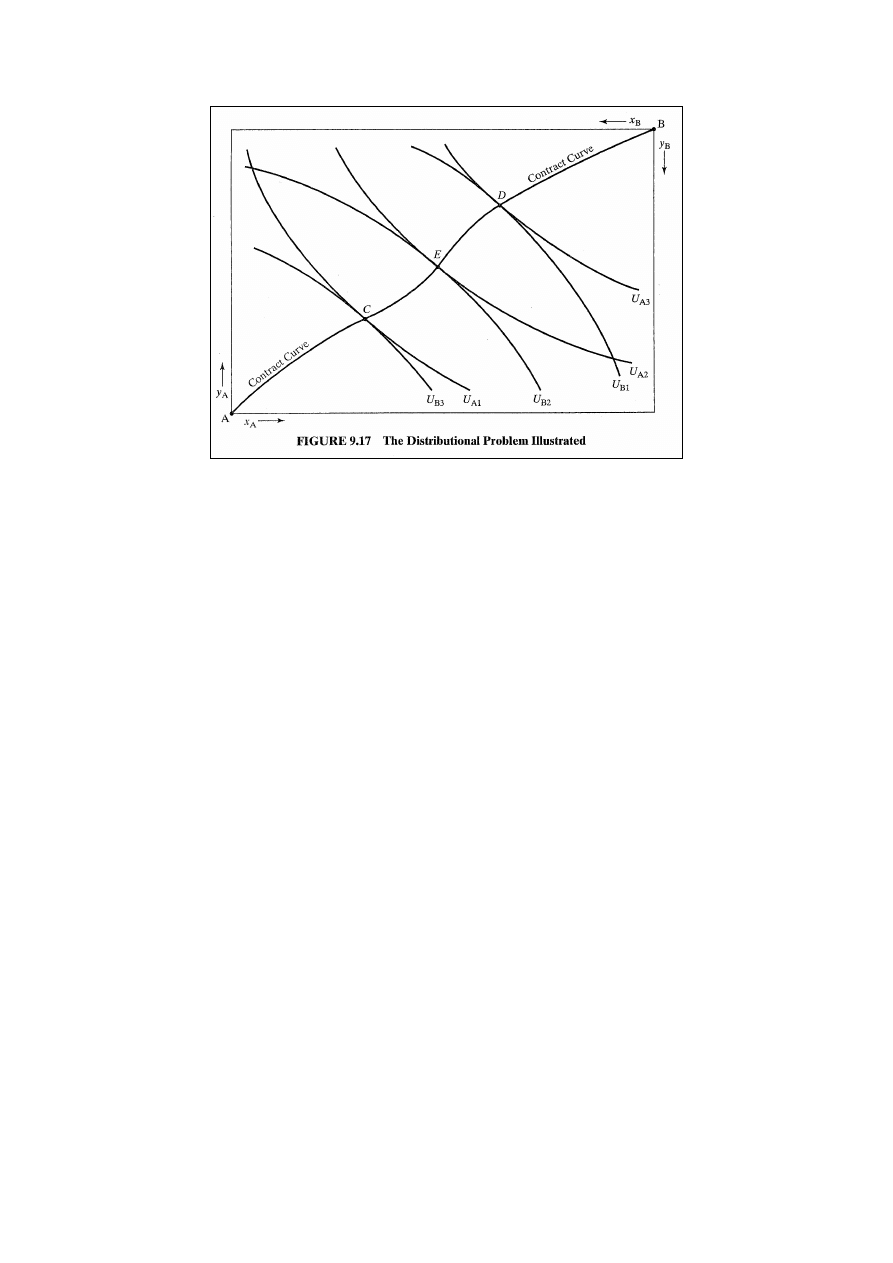
Osoba A preferuje D, a osoba B – C. Nawet po wprowadzeniu
równej alokacji w E, A będzie preferować D, a B – C.
Równowaga doskonale konkurencyjna jest jedynym optimum
w sensie Pareta, które zarówno jest korzystniejsze w sensie
Pareta w stosunku do wyposażenia początkowego, jak i
zgodne z linią ograniczenia budżetowego przechodzącą przez
punkt wyposażenia początkowego. (W niektórych
szczególnych przypadkach może istnieć więcej niż jedna
równowaga doskonale konkurencyjna dla danego wyposażenia
początkowego.) Istnieje jednak nieskończenie wiele optimów
w sensie Pareta wzdłuż krzywej kontraktowej, które
jednocześnie są korzystniejsze względem wyposażenia
początkowego, ale nie są równowagami doskonale
konkurencyjnymi. Dlatego ostateczna alokacja powinna być
osiągnięta w punkcie równowagi doskonale konkurencyjnej.

Optimum Pareto wybrane w procesie dochodzenia do
równowagi doskonale konkurencyjnej zależy od wyposażenia
początkowego. Jeżeli jedna osoba jest względnie „bogata” a
druga „biedna” w wyposażenie początkowe, to proces

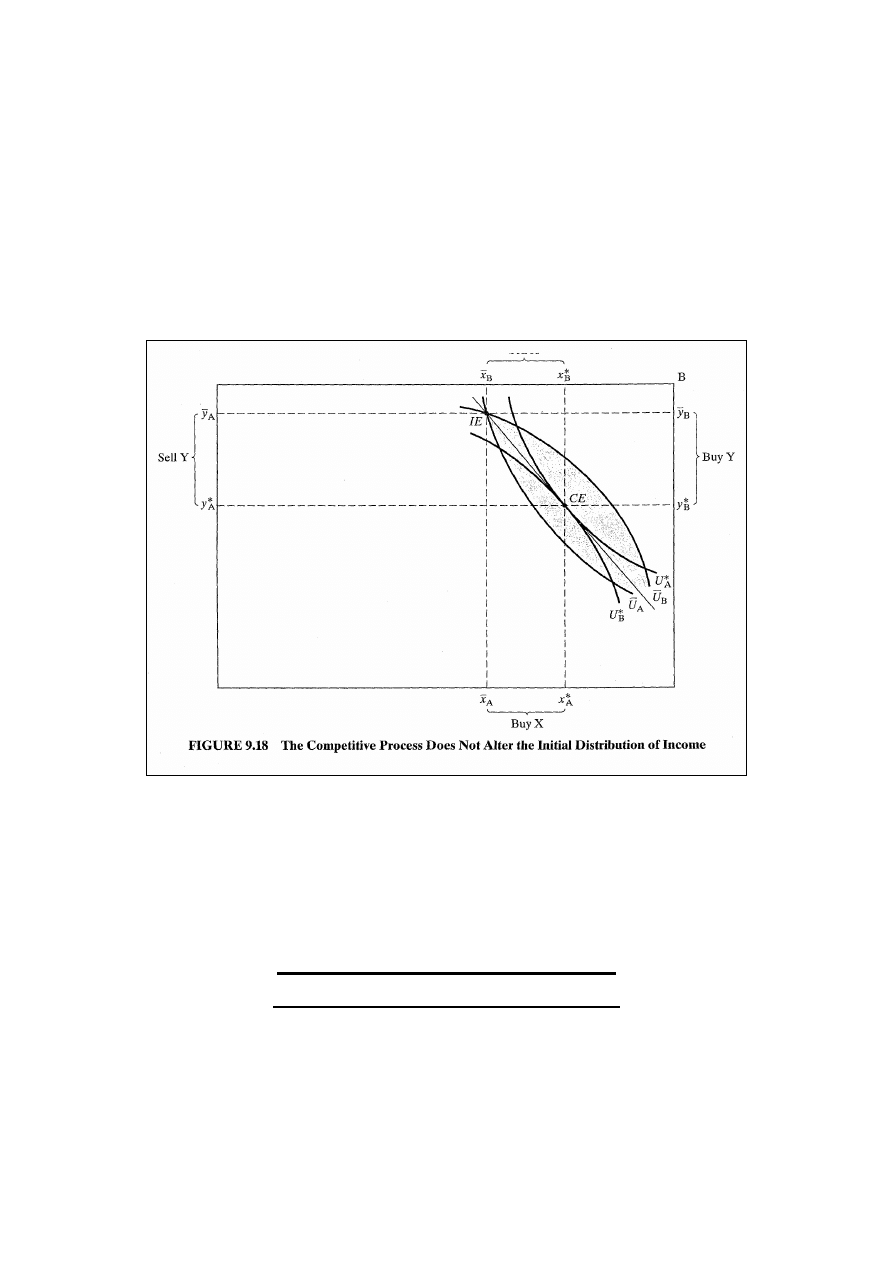
dochodzenia do równowagi doskonale konkurencyjnej poprawi
sytuację obu osób w porównaniu do punktu wyposażenia
początkowego i osiągnie optimum w sensie Pareta. Ale
nierówność (niesprawiedliwość) siły nabywczej nie ulegnie
zmianie pod działaniem sił rynkowych doskonale
konkurencyjnych. Rys. 9.18: w punkcie wyposażenia
początkowego osoba A posiada więcej obu dóbr.

W punkcie równowagi doskonale konkurencyjnej sytuacja obu
osób polepszyła się w porównaniu do wyposażenia
początkowego, ale A w dalszym ciągu konsumuje większą
część obu dóbr.

Inny proces alokacji zasobów

i optymalność w sensie Pareta

Dochodzenie do równowagi doskonale konkurencyjnej
prowadzi gospodarkę do optimum w sensie Pareta.
Jednocześnie w optimum Pareta niektórzy konsumenci mogą
być bardzo biedni, a inni bardzo bogaci w zależności od

wyposażenia początkowego. Ekonomiści nie oceniają
sprawiedliwości dystrybucji wyposażenia początkowego, ale
politycy i obywatele robią to. Jednym z celów ekonomii
dobrobyt jest oddziaływanie na efektywną dystrybucję
zasobów gwarantującą równiejszą dystrybucję konsumpcji
końcowej. Jeżeli osoba planująca zna preferencje
wszystkich członków społeczeństwa i całkowite zasoby dóbr,
to można znaleźć takie optimum w sensie Pareta, w którym
osiągana jest pożądana dystrybucja roszczeń dotyczących
konsumpcji i dobra są rozprowadzane do konsumpcji. Wtedy
jeśli jacyś konsumenci zdecydowaliby się na dokonanie
wymiany, to nie byłoby punktu do zrobienia tego, gdyż
oryginalna dystrybucja wyczerpała już korzyści z wymiany.
Drugie fundamentalne twierdzenie ekonomii dobrobytu
Przedstawione rozwiązanie wymaga aby planista miał więcej
informacji na temat preferencji konsumentów niż można
posiąść. Prostym rozwiązaniem redystrybucji jest zmiana
wyposażeń początkowych w kierunku wyrównania posiadania.
Po dokonaniu transferu wyposażeń początkowych jednostki
handlują między sobą uruchamiając proces dochodzenia do
równowagi doskonale konkurencyjnej, będącej optimum w
sensie Pareta.
Przy tych samych założeniach, jak te poczynione dla
pierwszego fundamentalnego twierdzenia ekonomii
dobrobytu, każdy punkt na krzywej kontraktowej może być
punktem równowagi doskonale konkurencyjnej dzięki
zręcznej zmianie wyposażeń początkowych. Jest to drugie
fundamentalne twierdzenie ekonomii dobrobytu przy czystej
wymianie.

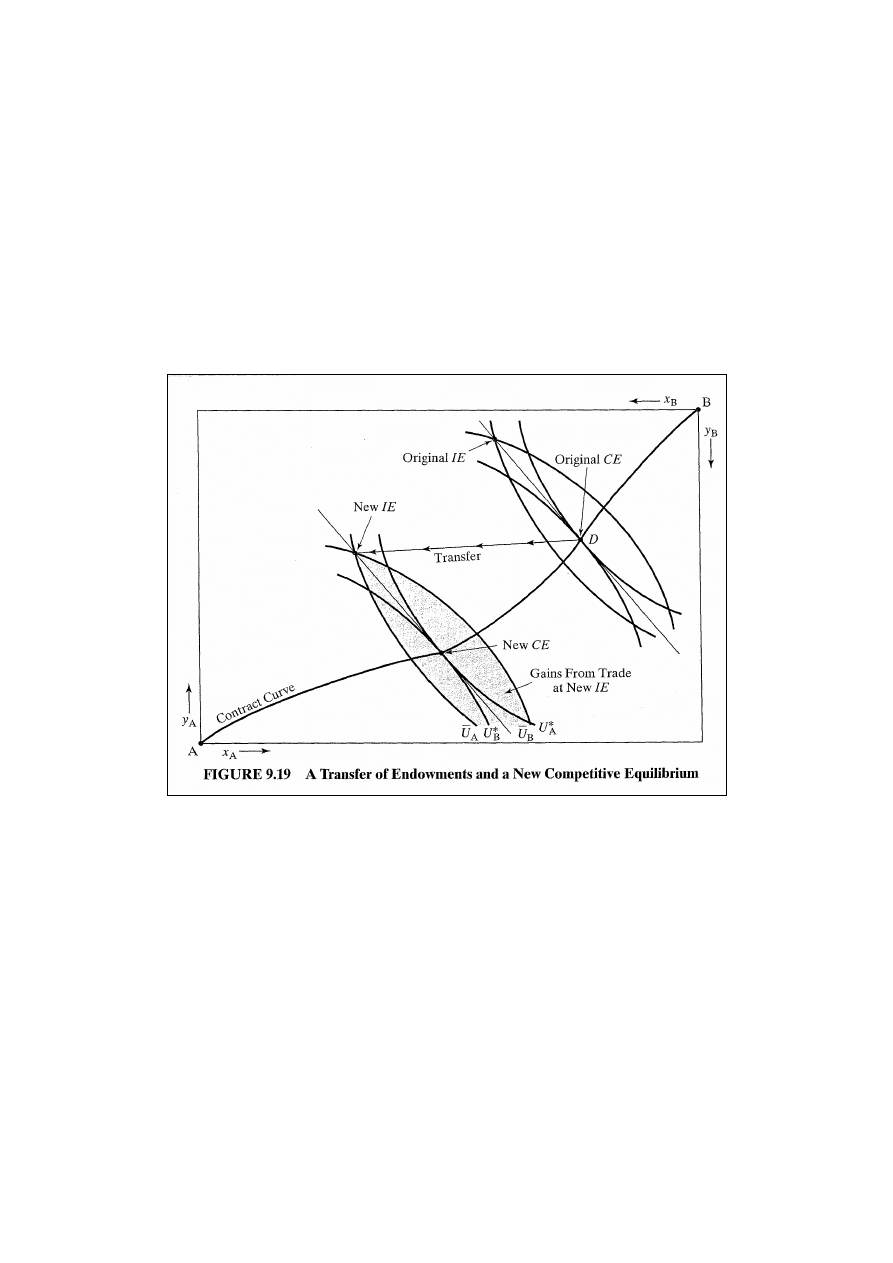
Rys. 9.19: ilustruje drugie fundamentalne twierdzenie
ekonomii dobrobytu: dla pierwotnego wyposażenia
początkowego równowaga doskonale konkurencyjna zostałaby
osiągnięta w punkcie D i osoba A byłaby względnie bogata, a
B – biedna. Nowa równowaga doskonale konkurencyjna w
punkcie F może być osiągnięta po przekazaniu części obu
dóbr osobie B i rozpoczęciu wymiany.