Oznaczenia :

Vmax

maksymalna prędkość (pąciągi pasażerskie)

km

h

km

h

Vt

maksymalna prędkość (pąciągi towarowe)

fdop

dopuszczalna prędkość podnoszenia się koła po rampie przechyłkowej

mm

s

ϕdop

dopuszczalna prędkość zmiany przyspieszenia na krzywej przejściowej

m

s

3

ap

dopuszczalne przyśpieszenie niezrównoważone dla pociągów pasażerskich

m

s

2

at

dopuszczalne przyśpieszenie niezrównoważone dla pociągów towarowych

m

s

2

Do obliczeń należy przyjąć

m

100

:=

m

3.6 fdop

⋅

=

sty

cz

na

w

ejs

cio

w

a

sty

cz

na

w

yjs

cio

w

a

za

krę

t w

p

ra

w

o!

W

(N

w

,E

w

)

m

s

3

ap 0.6

:=

m

s

2

ϕdop

0.5

:=

Przykładowe dane

R

1400

:=

Vmax 120

:=

Vt 60

:=

at 0.6

:=

Az1

146

:=

Az2

150

:=

Nw 3456.4521

:=

Ew

451.2427

−

:=

1 ) PRZECHYŁKA

hmin 11.8

Vmax

2

R

⋅

153 ap

⋅

−

:=

ZAOKRĄGLIĆ DO 5mm W GÓRĘ

hmin 29.571

=

to

hmin Ceil hmin 5

,

(

)

30

=

:=

hmax 11.8

Vt

2

R

⋅

153 at

⋅

+

:=

ZAOKRĄGLIĆ DO 5mm W DÓŁ

hmax 122.143

=

to

hmax Floor hmax 5

,

(

)

120

=

:=

przechyłka powinna się zawierać w przedziale <20 ; 150> mm

Do dalszych obliczeń przyjmujemy przechyłkę maksymalną h=hmax

hobl hmax 120

=

:=

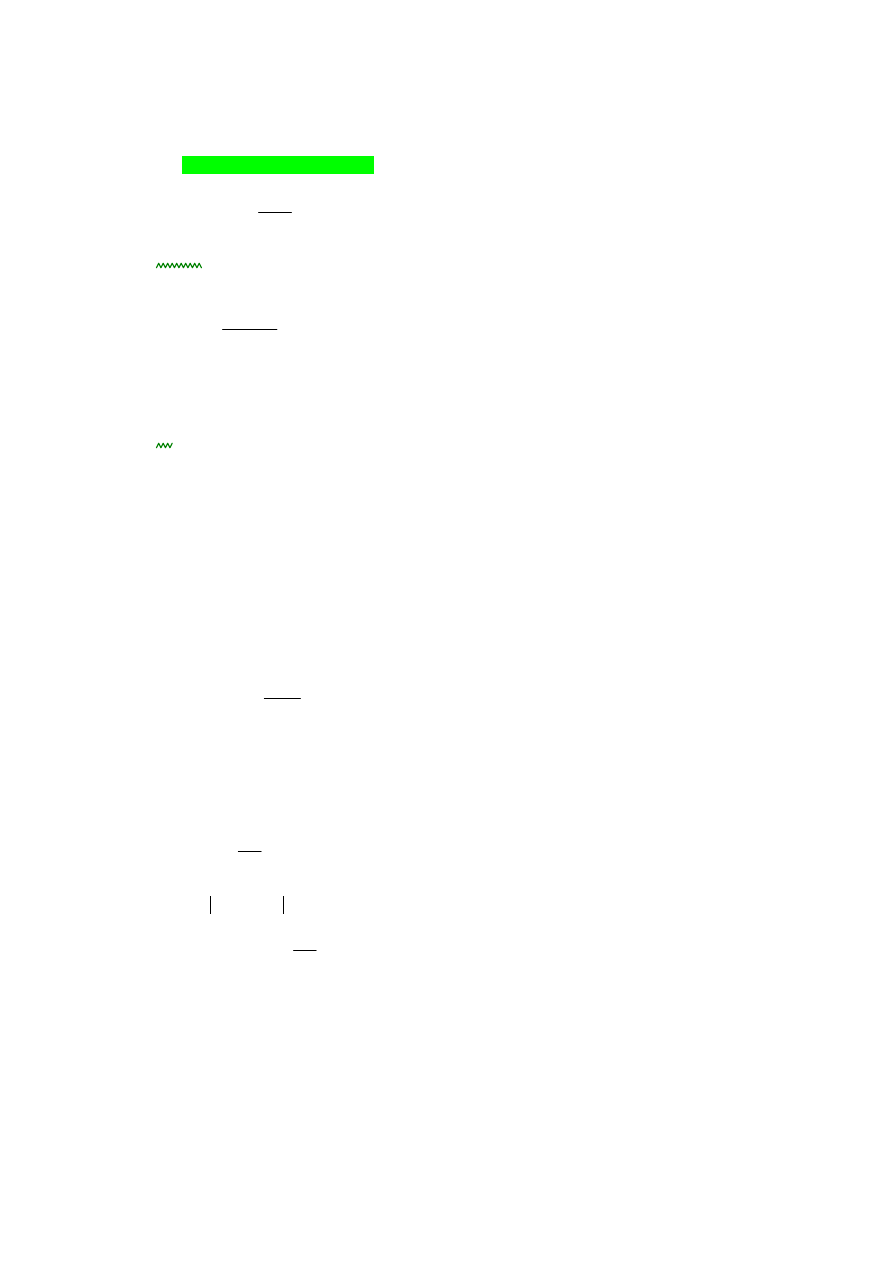
2 ) Wyznaczenie dlugosci krzywej przejściowej

zaokraglic do 5m w gore!!!

Lminf

Vmax

hmax

m

⋅

144

=

:=

Lminf

Ceil Lminf 5

,

(

)

145

=

:=

Lmin

ϕ

ap Vmax

⋅

m

0.72

=

:=

Powyższe wzory dotyczą minimalnej długości jaką może mieć krzywa przejściowa, z tego
powodu do dalszych obliczeń przyjmujemy wartość większą - i tak:

L

max Lminf Lminϕ

,

(

)

145

=

:=

3 ) Sprawdzenie warunku na minimalna długość łuku kołowego

Kmin max

Vmax

2.5

30

,










48

=

:=

minimalna długość łuku kołowego

Krzecz R β

⋅

=

kąt beta w radianach

β

α

2 ξ

⋅

−

=

ξ

asin

L

2 R

⋅









0.0518089

=

:=

rad

α

Az2

Az1

−

4

=

:=

alfa jest różnicą azymutów (w stopniach)

β

α

π

180

⋅

2 ξ

⋅

−

:=

Krzecz R β

⋅

47.326

−

=

:=

WARUNEK Krzecz Kmin

≥

NIE JEST SPEŁNIONY, ZMNIEJSZAM PRZECHYŁKĘ AŻ
DO SPEŁNIENIA WARUNKU

h

35

:=

L

Vmax

h

m

⋅

42

=

:=

L

Ceil L 5

,

(

)

45

=

:=

ξ

asin

L

2 R

⋅









0.016072

=

:=

rad

α

Az2

Az1

−

4

=

:=

alfa jest różnicą azymutów (w stopniach)

β

α

π

180

⋅

2 ξ

⋅

−

:=

Krzecz R β

⋅

52.737

=

:=

WARUNEK Krzecz Kmin

≥

JEST SPEŁNIONY DLA PRZECHYŁKI h=35mm

4) Styczne

UWAGA ZMAINA W OZNACZENIACH (TYLKO) NA RYSUNKACH:

ZAMIAST γ MA BYĆ α

ZAMIAST α MA BYĆ β

ξ

ξ

ξ

α

α

γ

γ

RYS 1

ξ

ξ

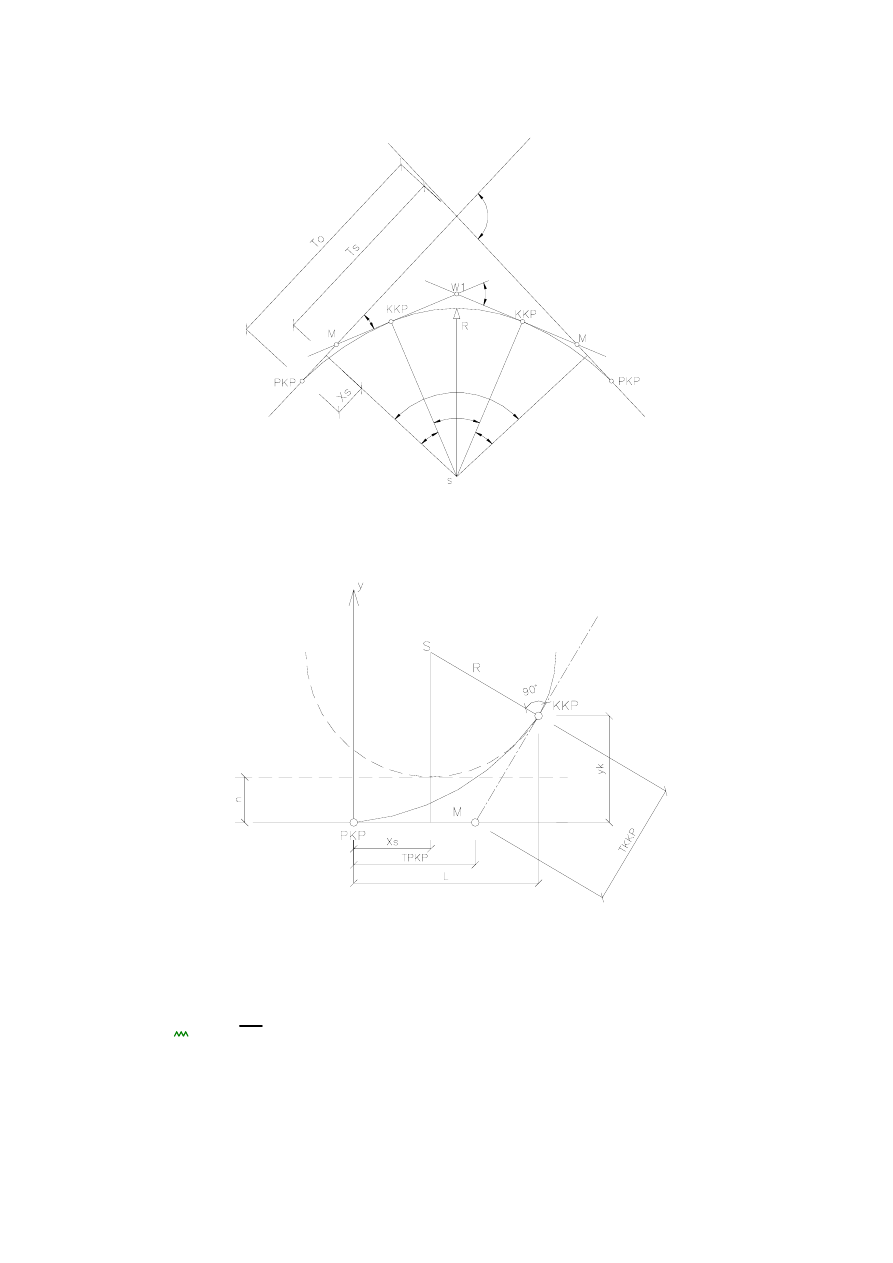
Rys 2

ξ

atan

L

2 R

⋅









0.01607

=

:=

ra

patrz rysunek 1 i pkt.3

xs L R sin ξ

( )

⋅

−

22.5029

=

:=

patrz rysunek 2

yk

L

2

6 R

⋅

0.2411

=

:=

patrz rys 2

nw yk R 1 cos ξ

( )

−

(

)

⋅

−

0.0603

=

:=

przesunięcie łuku kołowego do wewnątrz ukłądu
patrz rys 2

Ts

R

nw

+

(

)

tan

α

π

180

⋅

2













⋅

48.89118

=

:=

T0 Ts xs

+

71.394

=

:=

Tpkp

2
3

L

⋅

30

=

:=

Tkkp

L

3 cos ξ

( )

⋅

15.002

=

:=

TLuku R tan

β

2









⋅

26.371

=

:=

5 ) PUNKTY GŁÓWNE UKŁADU

DOWIĄZUJEMY SIĘ DO WIERZCHOŁKA TORU

PKP1

NPKP1 Nw T0 cos Az1

π

180

⋅

π

+









⋅

+

3515.6405

=

:=

EPKP1 Ew T0 sin Az1

π

180

⋅

π

+









⋅

+

491.1658

−

=

:=

PKP2

NPKP2 Nw T0 cos Az2

π

180

⋅









⋅

+

3394.623

=

:=

EPKP2 Ew T0 sin

Az2 π

⋅

180









⋅

+

415.5457

−

=

:=

M1

NM1 Nw

T0 Tpkp

−

(

)

cos Az1

π

180

⋅

π

+









⋅

+

3490.7694

=

:=

EM1 Ew

T0 Tpkp

−

(

)

sin Az1

π

180

⋅

π

+









⋅

+

474.39

−

=

:=

M2

NM2 Nw

T0 Tpkp

−

(

)

cos Az2

π

180

⋅









⋅

+

3420.6038

=

:=

EM2 Ew

T0 Tpkp

−

(

)

sin Az2

π

180

⋅









⋅

+

430.5457

−

=

:=

Az2

Az1

−

4

= różnica jest dodatnia więc łuk zakręca w prawo!!!

KKP1

PRAWO

NKKP1 NM1 Tkkp cos

Az1 π

⋅

180

ξ

+









⋅

+

3478.199

=

:=

EKKP1 EM1 Tkkp sin Az1

π

180

⋅

ξ

+









⋅

+

466.2019

−

=

:=

LEWO

NKKP1 NM1 Tkkp cos Az1

π

180

⋅

ξ

−









⋅

+

=

EKKP1 EM1 Tkkp sin Az1

π

180

⋅

ξ

−









⋅

+

=

KKP2

PRAWO

NKKP2 NM2 Tkkp cos Az2

π

180

⋅

π

+

ξ

−









⋅

+

3433.4736

=

:=

EKKP2 EM2 Tkkp sin Az2

π

180

⋅

π

+

ξ

−









⋅

+

438.2544

−

=

:=

LEWO

NKKP2 NM2 Tkkp cos Az2

π

180

⋅

π

+

ξ

+









⋅

+

=

EKKP2 EM2 Tkkp sin Az2

π

810

⋅

π

+

ξ

+









⋅

+

=

W1

PRAWO

NW1 NKKP1 TLuku cos Az1

π

180

⋅

ξ

+









⋅

+

3456.102

=

:=

EW1 EKKP1 TLuku sin Az1

π

180

⋅

ξ

+









⋅

+

451.8085

−

=

:=

LEWO

NW1 NKKP1 TLuku cos Az1

π

180

⋅

ξ

−









⋅

+

=

EW1 EKKP1 TLuku sin Az1

π

180

⋅

ξ

−









⋅

+

=