A. Zaborski, Łuk
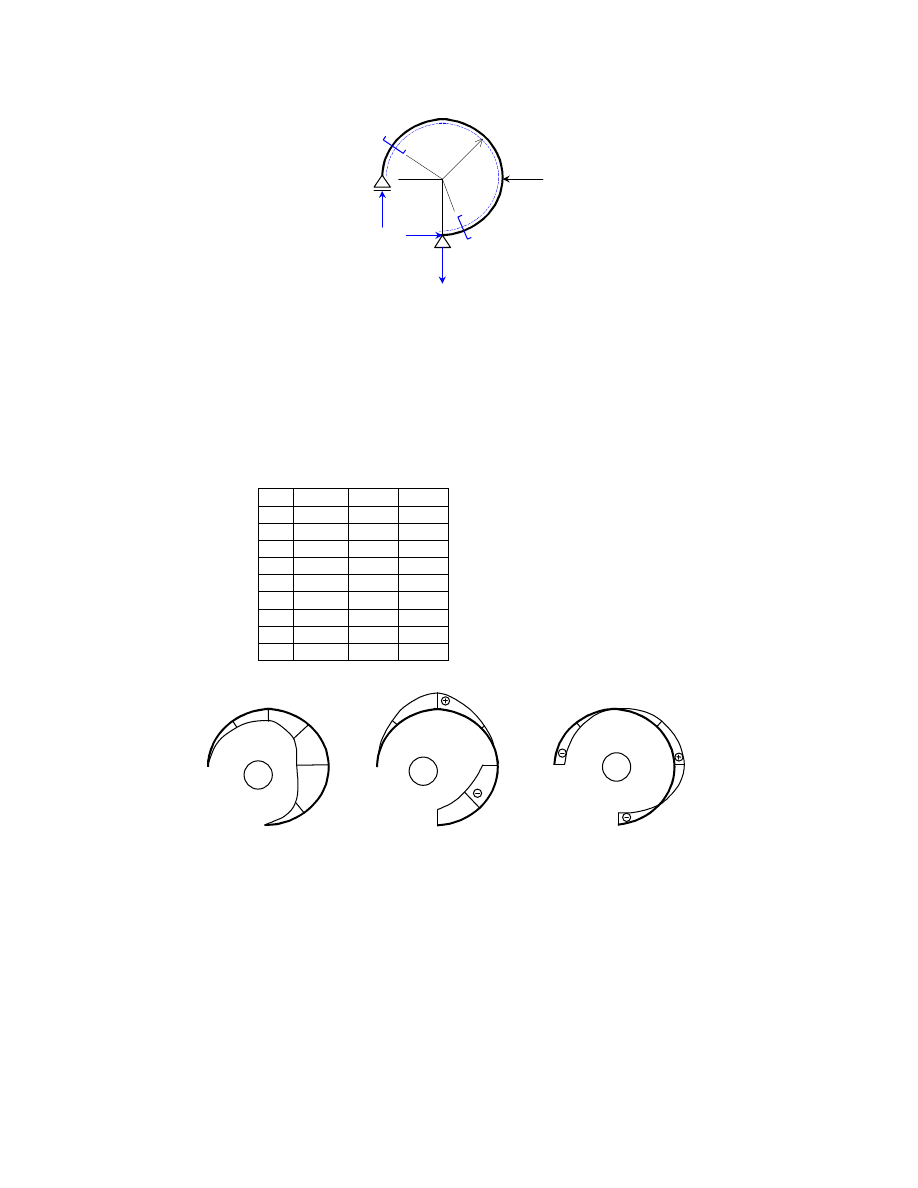
Łuk kołowy
3.5m
V
B
H
B
V
A
β
130 kN
α
Obliczenie reakcji:
R
A
= V
B
= H
B
= 130 kN
Równania sił przekrojowych:
0 <
α < 180°
M(
α) = R
A
3.5 (1 - cos
α)
Q(
α) = R
A
sin
α
N(
α) = - R
A
cos
α
0 <
β < 90°
M(
β) = V
B
3.5 (sin
β - cosβ +1)
Q(
β) = -V
B
cos
β - H
B
sin
β
N(
β) = V
B
sin
β - H
B
cos
β
Obliczenia zapisujemy w tabelce:
α
α
α
α
M
kNm Q kN
N
kN
0
0.0
0.0 -130.0
45
133.3
91.9
-91.9
90
455.0
130.0
0.0
135
776.7
91.9
91.9
180
910
0.0
130.0
β
β
β
β
M
Q
N
0
0.0 -130.0 -130.0
45
455.0 -183.8
0.0
90
910.0 -130.0
130.0
Wykresy:
455
910
776.7
455
133.3
M
183.8
130
130
91.92
130
91.92
Q
130
130
130
91.92
91.92
N
A. Zaborski, Łuk
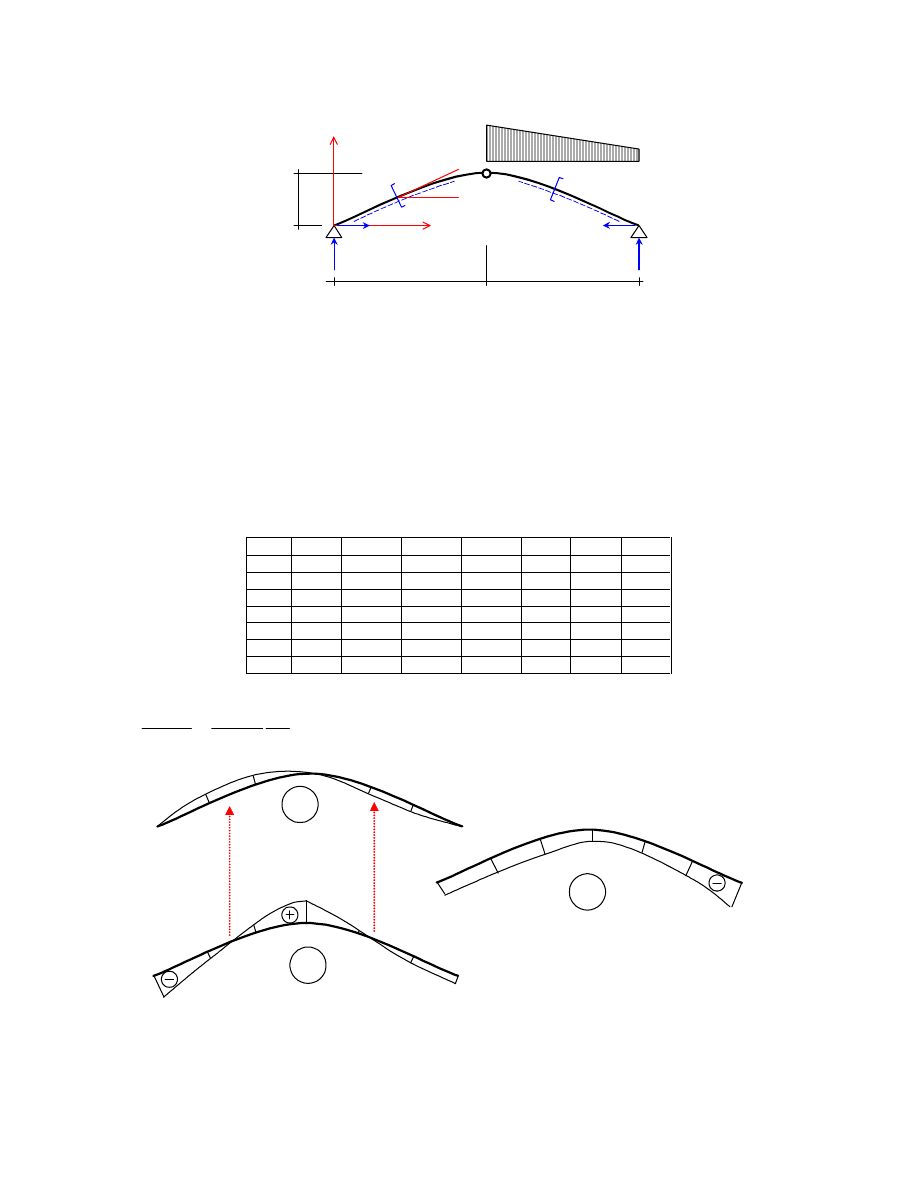
Łuk paraboliczny
α
V
B
H
B
V
A
H
A
3 m
3 m
1.5 m
y
x
15 kN/m
45 kN/m
Obliczenie reakcji:
H
A
= H
B
= 52.5 kN, V
A
= 26.25 kN, V
B
= 63.75 kN
Równanie łuku:
y(x) = a x
2
+ b x +c, z warunakami: y(0) = 0, y(3) = 1.5 m, y(6) = 0, skąd:
y(x) = -1/6 x
2
+ x
pochodna:
y’(x) = 1 – x/3 = tg
α
Równania sił przekrojowych:
0 < x < 3 m
M(x) = 26.25 x – 52.5 y
Q(x) = 26.25 cos
α - 52.5 sinα
N(x) = -26.25 sin
α - 52.5 cosα
3 m < x < 6 m
M(x) = 26.25 x – 52.5 y – 45/2 (x – 3)
2
+ 30/3 1/6 (x – 3)
3
Q(x) = 26.25 cos
α - 52.5 sinα - 45 (x – 3) |cosα| + 30/3 ½ (x –3)
2
|cos
α|
N(x) = -26.25 sin
α - 52.5 cosα - 45 (x – 3) |sinα| + 30/3 ½ (x –3)
2
|sin
α|
Obliczenia prowadzimy w tabelce:
x [m] y [m]
α
α
α
α
cos
α
α
α
α
sin
α
α
α
α
M
Q
N
0
0.000
0.7854
0.7071
0.7071
0.00 -18.56 -55.68
1
0.833
0.5880
0.8321
0.5547 -17.50
-7.28 -58.24
2
1.333
0.3218
0.9487
0.3162 -17.50
8.30 -58.11
3
1.500
0.0000
1.0000
0.0000
0.00
26.25 -52.50
4
1.333
-0.3218
0.9487
-0.3162
14.17
3.56 -54.15
5
0.833
-0.5880
0.8322
-0.5547
10.83
-7.28 -67.95
6
0.000
-0.7854
0.7071
-0.7071
0.00
-7.95 -82.20
Sprawdzenie, czy pochodna momentu zginającego po współrzędnej związanej z osią pręta jest równa sile
poprzecznej, np. w pierwszym przedziale:
)
Q(
sin
5
.
52
cos
25
.
26
cos
tg
5
.
52
cos
25
.
26
d
d
d
)
dM(
d
)
dM(
s
s
x
x
x
s
s
=
−
=
−
=
=
α
α
α
α
α
14.17
10.83
17.5
17.5
M
18.56
7.28
8.301
26.25
3.56
7.28
7.95
Q
55.68
58.24
58.11
52.5
54.15
67.95
82.2
N
ekstremum M
A. Zaborski, Łuk
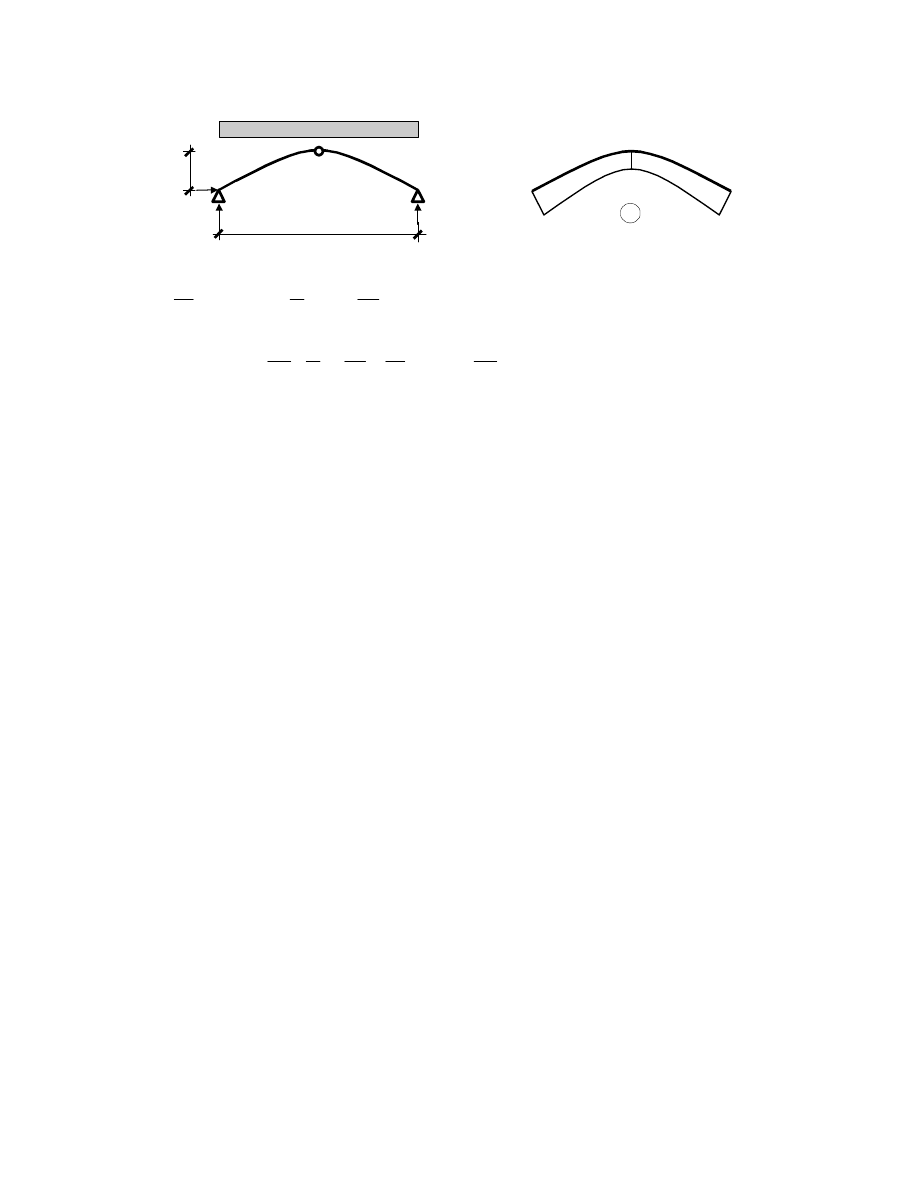
Przykład osi racjonalnej łuku parabolicznego
H
A
N
R
A
H
A
f
q
l
Określamy równanie osi łuku w postaci paraboli 2. stopnia o strzałce równej f i rozpiętości l oraz obliczamy
reakcje jak dla układu 3-przegubowego:
(
)
f
ql
H
ql
R
lx
x
l
f
y
A
A
8
,
2
,
4
2
2
2
=
=
−
−
=
.
Równanie momentów zginających ma postać:
(
)
0
2
4
8
2
2
)
(
2
2
2
2
2
=
=
−
−
−
−
=
−
−
=
K
qx
lx
x
l
f
f
ql
x
ql
qx
y
H
x
R
x
M
A
A
.
Jeśli moment zginający jest tożsamościowo równy zero, to i siła poprzeczna musi być tożsamościowo równa
zero i łuk pracuje jedynie na ściskanie. Łuk o takiej osi nazywamy łukiem o osi racjonalnej.