ŁUK KOŁOWY Z SYMETRYCZNYMI ŁUKAMI KLOTOIDY Dane: R, γ, L lub a.

γ=α+2τ, T₀=(R+H)tg γ/2, X₀=X_P-Rsin τ, X_S=X₀+Rsin γ/2, X_W'=X_S+Z'sin γ/2, Z'=[R/(cos α/2)]-R=R[1/(cos α/2)-1], Z=[(R+H)/(cos γ/2]-R, Y₀=R+H, Y_S=Y₀-Rcos γ/2, Y_W'=Y_S-Z'cos γ/2

DOKŁADNOŚĆ OSNOWY REALIZACYJNEJ Dokładność pomiaru kątów i boków w osnowie szczegółowej ustala się podczas wstępnej analizy, która bazuje na zachowaniu projektowanych odl. między osiami konstr. budowli.

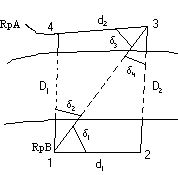
Zał. że dopuszczalna odchyłka rozstawu osi (1-1, 2-2) wynosi dl_t=±15mm, a śr. błąd realizacji rozstawu osi md_1-2= dl_t/3=5mm. Zakładając, że pkt. 1 zostanie wyniesiony od pkt-u 8 a pkt. 2 od pkt-u 7, to to rozstaw będzie równy d_1-2= d_7-8-d₁-d₂, błąd d_1-2 będzie wynosił m²d_1-2= m²d_7-8- m²d₁- m²d₂, gdzie md_7-8= md_1-2/√3. Na podst. wzoru md_7-8=±m₀√(fd_7-8(apa)^-1 fd_7-8) oblicza się dokładnośc pomiaru kątów i boków, gdzie błąd pojedynczego pomiaru m₀= md_7-8/(fd_7-8(apa)^-1 fd_7-8). Po obl. m₀ korzystamy z zał. koordynacji pomiarów kątowych i liniowych i przyjmując, że mα^cc/ρ^cc=md/d , obliczamy dokł. pomiarów linowych ze wzoru md=d (mα^cc/ρ^cc). Daje nam to dokładność z jaką musimy pomierzyć kąty i boki, aby otrzymać odpowiednie dokładności osi konstrukcyjnych.

PRZENIESIENIE WYSOKOŚCI PRZEZ PRZESZKODY WODNE

met. niwelacji trygonometrycznej zasada przedstawiona jest na rysun-ku.

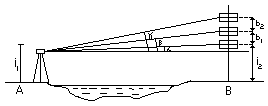
Przewyższenie ΔH można obliczyć trzykrotnie na podst. kątów α, β, γ. Chcąc zwiększyć dokładność wyz-naczenia ΔH należy przeprowadzić obserwacje jednocześnie z dwóch stanowisk po obu brzegach prze-szkody.

Na p-tach 2 i 4 ustawia się statywy z tarczami bisekcyjnymi i mierzy się wysokości tarcz nad

p-tami oraz między tarczami. Teodolity ustawia się na p-tach 1 i 3. Obserwacje ką-tów pionowych wykonuje się jed-nocześnie. Mierzy się również kąty poziome.

Dokł. określenia różnicy wys. tą met. oblicza się ze wzoru:

m_h=√[(tgα+(1-K/r)D₀)m_do]² +

(d_om/cos²α)² + (d_om_K/2r)²

α - kąt pionowy

K - współczynnik refrakcji

r - promień kuli ziemskiej

d_o - odległość między p-tami

Na błąd przyrostu wysokości naj-większy wpływ wywiera błąd po-miaru kąta pionowego, wpływ od-ległości nie ma większego znacze-nia.

ΔH=i_t + Dtgα - i_s + D²[(1-K)/2r]

METODY OBLICZANIA OBJĘTOŚCI MAS ZIEMNYCH

1)met. siatki kwadratów

Projektowana płaszczyzna dzieli obszar działki na części znajdujące się pod i nad tą płaszczyzną - inaczej na obszary wykopów i nasypów. Linia przecięcia pow-ierzchni terenu z powierzchnią projektowaną nazywa się linią robót zerowych. Na podstawie rzędnych istniejących i projekt-owanych, po odpowiednich obli-czeniach, otrzy-mujemy wielkość danego wykopu lub nasypu. Wzo-rem pozwalającym określić nam tę objętość jest wzór:

a)V=1/4(a²(h₁+h₂+h₃+h₄)), V=V_N+V_W, V_W=Sw(1/4(h₇+h₈)), V_N=S_N(1/4(h₅+h₆))

b)V=V_N+V_W, V_W=Sw(1/5(h₁+h₂+h₃)), V_N=S_N(1/3(h₄))

Pow. nasypu i wykopu określa się analitycznie, graficznie lub mechanicznie. Błąd wyznaczenia zależy przede wszystkim od długości boku kwadratu

2)met. przekrojów poprzecznych

Sposób ten jest powszechnie stosowany do obliczania robót ziemnych przy projektowaniu „budowli” o kształcie wydłużonym.

F₁, F₂ - pola powierzchni prze-krojów utworzonych z przecięcia terenu płaszczyznami pionowymi w miejscach przekrojów poprzecznych;

d - odległość między przekrojami

V=d/2 (F₁+F₂)

wzór ścisły na obliczenie objętości

V=d/3[F₁+F₂+√(F₁F₂)]

3)met. przekrojów poziomych z mapy warstwicowej

V = h/2 Σ(S_i+S_i+1) + Δh/3_*S_n

4)met. siatki trójkątów

V = a²/2 _* 1/3(h₁+h₂+h₃)

5)met. punktów rozproszonych

V = 1/3 S₁(h₁+h₂+h_3,) m_V²=(Vm_S/S)²+(S/3)²3m_h²+m_Vu²,

m_Vu² = 0,6 Q S√b, Q - współczynnik bogactwa mikro- rzeźby (0,005 - 0,01),

b - średnia długość celowej

Na dokł określenia objętości skła-dają się następujące błędy:

a) m_K - bł. ukształt. pow. terenu

ε = R - x; x = √(R²-a²/4)

a - bok kwadratu w met. siatki kw.

Błąd obliczonej objętości ze wzglę-du na ukształtowanie terenu wynosi

m_Vu² = S ε_SR = n a² ε_SR

b) wpływ błędu zagęszczenia terenu

D=V_W/W_N; V_W=V_N D ±0,02D V_N

0,02D - ustalona tolerancja stopnia zagęszczenia gruntu; wg Polskiej Normy 0,9<D<1,15

c) wpływ dokładności materiałów wyjściowych można to sprowadzić do wpływu dokładności wyznaczenia rzędnych terenu h.

1) V = S h₀

2) V = ΣS_i 1/KΣh_J

3) h₀ = V/S

4) h_J = h_J' ± m_hJ + u_J

Jeżeli do r-nia 3 podstawimy r-nie 4 to otrzymamy:

m_Vh = ±m₀√(S/K) + u₀S

u0 - bł. systemat. rzędnej wysokośc

m0 - bł. jednoznacznego określ. h

0,02m - niw. siatk.

0,10m - tachimetria

0,05m - p-ty rozproszone

0,05m - niw. przekrojów

0,20m - aerofotogrametria

REGULACJA TORÓW KOLEJOWYCH METODĄ „WYKRESU KĄTÓW”

x=LiCx, y=αiCy, dx=dLCx, dy=dαCy, c-współczynnik skali L=rα, dL=rdα, dα=dL/r, dx=CxdL, dy=Cy(dL/r), (dy/dx)=(Cy/Cx)(dL/rdL)=(Cy/Cx)(1/r), y=∫(Cr/r)dx, -równanie krzywej w przyjętym odwzorowaniu. W zależności od przyjętych krzywych wykres kątów będzie przyjmować różne kształty. Linia prosta r=∞, y=∫(Cr/r)dx=0-prosta równoległa do osi Y. Dla łuku kołowego r=R^y y=∫(Cr/r)dx y=(cr/R)x

Dla krzywej przejściowej o pochyłce zmieniającej się w sposób liniowy K/L=k/x, 1/(RL)=1/(rx), r=(RL)/x, y=∫(Cr/r)dx, y= (Cr/r)(x²/2)-równanie paraboli

---