ŁUK KOSZOWY Dane: t1, R1, R2, γ, Szukane: t, α1, α2,
Ukł. równania: α1+ α2+180o+180o- γ=360o 1) α1+ α2= γ 2) cos α2=(O1B)/(R2-R1), O1B=AC-O1C-AB=D- O1C-R2 , DE z ΔDEW →DE=t1cos[-(90o- γ)]=t1sin γ, O1C z Δ O1CD→ O1C=R1sin[-(90o- γ)]=-R1cos γ, więc cos α2=( t1sin γ+ R1cos γ- R2)/(R1-R2), dla sprawdzenia: t1=R1tg α1, t1'=R1tg (α1/2), WW1= t1- t1',
t2=R2tg α2, t2'=R2tg (α2/2), WW2= t2- t2'
PROJEKTOWANIE PŁASZ-CZYZN BILANSUJĄCYCH ROBOTY ZIEMNE
Każda płaszczyzna przechodząca przez środek ciężkości jest płasz-czyzną bilansującą roboty ziemne.
1)średnia wartość współrzędnych
XS=Σ xi/n YS=Σ yi/n ZS=Σ zi/n
2)jeżeli pł. bilansująca ma zadany kierunek najw. spadku α i wart. najw. spadku k to r-nie płaszcz. to:
(kcosα)x + (ksinα)y - z + Ho = 0
Ho = - XSkcosα - YSksinα + ZS
3)jeżeli projektowana płaszcz. ma przechodzić przez 2 p-ty
1 (x1, y1, z1) i 2 (x2, y2, z2) to
(x1-XS)kcosα + (y1-YS)ksinα -
(z1-ZS) =0
(x2-XS)kcosα + (y2-YS)ksinα -
(z2-ZS) =0
kcosα i ksinα dają tgα i liczymy α
4)jeżeli projektowana płaszczyzna ma przechodzić przez 1 dany p-t i ma określony max spadek wzdłuż kierunku α to mamy jedno r-nie;
(x1-XS)kcosα + (y1-YS)ksinα -
(z1-ZS) =0
5)jeżeli projektowana płaszczyzna ma przechodzić przez 1 dany p-t i ma określony max spadek k to mamy jedno r-nie;
(x1-XS)kcosα + (y1-YS)ksinα -
(z1-ZS) =0
i dołączamy r-nie sin2α+cos2α=1 i wyliczamy α
PRZENOSZENIE WSKAŹNI-KÓW KONSTRUKCYJNYCH
Przed przystąpieniem do obsługi geodezyjnej kondygnacji powta-rzalnych i wyznaczaniu wskaźni-ków konstrukcyjnych na poszcze-gólnych poziomach roboczych na-leży sporządzić szkic tyczenia, za-wierający rozmieszczenie osi konst-rukcyjnych zgodnie ze szkicem do-kumentacyjnym oraz osnowe bu-dowl.-montaż. Osnowa ta będzie służyć do przenoszenia osi konst-rukcyjnych na poszczególne kondy-gnacje.
1)met. stałej prostej
a)stawiamy teodol. na p-cie linii bazowej osnowy bud-mont., celuje-my na tarczę na końcu tej linii
b)poziomujemy teodol. przy każ-dym pomiarze
c)układamy łatę na stropie kondyg-nacji roboczej i ustawiamy ją pro-stop. do płaszcz. celowania
d)łatę ustawiamy tak, by obraz tar-czy sygn. znalazł się na pionowej kresce siatki celowniczej teodol.
e)zaznaczamy na stropie tyczony punkt. Czynności wykonujemy w 2 poł. lunety.
![]()
1)jeśli OK-OP=OK'-ΔK=OP'-ΔP
2)ΔK = ΔP/dP * dK
OK'-(ΔP/ dP) dK= OP'-ΔP
OK'dP-ΔPdK= dP OP'-ΔPdP
dP(OK'- OP')= ΔP(dK-dP)
poprawki trasowania
ΔP = [(OK'-OP')/(dK-dP)] * dP
ΔK = [OK'-OP'] + ΔP
analiza dokładności
1.bł centrowania teodol. 0,4mm
2.bł centrowania sygnału 0,4mm
3.niepionowość osi obr teod 0,9mm
4.bł celowania na tarczę 0,3mm
5.bł wprowadzenia sygn. w oś celo-wą 0,4mm
6.bł oznaczania wskaźnika 0,8mm
7.inne błędy 0,3mm
m = √(m12+m22+...m72) = ± 1,4mm
2)metoda rzutowania
Wyznacza się osie konstrukcyjne lub linie równoległe do tych osi dla ścian zewn. i wewn. Przenosi się też tą met. wszystkie typy osnowy wewn. na kondygnację roboczą.
1)teod. stawiamy na stanow. pozio-mujemy, celujemy pionową kreską na wskaźnik wyjściowy na bud.
2)w 2 poł. lunety wyzn. wskaźnik na krawędzi stropu wg kreski pion.
3)każdorazowo poziomujemy teod.
4)analogicznie wyzn. wskaźnik z drugiej strony budynku
5)wtyczyć teod. w linię przeniesio-nych wskaźników i za pomocą łaty realizacyjnej wyznaczamy wskaźni-ki ścian zewn.
p/d=P/D, czyli P=p(D/d)
analiza dokładności:
niepionowość osi obr. teod. 0,9mm
bł. celowania 0,3mm
bł wprowadzenia sygn w płaszcz. rzutowania 0,4mm
oznacz. wskaźnika na strope 0,8mm
m2 = m12+...m42 = 1,3mm
3)metoda biegunowa
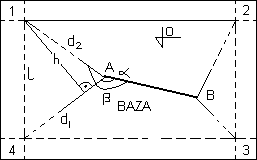
l2 = d12 + d22 - 2d1d2cos(β-α)
mL2 = cos2αmd12 + cos2αmd22 + h2mβ2 + h2mα2
analiza dokładności:
bł centrowania pionownika 0,3mm
bł poziomowania libelli 0,1mm
bł odczytu podziałki 0,7mm
bł oznaczenia p-tu na tarczy 0,5mm
m = 0,5mm
przy n kondygnacjach mn = 0,5√n
DOKŁADNOŚĆ TYCZENIA LOKALIZUJĄCEGO
Przedmiotem tyczenia lokalizującego jest określenie położenia względem osnowy realizacyjnej elementów projektowanego obiektuoraz oznaczenie ich w terenie w taki sposób aby wytyczane punkty mogły być wykorzystane po wykonaniu robót budowlano-motażowych.
Metoda biegunowa. Stabilizujemy w terenie dwa punkty A, B tworzące bazę i odkładając w terenie od tej osnowy dany kąt i odległość otrzymujemy punkt do wyniesienia. Na dokładność tyczenia mają wpływ:niedokładność osnowy, niedokł. wyzn. punktu osnowy, niedokł. czynności pomiarowych (centr. instrumentu 0,7(L/C)*e, odłożenie kąta:L(mα/ρ), odłożenie odległości:mL), niedokładność utrwalenia:
mog2=Σ4i=3mi2-uwzględnienie błędów osnowy
mwewn2=Σ4i=3mi2-wewn. błąd tyczenia
Analiza dokładności: mp=√(mx2+my2), Korzystając ze wzorów na wsp. punktu P Xp=XA+cosαd, Yp=YA+sinαd i różniczkując je otrzymujemy wzory na błąd położenia punktu P: mx2=[(δXp/δα)mα]2+[(δXp/δd)md]2,
my2=[(δYp/δα)mα]2+[(δYp/δd)md]2,
mx2=(-sinαd mα)2+(cosα md)2,
my2=(cosαd mα)2+(sinα md)2,
mp2= mα2d2+md2
Błąd długości:
dA-P=√ (XP-XA)2+(YP-YA)2
md2=(∂d/∂XP*mXP)2+(∂d/∂XA*mXA)2+(∂d/∂YP*mYP)2+(∂d/∂YA*mYA)2, gdzie:
∂d/∂XP=(XP-XA)/√[(XP-XA)2+(YP-YA)2 ]
∂d/∂XA=-(XP-XA)/√[(XP-XA)2+(YP-YA)2 ]
∂d/∂YP=(YP-YA)/√[(XP-XA)2+(YP- YA)2 ]
∂d/∂YA=-(YP-YA)/√[(XP-XA)2+(YP-YA)2 ]
Błąd kąta można wyzn. ze wzoru: mα/ρ=md/d
POZIOME SKŁADOWE PRZEMIESZCZEŃ PUNKTÓW
1)Metody pomiaru:ciąg poligonowy, sieć kątowo-liniowa, technika GPS, techniki klasyczne, niwelecja 2) Metody opracowania
a)uxp=xap-xop=fx(αa, βa, da)-fx(αo, βo, do); uyp=yap-yop=fy(αa, βa, da)-fy(αo, βo, do) b) uxp=fx(Δαa,o, Δβa,o, Δda,o); uyp=fy(Δαa,o, Δβa,o, Δda,o) Obserwacje kierunku na j-tym stanowisku -Vjk-Bjkdxk+Ajkdyk+Bjkdxj-Ajkdyj+sj=kjkobs-kjkprzybl Vik-popr, do kierunku; dxj,dyj-popr. do parametrów; dxk,dyk- popr. do parametrów; sj-niewiadoma określająca skręt pęku obserwacji; kjkobs-kierunek obs.; kjkprzybl-kierunek obl. na podst. (xp,yp) A=(Δxjk/djk)ρcc,B=(Δyjk/djk)ρcc Obserwacje kątów poziomych: Dla obs. liniowych: -Vij+cos αijdxj+sin αijdyj-cos αijdxi-sin αijdyi=dijobs-dijprzybl Dokładność:cov(x,y)=mo2(ATPA)-1 V(x)=mx2, V(y)=my2 BADANIE PIONOWOŚCI BUDOWLI METODĄ KĄTÓW Oparta jest na pomiarze kątów do niedostępnych punktów ze stanowisk dowolnie wybranych na placu budowy. Wielkość wychylenia i jego rzuty na osi współrzędnych ux i uy można obliczyć ze wzorów: Z pierwszego wcięcia: ux=(u2cos α1- u1cos α2)/sin(α2-α1) uy=(u2sin α1- u1sin α2)/sin(α2-α1) Z drugiego wcięcia: ux=(u3cos α2- u2cos α3)/sin(α3-α2) uy=(u3sin α2- u2sin α3)/sin(α3-α2) u=(diΔβ)/ρ Określamy również: αR=arctg(uy/ux)-azymut wychylenia u=ux/cos αR=uy/sin αR=√ux2+uy2-wielkość wychylenia . Metody opracowań: 1) Metoda analityczno-graficzna: a) Skartowanie stanowisk obserw. b)Obliczenie wartości u c)Wykreślenie wstęg wachań d) Określenie środka ciężkości trójkąta głędów e)Odczytanie wartości wychylenia
2)Metoda analityczna: a)Obserwacja kątów, b)Obl. (x,y) stanowisk obserwacyjnych c)Układamy poprawki typu AX+L=V przy zał. bezbłędności punktów na poziomie 0 d) Obl. dx, dy na i-tym poziomie
Równania poprawek: V1=sinφ1ux-cosφ1uy+u1 V2=sinφ2ux-cosφ2uy+u2 V3=sinφ3ux-cosφ3uy+u3 Rozwiązujemy układ metodą VTPV=min
Wyszukiwarka
Podobne podstrony:
Sciągi, ZESTAW 1, ŁUK KOŁOWY Z SYMETR
Finanse Sciągi Zestawienie ściąg z wzorami (51 str )
sciagi, Zestaw C, Zestaw C
Droga Obliczenie punktów przej łuk koszowego met rzędnych od cięciey Łuk II
Luk koszowy luk odwrotny
Sciągi, ZESTAW 7, WZÓR NA RÓWNANIE NATURALNE KLOTOIDY
sciagi, Zestaw D, Zestaw D
Sciągi, Zestaw 4, Zestaw 2
necka r1 r2, Psychologia UJ, Psychologia twórczości
K1 R1 R2, Edukacja, Elektrotechnika Magisterskie, Semestr 1, Maszyny Elektryczne
Sciągi, Zestaw 2, Zestaw 2
sciagi, Zestaw B, Zestaw B
Sciągi, ZESTAW 4, POSZERZENIE TORÓW KOLEJOWYCH
Sciągi, ZESTAW 02, POSZERZENIE TORÓW KOLEJOWYCH
Droga Obliczenie punktów przej łuk koszowego met rzędnych od cięciey Łuk I
Finanse Sciągi Zestawienie ściąg z wzorami (51 str )
Finanse Sciągi Zestawienie ściąg z wzorami (51 str )
Zestawy Miernictwo2, aaa, studia 22.10.2014, Materiały od Piotra cukrownika, materialy Kamil, płytka
projekt 2 Jerzy kordzikowski IM2 stacjonarne, zestaw3, Dane:
więcej podobnych podstron