STRUKTURA MECHANIZMÓW

Stopnie swobody
Jednym z podstawowych pojęć struktury mechanizmów jest liczba stopni swobody
mechanizmu. Można je zdefiniować opisując położenie ciała sztywnego (członu)
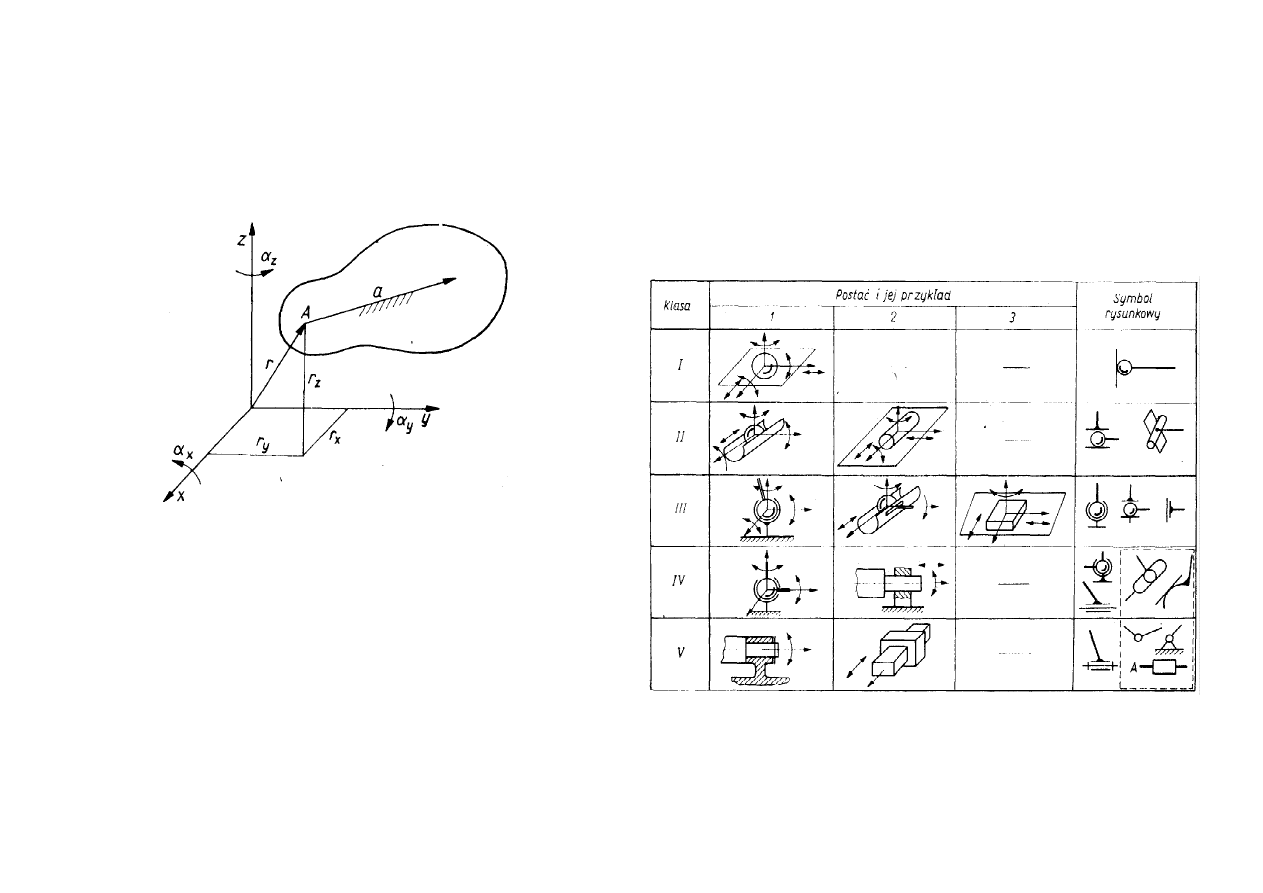
znajdującego się w przestrzeni (rys.).

Rys. Stopnie swobody ciała sztywnego

Położenie takiego ciała jest jednoznacznie określone przez 3 współrzędne

początku A wektora a sztywno związanego z tym ciałem, dwa kąty tego wektora z
dwiema (dowolnymi) osiami nieruchomego, prostokątnego układu odniesienia i
jeden kąt obrotu ciała wokół wektora, mierzony od dowolnej płaszczyzny
odniesienia. Każdy z trzech wymienionych kątów można wyrazić przez trzy kąty
obrotu wokół trzech osi układu prostokątnego. Tym samym, dowolne
przemieszczenie kątowe ciała w przestrzeni określa się jednoznacznie trzema
wypadkowymi kątami obrotu wokół trzech osi, a jego przemieszczenie liniowe —
trzema przemieszczeniami wzdłuż tych osi. Oznacza to, że dla określenia położenia
swobodnego ciała w przestrzeni potrzebna jest znajomość sześciu niezależnych
parametrów.

Liczbą stopni swobody nazywa się liczbę niezależnych parametrów

określających

jednoznacznie

położenie

pojedynczego

członu,

łańcucha

kinematycznego, względnie mechanizmu.

Łańcuch kinematyczny, względnie mechanizm składa się z członów

połączonych w tzw. pary kinematyczne. Oznacza to, że człony stykają się punktowo

lub powierzchniowo, z możliwością ruchów względnych. Wiąże się z tym utrata
pewnej liczby stopni swobody każdego członu. Połączenie członów w parę
kinematyczną nakłada na nie więzy.

Liczba stopni swobody jednego ciała względem drugiego, gdy ciała te nie

tworzą pary kinematycznej, wynosi 6. Połączenie w parę kinematyczną oznacza
ograniczenie tej liczby o co najmniej l i o co najwyżej 5 stopni swobody.

Z liczbami tymi wiąże się tradycyjnie klasę pary kinematycznej. Klasa I

zmniejsza całkowitą liczbę stopni o l, klasa II — o 2, klasa III — o 3, klasa IV — o 4,
a klasa V — o 5. W literaturze anglosaskiej zwykle rozróżnia klasy się na podstawie
pozostawionych stopni swobody. Na przykład „para obrotowa o jednym stopniu
swobody" jest odpowiednikiem stosowanej w tej książce pary obrotowej V klasy.

Klasyfikacja par kinematycznych

Klasa paty kinematycznej określa liczbę odjętych stopni swobody. Pozostałe stopnie
swobody mogą dotyczyć ruchu obrotowego i postępowego. Wiąże się z tym pojęcie
postaci klasy kinematycznej (numer l; 2 lub 3). Numer postaci rośnie wraz z uby-
waniem liczby możliwych ruchów obrotowych.
W tabl. podano najprostsze, wybrane przykłady par kinematycznych. Niektóre z nich
dotyczą tworzenia par kinematycznych występujących jako elementy handlowe
produkowane przez wyspecjalizowane firmy. Przykładem mogą tu być łożyska
toczne.

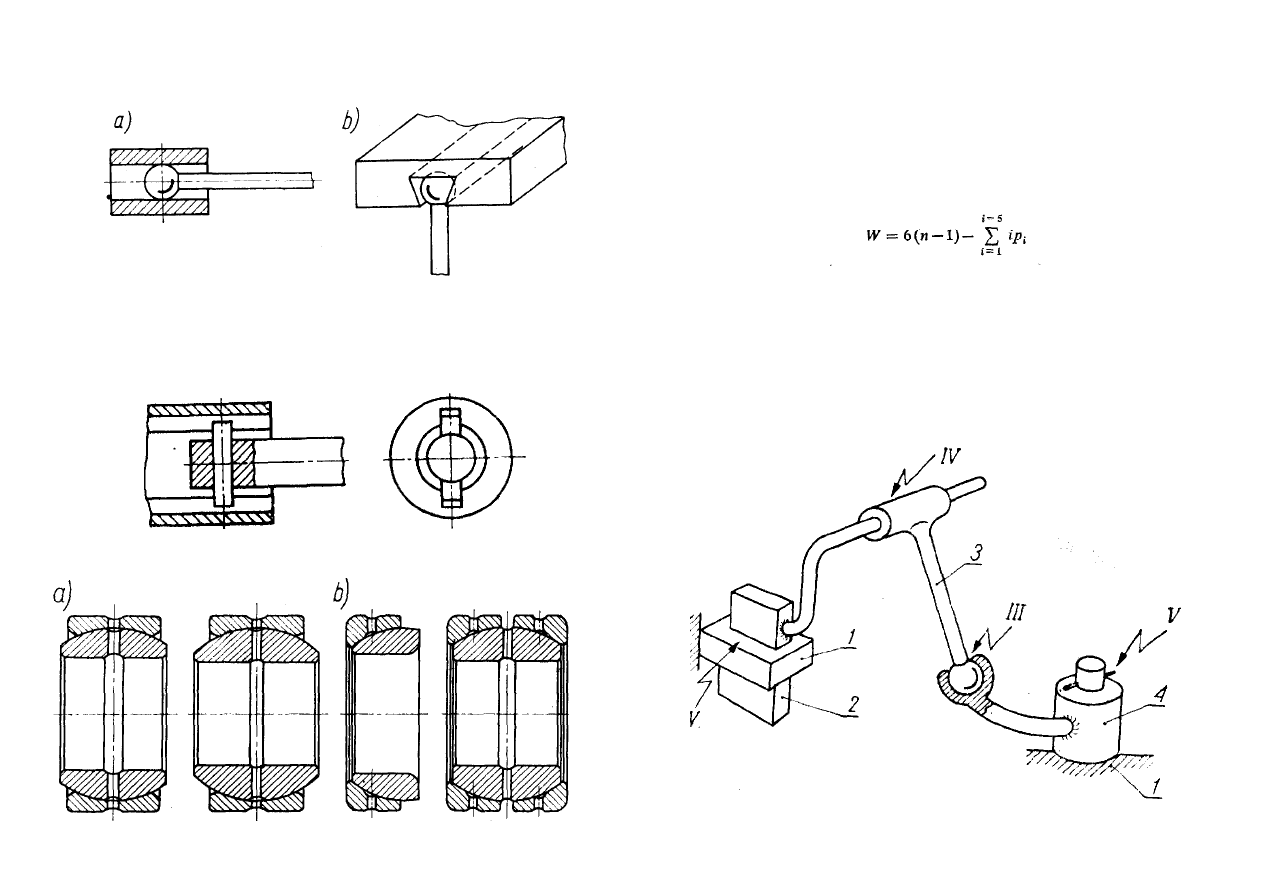
Na rysunku poniżej pokazano przykłady techniczne par kinematycznych II klasy

l postaci. Uzyskano je przez pasowanie suwliwe kuli z: a) cylindrem, b) rowkiem
pryzmatycznym.

Rys. Przykłady techniczne par II klasy l postaci

Podobne zamknięcie kinematyczne występuje w parze II klasy 2 postaci (rys.). Para
taka może być zastosowana w konstrukcji sprzęgła przenoszącego niewielkie
obciążenia.

Rys. Techniczne rozwiązanie pary II klasy 2 postaci

Rys. Ślizgowe łożyska wahliwe

Ruchliwość mechanizmów
Łańcuch kinematyczny członów połączonych w pary kinematyczne z jednym członem
(podstawą) nieruchomym jest mechanizmem. Ruchliwością mechanizmu nazywa się
liczbę stopni swobody tworzącego go łańcucha kinematycznego obliczoną względem
nieruchomego członu (podstawy). Ruchliwość jest ważnym wskaźnikiem dla
konstruktora, ponieważ jest ona równa liczbie niezależnych napędów jakie należy
zastosować w danym mechanizmie, ażeby uzyskać jego jednoznaczny ruch.
Ruchliwość W mechanizmu przestrzennego oblicza się ze wzoru

gdzie: n — liczba członów, i — klasa pary kinematycznej, p

i

— liczba par kine-

matycznych klasy i.
W mechanizmie przestrzennym, którego każdy człon traktowany jako swobodne ciało
sztywne w przestrzeni ma 6 stopni swobody, mogą wystąpić wszystkie rodzaje par
kinematycznych.

Przykład

Na rysunku pokazany jest przestrzenny czworobok przegubowy z zaznaczeniem klasy
par kinematycznych.

Rys. Przestrzenny czworobok przegubowy

Liczba członów n wynosi tu 4. Liczby par kinema

tycznych poszczególnych klas p

1

= 0; p

2

=

0; p

3

= l; p

4

= l oraz p

5

= 2. Podstawiając te dane do wzoru, otrzymuje się

l

2

-

5

-

l

4

-

l

3

-

0

2

-

0

1

-

1)

-

6(4

W

=

⋅

⋅

⋅

⋅

=

Ruchliwość tego mechanizmu jest więc równa jedności i tylko jeden niezależny napęd potrzebny
jest dla uzyskania jednoznacznego ruchu mechanizmu.

Przyk

ł

ad

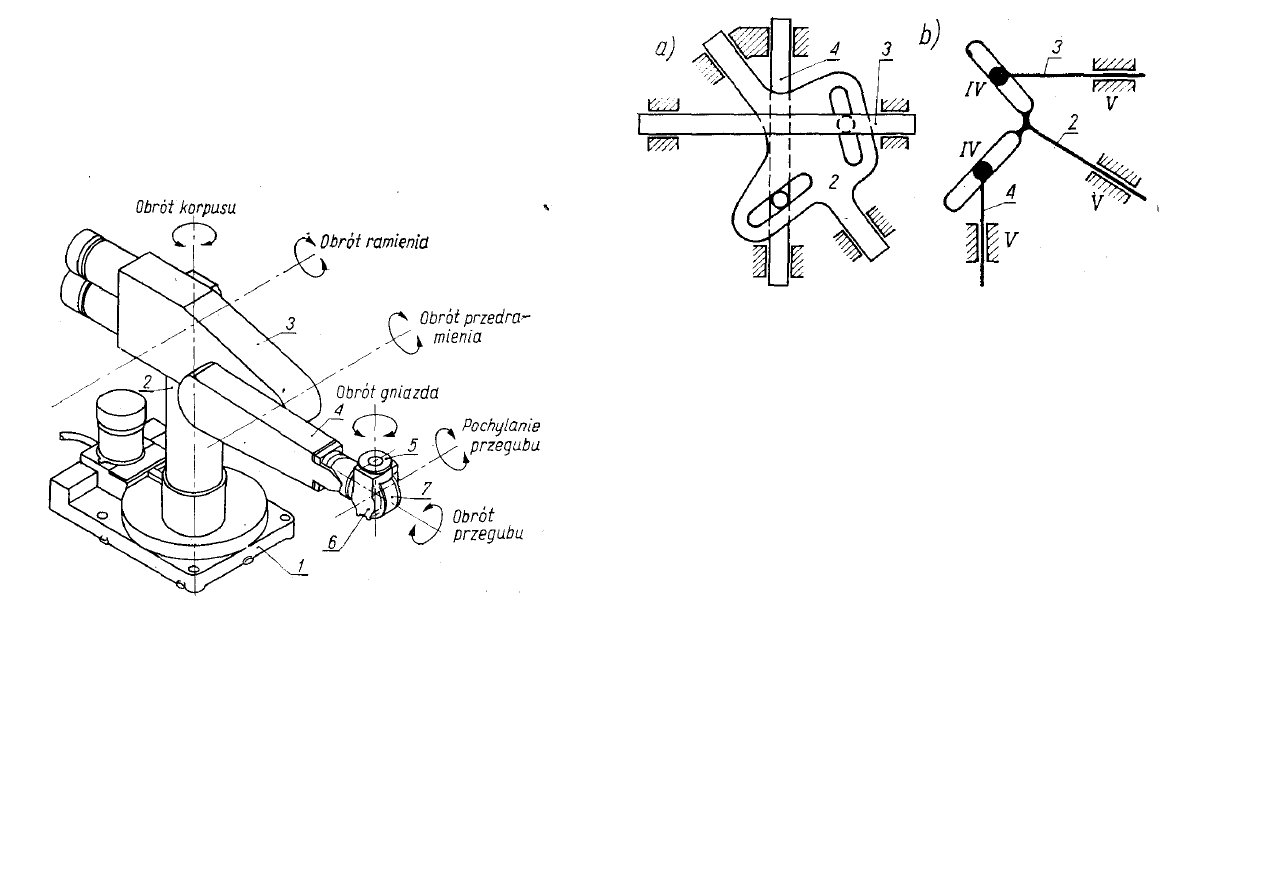
Uproszczony rysunek współczesnego robota przemysłowego przedstawiono na rys.:

Ruchy są wyłącznie obrotowe. Z danych wynika, że n = 7 oraz p

5

= 6. Po podstawieniu tych

danych do wzoru otrzymano W= 6 i taka sama liczba niezależnych napędów stosowana jest w
tego typu robocie w celu uzyskania jednoznacznego ru

c

hu chwytaka umieszczonego w

gnieździe.

W mechanizmach płaskich wszystkie człony poruszają się w płaszczyznach wzajemnie

równoległych. Odbiera to każdemu swobodnemu członowi 3 stopnie swobody z ogólnej liczby 6
jaką ma on w przestrzeni. Dwa człony tworzące parę kinematyczną mogą więc być pozbawione
co najwyżej 2 stopni swobody. Tym samym w mechanizmach płask

i

ch występują tylko pary

kinematyczne IV i V klasy. W tablicy oznaczono obszarem A te pary kinematyczne, które
dotyczą mechanizmów płaskich. Pary te mogą również występować w mechanizmach
przestrzennych. Odpowiedni wariant wzoru przybiera postać:

W=3(n-1)-2p

5

-p

4

.

Rys. Mechanizm:

a) pół-konstrukcyjny, b) schemat strukturalny

Przed przystąpieniem do obliczania ruchliwości mechanizmu należy zastosować pewne
uproszczenia jego struktury, polegające na usunięciu członów, których obecność nie ma
wpływu na ruch mechanizmu. Zabieg taki nazywa się tworzeniem schematu
strukturalnego. Schemat taki powinien być również pozbawiony powtórzeń par
kinematycznych, które są niezbędne w konstrukcyjnej realizacji mechanizmu, lecz nie
mają wpływu na jego ruch. Przykład schematu strukturalnego, utworzonego na podstawie
pół-konstrukcyjnego rysunku rzeczywistego mechanizmu, pokazano na rys. Jego dane to:
n =4, p

4

=2 oraz p

5

=3, czyli W= 3 • 3-2 • 3-2= l.

Mechanizmy o racjonalnej konstrukcji

Powtórzenia par kinematycznych i inne dodatkowe więzy nałożone na mechanizm

powodują, że rzeczywista ruchliwość mechanizmu W równa jest

W'=W+b

gdzie b oznacza dodatkowe więzy nałożone na mechanizm, zwane w dalszym ciągu
więzami biernymi. Jeżeli założy się, że rzeczywista ruchliwość mechanizmu W jest znana,
to można otrzymać wzór, który pozwala na obliczenie liczby biernych więzów w
mechanizmie

b=W’ -W

Liczba b pozwala na ocenę jakości realizacji technicznej dowolnego mechanizmu.

Konstrukcję mechanizmu uznaje się za racjonalną, gdy b ma wartość zerową lub możliwie
małą. Mechanizmy racjonalne cechuje:

— niewrażliwość na znaczne błędy wykonania. Oznacza to niski koszt ich wykonania;
— łatwość montażu bez wstępnej selekcji części;
— łatwość napraw wynikająca z łatwości montażu i prawie" całkowitej zamienności

części;

— Całkowita lub częściowa eliminacja docierania.

Warto przypomnieć, że w pewnych przypadkach obecność biernych więzów w

mechanizmach jest uzasadniona potrzebą przenoszenia znacznych obciążeń, których po
usunięciu biernych więzów mechanizm nie jest w stanie przenieść.

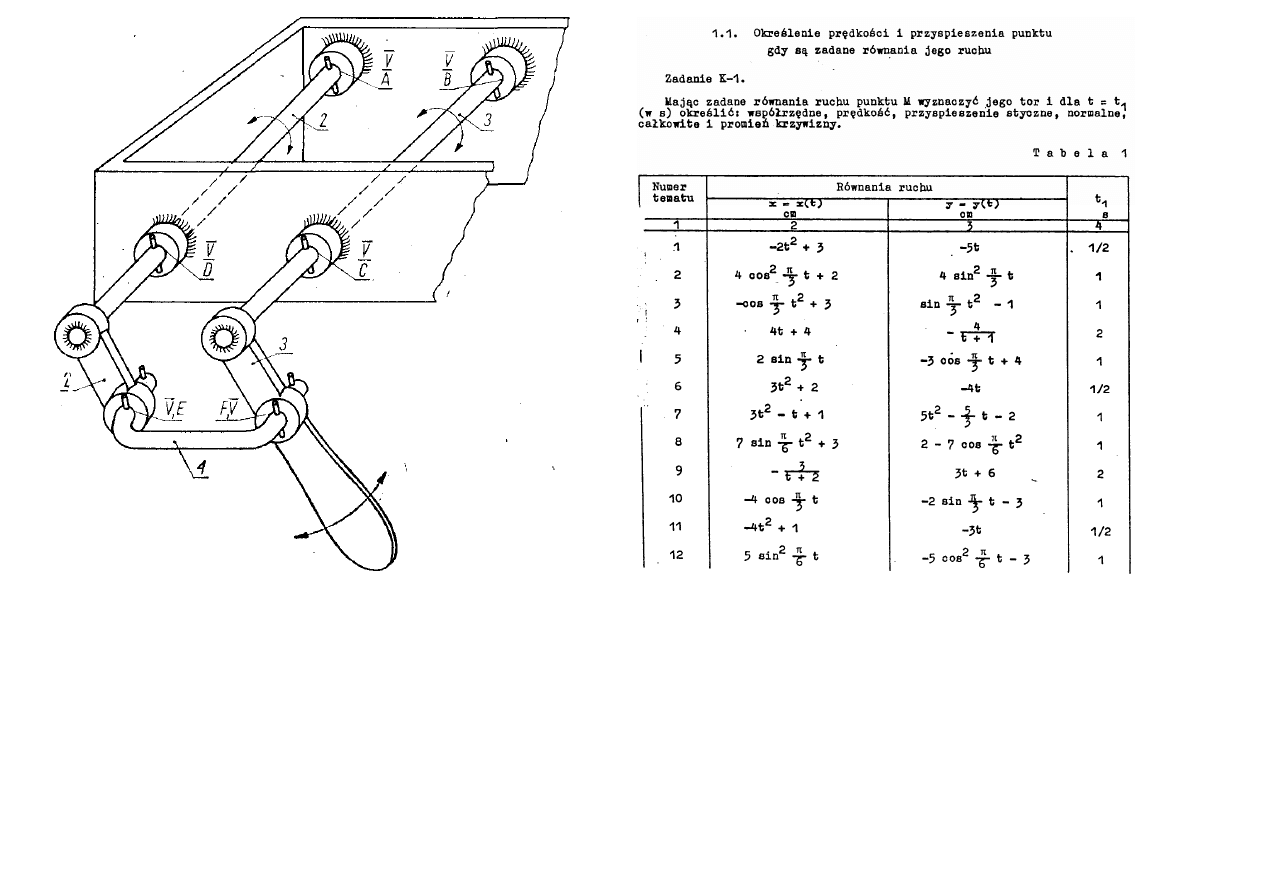
Rys. Przykład niewłaściwej konstrukcji z biernymi więzami

Kinematyka mechanizmów

Kinematyka (od greckiego słowa „kinema" — ruch) jest działem mechaniki, który zajmuje się badaniem
ruchu mechanizmów w oderwaniu od przyczyn (sił), które ten ruch powodują. Uzasadnia to stosowaną
często zamiennie ze słowem kinematyka nazwę geometria ruchu.

W kinematyce występują tylko dwie jednostki: długości (przemieszczenia) i czasu. Dzieli się ona na

dwa podstawowe działy: l) analiza i 2) synteza. Analiza dotyczy badania ruchu istniejących mechanizmów.
Synteza — projektowania mechanizmów wykonujących określony ruch.

Metody stosowane w kinematyce można podzielić na trzy grupy:

— metody wykreślne,

— metody analityczne,

— metody numeryczne.