MATLAB

Charakterystyka środowiska

Mathworks Inc.

www.mathworks.com

.

Podstawowe właściwości:

• możliwość pracy w trybie interakcyjnym

• możliwość pracy w trybie wsadowym (interpretacja

skryptów tzw. M – plików) oraz realizacja
skompilowanych plików typu MEX (automatyzacja
procesu przetwarzania dużej ilości danych)

• możliwość wywoływania programów napisanych w

innych językach np. C++, Fortran

• możliwość korzystania z możliwości obliczeniowych

Matlaba z poziomu innych programów napisanych w
C++, Fortranie

• możliwość zmiany platformy sprzętowej (łatwe

przenoszenie m- skryptów na inne platformy)

• otwarta architektura pakietu – łatwość wzbogacania

bibliotek własnymi (pozyskanymi) funkcjami (inaczej niż
np. STATISTICA)

• możliwość budowy własnego interfejsu (dostępne

elementy interfejsu użytkownika takie jak: przyciski,
listy, menu itd… (możliwość budowy profesjonalnie
wyglądającej aplikacji)

• bardzo rozbudowane możliwości graficznej prezentacji

wyników z możliwością eksportu (zapisu) rysunku w
wielu formatach

• grafika obiektowo zorientowana

• łatwość importu i eksportu danych z (do) plików

binarnych i tekstowych

• możliwość bezpośredniej współpracy ze sprzętem

pomiarowym (także procesory sygnałowe)

• zaawansowana algebra macierzy

• możliwość pracy z liczbami zespolonymi

• setki gotowych funkcji

• łatwość kodowania operacji (przejrzysty i prosty język

wysokiego poziomu)

• bardzo bogata biblioteka modułów:

- sieci neuronowe,
- logika rozmyta,
- algebra symboliczna
- optymalizacja
- identyfikacja systemów
- przetwarzanie cyfrowe sygnałów
- rozwiązywanie równań różniczkowych
cząstkowych
- pakiet do modelowania analogowego

(SIMULINK)

- transformata falkowa
- eksperymentalna analiza modalna (identyfikacja

postaci drgań i częstotliwości)

• możliwość pracy z multimediami (np. obsługa karty

dźwiękowej pozwala na wykorzystanie tego urządzenia
jako „przetwornika A/C”)

• możliwość tworzenia animacji

• środowisko zintegrowane (Edytor/Debugger)

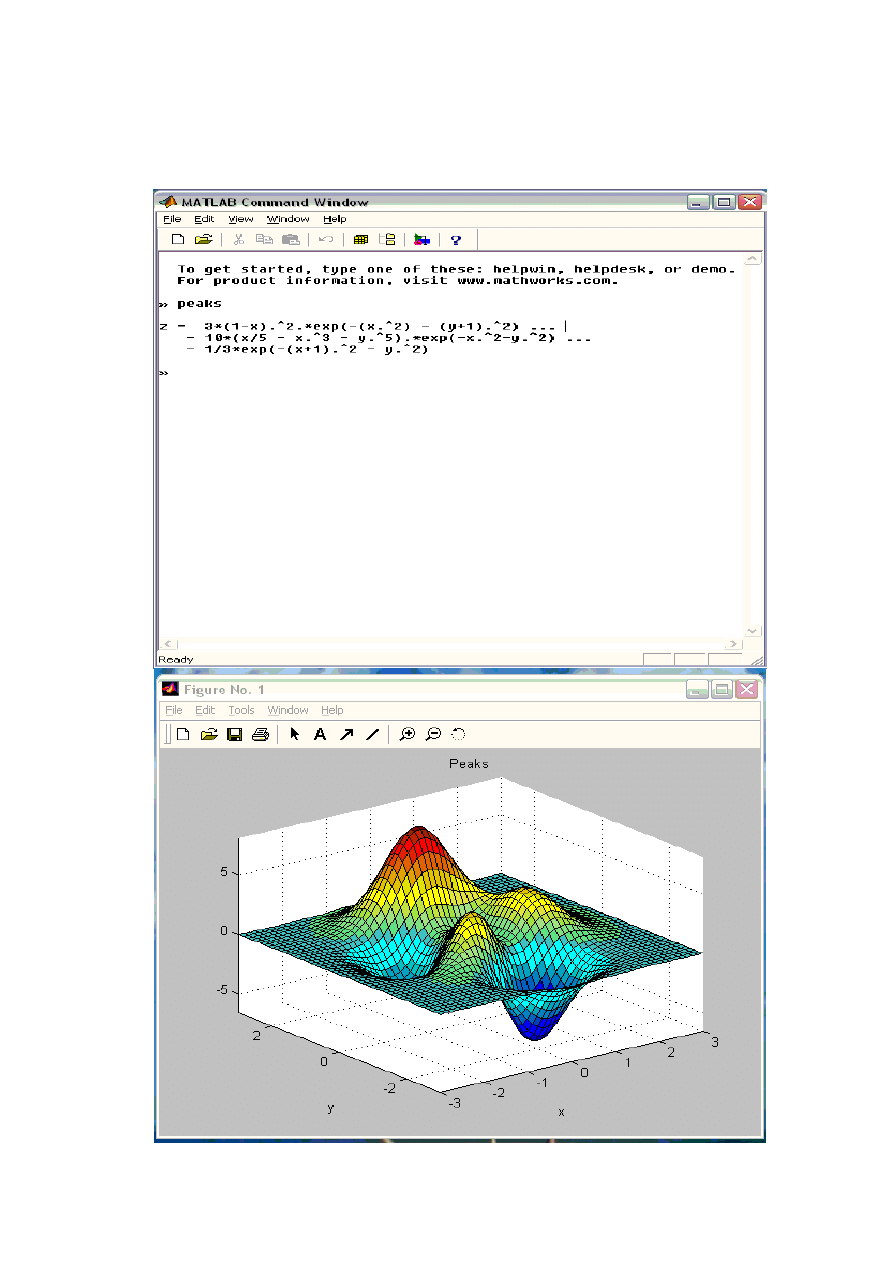
Praca z MATLABEM

Ver.4, 5

ver 6.

*Praca interaktywna poprzez bezpośrednie podawanie
komend
* Uruchamianie m- skryptów poprzez podanie nazwy
skryptu (lub uruchomienie z menu) z zapisanymi
poleceniami

Praca z debuggerem (ver 5 i 6)

*breakpoints
*step
*step in
*step out

Błędy składni (syntaktyczne) są wyłapywane tuż przed
uruchomieniem skryptu. Matlab podaje dokładną
informację o pochodzeniu błędu.
W trakcie działania programu wyłapywane są również
błędy semantyczne np. niezgodność wymiarów tablic itp…

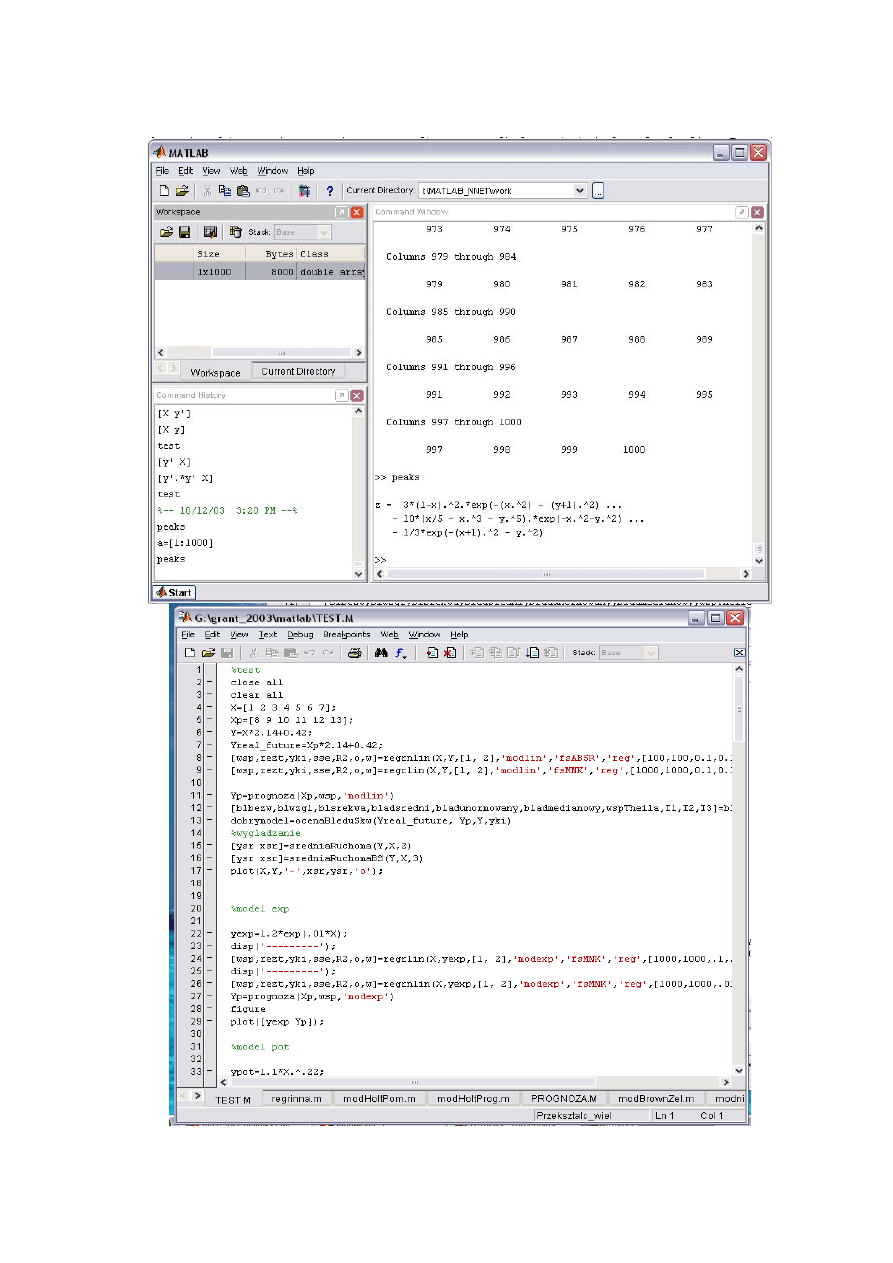
Foldery robocze

Standardowo pliki użytkownika obsługiwane są w folderze
„work” (ver 5, 6) każdy inny folder użytkownika należy
wskazać wybierając opcję FILE/SET PATH
W ver 4. odpowiednich zmian dokonuje się w tekstowym
pliku konfiguracyjnym matlabrc.m

Podstawowe działania

Przypisania

>> zmienna = wyrażenie

>> a=2*3.14

odpowiedź:
a= 6.28

>>zmienna = wyrażenie;

>> b = a*a;

odpowiedź: brak
b ma wartość 39.4384

>> wyrażenie


>> b-10

odpowiedź:
ans = 29.4384

Wywołanie funkcji

zmienna = nazwa funkcji (parametry)

a = fft (x);
[a b] = licz (1 , 6);

Umieszczanie komentarzy

% komentarz do końca linii

r=1.2;
a = 3.14*r*r; %a zawiera pole koła
% b = 2*3.14 *r – to się nie wykona

Wprowadzanie danych (1)

Wektor = [1 2 3 4 5 6 7 8];

Macierz = [1 2 3; 4 5 6; 7 8 9]
%wiersze oddziela średnik

odpowiedź:
Macierz = 1 2 3
4 5 6
7 8 9

Tablicowanie danych

Min:krok:max
Min:max

np.
Wektor = 1:1:8;
Wektor = 1:8;
Macierz = [1:3; 4:6; 7:9];

InnyWektor=0:0.1:5;

Łączenie macierzy

A=[1:3;4:6]

A =

1 2 3
4 5 6

>> B=[7:9;10:12]

B =

7 8 9
10 11 12

>> C=[A B]

C =

1 2 3 7 8 9
4 5 6 10 11 12

>> C=[A; B]

C =

1 2 3
4 5 6
7 8 9
10 11 12

Zapisywanie łańcuchów tekstowych

Zmienna = ‘treść’;

tekst = ‘Matlab jest OK’;

Dostęp do elementów macierzy

zmienna = zmienna(index1, index2)
zmienna(index1, index2)


A = [1 2 3;
4 5 6;
7 8 9];

b=A(1,2)

odpowiedź:
b=2

A(3,2)

odpowiedź:
ans = 8

operator zakresu „:”

A = [1 2 3;
4 5 6;
7 8 9];
B= A(:,1)

odpowiedź:
B =

1
4
7


B=A(1:2,:)
odpowiedź:
B =
1 2 3
4 5 6

B=A(1:2, 2:3)
odpowiedź:
B =
2 3
5 6

A(:,1)= [ 7 ;7; 7]

odpowiedź:

A =

7 2 3
7 5 6
7 8 9


Wektor= 1:10;
InnyWektor=Wektor(1:2:10)

odpowiedź:

InnyWektor =

1 3 5 7 9

Operatory rozmiaru

[wierszy, kolumn] =size(zmienna)
size(zmienna)

size(Wektor)

odpowiedź
ans = 1 10

[w k]=size(A)

w =

3


k =

3

dlugosc =length (zmienna)
length(zmienna)


C=[1:10;2:11];

Dl=length (C)

Dl = 10

Znaki i operatory specjalne – podsumowanie

=

przypisanie

A=B

[ ]

wyszczególnienie elementów podczas tworzenia

macierzy, wektorów

A=[ 1:5:100];

( ) odwołanie do elementów tablicy, ustalanie
kolejności operacji, przekazywanie parametrów
do funkcji

A=B(1,2)

D=A*(B+C);

E= sin(2*3.14+0.1);

. znak kropki dziesiętnej (bez względu na ustawienia
w Windows)

pi=3.14

… kontynuacja polecenia w następnej linii

A= zmienna1-zmienna2+zmienna3 * …
zmienna4;

, separator indeksów, argumentów wywołań funkcji

A=B(1 , 1:3)
A=[1,2,3]; % zamiast A=[1 2 3]


E= licz(1,alfa);

; koniec wiersza macierzy, blokada odpowiedzi
Matlaba

A=[1 2; 0 4;0 1];
Brak odpowiedzi

A=[1 2; 0 4; 0 1]
odpowiedź:
A= 1 2
0 4
0 1

% komentarz

: operator zakresu elementów, tablicowanie wartości

A= B(1:3)

A=1:2:6;

‘ ‘ zapis łańcuchów

‘To jest ciąg znaków – łańcuch’

Operatory arytmetyczne

+ dodawanie

C=A+B +3.0;

- odejmowanie

C= A-B

* mnożenie macierzy (zgodność ilości kolumn i wierszy),
mnożenie macierzy i stałej

C=A*B
C=4*A;

.* mnożenie elementów wektora (macierzy)

A=[1 2];
B=[3 4];

C=A.*B

C=[1*3 2*4]= [3 8]

^ Podnoszenie do potęgi (macierzowe)

C=A^2;

.^ Podnoszenie do potęgi tablicowe

C=[1 2].^2
C=[1 4]

/ dzielenie macierzowe, lub przez stałą (\ dzielenie
lewostronne)

A/B ( A*inv(B))

A\B ( inv(A)*B)

./ dzielenie tablicowe

A./B - każdy element A przez odpowiadający mu
element B

A.\B (B./A)

‘ transpozycja macierzy (przekształcenie wektora)

A=[1 2
3 4]
B=A’

B= 1 3
2 4

W=[1 2 3 4];

W’
ans= 1
2
3
4

Operatory logiczne

== operator równości

a=3.14;
b=pi;

a= =b - zwraca 1 (prawda) jeżeli a jest dokładnie

równe b inaczej zwraca 0 (fałsz)

<, > ,>=, <=, ~= operatory relacji

a<b % 1 prawda (mniejsze)
a>b % 0 fałsz (większe)
a<=b %1 prawda (mniejsze równe)
a>=b % 0 fałsz (większe równe)
a~=b % 1 prawda (różne)

& operator logiczny “i”

wyr1 & wyr2 &….


wyr1 P F P F
wyr2 P P F F
wyr1 & wyr2 P F F F

a<b & b>3 % 1 prawda

| operator logiczny „lub”

wyr1 | wyr2

wyr1 P F P F
wyr2 P P F F
wyr1 | wyr2 P P P F

a <b | a<0 % 1 prawda

~ operator negacji

~wyr

wyr P F
~wyr F P

~(a>b) % 1 prawda


xor - operator różnicy symetrycznej

xor (wyr1,wyr2)

wyr1 P F P F
wyr2 P P F F
xor(wyr1,wyr2) F P P F

Operatory logiczne w zastosowaniu do macierzy

A=[1 2 3;
4 5 6;
7 8 9]
» B=A>3
B =
0 0 0
1 1 1
1 1 1

C=A(B)
C =
4
7
5
8
6
9

W=[1 2 3 4 5 6 7];
» D=W>3 & W<6
D =
0 0 0 1 1 0 0

» W(D)

ans =

4 5

Funkcje logiczne

all – wszystkie elementy wektora są niezerowe

W=[ 1 2 3];
all (W)

ans = 1

A=[ 1 2 3;
4 5 0;
6 7 8];

all (A)
ans = 1 1 0

any – jakikolwiek element wektora jest niezerowy

any(A)

ans= 1 1 1

isinf – argument jest +Inf lub – Inf

isinf(1/0)
Warning: Divide by zero
ans = 1

isempty – argument jest macierzą pustą

a =

[]

» isempty(a)

ans =

1
strcmp – porównywanie łańcuchów

la=’aab’;

strcmp(la,'aac')

ans = 0

%odwołania do elementów łańcucha jak do elementów
%tablicy

o=’aac’;
strcmp(la(1:2),o(1:2))
ans =1

isreal – wszystkie elementy argumentu są rzeczywiste

a=[1i+2 2i+1 ;0i+3 0i+4]

a =

2.0000 + 1.0000i 1.0000 + 2.0000i
3.0000 4.0000

» isreal(a)

ans = 0

Zmienne specjalne i stałe

ans – zmienna robocza
i,j - jednostki urojone

1

−

lzesp=2i+3;

pi - 3.14159265358979…

realmax – największa dostępna liczba rzeczywista
1.797693134862316e+308

realmin – najmniejsza dostępna liczba rzeczywista
2.225073858507202e-308

Niektóre polecenia środowiska

who - informacja o wszystkich zmiennych

>> who

Your variables are:

a b

whos – zaawansowana informacja o zmiennych

>> whos
Name Size Bytes Class

a 2x3 48 double array
b 2x3 48 double array

clear – likwidowanie definicji zmiennych (zwalnianie
pamięci)

clear all – wszystkie zmienne
clear zmienna – konkretna zmienna


help wyrażenie – uzyskiwanie informacji o funkcjach
(wyrażeniach)
np. help fft
help isinf

save – zapis danych do pliku

save ‘dane.txt’ A –ascii
%zapis macierzy A do pliku „dane.txt” w trybie tekstowym

save ‘dane.dta’ A
% zapis w trybie binarnym

save dane A
%zapis macierzy A jako plik „dane.mat”
% możliwość odczytu przez program

save dane
%zapis wszystkich danych z przestrzeni roboczej do pliku
dane.mat

Wprowadzanie danych(2)

load – odczyt danych pliku
save ‘dane.txt’ A –ascii
……..
load ‘dane.txt’
srednia=dane/length(dane);

save dane A
…..
load dane

save dane
….
load dane

quit, exit – zakończenie pracy z MATLABEM
format – zmiana formatu wyświetlania liczb

format short (5 cyfr)
pi
ans = 3.1416


pi*1000
ans =3.1416e+003

format long (15 cyfr)
format rat - prezentacja w postaci ułamka

format short
B =
1.1000 2.1000 3.1000
4.1000 5.1000 0.1000
6.1000 7.1000 8.1000
format rat
B =

11/10 21/10 31/10
41/10 51/10 1/10
61/10 71/10 81/10

Priorytety operatorów

* potęgowanie macierzowe i tablicowe (^, .^), transpozycja

(‘)
* jednoargumentowa zmiana znaku (-)

-a

* mnożenie, dzielenie
* dodawanie, odejmowanie

a=[1 2 3]

a =

1 2 3

» b=[3 4 5]

b =

3 4 5

» a+b.^2

ans =

10 18 28

Wprowadzanie danych (3)

zeros(k,w) - wypełnianie macierzy zerami

A=zeros(1,5)

A = 0 0 0 0 0

B=zeros(size(A)); % zagnieżdżanie poleceń

ones(w,k) - wypełnianie jedynkami

rand(w,k) – losowanie zmiennych o rozkładzie jednorodnym
(funkcja gęstości prawdopodobieństwa prostokątna). Zakres
liczb od 0 do 1.

randn(w,k) - losowanie zmiennych o rozkładzie normalnym.
Wariancja 1, średnia 0.

Podstawowe funkcje

max – szukanie wartości maksymalnej
[ wartość index] =max(tablica)

t=[1 2 10 4 5 0 ];
» [w i]=max(t)

w = 10
i = 3

w=max(t)
w=10

[ wartość index] =max(macierz)

M=[1 2 3; 4 5 6;0 9 2]
M =

1 2 3
4 5 6
0 9 2

» [w i]=max(M)

w =

4 9 6

i =

2 3 2

min – analogicznie do max

sum- wyznaczanie sumy elementów

zmienna=sum (wektor)

s=sum(t)
s=22
nowywektor=sum (macierz)

sum(M)

ans = 5 16 11

mean – wyznaczenie wartości średniej


format rat
mean(M)

ans =

5/3 16/3 11/3

abs – wyznaczanie modułu

M=
0 + 3.1416i 0.6931 + 3.1416i 1.0986 + 3.1416i
1.3863 + 3.1416i 1.6094 + 3.1416i 1.7918 + 3.1416i
-Inf 2.1972 + 3.1416i 0.6931 + 3.1416i

abs (M)

ans =

3.1416 3.2172 3.3281
3.4339 3.5299 3.6166
Inf 3.8337 3.2172

M =

-1 -2 -3
-4 -5 -6
0 -9 -2

abs(M)

ans =

1 2 3
4 5 6
0 9 2

sign – funkcja znaku

sign(M)

ans =

-1 -1 -1
-1 -1 -1
0 -1 -1

sqrt – pierwiastek kwadratowy

k=sqrt(-1)
k =

0 + 1.0000i

std – odchylenie standardowe
median - mediana

M =

-1 -2 -3
-4 -5 -6
0 -9 -2


» median(M)

ans =

-1 -5 -3

round – zaokrąglenie do najbliżej liczby całkowitej

M =

0.2500 0.5000 0.7500
1.0000 1.2500 1.5000
0 2.2500 0.5000

» round(M)

ans =

0 1 1
1 1 2
0 2 1

floor - zaokrąglenie w dół w kierunku –inf

M =

-0.5000 0.5000 0.7500
1.0000 1.2500 1.5000
0 2.2500 0.5000

» floor(M)

ans =
-1 0 0
1 1 1
0 2 0

fix – zaokrąglenie w dół w kierunku zera
fix(M)

ans =

0 0 0
1 1 1
0 2 0

ceil - zaokrąglenie w górę w kierunku + Inf
ceil(M)

ans =

0 1 1
1 2 2
0 3 1

end – ostatni element macierzy

A=[1 2 3; 4 5 6; 7 8 9]

A =

1 2 3
4 5 6
7 8 9

>> A(1,end)

ans =

3

>> A(:,end)

ans =

3
6
9

[ ] – macierz pusta

%Usunięcie elementów macierzy

A=[1 2 3; 4 5 6; 7 8 9]

A =

1 2 3
4 5 6
7 8 9

A(:,1)=[]

A =

2 3
5 6
8 9

[ ] – wybór elementów macierzy wymienionych jako
elementy wektora

A=[1 2 3; 4 5 6; 7 8 9]
B=A([1 3],:)

B =

1 2 3
7 8 9

eye – macierz jednostkowa

A=eye(5)

ans =

1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

eye(2,4)

ans =

1 0 0 0
0 1 0 0

Tworzenie macierzy przez zdefiniowanie jej elementu
B(2,3)=3

B =

0 0 0
0 0 3

diag – elementy na przekątnej macierzy

A=[1 2 4; 5 6 7; 8 9 10]

A =

1 2 4
5 6 7
8 9 10

>> diag(A)

ans =

1
6
10


det – wyznacznik macierzy

wyzn=det(A)


inv – macierz odwrotna

A=rand(3,3);
I=inv(A)*A;

fliplr – zamiana kolejności elementów (elementów w
wierszach)

A =

1 2 4
5 6 7
8 9 10

>> fliplr(A)

ans =

4 2 1
7 6 5
10 9 8

flipud – analogicznie w kolumnach

findstr – poszukiwanie wystąpienia znaków w określonym
łańcuchu

s =’Matlab jest matematycznym laboratorium ’;
findstr(s,'a')
ans=
2 5 14 18 28 32
s(ans)

ans =

aaaaaa

findstr(s,'mat')

ans =

13 17

s(ans)

ans =

mm

findstr(s,'k')

ans =

[]
disp - wyświetlanie łańcucha na ekranie

disp(‘Ten tekst będzie wyświetlony na ekranie’);


‘Ten tekst będzie wyświetlony na ekranie’
ans =
‘Ten tekst będzie wyświetlony na ekranie’

num2str – zamiana wartości liczbowej na łańcuch
(str2num – funkcja odwrotna)
tekst=num2str(pi);
disp([‘Wartość liczby pi wynosi :’ tekst]);
Wartość liczby pi wynosi :3.1416

input – wprowadzanie danych z klawiatury (zastosowanie
w m.skrypcie)
zmienna=input(tekst);
zmienna_tekstowa = input(tekst,’s’);

r = input('podaj a ')
podaj a 2

r =

2

>> r*r

ans =

4

r =input ('podaj a ','s')
podaj a 3
r =
3
>> str2num(r).^2
ans =
9

pause – wstrzymanie programu
pause(n) – na n- sekund
pause – aż do naciśnięcia klawisza

roots – oblicza pierwiastki wielomianu

%W=x+2 - wektor współczynników wielomianu [1 2]

roots([1 2])

ans =

-2

%W=3x

2

+8x+2

x=roots([3 8 2])

x =

-2.3874
-0.2792

>> 3*x(1)^2+8*x(1)+2

ans =

0

x=roots([3 3 2])

x =

-0.5000 + 0.6455i
-0.5000 - 0.6455i

poly – wyznacza współczynniki wielomainu na podstawie
pierwiastków

wsp=[2 3 4]

wsp =

2 3 4

>> r=roots(wsp)

r =

-0.7500 + 1.1990i
-0.7500 - 1.1990i

>> poly(r)

ans =

1.0000 1.5000 2.0000

>> wsp/2

ans =

1.0000 1.5000 2.0000

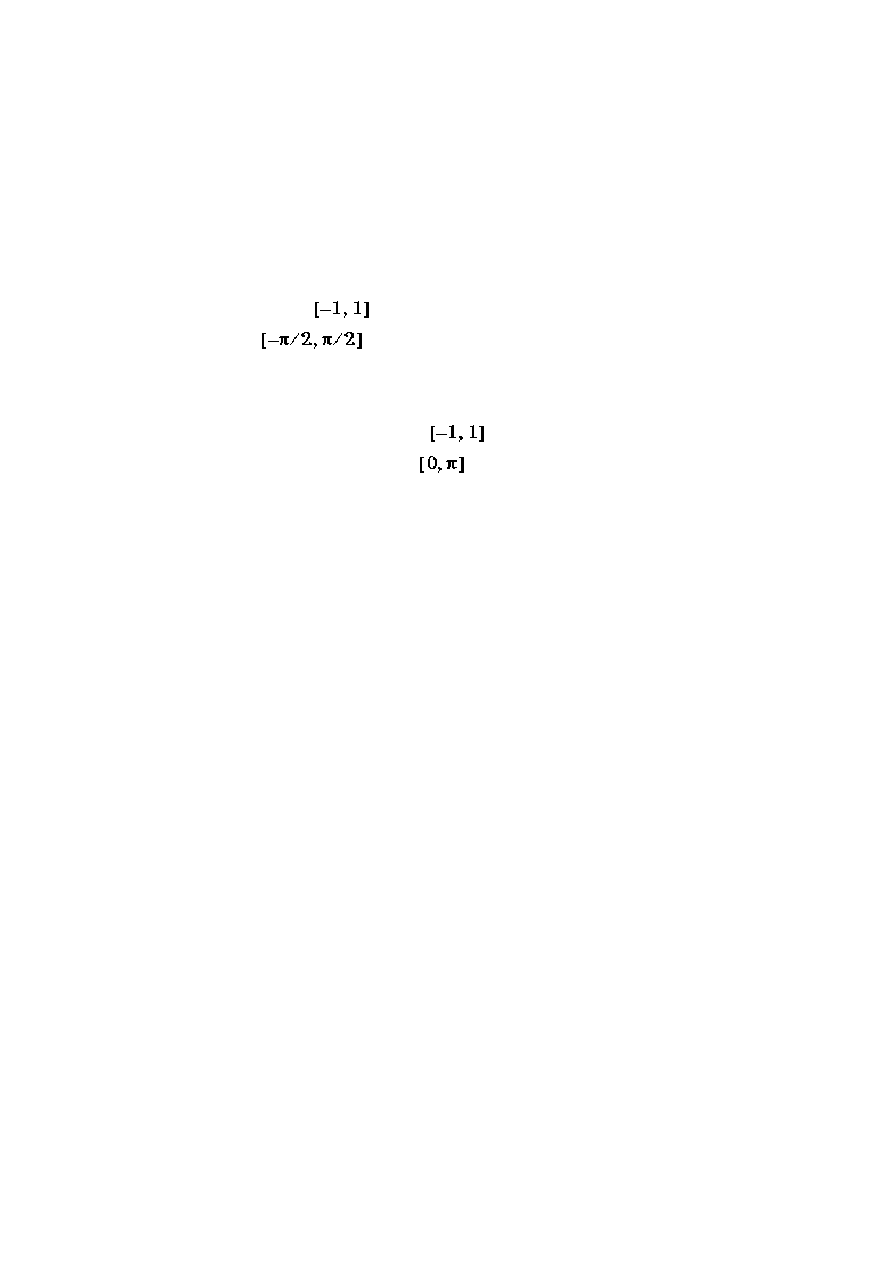
Ważniejsze funkcje matematyczne

sin(kąt) – sinus. Argument w radianach.
cos(kąt) – cosinus. Argument w radianach
asin(argument) – arcsine (funkcja odwrotna do sinusa).
Wartości rzeczywiste funkcja ma w zakresie
argumentów

.

Wynik podawany jest w radianach w

zakresie

. .

acos (argument)– arccosine (funkcja odwrotna do
cosinusa) . Wartości rzeczywiste funkcja ma w
zakresie argumentów

.

Wynik podawany jest w

radianach w zakresie

.

tan(x) –tangens
atan(x) – arcustangens - analogicznie

exp(x) - e

x

log(x) – logarytm naturalny z x
log2(x) – logarytm o podstawie 2 z x
log10(x) – logarytm dziesiętny z x

eig – wartości własne i wektory własne macierzy

d = eig(A) – zwraca wektor wartości własnych macierzy A

[V,D] = eig(A) wartości własne (D) i wektory własne (V)
macierzy A

.

Problem wartości własnych sprowadza się do wyznaczenia
nietrywialnych rozwiązań równania:
A*V = V*D.
fft(x) – transformata Fouriera (N potęga dwójki jak i nie)
ifft(x) – odwrotna transformata Fouriera

Struktury

Grupowanie danych

Nazwa_zmiennej.nazwa_pola

a.czas=1;
a.peak= 4.56;
a.rms= 3.24;


a =

czas: 1
peak: 4.5600
rms: 3.2400


a.czas+1

ans =

2

a(2).czas=20

a =

1x2 struct array with fields:
czas
peak
rms

» a(2)

ans =

czas: 20
peak: []
rms: []


a(1).czas+a(2).czas

ans =

30

Usuwanie pola

rmfield(zmienna, nazwa pola)
rmfield(tablica,nazwa pola)

a=rmfield(a,'peak')

a =

1x2 struct array with fields:
czas
rms

» a(1)

ans =

czas: 10
rms: 3.2400