1
OBLICZENIA STATYCZNE WI
ĘŹBY DACHOWEJ
1. Podstawa oblicze
ń
1.
PN-EN 1995-1-1:2010 Eurokod 5: Projektowanie konstrukcji drewnianych. Część 1-1:
Postanowienia ogólne. Reguły ogólne i reguły dotyczące budynków
2.
PN-EN 1990:2004 Eurokod. Podstawy projektowania konstrukcji
3.
PN-EN 1991-1-1:2004 Eurokod 1: Oddziaływania na konstrukcje. Część 1-1: Oddziaływania
ogólne. Ciężar objętościowy, ciężar własny, obciążenia użytkowe w budynkach
4.
PN-EN 1991-1-3:2005 Eurokod 1: Oddziaływania na konstrukcje. Część 1-3: Oddziaływania
ogólne – Obciążenie śniegiem
5.
PN-EN 1991-1-4:2008 Eurokod 1: Oddziaływania na konstrukcje. Część 1-4: Oddziaływania
ogólne. Oddziaływania wiatru.
6.
EN 338:2009 Drewno konstrukcyjne - Klasy wytrzymałości
2. Zestawienie obci
ążeń działających na konstrukcję dachową
3. OBLICZENIA WI
ĘŹBY DACHOWEJ wg [1]
3.1.
Dane do projektowania
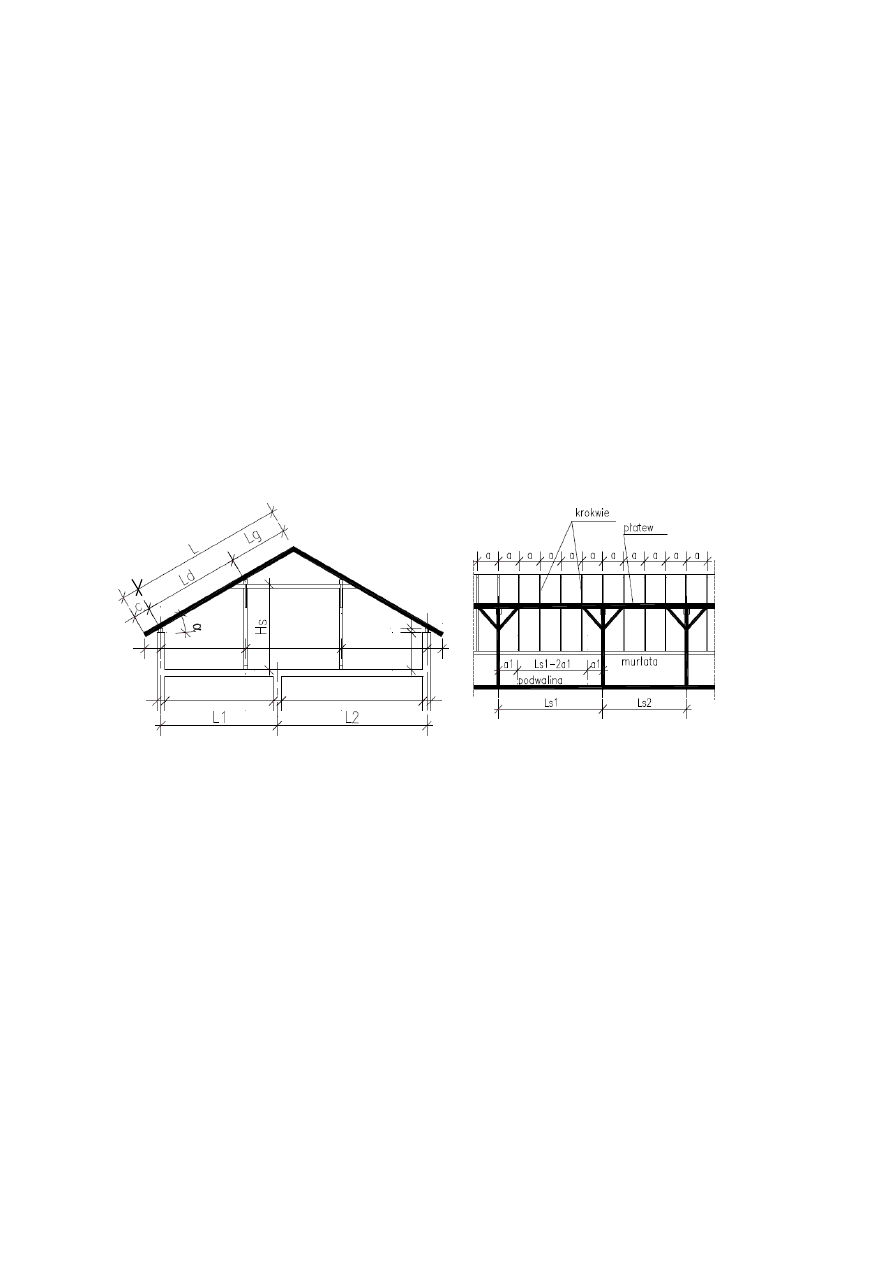
Przekrój poprzeczny wiązara płatwiowo-kleszczowego
Przekrój podłużny
α = ....., L=(L
1
+L
2
)/(2cos α) =
L
d
=2L/3 =
L
g
=L/3 =
a – rozstaw krokwi (0,8-1,2) m, a =
a
1
– wysięg mieczy (0,5-1,0) m, a
1
=
L
s1
i L
s2
- rozstaw słupków,
H
s
– wysokość słupka
Klasa użytkowania konstrukcji
−
Klasa trwania obciążeń:
pokrycie dachowe
−
obciążenie śniegiem
−
obciążenie wiatrem
−
Klasa drewna
−
............, dane materiałowe wg [6]
γ
M
– częściowy współczynnik bezpieczeństwa
γ
M
=
k
mod
– współczynnik modyfikacyjny (dla obciążenia
o najkrótszym czasie trwania)
k
mod
=
f
c,0,k
– wytrzymałość charakterystyczna na ściskanie
f
c,0,k
=
f
c,90,k
– wytrzymałość charakterystyczna na ściskanie
w poprzek włókien
f
c,90,k
=
2
f
m,k
– wytrzymałość charakterystyczna na zginanie
f
m,k
=
f
c,0,d
– wytrzymałość obliczeniowa na ściskanie
=
=
k
c
M
d
c
f
k
f
,
0
,
mod
.
0
.
γ
f
c,90,d
– wytrzymałość obliczeniowa na ściskanie
w poprzek włókien
=
=
k
c
M
d
c
f
k
f
,
90
,
mod
.
90
.
γ
f
m,d
– wytrzymałość obliczeniowa na zginanie
=
=
k
m
M
d
m
f
k
f
,
mod
.
γ
E
0,mean
– średni moduł sprężystości wzdłuż włókien
E
0,mean
=
E
0,05
– 5% kwantyl modułu sprężystości wzdłuż włókien
E
0,05
=
G
mean
– średni moduł odkształcenia postaciowego
G
mean
=
3.2. WYMIAROWANIE STATYCZNE KROKWI
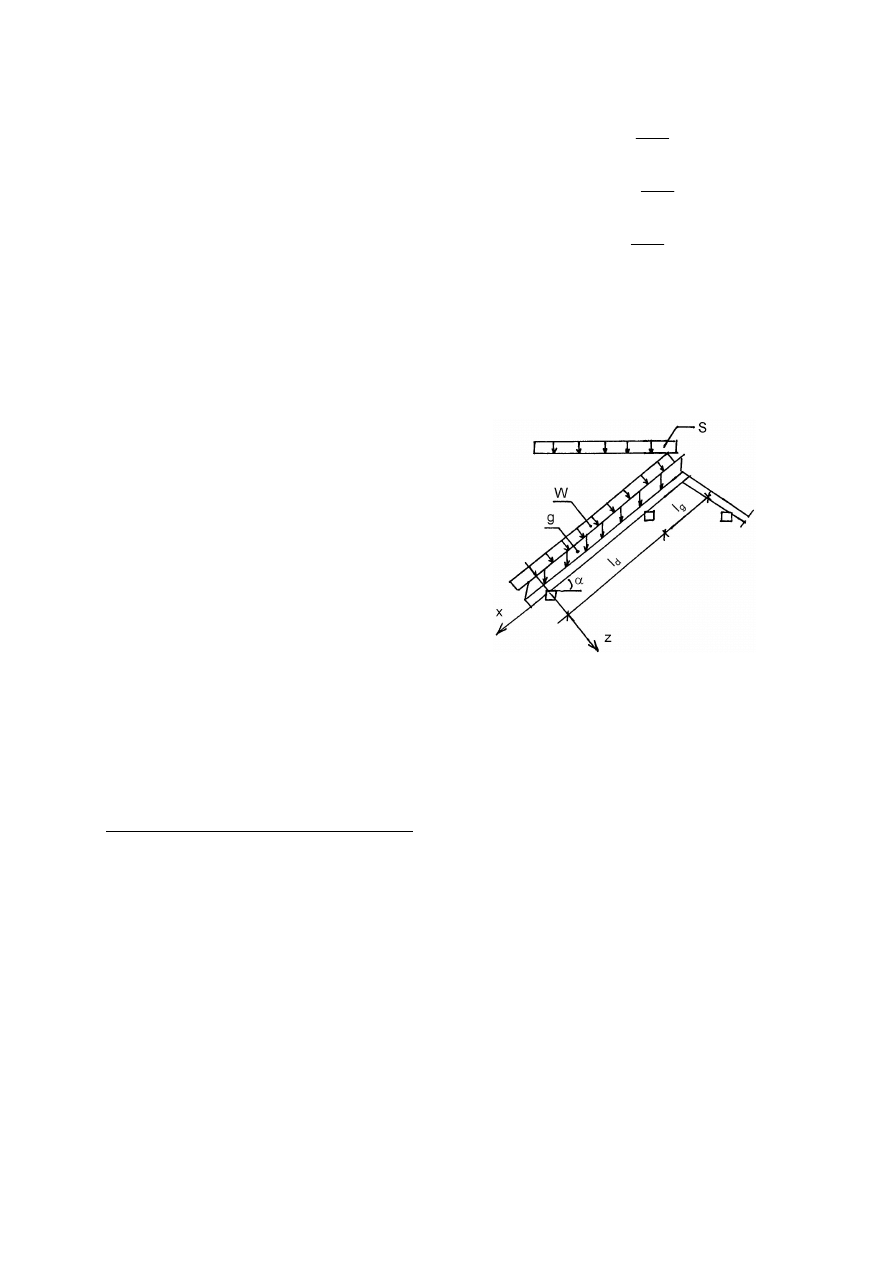
3.2.1. Schemat statyczny krokwi
Jako schemat statyczny krokwi przyjęto belkę
swobodnie podpartą (na murłacie i płatwi)
o rozpiętości obliczeniowej l
d
.
l
d
– długość dolnego odcinka krokwi, l
d
=
l
g
– długość górnego odcinka krokwi, l
g
=
a – maks. rozstaw osiowy krokwi,
a = …………. m
3.2.2. Podstawowe kombinacje obci
ążeń
Współczynniki wartości kombinacyjnej obciążenia zmiennego (od wiatru lub śniegu):
Ψ
01
=
,
Ψ
02
=
współczynnik redukcyjny
ξ=
Obciążenia obliczeniowe (na 1mb krokwi)
a) prostopadłe do połaci dachu
q`
z
= (
γ
G
· G
k
·cosα +
γ
Q1
· Ψ
01
·Q
k1
·cos
2
α + Ψ
02
·
γ
Q2
· Q
k2
)·a
………………………………………………………………..…=…………..kN/m
q``
z
= (
ξ
·
γ
G
· G
k
·cosα +
γ
Q1
· Q
k1
·cos
2
α + Ψ
02
·
γ
Q2
· Q
k2
)·a
………………………………………………………………..…=…………..kN/m
q
z
= …………………… kN/m
(przyjmujemy wartość mniej korzystną)
b) równoległe do połaci dachu
q`
x
= (
γ
G
· G
k
·sinα +
γ
Q1
· Ψ
01
· Q
k1
·cosα sinα)·a
………………………………………………………………..…=…………..kN/m
q``
x
= (
ξ
·
γ
G
· G
k
·sinα +
γ
Q1
· Q
k1
·cosα sinα)·a
………………………………………………………………..…=…………..kN/m
q
x
= …………………… kN/m
(przyjmujemy wartość mniej korzystną)
3
Obciążenia charakterystyczne (na 1mb krokwi)
a) prostopadłe do połaci dachu
q
zk(G)
= G
k
·cosα ·a =………………………..=………..kN/m
q
zk(S)
= Q
k1
·cos
2
α ·a =………………………=………..kN/m
q
zk(W)
= Q
k2
·a =…………………………….=………...kN/m
3.2.3. Sprawdzenie stanu granicznego no
śności - SGN
Siły wewnętrzne w krokwi (krokiew pracuje na zginanie z osiową siłą ściskającą)
=
⋅
=
8
2
d
z
y
l
q
M
………….………
=
=
⋅
=
2
d
x
x
l
q
N
……….…………..
=
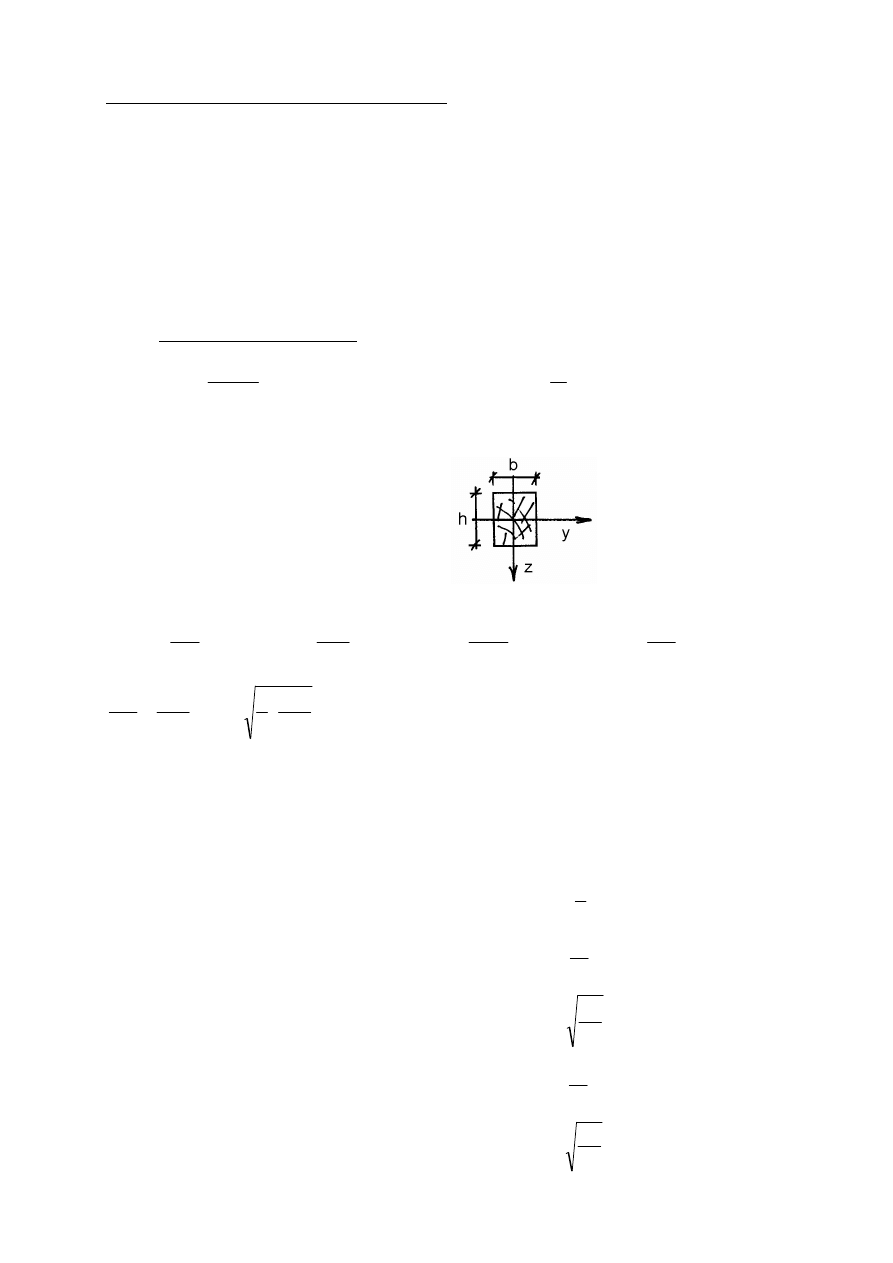
3.2.3.1. Wstępne określenie wymiarów przekroju (z uwzględnieniem tylko zginania)
b – szerokość przekroju
h – wysokość przekroju
h = 2÷3b, h ≤ 4b
Naprężenia w krokwi przy uwzględnieniu tylko zginania wynoszą:
d
m
y
y
d
m
y
y
d
y
m
f
M
W
f
W
M
,
,
,
,
≥
⇒
≤
=
σ
6
2
h
b
W
y
⋅
=
6
9
3
3
b
W
b
h
y
≅
⇒
≅
=
⋅
≥
⇒
≥
3
,
,
3
3
2
6
9
d
m
y
d
m
y
f
M
b
f
M
b
Przyjęto
b = ……………..,
h = ……………..
Charakterystyki geometryczne przekroju:
Pole przekroju poprzecznego krokwi
A
d
= b·h > 40cm
2
=
Wskaźnik wytrzymałości przekroju względem osi y
=
=
2
6
1
bh
W
y
Moment bezwładności przekroju względem osi y
=
=
3
12
1
bh
I
y
Promień bezwładności przekroju względem osi y
=
=
d
y
y
A
I
i
Moment bezwładności przekroju względem osi z
=
=
h
b
I
z
3
12
1
Promień bezwładności przekroju względem osi z
=
=
d
z
z
A
I
i
4
3.2.3.2. Sprawdzenie nośności krokwi z uwzględnieniem złożonego stanu naprężeń
Naprężenia ściskające:
=
=
d
x
d
c
A
N
,
0
,
σ
………………
=
Naprężenia zginające:
=
=
y
y
d
y
m
W
M
,
,
σ
………………
=
µ
y
– współczynnik długości wyboczeniowej
µ
y
= 1,0
l
c,y
– długość wyboczeniowa krokwi
l
c,y
= l
d
·µ
y
=
λ
y
– smukłość krokwi, λ
y
≤ 150 dla prętów
jednolitych
=
=
y
y
c
y
i
l
,
λ
λ
rel
,
y
– smukłość względna
=
=
05
,
0
,
0
,
,
E
f
k
c
y
y
rel
π
λ
λ
Jeżeli λ
rel
,
y
≤
0,3
Aby nośność krokwi nie została przekroczona, powinien być spełniony warunek:
1
,
,
,
2
,
0
,
,
0
,
≤
+
d
m
d
y
m
d
c
d
c
f
f
σ
σ
Jeżeli λ
rel
,
y
> 0,3
=
+
−
+
⋅
=
]
)
(
)
3
,
0
(
1
[
5
,
0
2
,
,
y
rel
y
rel
c
y
k
λ
λ
β
……………………………………..=
β
c
– współczynnik dotyczący prostoliniowości elementów,
określony dla drewna litego
=
−
+
=
2
,
2
,
)
(
)
(
1
y
rel
y
y
y
c
k
k
k
λ
………………………………..=
Aby nośność elementu nie została przekroczona, powinien być spełniony warunek:
1
,
,
,
,
,
,
,
,
0
,
≤
+
⋅
d
y
m
d
y
m
d
o
c
y
c
d
c
f
f
k
σ
σ
…………………….+…………………..≤1
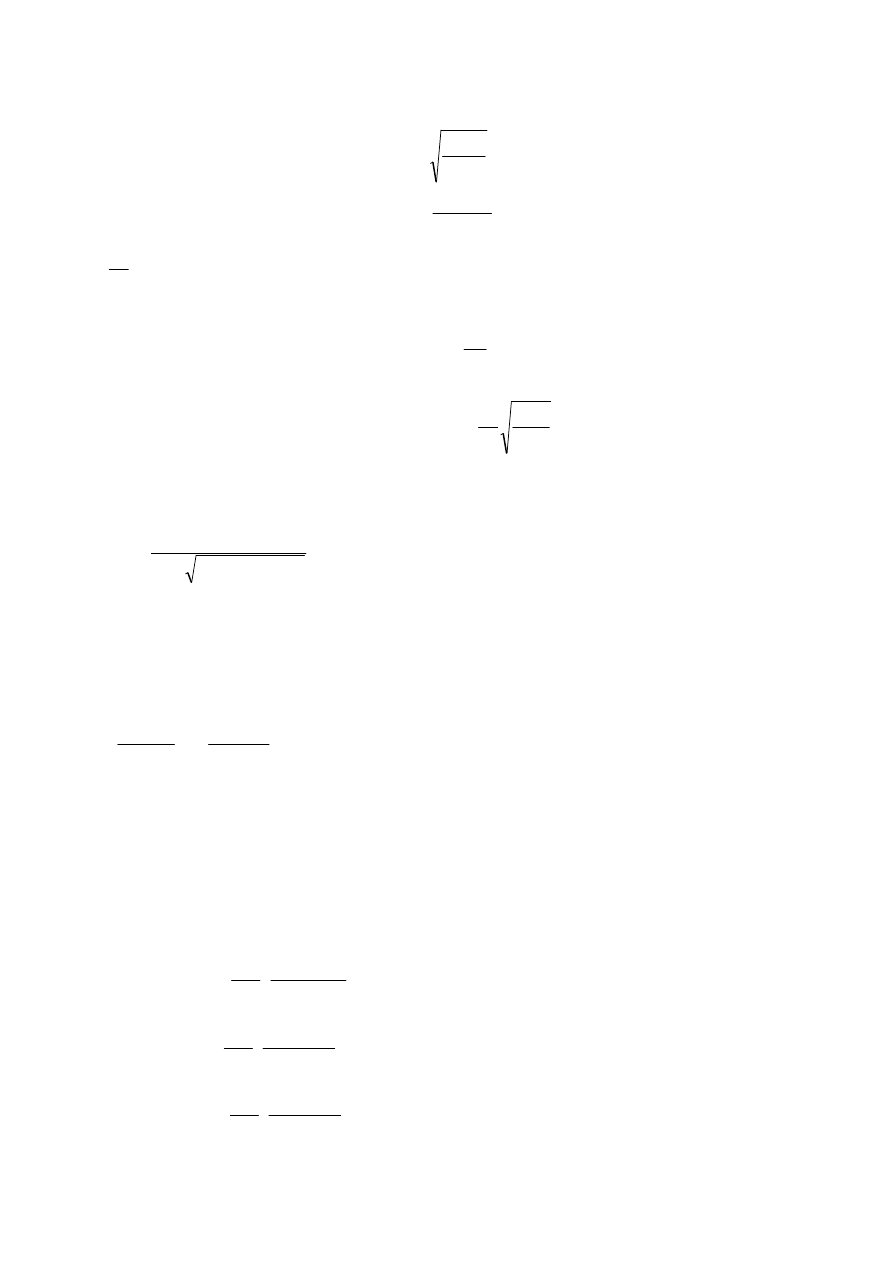
5
3.2.3.3. Sprawdzenie stateczności krokwi jako belki zginanej i ściskanej
Smukłość względna przy zginaniu
crit
m
k
m
m
rel
f
,
,
,
σ
λ
=
,
Naprężenie krytyczne przy zginaniu
05
,
0
2
,
78
,
0
E
l
h
b
ef
crit
m
⋅
⋅
=
σ
=
d
ef
l
l
l
ef
=
=
crit
m,
σ
Smukłość krokwi względem osi z
=
=
z
z
c
z
i
l
,
λ
Smukłość względna względem osi z
=
=
05
,
0
,
0
,
,
E
f
k
c
z
z
rel
π
λ
λ
=
+
−
+
⋅
=
]
)
(
)
3
,
0
(
1
[
5
,
0
2
,
,
z
rel
z
rel
c
z
k
λ
λ
β
=
−
+
=
2
,
2
,
)
(
)
(
1
z
rel
z
z
z
c
k
k
k
λ
Współczynnik stateczności giętej
k
crit =
Ze względu na stateczność naprężenia w krokwi powinny spełniać warunek:
1
,
0
,
,
,
0
,
2
,
,
≤
+
d
c
z
c
d
c
d
m
crit
d
m
f
k
f
k
σ
σ
……………………+………………….≤1
3.2.4. Sprawdzenie stanu granicznego użytkowalności
3.2.4.1. Ugięcia chwilowe
l
d
/h =
a)
jeżeli l
d
/h ≥ 20:
=
⋅
⋅
⋅
=
=
y
mean
d
G
zk
G
M
G
inst
I
E
l
q
u
u
,
0
4
)
(
)
(
)
(
384
5
…………………………………=
=
⋅
⋅
⋅
=
=
y
mean
d
S
zk
S
M
S
inst
I
E
l
q
u
u
,
0
4
)
(
)
(
)
(
384
5
………………………………….=
=
⋅
⋅
⋅
=
=
y
mean
d
W
zk
W
M
W
inst
I
E
l
q
u
u
,
0
4
)
(
)
(
)
(
384
5
………………………………….=
6
b)
jeżeli l
d
/h < 20
=
+
=
2
)
(
)
(
2
,
19
1
d
G
M
G
inst
l
h
u
u
………………………………….=
=
+
=
2
)
(
)
(
2
,
19
1
d
S
M
S
inst
l
h
u
u
…………………………………….=
=
+
=
2
)
(
)
(
2
,
19
1
d
W
M
W
inst
l
h
u
u
……………………………………=
3.2.4.2. Ugięcia końcowe
k
def
- współczynnik dla drewna i materiałów drewnopochodnych modyfikujący odkształcenie w
zależności od czasu trwania odkształcenia
k
def
=
Ψ
2,1
- współczynnik dla quasi-stałych wartości oddziaływań zmiennych
Ψ
0,2
– współczynnik dla wartości kombinacji oddziaływań zmiennych
u
fin,G
= u
inst,G
·(1+k
def
)=……………………………..=
u
fin,S
= u
inst,S
·(1+ Ψ
2,1
·k
def
)=…………………………=
u
fin,W
= u
inst,W
·( Ψ
0,2
+ Ψ
2,2
·k
def
)=…………………………=
u
fin
= u
fin,G
+ u
fin,S
+ u
fin,W=……………………………………….=
Ugięcie dopuszczalne wynosi:
=
=
200
,
d
fin
net
l
u
Aby stan graniczny użytkowania elementu nie został przekroczony, powinien być spełniony
warunek:
U
fin
= .................................... ≤ u
net,fin
= .....................................
7
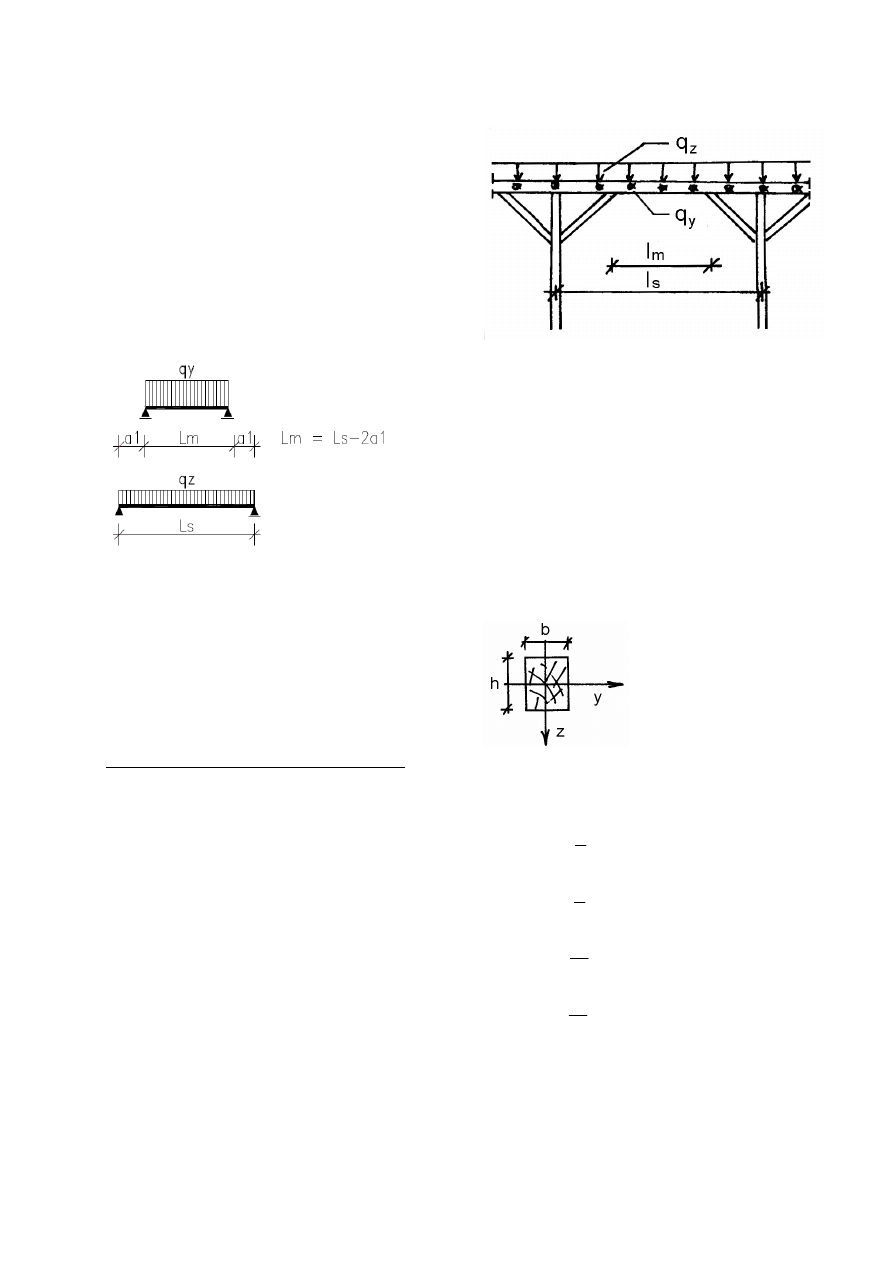
3.3. WYMIAROWANIE STATYCZNE PŁATWI
3.3.1. Schemat statyczny płatwi
Jako schemat statyczny płatwi przyjęto belkę
swobodnie podpartą, o rozpiętości obliczeniowej
w
kierunku
pionowym
l
m
i
rozpiętości
obliczeniowej w kierunku poziomym l
s
.
l
s
– rozpiętość płatwi między słupkami, l
s
=
l
m
– rozpiętość płatwi między mieczami, l
m
=
Założono wstępnie wymiary płatwi:
b – szerokość przekroju, b =
h – wysokość przekroju, h =
h ≤ 4b
Charakterystyki geometryczne przekroju:
Pole przekroju poprzecznego płatwi
A
d
= b·h =
Wskaźnik wytrzymałości przekroju względem osi y:
=
=
2
6
1
bh
W
y
Wskaźnik wytrzymałości przekroju względem osi z:
=
=
h
b
W
z
2
6
1
Moment bezwładności przekroju względem osi y:
=
=
3
12
1
bh
I
y
Moment bezwładności przekroju względem osi z:
=
=
h
b
I
z
3
12
1
G
k.płatwi
– ciężar własny 1mb płatwi
ρ
d
– ciężar objętościowy drewna
G
k.płatwi
= A
d·
ρ
d
=
8
3.3.2. Podstawowe kombinacje obciążeń
Obciążenia obliczeniowe (na 1mb płatwi)
a) pionowe
q`
z
= (l
g
+ ½ l
d
)(
γ
G
· G
k
+
γ
Q1
· Ψ
01
·Q
k1
·cosα + Ψ
02
·
γ
Q2
· Q
k2
·cosα) +
γ
G·
G
k.płatwi
…………………………………………………………………………=………..
kN/m
q``
z
= (l
g
+ ½ l
d
)(
ξ
·
γ
G
· G
k
+
γ
Q1
· Q
k1
·cosα + Ψ
02
·
γ
Q2
· Q
k2
·cosα) +
γ
G
·G
k.płatwi
…………………………………………………………………………=………..
kN/m
q
z
= …………………… kN/m
(przyjmujemy wartość mniej korzystną)
b) poziome
q
y
= (l
g
+ ½ l
d
) (Ψ
02
·
γ
Q2
· Q
k2
· sinα) =………………………………………=……….
kN/m
Obciążenia charakterystyczne (na 1mb płatwi)
a) pionowe
q
zk(G)
= (l
g
+ ½ l
d
) · G
k
+ G
płatwi
=……………..……………….=…........kN/m
q
zk(S)
= (l
g
+ ½ l
d
) · Q
k1
· cosα =………………………………..=……….kN/m
q
zk(W)
= (l
g
+ ½ l
d
) · Q
k2
· cosα =………………………………=………..kN/m
b) poziome
q
yk(G)
= 0,
q
yk(S)
= 0,
q
yk(W)
= (l
g
+ ½ l
d
)·Q
k2
·sinα = ....................................=…….... kN/m
3.3.3. Sprawdzenie stanu granicznego nośności
3.3.3.1. Siły wewnętrzne w płatwi
=
⋅
=
8
2
m
z
y
l
q
M
………….……….
=
=
⋅
=
8
2
s
y
z
l
q
M
……………………..
=
3.3.3.2. Sprawdzenie nośności płatwi z uwzględnieniem złożonego stanu naprężeń
Naprężenia zginające:
=
=
y
y
d
y
m
W
M
,
,
σ
………..….
=
=
=
z
z
d
z
m
W
M
,
,
σ
……….……..
=
Aby nośność elementu nie została przekroczona, powinny być spełnione warunki:
1
,
,
,
,
,
,
,
,
≤
+
d
z
m
d
z
m
d
y
m
d
y
m
m
f
f
k
σ
σ
,
1
,
,
,
,
,
,
,
,
≤
+
d
y
m
d
z
m
m
d
y
m
d
y
m
f
k
f
σ
σ
k
m
– współczynnik redystrybucji naprężeń zginających w przekroju
k
m
=
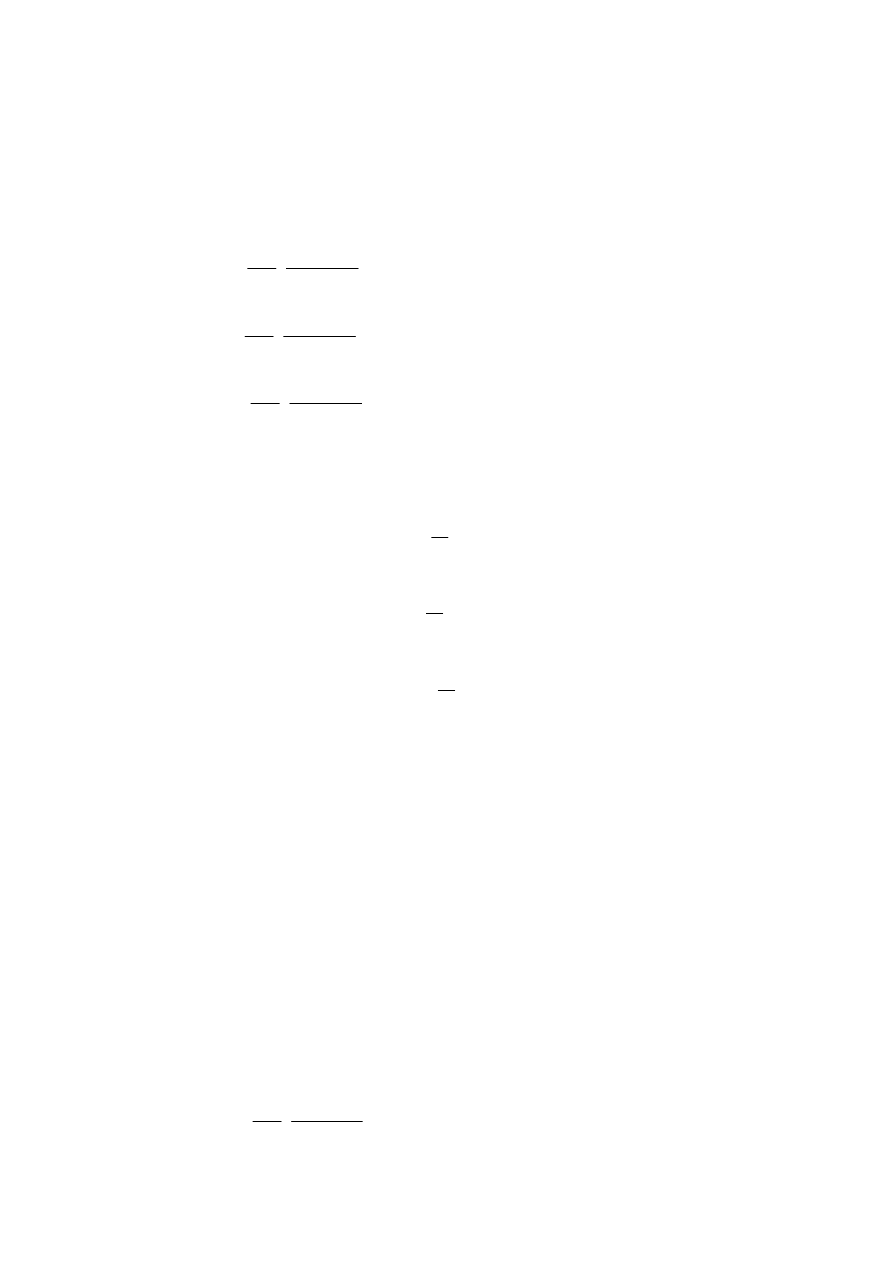
9
3.3.4. Sprawdzenie stanu granicznego użytkowalności - SGU
3.3.4.1. Ugięcia chwilowe pionowe (w kierunku z)
l
m
/h =
a)
jeżeli l
m
/h ≥ 20:
=
⋅
⋅
⋅
=
=
y
mean
m
G
zk
G
M
z
G
inst
z
I
E
l
q
u
u
,
0
4
)
(
)
(
_
,
_
384
5
……………………………………….=
=
⋅
⋅
⋅
=
=
y
mean
m
S
zk
S
M
z
S
inst
z
I
E
l
q
u
u
,
0
4
)
(
)
(
_
,
_
384
5
…………………………………………=
=
⋅
⋅
⋅
=
=
y
mean
m
W
zk
W
M
z
W
inst
z
I
E
l
q
u
u
,
0
4
)
(
)
(
_
,
_
384
5
………………………………………..=
b)
jeżeli l
m
/h < 20
=
+
=
+
=
2
)
(
_
)
(
_
)
(
_
,
_
2
,
19
1
m
G
M
z
G
T
z
G
M
z
G
inst
z
l
h
u
u
u
u
………………………………….=
=
+
=
+
=
2
)
(
_
)
(
_
)
(
_
,
_
2
,
19
1
m
S
M
z
S
T
z
S
M
z
S
inst
z
l
h
u
u
u
u
……………………………………=
=
+
=
+
=
2
)
(
_
)
(
_
)
(
_
,
_
2
,
19
1
m
W
M
z
W
T
z
W
M
z
W
inst
z
l
h
u
u
u
u
……………………………………=
3.3.4.2. Ugięcia końcowe pionowe (w kierunku z)
u
z,fin,G
= u
z,inst,G
·(1+k
def
)=………………………..=
u
z,fin,S
= u
z,inst,S
·(1+ Ψ
2,1
·k
def
)=………………………=
u
z,fin,W
= u
z,inst,W
·( Ψ
0,2
+ Ψ
2,2
·k
def
)=…………………….=
u
z,fin
= u
z,fin,G
+ u
z,fin,S
+ u
z,fin,W
=…………………………………….=
3.3.4.3. Ugięcia chwilowe poziome (w kierunku y)
l
s
/b =
a)
jeżeli l
s
/b ≥ 20:
0
)
(
_
,
_
=
=
G
M
y
G
inst
y
u
u
,
0
)
(
_
,
_
=
=
S
M
y
S
inst
y
u
u
=
⋅
⋅
⋅
=
=
z
mean
s
W
yk
W
M
y
W
inst
y
I
E
l
q
u
u
,
0
4
)
(
)
(
_
,
_
384
5
.............................................=
10
b)
jeżeli l
s
/b < 20
0
)
(
_
)
(
_
,
_
=
+
=
G
T
y
G
M
y
G
inst
y
u
u
u
0
)
(
_
)
(
_
,
_
=
+
=
S
T
y
S
M
y
S
inst
y
u
u
u
=
+
=
+
=
2
)
(
_
)
(
_
)
(
_
,
_
2
,
19
1
s
W
M
y
W
T
y
W
M
y
W
inst
y
l
b
u
u
u
u
.................................................=
3.3.4.4. Ugięcia końcowe poziome (w kierunku y)
u
y,fin,G
= 0,
u
y,fin,S
= 0,
u
y,fin,W
= u
z,inst,W
·( Ψ
0,2
+ Ψ
2,2
·k
def
) = ………………………….=
u
y,fin
= u
y,fin,G
+ u
y,fin,S
+ u
y,fin,W
= ………………………………..=
3.3.4.5. Ugięcia końcowe wypadkowe
=
+
=
2
,
2
,
)
(
)
(
fin
y
fin
z
fin
u
u
u
Ugięcie dopuszczalne wynosi:
=
=
200
,
,
m
z
fin
net
l
u
…….,
=
=
200
,
,
s
y
fin
net
l
u
……..,
.
..........
)
(
)
(
2
)
,
,
2
)
,
,
,
=
+
=
y
fin
net
z
fin
net
fin
net
u
u
u
Aby stan graniczny użytkowania płatwi nie został przekroczony, powinien być spełniony
warunek:
u
fin
= ........ ≤ u
net,fin
= ..........
3.4. WYMIAROWANIE STATYCZNE SŁUPKA
3.4.1. Schemat statyczny słupka
Wysokość słupka, h
s
=
Odległość między słupkami (z lewej strony słupka), l
sL
=
Odległość między słupkami (z prawej strony słupka), l
sP
=
l
s
= ½ (l
sL
+ l
sP
) =
Założono wstępnie wymiar słupka:
a = (a
min
= 10cm)
A
brutto
= a
2
= .........
(słupek o przekroju kwadratowym)
Wymiary miecza:
a
m
= b
m
= h
m
=
11
Charakterystyki geometryczne przekroju:
Szkic połączenia słupka z mieczami:
A
d
= A
netto
– jeśli symetryczne osłabienia naruszają krawędzie słupka
A
d
= A
brutto
– jeśli osłabienia nie naruszają krawędzi słupka i nie są większe niż 25% przekroju
brutto
A
d
= 4/3A
netto
– jeśli osłabienia nie naruszają krawędzi słupka i są większe niż 25% przekroju
brutto
Pole obliczeniowe przekroju poprzecznego słupka A
d
=
Moment bezwładności przekroju
=
=
4
12
1
a
I
Promień bezwładności przekroju
=
=
br
A
I
i
Ciężar własny słupka wraz z mieczami
G
słupka
= (a
2
·h
s
+ 2·a
m
·b
m
·h
m
)·ρ
d
·γ
G
[kN] =
3.4.2. Sprawdzenie stanu granicznego nośności
3.4.2.1. Siły wewnętrzne w słupku
N = q
z
l
s
+ G
słupka
= …………………………….=
q
z
– obciążenie pionowe na 1mb płatwi
3.4.2.2. Sprawdzenie nośności słupka
Naprężenia w słupku od ściskania (bez uwzględniania wyboczenia):
=
=
d
d
c
A
N
,
0
,
σ
………..=
µ
y
– współczynnik długości wyboczeniowej
µ
y
= 1,0
l
c,y
– długość wyboczeniowa słupka
l
c,y
= h
s
·µ
y
=
λ
y
– smukłość słupka, λ
y
≤ 150
=
=
y
y
c
y
i
l
,
λ
σ
c,crit
– naprężenia krytyczne przy ściskaniu
=
=
2
05
,
0
2
,
,
)
(
y
y
crit
c
E
λ
π
σ
λ
rel
,
y
– smukłość względna
=
=
05
,
0
,
0
,
,
E
f
k
c
y
y
rel
π
λ
λ
12
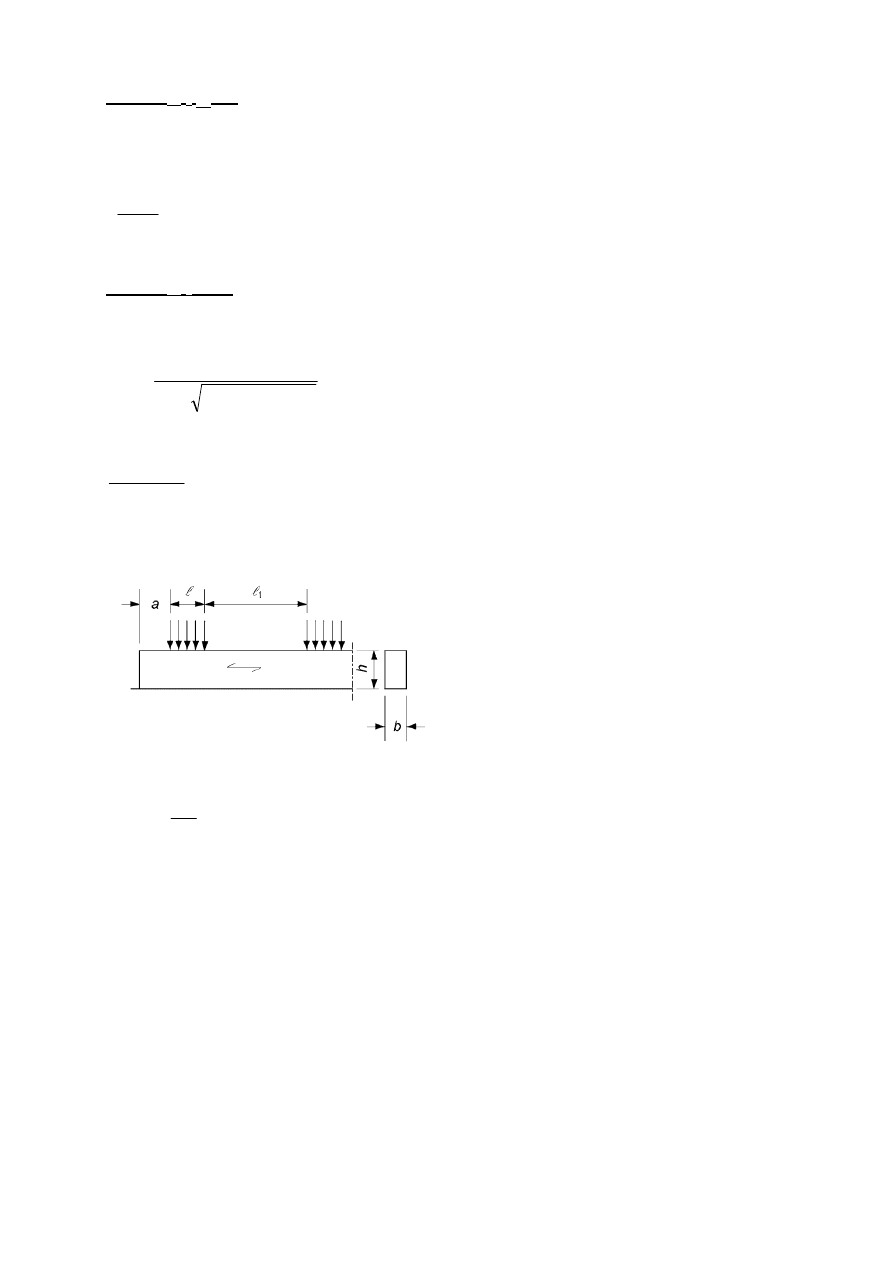
Jeżeli λ
rel
,
y
≤
0,3
Aby nośność słupka nie została przekroczona, powinien być spełniony warunek:
1
2
,
0
,
,
0
,
≤
d
c
d
c
f
σ
………………………≤1
Jeżeli λ
rel
,
y
> 0,3
=
+
−
+
⋅
=
]
)
(
)
3
,
0
(
1
[
5
,
0
2
,
,
y
rel
y
rel
c
y
k
λ
λ
β
β
c
= 0,2
=
−
+
=
2
,
2
,
)
(
)
(
1
y
rel
y
y
y
c
k
k
k
λ
…………………………………..=
Aby nośność słupka nie została przekroczona, powinien być spełniony warunek:
1
,
0
,
,
,
0
,
≤
⋅
d
c
y
c
d
c
f
k
σ
………………………….≤1
3.4.3. Sprawdzenie docisku słupka do podwaliny
Schemat docisku słupka do podwaliny
l - efektywna długość kontaktu wzdłuż włókien l
=
A
ef
- efektywne pole docisku
A
ef
=
Naprężenia dla docisku prostopadle do włókien:
=
=
ef
d
c
A
N
,
90
,
σ
………………..=
k
c,90
– współczynnik uwzględniający rozkład obciążenia, możliwość powstania pęknięć oraz
stopień odkształcania przy ściskaniu
k
c,90
=
Aby nośność podwaliny nie została przekroczona, powinien być spełniony warunek:
σ
c,90,d
≤ k
c,90
·
f
c,90,d
…………..≤………………………….