PROJEKT 2 CZĘŚĆ 2

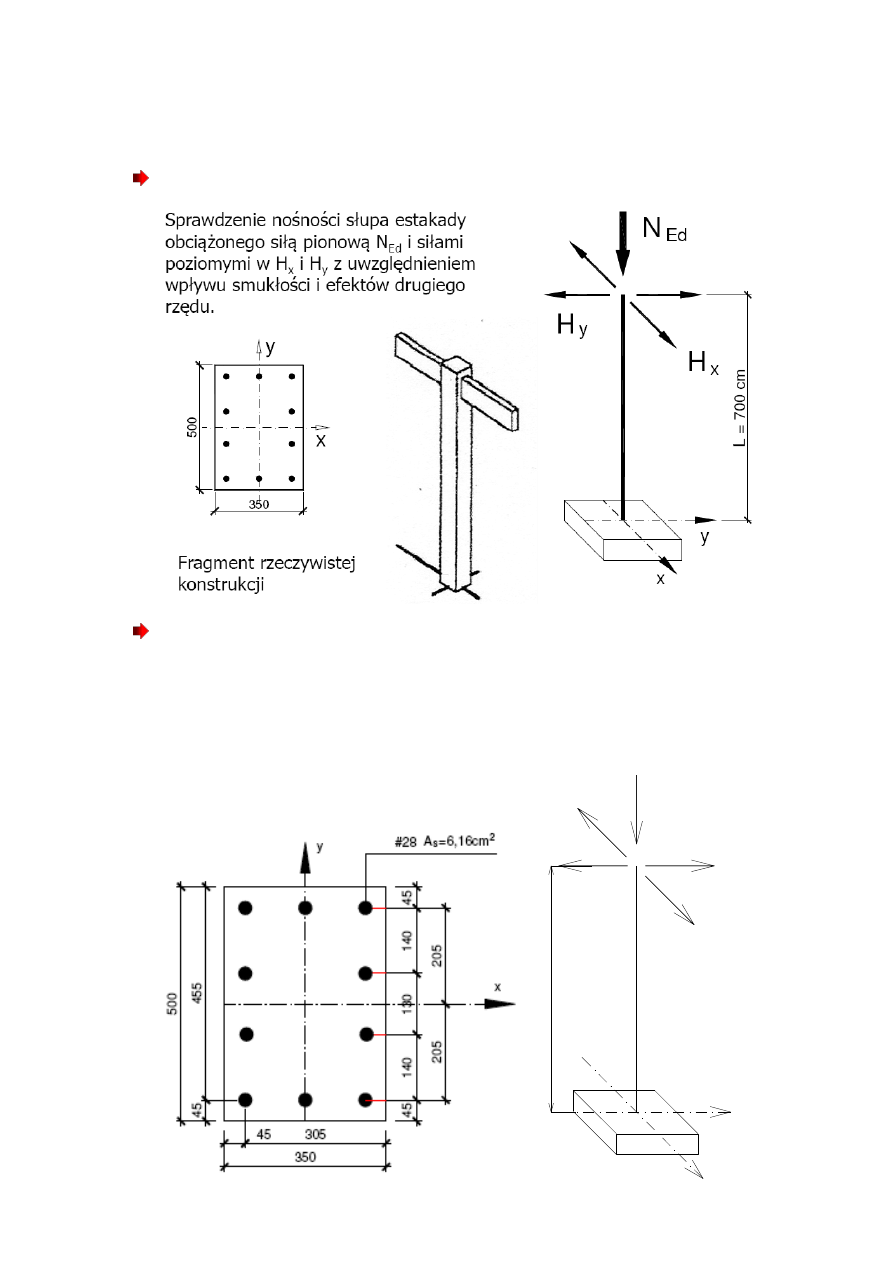
„Sprawdzenie nośności słupa estakady”

Cel ćwiczenia

Dane:

Beton C30/37: f

cd

= f

ck

/

γ

c

= 30/1,4 = 21,43MPa

Stal BSt500: f

yd

= f

yk

/y

s

= 500/1,15 = 435MPa

Moduł sprężystości: E

s

= 200GPa

ε

yd

= f

yd

/E

s

= 435/200000 = 2,18‰

l

col

=

800cm

N

Ed

=791 kN

H

Ed,y

=±6 kN

H

Ed,x

=±12 kN

y

x

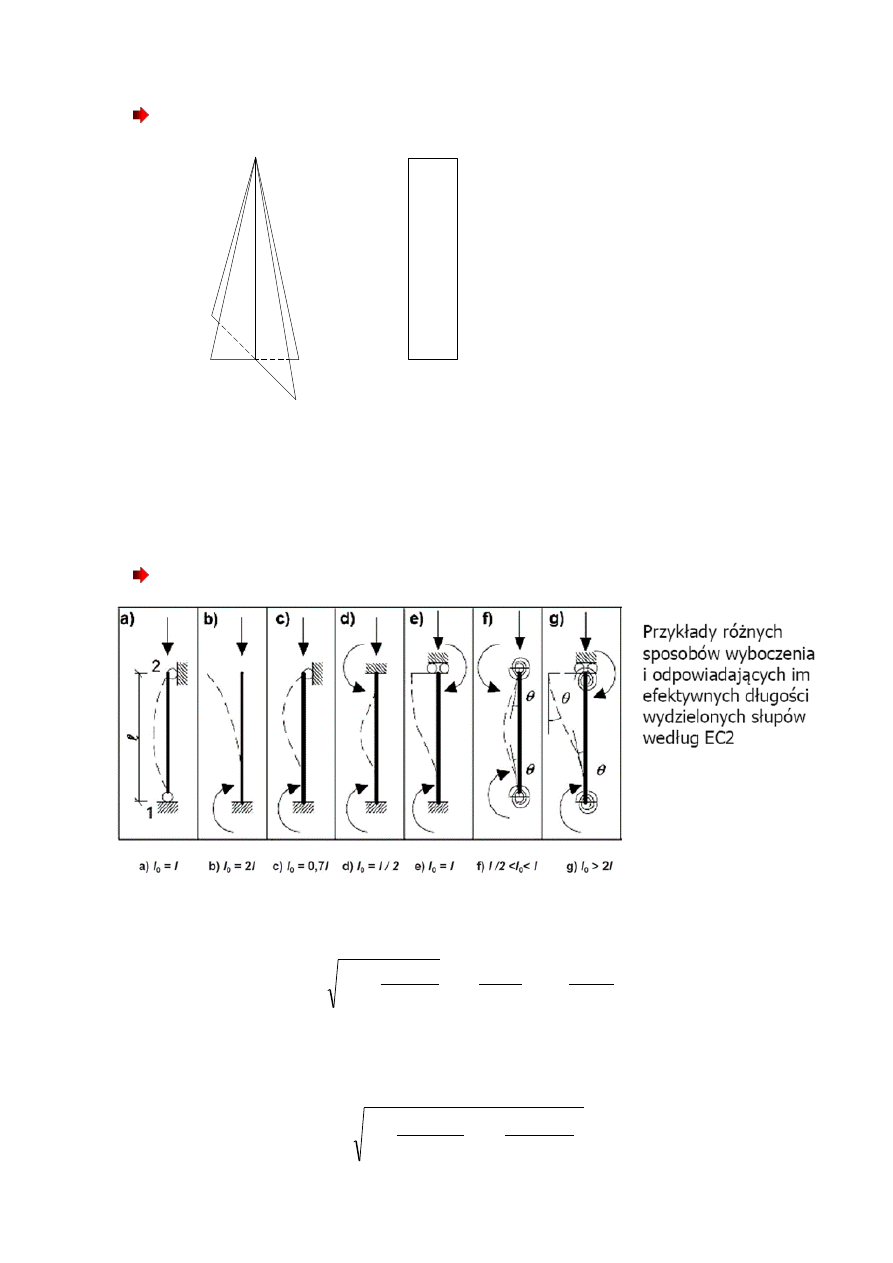
Siły pierwszego rzędu:

M

1,x

=48kN

791 kN

M

1

N

Ed

Siły pierwszego rzędu
bez uwzględniania
imperfekcji

M

1,y

=96kN

M

1,y

-

moment względem osi y, zginanie w płaszczyźnie x-x

M

1,x

-

moment względem osi x, zginanie w płaszczyźnie y-y

Długość efektywna słupa w płaszczyźnie x-x i y-y

Efektywna długość w elementach ściskanych dla układu nieusztywnionego (o
węzłach przesuwnych), wyznacza się ze wzoru:

k -

względna podatność podpór na końcach 1 i 2

natomiast dla układu usztywnionego ze wzoru:

gdzie:





































2

2

1

1

0

k

0,45

k

1

k

0,45

k

1

0,5l

l



























































2

2

1

1

2

1

2

1

col

0

k

1

k

1

,

k

1

k

1

,

k

k

k

k

10

1

max

l

l

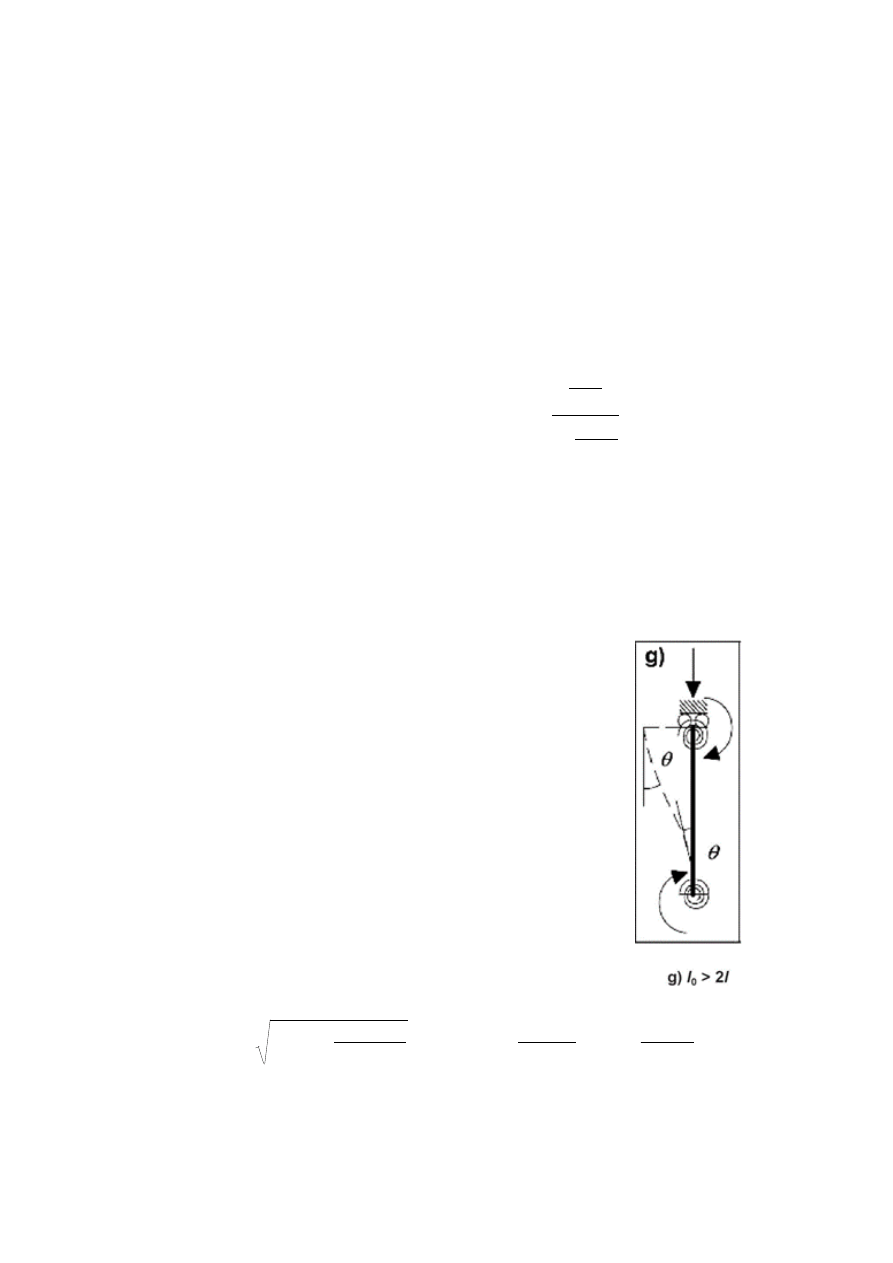
k

– względna podatność podpór na końcach 1 i 2

k =

θ/M · EI/l

θ – kąt obrotu podpory

k = 0 zamocowanie całkowicie sztywne (zaleca się przyjmować 0,1)

k = ∞ pełen przegub (zaleca się przyjmować dużą wartość, np. 10)

Kąt θ można odczytać wykonując analizę statyczną układu w programie
komputerowym, w przypadku braku takich danych można skorzystać z metody
uwzględniającej sztywność elementów połączonych w węźle, ze wzoru
zaczerpniętego z UK National Annex:

J

– moment bezwładności przekroju niezarysowanego.

Sztywności sąsiednich słupów nie mogą różnić się bardziej niż o 10 %.

W przykładzie mamy układ nieusztywniony.

PŁASZCZYZNA Y-Y

-

podatność podpory dolnej - zamocowanie: k

1

= 0,1

-

podatność końca górnego - swobodny koniec: k

2

= 10































































08

,

2

10

1

10

1

1

,

0

1

1

,

0

1

;

41

,

1

10

1

,

0

10

1

,

0

10

1

max

0

,

8

0 y

l

1

,

0

2







b

b

c

c

l

EJ

l

EJ

k

m

l

y

64

,

16

08

,

2

0

,

8

,

0







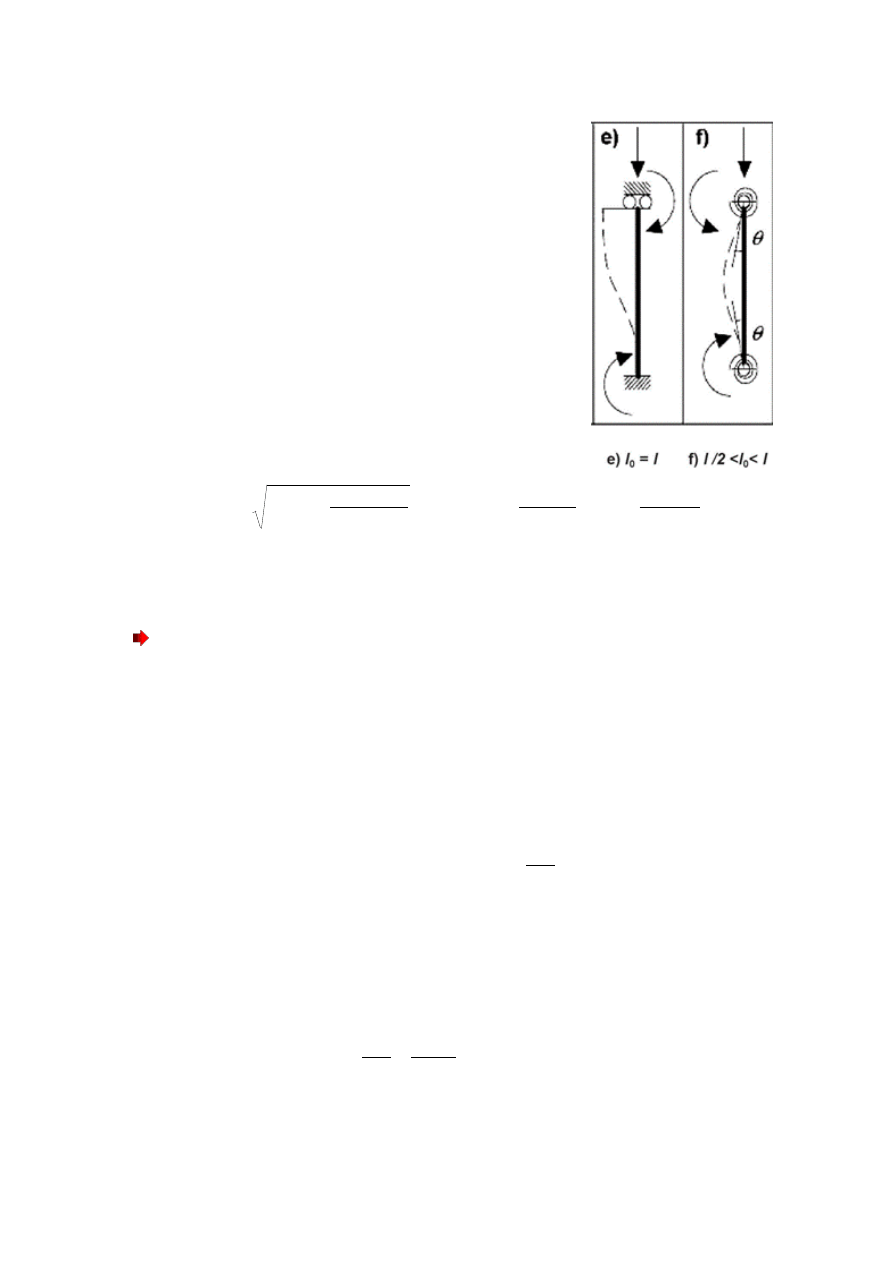
PŁASZCZYZNA X-X

-

podatność podpory dolnej - zamocowanie: k

1

= 0,1

-

podatność końca górnego - belka, przyjęto: k

2

= 0,5

(proszę przyjąć 0,1*i, i - ilość liter w imieniu)

Imperfekcje:

Analizując konstrukcje i ich elementy, należy uwzględniać niekorzystne

wpływy możliwych odchyłek geometrycznych konstrukcji (chodzi tu o odchylenie od

zaplanowanego kształtu) i zmian położenia obciążeń, są to tzw. imperfekcje

geometryczne.

Wpływ imperfekcji na wydzielone elementy można uwzględnić jako mimośród

e

i

, który w uproszczeniu można obliczyć jako:

l

o

-

długość efektywna słupa

h -

wysokość przekroju

Mimośród wg wzoru powyżej należy uwzględnić w płaszczyźnie, w której efekt

będzie bardziej niekorzystny, w przykładzie przyjęto, że będzie to płaszczyzna, w

której słup ma większą długość wyboczeniową czyli y-y:































































45

,

1

5

,

0

1

5

,

0

1

1

,

0

1

1

,

0

1

;

35

,

1

5

,

0

1

,

0

5

,

0

1

,

0

10

1

max

0

,

8

0 x

l

mm

y

l

y

i

e

6

,

41

400

16640

400

0

,







mm

e

y

i

6

,

41

,



Ed

y

i

x

i

N

e

M





,

,

400

0

l

i

e



m

l

x

60

,

11

45

,

1

0

,

8

,

0







zatem moment przy podporze:

Natomiast w płaszczyźnie x-x:

791 kN

M

0Ed

N

Ed

Siły pierwszego rzędu
z uwzględnieniem
imperfekcji

M

0Ed,x

=81kN

M

0Ed,y

=96kN

M

0Ed,x

=33kN

Kryterium smukłości

Efekty drugiego rzędu należy uwzględnić, jeżeli smukłość λ w danej płaszczyźnie
przekracza smukłość graniczną λ

lim

:

gdzie:

Ed

y

i

x

x

Ed

N

e

M

M







,

,

1

,

0

kNm

M

x

i

9

,

32

791

0416

,

0

,







kNm

M

x

Ed

9

,

80

9

,

32

48

,

0







y

y

Ed

M

M

,

1

,

0



kNm

M

y

Ed

96

,

0



n

ABC

20

lim





x

Ed

x

Eqp

M

M

t

x

ef

,

0

,

0

)

,

(

,











y

Ed

y

Eqp

M

M

t

y

ef

,

0

,

0

)

,

(

,











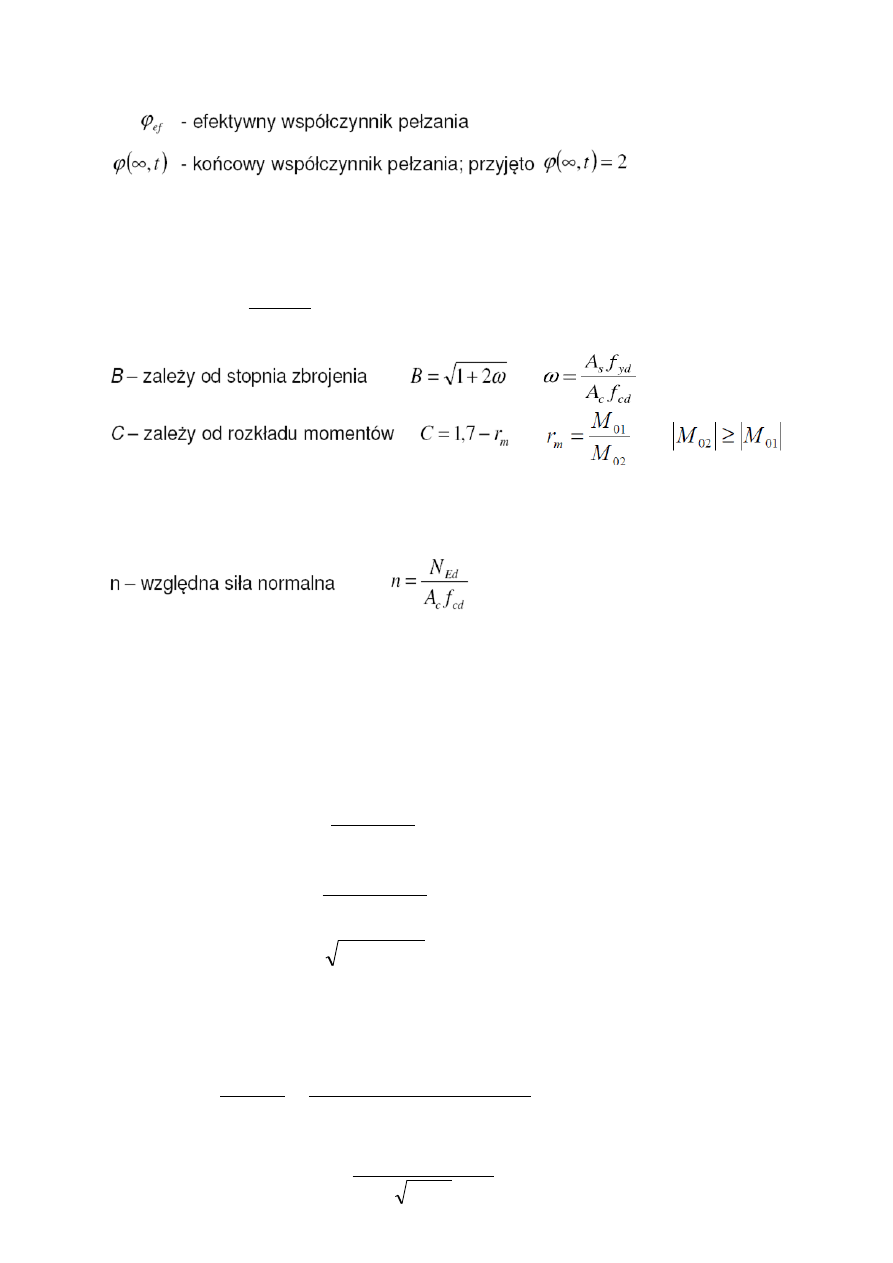
M

0Eqp

-

moment zginający wywołany przez prawie stałą kombinacje obciążeń

M

0Ed

= M

1

-

moment zginający wywołany przez obliczeniową kombinacją obciążeń

Można przyjąć:

,

,

w układach nieusztywnionych zaleca się przyjmować C=0,7

M

01

, M

02

-

momenty I rzędu na końcach słupa

Dla naszego słupa mamy zatem:

PŁASZCZYZNA X-X

PŁASZCZYZNA Y-Y

211

,

0

43

,

21

50

,

0

35

,

0

791













MPa

m

m

kN

f

A

N

n

cd

C

Ed

6

,

1

8

,

0

2

,







x

ef



8

,

0

0

0



Ed

Eqp

M

M

6

,

1

8

,

0

2

,







y

ef



76

,

0

6

,

1

2

,

0

1

1









A

71

,

0

43

,

21

50

35

435

16

,

6

10















55

,

1

71

,

0

2

1









B

7

,

0



C

9

,

35

211

,

0

7

,

0

55

,

1

76

,

0

20

lim,

lim,













y

x





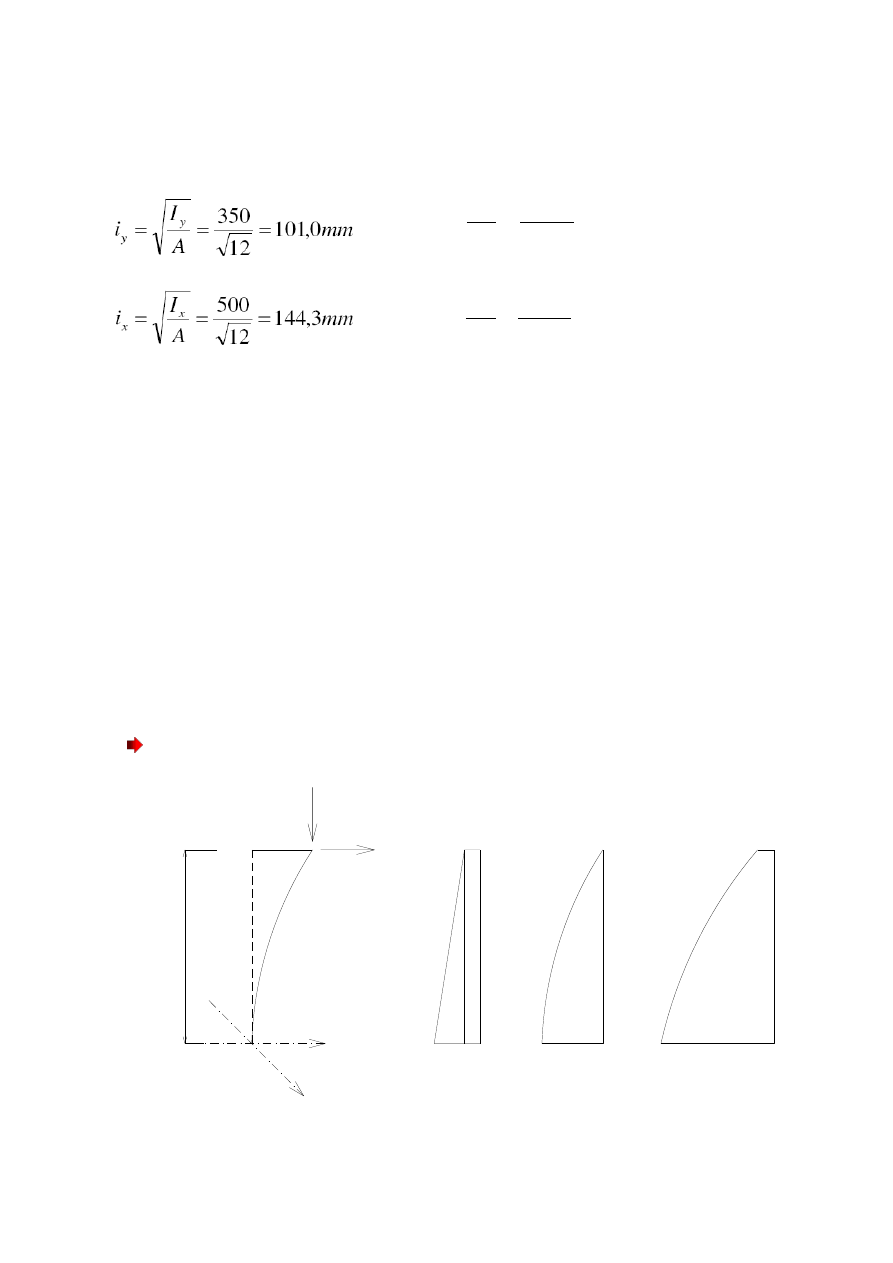
Smukłość elementu w poszczególnych płaszczyznach wynosi:

Zatem:

- płaszczyzna x-x:

- płaszczyzna y-y:

W obydwu płaszczyznach smukłość przekracza wartość graniczną, zatem w obydwu
trzeba uwzględnić efekty drugiego rzędu.

Efekty drugiego rzędu można uwzględnić w każdej z płaszczyzn jedną z dwóch
metod:

-

metodą nominalnej sztywności

-

metodą nominalnej krzywizny.

Efekty drugiego rzędu - metoda nominalnej krzywizny (płaszczyzna y-y)

l

c

ol

=

800cm

N

Ed

=791 kN

H

Ed,y

=6 kN

y

x

M

0Ed

M

0Ed,x

=81kN

M

0Ed,x

=33kN

e

2,y

M

2,x

+

=

M

Ed,x

6

,

114

0

,

101

11600

0







y

x

x

i

l



6

,

115

144

16640

0







x

y

y

i

l



9

,

35

6

,

114

lim,







x

x





9

,

35

6

,

115

lim,







y

y





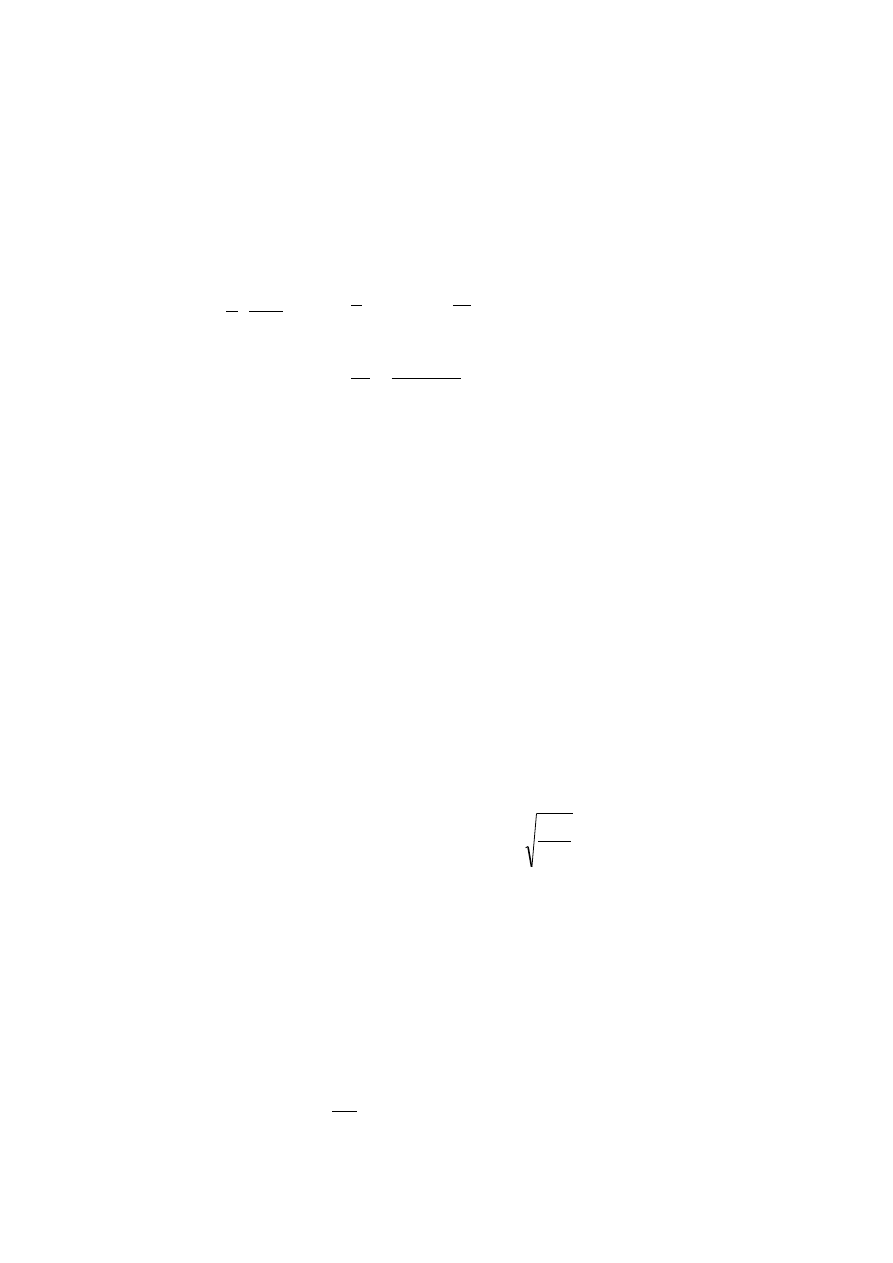
W metodzie nominalnej krzywizny znajdujemy całkowity moment M

Ed

poprzez

obliczenie momentu od efektów drugiego rzędu M

2

oraz dodanie go do momentu I

rzędu z uwzględnieniem imperfekcji M

0Ed

, dla płaszczyzny y-y:

M

Ed,x

= M

0Ed,x

+ M

2,x

,

gdzie:

M

2,x

= N

Ed

·e

2,y

Efekty drugiego rzędu uwzględniamy wyznaczając mimośród e

2

:

1

/

r

- krzywizna

l

0

-

długość efektywna w danej płaszczyźnie

c

-

współczynnik zależny od rozkładu krzywizny momentu II rzędu

K

r

-

współczynnik poprawkowy zależny od siły podłużnej, wg wzoru 5.36

K

φ

-

współczynnik zależny od pełzania, wg wzoru 5.37

ε

yd

- odkształcenie odpowiadające granicy plastyczności

d

-

dla danej płaszczyzny, dla zbrojenia rozmieszczonego na dwóch bokach

przekroju d jest

wysokością użyteczną przekroju, dla zbrojenia rozłożonego na

wszystkich

bokach należy skorzystać ze wzoru:

gdzie:

I

s

-

moment bezwładności zbrojenia dla zginania w płaszczyźnie y-y, liczony

względem osi x (w drugiej płaszczyźnie analogicznie)

A

s

- pole zbrojenia

Po wyznaczeniu mimośrodu e

2

, doko

nujemy sprawdzenia z wartością minimalną

mimośrodu:

c

l

r

e

y

y

2

,

0

,

2

1





0

1

1

r

K

K

r

r









y

yd

d

r





45

,

0

1

0



x

s

y

i

h

d

,

5

,

0







s

x

s

x

s

A

I

i

,

,



)

20

;

30

max(

,

0

mm

h

e

y

y



czyli zweryfikowana wartość momentu całkowitego ma postać:

Efekty drugiego rzędu - metoda nominalnej sztywności (płaszczyzna y-y)

W metodzie nominalnej sztywności całkowity moment uzyskujemy mnożąc moment
pierwszego rzędu przez współczynnik zwiększający:

gdzie jest siłą krytyczną obliczoną dla sztywności nominalnej EI:

l

0

-

długość efektywna w danej płaszczyźnie

K

c

-

współczynnik zależny od wpływów zarysowania, pełzania, wg wzoru 5.22

K

s

-

współczynnik zależny od udziału zbrojenia, wg wzoru 5.22

I

c

-

moment bezwładności przekroju betonu

I

s

-

moment bezwładności prętów zbrojenia względem środka ciężkości

przekroju betonowego

E

cd

-

obliczeniowa wartość modułu sprężystości betonu, wg wzoru 5.20

E

s

-

moduł sprężystości stali, E

s

=200GPa

natomiast współczynnik β zależy od rozkładu momentu pierwszego i drugiego rzędu,
wg wzoru 5.29.

Ed

y

Ed

x

Ed

x

Ed

N

e

N

M

M

















,

0

,

,

;

max

*































1

1

,

0

,

Ed

B

x

Ed

x

Ed

N

N

M

M



2

,

0

2

,

y

x

y

B

l

EI

N





x

s

s

s

x

c

cd

c

x

I

E

K

I

E

K

EI

,

,





Po wyznaczeniu momentu całkowitego również sprawdzamy czy uzyskany mimośród
jest większy od minimalnego. Zweryfikowana postać momentu ma postać
analogiczną:

Zginanie ukośne

Po wyznaczeniu wartości M

Ed,x

, M

Ed,y

zgodnie z założoną metodą należy sprawdzić

nośność dla zginania ukośnego.

Sprawdzanie zginania ukośnego można pominąć gdy smukłości w dwóch
płaszczyznach spełniają warunki:

i

oraz gdy spełniony jest jeden z warunków: lub

gdzie mimośrody:

natomiast b

eq

, h

eq

oznaczają wymiary zastępcze przekroju:

a i

x

, i

y

to promienie bezwładności względem danej osi.

Jeżeli powyższe warunki są spełnione to można sprawdzać oba kierunki niezależnie:

i

Ed

y

Ed

x

Ed

x

Ed

N

e

N

M

M

















,

0

,

,

;

max

*

)

20

;

30

max(

,

0

mm

h

e

y

y



2



x

y





2



y

x





2

,

0





z

eq

eq

y

e

b

h

e

2

,

0





y

eq

eq

z

e

h

b

e

Ed

x

Ed

y

N

M

e

,



Ed

y

Ed

x

N

M

e

,



12

x

eq

i

h



12

y

eq

i

b



0

,

1

,

,



x

Rd

x

Ed

M

M

0

,

1

,

,



y

Rd

y

Ed

M

M

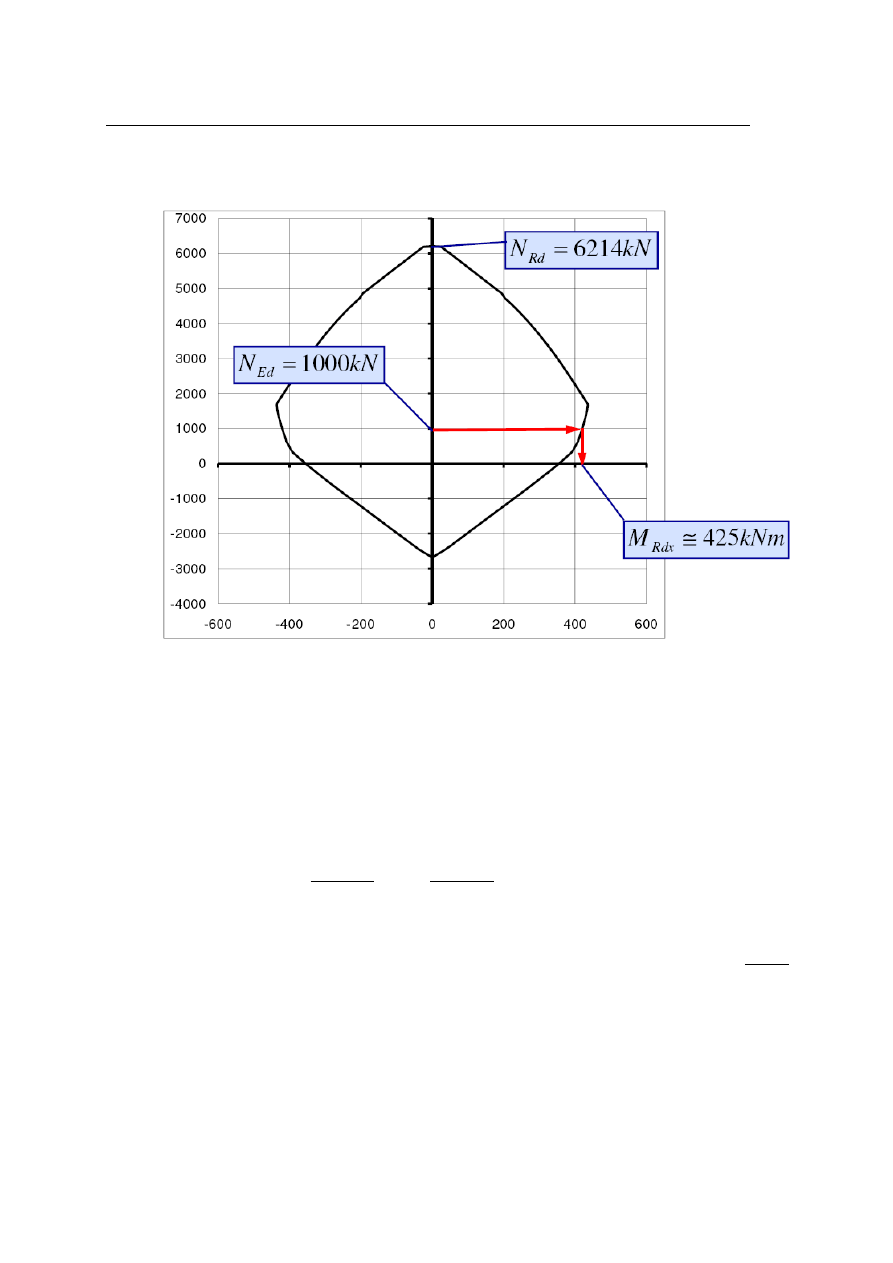
Jeżeli powyższe warunki nie są spełnione to należy uwzględnić zginanie ukośne.

Z krzywych interakcji w poszczególnych płaszczyznach odczytujemy nośność
przekroju na zginanie przy zadanej sile, np.: dla siły 1000kN:

W przykładzie przedstawionym na początku należałoby wyznaczyć nośność dla siły
N

Ed

=791kN dla krzywej interakcji w płaszczyźnie y-y - M

Rd,x

i analogicznie x-x - M

Rd,y

.

Następnie sprawdzamy warunek zginania ukośnego wg wzoru 5.39:

gdzie wykładnik potęgi

α

należy ustalić wg 5.8.9 (4) w zależności od stosunku

0

,

1

,

,

,

,





































y

Rd

y

Ed

x

Rd

x

Ed

M

M

M

M

Rd

Ed

N

N