Mechanika Techniczna

i Wytrzymaªo±¢ Materiaªów

Cz¦±¢ I - ‘rodki Ci¦»ko±ci

dr in». Waldemar Samodulski

2010

1.1 Wprowadzenie

Przedmiot Mechanika Techniczna jest dziaªem zyki zajmuj¡cym si¦ ustalaniem

ogólnych praw równowagi oraz ruchu ciaª materialnych. Prawa te stosujemy do

wyidealizowanych schematów w ciaªach rzeczywistych, którymi s¡ punkt mate-

rialny oraz ciaªo doskonale sztywne.

1.2 Przestrzenny ukªad siª równolegªych. ‘rodek

siª równolegªych

Rozwa»my ogólny przypadek n siª równolegªych F

1

, F

2

, ... F

i

... F

n

, przyªo»o-

nych do punktów A

1

, A

2

, ... A

i

... A

n

. Je»eli suma miar tych siª wzgl¦dem osi

równolegªej do ich linii dziaªania jest ró»na od zera, to mo»emy siªy te zast¡pi¢

jedn¡ siª¡ wypadkow¡ W .

Rys. 1 - Ukªad siª równolegªych

W =

i=n

X

i=1

F

i

(1.1)

gdzie F

i

i W oznaczaj¡ miary siªy F

i

i wypadkowej W wzgl¦dem osi równo-

legªej (rys. 1).

Zaªó»my, »e wszystkie siªy F

1

... F

i

... F

n

zostaªy obrócone o ten sam k¡t

alfa przy niezmienionych punktach przyªo»enia tych siª oraz ich warto±ciach.

Zauwa»amy, »e punkt przyªo»enia C wypadkowej nie zmienia si¦ oraz jej warto±¢
W

pozostaje staªa.

Punkt C nazywamy ±rodkiem siª równolegªych.

1

Moment siªy wypadkowej W wzgl¦dem osi O

y

:

M

y

= W x

c

(1.2)

Moment siªy F przyªo»onej w punkcie A

i

:

M

i

y = F

i

x

i

(1.3)

Korzystaj¡c z twierdzenia o momencie wypadkowej ukªadu siª otrzymujemy:

W x

c

=

i=n

X

i=1

F

i

x

i

(1.4)

st¡d otrzymujemy wspóªrz¦dn¡ x

c

±rodka siª równolegªych:

x

c

=

P

i=n
i=1

F

i

x

i

P

i=n
i=1

F

i

(1.5)

post¦puj¡c analogicznie otrzymujemy pozostaªe wspóªrz¦dne prostok¡tne ±rodka

siª równolegªych:

y

c

=

P

i=n
i=1

F

i

y

i

P

i=n
i=1

F

i

(1.6)

z

c

=

P

i=n
i=1

F

i

z

i

P

i=n
i=1

F

i

(1.7)

1.3 ‘rodki ci¦»ko±ci

Powszechnie spotykanym przykªadem siª równolegªych s¡ siªy ci¦»ko±ci. Siªy te

mo»emy trakowa¢ jako równolegªe, gdy» wymiary ciaª w zastosowaniach tech-

nicznych s¡ znikomo maªe w porównaniu z promieniem kuli ziemskiej. Wypad-

kow¡ siª ci¦»ko±ci mo»emy umie±ci¢ na staªe w ±rodku ci¦»ko±ci C, niezale»nie

od poªo»enia ciaªa.

W miejsce siª F

i

do wzorów (1.5), (1.6), (1.7) wstawiamy G

i

= V

i

∗ γ

, gdzie V

i

- obj¦to±¢ elementu ciaªa, γ - ci¦»ar wªa±ciwy ciaªa.

Wzory (1.5), (1.6), (1.7) przyjmuj¡ wtedy posta¢:

x

c

=

P

i=n
i=1

G

i

x

i

P

i=n
i=1

G

i

=

P

i=n
i=1

V

i

γx

i

P

i=n
i=1

V

i

γ

=

P

i=n
i=1

V

i

x

i

P

i=n
i=1

V

i

(1.8)

y

c

=

P

i=n
i=1

G

i

y

i

P

i=n
i=1

G

i

=

P

i=n
i=1

V

i

γy

i

P

i=n
i=1

V

i

γ

=

P

i=n
i=1

V

i

y

i

P

i=n
i=1

V

i

(1.9)

z

c

=

P

i=n
i=1

G

i

z

i

P

i=n
i=1

G

i

=

P

i=n
i=1

V

i

γz

i

P

i=n
i=1

V

i

γ

=

P

i=n
i=1

V

i

z

i

P

i=n
i=1

V

i

(1.10)

2

Wyst¦puj¡ce wy»ej sumy sko«czone po przej±ciu do granicy zamieniaj¡ si¦

w caªki obj¦to±ciowe rozci¡gni¦te na caª¡ obj¦to±¢ ciaªa.

x

c

=

R ρxdv

m

(1.11)

y

c

=

R ρydv

m

(1.12)

z

c

=

R ρzdv

m

(1.13)

Gdzie: ρ - g¦sto±¢ ciaªa wyra»ona w [

kg

m

3

], m - masa caªkowita ciaªa wyra»ona

w [kg] i okre±lona wzorem m = R ρdv

Caªki wyst¦puj¡ce w licznikach wzorów (1.11), (1.12), (1.13) nosz¡ nazw¦

momentów statycznych ciaªa materialnego wzgl¦dem pªaszczyzn ukªadu wspóª-

rz¦dnych:

R ρxdv

- moment statyczny ciaªa wzgl¦dem pªaszczyzny O

yz

R ρydv

- moment statyczny ciaªa wzgl¦dem pªaszczyzny O

xz

R ρzdv

- moment statyczny ciaªa wzgl¦dem pªaszczyzny O

xy

1.3.1 ‘rodki ci¦»ko±ci linii

Wzory (1.8), (1.9), (1.10) mo»emy zastosowa¢ do wyznaczenia poªo»enia ±rodka

ci¦»ko±ci w ogólnym przypadku dla linii przestrzennej o staªym ci¦»arze jednost-

kowym q, wówczas G

i

= l

i

q

x

c

=

P

i=n
i=1

ql

i

x

i

P

i=n
i=1

ql

i

=

P

i=n
i=1

l

i

x

i

P

i=n
i=1

l

i

(1.14)

y

c

=

P

i=n
i=1

ql

i

y

i

P

i=n
i=1

ql

i

=

P

i=n
i=1

l

i

y

i

P

i=n
i=1

l

i

(1.15)

z

c

=

P

i=n
i=1

ql

i

z

i

P

i=n
i=1

ql

i

=

P

i=n
i=1

l

i

z

i

P

i=n
i=1

l

i

(1.16)

Przedstawione powy»ej sumy zast¦pujemy caªk¡ i otrzymujemy:

x

c

=

R

l

xdl

l

, y

c

=

R

l

ydl

l

, z

c

=

R

l

zdl

l

(1.17)

gdzie l jest dªugo±ci¡ caªkowit¡ linii.

3

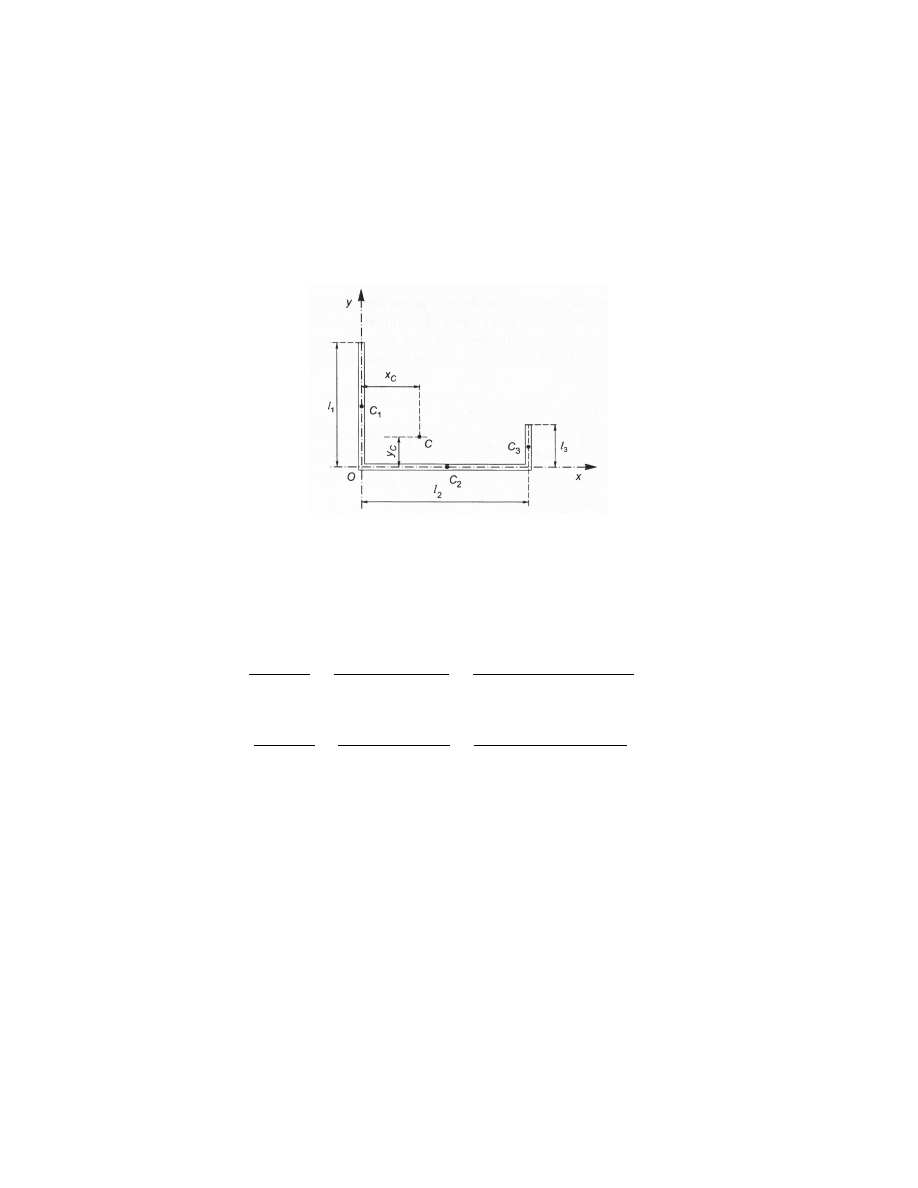
Przykªad 1
Wyznaczy¢ poªo»enie ±rodka ci¦»ko±ci jednorodnej linii ªamanej przedstawionej

na rys. 2. Dªugo±ci poszczególnych odcinków linii wynosz¡: l

1

=20cm, l

2

=30cm,

l

3

=10cm.

Rys. 2 - ‘rodek ci¦»ko±ci jednorodnej linii

Poniewa» mamy do czynienia z lini¡ pªask¡, zastosowanie maj¡ wzory (1.14),

(1.15).

Podstawiaj¡c warto±ci wspóªrz¦dnych ±rodka ci¦»ko±ci odcinków l

1

, l

2

, l

3

otrzy-

mujemy:

x

c

=

P

i=3
i=1

l

i

x

i

P

i=3
i=1

l

i

=

l

1

x

1

+ l

2

x

2

+ l

3

x

3

l

1

+ l

2

+ l

3

=

20 ∗ 0 + 30 ∗ 15 + 10 ∗ 30

20 + 30 + 10

= 12, 5cm

y

c

=

P

i=3
i=1

l

i

y

i

P

i=3
i=1

l

i

=

l

1

y

1

+ l

2

y

2

+ l

3

y

3

l

1

+ l

2

+ l

3

=

20 ∗ 10 + 30 ∗ 0 + 10 ∗ 5

20 + 30 + 10

= 4, 25cm

4

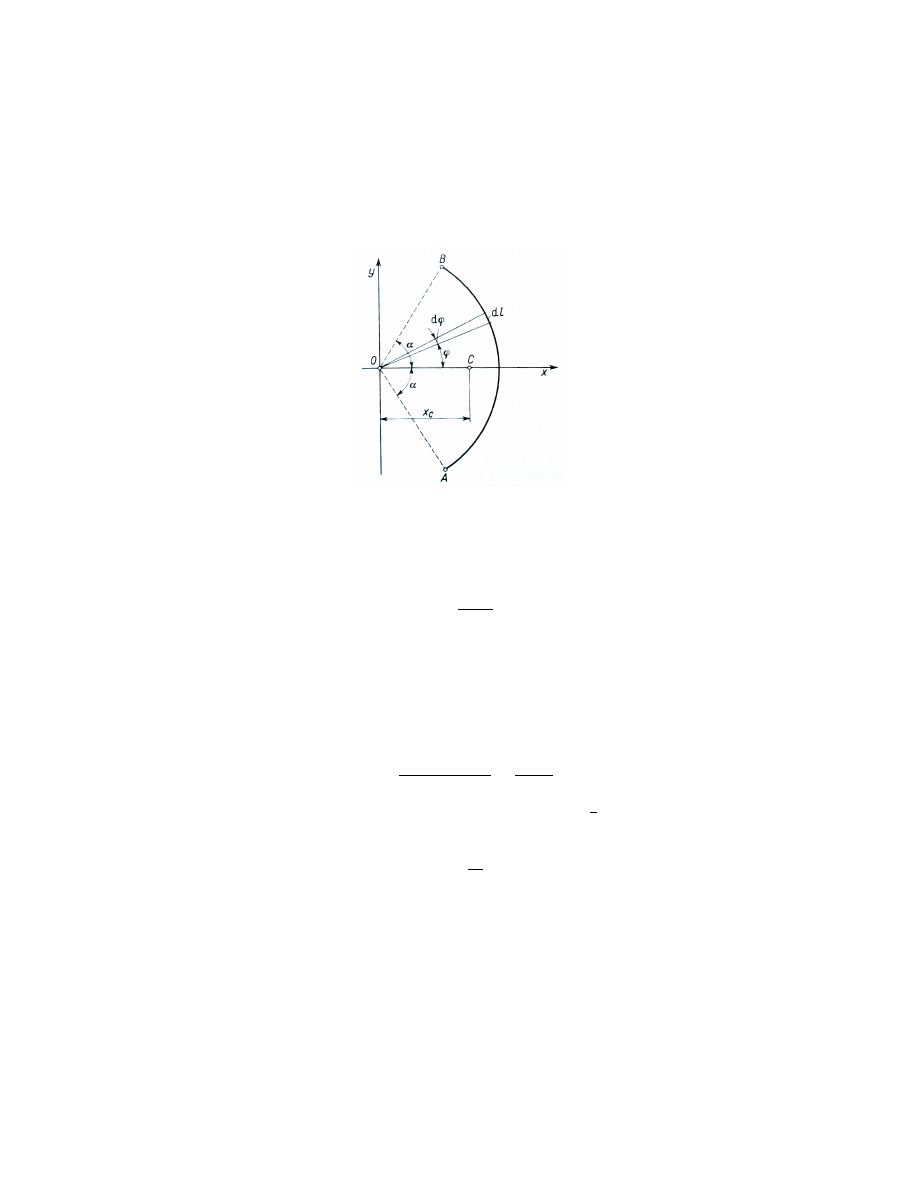
Przykªad 2
Wyznaczy¢ poªo»enie ±rodka ci¦»ko±ci ªuku okr¦gu o promieniu r

Rys. 3 - ‘rodek ci¦»ko±ci jednorodnego ªuku

(patrz rys.3). Ze wzgl¦du na symetri¦ ªuku, poªo»enie ±rodka ci¦»ko±ci okre±la

tylko jedna wspóªrz¦dna le»¡ca na osi O

x

zgodnie ze wzorem (7).

x

c

=

R

l

xdl

l

gdzie: l = 2rα (dªugo±¢ ªuku)

dl = r ∗ dφ

x = r cos φ

po podstawieniu otrzymujemy:

x

c

=

r

2

R

α

−α

cosφ dφ

2rα

=

rsinα

α

Je»eli do otrzymanego powy»ej wyniku podstawimy α =

π

2

, uzyskamy wspóª-

rz¦dn¡ x

c

okre±laj¡c¡ poªo»enie ±rodka ci¦»ko±ci dla póªokr¦gu:

x

c

=

2r

π

5

1.3.2 ‘rodki ci¦»ko±ci powierzchni

‘rodek ci¦»ko±ci gury pªaskiej le»y na prostej b¦d¡cej osi¡ symetrii mecha-

nicznej. Dla prostok¡ta lub równolegªoboku ±rodek ci¦»ko±ci le»y na przeci¦ciu

dwóch osi symetrii mechanicznej. W przypadku dowolnego trójk¡ta ±rodek ci¦»-

ko±ci musi le»e¢ na przeci¦ciu ±rodkowych, czyli w 1/3 wysoko±ci od podstawy.

Podstawiaj¡c do wzorów (1.5), (1.6), (1.7) v

i

= A

i

δ

, gdzie A

i

- pole powierzchni

gury, δ - grubo±¢ gury otrzymujemy:

x

c

=

P

i=n
i=1

A

i

x

i

P

i=n
i=1

A

i

, y

c

=

P

i=n
i=1

A

i

y

i

P

i=n
i=1

A

i

(1.18)

lub w postaci caªkowej:

x

c

=

R

A

A

i

x

i

A

, y

c

=

R

A

A

i

y

i

A

(1.19)

Wyra»enia w licznikach nazywamy momentami statycznymi gury pªaskiej

wzgl¦dem osi:

S

y

=

R

A

x dA

- moment statyczny wzgl¦dem osi y

S

x

=

R

A

y dA

- moment statyczny wzgl¦dem osi x

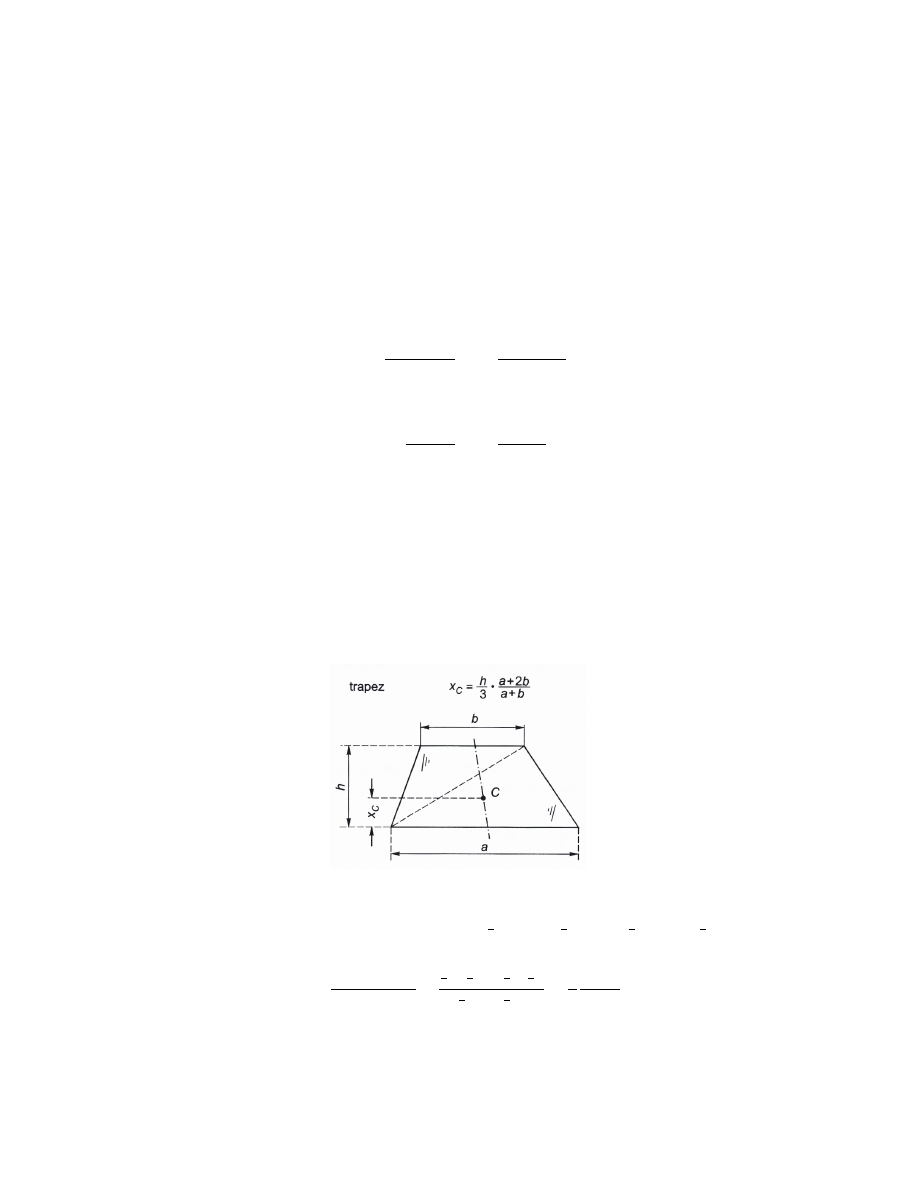
Przykªad 1
Trapez o podstawach a i b oraz wysoko±ci h mo»emy traktowa¢ jako sum¦ dwóch

trójk¡tów (rys. 4).

Rys. 4 - ‘rodek ci¦»ko±ci trapezu

Po podstawieniu do wzoru (1.18) A

1

=

1
2

ah

, x

1

=

1
3

h

, A

2

=

1
2

bh

, x

2

=

2
3

h

otrzymamy:

x

c

=

A

1

x

1

+ A

2

x

2

A

1

+ A

2

=

1
2

ah

1
3

h +

1
2

bh

2
3

h

1
2

ah +

1
2

bh

=

h

3

a + 2b

a + b

6

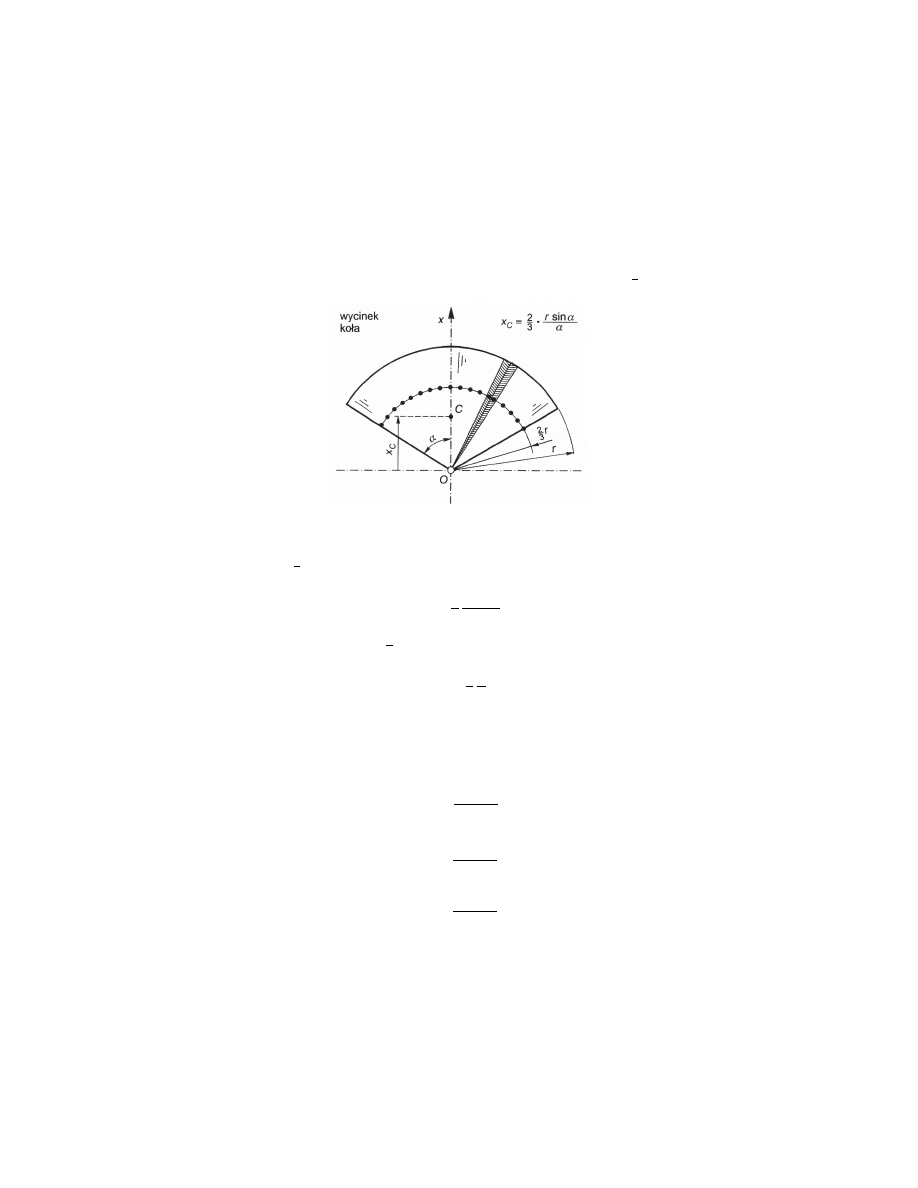
Przykªad 2
W celu wyznaczenia ±rodka ci¦»ko±ci C wycinka koªa o promieniu r i k¡cie

rozwarcia 2α, dzielimy pole wycinka na elementarne trójk¡ty o podstawie równej
rdφ

.

‘rodki ci¦»ko±ci tych trójk¡tów znajduj¡ si¦ na ªuku o promieniu

2
3

r

.

Rys. 5 - ‘rodek ci¦»ko±ci wycinka koªa

Podstawiaj¡c

2
3

r

do wzoru na ±rodek ci¦»ko±ci ªuku otrzymujemy:

x

c

=

2

3

rsinα

α

dla póªkola wstawiaj¡c α =

π

2

otrzymujemy:

x

c

=

4

3

r

π

1.3.3 ‘rodki ci¦»ko±ci bryª

Poªo»enie ±rodka ci¦»ko±ci bryªy okre±lone jest wzorami:

x

c

=

R ρxdv

m

(1.20)

y

c

=

R ρydv

m

(1.21)

z

c

=

R ρzdv

m

(1.22)

Za ich pomoc¡ wyznaczymy poªo»enie ±rodka ci¦»ko±ci jednorodnego sto»ka.

‘rodek ci¦»ko±ci C b¦dzie le»aª na osi symetrii sto»ka - O

z

.

7

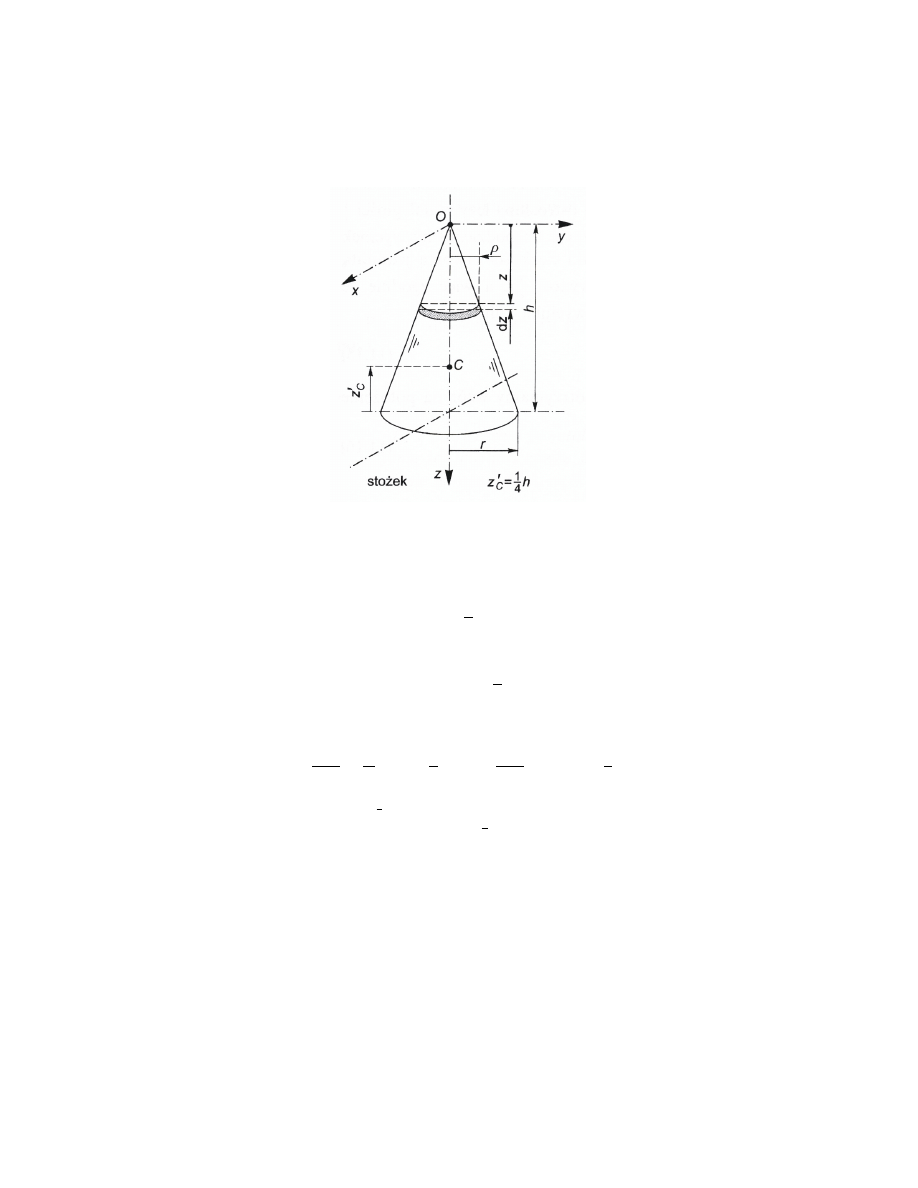
Rys. 5 - ‘rodek ci¦»ko±ci sto»ka

Rozpatrzmy elementarny kr¡»ek o grubo±ci dz w odlegªo±ci z od wierzchoªka

sto»ka. Promie« tego kr¡»ka wynosi:

ρ =

z

h

r

(1.23)

Obj¦to±¢ elementarnego kr¡»ka wynosi:

dV = πρ

2

dz = π(

z

h

r)

2

dz

Korzystaj¡c ze wzoru (1.22) otrzymujemy:

z

c

=

Z

V

zdV

V

=

1

V

Z

h

0

zπ(

z

h

r)

2

dz =

πr

2

V h

2

Z

h

0

z

3

dz =

3

4

h

(1.24)

gdzie obj¦to±¢ sto»ka V =

1
3

πr

2

h

‘rodek ci¦»ko±ci sto»ka le»y w odlegªo±ci

1
4

h

od podstawy sto»ka. Wynik ten

dotyczy równie» sto»ków uko±nych oraz ostrosªupów o dowolnych podstawach.

8

1.4 Zadania do samodzielnego rozwi¡zania

1.4.1 Zadanie nr 1

Wyznaczy¢ poªo»enie ±rodka ci¦»ko±ci gury pªaskiej przedstawionej na rys.

Rys. 7

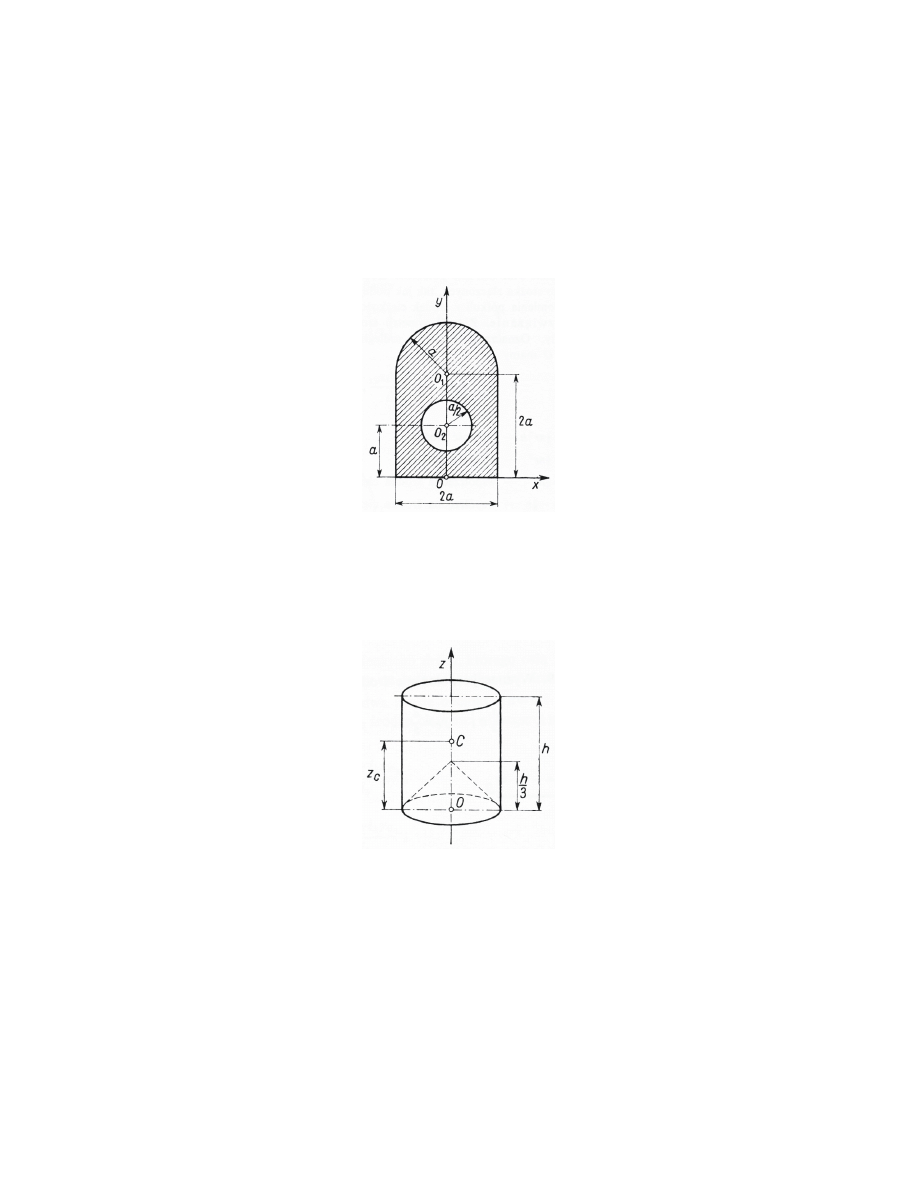
1.4.2 Zadanie nr 2

Z jednorodnego walca wydr¡»ono sto»ek, tak jak przedstawia Rys. 7 Okre±li¢

poªo»enie ±rodka ci¦»ko±ci otrzymanego ciaªa.

Rys. 8

Bibliograa:

(1) Mechanika Ogólna Tom I, PWN Warszawa 2008

(2) T. Niezgodzi«ski - Mechanika Ogólna, Wydawnictwo Naukowe PWN 2010

9