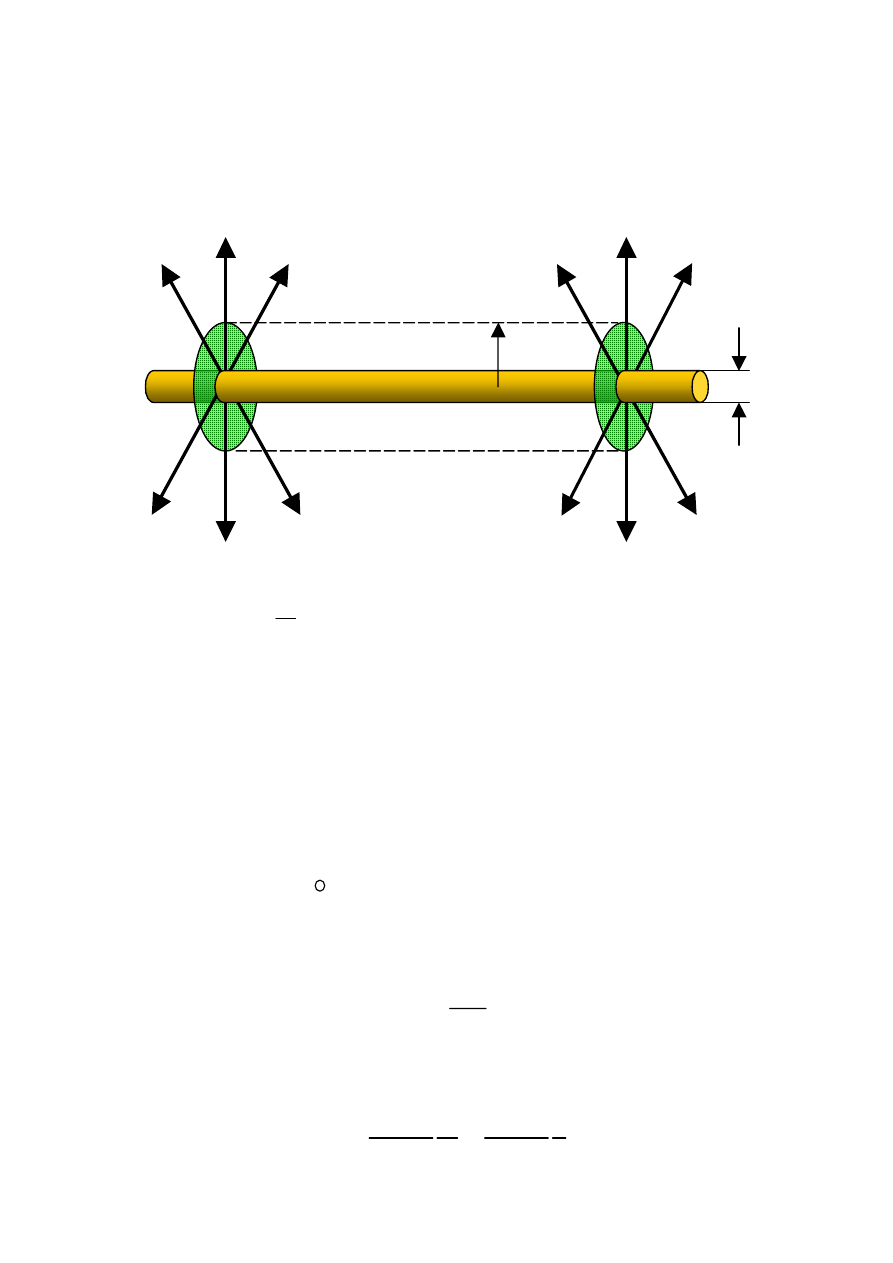
Pole elektryczne nieskończenie długiego walca prostego z

równomiernie rozłożonym na jego powierzchni ładunkiem

liniowym

E

E

S

G

q

l

2R

r

l

Gaussa

rl

S

l

Q

q

G

l

ia

powierzchn

2

;

−

=

=

π

Oba strumienie natężenia pola przez obie podstawy walca o
promieniu r są równe zeru: E

= E

n

= 0. Natomiast wszędzie na

całej pobocznicy walca, czyli na powierzchni Gaussa, jest E

= E

n

= const, zatem

0

0

oraz

2

d

εε

Φ

π

Φ

Q

rl

E

ES

S

E

EdS

G

S

S

G

G

=

⋅

=

=

=

=

∫

∫

r

q

rl

Q

E

l

1

2

1

2

0

0

πεε

πεε

=

=

Potencjał w polu elektrycznym nieskończenie długiego walca

naładowanego równomiernie ładunkiem liniowym

∫

−

=

⇒

−

=

−

=

x

E

x

E

d

d

d

grad

ϕ

ϕ

ϕ

Ogólnie

C

r

q

r

r

q

l

l

+

−

=

−

=

∫

ln

2

d

2

0

0

πεε

πεε

ϕ

Różnica potencjałów między dwoma dowolnymi punktami pola
odpowiednio w odległościach r

1

i r

2

(r

2

> r

1

) od osi naładowanego

walca

(

)

1

2

0

1

2

0

0

0

2

1

ln

2

ln

ln

2

ln

2

d

2

d

2

1

2

1

1

2

r

r

q

r

r

q

r

q

r

r

q

r

E

l

l

r
r

l

r

r

l

r

r

πεε

πεε

πεε

πεε

ϕ

ϕ

=

−

=

=

=

−

=

−

∫

∫

Wobec warunku: r

2

> r

1

jest

ϕ

1

>

ϕ

2

, czyli potencjał maleje wraz z

odległością od naładowanego, nieskończenie długiego walca.

R

r

E

0

E,

q

l

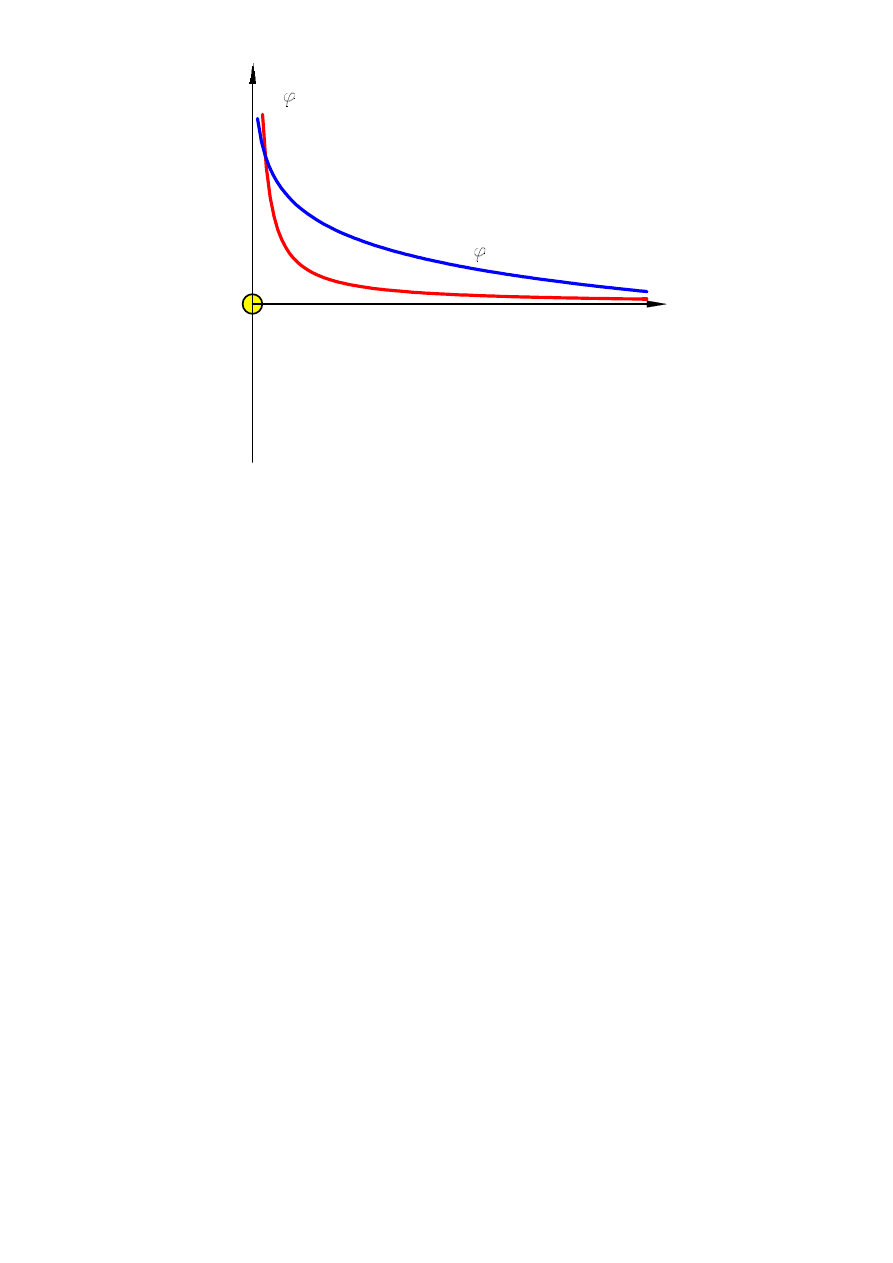
Rozkłady natężenia pola i potencjału dla nieskończenie długiego

walca naładowanego ze stałą gęstością liniową q

l