Dodatek A.
Dwójkowo i szesnastkowo

Podstawy arytmetyki poznaliśmy w tak zamierzchłej przeszłości, że trudno sobie wyobrazić co by
było, gdybyśmy nie posiadali tej wiedzy. Gdy patrzymy na znaki 145, to natychmiast wiemy, że
chodzi o liczbę „sto czterdzieści pięć”.

Zrozumienie sposobu funkcjonowania systemu dwójkowego i szesnastkowego wymaga innego
spojrzenia na liczbę 145, a mianowicie postrzegania jej nie jako liczby, ale jako jej kodu.

Na początku wyobraź sobie powiązanie pomiędzy liczbą trzy a „3”. Cyfra „3” jest znaczkiem na
papierze; liczba trzy jest ideą. Cyfra służy do reprezentowania liczby.

To rozróżnienie może być łatwiejsze do zrozumienia, jeśli uświadomimy sobie, że zarówno trzy
jak i 3, |||, III oraz *** reprezentują tę samą ideę liczby trzy.

W systemie dziesiętnym (czyli, jak mówią matematycy, o podstawie 10) do reprezentowania
wszystkich liczb używamy cyfr 0, 1, 2, 3, 4, 5, 6, 7, 8 oraz 9. Jak jest reprezentowana liczba 10?

Można sobie wyobrazić, że do reprezentowania liczby dziesięć używamy litery A, lub że
używamy zapisu IIIIIIIIII. Rzymianie używali znaku X. W systemie arabskim, z którego obecnie
korzystamy, do reprezentowania wartości wykorzystujemy cyfry i ich pozycje. Pierwsza (położona
najbardziej na prawo) kolumna jest używana dla jedynek, a druga (w lewą stronę) jest używana dla
dziesiątek. Tak więc liczba piętnaście jest reprezentowana jako 15 (czytaj: „jeden, pięć”), czyli
jedna dziesiątka i pięć jedynek.

Pojawia się regularność, dzięki której można dokonać pewnej generalizacji:

1. System o podstawie 10 używa cyfr od 0 do 9.

2. Kolumny

są potęgami dziesięciu: 1, 10, 100, itd.

3. Jeśli trzecia kolumna reprezentuje setki, to największą liczbą, jaką można zapisać w dwóch

kolumnach, jest 99. Innymi słowy, w n kolumnach możemy reprezentować liczby od 0 do
(10

n

–1). Tak więc, w trzech kolumnach możemy reprezentować liczby od 0 do (10

3

–1), czyli

od 0 do 999.

Inne podstawy

To, że korzystamy z podstawy 10, nie jest przypadkiem: w końcu mamy po dziesięć palców.
Można sobie jednak wyobrazić inną podstawę. Używając reguł określonych dla podstawy 10,
możemy opisać podstawę 8:

1. System o podstawie 8 używa cyfr od 0 do 7.

2. Kolumny

są potęgami ośmiu: 1, 8, 64, itd.

3. W n kolumnach możemy zapisywać liczby od 0 do 8

n

–1.

W celu rozróżniania liczb o różnych podstawach, podstawy zapisujemy jako indeks dolny tuż za
ostatnią cyfrą liczby. Liczba piętnaście przy podstawie 10 jest zapisywana jako 15

10

i odczytywana

jako „jeden, pięć, dziesiętnie”.

Tak więc, reprezentując liczbę 15

10

w systemie o podstawie 8, napisalibyśmy 17

8

. Należy ją

odczytywać jako „jeden, siedem, ósemkowo”. Zwróć uwagę, że można to odczytywać jako
„piętnaście”, gdyż tę wartość reprezentuje.

Dlaczego 17? Jedynka oznacza jedną ósemkę, a siódemka oznacza siedem jedynek. Jedna ósemka
plus siedem jedynek daje piętnaście. Weźmy piętnaście gwiazdek:

***** *****
*****

Naturalnym działaniem będzie utworzenie dwóch grup: grupy dziesięciu gwiazdek i grupy pięciu
gwiazdek. Dziesiętnie byłyby one reprezentowane jako 15 (jedna dziesiątka i pięć jedynek).
Można także pogrupować gwiazdki następująco:

**** *******
****

to jest, jako osiem gwiazdek i siedem. W systemie ósemkowym zapisalibyśmy to jako 17

8

, czyli

jako jedną ósemkę i siedem jedynek.

Wokół podstaw

Liczbę piętnaście możemy w systemie dziesiętnym zapisywać jako 15, w systemie
dziewiątkowym jako 16

9

, w systemie ósemkowym jako 17

8

, a czy w systemie siódemkowym jako

21

7

. Dlaczego 21

7

? W systemie siódemkowym nie ma cyfry 8. Aby wyrazić liczbę piętnaście,

potrzebujemy dwóch siódemek i jednej jedynki.

Jak można to uogólnić? Aby zamienić liczbę o podstawie 10 na liczbę o podstawie 7, pomyśl o
kolumnach: w systemie siódemkowym występują kolumny dla jedynek, siódemek, czterdziestek
dziewiątek, trzysta czterdziestek trójek i tak dalej. Dlaczego takie kolumny? Ponieważ
reprezentują 7

0

, 7

1

, 7

2

, 7

4

i tak dalej.

Pamiętajmy, że dowolna liczba podniesiona do zerowej potęgi (na przykład 7

0

) równa się 1, każda

liczba podniesiona do pierwszej potęgi (na przykład 7

1

) równa się samej sobie, każda liczba

podniesiona do drugiej potęgi równa się wynikowi przemnożenia jej przez siebie (7

2

= 7*7 = 49),

a każda liczba podniesiona do trzeciej potęgi odpowiada trzykrotnemu przemnożeniu jej przez
siebie (7

3

= 7*7*7 = 343).

Wykonaj tabelę:

Kolumna

4 3 2 1

Potęga 7

3

7

2

7

1

7

0

Wartość 343

49

7

1

Pierwszy wiersz reprezentuje numer kolumny. Drugi wiersz reprezentuje potęgę siódemki. Trzeci
wiersz reprezentuje wartość dziesiętną każdej liczby w drugim wierszu.

Aby zamienić wartości dziesiętne na liczby siódemkowe, postępuj zgodnie z poniższą procedurą:
sprawdź liczbę i zdecyduj, której kolumny użyć jako pierwszej. Jeśli liczbą jest na przykład 200,
wiemy, że kolumna 4 (343) będzie zawierała 0 i nie musimy się nią martwić.

Aby dowiedzieć się, ile 49-ek jest w liczbie 200, podzielimy 200 przez 49. Otrzymujemy 4, więc
w kolumnie trzeciej umieszczamy cyfrę 4 i sprawdzamy resztę z dzielenia: 4. W liczbie 4 nie ma
żadnej siódemki, więc w kolumnie siódemek umieszczamy cyfrę 0. W liczbie cztery są cztery
jedynki, więc w kolumnie jedynek umieszczamy cyfrę 4. Odpowiedzią jest 404

7

.

Kolumna

4 3 2 1

Potęga 7

3

7

2

7

1

7

0

Wartość 343

49

7

1

200

siódemkowo

0 4 0 4

Wartość
dziesiętna

0

4*49 = 196

0

4*1 = 4

W tym przykładzie cyfra 4 w trzeciej kolumnie reprezentuje wartość dziesiętną 196, a cyfra 4 w
pierwszej kolumnie reprezentuje wartość 4. 196+4 = 200. Tak więc 404

7

= 200

10

.

Przejdźmy następnego przykładu.

Aby zamienić liczbę 968 na liczbę szóstkową:

Kolumna 5

4

3

2

1

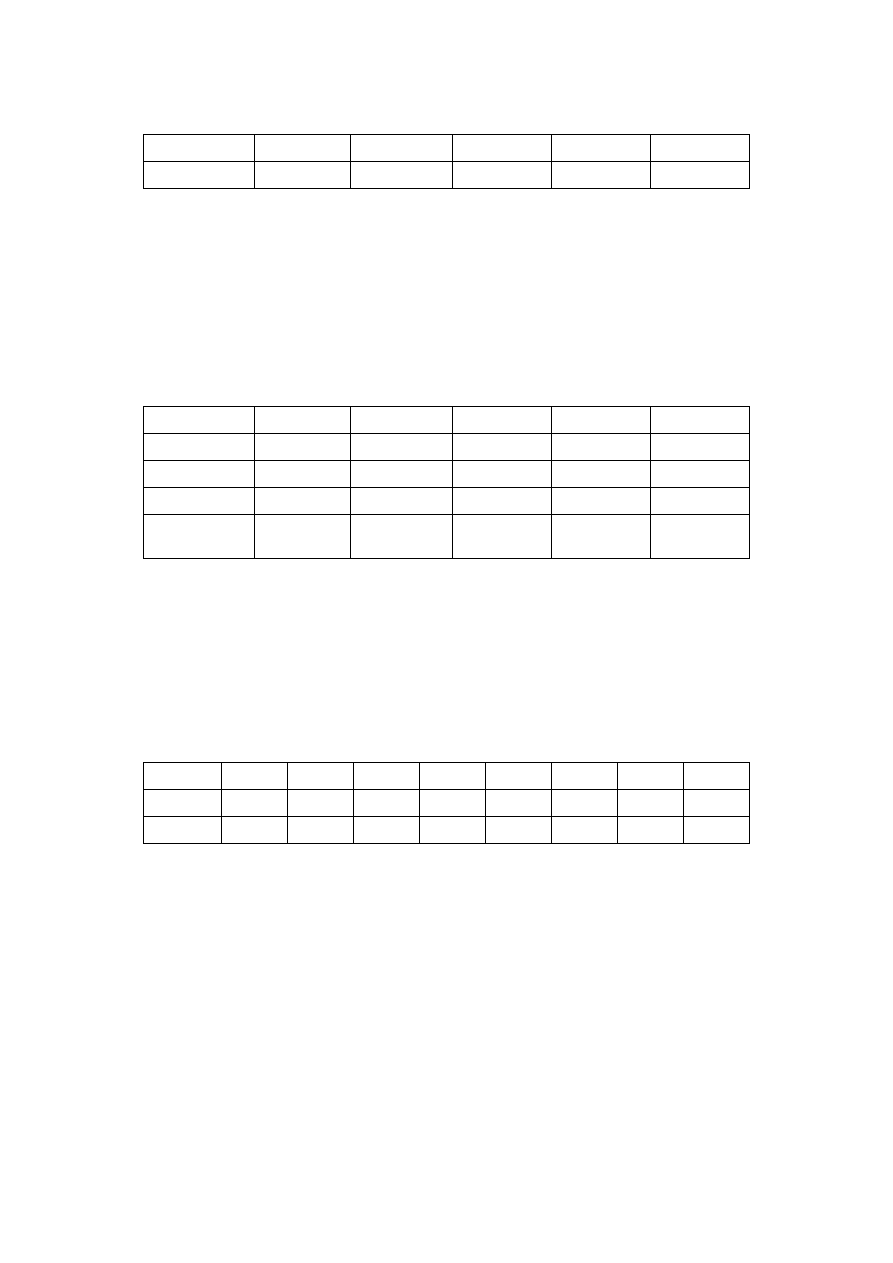
Potęga 6

4

6

3

6

2

6

1

6

0

Wartość 1296 216

36

6

1

Sprawdź, czy wiesz, dlaczego kolumny reprezentują takie wartości. Pamiętaj, że 6

3

= 6*6*6 = 216.

Aby wyznaczyć reprezentację liczby 986 w systemie szóstkowym, zaczniemy od kolumny 5. Ile
1296-tek mieści się w 986? Żadna, więc w kolumnie 5. zapisujemy 0. Jeśli podzielimy 968 przez
216, to otrzymamy 4 z resztą 104. W kolumnie 4. znajdzie się cyfra 4. To jest, ta kolumna będzie
reprezentować 4*216 (864).

Musimy teraz wyrazić pozostałą wartość (968-864 = 104). Podzielenie 104 przez 36 daje 2 z resztą
32. Kolumna trzy będzie zawierać cyfrę 2. Podzielenie 32 przez 6 daje 5 z resztą 2. Tak więc
otrzymujemy liczbę 4252

6

.

Kolumna 5

4

3

2

1

Potęga 6

4

6

3

6

2

6

1

6

0

Wartość 1296 216

36

6

1

986 szóstkowo

0

4

2

5

2

Wartość
dziesiętna

0 4*216=864

2*36=72

5*6=30

2*1=2

864+72+30+2 = 968

Dwójkowo

Ostatecznym etapem tego systemu jest system o podstawie 2. Są w nim tylko dwie cyfry: 0 i 1.
Kolumny to

Kolumna

8 7 6 5 4 3 2 1

Potęga 2

7

2

6

2

5

2

4

2

3

2

2

2

1

2

0

Wartość

128 64 32 16 8 4 2 1

Aby zamienić liczbę 88 na liczbę dwójkową, postępujemy zgodnie z tą samą procedurą: w 88 nie
ma 128-ek, więc w kolumnie ósmej wpisujemy cyfrę 0.

W 88 jest jedna sześćdziesiątka czwórka, więc do kolumny 7 wpisujemy cyfrę 1. Zostaje nam
reszta wynosząca 24. W 24 nie ma trzydziestek dwójek, więc kolumna 6 zawiera cyfrę 0.

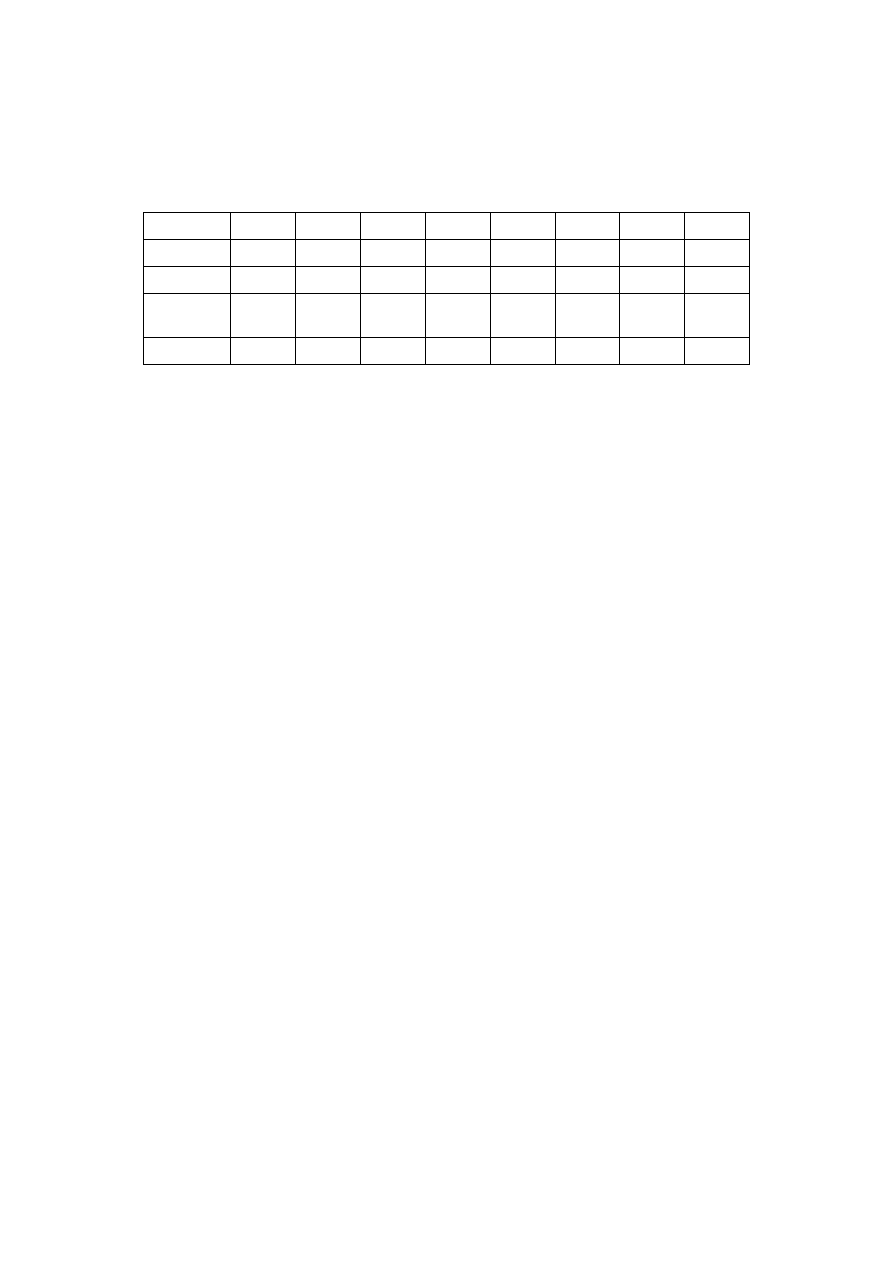
W 24 mieści się jedna szesnastka, więc kolumna pięć zawiera cyfrę 1. Pozostaje nam reszta 8. W 8
jest jedna ósemka, więc kolumna 4. będzie zawierać cyfrę 1. Nie ma już żadnej reszty, więc
pozostałe kolumny będą zawierać zera.

Kolumna

8 7 6 5 4 3 2 1

Potęga 2

7

2

6

2

5

2

4

2

3

2

2

2

1

2

0

Wartość

128 64 32 16 8 4 2 1

88
dwójkowo

0 1 0 1 1 0 0 0

Wartość

0 64 0 16 8 0 0 0

Aby sprawdzić wynik, zamieńmy to z powrotem na liczbę o podstawie dziesięć:

1 * 64 = 64
0 * 32 = 0
1 * 16 = 16
1 * 8 = 8
0 * 4 = 0
0 * 2 = 0
0 * 1 = 0
88

Dlaczego podstawa 2?

Podstawa 2 pełni ważną rolę w programowaniu, gdyż dokładnie odpowiada temu, co może być w
komputerze reprezentowane. Komputery w rzeczywistości nie wiedzą nic o literach, cyfrach,
instrukcjach czy programach. W swoim rdzeniu są jedynie układami elektronicznymi, w których w
danym punkcie może występować większe albo bardzo małe napięcie.

Aby zachować prostotę konstrukcji, inżynierowie nie traktują napięcia jako skali relatywnej
(niskie napięcie, wyższe napięcie, bardzo wysokie napięcie czy ogromne napięcie), ale raczej jako
skalę o dwóch stanach („napięcie wystarczające” lub „napięcie niewystarczające”). Zamiast jednak
mówić „wystarczające” lub „niewystarczające”, mówią po prostu „tak” lub „nie”. Tak lub nie,
czyli prawda lub fałsz, może być reprezentowane jako 1 lub 0. Zgodnie z konwencją, 1 oznacza
prawdę lub Tak, ale to tylko konwencja; równie dobrze mogłoby oznaczać fałsz lub Nie.

Gdy zauważysz tę regułę, potęga systemu dwójkowego objawi się w całej okazałości: za pomocą
zer i jedynek można oddać stan każdego układu (jest napięcie lub go nie ma). Wszystkie
komputery znają tylko dwa stany: włączony = 1 oraz wyłączony = 0.

Bity, bajty, nible

Gdy podjęto decyzjęm by reprezentować prawdę i fałsz jedynkami i zerami, bardzo ważne stało
się pojęcie bitu (od binary digit, cyfra binarna

1

). Ponieważ pierwsze komputery mogły przesłać

jednocześnie osiem bitów, więc naturalnie pierwszy kod zapisywano, używając liczb 8-bitowych
— nazywanych bajtami (ang. byte).

UWAGA W gwarze programistycznej połówka bajtu (4 bity) jest nazywana niblem (ang. nybble).

Za pomocą ośmiu bitów można reprezentować do 256 różnych wartości. Dlaczego? Sprawdź
kolumny: gdy wszystkie osiem bitów jest ustawionych (1), wartością jest 255
(128+64+32+16+8+4+2+1). Jeśli nie jest ustawiony żaden (wszystkie bity są wyzerowane, czyli
mają wartość 0), wtedy wartością jest 0. Od 0 do 255 to 256 możliwych stanów.

Co to jest KB?

Okazuje się, że 2

10

(1024) to w przybliżeniu 10

3

(1 000). Ten związek był zbyt dobry, aby go nie

zauważyć, więc komputerowi specjaliści zaczęli nazywać 2

10

bajtów kilobajtem, czyli KB,

zapożyczając przedrostek kilo (k) oznaczający tysiąc. Dla wskazania, że chodzi o wartość 1024, a
nie 1000, „komputerowe kilo” oznacza się dużą literą K.

Również 1024*1024 (1 048 576) jest na tyle bliskie miliona, że otrzymało oznaczenie 1 MB, czyli
megabajt, zaś 1 024 megabajtów jest nazywanych gigabajtem (giga to przedrostek oznaczający
tysiąc milionów, czyli miliard).

Liczby dwójkowe

Komputery kodują każdą wartość za pomocą zer i jedynek. Instrukcje maszynowe są zakodowane
jako serie jedynek i zer, następnie są interpretowane przez układy procesora. Zestawy zer i
jedynek mogą być zamienione na liczby, ale traktowanie tych liczb jako posiadających jakieś
specyficzne znaczenie byłoby błędem.

Na przykład, procesor Intel 8086 interpretuje wzorzec bitów 1001 0101 jako instrukcję.
Oczywiście, możemy zamienić te bity na liczbę dziesiętną 149, ale ta wartość sama w sobie nie ma
dla nas żadnego znaczenia.

Czasem liczby są instrukcjami, czasem wartościami, a czasem kodami. Jednym z ważnych,
standardowych zestawów kodów jest zestaw ASCII. W zestawie tym każda litera, cyfra i znak
przestankowy ma przydzieloną siedmiobitową reprezentację. Na przykład, mała litera „a” jest

1

A także od „kawałka” informacji, gdyż bit to po angielsku także „kawałek.” —

przyp. tłum.

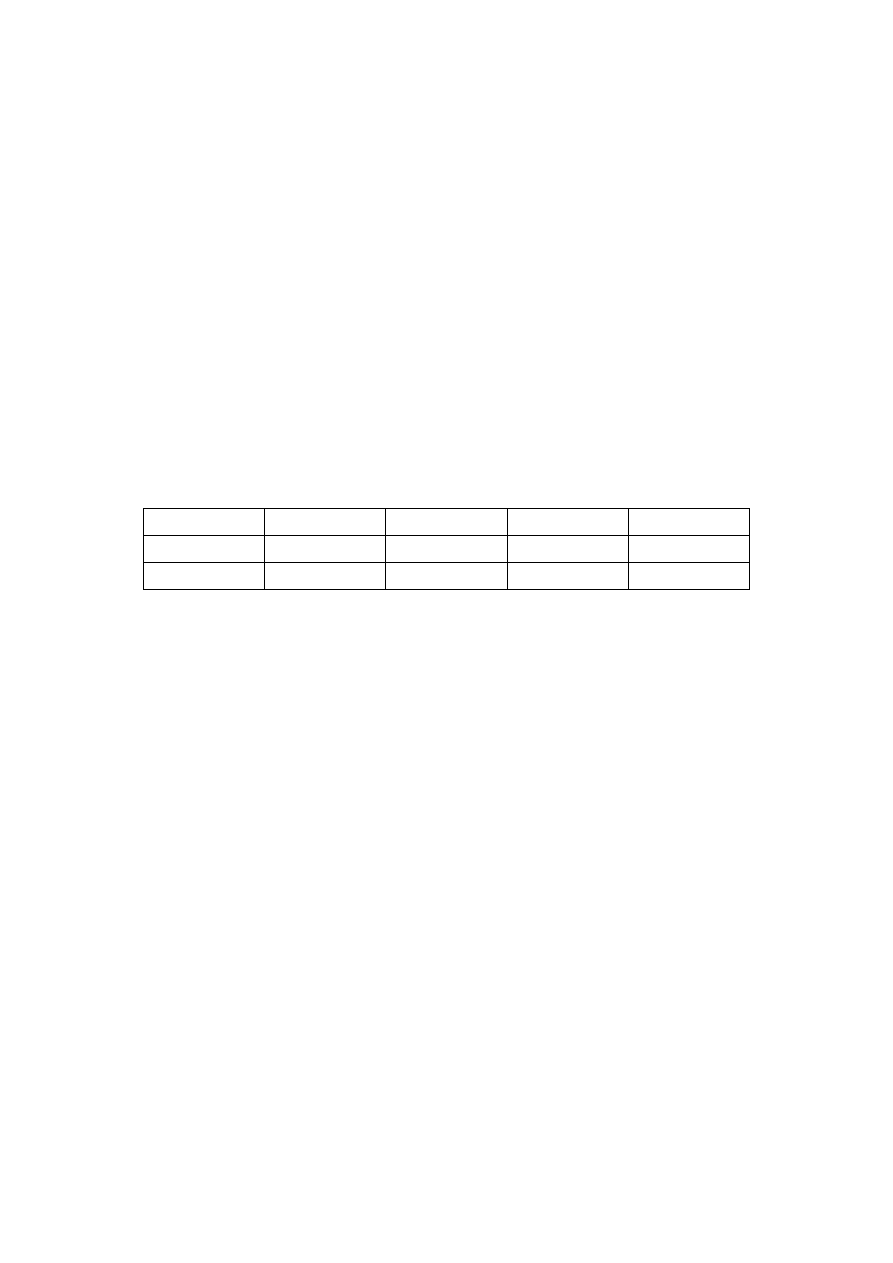
reprezentowana jako 0110 0001. Nie jest to liczba, choć można ją zamienić na liczbę 97 w
systemie dziesiętnym (64+32+1). Właśnie w tym sensie mówi się, że litera „a” to 97 w ASCII,
choć w rzeczywistości kodem litery „a” jest dwójkowa reprezentacja wartości 97 (0110 0001), a
wartość dziesiętna 97 stanowi tylko ułatwienie dla ludzi.

Szesnastkowo

Ponieważ liczby dwójkowe są trudne do odczytania, stworzono prostszy sposób ich
reprezentowania. Przejście z systemu dwójkowego na dziesiętny wymaga sporo przeprowadzenia
skomplikowanych operacji na liczbach, ale okazuje się, że przejście z podstawy 2 do podstawy 16
jest proste, gdyż istnieje bardzo dobry skrót.

Aby zrozumieć ten proces, musisz najpierw zrozumieć system o podstawie 16, zwany systemem
szesnastkowym lub heksadecymalnym. Przy podstawie 16 mamy do dyspozycji szesnaście cyfr: 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E oraz F. Ostatnie sześć znaków, litery od A do F, zostały
wybrane, ponieważ łatwo można je wpisać z klawiatury (i wyświetlić na wyświetlaczu
siedmiosegmentowym). Kolumny w systemie szesnastkowym to:

Kolumna

4 3 2 1

Potęga 16

3

16

2

16

1

16

0

Wartość 4096

256

16

1

Aby zamienić liczbę z systemu szesnastkowego na dziesiętny, możemy mnożyć. Tak więc liczba
F8C reprezentuje:

F * 256 = 15 * 256 = 3840
8 * 16 = 128
C * 1 = 12 * 1 = 12
3980

(Pamiętaj, że F

16

to 15

10

)

Najlepiej przeprowadzić zamianę liczby FC na dwójkową, zamieniając ją najpierw na liczbę
dziesiętną, a następnie na dwójkową:

F * 16 = 15 * 16 = 240
C * 1 = 12 * 1 = 12
252

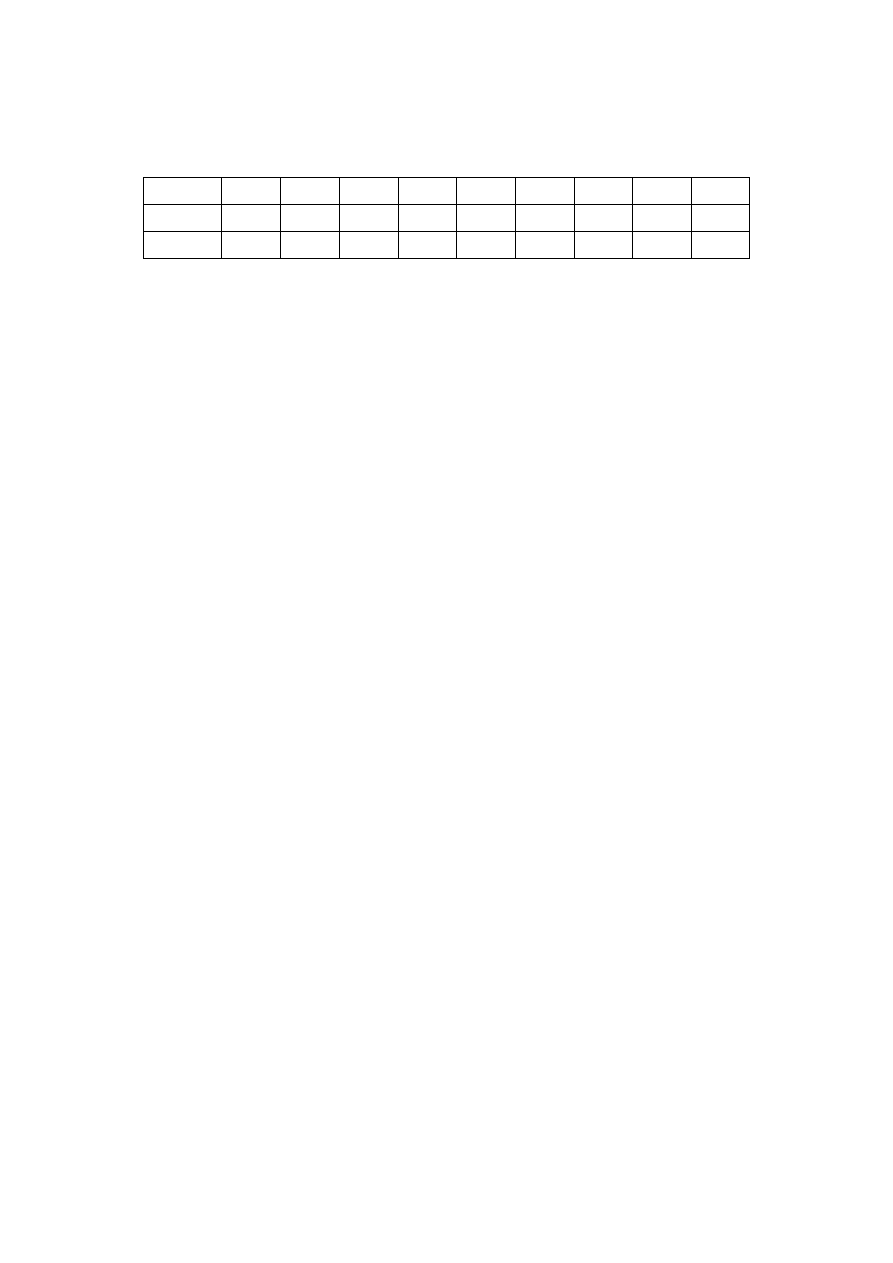
Zamiana 252 na liczbę dwójkową wymaga użycia tablicy:

Kolumna

9 8 7 6 5 4 3 2 1

Potęga 2

8

2

7

2

6

2

5

2

4

2

3

2

2

2

1

2

0

Wartość

256

128

64 32 16 8 4 2 1

Nie ma 256-ek.

1*128 = 128. 252–128 = 124

1*64 = 64. 124–64 = 60

1*32 = 32. 60–32 = 28

1*16 = 16. 28–16=12

1*8 = 8. 12–8 = 4

1*4 = 4. 4–4 = 0

0*2 = 0

0*1 = 0

124+60+28+12+4 = 252.

Tak więc FC

16

w systemie dwójkowym to 1111 1100.

Okazuje się, że gdy potraktujemy tę liczbę dwójkową jako dwa zestawy czterech cyfr (1111 1100),
możemy dokonać „magicznego” przekształcenia.

Prawy zestaw to 1100. Dziesiętnie to 12, a szesnastkowo C. (1*8 + 1*4 + 0*2 + 0*1).

Lewy zestaw to 1111, czyli dziesiętnie 15, a szesnastkowo F.

Tak więc mamy:

1111 1100
F C

Umieśćmy dwie cyfry szesnastkowe razem i otrzymamy FC, które jest wartością szesnastkową
binarnej liczby 1111 1100. Ten skrót działa! Możemy wziąć liczbę binarną o dowolnej długości,
podzielić ją na zestawy po cztery bity, zamienić każdy z zestawów na cyfrę szesnastkową i
połączyć otrzymane cyfry tak, aby otrzymać wynik w systemie szesnastkowym. Oto dużo większa
liczba:

1011 0001 1101 0111

Aby sprawdzić, czy nasze założenia są właściwe, najpierw zamieńmy tę liczbę na dziesiętną.

Wartości kolumn możemy obliczyć poprzez ich podwajanie. Kolumna położona najbardziej na
prawo ma wartość 1, następna 2, następne 4, 8, 16 i tak dalej.

Zaczniemy od kolumny położonej najbardziej na prawo, która, licząc dziesiętnie, ma wagę 1.
Mamy jedynkę, więc ta kolumna jest warta 1. Następna kolumna ma wagę 2. W tej kolumnie także
mamy jedynkę, więc dodajemy 2 i otrzymujemy sumę wynoszącą 3.

Następna kolumna ma wagę 4 (podwajamy wagę poprzedniej kolumny). W związku z tym
otrzymujemy 4+2+1=7.

Kontynuujemy tę procedurę dla kolejnych kolumn:

1x1 1
1x2 2
1x4 4
0x8 0
1x16 16
0x32 0
1x64 64
1x128 128
1x256 256
0x512 0
0x1024 0
0x2048 0
1x4096 4 096
1x8192 8 192
0x16384 0
1x32768 32 768
Razem 45 527

Zamiana na liczbę szesnastkową wymaga zastosowania tablicy z wartościami szesnastkowymi.

Kolumna

4 3 2 1

Potęga 16

3

16

2

16

1

16

0

Wartość 4096

256

16

1

Mamy jedenaście 4096-ek (45 056) z resztą 471. W 471 jest jedna 256-ka z resztą 215. W 215 jest
trzynaście 16-ek (208) z resztą 7. Tak więc szukana liczba szesnastkowa to B1D7.

Sprawdzamy obliczenia:

B (11) * 4096 = 45 056
1 * 256 = 256
D (13) * 16 = 208
7 * 1 = 7
Razem 45 527

Skrócone rozwiązanie polega na podzieleniu pierwotnej liczby dwójkowej 1011000111010111 na
grupy po cztery bity: 1011 0001 1101 0111. Każdą z grup można wtedy przedstawić jako cyfrę
szesnastkową:

1011 =
1 x 1 = 1
1 x 2 = 2
0 x 4 = 0
1 x 8 = 8
Razem 11
Hex: B

0001 =
1 x 1 = 1
0 x 2 = 0
0 x 4 = 0
0 x 8 = 0
Razem 1
Hex: 1

1101 =
1 x 1 = 1
1 x 2 = 0
1 x 4 = 4
1 x 8 = 8
Razem 13
Hex: D

0111 =
1 x 1 = 1
1 x 2 = 2
1 x 4 = 4
0 x 8 = 0
Razem 7
Hex: 7

Razem Hex: B1D7

Voila! Skrócona procedura zamiany, liczby dwójkowej na szesnastkową, dała nam ten sam wynik,
co wersja dłuższa.

Przekonasz się, że programiści bardzo często korzystają z liczb szesnastkowych; ale okaże się
także, że bardzo długo można się bez nich obejść!