Temat: Klasyfikacja i ogólna charakterystyka ruchu ciała, zasady dynamiki, drgania.

1. Ruch ciała

Ruch określamy ogólnie jako zmianę położenia ciała materialnego względem układu odniesienia, tj.
względem innego ciała lub zbioru ciał uważanych za pozostające w spoczynku.
Ruch bezwzględny – jest ruchem odniesionym względem układu stałego, (czyli pozostającego w
bezwzględnym spoczynku)
Ruch względny – jest to ruch rozpatrywany względem ruchomego układu odniesienia
Tor punktu – jest to linia utworzona przez kolejne położenia poruszającego się punktu
Ruch prostoliniowy występuje jako: jednostajny i zmienny.
Ruch krzywoliniowy występuje również jako: jednostajny i zmienny.

2. Ruch prostoliniowy jednostajny

Stosunek drogi s do czasu t, w którym ta droga została przebyta,
nazywamy prędkością poruszającego się punktu

.

v =

t

s

gdzie: v – prędkość, s – droga, t – czas

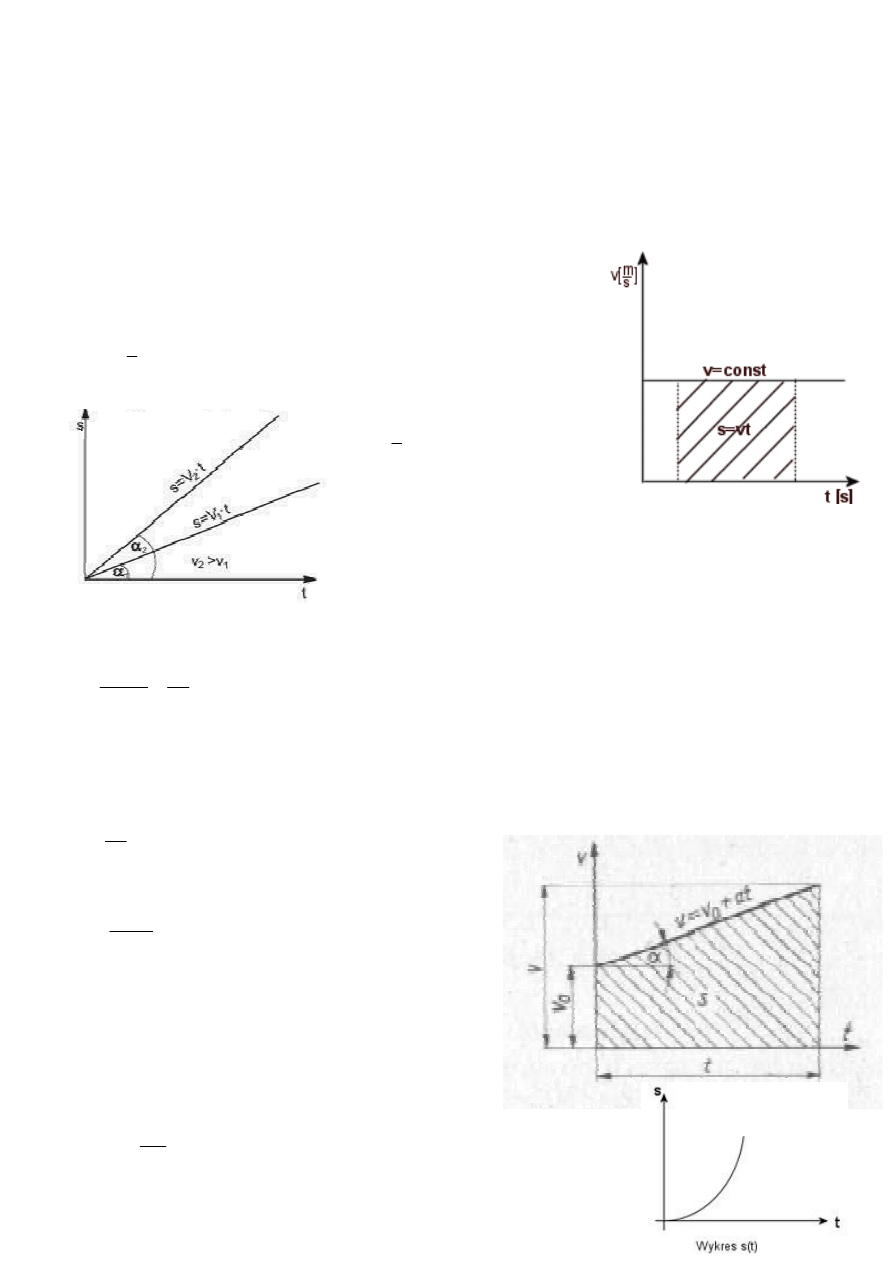
s = v * t

tg α =

t

s

, czyli tg α = v

Tangens kąta nachylenia linii
wykresu drogi do osi odciętych przedstawia w przyjętej podziałce
prędkość danego ruchu.

3. Ruch prostoliniowy zmienny

Stosunek przyrostu drogi ∆s do przyrostu czasu ∆t przedstawia wartość prędkości średniej punktu.

gdzie ∆s – przyrost (odcinka) drogi, ∆t – przedział czasu

W ruchu zmiennym prędkość ciała zmienia się, jeśli prędkość rośnie to mamy ruch przyśpieszony, jeżeli
ruch maleje to mamy ruch opóźniony.
Ruch jednostajnie zmienny – to taki ruch, w którym przyśpieszenie jest wartością stałą.
Ruch niejednostajnie zmienny – to taki ruch, w którym przyśpieszenie w czasie ruchu rośnie lub maleje.

a =

t

v

∆

∆

a – przyśpieszenie (które przyjmuje wartości

dodatnie w ruchu jednostajnie przyśpieszonym oraz
ujemne w ruchu jednostajnie opóźnionym).

a =

t

v

v

0

−

gdzie: t – całkowity czas trwania ruchu od

położenia A

0

do A, v

0

– prędkość początkowa, którą

ciało ma w punkcie A

0

, v – prędkość w dowolnym

punkcie A.
v = v

0

+ a*t

gdzie:
t – całkowity czas trwania ruchu od położenia A

0

do A,

v

0

– prędkość początkowa, którą ciało ma w punkcie A

0

,

a – przyśpieszenie w ruchu jednostajnie zmiennym

s = s

0

+

2

2

at gdzie: s

0

– droga początkowa, a – przyśpieszenie w ruchu

jednostajnie zmiennym,
t – czas trwania ruchu.

t

s

t

t

s

s

v

∆

∆

=

−

−

=

1

2

1

2

4. Ruch krzywoliniowy

Ruch krzywoliniowy jednostajny – to taki ruch, w
którym wartość wektora nie zmienia się, a zmienia się
kierunek i nachylenie,
Ruch krzywoliniowy zmienny – w takim ruchu oprócz
zmiany kierunku i nachylenia wektora prędkości zmienia
się również wartość prędkości.

a

śr

=

t

v

∆

∆

→

5. Ruch jednostajny po okręgu

Punkt materialny porusza się ruchem jednostajnym po okręgu
o promieniu r, przebywając w równych odstępach czasu t
równe drogi wg łuków A

0

A

1

, A

1

A

2

, A

2

A

3

.

v =

t

s

gdzie: s – droga, t – czas trwania ruchu.

- droga jest łukowa więc:
s = r * α gdzie: r – promień łuku,
α – kąt (w radianach) który przebył punkt to:

v = r

t

α

Prędkość kątowa – jest to stosunek kąta α (w radianach), który
przebył punkt w czasie t, do wartości tego czasu

ω =

t

α

⎥⎦

⎤

⎢⎣

⎡

s

rad

Prędkość w ruchu obrotowym ma postać:
v = r * ω
gdzie: r – promień łuku, ω – prędkość kątowa

6. Ruch obrotowy jednostajny ciała sztywnego dookoła stałej osi

Prędkość kątowa (prędkość obrotowa)w ruchu jednostajnym jest stała. Wyrażamy ją w obr/min. przy
wykonaniu pełnego obrotu (tzn. 360

o

).

α = 360

o

= 2 π [rad] ω =

t

α

gdzie: α = 2 π, t = 1 min = 60 s. stąd: ω =

60

2

π

⎥⎦

⎤

⎢⎣

⎡

s

rad

- jeżeli ciało wykonuje n obrotów w czasie 1 min. to prędkość kątowa wynosi:

ω =

60

2 n

π

⎥⎦

⎤

⎢⎣

⎡

s

rad

czyli ω =

30

n

π

⎥⎦

⎤

⎢⎣

⎡

s

rad

- prędkość dowolnego punktu nie leżącego na osi obrotu zapisujemy: v = r * ω czyli:

ze wzoru ω =

60

2 n

π

mamy: v = r

60

2 n

π

a ponieważ 2r = d otrzymujemy: v =

60

d

n

π

[obr/min]

7. Zasady dynamiki

Zasada 1.
Ciało pozostaje w spoczynku lub w ruchu jednostajnym prostoliniowym, jeżeli na ciało nie działa żadna siła
lub działające siły się równoważą.
Wnioski:
- ciało w spoczynku nie może rozpocząć ruchu bez zadziałania na niego siły,
- jeżeli na poruszające się ciało nie działa żadna siła lub siły równoważą się, to może się ono poruszać
ruchem prostoliniowym jednostajnym,
- ruch jednostajny lub krzywoliniowy ciało może wykonywać tylko na skutek działania nań siły.

Zasada 2
Każda siła przyłożona do ciała nadaje temu ciału przyśpieszenie.
Przyśpieszenie jest skierowane wzdłuż linii działania przyłożonej siły, a
jego wartość jest wprost proporcjonalna do wartości siły.

→

→

= a

m

F

gdzie: F – siła działająca [N],

a – przyśpieszenie ruchu [1 m/s

2

], m – masa poruszającego się ciała [kg].

Zasada 3.
Każdemu działaniu towarzyszy równe, lecz przeciwnie zwrócone
przeciwdziałanie.
Siła G = sile R, siły się równoważą i pozostaje w spoczynku ciało m.

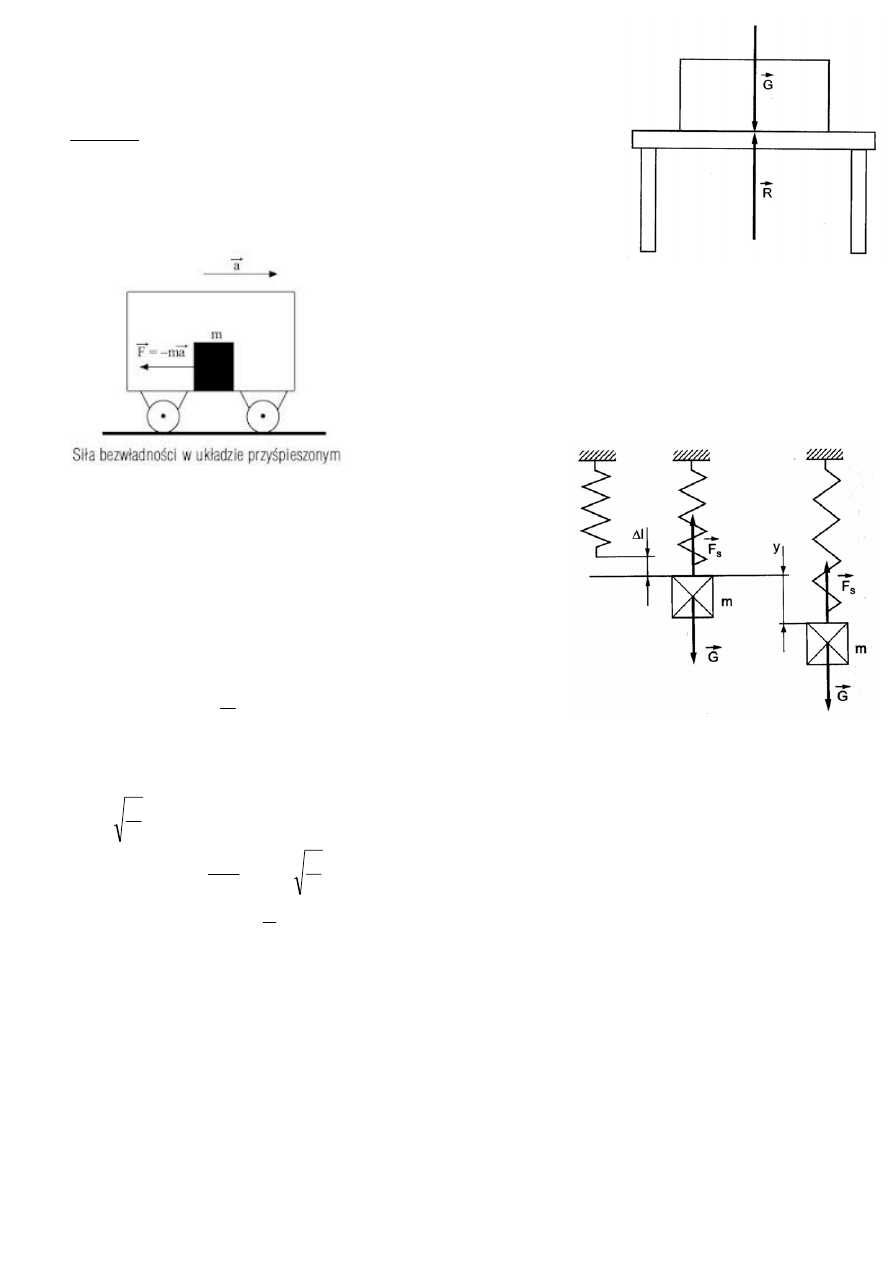
8. Siła bezwładności.

- występuje w początkowej fazie
ruchu, kiedy ciało rozpoczyna ruch lub w fazie ostatniej nagłego
zatrzymania.

→

−

=

a

m

→

b

F

gdzie: F

b

– siła bezwładności, m – masa ciała, a –

przyśpieszenie (opóźnienie) działające na ciało

9. Drgania swobodne.

F

s

= G = c ∆l gdzie: c – stała sprężyny, ∆l – wydłużenie

sprężyny pod wpływem zawieszonego ciężaru
F

s

= c (∆l + y) - przy uwzględnieniu wychylenia ze stanu

równowagi do położenia skrajnego,
y – wartość wychylenia sprężyny z położenia równowagi
- uwzględniając II zasadę dynamiki mamy:
m a = G – F

s

a: G = c ∆l F

s

= c (∆l + y) więc:

m a = c ∆l – c ∆l – c ∆l mamy: m a = c – ∆l

otrzymujemy: a = -

y

m

c

gdzie: c – stała sprężyny,

∆l – wydłużenie sprężyny pod względem zawieszonego ciężaru, m – masa, G – obciążenie sprężyny,
a – przyśpieszenie, y – wartość wychylenia sprężyny z położenia równowagi,
- częstość kątowa drgań swobodnych:

ω =

m

c

- okres drgań: T =

ω

π

2

=

c

m

π

2

T – okres drgań, czyli czas, w którym masa wykona pełny cykl drgania

- częstotliwość drgań: v =

T

1

10. Drgania wymuszone.

- powstają na skutek działania siły okresowo zmiennej, zwanej siłą wymuszającą, (przykład huśtania się na
huśtawce, czyli wprawiania jej w ruch poprzez wychylanie się)

11. Rezonans

- zjawisko bardzo niekorzystne zachodzące wtedy, gdy częstotliwość drgań własnych jest równa
częstotliwości pojawiania się siły zewnętrznej. W budowie maszyn oblicza się np. prędkości rezonansowe
i na ich podstawie dobiera się parametry maszyn tak żeby maszyna pracowała poza zakresem rezonansu.