Wprowadzenie do MATLABA

Dr in

ż. Mirosław Kwiesielewicz

Wydzia

ł Elektrotechniki i Automatyki

Politechnika Gda

ńska

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

2

Funkcje środowiska
MATLAB/SIMULINK

MATLAB - ang. matrix laboratory

Środowisko do obliczeń numerycznych



analiza numeryczna



operacje na macierzach



przetwarzanie sygna

łów



prezentacja graficzna wyników



przyborniki (toolbox) z procedurami i
funkcjami specyficznymi dla danej dziedziny
nauki

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

3

Podstawowe informacje o pakiecie
MATLAB



Pierwotnie napisany w FORTRANIE



Obecny MATLAB napisany w C przez firm

ę

MathWorks



Mo

żliwość tworzenia własnych procedur i

funkcji



Mo

żliwość dołączania procedur w języku C

lub FORTRAN

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

4

ŚRODOWISKO MATLAB/SIMULINK

MATLAB

SIMULINK

SIMULINK Extensions

•SIMULINK Accelerator

•Real-Time Workshop

Bloksets

MATLAB Extensions
•MATLAB Compiler
•MATLAB C Math

Library
Tollboxes
•Control System
•Communication
•Financial

•Frequency Domain

System Identification

•Fuzzy Logic

•High-Order Spectral

Analysis
•Image Processing
•LMI Control

•Model Predictive

Control

•-Analysis and

Synthesis

•NAG



Foundation

•Neural Network
•Optimization

•Partial Differential

Equations

•QFT Control Design
•Robust Control
•Signal Processing
•Spline
•Statistics
•Symbolic Math
•System Identification

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

5

Przyborniki 1



The Signal Processing Toolbox -
przetwarzanie sygna

łów; projektowanie i

analiza filtrów cyfrowych; estymacja widma
(analiza FFT)



The Control System Toolbox - systemy
sterowania i regulacji; odpowiedzi czasowe i
cz

ęstotliwościowe układów; przekształcenie

Laplace’a i Fouriera



Simulink - symulacja systemów
dynamicznych

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

6

Przyborniki 2



The System Identification Toolbox -
identyfikacja; estymacja modeli



The Optimization Toolbox - zagadnienia
optymalizacyjne z ograniczeniami



The Neural Network Toolbox - sieci
neuronowe



The Robust-Control Toolbox - uk

łady

sterowania krzepkiego

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

7

Przyborniki 3



The Fuzzy Logic Toolbox - logika rozmyta



The Genetic Algorithms Toolbox -
optymalizacja z wykorzystaniem algorytmów
genetycznych; nie jest to produkt firmy
Mathworks



The Model Predictive Control Toolbox

sterowanie predykcyjne

Nowo

ści: http://www.mathworks.com/

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

8

Ścieżka dostępu



MATLAB wykorzystuje definicj

ę ścieżki dostępu w

celu znalezienia M-plików



M-pliki znajduj

ą się w odpowiednio zorganizowanych

katalogach i podkatalogach



Je

śli wprowadzimy pewną nazwę nazwa w linii

MATLABA to interpretator linii polece

ń wykona

nast

ępujące czynności

– Sprawdzi, czy nazwa jest zmienn

ą

– Sprawdzi, czy nazwa jest funkcj

ą wbudowaną

– Poszuka pliku nazwa.m w bie

żącym katalogu

– Przejrzy katalogi, zgodnie z stawion

ą ścieżką

dost

ępu

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

9

Zmiana ścieżki dostępu



Mo

żna wyświetlić oraz zmienić ścieżkę

dost

ępu na czas bieżącej sesji wykorzystując

funkcje path, addpath i rmpath

– polecenie path zwraca bie

żące ustawienia

– path(s), gdzie s

łańcuchem ustawia

ścieżkę zgodnie z s

– addpath /home/lib oraz (path, ‘/home/lib’)

dodaj

ą nową ścieżkę do istniejącej

– rmpath /home/lib usuwa t

ą ścieżkę

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

10

Plik startowy - startup.m



W trakcie startu MATLAB automatycznie
wykonuje plik matlabrc.m oraz startup.m
o ile istnieje



Plik startup.m pozwala u

żytkownikowi

na dokonanie w

łasnych ustawień



Przyk

ładowo w pliku startup.m można

umie

ścić polecenie

addpath /home/me/mytools



Plik ten na pececie nale

ży umieścić w

katalogu

.../toolbox/local

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

11

Katalog bieżący



Do pracy z plikami *.M oraz *.MAT przyj

ęty

jest bie

żący katalog



Na pececie jest to katalog ustawiony w
skrócie do wywo

łania MATLABA



Zmiany bie

żącego katalogu na pececie

mo

żna dokonać za pomocą polecenia cd



Wy

świetlenie plików z danego katalogu

dokonuje si

ę poleceniem what

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

12

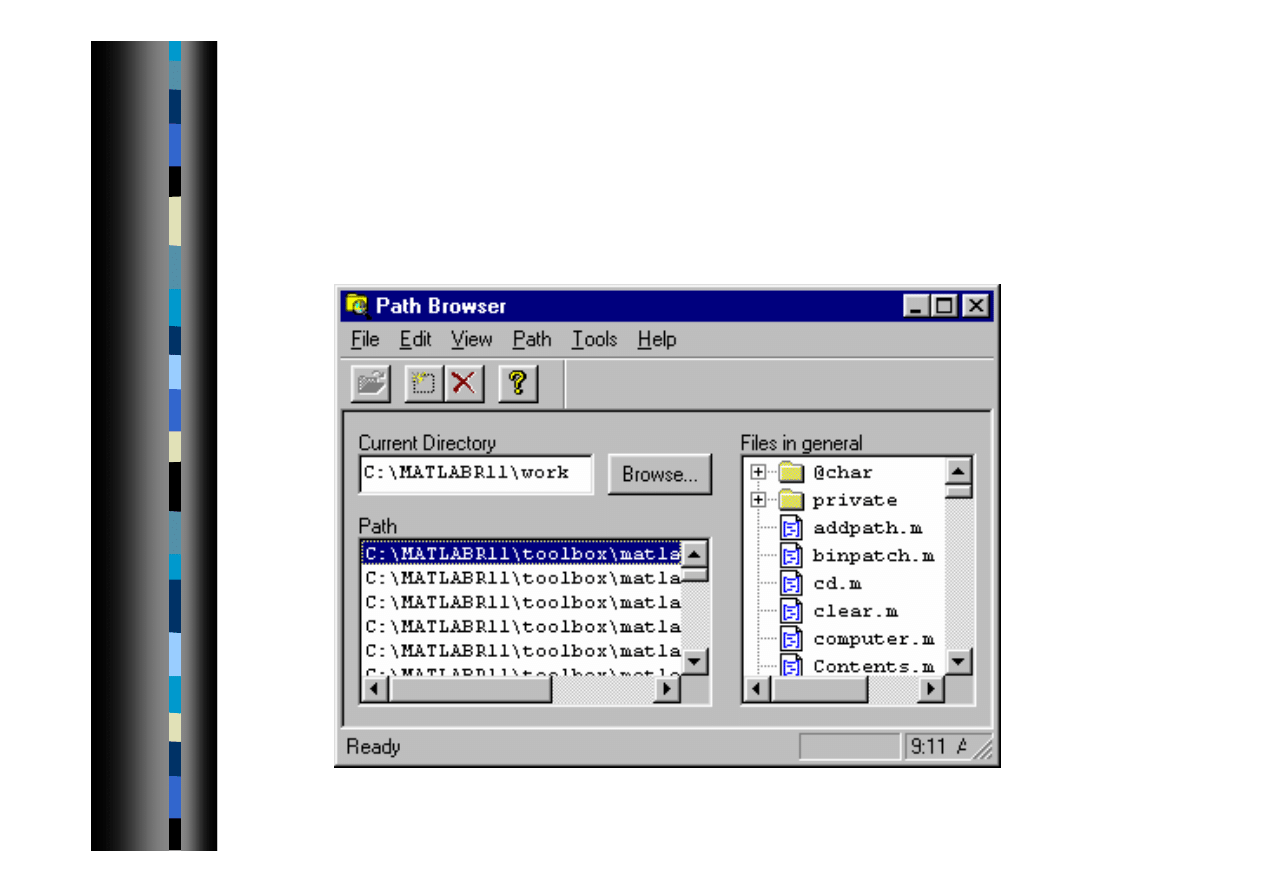
Przeglądarka ścieżek dostępu

Menu>File>PathBrowser

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

13

System podpowiedzi



Polecenie help

help magic



Okno help



Polecenie lookfor

lookfor inverse



Dokumentacja na kr

ążku lub sieci lokalnej



Dokumentacja ksi

ążkowa



Strony WWW firmy Mathworks

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

14

Typy i nazwy zmiennych



MATLAB operuje tylko na jednym typie
danych - na macierzach



Wektory i skalary s

ą szczególnymi

przypadkami macierzy, tzn. posiadaj

ącymi

jeden wiersz lub/i jedn

ą kolumnę



Nazwy zmiennych rozpoczynaj

ą się od litery,

a nast

ępnie może wystąpić dowolna

kombinacja liter, cyfr i znaków podkre

ślenia



Pami

ętanych jest 19 pierwszych znaków

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

15

Nazwy i definicje zmiennych



MATLAB rozró

żnia duże i małe litery w

nazwach zmiennych oraz polece

ń

– polecenia standardowe nale

ży pisać

ma

łymi literami

– do nazywania w

łasnych programów i

zmiennych mo

żna używać małych i dużych

liter



Definiowanie typu i wielko

ści zmiennej

odbywa si

ę automatycznie

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

16

Metody wprowadzania danych



konsola



generowane przez wewn

ętrzne lub

zewn

ętrzne funkcje lub procedury



zbiory dyskowe

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

17

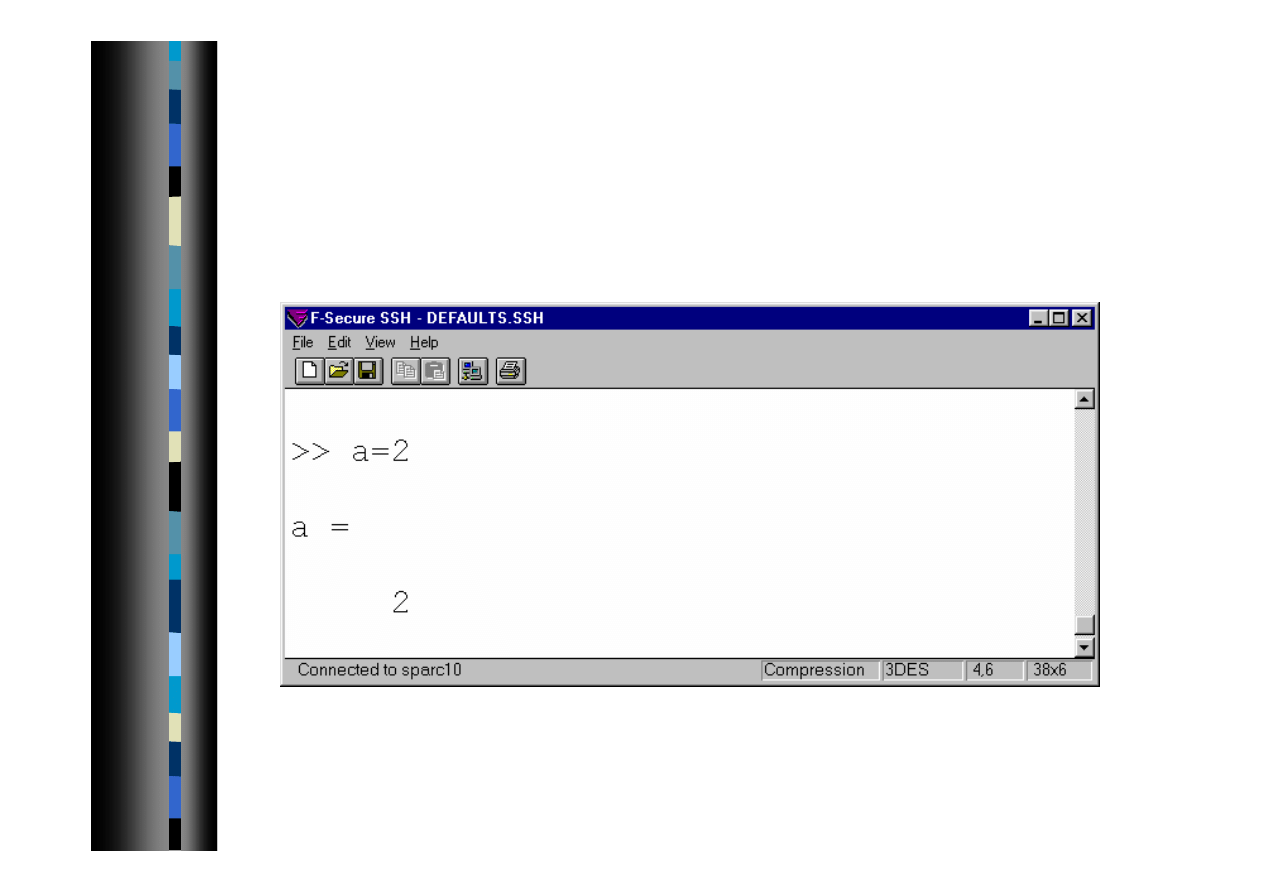
Wprowadzanie danych - skalar

Skalar

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

18

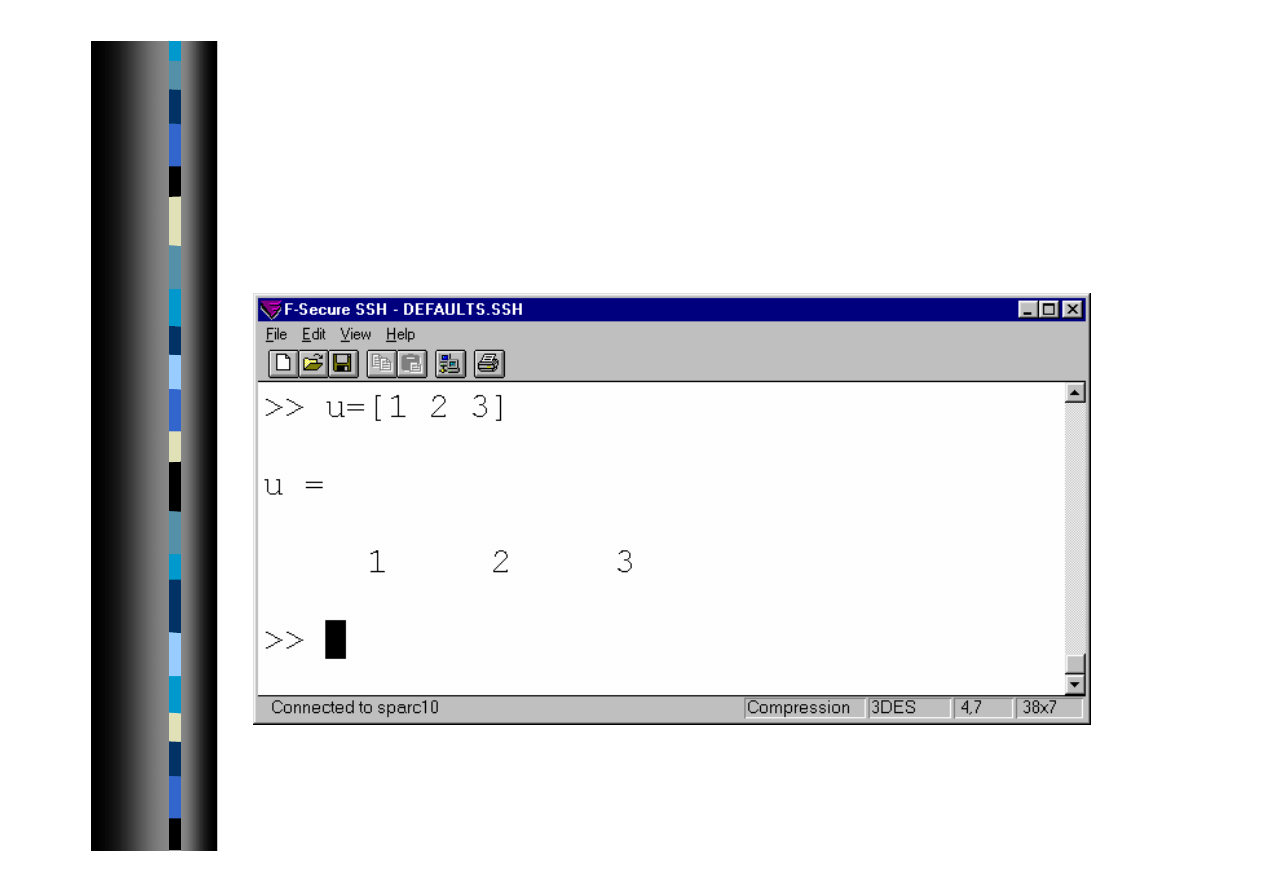
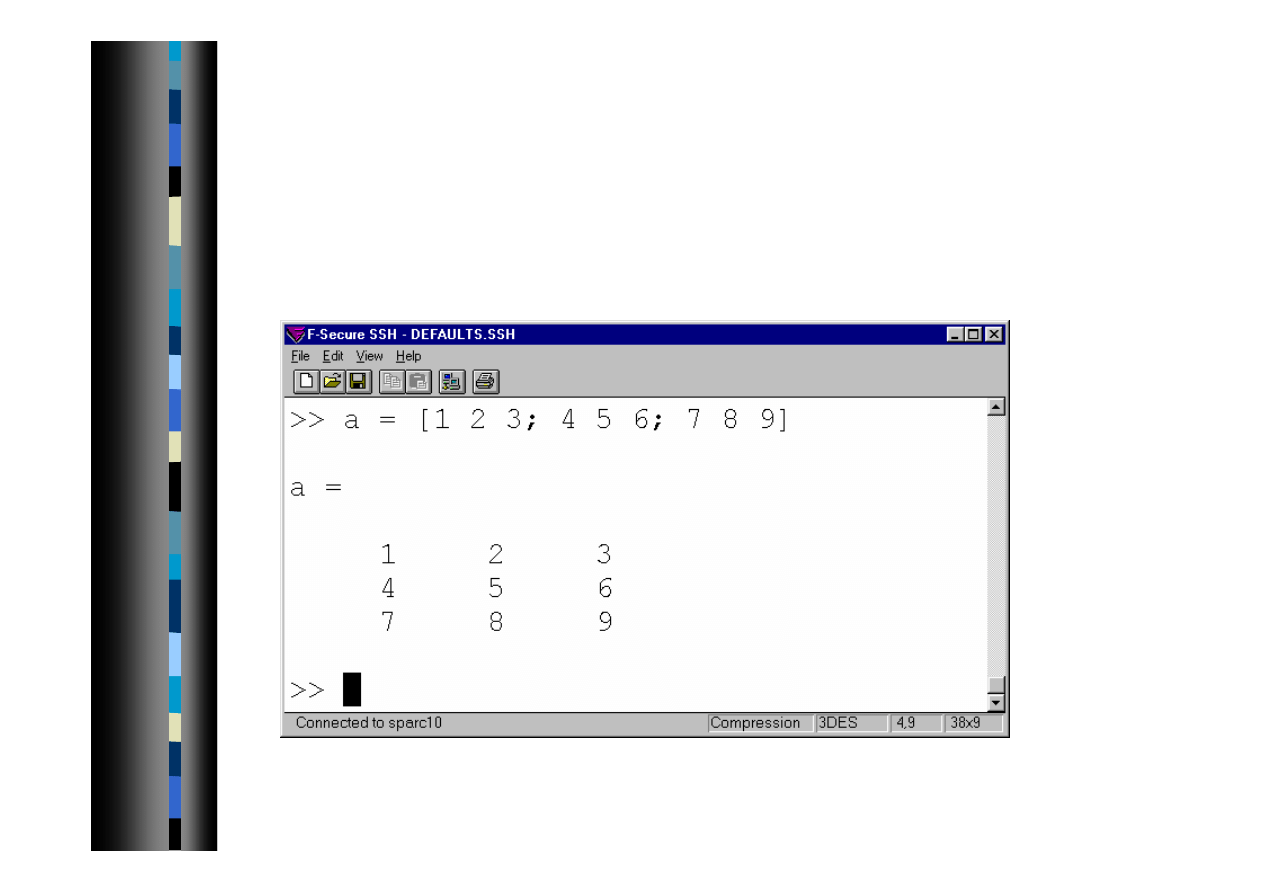
Wprowadzanie danych - wektor

Wektor

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

19

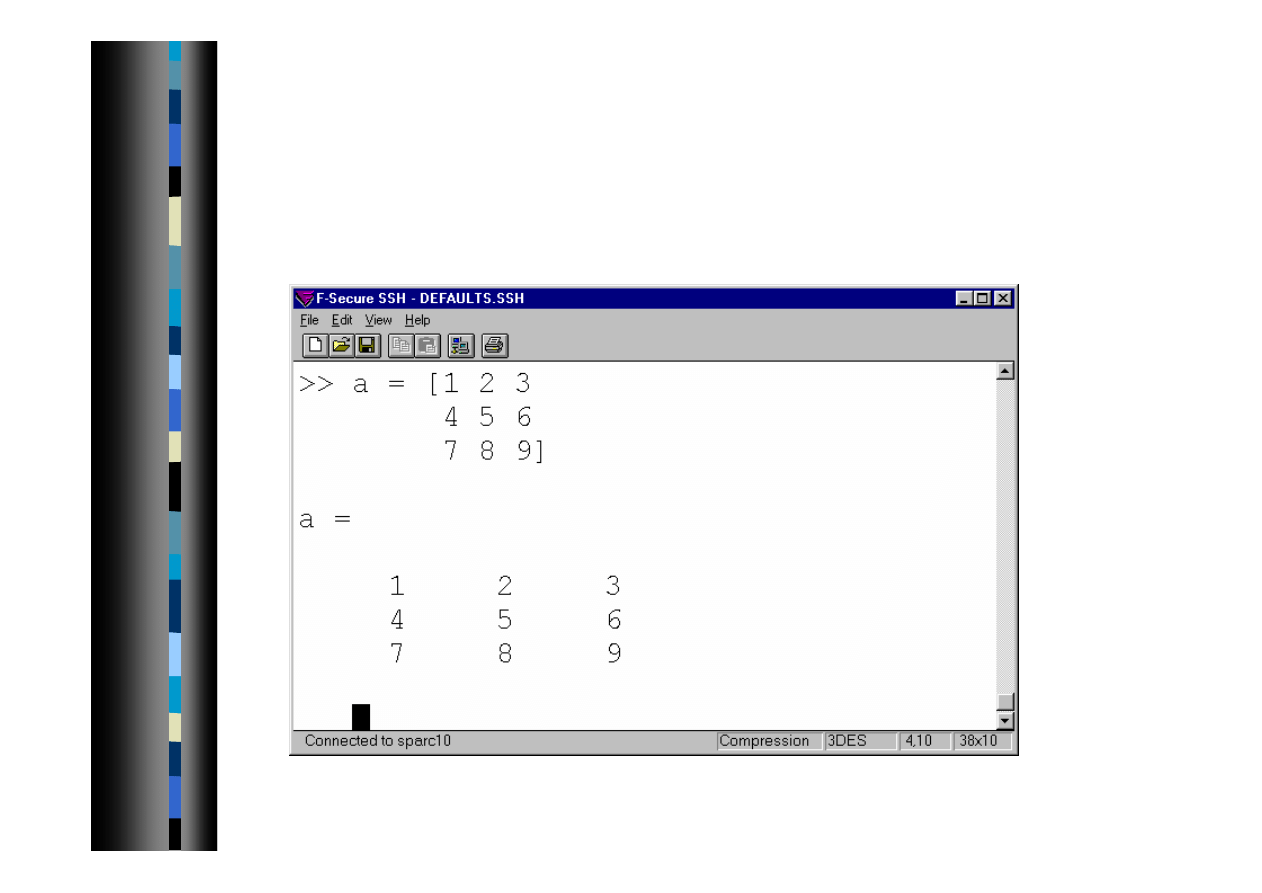
Wprowadzanie danych - macierz

Macierz

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

20

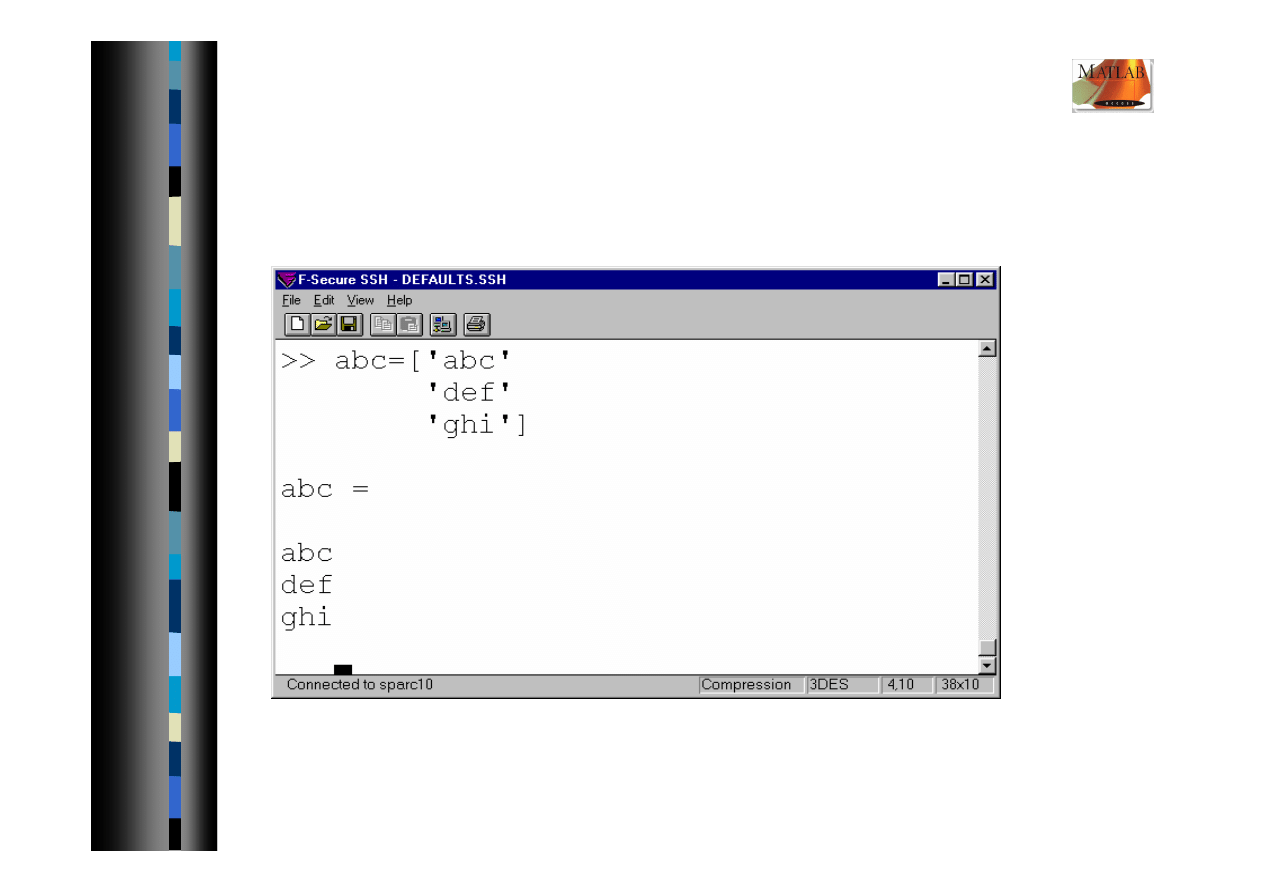
Wprowadzanie danych - macierz

Macierz

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

21

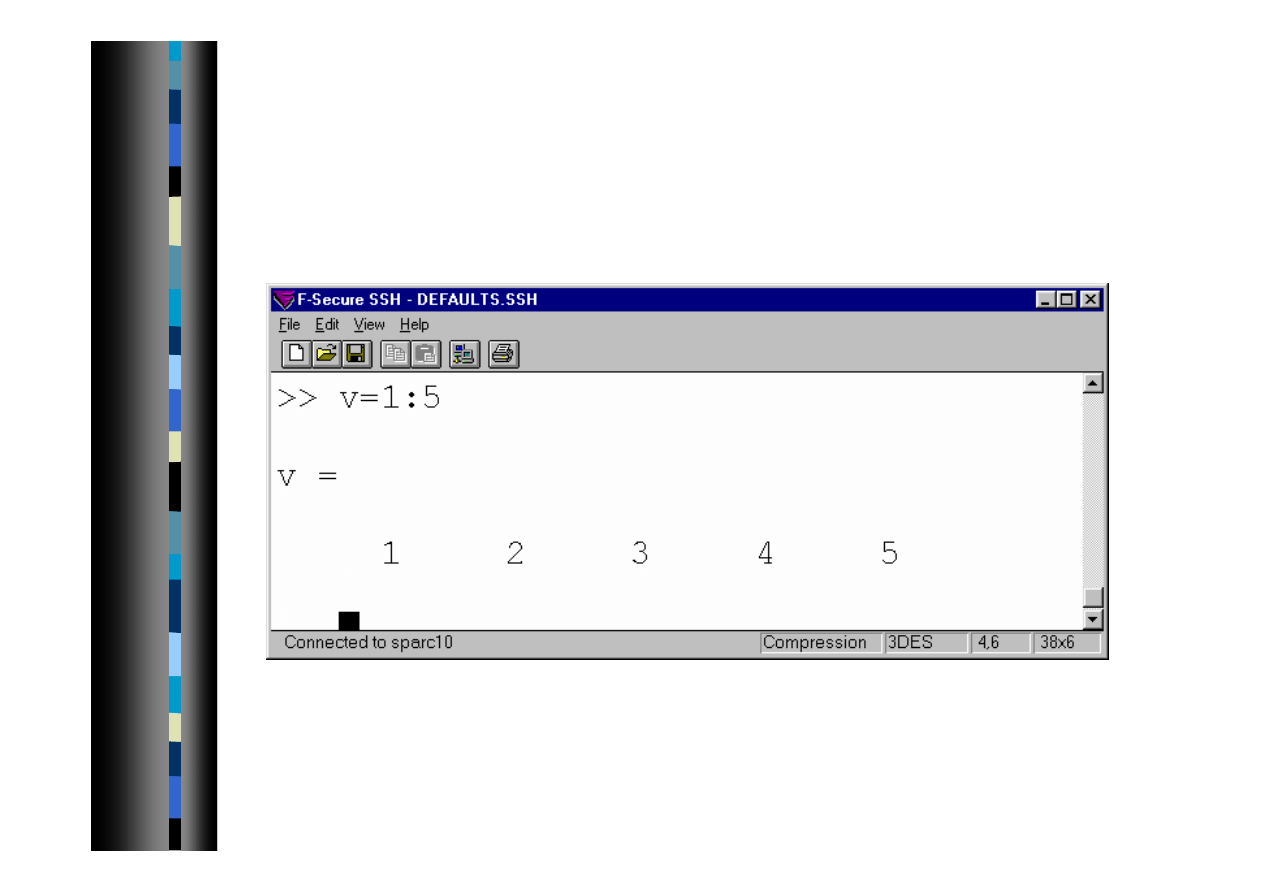
Wprowadzanie danych

- macierz znakowa

Macierz znakowa

Uwaga: macierz abc jest wymiaru 3x3

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

22

Wprowadzanie danych - c.d.

Szybkie tworzenie wektorów

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

23

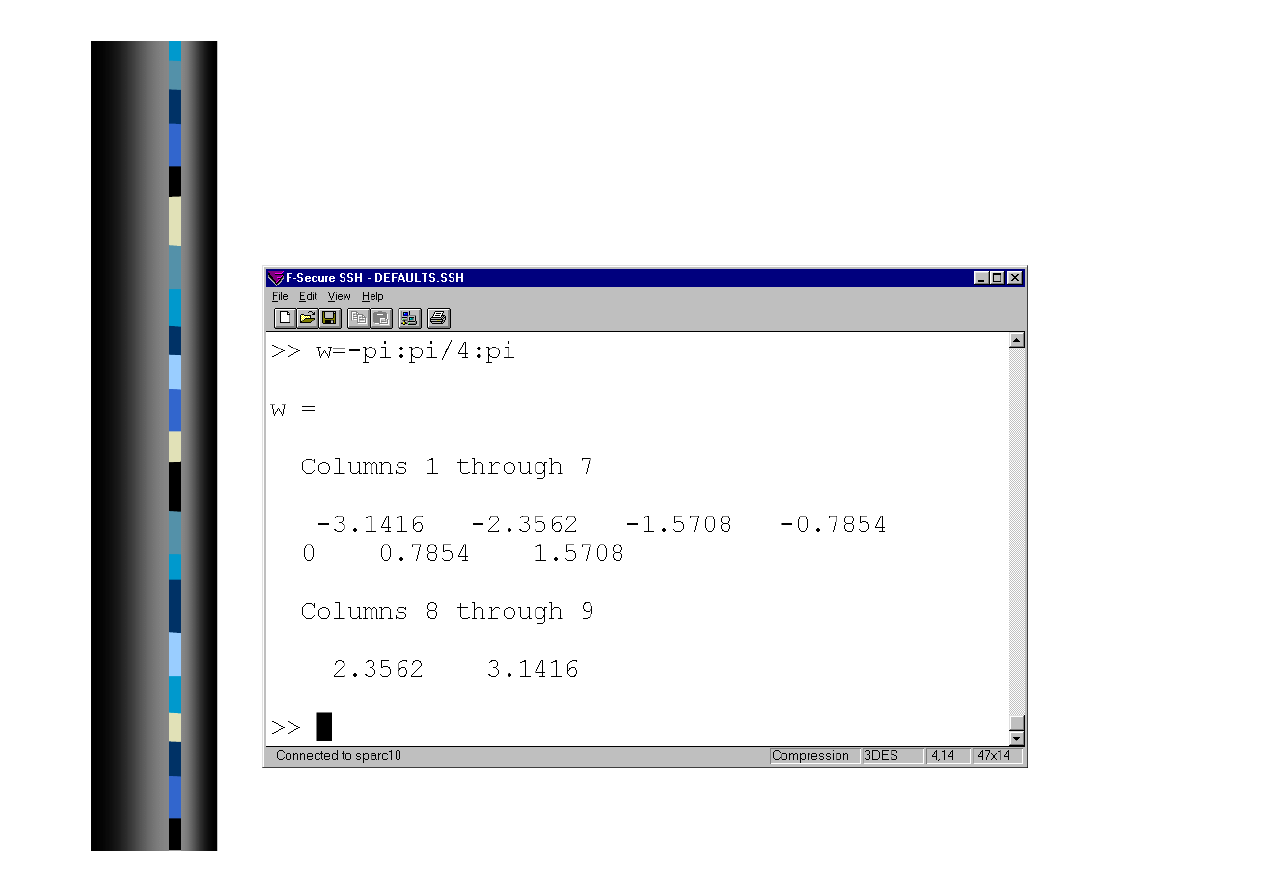
Wprowadzanie danych - c.d.

Szybkie tworzenie wektorów

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

24

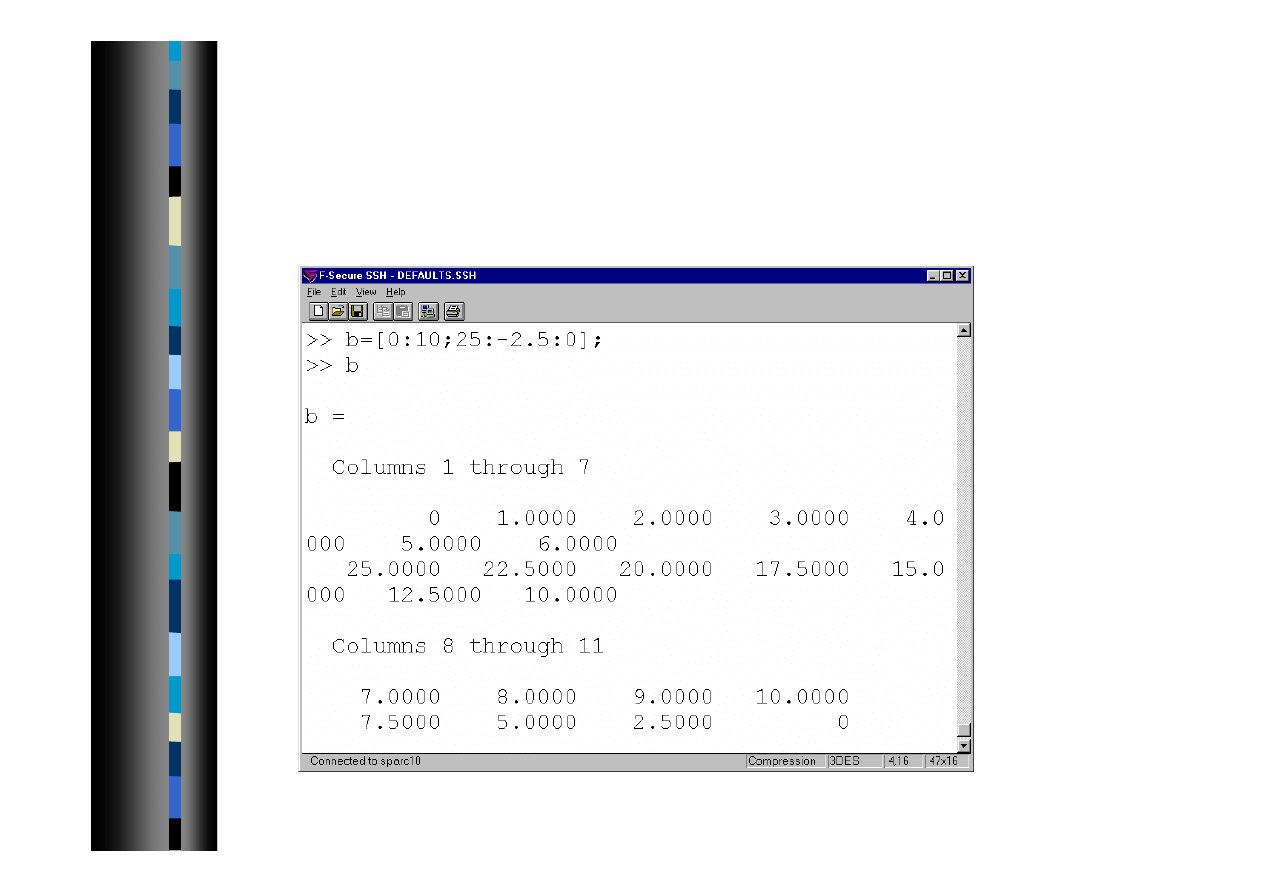
Wprowadzanie danych - c.d.

Szybkie tworzenie macierzy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

25

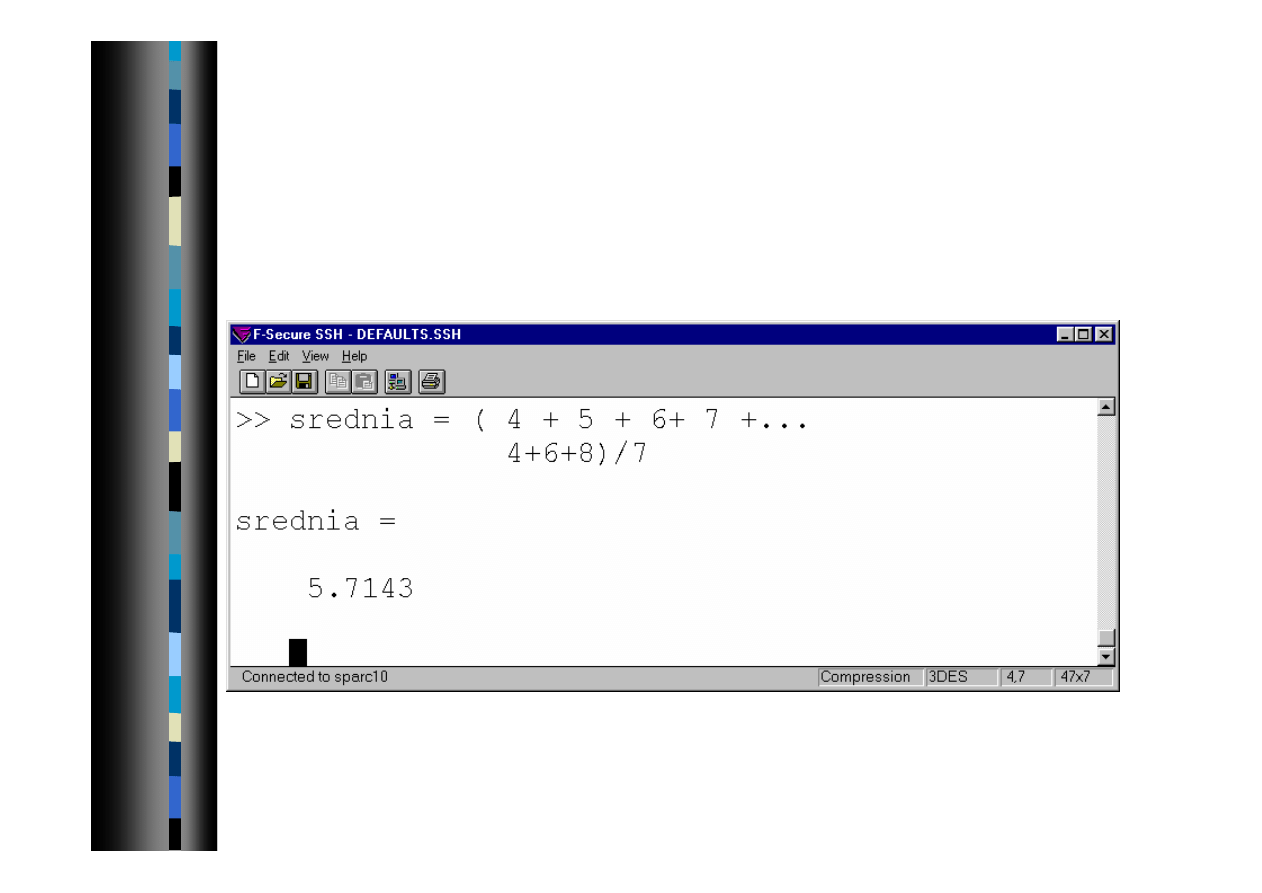
Wprowadzanie danych - c.d.

Obszerne polecenia

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

26

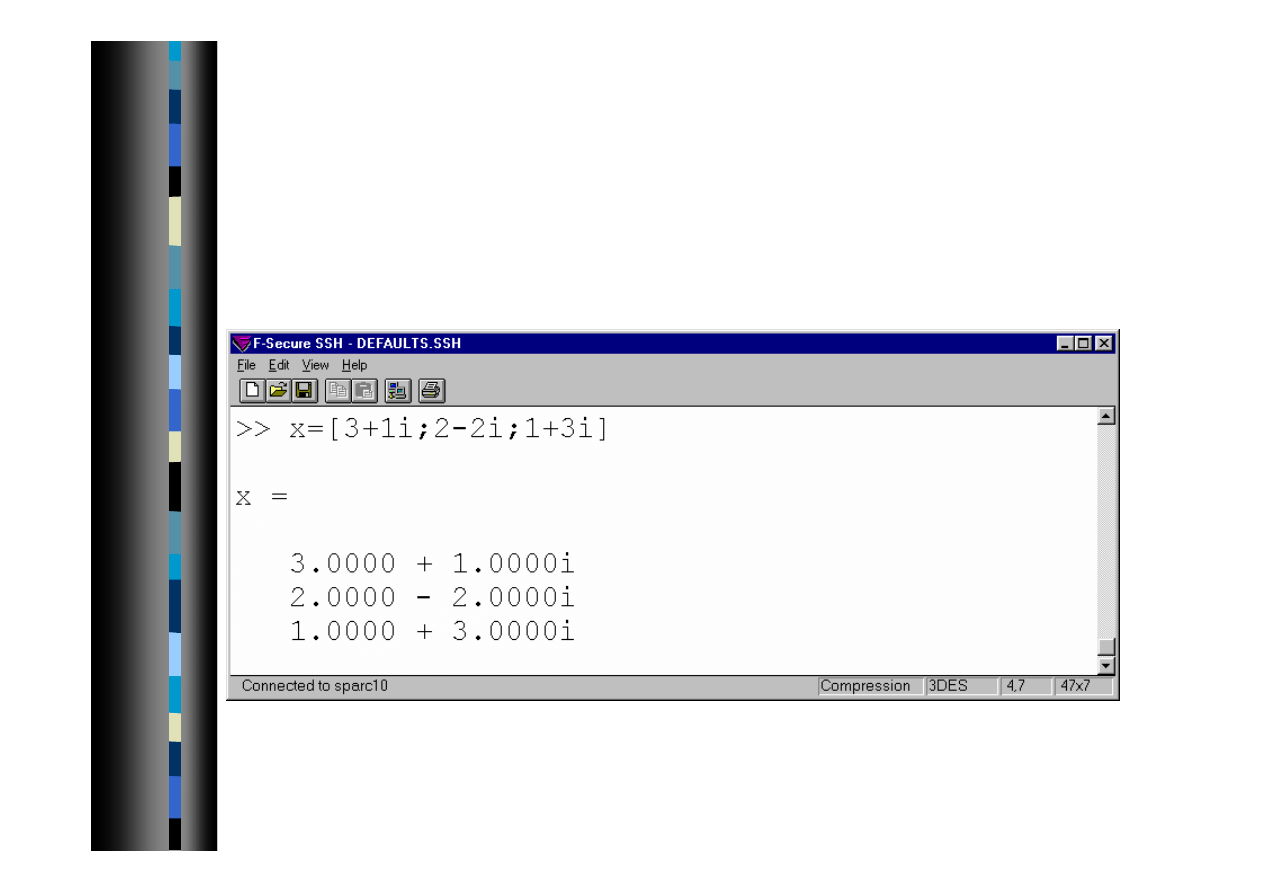
Wprowadzanie danych - c.d.

Wektory i macierze zespolone

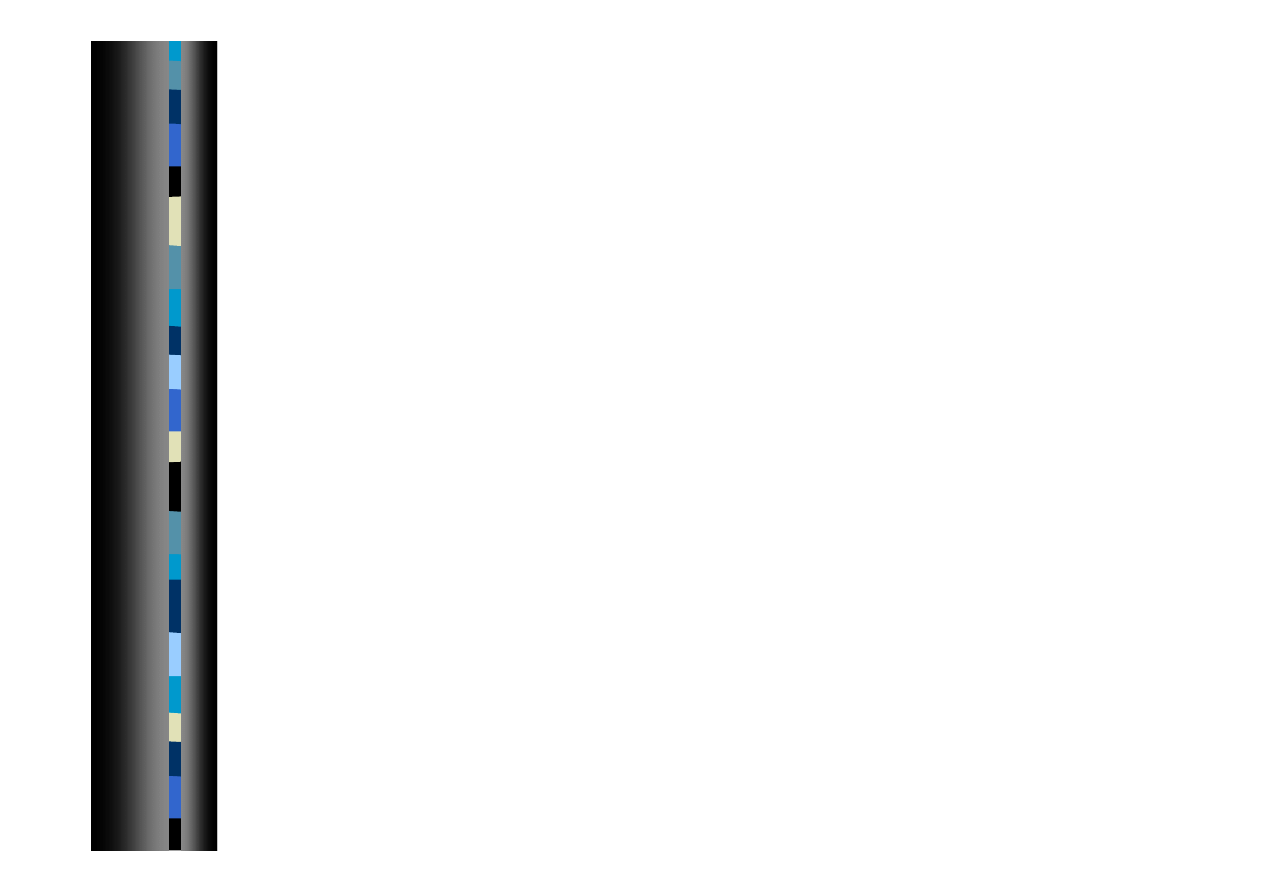
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

27

Wprowadzanie danych - funkcje specjalne

Funkcje specjalne

•pi

- generuje liczbę pi

•Inf

- generuje symbol nieskończony „1/0”

•NaN - generuje symbol nieoznaczony „Inf/Inf” czy „0/0”

Uwagi. Pojawienie się podczas obliczeń symboli „Inf”, czy
„NaN” nie powoduje błędu i wartości te mogą być użyte do
dalszych obliczeń. Rezultatem obliczeń z argumentem
„NaN” będzie również „NaN”. „Inf” i „NaN” nie są
interpretowane jako komendy graficzne.

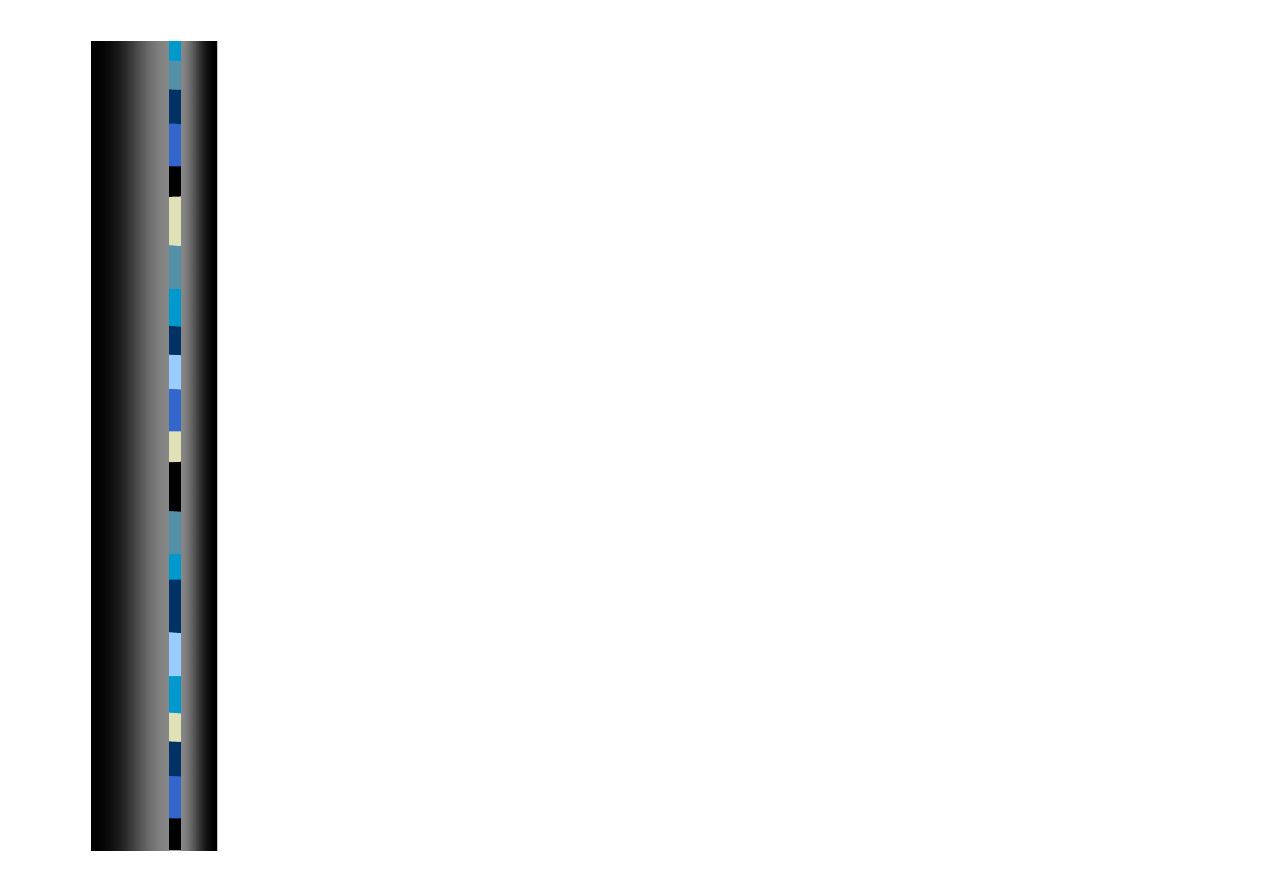
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

28

Wprowadzanie danych - c.d.

Generacja macierzy za pomocą zewnętrznej procedury

W katalogu roboczym tworzymy plik tekstowy genmatC.m
zawierający:

C = [1 0 2

0 3 0

4 0 5];

Wydanie polecenia

>>genmatC

spowoduje zdefiniowanie macierzy C.

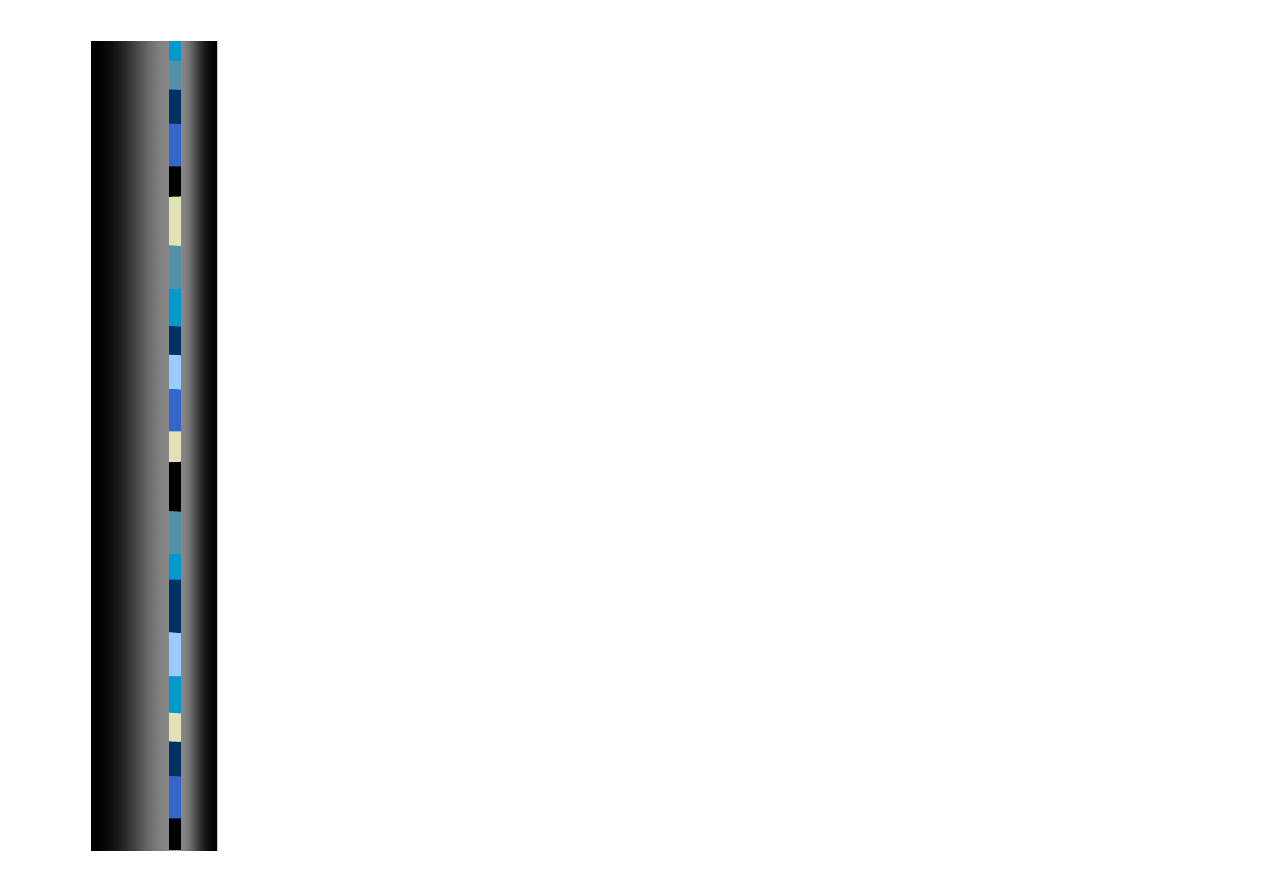
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

29

Wprowadzanie danych

Wczytywanie danych jako macierz

W katalogu roboczym tworzymy plik tekstowy D.txt
zawierający:

1 0 2

0 3 0

4 0 5

Wydanie polecenia

>>load D.txt

spowoduje zdefiniowanie macierzy D.

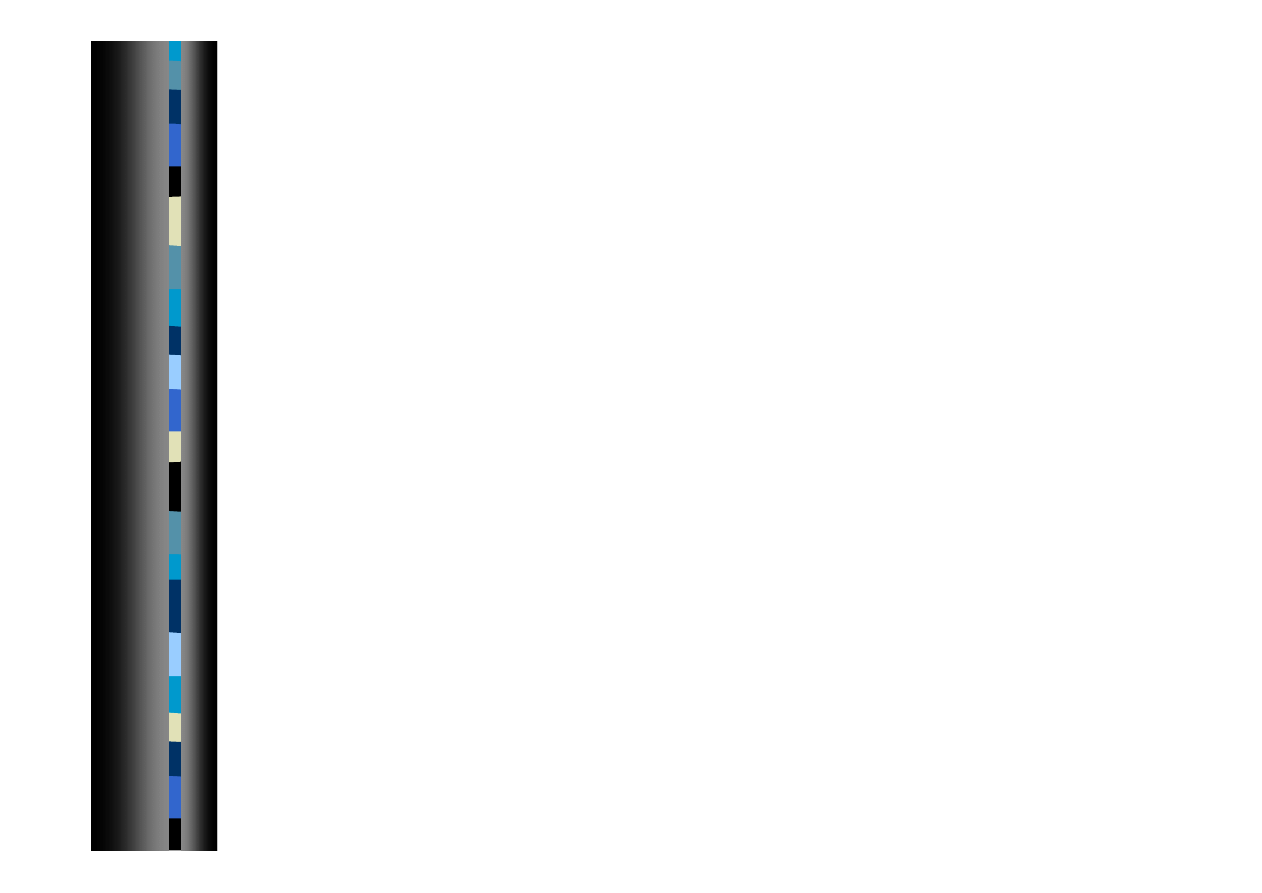
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

30

Wprowadzanie danych

Wczytywanie danych jako macierz - uwagi



W przedstawiony sposób mo

żna wczytywać

tylko liczby rzeczywiste.



Liczby zespolone trzeba przedstawi

ć w

postaci dwóch liczb rzeczywistych, a po
wczytaniu odtworzy

ć z nich liczbę zespoloną.

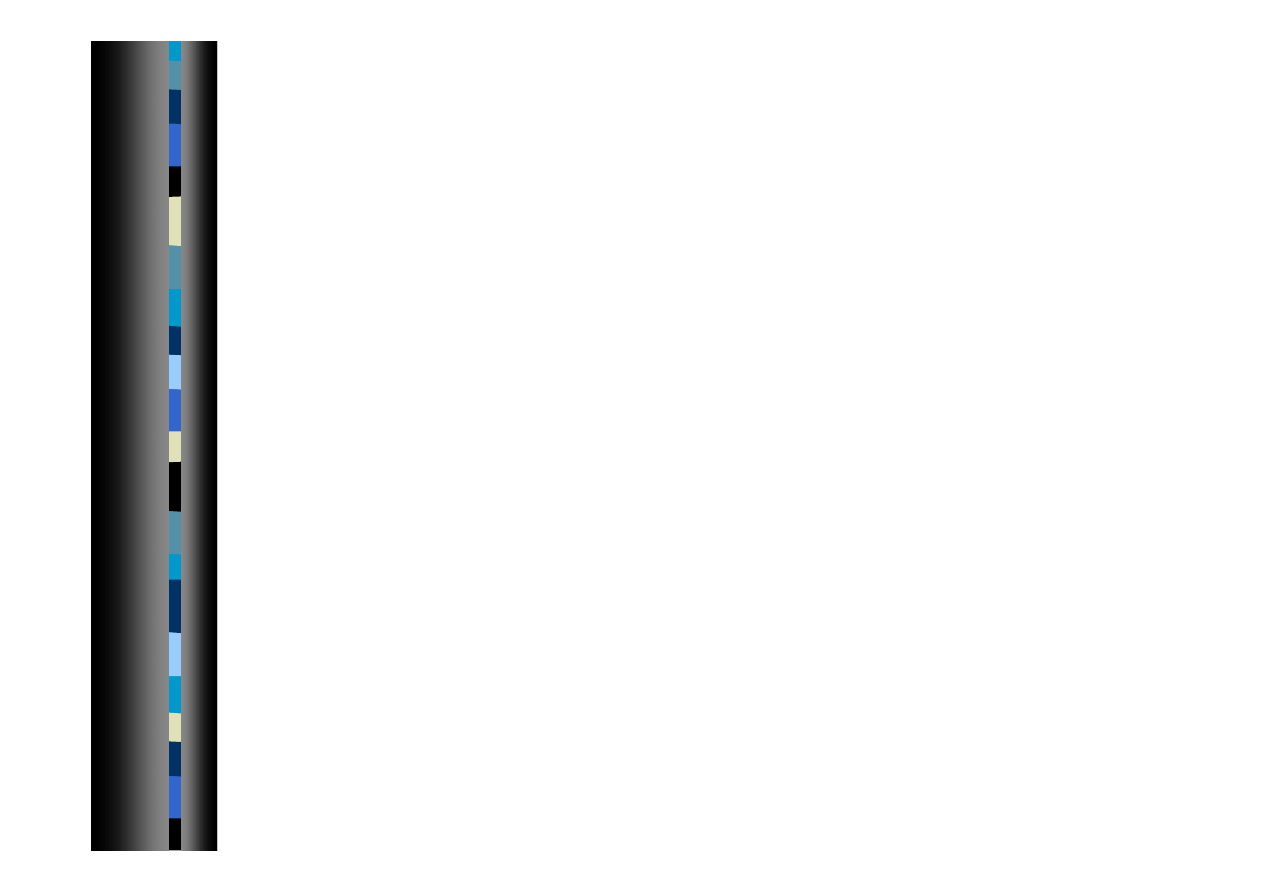
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

31

Reprezentacja danych w pamięci i na
ekranie



Dane liczbowe w pami

ęci MATLABA

– liczby rzeczywiste 8-bajtowe

– liczby zespolone 16-bajtowe

– znak 8-bajtów



Macierze mog

ą być pamiętane w formie

– g

ęstej

– rzadkiej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

32

Polecenia dotyczące pamięci 1

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

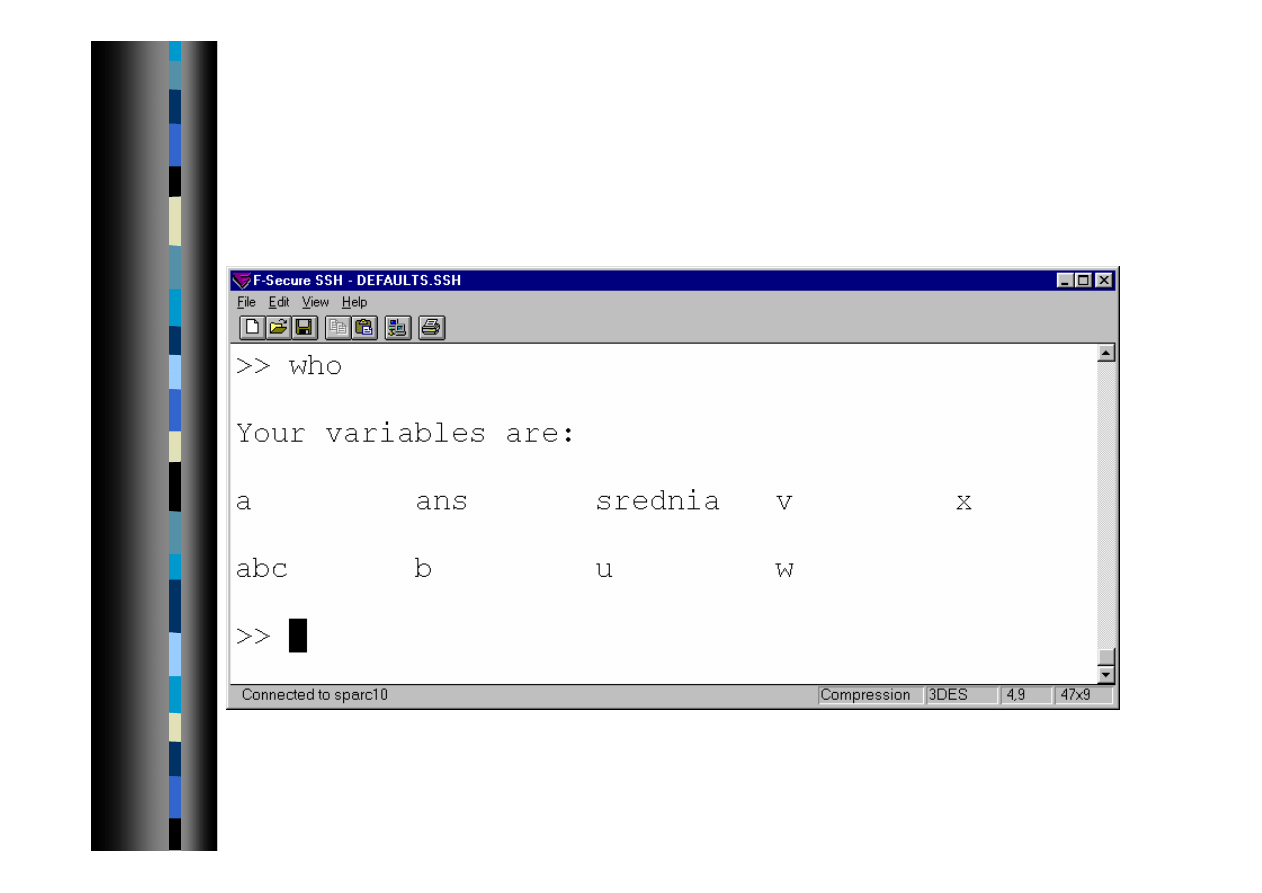
33

Polecenia dotyczące pamięci 2

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

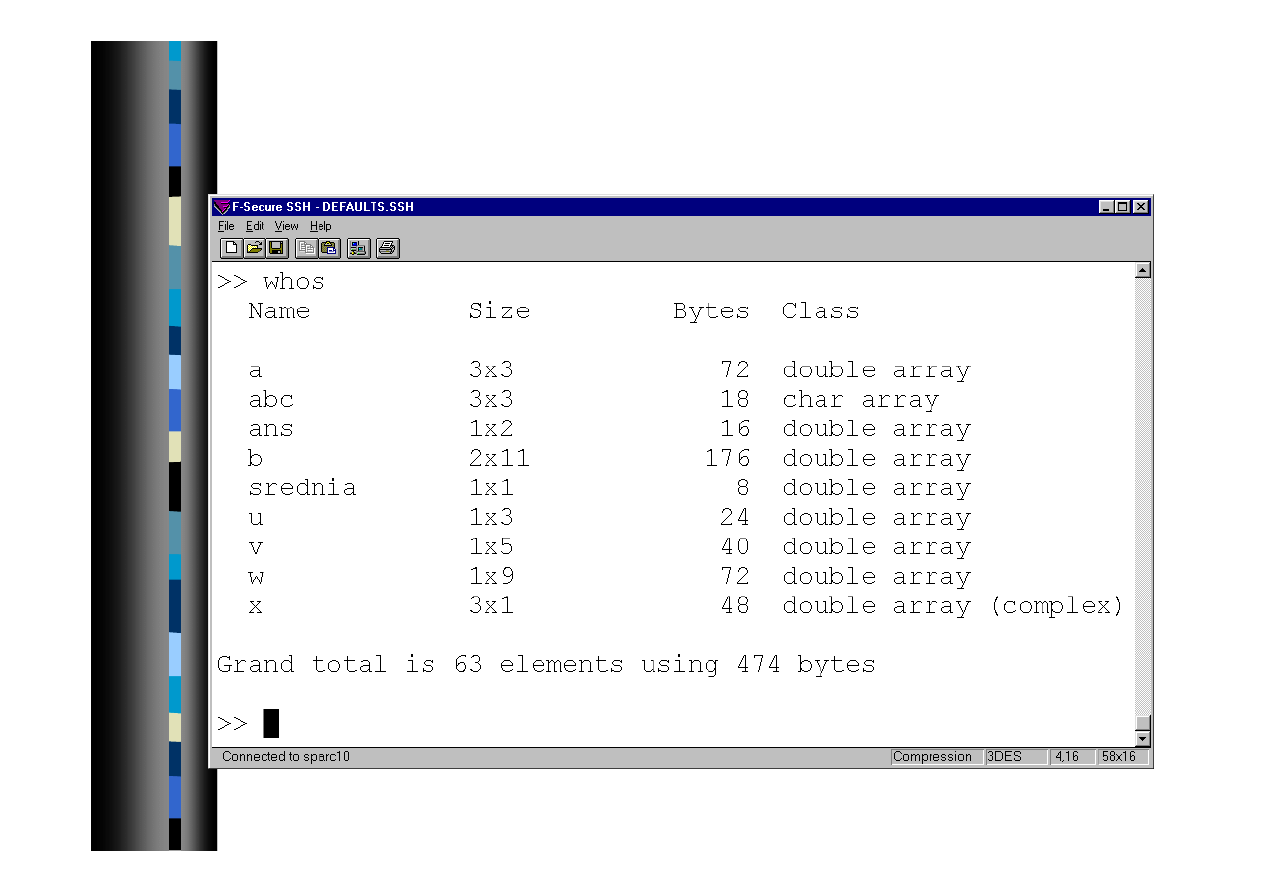
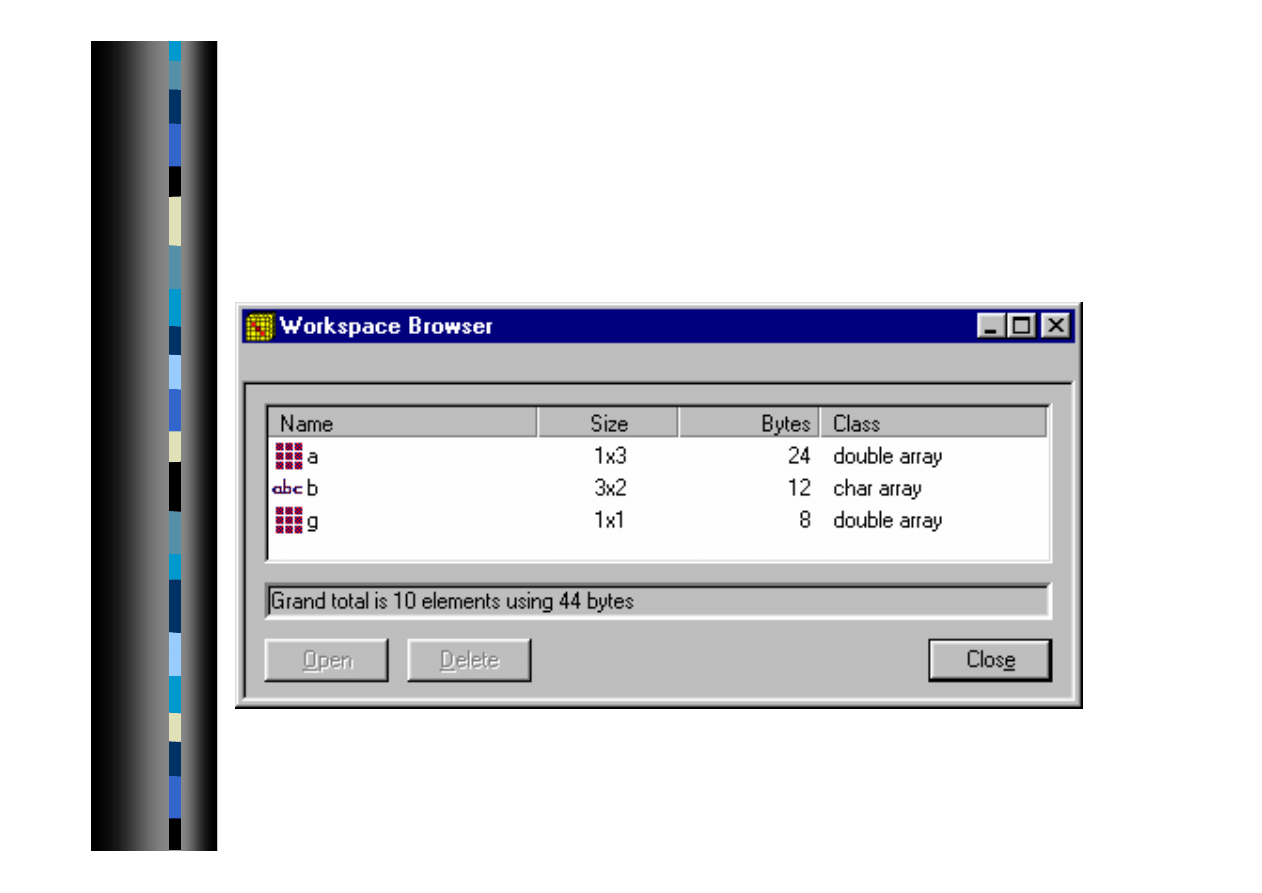
34

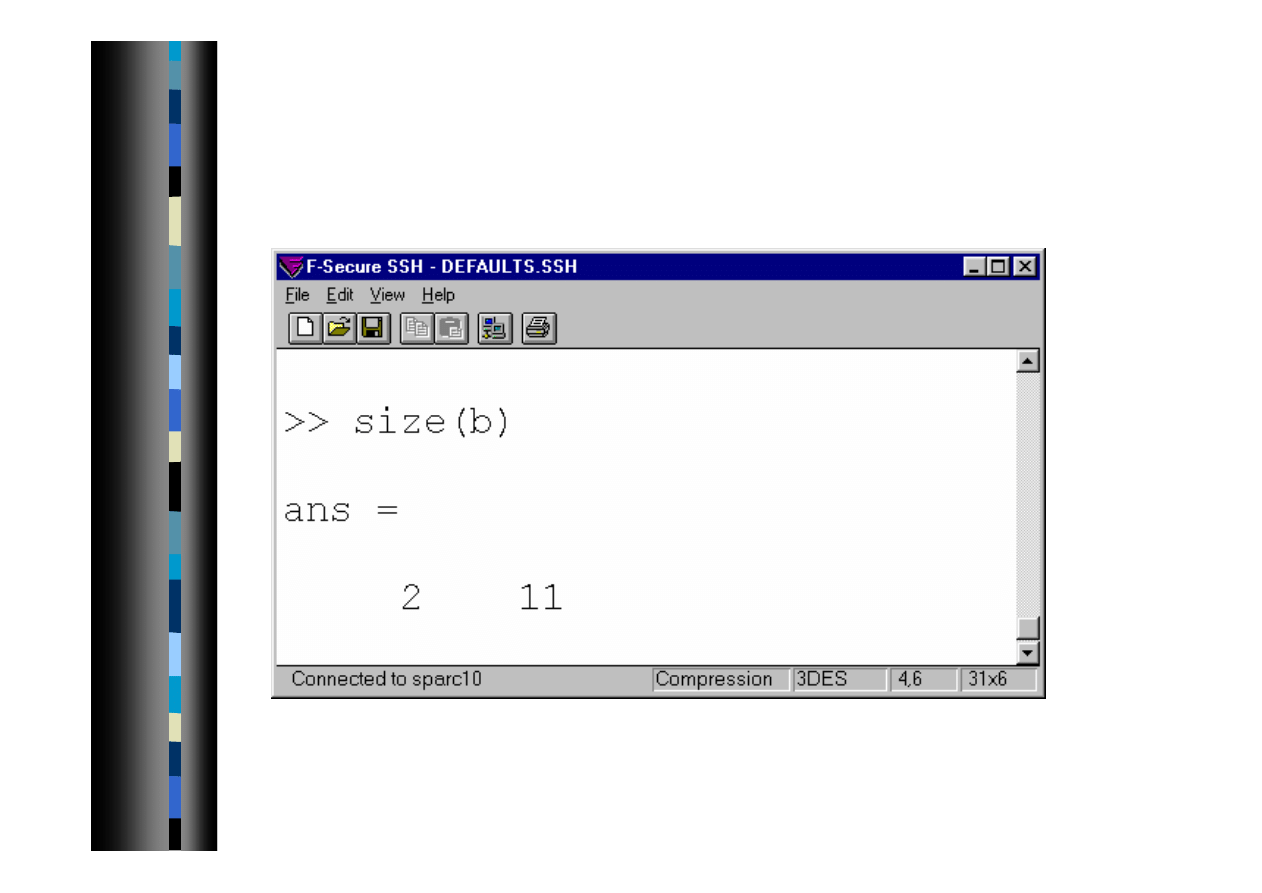
Przeglądarka pamięci

Menu>File>ShowWorkSpace

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

35

Wymiary pojedynczej macierzy

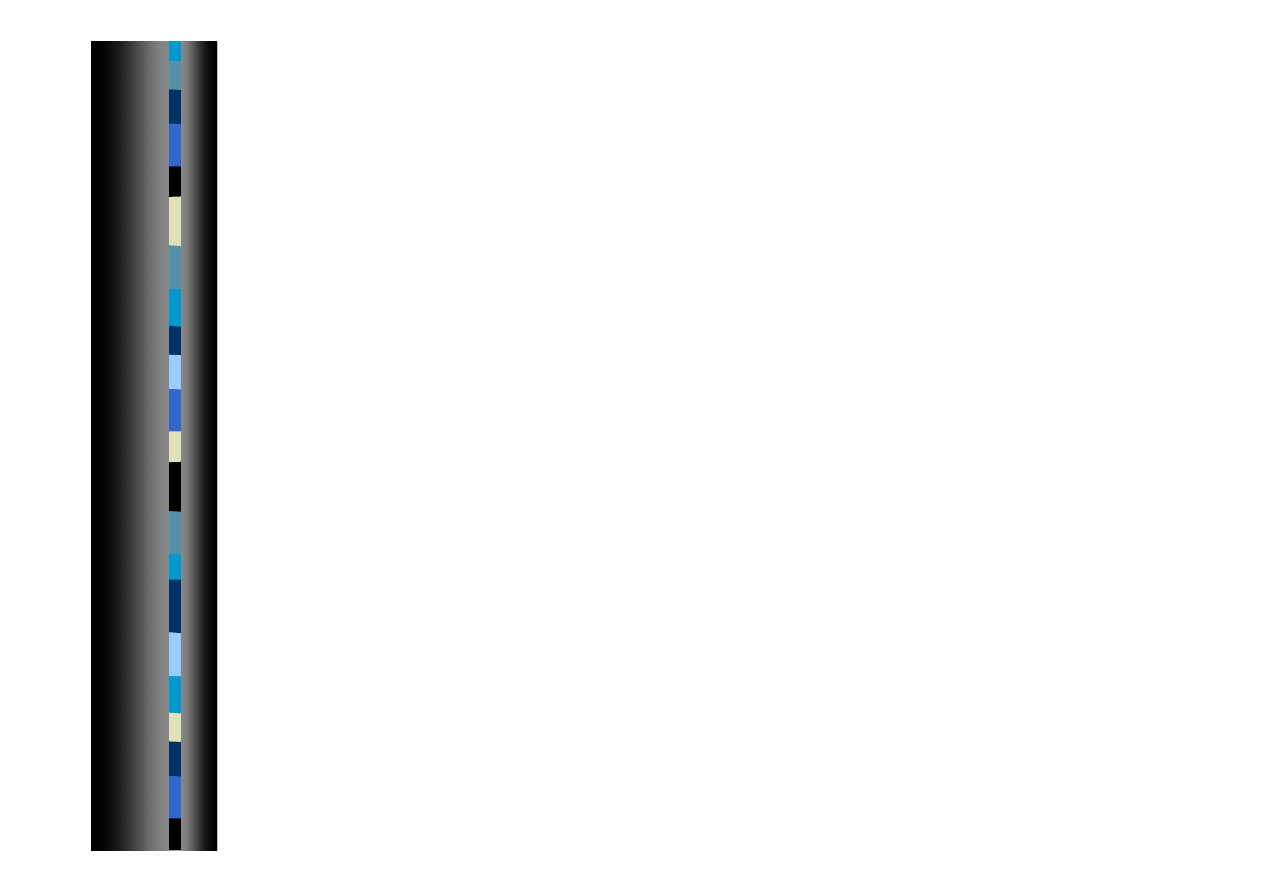
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

36

Formaty liczb na konsoli

Format

Opis

Przyk

ład

short
short e
long
long e
bank
hex
+
compact

Krótki
Krótki z wyk

ładnikiem

D

ługi

D

ługi z wykładnikiem

Bardzo krótki
Szesnastkowy
Tylko znak liczb
Zwarty w pionie

3.1416
3.14.16e+00
3.14159265358979
3.14159265358979e+00
3.14
400921fb54442d18
++

Format mo

żna zmieniać poleceniem format

>>format long e

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

37

Edycja linii komend

Klawisz

Funkcja

,^P
,^N
,^B
,^F
Delete
^L
^R
^A
^E
^U
^T
^D
^K

Przywo

łaj poprzednią linię

Przywo

łaj następną linię

Przesu

ń kursor w lewo o jeden znak

Przesu

ń kursor w prawo o jeden znak

Usu

ń znak

Przesu

ń kursor w lewo o jeden wyraz

Przesu

ń kursor w prawo o jeden wyraz

Przesu

ń kursor do początku linii

Przesu

ń kursor do końca linii

Usu

ń bieżącą linię

Prze

łącz tryb pisania

Usu

ń znak pod kursorem

Usu

ń do końca linii

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

38

Zarządzanie przestrzenią roboczą 1



Zwolnienie pami

ęci używanej przez zmienną

>> v = [ ]



Usuni

ęcie zmiennej z pamięci

>> clear v



Po zwolnieniu pami

ęci jej konsolidacja

>> pack



Zachowanie przestrzeni roboczej w pliku

>> save

zapis do pliku matlab.mat

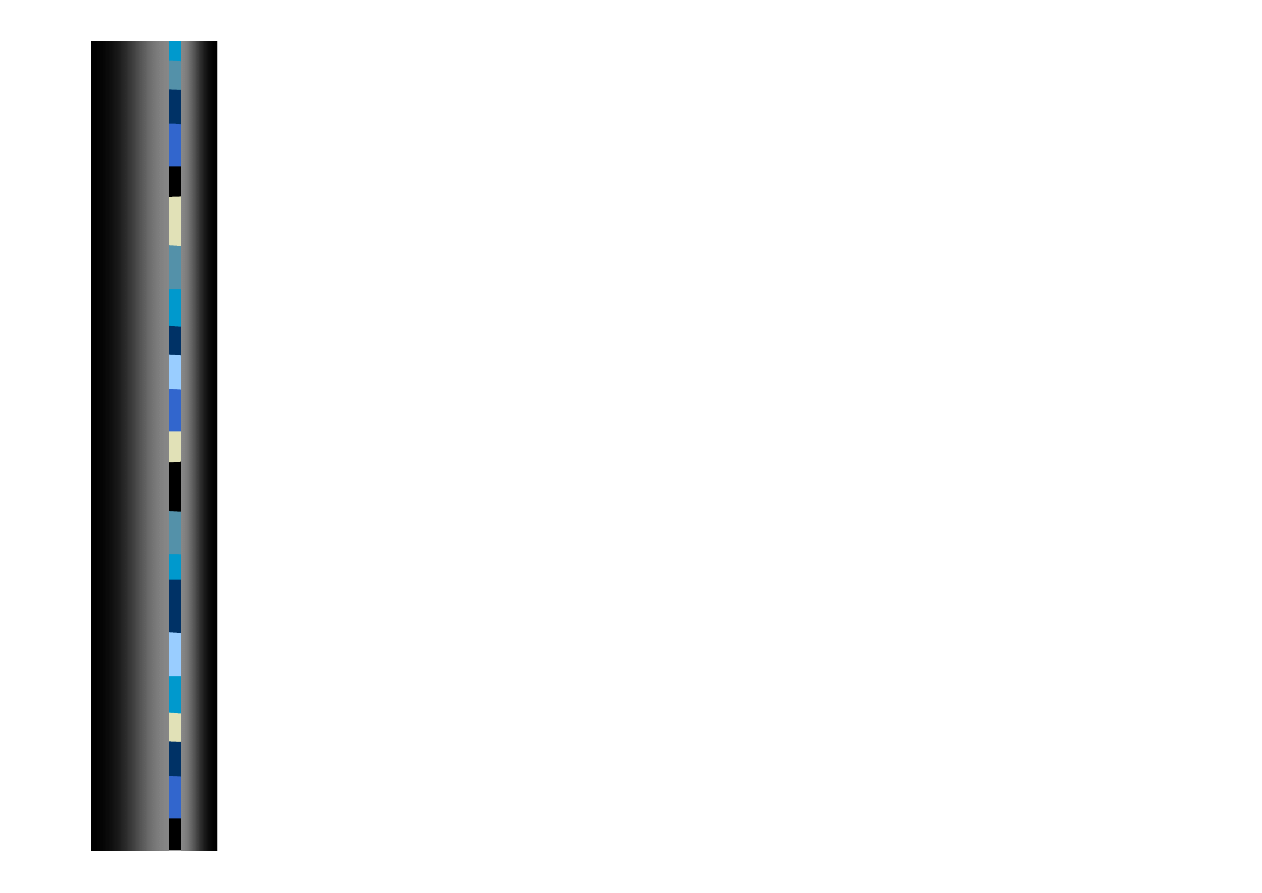
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

39

Zarządzanie przestrzenią roboczą 2



Zapisanie wybranych zmiennych do pliku

>> save abc A B C



Zapisanie zmiennych w pliku tekstowym

>> save abc.dat A -ascii



Zmiana katalogu

>> cd path



Wy

świetlenie plików związanych z MATLAem

>> what path

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

40

Operacje na macierzach 1

Transpozycja macierzy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

41

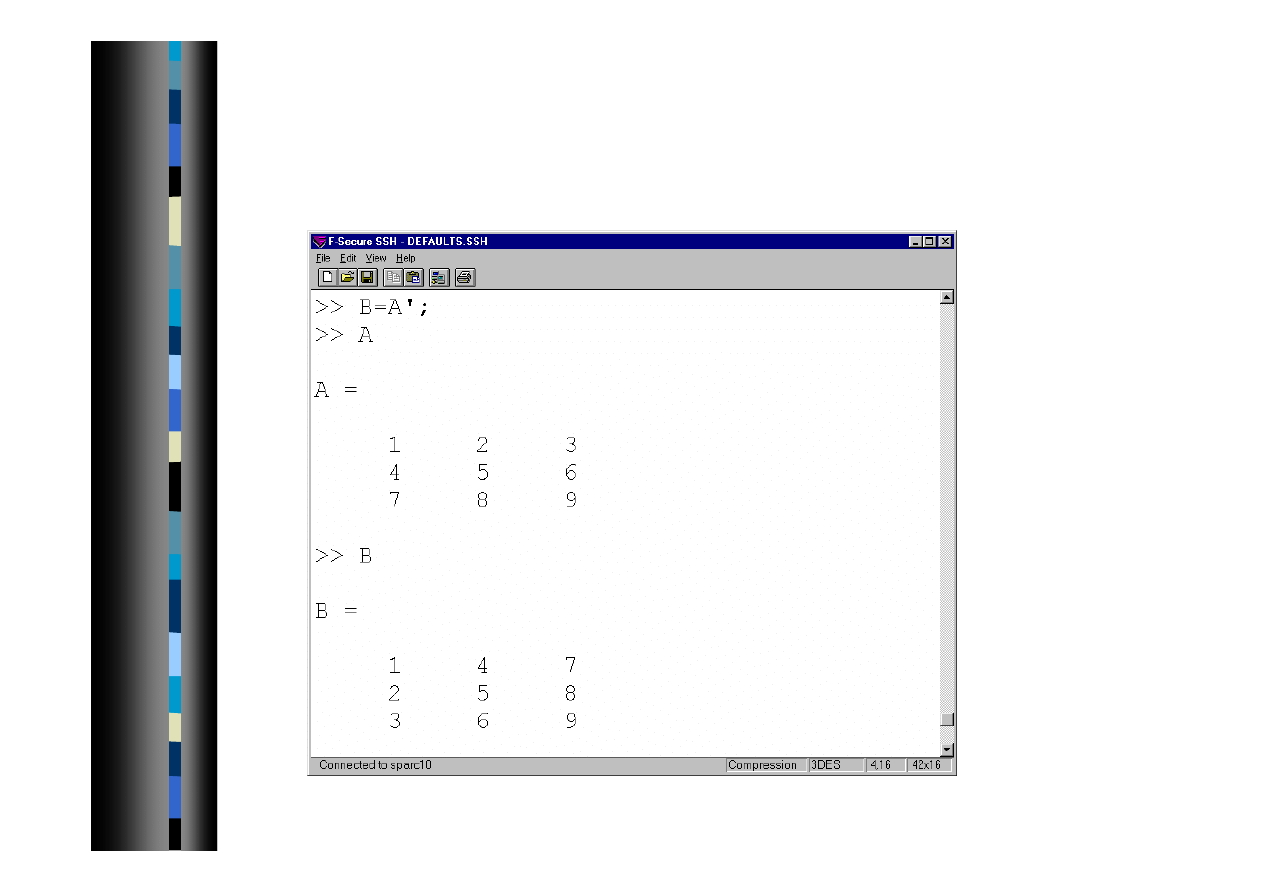
Operacje na macierzach 2

Transpozycja macierzy (wektora)

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

42

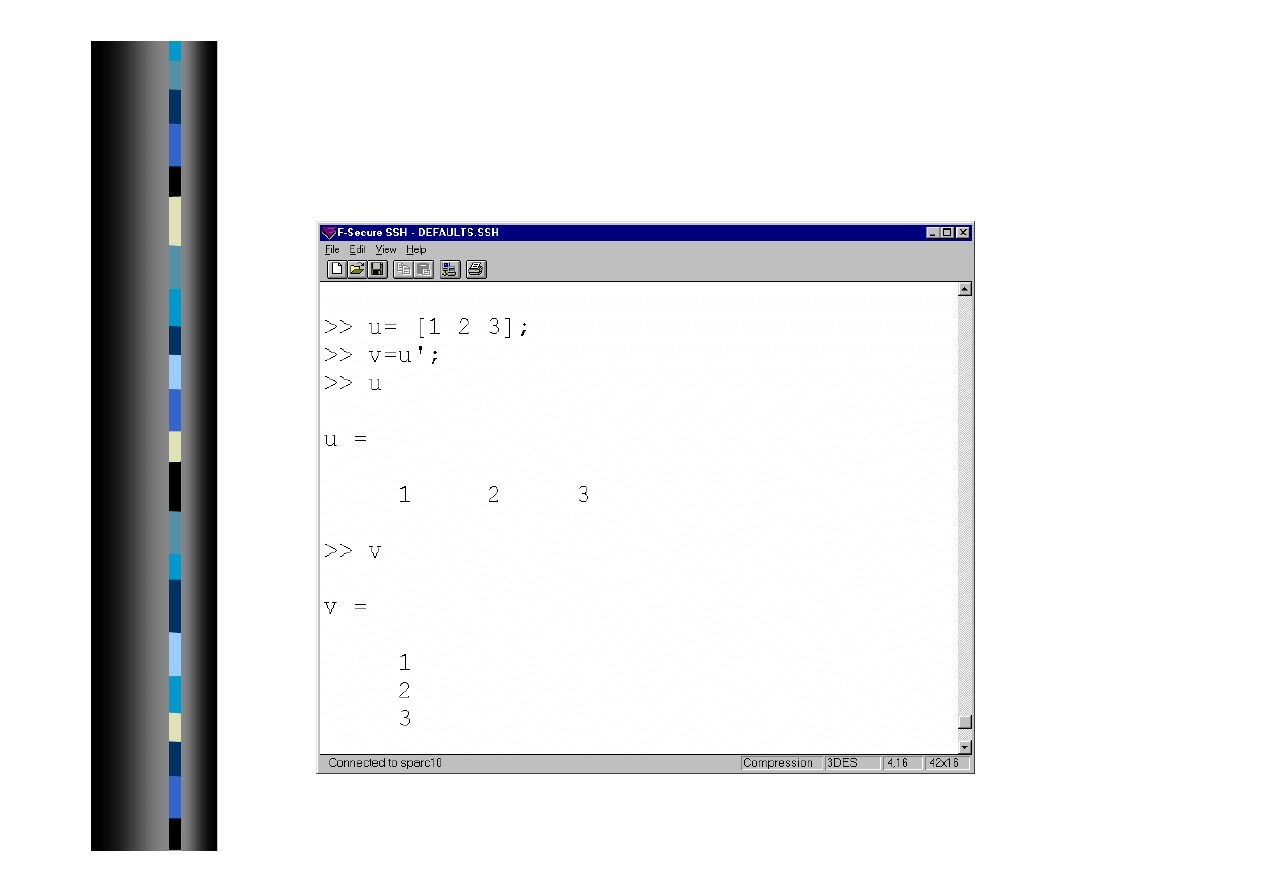
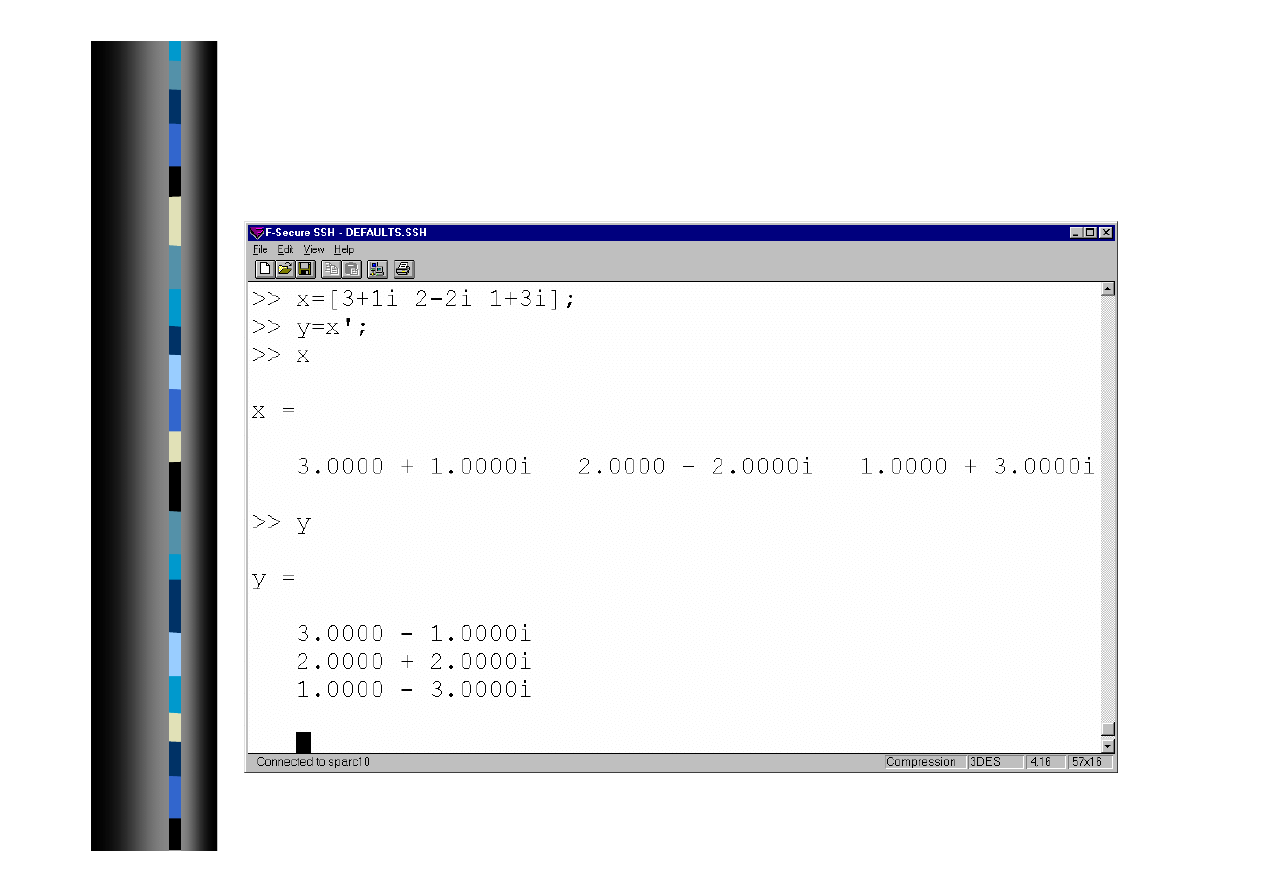
Operacje na macierzach 3

Transpozycja macierzy zespolonej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

43

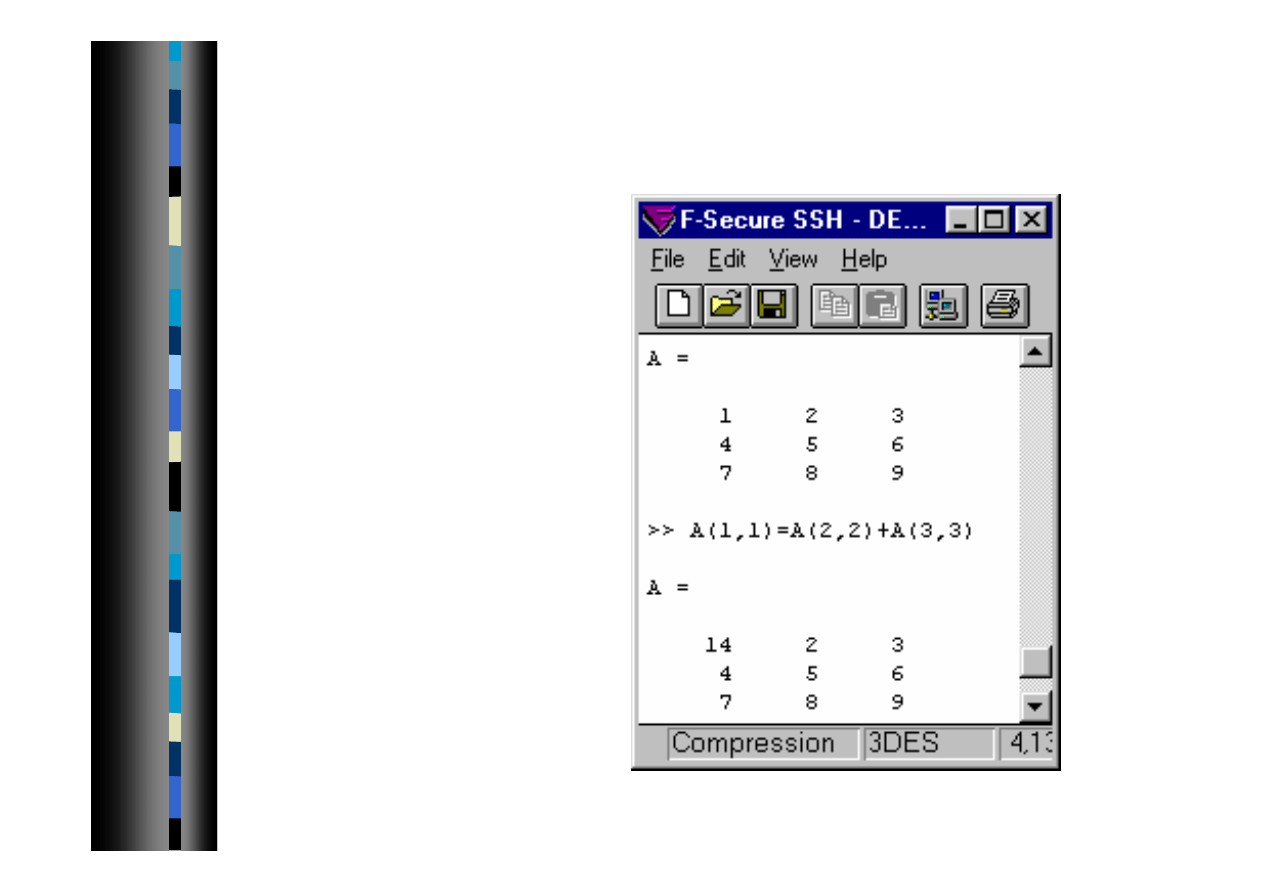
Operacje na macierzach 4



Dodawanie i odejmowanie macierzy (+/-)
zdefiniowane dla

– dwóch macierzy tych samych wymiarów

– macierzy i skalara; skalar dodawany

(odejmowany) do (od) ka

żdego elementu

macierzy



Mno

żenie macierzy (*)

– dwóch macierzy o odpowiednich wymiarach

– Macierzy przez skalar (mno

żenie każdego

elementu macierzy)

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

44

Operacje na macierzach 5



Dzielenie macierzy

– X = A\B jest rozwi

ązaniem układu A*X = B

– X = B/A jest rozwi

ązaniem układu X*A = B

– Dzielenie macierzy przez skalar (dzielenie

ka

żdego elementu macierzy)



Pot

ęgowanie macierzy (^)

Zdefiniowane dla macierzy kwadratowej w
wyk

ładnika skalarnego

– dla k ca

łkowitego k-krotne mnożenie

– dla k rzeczywistego - rozk

ład na wartości

w

łasne

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

45

Indeksowanie macierzy i wektorów



Do pojedynczych
indeksów mo

żna się

odwo

ływać poprzez

podanie indeksów w
nawiasach zwyk

łych



Je

śli indeks jest

wyra

żeniem, to jest

ono zaokr

ąglane do

najbli

ższej liczby

ca

łkowitej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

46

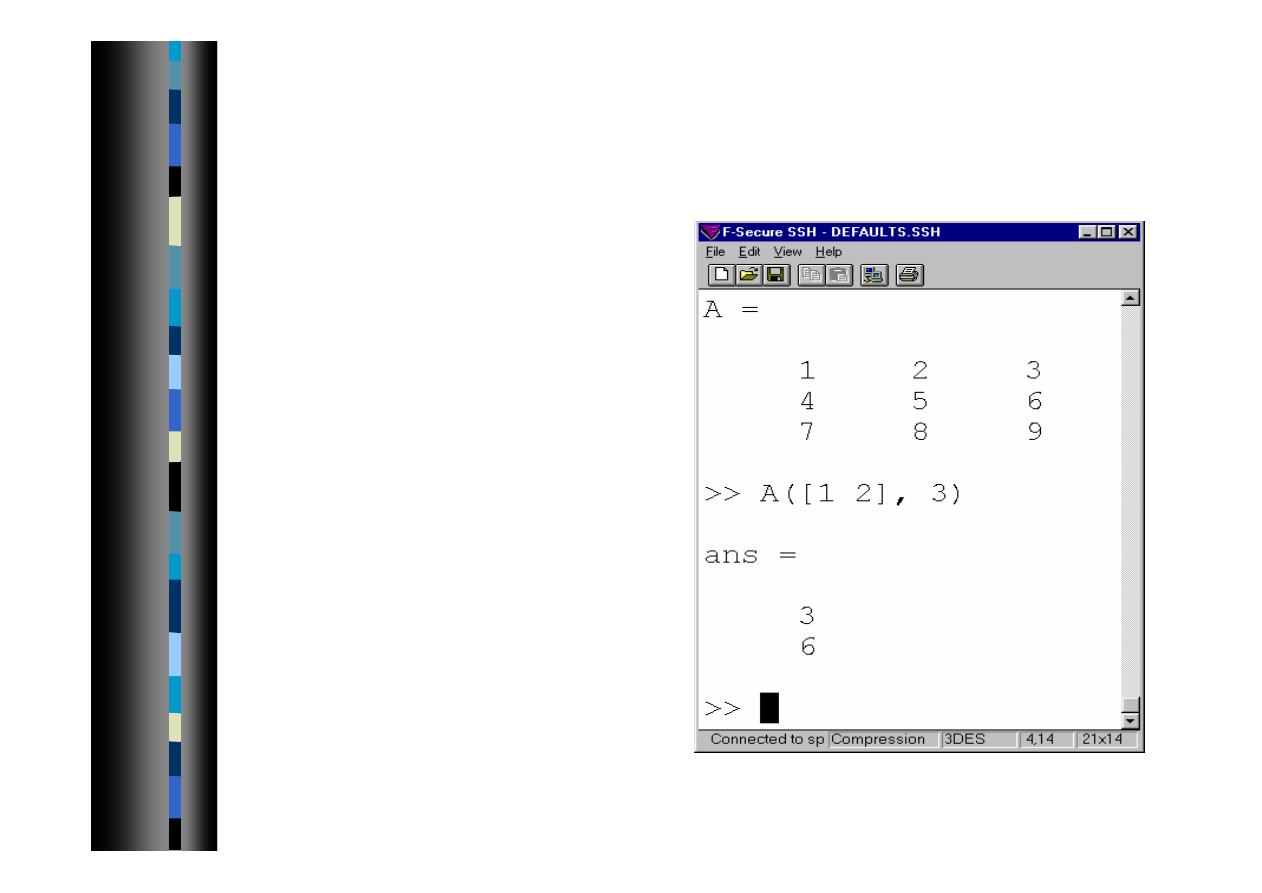
Indeksowanie macierzy 1



Indeks mo

że być również

wektorem; elementy
wektora wskazuj

ą wtedy

wiersze i/lub kolumny, do
których si

ę odnosimy



Je

śli u i v są wektorami to

A(u,v) generuje macierz,
w której wiersze s

ą

wymienione w wektorze u,
a kolumny w wektorze v.

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

47

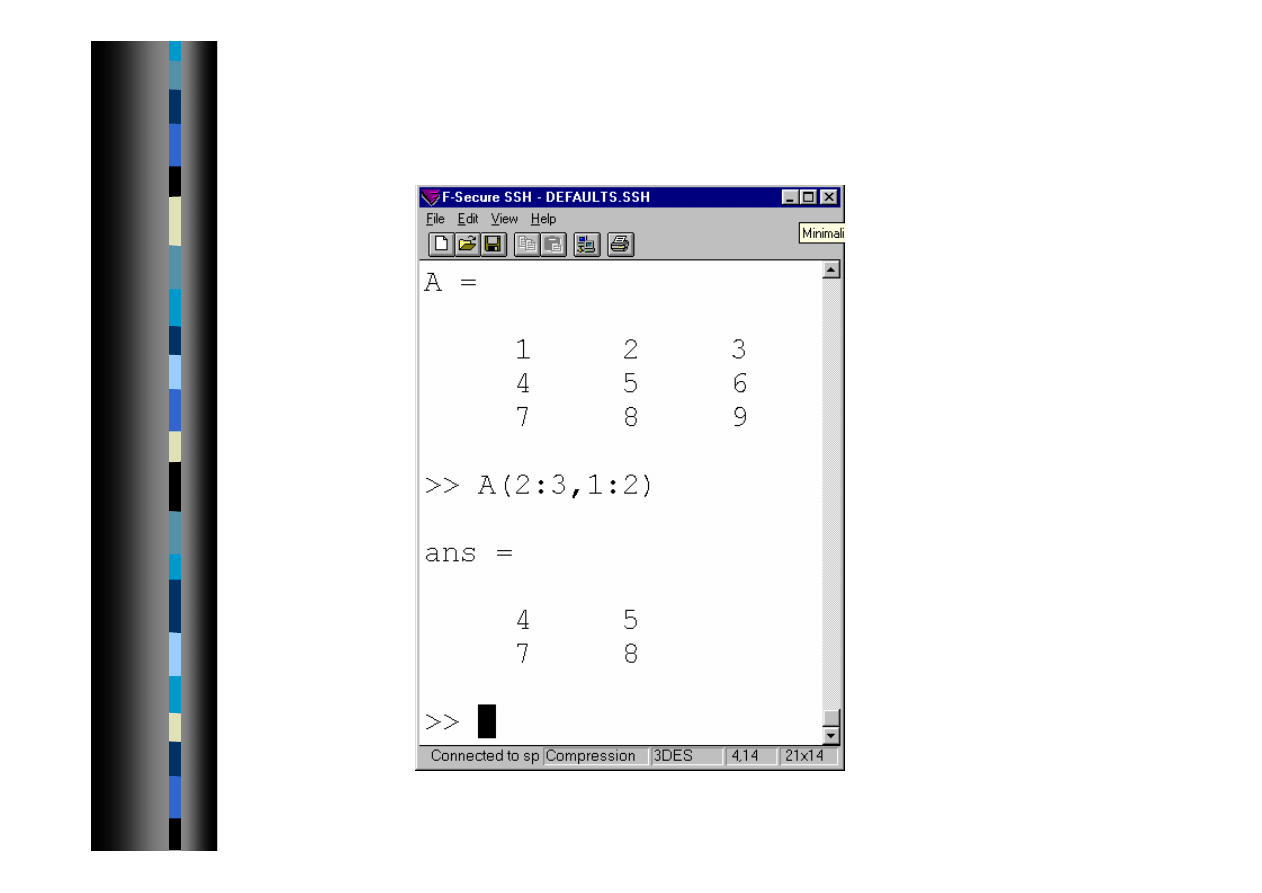
Indeksowanie macierzy 2

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

48

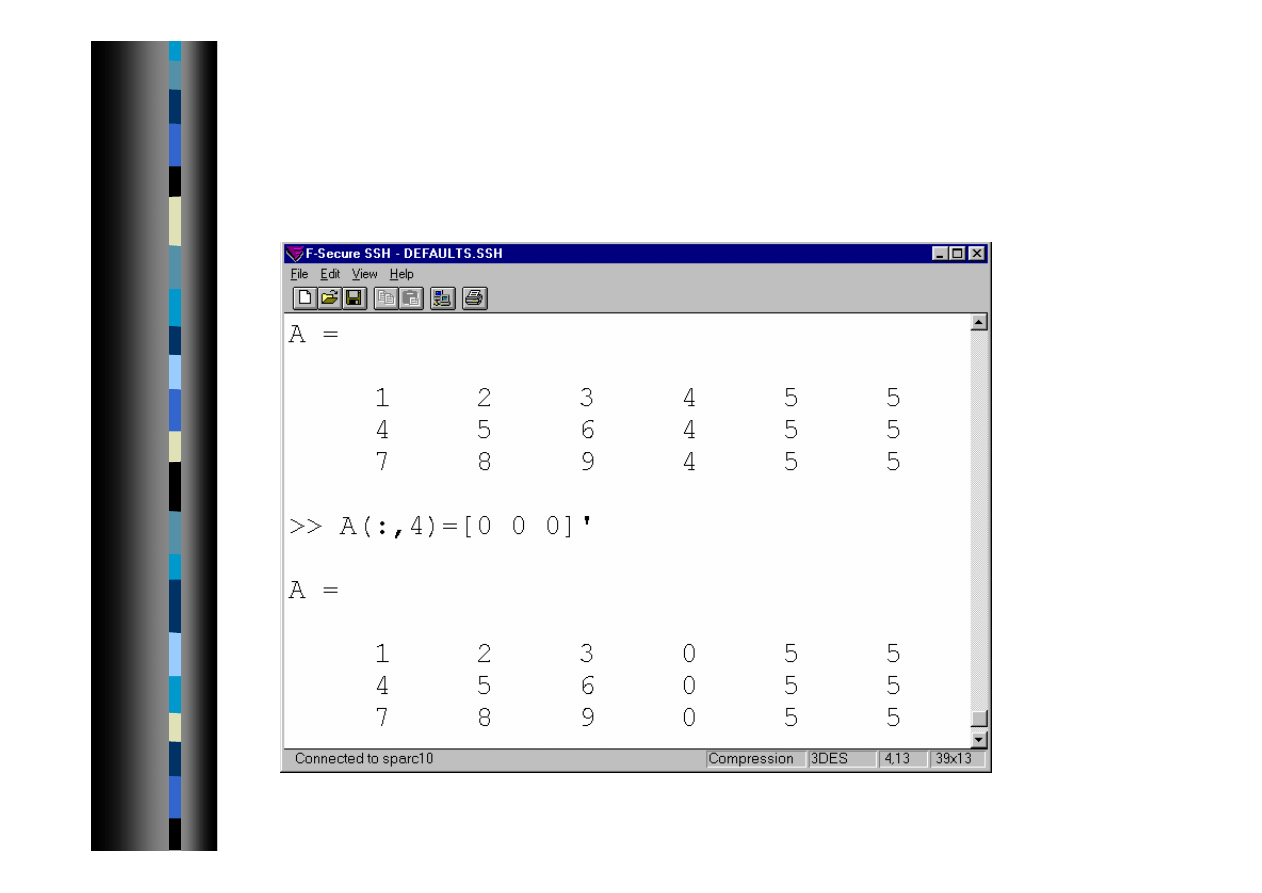
Indeksowanie macierzy 3

Do całej kolumny lub wiersza można odwołać się
używając w miejsce indeksu dwukropka

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

49

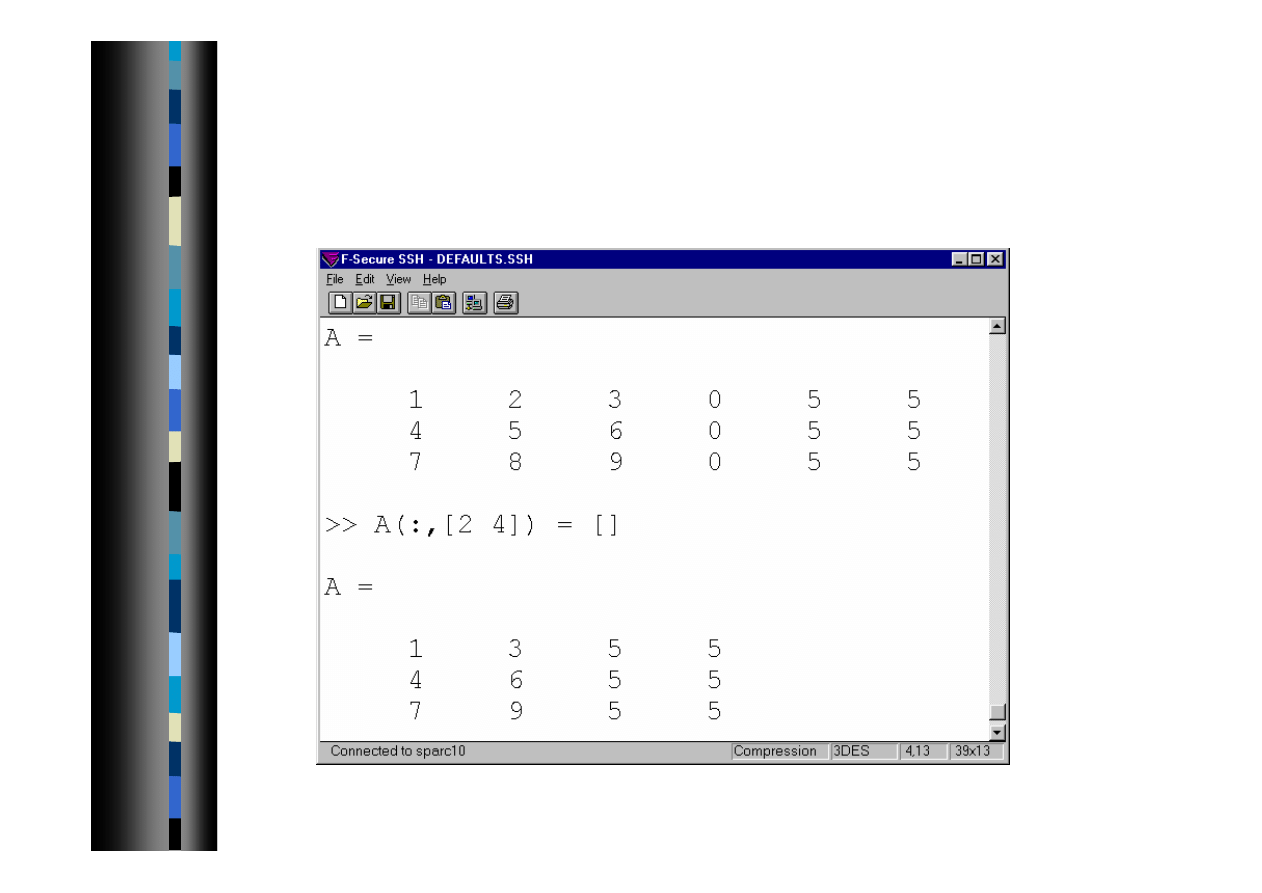
Indeksowanie macierzy 4

W celu usunięcia kolumn lub i wierszy - przyporządkowanie
macierzy pustej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

50

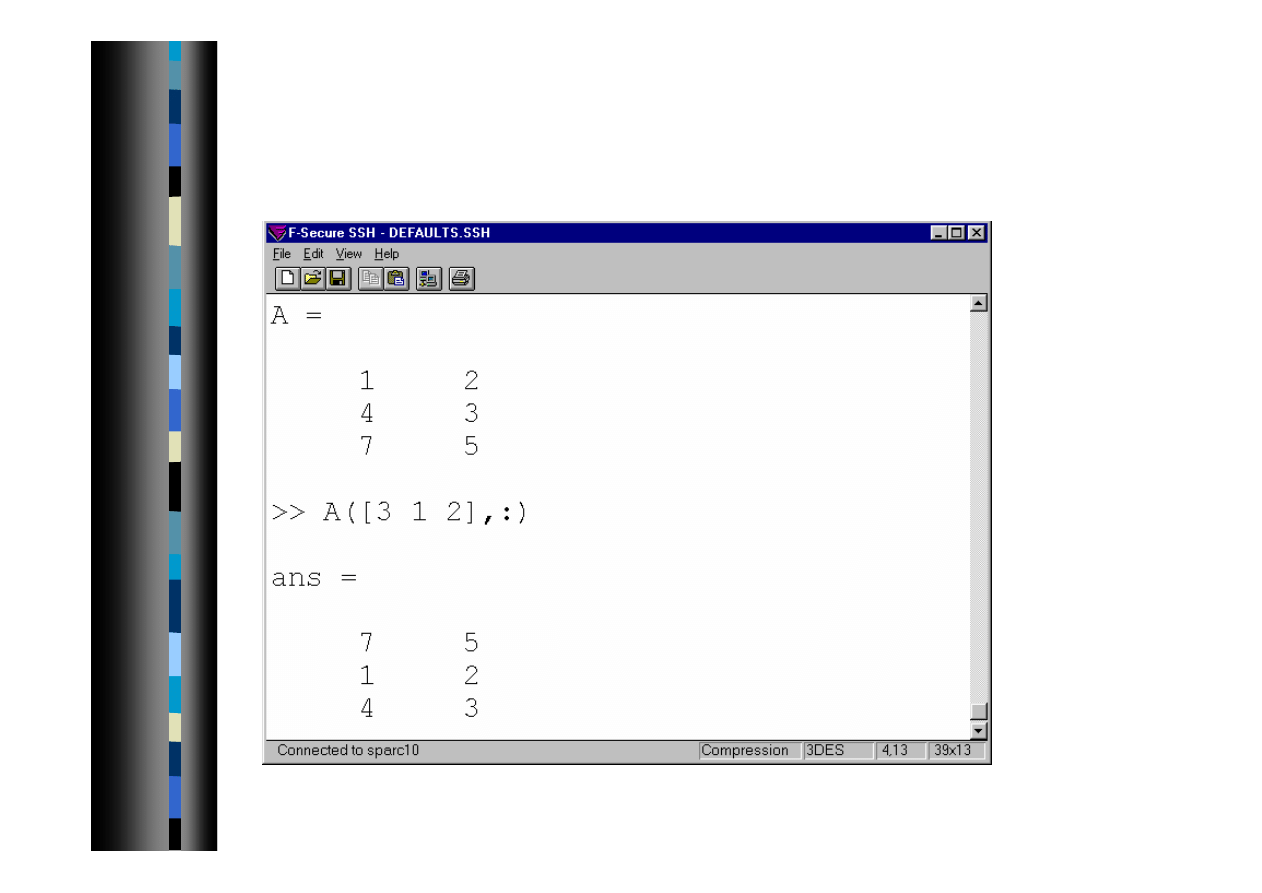
Indeksowanie macierzy 5

Permutacja wierszy lub/i kolumn - kolejność wierszy 3, 2 1

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

51

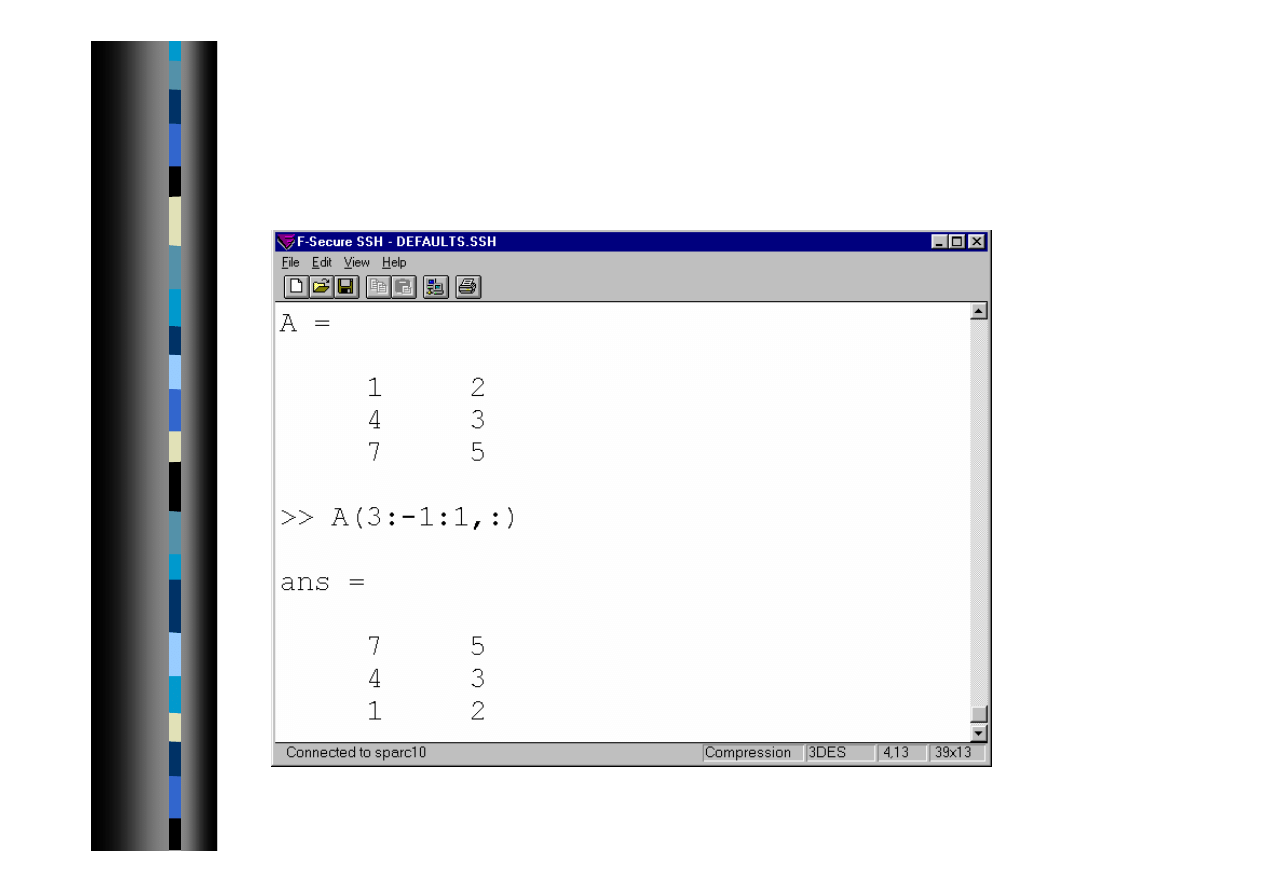
Indeksowanie macierzy 6

Permutacja wierszy lub/i kolumn - odwrotna kolejność

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

52

Indeksowanie macierzy - użycie „:”

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

53

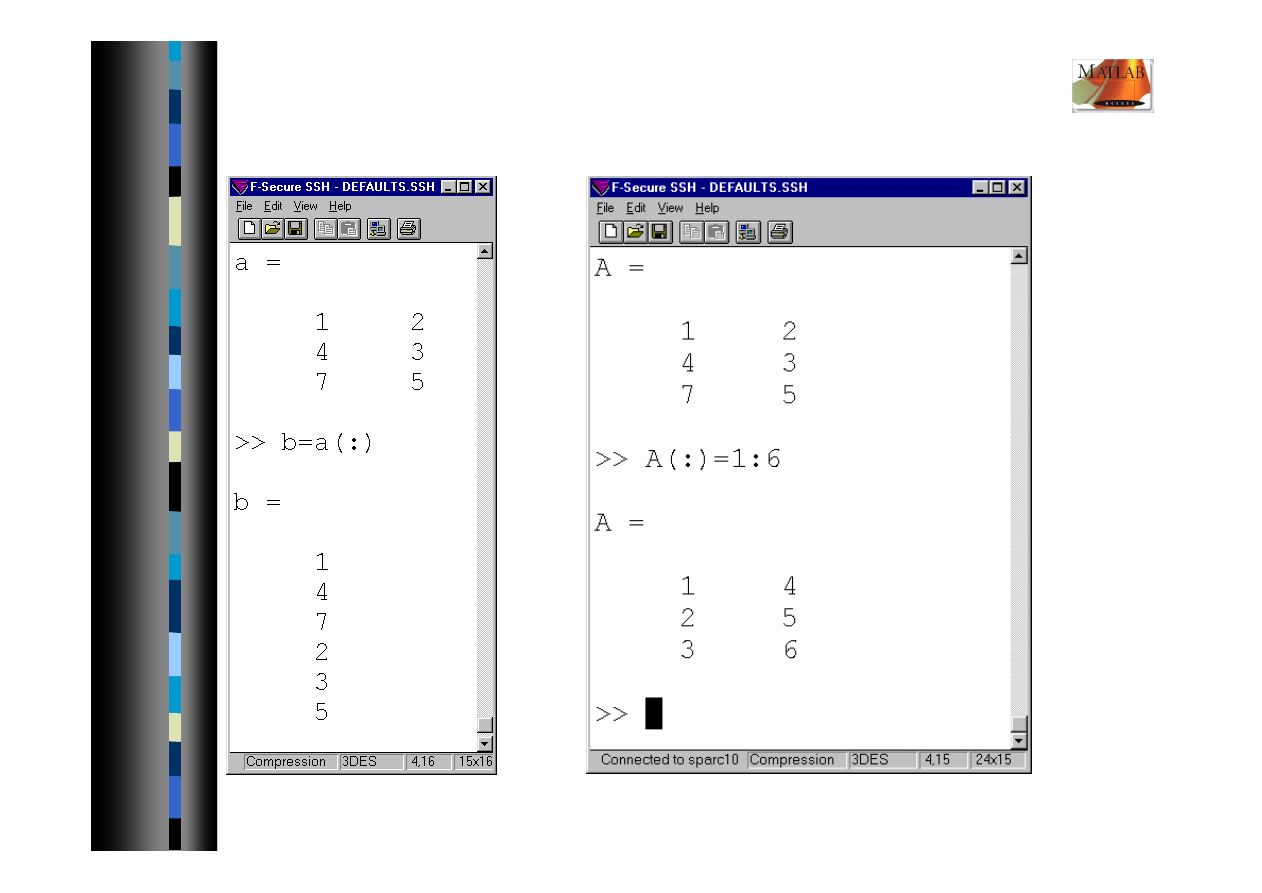
Ekstrakcja podmacierzy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

54

Funkcje modyfikujące i tworzące macierz



diag - tworzenie macierzy diagonalnej lub
ekstrakcja g

łównej przekątnej



fliplr - ustrzanie odbicie macierzy w poziomie



flipud - lustrzane odbicie macierzy w pionie



reshape - zmiana rozmiarów macierzy



rot90 - obrót macierzy o 90 stopni



tril - ekstrakcja macierzy trójk

ątnej dolnej



triu - ekstrakcja macierzy trójk

ątnej górnej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

55

Tworzenie macierzy specjalnych



compan - macierz stowarzyszona



gallery - kilka ma

łych macierzy testowych



hadamard - macierz Hadamarda



hankel - macierz Hankela



hilb - macierz Hilberta



invhilb - macierz odwrotna Hilberta



kron - iloczyn tensorowy Koroneckera



magic - magiczny kwadrat



toeplitz - macierz Toeplitza



vander - macierz Vandermonde’a



wilkinson - macierz testowa Wilkinsona dla
zagadnie

ń własnych

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

56

Tworzenie innych użytecznych macierzy



zeros - macierz zer



ones - macierz jedynek



eye - macierz jednostkowa



rand - macierz losowa o rozk

ładzie równomiernym



randn - macierz losowa o rozk

ładzie normalnym



linspace - liniowo zmienny wektor



logspace - logarytmicznie zmienny wektor



meshgrid - tablice X i Y dla trójwymiarowych
wykresów

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

57

Funkcje macierzowe



cond - wska

źnik uwarunkowania macierzy



rcond - estymator odwrotno

ści

uwarunkowania macierzy



norm - norma macierzy lub wektora



det - wyznacznik



trace - suma elementów diagonalnych



rank - rz

ąd macierzy



null - j

ądro macierzy



orth - obraz macierzy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

58

Układy równań liniowych



chol - dekompozycja Cholesky’ego



lu - dekompozycja LU



qr - dekompozycja QR



nnls - nieujemne najmniejsze kwadraty



lscov - najmniejsze kwadraty przy znanej
kowariancji



inv - odwrotno

ść macierzy



pinv - pseudoodwrotno

ść macierzy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

59

Wartości własne i szczególne



eig - warto

ści własne i wektory własne



poly - wielomian charakterystyczny



polyeig - wielomianowy problem w

łasny



hess - macierz Hessenberga



qz - uogólnione warto

ści własne



schur - dekompozycja Shur’a



svd - dekompozycja wed

ług wartości

szczególnych

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

60

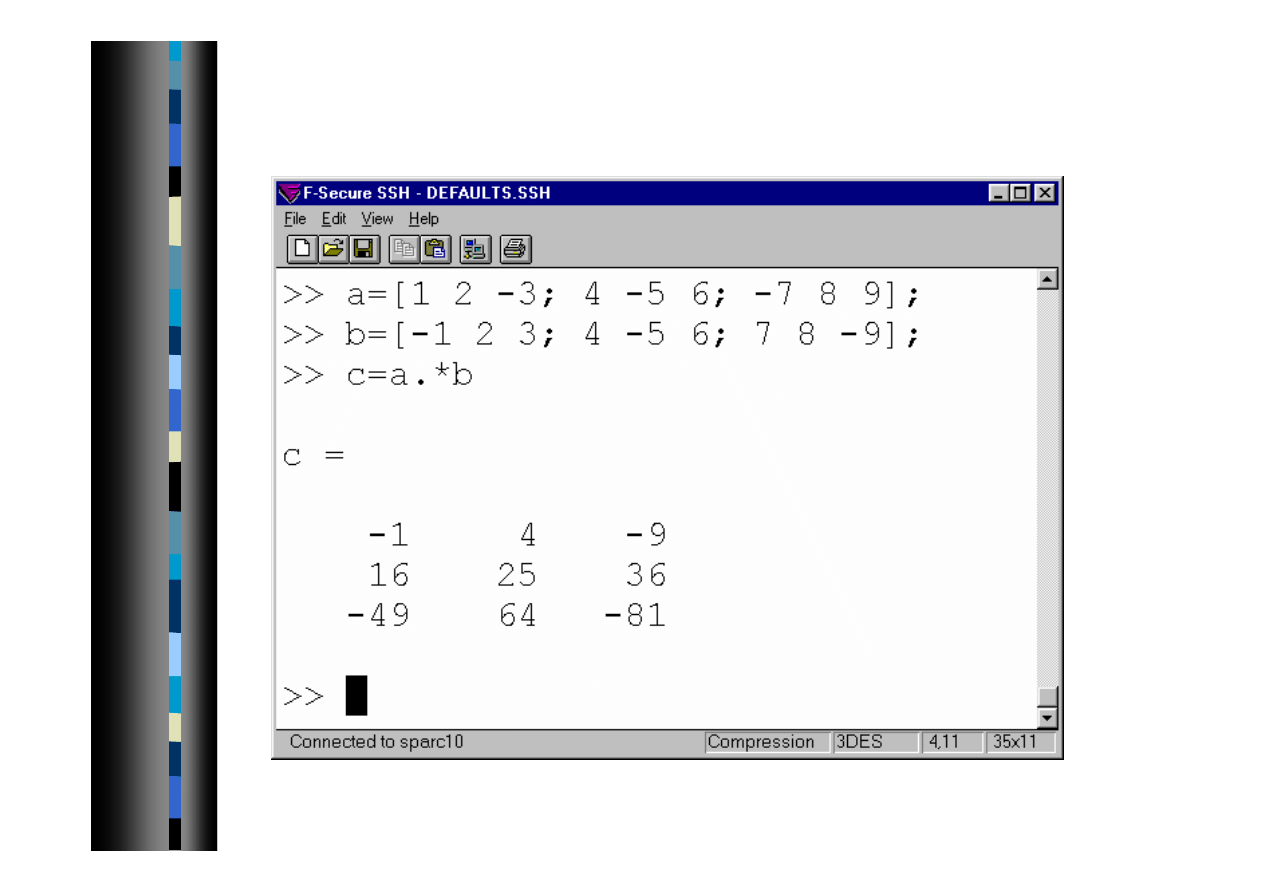
Operacje na tablicowe na macierzach



Dost

ępne są operacje .* ./ .\ .^, które

wykonuje si

ę element po elemencie macierzy



Macierze musz

ą być tych samych wymiarów



W przypadku mno

żenia liczby przez macierz

przed kropk

ą powinna wystąpić spacja, np..:

z = 2 .^[x y]



Dodawanie i odejmowanie tablicowe s

ą

zdefiniowane tak samo jak dla macierzy.

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

61

Mnożenie tablicowe

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

62

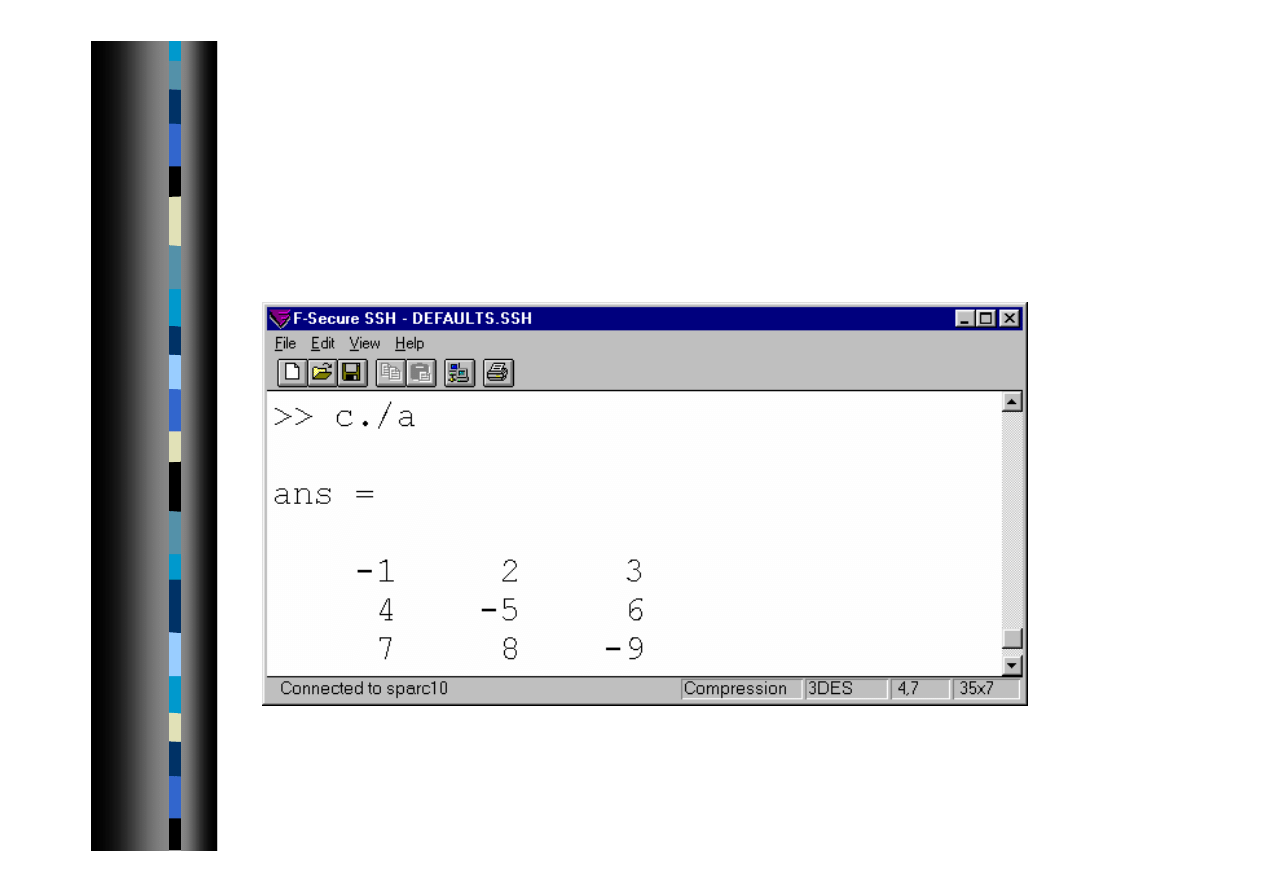
Dzielnie tablicowe ./ (prawe)

Ilorazy elementów z tablic c i a o tych samych indeksach

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

63

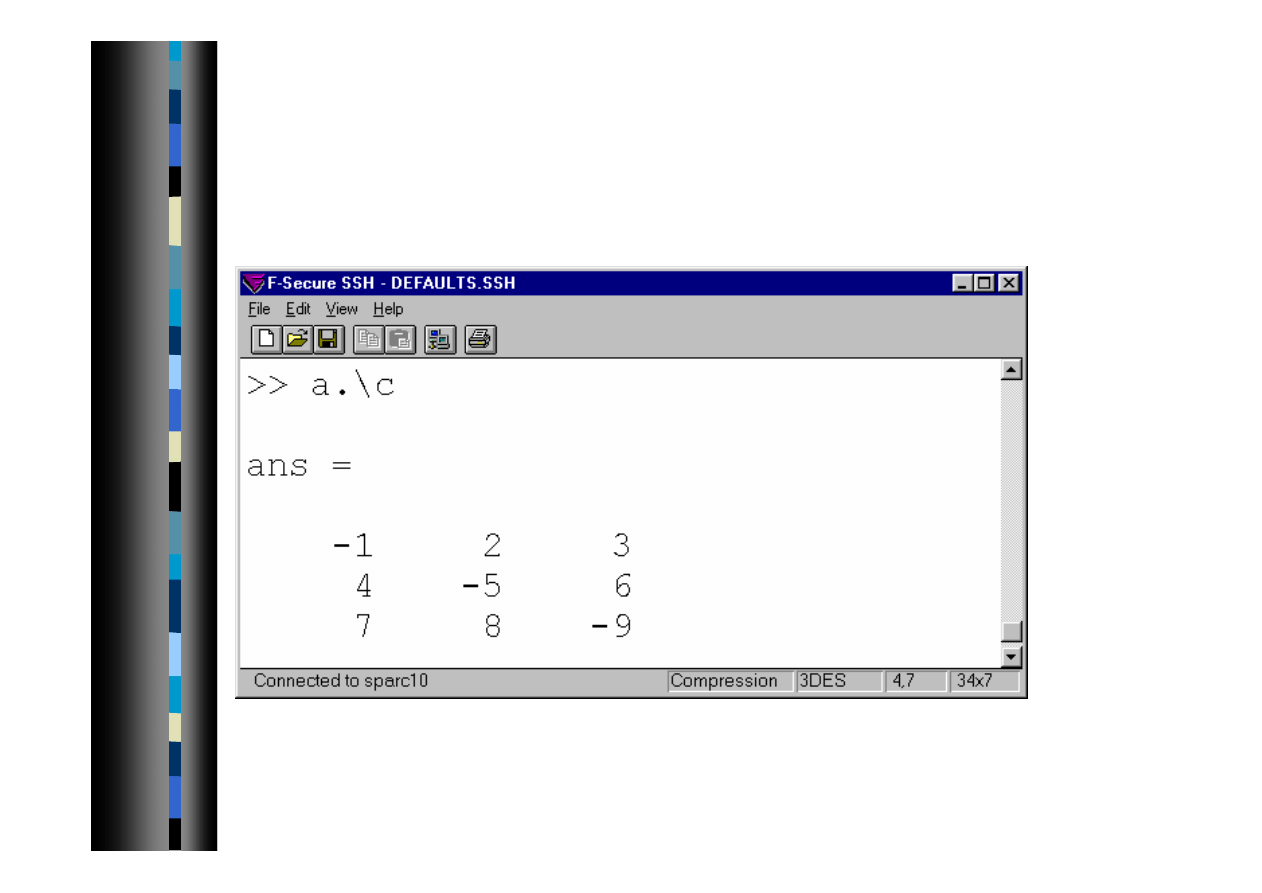
Dzielenie tablicowe .\ (lewe)

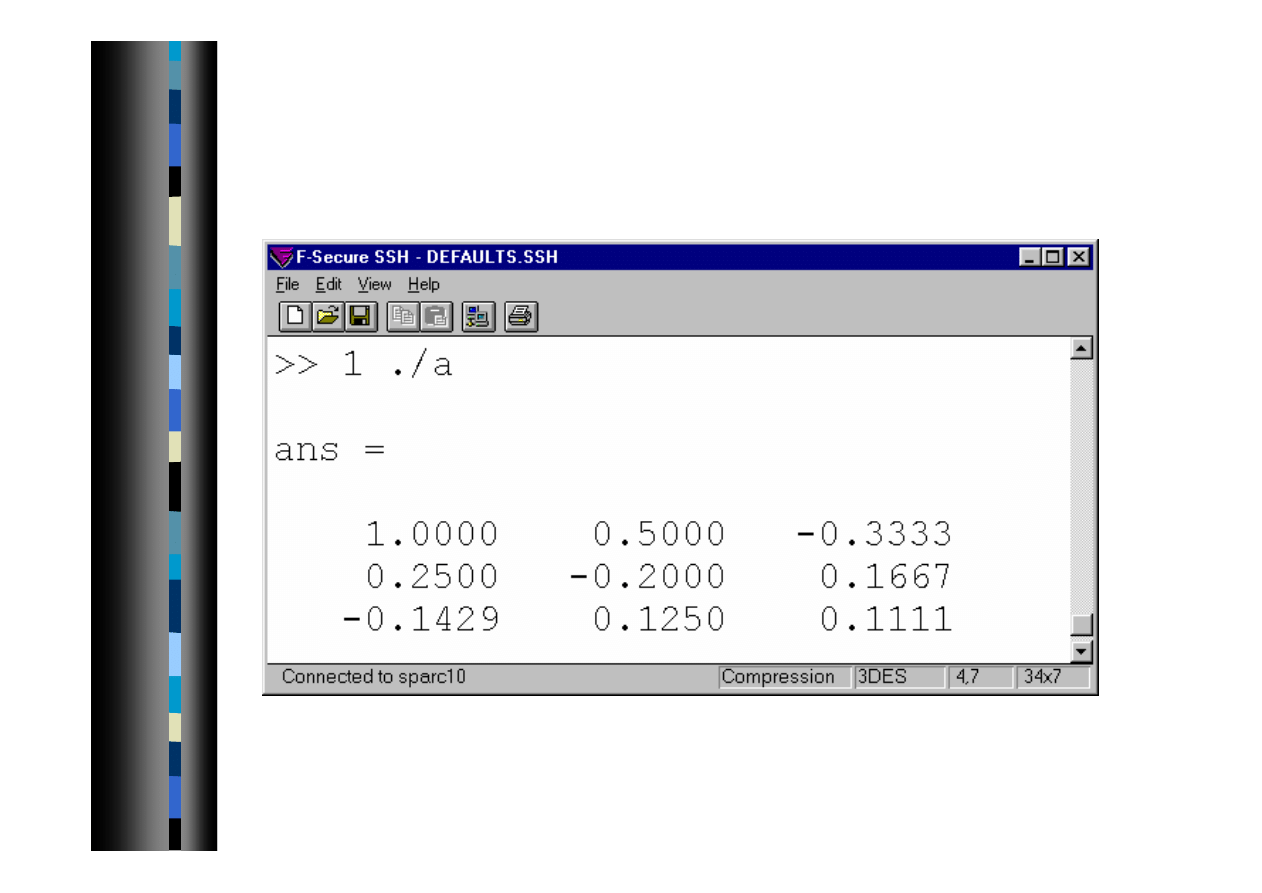
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

64

Mnożenie i dzielenie przez skalar

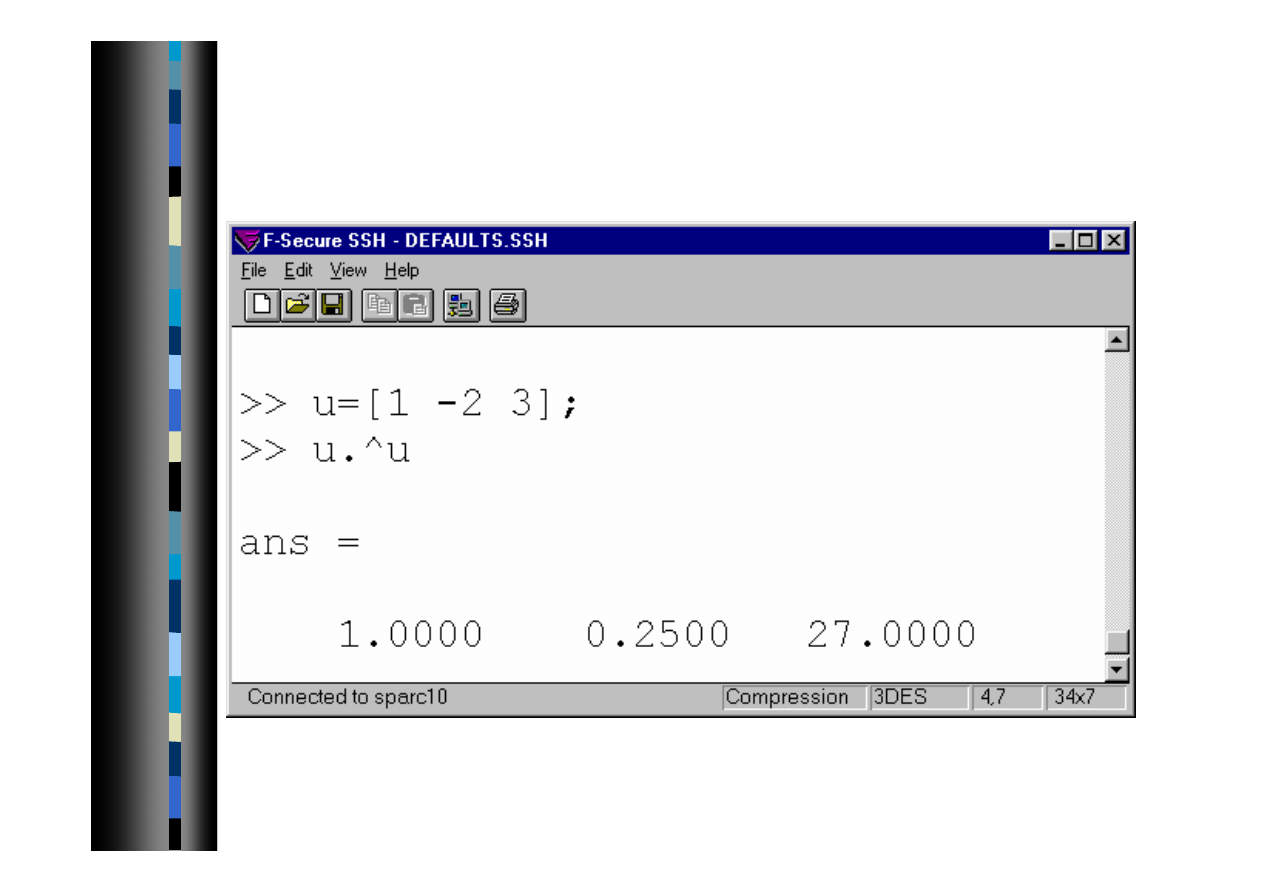
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

65

Potęgowanie tablicowe .^

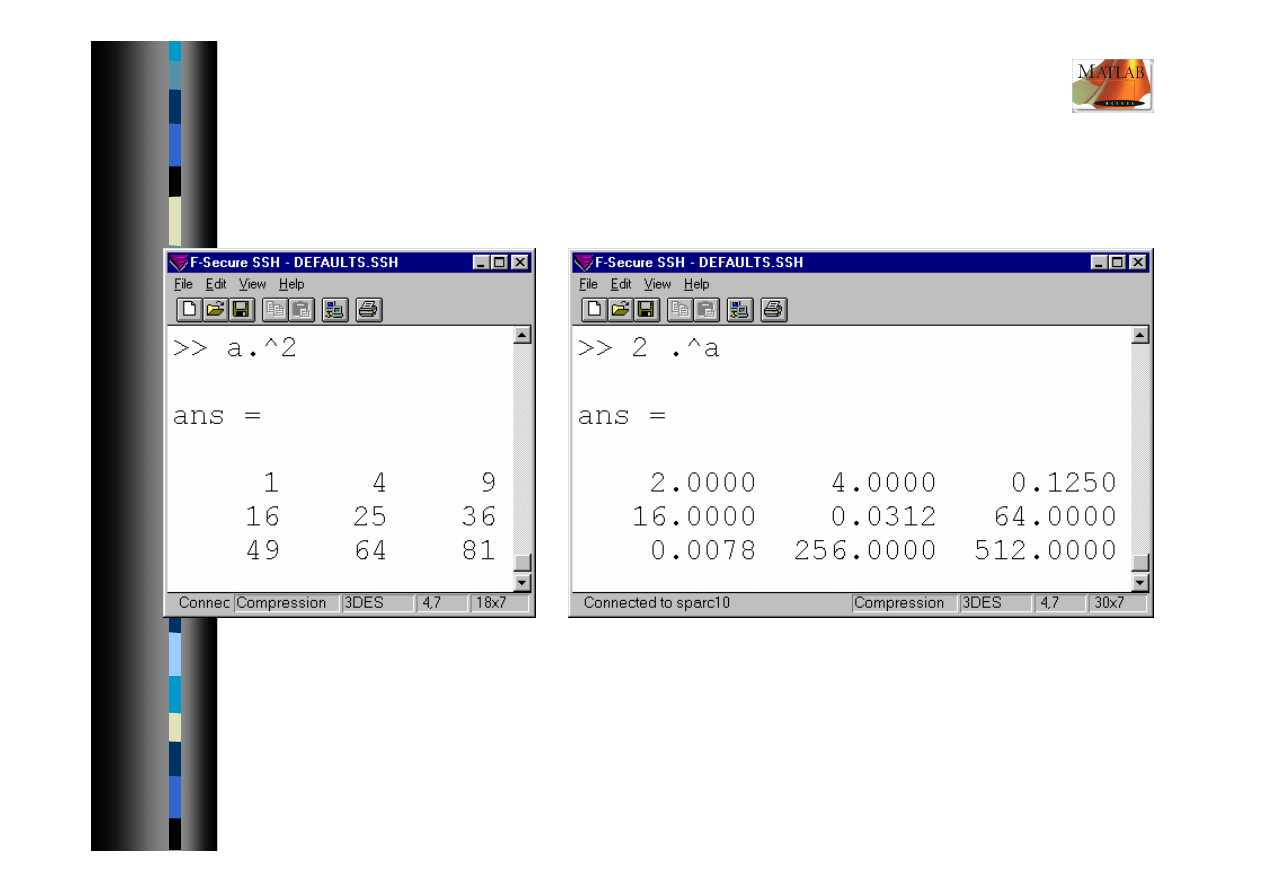
2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

66

Potęgowanie tablicowe .^ (skalary)

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

67

Operacje relacyjne i logiczne



<

mniejszy



<

mniejszy b

ądź równy



>

wi

ększy



>= wi

ększy bądź równy



== równy



~= ró

żny



&

logiczne and



|

logiczne or



~

logiczne not

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

68

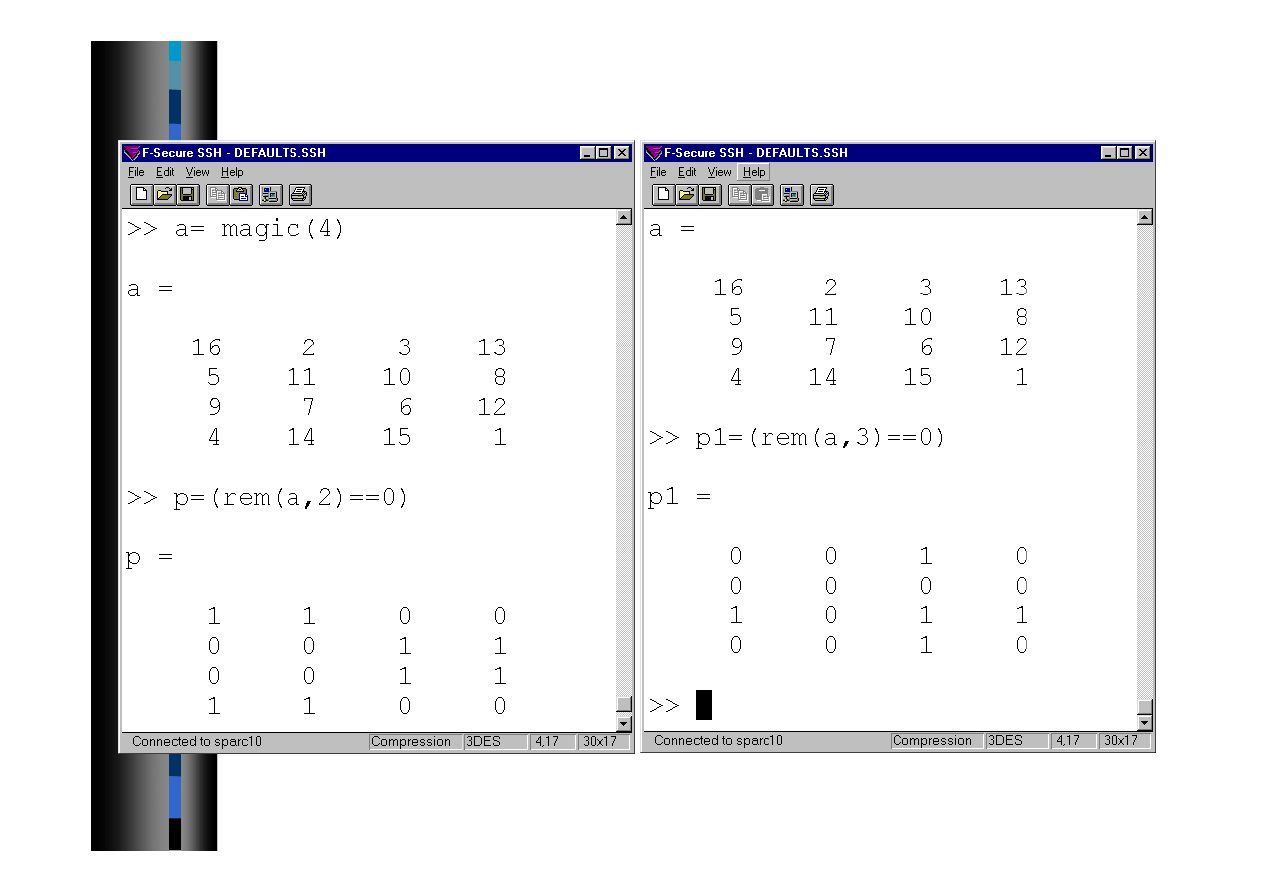
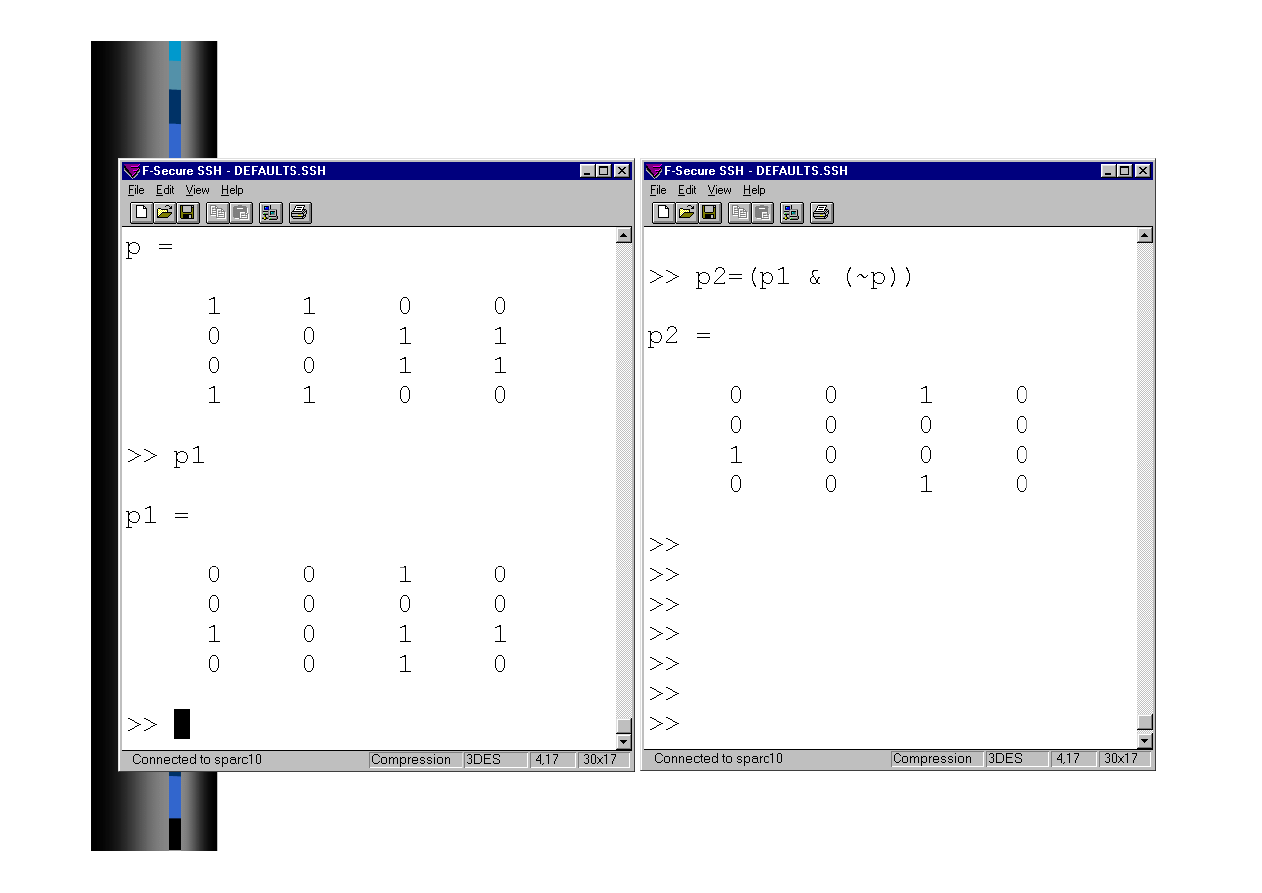
Operacje relacyjne i logiczne - przykład

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

69

Operacje logiczne - przykład

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

70

Funkcje relacyjne i logiczne



exist - prawda, je

śli funkcja albo zmienna jest zdefiniowana



any - prawda, je

śli którykolwiek z elementów wektora jest

prawdziwy



all - prawda, je

śli wszystkie elementy wektora są prawdziwe



find - znajduje indeksy elementów niezerowych



isnan - prawda dla NaN



isinf - prawda dla elementów niesko

ńczonych



finite - prawda dla elementów sko

ńczonych



isempty - prawda dla macierzy pustej



isreal - prawda dla macierzy rzeczywistej



issparse - prawda dla macierzy rzadkiej



isstr - prawda dla macierzy tekstowej



isglobal - prawda dla zmiennej globalnej

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

71

Funkcje trygonometryczne



sin - sinus



cos - cosinus



tan - tangens



asin - arcus sinus



acos - arcus cosinus



atan - arcus tangens



atan2 - arcus tanges w
czterech

ćwiartkach



sinh - sinus hiperboliczny



cosh - cosinus
hiperboliczny



tanh - tangens
hiperboliczny



asinush - arcus sinus
hiperboliczny



acosh - arcus cosinus
hiperboliczny



atanh - arcus tangens
hiperboliczny

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

72

Funkcje elementarne



abs - warto

ść

bezwzgl

ędna



angle - faza



conj - sprz

ężenie



imag - cz

ęść urojona



real - cz

ęść rzeczywista



fix - zaokr

ąglenie w

kierunku 0



floor zaokr

ąglenie w

kierunku -



ceil - zaokr

ąglenie w

kierunku +



round - zaokr

ąglenie do

najbli

ższej całkowitej



rem - reszta z dzielenia



sign - znak



exp - funkcja wyk

ładnicza



log - logarytm naturalny



log10 - logarytm dziesi

ętny



sqrt - pierwiastek
kwadratowy

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

73

Funkcje specjalne 1



besselj - funkcja Bessela pierwszego rodzaju



bessely - funkcja Bessela drugiego rodzaju



besseli - zmodyfikowana funkcja Bessela
pierwszego rodzaju



besselk - zmodyfikowana funkcja Bessela drugiego
rodzaju



beta - funkcja beta



ellipj - eliptyczne funkcje Jakobiego



ellipke - pe

łna całka eliptyczna



erf - funkcja b

łędu

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

74

Funkcje specjalne 2



gamma - funkcja Gamma



gcd - najwi

ększy wspólny podzielnik



lcm - najmniejsza wspólna wielokrotno

ść



rat - aproksymacja u

łamkiem



cart2sph - zmiana wspó

łrzędych z kartezjańskich na

sferyczne



cart2pool - zmiana wspó

łrzędych z kartezjańskich na

polarne



pool2cart - zmiana wspó

łrzędych z polarnych na

kartezja

ńskie



sph2cart - zmiana wspó

łrzędych ze sferycznych na

kartezja

ńskie

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

75

Wielomiany



roots - pierwiastki wielomianu



poly - wielomian na podstawie pierwiastków



polyval - warto

ść wielomianu



polyvalm - warto

ść wielomianu w sensie

macierzowym



residue - rozk

ład na ułamki proste



polyfit - dopasowanie wielomianu do danych



polyder - pochodna wielomianu



conv - mno

żenie wielomianów



deconv - dzielenie wielomianów

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

76

Operacje podstawowe i interpolacja



max - element maksymalny



min - element minimalny



mean -

średnia



median - mediana



std - odchylenie standardowe



sort - sortowanie w porz

ądku rosnącym



sum - suma



prod - iloczyn



interp1 - 1-wymiarowa interpolacja



interp2 - 2-wymiarowa interpolacja



interpft - interpolacja z wykorzystaniem FFT



spline - interpolacja przy pomocy splajnów

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

77

Filtrowanie sygnałów i transformata Fouriera



filter - 1-wymiarowy filtr cyfrowy



filter2 - 2-wymiarowy filtr cyfrowy



fft - szybka transformata Fouriera



fft2 - 2-wymiarowa szybka transformata
Fouriera



ifft - odwrotna szybka transformata Fouriera



ifft2 - odwrotna 2-wymiarowa szybka
transformata Fouriera

2007-10-08

M. Kwiesielewicz. Wprowadzenie do MATLABA

78

Operacje na funkcjach



fmin - minimalizacja funkcji jednej zmiennej



fmins - minimalizacja funkcji wielu zmiennych



fzero - miejsca zerowe funkcji jednej
zmiennej