
Estymatory średniej i dyspersji
1
Estymatory średniej i dyspersji.
Zakładamy, że w czasie doświadczenia otrzymaliśmy zestaw
n
wartości
zmiennej losowej
X
o pewnym rozkładzie prawdopodobieństwa (gęsto-
ści prawdopodobieństwa).
{
}
n
x
x
x
x
,...
,
,
3
2
1
Prawdopodobieństwo otrzymania dowolnej z tych wartości wynosi
)
(
i
x
P
albo
dx
x
p
dx
x
x
dP
i
i
i
⋅
=
+
)
(
)
,
(
odpowiednio dla zmiennej dyskretnej albo ciągłej.
Jeżeli możemy założyć, że kolejne wartości są niezależne, to prawdopo-
dobieństwo otrzymania całego ich zestawu
{
}
n
x
x
x
x
,...
,
,
3
2
1
wynosi
)
(
})
({
1
i
n
i
i
x
P
x
P
=
∏
=
dla zmiennej dyskretnej albo
(
)
dx
x
p
x
dP
i
n
i
i
⋅
∏
=
=
)
(
})
({
1
dla zmiennej ciągłej. Prawdopodobieństwo to
zależy od samych wartości
}
{
i
x
i od postaci rozkładu prawdopodobień-
stwa. Na przykład dla rozkładu normalnego
)
,
(
σ
µ
N
dx
x
dx
x
x
dP
i
i
i
⋅
−
−
=
+
2
2
1
exp
2
1
)
,
(
σ
µ
π
σ
prawdopodobieństwo będzie zależało od średniej i dyspersji tego rozkła-
du.
⋅
−
−
∏
=
=
dx
x
x
dP
i
n
i
i
2
1
2
1
exp
2
1
})
({
σ
µ
π
σ
( )
dx
x
x
dP
n
i
n
i
i
n
i
1
1
2
2
1
exp
2
1
})
({
=
=
∏
⋅
−
−
=
∑
σ
µ
π
σ
Funkcja
−
−
=
∑
=
n
i
i
n
i
x
x
p
1
2
2
1
exp
2
1
)
,
};
({
σ
µ
π
σ
σ
µ
ma sens funkcji rozkładu gęstości prawdopodobieństwa otrzymania ze-
stawu wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
.

Estymatory średniej i dyspersji
2
Metoda największej wiarogodności
Wykonując pomiary nie znamy wartości mierzonej, tzn. nie znamy para-
metrów
µ
i
σ
rozkładu
)
,
};
({
σ
µ
i
x
p
i celem pomiarów jest ich wyzna-
czenie. Możemy jednak przypuszczać, że to co się wydarzyło, to znaczy,
że otrzymaliśmy zestaw konkretnych wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
, było naj-
bardziej prawdopodobne. Zamiast zatem pytać jakie są faktyczne warto-
ści parametrów
µ
i
σ
(na to pytanie zwykle nie można odpowiedzieć),
możemy zapytać o coś innego.
Dla uproszczenia załóżmy jeszcze, że interesuje nas tylko wartość śred-
nia, a dyspersję albo znamy skądinąd, albo nie jest nam potrzebna jej
wartość.
To inne pytanie brzmi:
Dla jakiej wartości
'
µ
hipotetycznej średniej rozkładu otrzymanie
zestawu wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
jest najbardziej prawdopodobne?
Czyli dla jakiej wartości
'
µ
funkcja
−
−
=
∑
=
n
i
i
n
x
p
1
2
'
2
1
exp
2
1
)
'
(
σ
µ
π
σ
µ
osiąga maksimum przy ustalonych
{
}
n
x
x
x
x
,...
,
,
3
2
1
i
σ
.
Na takie pytanie można odpowiedzieć, i to stosunkowo łatwo, chodzi
bowiem o znalezienie maksimum funkcji jednej zmiennej.
Funkcja
)
'
(
µ
p
osiąga maksimum kiedy wartość sumy
2
1
'
∑
=
−
n
i
i
x
σ
µ
jest minimalna. Oznacza to, że pochodna sumy przyjmuje wartość zero
0
'
'
2
1
=
−
∂
∂
∑
=
n
i
i
x
σ
µ
µ

Estymatory średniej i dyspersji
3
Pochodna wynosi
∑
∑
∑
=
=
=
−
−
=
−
−
=
−
∂
∂
n
i
i
n
i
i
n
i
i
x
x
x
1
1
2
1
'
2
1
'
2
'
'
σ
µ
σ
σ
σ
µ
σ
µ
µ
i osiąga zero gdy zeruje się suma
0
'
1
=
−
∑
=
n
i
i
x
σ
µ
σ
σ
µ
⋅
=
−
∑
=
0
'
1
n
i
i
x
0
'
1
=
−
∑
=
µ
n
x
n
i
i
czyli gdy
'
µ
jest równe średniej arytmetycznej wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
∑
=
=
n
i
i
x
n
1
1
'
µ
Wartość
'
µ
jest estymatorem największej wiarogodności wartości śred-
niej rozkładu
)
,
(
σ
µ
N
.
Jeżeli
{
}
n
x
x
x
x
,...
,
,
3
2
1
są wynikami bezpośrednich pomiarów wielkości
fizycznej
X
, to ich średnia arytmetyczna jest najlepszym oszacowaniem
wartości
X
. Oprócz szacunku samej wartości musimy podać też nie-
pewność oszacowania, czyli pierwiastek wariancji
'
µ
. Oznaczmy ją
przez
)
'
(
µ
V
.
=
∑
i
x
n
V
V
1
)
'
(
µ
W celu obliczenia wartości prawej strony możemy wykorzystać wprowa-
dzone poprzednio prawo przenoszenia niepewności (w istocie było to
prawo przenoszenia wariancji, które dla naszych celów przekształciliśmy
w prawo przenoszenia niepewności), a właściwie pewne specjalne wzory
wyprowadzone z tego prawa.
( )
∑
∑
⋅
=
i
i
x
V
n
x
n
V
2
1
1
Jeżeli wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
są niezależne, to
( )
2
)
(
σ
⋅
=
=
∑
∑
n
x
V
x
V
i
i

Estymatory średniej i dyspersji
4
Ostatecznie
n
n
n
V
2
2
2
1
)
'
(
σ
σ
µ
=
⋅
=
Czyli wynik serii pomiarów mógłby wyglądać na przykład tak:
∑
=
=
=
n
i
i
x
n
X
1
1
µ
,
σ
n
X
u
1
)
(
=
.
♦
Załóżmy teraz, że znamy wartość średnią rozkładu
µ
, a chcielibyśmy
znaleźć estymator dyspersji tego rozkładu
'
σ
.
Jeżeli
'
σ
ma być estymatorem największej wiarogodności, to tym razem
funkcja
−
−
=
∑
=
n
i
i
n
x
p
1
2
'
2
1
exp
2
'
1
)
'
(
σ
µ
π
σ
σ
ma osiągnąć maksimum ze względu na
'
σ
, czyli
0
)
'
(
'
=
∂
∂
σ
σ
p
0
'
2
1
exp
2
'
1
'
1
2
=
−
−
∂
∂
∑
=
n
i
i
n
x
σ
µ
π
σ
σ
0
'
)
(
2
'
1
2
'
1
2
'
1
1
3
2
(...)
(...)
2
1
=
−
+
−
∑
=
−
−
−
n
i
i
n
n
x
e
e
n
σ
µ
π
σ
π
σ
π
σ
0
'
)
(
2
'
1
2
'
1
'
1
3
2
(...)
(...)
=
−
+
−
∑
=
−
−
n
i
i
n
n
x
e
e
n
σ
µ
π
σ
π
σ
σ
Po podzieleniu stronami przez
(...)
2
'
1
−
e
n
π
σ
otrzymujemy
2
1
3
2
'
0
'
)
(
'
σ
σ
µ
σ
⋅
=
−
+
−
∑
=
n
i
i
x
n

Estymatory średniej i dyspersji
5
(
)
0
'
1
2
2
=
−
+
−
∑
=
n
i
i
x
n
µ
σ
czyli
(
)
∑
=
−
=
n
i
i
x
n
1
2
2
1
'
µ
σ
(
)
∑
=
−
=
n
i
i
x
n
1
2
1
'
µ
σ
Estymatorem największej wiarogodności wariancji rozkładu
)
,
(
σ
µ
N
jest
2
'
σ
– średni kwadrat odchylenia wartości
{
}
n
x
x
x
x
,...
,
,
3
2
1
od wartości
średniej tego rozkładu, a estymatorem dyspersji jest
'
σ
.
Najczęściej nie znamy żadnego parametrów rozkładu i musimy je osza-
cować tylko na podstawie uzyskanych wartości doświadczalnych
{
}
n
x
x
x
x
,...
,
,
3
2
1
.
Nie zmienia to sposobu wyznaczenia wartości
'
µ
i w dalszym ciągu naj-
lepszym estymatorem (w sensie metody największej wiarogodności) po-
zostaje średnia arytmetyczna.
∑
=
=
n
i
i
x
n
1
1
'
µ
.
Do wyznaczenia estymatora dyspersji (albo wariancji) potrzebna jest
znajomość wartości średniej rozkładu. Jeżeli użyjemy w tym celu warto-
ści
'
µ
zamiast
µ
, to moglibyśmy zapisać
(
)
∑
=
−
=
n
i
i
x
n
1
2
2
'
1
'
µ
σ
.
Okazuje się jednak, że taki estymator jest obciążony, to znaczy, że war-
tość średnia
2
'
σ
jest różna od
2
σ
. W statystyce dowodzi się, że
2
2
)
'
(
σ
σ
<
E
.

Estymatory średniej i dyspersji
6
Rzeczywiście
(
)
(
)
=
−
+
−
=
−
=
∑
∑
=
=
n
i
i
n
i
i
x
n
E
x
n
E
E
1
2
1
2
2
)
'
(
)
(
1
'
1
)
'
(
µ
µ
µ
µ
σ
[
]
=
−
−
−
=
∑
=
n
i
i
x
n
E
1
2
)
'
(
)
(
1
µ
µ
µ
[
]
=
−
+
−
−
−
−
=
∑
=
n
i
i
i
x
x
n
E
1
2
2
)
'
(
)
'
)(
(
2
)
(
1
µ
µ
µ
µ
µ
µ
=
−
+
−
−
−
−
=
∑
∑
=
=
2
1
1
2
)
'
(
1
)
(
1
)
'
(
2
)
(
1
µ
µ
µ
µ
µ
µ
n
n
x
n
x
n
E
n
i
i
n
i
i
=
−
+
−
−
−
=
∑
=
2
2
1
2
)
'
(
)
'
(
2
)
(
1
µ
µ
µ
µ
µ
n
i
i
x
n
E
=
−
−
−
=
∑
=
2
1
2
)
'
(
)
(
1
µ
µ
µ
n
i
i
x
n
E
(
) (
)
=
−
−
−
=
∑
=
2
1
2
)
'
(
)
(
1
µ
µ
µ
E
x
E
n
n
i
i
(
) (
)
)
'
(
)
(
)
'
(
)
(
2
2
µ
µ
µ
µ
V
x
V
E
x
E
i
−
=
−
−
−
=
Czyli
( )
2
2
2
2
1
1
'
σ
σ
σ
σ
n
n
n
E
−
=
−
=
i
(
)
∑
=
−
−
=
n
i
i
x
n
s
1
2
2
'
1
1
µ
jest już nieobciążonym estymatorem wariancji.
Po uwzględnieniu ostatniego wzoru wynik pomiarów można by przed-
stawić następująco:
∑
=
=
=
n
i
i
x
n
x
X
1
1
,
(
)
∑
−
−
−
=
n
i
i
x
x
n
n
X
u
1
2
)
1
(
1
)
(
.
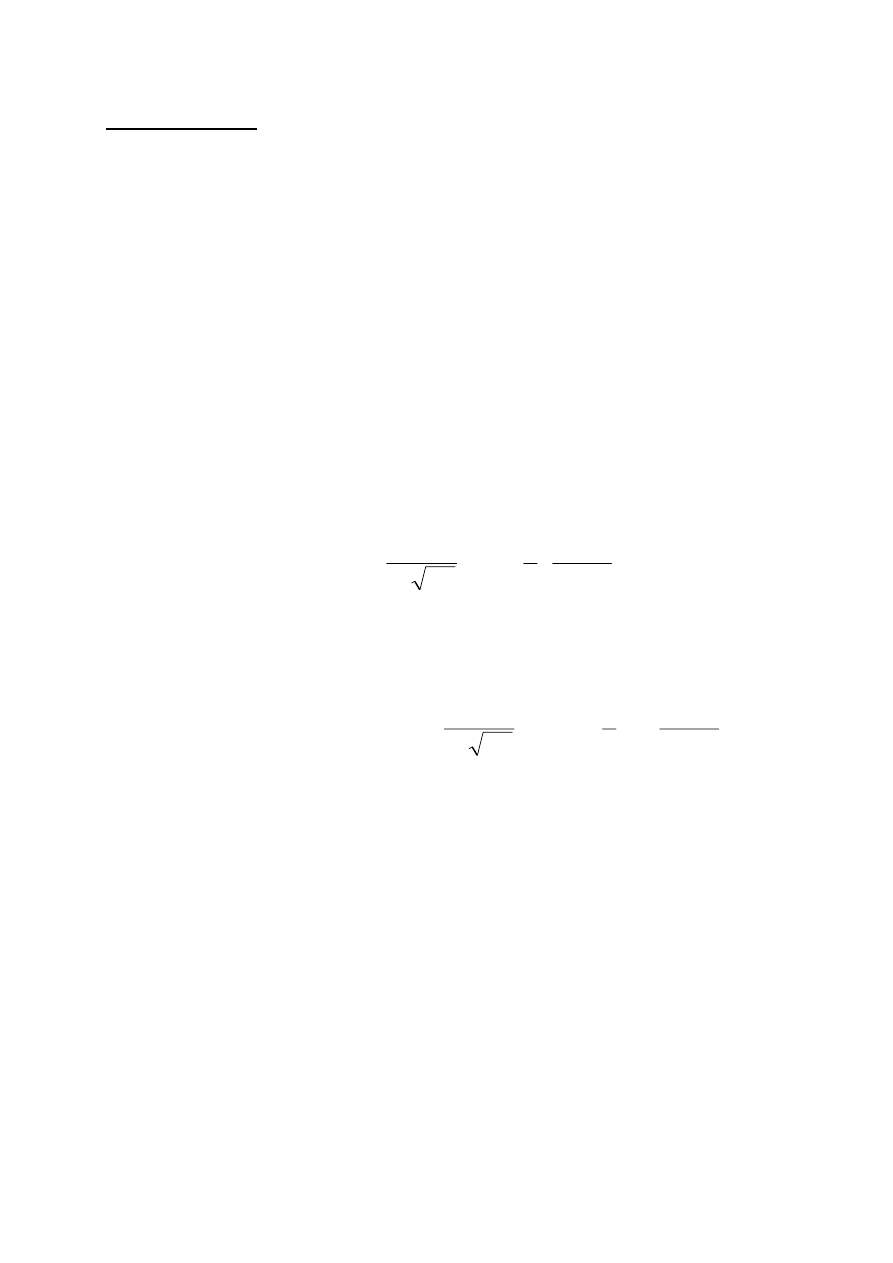
Estymatory średniej i dyspersji
7
Średnia ważona
We wzorze
(
)
dx
x
P
x
dP
i
n
i
i
⋅
∏
=
=
)
(
})
({
1
wcale nie jest konieczne, żeby wszystkie
i
x
miały dokładnie takie same
rozkłady. Równie dobrze moglibyśmy zapisać
(
)
∏
=
⋅
=
n
i
i
i
i
dx
x
p
x
dP
1
)
(
})
({
a funkcja
∏
=
=
n
i
i
i
i
x
p
x
p
1
)
(
})
({
miałaby taką samą interpretację jak poprzednio.
Załóżmy, że rozkłady
−
−
=
2
2
1
exp
2
1
)
,
;
(
i
i
i
i
i
i
x
x
p
σ
µ
π
σ
σ
µ
mają wszystkie tę samą wartość średnią i różne dyspersje.
Wtedy rozkład gęstości prawdopodobieństwa otrzymania ciągu wartości
{
}
n
x
x
x
,...
,
2
1
wyniesie
−
−
⋅
=
=
∑
∏
∏
=
=
=
n
i
i
i
n
i
i
n
i
i
i
i
i
x
x
p
x
p
1
2
1
1
2
1
exp
2
1
)
,
;
(
})
({
σ
µ
π
σ
σ
µ
.
Taki przypadek odpowiada sytuacji, kiedy kolejne wartości
{
}
n
x
x
x
,...
,
2
1
wyznaczono niezależnie metodami różniącymi się precyzją scharaktery-
zowaną różnymi wartościami
i
σ
.

Estymatory średniej i dyspersji
8
Stosując metodę największej wiarogodności do wyznaczenia estymatora
wartości średniej
µ
będziemy szukali maksimum funkcji
−
−
⋅
=
∑
∏
=
=
n
i
i
i
n
i
i
x
p
1
2
1
'
2
1
exp
2
1
)
'
(
σ
µ
π
σ
µ
.
Podobnie jak poprzednio odpowiada to znalezieniu minimum sumy
∑
=
−
n
i
i
i
x
1
2
'
σ
µ
0
'
2
'
'
1
2
1
2
=
−
−
=
−
∂
∂
∑
∑
=
=
n
i
i
i
n
i
i
i
x
x
σ
µ
σ
µ
µ
Stąd
0
'
1
2
1
2
=
−
∑
∑
=
=
n
i
i
n
i
i
i
x
σ
µ
σ
∑
∑
=
=
=
n
i
i
n
i
i
i
x
1
2
1
2
1
'
σ
µ
σ
i ostatecznie
(
)
( )
∑
∑
=
=
=
n
i
i
n
i
i
i
x
1
2
1
2
1
'
σ
σ
µ
W celu ustalenia wariancji tego estymatora obliczamy pochodne cząst-
kowe:
(
)
( )
( )
∑
∑
∑
=
=
=
=
∂
∂
=
∂
∂
n
i
i
i
n
i
i
n
i
i
i
i
i
x
x
x
1
2
2
1
2
1
2
1
1
1
'
σ
σ
σ
σ
µ
i zgodnie z prawem przenoszenia wariancja wynosi
( )
( )
[
]
( )
∑
∑ ∑
∑ ∑
=
=
=
=
=
2
1
2
2
2
1
2
2
2
2
1
1
1
1
1
1
)
'
(
i
n
i
i
i
n
i
i
i
i
V
σ
σ
σ
σ
σ
σ
µ

Estymatory średniej i dyspersji
9
Niepewności względne
Może się zdarzyć, że znamy względne wartości
i
σ
nie znając przy tym
ich wartości bezwzględnych. Wprowadzimy czynniki wagowe (wagi)
i
w
i
i
kw
σ
1
=
gdzie
k
jest pewną stałą. Znajomość względnych niepewności odpowia-
da znajomości wartości wag
i
w
nawet jeżeli
i
σ
pozostają nieznane.
Wtedy
(
)
( )
(
)
( )
(
)
( )
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
=
=
=
n
i
i
n
i
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
i
w
x
w
kw
x
kw
x
1
1
1
1
1
2
1
2
1
'
σ
σ
µ
W celu ustalenia wariancji tak obliczonej średniej wprowadzimy nową
wielkość – średnią ważoną wariancję wyników
2
σ
1
'
1
)
'
(
2
2
2
2
−
−
=
−
−
=
∑
∑
∑
∑
n
n
w
x
w
n
n
w
x
w
i
i
i
i
i
i
µ
µ
σ
Wartość w nawiasie jest różnicą średniego ważonego kwadratu wyników
i kwadratu średniej ważonej wyników. Pozostały czynnik uwzględnia fakt,
że wartość
'
µ
została obliczona z tych samych wyników, zmniejszając
liczbę stopni swobody.
Przez analogię z wcześniej otrzymanymi związkami możemy zapisać, że
wariancja
'
µ
wynosi
−
−
=
=
∑
∑
2
2
2
'
1
1
)
'
(
µ
σ
µ
i
i
i
w
x
w
n
n
V
Jeżeli chcielibyśmy znaleźć nieznane dotąd wartości
k
i
i
σ
, to możemy
przyrównać
∑
∑
=
=
i
i
w
k
n
1
1
1
2
2
σ
σ
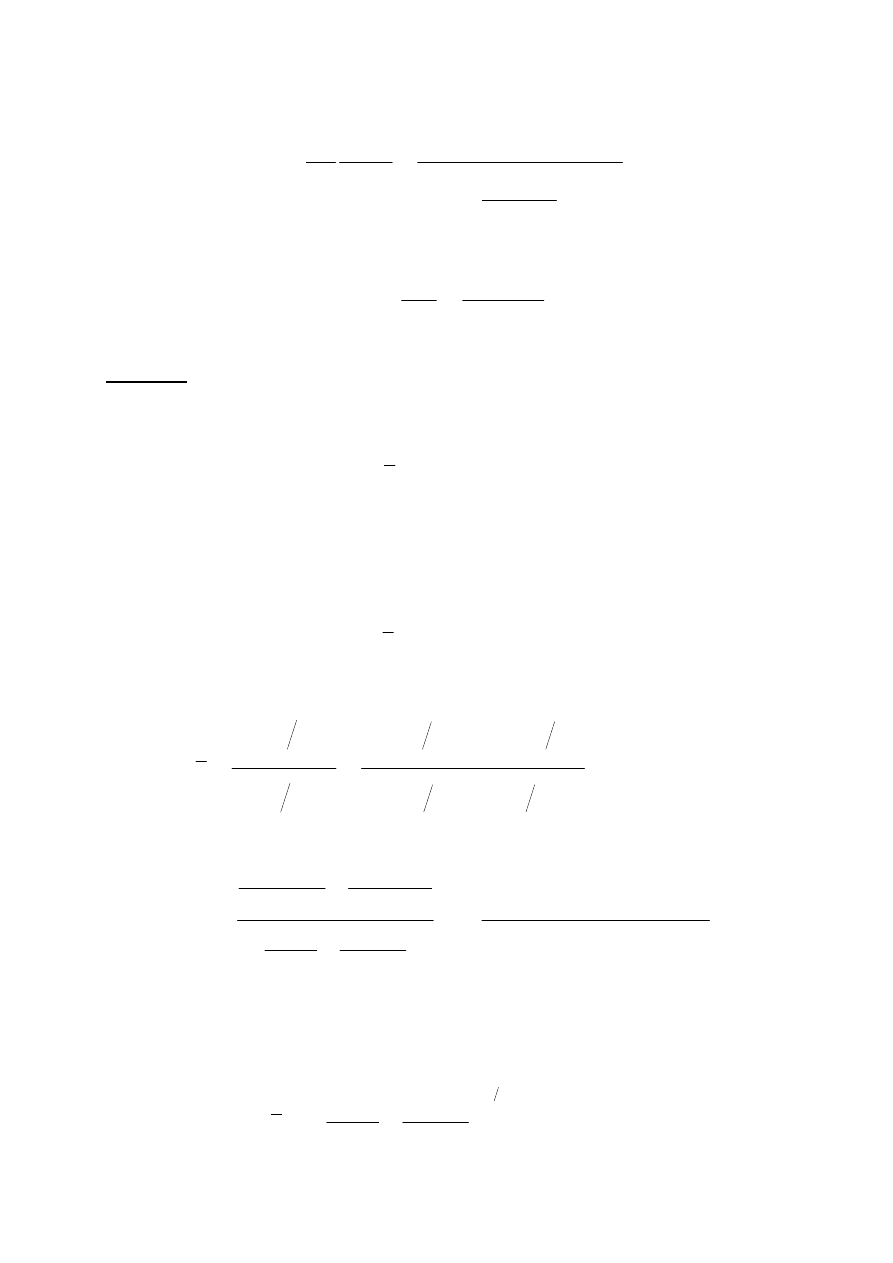
Estymatory średniej i dyspersji
10
czyli
−
−
=
=
∑
∑
∑
∑
2
2
2
'
1
1
µ
σ
i
i
i
i
i
w
x
w
w
n
w
n
k
oraz
i
i
i
i
nw
w
kw
∑
=
=
2
2
1
σ
σ
Przykład
Studentka przeprowadza doświadczenie w celu określenia napięcia
ogniwa normalnego. Wykonuje 40 pomiarów przy pomocy pewnego
przyrządu i znajduje, że
V
0220
,
1
1
=
x
z odchyleniem standardowym
V
010
,
0
1
=
s
Po przyjrzeniu się wynikom zauważa, że mogłaby ulepszyć układ pomia-
rowy i zmniejszyć niepewność o czynnik 2,5
V
0040
,
0
2
=
s
. Wykonuje
kolejnych 10 pomiarów, które dają
V
0180
,
1
2
=
x
Średnia wyników wszystkich wykonanych pomiarów wynosi
(
)
( )
(
) (
)
( ) ( )
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
+
+
=
=
40
1
10
1
2
2
2
1
10
1
2
2
2
40
1
2
1
1
50
1
2
50
1
2
1
1
1
i
i
i
i
i
i
i
i
i
i
i
s
s
s
x
s
x
x
x
σ
σ
V
25
,
6
00
,
4
018
,
1
25
,
6
022
,
1
00
,
4
V
004
,
0
10
01
,
0
40
004
,
0
018
,
1
10
01
,
0
022
,
1
40
2
2
2
2
+
⋅
+
⋅
=
+
⋅
+
⋅
=
V
019561
,
1
=
Niepewność wartości średniej napięcia
V
000987
,
0
004
,
0
10
01
,
0
40
)
(
2
1
2
2
=
+
=
−
x
u

Estymatory średniej i dyspersji
11
Ostateczny wynik należy zapisać w formie
V
01956
,
1
=
x
,
V
00099
,
0
)
(
=
x
u
lub alternatywnie
V
)
99
(
01956
,
1
=
x
Niepewność końcowego wyniku jest mniejsza od niepewności uzyska-
nych w każdej z części doświadczenia
V
0016
,
0
V
40
01
,
0
)
(
1
=
=
x
u
,
V
0013
,
0
V
10
004
,
0
)
(
2
=
=
x
u
Co by było gdyby studentka nie znała bezwzględnych wartości niepew-
ności swoich pomiarów, a tylko wiedziała (np. od prowadzącego zajęcia),
że zostały zmniejszone w drugiej części o czynnik 2,5?
Średnią ważoną może obliczyć w taki sposób
1
1
2
1
1
=
=
s
w
,
2
2
2
2
5
,
2
1
=
=
s
w
(
)
( )
V
01956
,
1
V
5
,
2
10
1
40
018
,
1
5
,
2
10
022
,
1
1
40
2
2
1
1
=
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
=
∑
∑
=
=
n
i
i
n
i
i
i
w
x
w
x
Niepewność średniej ważonej wyniesie wtedy
−
⋅
+
+
=
−
−
=
∑
∑
∑
∑
=
=
2
2
10
1
2
2
2
40
1
2
1
2
2
5
,
2
10
40
5
,
2
39
1
1
1
)
(
x
x
x
x
w
x
w
n
x
u
i
i
i
i
i
i
i
Estymatory średniej i dyspersji
12
Przykład
Student wykonał 100 niezależnych pomiarów długości drewnianego
klocka. Wyniki, po korekcie błędów systematycznych, mieszczą się w
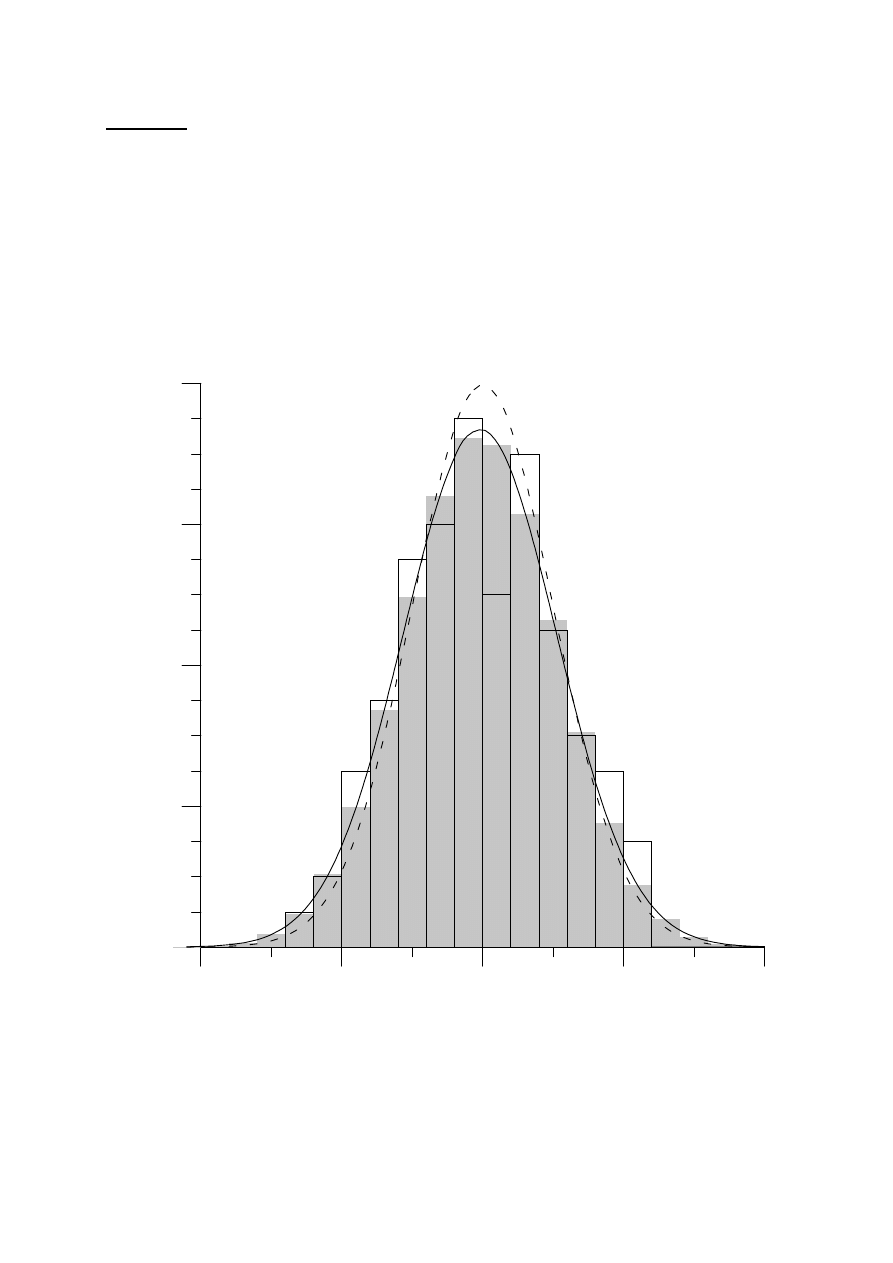
przedziale od około 18 do 22 cm i wiele z nich powtarza się. Na wykresie
przedstawiono je w postaci histogramu (słupki narysowane cienką ciągłą
linią) o szerokości przedziału 0,2 cm. Jeżeli obserwowany rozkład wyni-
ka z błędów przypadkowych, to jest bardzo prawdopodobne, że da się
opisać przy pomocy rozkładu Gaussa (normalnego). Rozkład narysowa-
ny linia ciągłą odpowiada parametrom wyznaczonym z wyników pomia-
rów: średnia 19,98 cm i odchylenie standardowe 0,54 cm.
18.00
19.00
20.00
21.00
22.00
długość zmierzona, cm
0
4
8
12
16
lic
zb
a p
omi
arów
Histogram z szarych słupków jest wyliczony z tego rozkładu normalnego
i przedstawia oczekiwaną (średnią) liczbę pomiarów w każdym przedzia-
le. Rozkład narysowany linią przerywaną odpowiada
)
50
,
0
;
00
,
20
(
N
.

Estymatory średniej i dyspersji
13
Usuwanie wyników odstających
Załóżmy, że wśród wyników zanotowanych przez studenta w karcie po-
miarowej znalazł się jeden wyraźnie inny od pozostałych – 91,2 cm.
Zwykle w takim przypadku nie ma wątpliwości, że nastąpiła pomyłka
przy zapisywaniu wyniku i wynik odrzuca się jako tzw. błąd gruby. Sytu-
acja wygląda jednak inaczej jeżeli odstający wynik wynosiłby np. 22,2
cm. Jeżeli w zestawie 100 wyników wartość 21,2 zastąpimy przez 22,2,
to średnia i odchylenie standardowe zmienią się odpowiednio na 19,99 i
0,54. Odległość wyniku od średniej wynosi prawie 4 odchylenia standar-
dowe. Z rozkładu Gaussa
)
54
,
0
;
99
,
19
(
N
można wyliczyć, że prawdo-
podobieństwo przypadkowego pojawienia się rezultatu, który jest nie-
mniej oddalony od średniej wynosi około 12
⋅
10
-5
, to znaczy że spodzie-
wana liczba wyników
≥
22,2 cm (lub
≤
17,78 cm) wynosi 12
⋅
10
-5
×
100 =
0,012. Czy tak mało prawdopodobny rezultat możemy odrzucić?
Kryterium Chauveneta
Odstający rezultat
0
x
można odrzucić, jeżeli spodziewana liczba takich
przypadków, że
|
|
|
|
0
x
x
x
x
−
≥
−
5
,
0
|)
|
|
(|
0
<
−
≥
−
⋅
=
x
x
x
x
P
N
n
Kryterium Chauveneta należy stosować z dużą ostrożnością, mając
pewność, że potrafimy poprawnie obliczyć prawdopodobieństwo
|)
|
|
(|
0
x
x
x
x
P
−
≥
−
, co zwykle oznacza, że musimy znać faktyczny roz-
kład prawdopodobieństwa w danych warunkach.
Wyszukiwarka
Podobne podstrony:
Estymatory średniej i dyspersji
Estymacja parametr w rozkladu prawdopodobienstwa, Estymacja parametrów rozkładu prawdopodobieństwa:
uklady dyspersyjne
wieki średnie
Wyklad 4 srednia dorosloscid 8898 ppt
rozwojowka slajdy, Wyklad 5 Srednia doroslosc teoria czasowa
sredni wiek pps
rozwojowka slajdy, Wyklad 3 srednia doroslosc
Mój region w średniowieczu
Estymacja 2
Średniowiecze prezentacja
HMG Wyklad 2 Sredniowiecze
Piśmiennictwo w średniowieczu
POWTÓRKA SREDNIOWIECZE
Nomogram doboru średnic przewodów c o 3 14 mmH2O
Katechizm rzymsko katolicki średni dla Archidiecezyi Gnieźnieńskiej i Poznańskiej 1871
więcej podobnych podstron