Ć w i c z e n i e 13

POMIAR REZYSTANCJI ZA POMOCĄ MOSTKA PRĄDU

STAŁEGO

Celem ćwiczenia jest wyznaczenie rezystancji:

1. rezystora pierwszego,
2. rezystora drugiego,
3. układu tych rezystorów połączonych równolegle,
4. układu tych rezystorów połączonych szeregowo.

Każdy z ćwiczących zapisuje wszystkie wykonywane pomiary. Zaleca się by prowadzący dokonał
podziału zagadnień do opracowania pomiędzy ćwiczących. Jeżeli prowadzący nie zaleci inaczej
każdy ćwiczący opracowuje całość ćwiczenia.

13.1 Wstęp teoretyczny

Różne metody pomiarowe zostały omówione we Wstępie do Teorii Błędów pkt. 1. „Wiadomości z
podstaw metrologii”. Za najdokładniejsze metody porównania bezpośredniego są uważane metody
zerowe. Porównanie wartości mierzonej z wartością wzorcową odbywa się w nich za pomocą ukła-
du pomiarowego, w którym przez zmianę parametrów układu pomiarowego doprowadza się do za-
niku napięcia lub prądu w kontrolowanej gałęzi obwodu. Wskaźnik służący do zaobserwowania
tego stanu ( np. galwanometr) nazywamy wskaźnikiem równowagi. Na dużą dokładność pomiarów
metodami zerowymi wpływa duża precyzja wykonania wzorców oraz wysoka czułość wskaźników
równowagi. Przy metodzie zerowej można zatem jako pomijalnie małe odrzucić błędy systematycz-
ne. Pozostają jedynie błędy przypadkowe. Można wyróżnić metody zerowe mostkowe oraz kom-
pensacyjne. Przy pomiarach rezystancji R (opór czynny) oraz reaktancji X (X

C

=1/

ω

C;

L

X

L

ω

=

-

opór bierny) obwodów elektrycznych zarówno przy prądzie stałym jak i zmiennym najczęściej sto-
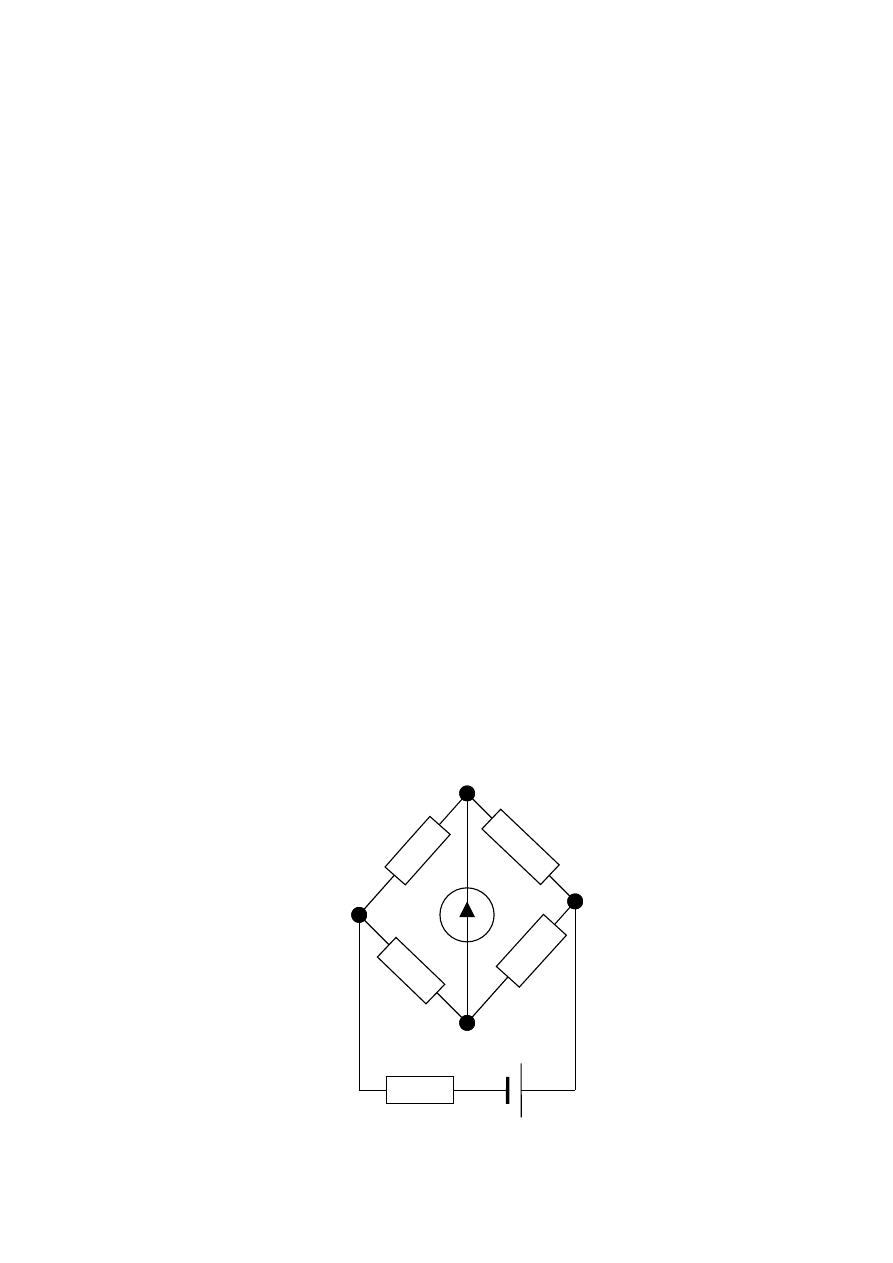
suje się układy zwane mostkowymi. Są to układy schematycznie przedstawione na Rys. 13.1

Rys. 13.1 Schemat układu mostkowego.

C

Z

1

Z

2

A Z

5

B

Z

3

Z

4

- +

Ramionami mostka są impedancje Z

1

, Z

2

, Z

3

, Z

4

gdzie :

2

2

)

(

L

C

X

X

R

Z

+

+

=

. Na przekątnej w

punktach C, D włączony jest wskaźnik równowagi, np. galwanometr o impedancji Z

5

. Wskaźnik ten

jest włączony jak „most” między równolegle połączonymi gałęziami (Z

1

+ Z

2

) oraz (Z

3

+Z

4

). W

punktach A, B mostek jest zasilany ze źródła prądu o sile elektromotorycznej E i impedancji we-
wnętrznej Z

6

. Oprócz mostków stałoprądowych mogą wystąpić mostki zasilane źródłem zmienno-

prądowym. W tym przypadku zamiast źródła stałoprądowego na Rys. 13.1 należy podstawić źródło
zmiennoprądowe zaś na impedancje występujące w schemacie składają się rezystancje, pojemności
oraz indukcyjności własne i wzajemne.
Mostek stałoprądowy w układzie czteroramiennym nazywa się mostkiem Wheatstone’a i jest naj-
bardziej rozpowszechniony przy pomiarach rezystancji. W jego skład wchodzą cztery ramiona opo-
rowe R

1

, R

2

, R

3

, R

4

, wskaźnik równowagi – galwanometr o rezystancji R

5

oraz źródło o sile elektro-

motorycznej E i rezystancji wewnętrznej R

6

.

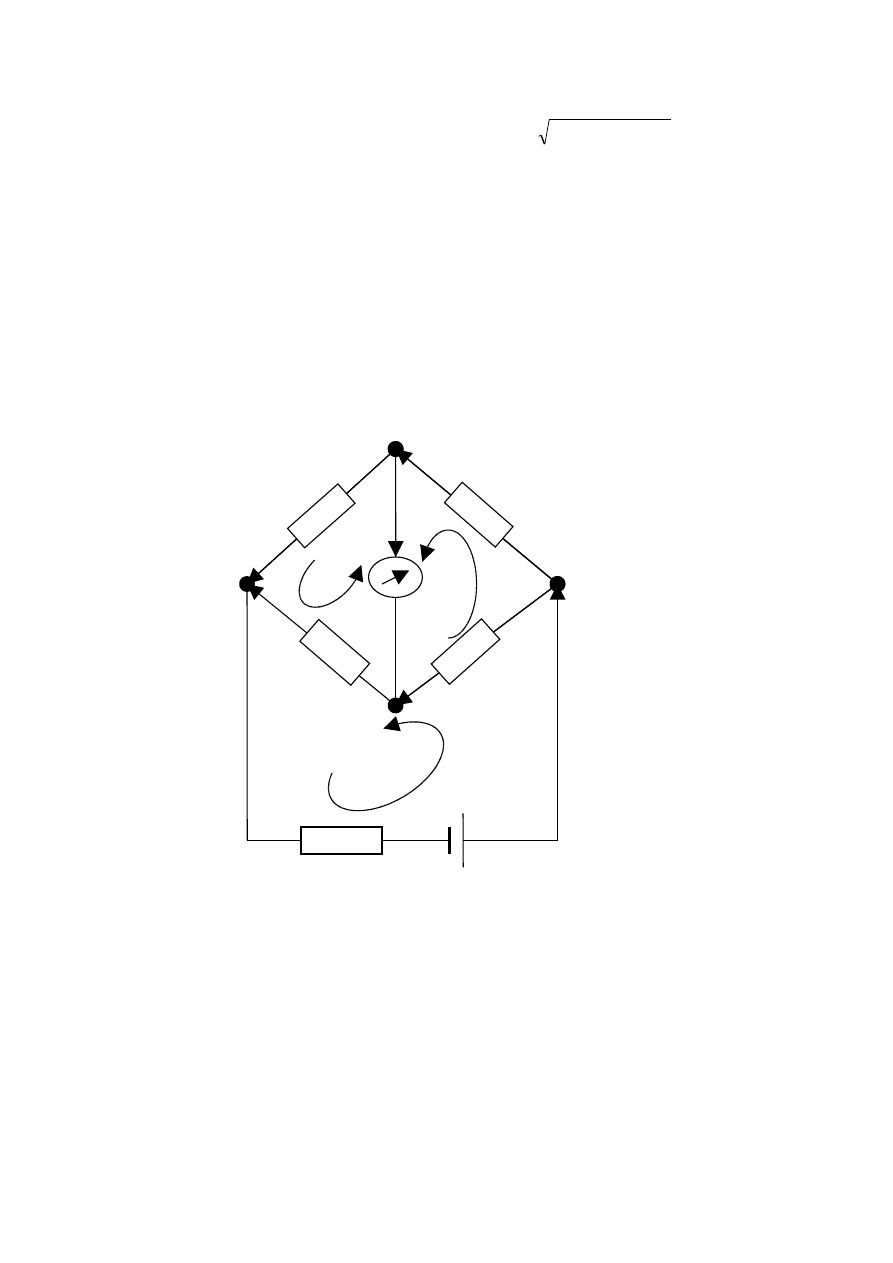
Rys. 13.2. Mostek Wheatstone’a

Aby wyznaczyć zależność na nieznaną rezystancję korzystamy z podstawowych praw zachowania
ładunku i energii, które dla przypadku obwodów elektrycznych przyjmują postać pierwszego pierw-
szego drugiego prawa Kirchhoffa. Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływają-
cych i suma prądów wypływających z węzła są sobie równe. Oznaczając jako dodatnie prądy wpły-
wające a jako ujemne wypływające pierwsze prawo Kirchhoffa zapisujemy w postaci:

∑

=

=

n

k

k

I

1

0

(13.1)

gdzie: n - liczba gałęzi zbiegających się w węźle, I

k

– prąd płynący w k-tej gałęzi.

C

I

2

R

1

I

5

R

2

I

1

R

5

A III II

B

I

4

R

4

R

3

I

3

D

I

6

I

- +

Drugie prawo, zwane również twierdzeniem o oczkach sieci elektrycznej, mówi, że suma zmian po-
tencjału napotykanych przy dokonywaniu obiegu wokół dowolnego obwodu ( oczka) jest równa
zeru. Zmiana potencjału może być spowodowana zarówno spadkiem napięcia na rezystancji jak i
źródłem siły elektromotorycznej. Dla schematu z Rys. 13.2. mamy zatem trzy równania na spadki
napięć w oczkach:

- 1 oczko

4

4

3

3

6

6

I

R

I

R

I

R

E

+

+

=

- 2 oczko

3

3

5

5

2

2

0

I

R

I

R

I

R

−

+

=

(13.2)

- 3 oczko

5

5

4

4

1

1

0

I

R

I

R

I

R

−

−

=

oraz trzy równania na sumy prądów w węzłach:

- węzeł A

0

4

6

1

=

+

−

I

I

I

- węzeł B

0

2

3

6

=

−

−

I

I

I

(13.3)

- węzeł C

0

1

5

2

=

−

−

I

I

I

Jest to układ sześciu równań z sześcioma niewiadomymi prądami. Korzystając z metody podstawia-
nia lub macierzowej wyznaczymy prąd I

5

.

M

R

R

R

R

E

I

4

2

3

1

5

−

=

(13.4)

gdzie:

)

(

)

(

)

)(

(

)

)(

(

)

(

2

1

4

3

4

3

2

1

3

2

4

1

6

4

3

2

1

5

4

3

2

1

6

5

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

M

+

+

+

+

+

+

+

+

+

+

+

+

+

+

=

W warunkach równowagi mostka ( prąd I

5

=0) otrzymujemy:

4

3

2

1

R

R

R

R

R

x

=

=

(13.5)

W celu uzyskania równowagi mostka należy regulować wzorcowy opornik R

4

przy stałym stosunku

R

2

/R

3

lub stosunek rezystancji R

2

/R

3

utrzymując niezmienną wartość rezystancji wzorcowej R

4

. W

tym ćwiczeniu wykorzystuje się drugą metodę (Rys. 13.3).

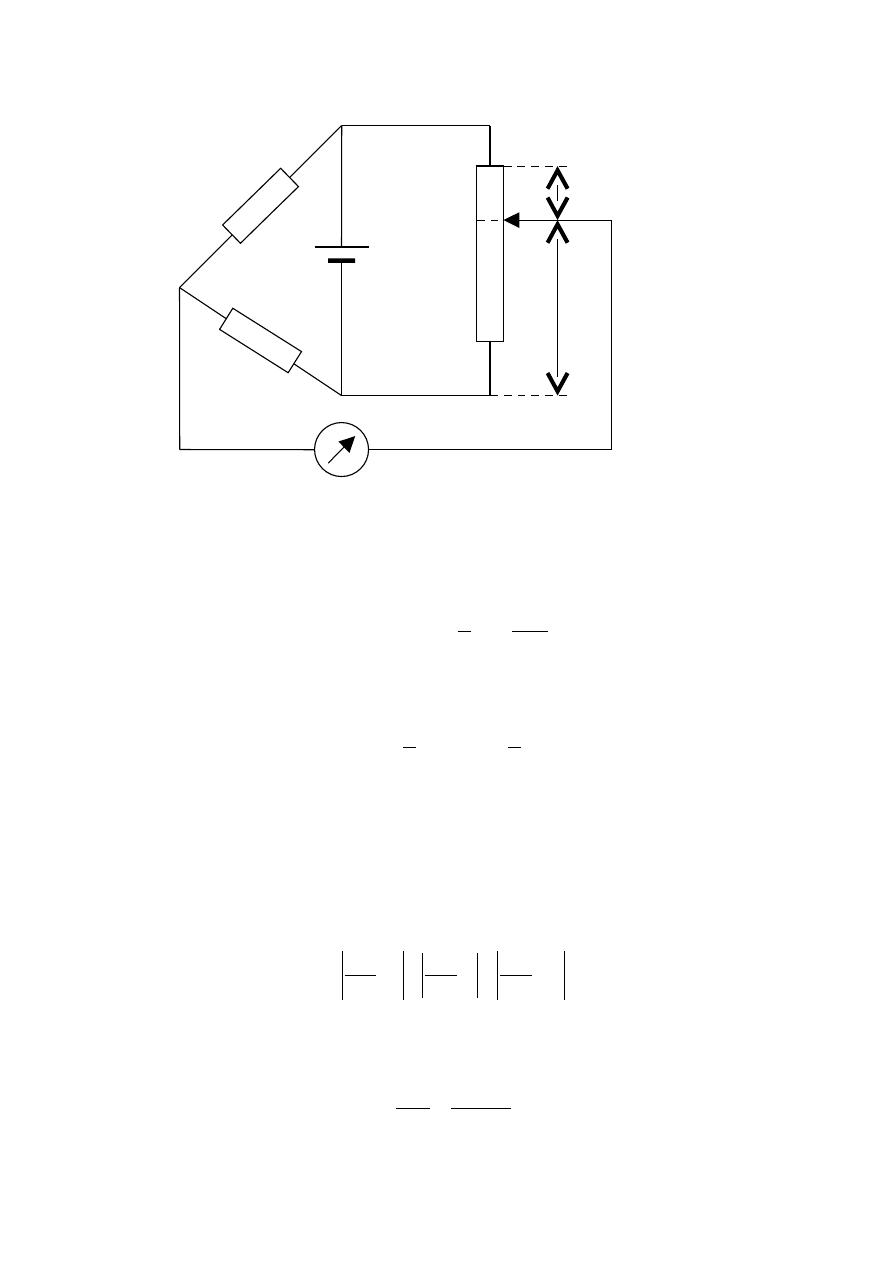
Rys. 13.3 . Metoda równoważenia mostka Wheatstone’a

W przypadku, gdy oporniki R

2

, R

3

zostały zastąpione drutem ślizgowym, warunek równowagi

mostka ma postać:

2

2

4

3

2

4

l

l

l

R

l

l

R

R

X

−

=

=

(13.6)

oznaczenia:

3

2

l

l

l

+

=

- całkowita długość drutu,

ρ

- opór właściwy drutu, S – powierzchnia prze-

kroju drutu, gdyż

S

l

R

2

2

⋅

=

ρ

;

S

l

R

3

3

⋅

=

ρ

;

(13.7)

13.1.1. Dokładność metody.

Rozpatrzmy zależność 13.6 z której metodą pośrednią określamy wartość nieznanej rezystancji R

X

.

Mierząc l

2

i popełniając błąd

2

l

∆

. Wartość l oraz R

4

zostały zmierzone ze znacznie większą precy-

zją. Załóżmy, że błędy wynoszą odpowiednio l

∆

oraz

4

R

∆

. Jeżeli przyjąć, że podane błędy są war-

tościami granicznymi, to maksymalny (graniczny) błąd pomiaru R

X

stanowi sumę wartości bez-

względnych błędów cząstkowych :

4

4

2

2

R

R

R

l

l

R

l

l

R

R

X

X

X

X

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

=

∆

(13.8)

Przy pominięciu wkładów od błędu l

∆

oraz

4

R

∆

jako znacznie mniejsze od wkładu od

2

l

∆

wzór na

błąd względny przyjmuje postać:

)

(

2

2

2

l

l

l

l

l

R

R

X

X

−

∆

⋅

=

∆

(13.9)

C

R

X

R

2

l

2

B

A

R

3

l

3

R

4

D

Błąd ten osiąga minimum, kiedy mianownik osiąga maksimum tzn. dla

3

2

2

czyli

2

l

l

l

l

=

=

co daje

R

2

= R

3

. Podstawiając ten warunek do 13.9 uzyskuje się:

l

l

R

R

X

X

2

2

∆

=

∆

(13.10)

Wniosek: minimalny błąd pomiaru wielkości R

X

jest wtedy, gdy jego wartość mało różni się od R

4

.

13.2. Opis układu pomiarowego.

Schemat montażowy przedstawiony jest na stole pomiarowym, ale zasada jest zgodna z Rys. 13.3.
Ramię AC- odpowiada mierzonej rezystancji R

X

, zaś ramię AD – rezystancji zatyczkowej R

4

. Wiel-

kości rezystancji R

2

i R

3

zależą od położenia suwaka reochordu długości 1 m. Przy przesuwaniu

jego suwaka zmieniają się wielkości rezystancji R

2

i R

3

, a w związku z tym ich stosunek a zarazem

stosunek długości odcinków reachordu. Pomiar nieznanej rezystancji sprowadza się do takiego zna-
lezienia położenia suwaka reochordu ( po uprzednim dobraniu za pomocą rezystora zatyczkowego
odpowiedniej wartości rezystancji R

4

), przy którym prąd nie płynie przez galwanometr. Powyższa

operacja nosi nazwę równoważenia mostka, a mostek przez który prąd nie płynie nazywa się zrów-
noważonym.
Na schemacie montażowym dodatkowo zainstalowano komutator służący do zamiany miejscami re-
zystancji włączonych w ramiona mostka bez przełączania przewodów. Stosowanie komutatora jest
wskazane z tego powodu, że drut reochordu nie bywa całkowicie jednorodny wzdłuż całej długości
i dlatego stosunek R

2

/ R

3

nie jest dokładnie równy stosunkowi l

2

/ l

3

. Przy końcowych obliczeniach

należy brać średnią arytmetyczną wartości l

2

i l

3

z wielkości znalezionych przy dwóch położeniach

komutatora. Drugim elementem różniącym układ pomiarowy od schematu jest podwójny klucz K

1

,

którym można otwierać i zamykać obwód prądu jak i obwód galwanometru. Jego konstrukcja po-
zwala przy naciśnięciu zamykać najpierw obwód prądu a po nim obwód galwanometru zaś przy
otwieraniu – odwrotnie. Zastosowanie klucza pozwala włączać obwód na krótki okres, co zapobie-
ga nagrzewaniu się drutu a jednocześnie zapobiega galwanometr przed przeciążeniem. Dodatko-
wym zabezpieczeniem galwanometru jest klucz K

3

, za pomocą którego można włączać szeregowo

dodatkowy rezystor przy wstępnym równoważeniu mostka. Dla dokładnego zrównoważenia mostka
, klucz K

3

trzeba zamknąć. Obwód zasilany jest prądem stałym.

13.3. Przebieg pomiarów

1. Porównać elementy układu pomiarowego ze szkicem na rysunku 13.3.
2. Sprawdzić czy na na rezystorze zatyczkowym ustawiona jest rezystancja około 100

Ω

.

3. Sprawdzić, czy komutator znajduje się w jednym z położeń roboczych (1 albo 2), a nie pomię-

dzy nimi.

4. Włożyć jeden z badanych rezystorów do uniwersalnego gniazda pomiarowego w taki sposób by

zamknąć gałąź pomiarową mostka.

5. Ustawić suwak w połowie długości reochordu przy otwartym kluczu, zaś na rezystancji za-

tyczkowej dobrać taką rezystancję aby przy zamykaniu klucza przez galwanometr popłynął jak
najmniejszy prąd.

6. Całkowite wyzerowanie wskazań galwanometru osiągamy przez minimalne zmiany w położe-

niu suwaka reochordu (np. zakres 450 – 550 mm) przy zamykanym na krótko kluczu.

7. Czynności według punktów 5-6 przeprowadzić dla tego samego rezystora, ale przeciwnego po-

łożenia komutatora.

8. Powyższe czynności powtórzyć dla:

●

drugiej rezystancji,

●

obu rezystancji połączonych szeregowo,

●

obu rezystancji połączonych równolegle.

Zaleca się nie poprzestać na pojedynczym pomiarze, ale wykonać każdy z cykli pomiarów
przez każdego z ćwiczących. Do opracowania bierzemy wtedy wartości średnie odpowiednich
wielkości.

W przypadku pomiarów rezystancji powyżej 10

Ω

niepewności powodowane złym odczytem poło-

żenia suwaka przewyższają niepewności ustawienia opornika zatyczkowego.

13.4. Opracowanie wyników pomiarów.

1. Wykonać obliczenia wartości mierzonych rezystancji: pierwszej, drugiej oraz ich połączenia

szeregowego i równoległego korzystając ze wzoru (13.6).

2. Obliczyć niepewności wyznaczenia powyższych rezystancji korzystając ze wzoru (13.10). Błąd

2

l

∆

obliczyć za pomocą następującego wzoru

2

2

2

2

1

2

2

2

l

l

l

l

l

śr

śr

−

+

−

=

∆

,

gdzie

2

2

1

2

l

i

l

oznaczają długości odcinka przy różnych położeniach komutatora.

Jeżeli tak otrzymany wynik jest mniejszy od dokładności odczytu położenia reochordu, to za

2

l

∆

należy przyjąć dokładność odczytu.

3. Wykorzystując wyniki pomiarów rezystancji i niepewności wartości średnich porównać z wyni-

kami uzyskanymi dla połączenia szeregowego i równoległego.

L i t e r a t u r a

[1] M. Łaciński, Miernictwo elektryczne, PWN, Warszawa 1974
[2] A. Piekara , Elektryczność i magnetyzm, PWN, Warszawa, 1970