1. C

ZĘŚĆ TEORETYCZNA

Parowanie to przejście cieczy w parę. Proces polegający na odrywaniu się cząstek wody od
wilgotnej powierzchni (np. oceanu, gruntu, roślin) i przechodzeniu jej do powietrza jako
drobiny pary wodnej, podczas którego pobierana jest energia z otoczenia (do wyparowania 1
g wody o temperaturze 0°C potrzeba 597 cal).

Wielkość parowania wyrażona w mm grubości wody, która wyparowuje w jednostce czasu,
zależy od: temperatury otoczenia i ciała parującego, wilgotności powietrza, prędkości jego
ruchu i ciśnienia atmosferycznego.

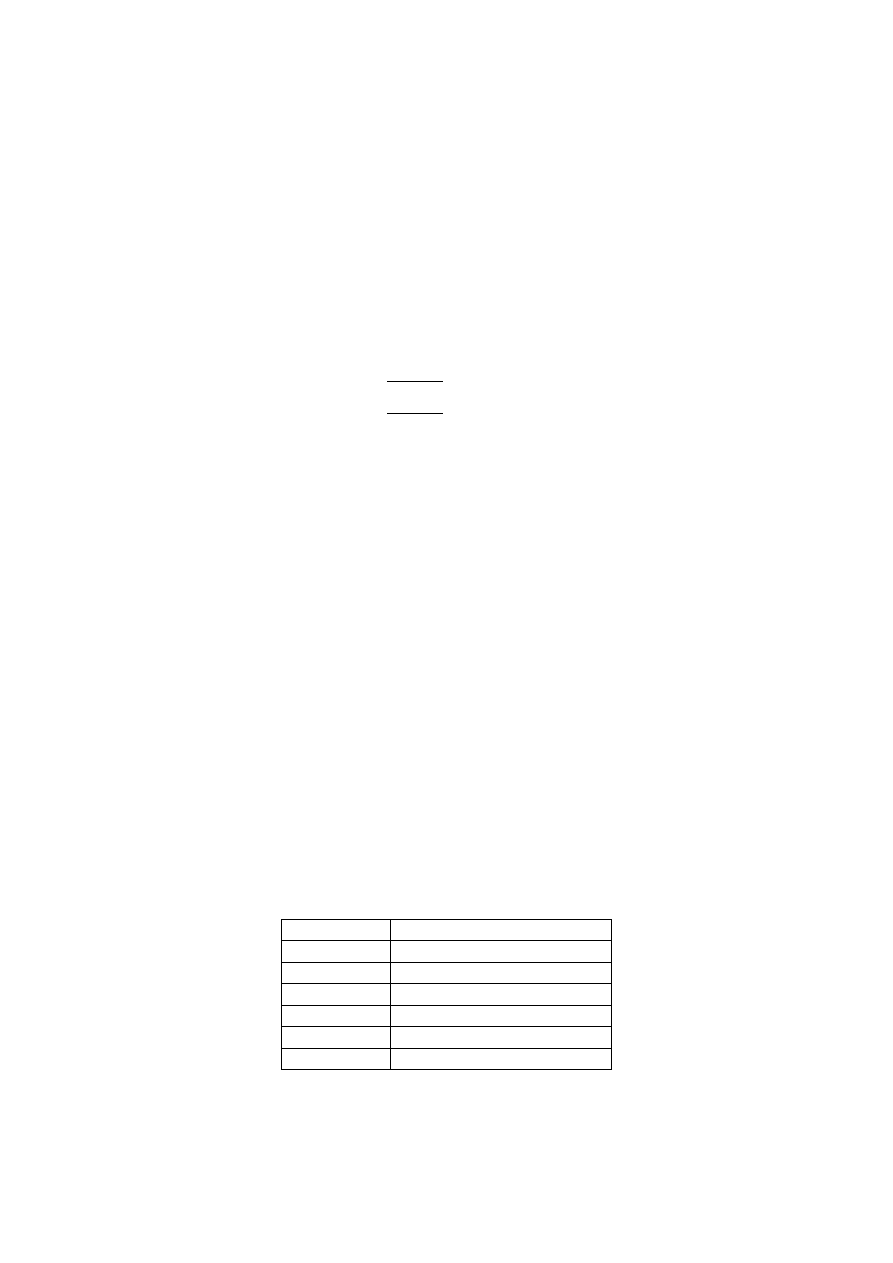
Szybkość parowania cieczy z jednostki powierzchni wyrażana jest wzorem

√

gdzie: m - masa molowa cieczy, k - stała Boltzmanna, T - temperatura bezwzględna, p

0

-

prężność pary nasyconej w danej temperaturze, p - aktualna prężność pary nad cieczą. Wzrost
temperatury i prędkości wiatru wzmaga parowanie, natomiast wilgotne otoczenie i wysokie
ciśnienie osłabiają je.

Szybkość parowania osiąga wartość maksymalną w próżni. Parowanie w całej objętości
cieczy określane jest jako wrzenie. Do pomiaru parowania wykorzystuje się ewaporometry.
Procesem przeciwnym do parowania jest kondensacja.

Ciepło parowania to ilość energii potrzebnej do odparowania jednostki masy danej substancji
przy stałym ciśnieniu i temperaturze. W układzie SI jednostką ciepła parowania jest J/kg.
Stosuje się też jednostkę J/mol.

Ciepło parowania zależy silnie od ciśnienia (i temperatury) malejąc wraz ze wzrostem
temperatury i osiągając 0 w punkcie krytycznym.

Jeżeli nie podano dla jakiego ciśnienia określono ciepło parowania, to uznaje się, że określono
je dla ciśnienia atmosferycznego.

Substancja

Ciepło parowania [kJ/kg]

Aluminium

10.500

Żelazo

6.340

Woda

2.257

Etanol

879

Wodór

454

Rtęć

301

Ciepło parowania możemy obliczyć również ze wzoru:

Gdzie:
Q

p

– energia potrzebna do wyparowania tej ilości substancji,

m – masa substancji,
R – ciepło parowania

Aby układ składający się z cieczy i pary nasyconej znalazł się w stanie równowagi konieczne
jest zapewnienie ściśle określonej temperatury oraz ciśnienia pary nasyconej. Wszelka zmiana
temperatury wywołują zmianę ciśnienia pary nasyconej.
Równanie Clausiusa-Clapeyrona to równanie opisujące zależność między zmianą ciśnienia a
zmianą temperatury wzdłuż krzywej fazowej dla przemiany fazowej układu
jednoskładnikowego:

dp/dT – pochodna ciśnienia po temperaturze w warunkach równowagi przemiany
fazowej (wzdłuż krzywej przemiany fazowej),
L – ciepło przemiany fazowej,
T – temperatura,
ΔV – zmiana objętości w wyniku przemiany fazowej.

Równanie jest poprawne dla wszystkich przemian fazowych (parowanie, topnienie,
sublimacja).

Dla przemiany cieczy w gaz, w temperaturze znacznie niższej od temperatury punktu
krytycznego można pominąć objętość cieczy, oraz używając równanie gazu doskonałego:

Równanie może przyjąć postaci:

[

(

)]

Równanie umożliwia określenie zmiany temperatury przemiany fazowej przy zmianie
ciśnienia lub zmianę ciśnienia przemiany przy zmianie temperatury.

Podczas parowania i sublimacji następuje wzrost objętości (gaz ma większą objętość niż
ciecz), co przy dodatniej wartości temperatury T i ciepła przemiany fazowej L prowadzi do
wniosku, że wraz ze wzrostem temperatury rośnie też ciśnienie pary nasyconej lub wzrost
ciśnienia powoduje wzrost temperatury przemiany fazowej.

Podczas przemiany ciała stałego w ciecz dla większości substancji też następuje wzrost
objętości, co skutkuje wzrostem temperatury przemiany, przy wzroście ciśnienia. Niektóre

substancje (np woda) zmniejszają objętość podczas topnienia, co skutkuje tym, że wzrost
ciśnienia powoduje zmniejszenie temperatury przemiany fazowej.

Pojemność cieplna to wielkość fizyczna, która charakteryzuje ilość ciepła, jaka jest niezbędna
do zmiany temperatury ciała o jednostkę temperatury.

Gdzie
– Zmiana ciepła
– Zmiana temperatury

2. W

YNIKI I OBLICZENIA

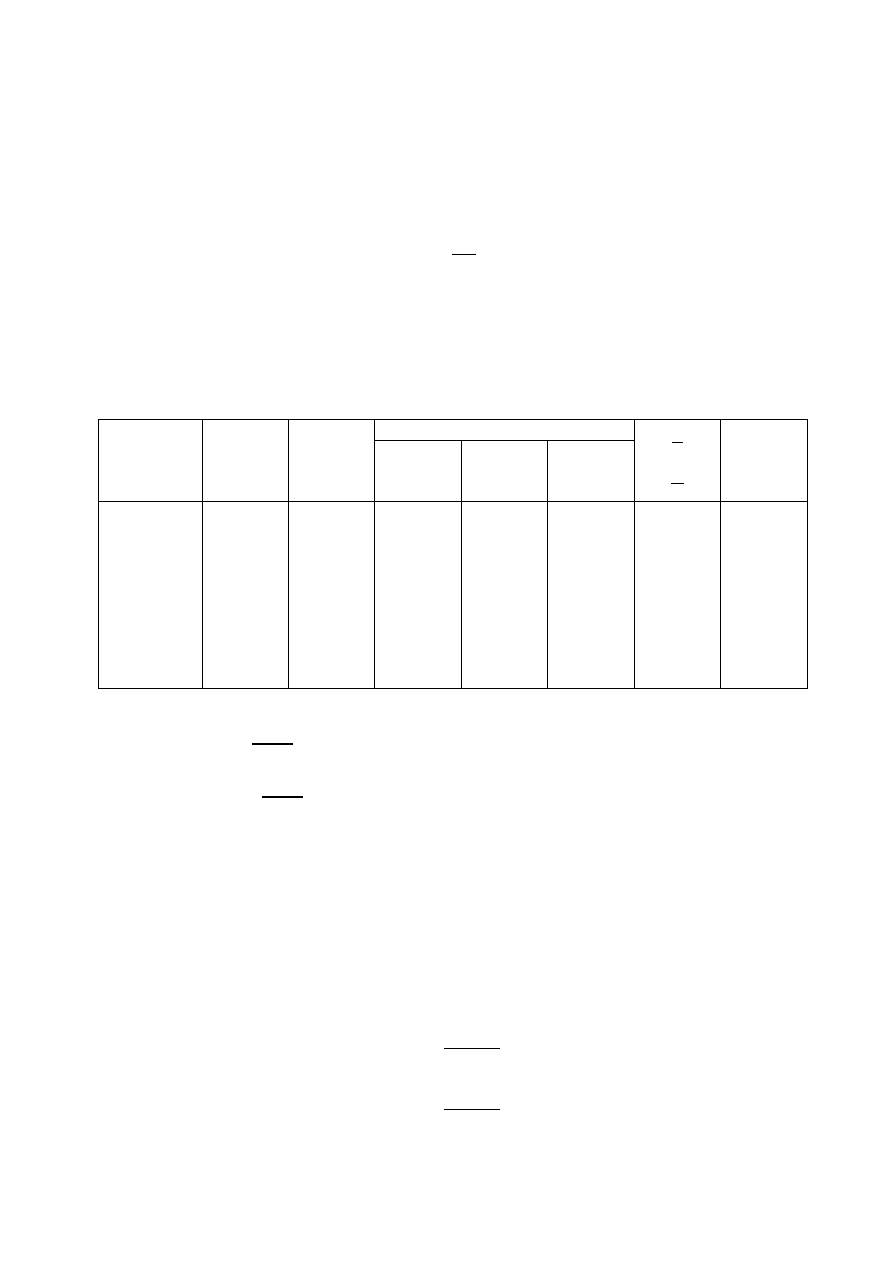
Nr pomiaru

t

[oC]

T

[K]

Odczyt

[

]

Góra

Dół

p

1
2
3
4
5
6
7
8
9

34
35
36
37
39
40
42
43
45

307,15
308,15
309,15
310,15
312,15
313,15
315,15
316,15
318,15

406
406
407
407
408
409
410
412
413

372
370
368
368
367
366
365
363
361

34
36
39
39
41
43
45
49
52

0,00326
0,00324
0,00324
0,00322
0,00320
0,00319
0,00317
0,00316
0,00314

1,531
1,556
1,591
1,591
1,613
1,633
1,653
1,690
1,716

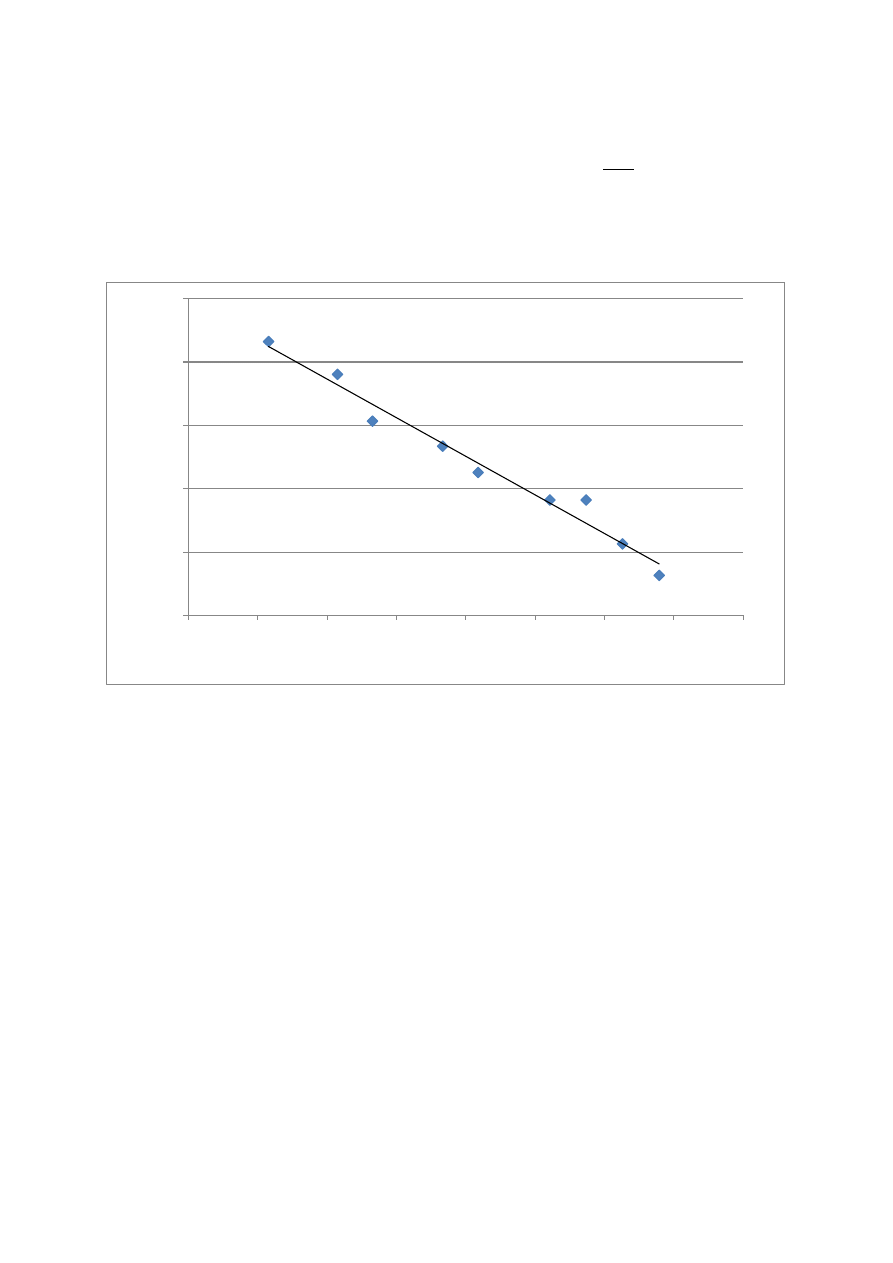
Z zależności

wynika, że wykreślenie logarytmu ciśnienia pary

nasyconej w funki odwrotności temperatury daje prostą o współczynniki

kierunkowym

.

a=-1445,591

b=6,248

y=-1445,591x + 6,248

Ciepło parowania

3. W

NIOSKI



Wraz ze wzrostem temperatury wzrasta ciśnienie



Powyższa zależność umożliwia obliczenie ciepła parowania, które wyniosło
27,679 kJ/mol

Wartości otrzymane w obliczeniach różnią się od wartości tablicowych. Powodem tego
mogą być błędy w odczycie, a także fakt, że podczas włączenia dopływu powietrza
zmniejszała się temperatura, przez co dokładne odczytanie wyników było bardzo trudne.
Dodatkowo na zafałszowanie wyników mogły mieć wpływ zanieczyszczenia cieczy.

1,5

1,55

1,6

1,65

1,7

1,75

0,00312

0,00314

0,00316

0,00318

0,00320

0,00322

0,00324

0,00326

0,00328

lo

g

p

1/T [1/K]