Dwufazowe silniki wykonawcze (DSW):
-1-
Budowa:
Silnik składa się z dwóch uzwojeń stojana przesuniętych względem siebie pod kątem
prostym. Najczęściej są to identyczne uzwojenia, z których jedno pełni rolę uzwojenia
wzbudzenie a drugie uzwojenia sterującego. Wirnik może mieć różne wykonanie:
a) klasyczne – wirnik klatkowy, długi wirnik (L/D=2..3), szczelina powietrzna:
0.025..0.1 mm
b) wirnik kubkowy (silnik Ferrarisa) – kubek najczęściej z aluminium o grubości ok. 0.2 do
1mm, szczelina powietrzna ok. 0.3..1.5 mm
-2-
-3-
c) silniki klatkowe o małym momencie bezwładności:
d) silniki z wirnikami ferromagnetycznymi
e) silniki o innych topologiach: silniki tarczowe: płaskie uzwojenia drukowane (tarcza)
wirnika oraz uzwojenia drukowane stojana (druk o grubości ok. 0.01..0.5mm); dopuszczalna
gęstość prądu w pracy dorywczej do 100A/mm
2
-4-
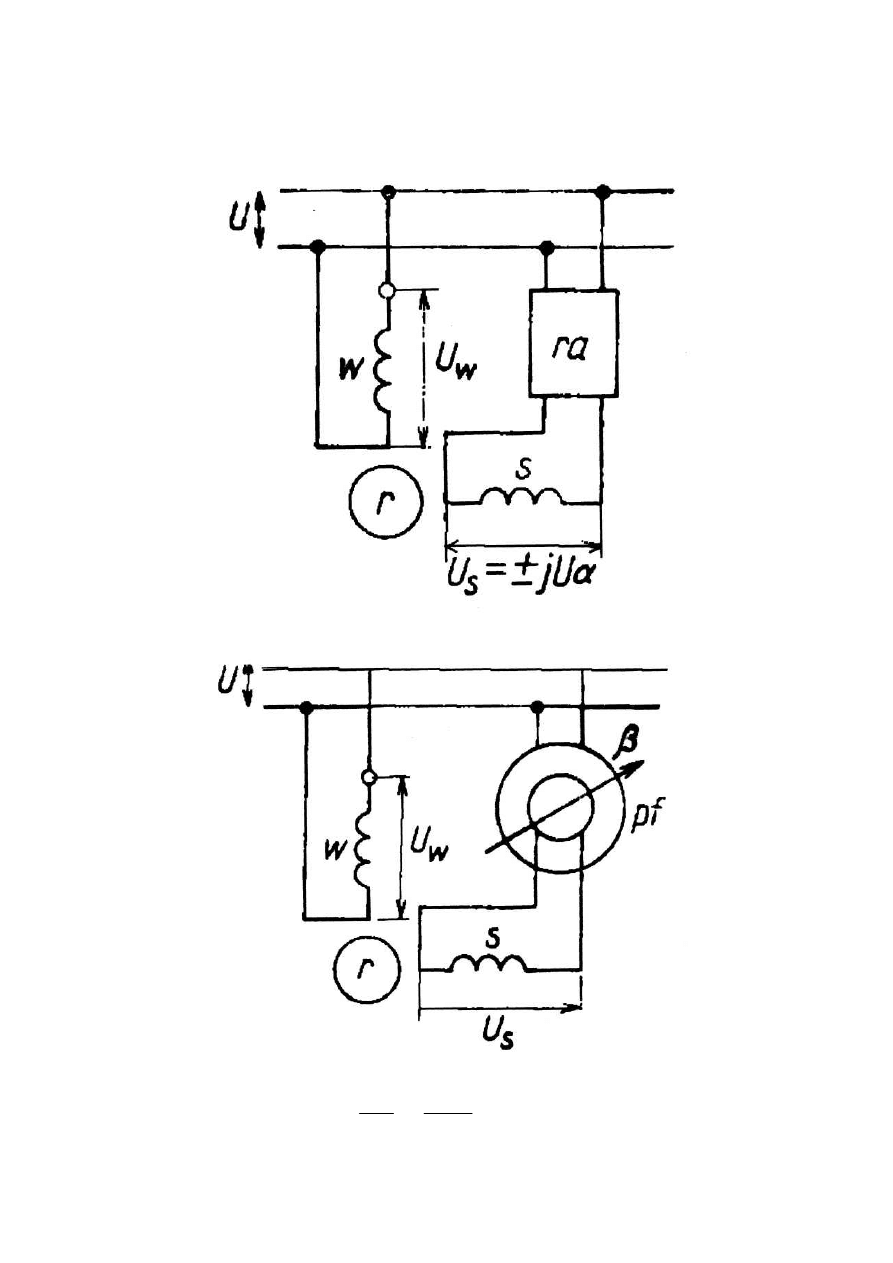
Sposoby sterowania:
a) amplitudowe
α=π/2 U
st
=var
b) fazowe
α=var U
st
=const
α
j
wzb
st
e
U
U
−
⋅
=
-5-
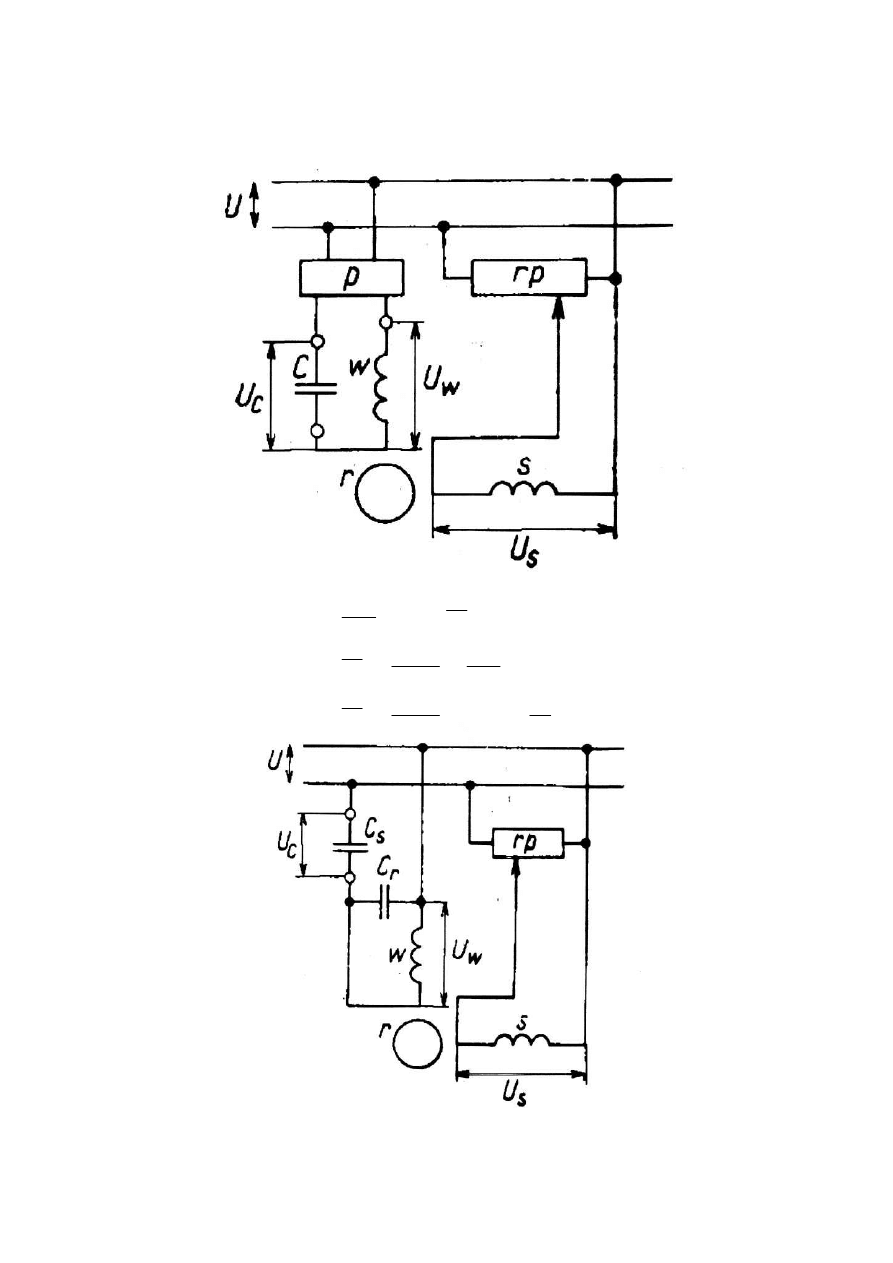
c) amplitudowo-fazowe
α=var U
st
=var
c
C
wzb
C
wzb
e
st
I
jX
U
U
U
U
U
U
U
⋅
+
=
+
=
⋅
=
α
-6-
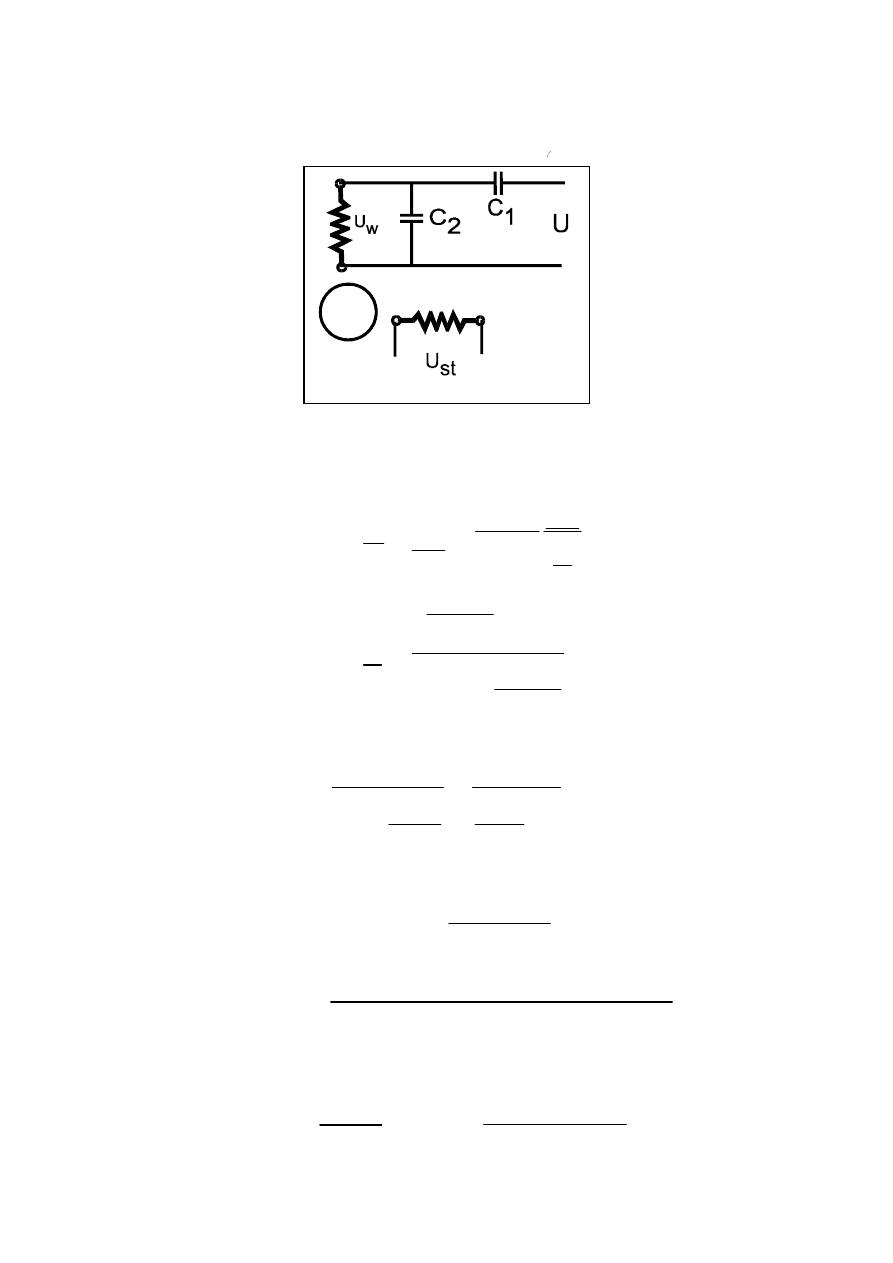
Dobór pojemności do sterowania amplitudowo-fazowego
Załóżmy, że Ze
j
ϕ
jest impedancją uzwojenia wzbudzającego przy wirniku nieruchomym.
Chcemy znaleźć pojemności C
1
i C
2
, przy których napięcie na uzwojeniu wzbudzenia będzie
równe kUe
j
ψ
. Warunek ten będzie spełniony, gdy:
2
2
1
1
1
1
C
j
Ze
Ze
C
j
Z
Z
U
C
j
U
U
j
j
w
w
ω
ω
ω
ϕ
ϕ
+
=
=
−
Po przekształceniach otrzymamy:
1
1
2
1
−
=
+
−
−
k
e
Z
j
e
C
C
j
j
ψ
ϕ
ω
Porównując części rzeczywiste i urojone wyrażenia znajdujemy zależności na C
1
i C
2
:
ψ
ω
ϕ
sin
cos
1
Z
k
C
⋅
=
ψ
ω
ϕ
ψ
ψ
ϕ
sin
cos
)
cos
(
sin
sin
2
Z
k
C
−
−
⋅
=
Dla przypadku pola kołowego przy rozruchu: k=1 oraz
ψ=π/2 otrzymamy:
ω
ϕ
Z
C
cos
1
=
ω
ϕ
ϕ
Z
C
cos
sin
2
−
=
-7-
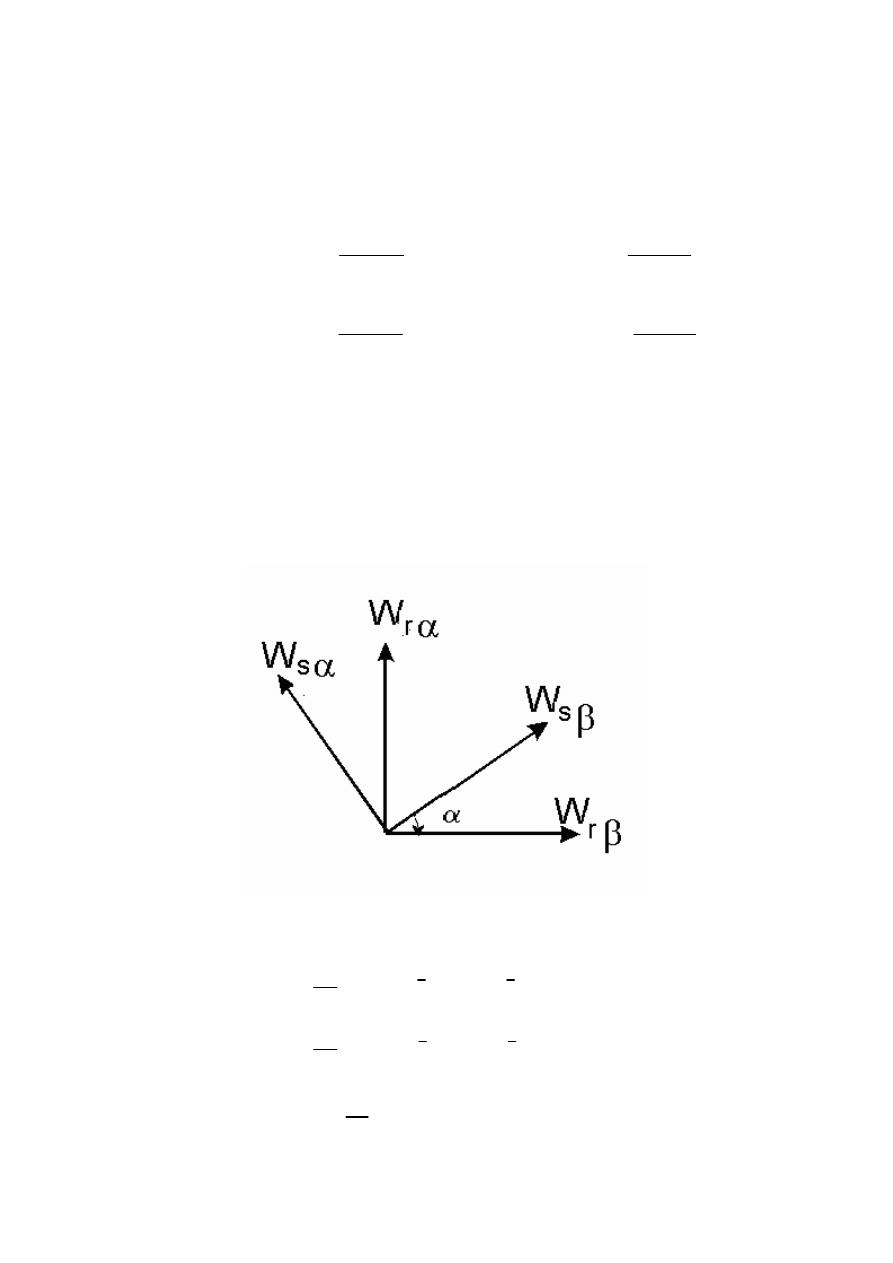
DYNAMIKA DWUFAZOWEGO SILNIKA WYKONAWCZEGO
Przyjmijmy, że model silnika da się sprowadzić do silnika o dwóch uzwojeniach w stojanie i
wirniku przesuniętych na obwodzie o kat 90
°. Kąt pomiędzy uzwojeniami stojana i wirnika jest
równy
α. Silnik taki można opisać wzorami:
u
R i
d
dt
u
R i
d
dt
u
R i
d
dt
u
R i
d
dt
s
s s
s
s
s s
s
r
r r
r
r
r r
r
α
α
α
β
β
β
α
α
α
β
β
β
ψ
ψ
ψ
ψ
=
+
=
+
=
+
=
+
gdzie:
α
α
ψ
α
α
ψ
α
α
ψ
α
α
ψ
β
α
β
β
β
α
α
α
β
α
β
β
β
α
α
α
cos
sin
sin
cos
cos
sin
sin
cos
s
s
r
r
r
s
s
r
r
r
r
r
s
s
s
r
r
s
s
s
Mi
Mi
i
L
Mi
Mi
i
L
Mi
Mi
i
L
Mi
Mi
i
L
+
−
=
+
+
=
+
+
=
−
+
=
Po pomnożeniu równań z indeksem
β przez j i dodaniu stronami odpowiednich równań
otrzymamy:
ψ
ψ
α
α
s
s s
r
j
r
r r
s
j
L i
Mi e
L i
Mi e
=
+
=
+
−
Gdzie wielkości zespolone określone są przez indeksy
α i β w sposób następujący:
w
w
jw
=
+
α
β
Pomnożenie równań wirnika przez wielkość Ce
j
α
powoduje przekształca równań silnika do
postaci:
-8-
ψ
ψ
s
s s
s
L i
Mi
L i
Mi
r
r
r
r
=
+
=
+
'
'
'
'
Oraz:
dt
d
e
i
e
R
u
e
dt
d
i
R
u
r
r
r
j
j
r
j
s
s
s
s
ψ
ψ
α
α
α
+
=
+
=
Biorąc pod uwagę, że:
dt
d
e
e
dt
dα
j
dt
e
d
dt
d
r
r
r
j
r
j
j
ψ
ψ
ψ
ψ
α
α
α
+
=
=
)
(
'
'
'
r
j
dt
dα
j
dt
d
dt
d
e
r
r
ψ
ψ
ψ
α
-
=
otrzymamy:
'
'
'
'
r
r
s
s
s
s
dt
dα
j
dt
d
i
R
u
dt
d
i
R
u
r
r
r
ψ
ψ
ψ
-
+
=
+
=
Przy czym wielkości wirnika zostają w ten sposób sprowadzone do układu stacjonarnego
(związanego z nieruchomym układem odniesienia).
Wzór na moment elektromagnetyczny uzyskamy po analizie na zależności napięciowe
pomnożone przez odpowiednio sprzężony prąd stojana i wirnika:
u i
R i i
d
dt
i
u i
R i i
d
dt
i
i
s
s s
s
r r
r r r
r
r r
s
s
s
r
*
*
*
' *
' *
'
' *
' ' *
=
+
=
+
ψ
ψ
α ψ
- j
d
dt
Odpowiadające sobie wielkości to odpowiednio: moc doprowadzana do stojana, wirnika oraz
straty mocy na rezystancjach stojana i wirnika, moc zgromadzona w polu magnetycznym
(iloczyn pochodnej strumienia i prądu) oraz moc mechaniczna. Moc chwilowa w układzie alfa-
beta jest równa:
}
Re{
*
s
i
u
i
u
i
u
s
=
+
β
β
α
α
-9-

Stąd moment elektromechaniczny jest równy:
}
i
ψ
{j
p
M
ω
dt
dα
}
i
ψ
dt
dα
{-j
ω
p
=
ω
P
=
M
'*
r
'
r
e
'*
r
'
r
m
m
e
Re
Re
−
=
=
Podstawiając za strumień zależność [5] otrzymamy po uwzględnieniu, że:
'*
r
'
r
r
i
i
L
- jest liczbą rzeczywistą, oraz że:
}
i
{i
}=
i
{i
'
r
*
'*
r
s
s
Im
Re
Otrzymamy następujący wzór na moment elektromagnetyczny:
}
i
i
{j
pM
M
'
r
*
s
e
Im
−
=
Wyprowadzone równania należy uzupełnić równaniem dynamiki masy wirującej:
d
dt
J
M
M
m
e
ω
=
−
1
0
(
)
-10-
STAN USTALONY DWUFAZOWEGO SILNIKA WYKONAWCZEGO PRZY
SYMETRYCZNYM ZASILANIU
Jako stan wyjściowy do analizy stanu ustalonego przyjmijmy równania dynamiki silnika
opisanego zależnościami:
ψ
ψ
s
s s
s
L i
Mi
L i
Mi
r
r
r
r
=
+
=
+
'
'
'
'
Oraz:
'
r
'
'
'
'
s
s
s
s
ψ
dt
dα
-j
dt
ψ
d
i
R
u
dt
ψ
d
i
R
u
r
r
r
r
+
=
+
=
}
i
i
{j
pM
M
'
r
*
s
Im
−
=
Przyjmijmy, że napięcia zasilające silnik można opisać zależnościami:
)
sin(
2
cos
2
1
1
t
U
u
t
U
u
s
s
ω
ω
β
α
=
=
Stąd w wielkościach zespolonych napięcie zasilające można przedstawić w postaci:
u
Ue
s
j
t
= 2
1
ω
Przyjmijmy, że wirnik jest zwarty oraz, że analizy dokonujemy przy założeniu, że prędkość
mechaniczna jest stała. Załóżmy, że prądy oraz strumienie są sinusoidalne i symetryczne w obu
fazach, stąd:
t
j
s
s
e
I
i
1
2
ω
=
t
j
e
I
i
r
r
1
'
'
2
ω
=
Operacja sprowadzenia wielkości wirnika na stronę stojana powoduje, że można łatwo określić
zależności pomiędzy kolejnymi składnikami indukcyjności własnych i wzajemnych:
'
'
r
r
L
M
L
L
M
L
s
s
δ
δ
+
=
+
=
Wzór powyższy można zinterpretować jako rozdzielenie strumienia skojarzonego z uzwojeniem
stojana (wirnika) na strumień rozproszenia i strumień główny.
-11-

W takiej sytuacji w stanie elektromagnetycznie ustalonym można dokonać różniczkowania
opisanego we wzorach [2]. Otrzymamy po przekształceniach:
)
(
0
'
'
1
'
1
'
1
1
s
r
r
s
r
r
r
s
s
s
s
I
M
I
L
j
I
M
j
I
L
j
I
R
I
M
j
I
L
j
I
R
U
r
r
+
−
+
+
=
+
+
=
ω
ω
ω
ω
ω
Wprowadzenie do równań fikcyjnego prądu (magnesującego):
'
r
I
I
I
s
+
=
µ
Przekształca równania [9] do postaci:
µ
µ
δ
ω
ω
ω
ω
ω
ω
δ
I
M
j
I
L
j
I
R
I
M
j
I
L
j
I
R
U
r
r
s
s
s
s
r
r
)
(
)
(
0
1
'
1
'
1
1
−
+
−
+
=
+
+
=
Dzieląc równania wirnika przez:
1
1
ω
ω
ω
−
=
s
Otrzymamy znane z teorii maszyn elektrycznych równania opisujące maszynę indukcyjną
symetryczną:
µ
µ
δ
ω
ω
ω
ω
δ
I
M
j
I
L
j
I
s
R
I
M
j
I
L
j
I
R
U
r
r
s
s
s
s
r
r
1
'
1
'
1
1
0
+
+
=
+
+
=
Przy idealnym biegu jałowym możemy zatem przyjąć, że równanie stanu ustalonego przyjmie
postać:
s
s
s
s
I
M
L
j
I
R
U
)
(
1
+
+
=
δ
ω
Z pomiarów przy idealnym biegu jałowym (należy napędzić silnik dwufazowy maszyną prądu
stałego do uzyskania prędkości synchronicznej) otrzymamy, po pominięciu strat w żelazie, sumę
indukcyjności głównej M i indukcyjności rozproszenia L. Rezystancję stojana określamy metodą
bezpośredniego pomiaru. Symetryczne zwarcie pomiarowe umożliwia pomiar impedancji
zwarcia, która w tym przypadku jest równa (przy założeniu, że indukcyjność rozproszenia
stojana i wirnika są sobie takie same i równa X ):
)
(
)
(
'
'
X
X
j
R
jX
R
jX
jX
R
Z
r
r
s
+
+
+
+
+
=
µ
µ
Rozważania opisane wyżej można uogólnić na składową zgodną i przeciwną napięcia
zasilającego, traktując, że wzór [5] dotyczy składowej zgodnej a napięcie składowej przeciwnej
wyrazimy zależnością:
t
j
s
e
U
u
1
2
ω
−
−
=
Przyjmując że składowa przeciwna związana jest z polem wirującym przeciwnie do prędkości
silnika otrzymując zmodyfikowany wzór [11]:
−
−
−
−
−
−
−
+
+
+
+
=
+
+
=
µ
µ
δ
ω
ω
ω
ω
ω
ω
δ
I
M
j
I
L
j
I
R
I
M
j
I
L
j
I
R
U
r
r
s
s
s
s
r
r
)
(
)
(
0
1
'
1
'
1
1
-12-
Równania [18] i [11] opisują stan ustalony
silnika przy stałej prędkości obrotowej dla

dowolnego układu napięć zasilających. Dla równań tych można stworzyć równoważny schemat
zastępczy podawany w literaturze [Owczarek, Elektryczne maszynowe elementy automatyki,
WNT, Warszawa 1983, str. 207], przy czym zależność pomiędzy poślizgiem s a prędkością
względną
ν można przedstawić jako:
ν
−
= 1
s
- dla składowej zgodnej
ν
+
= 1
s
- dla składowej przeciwnej
-13-
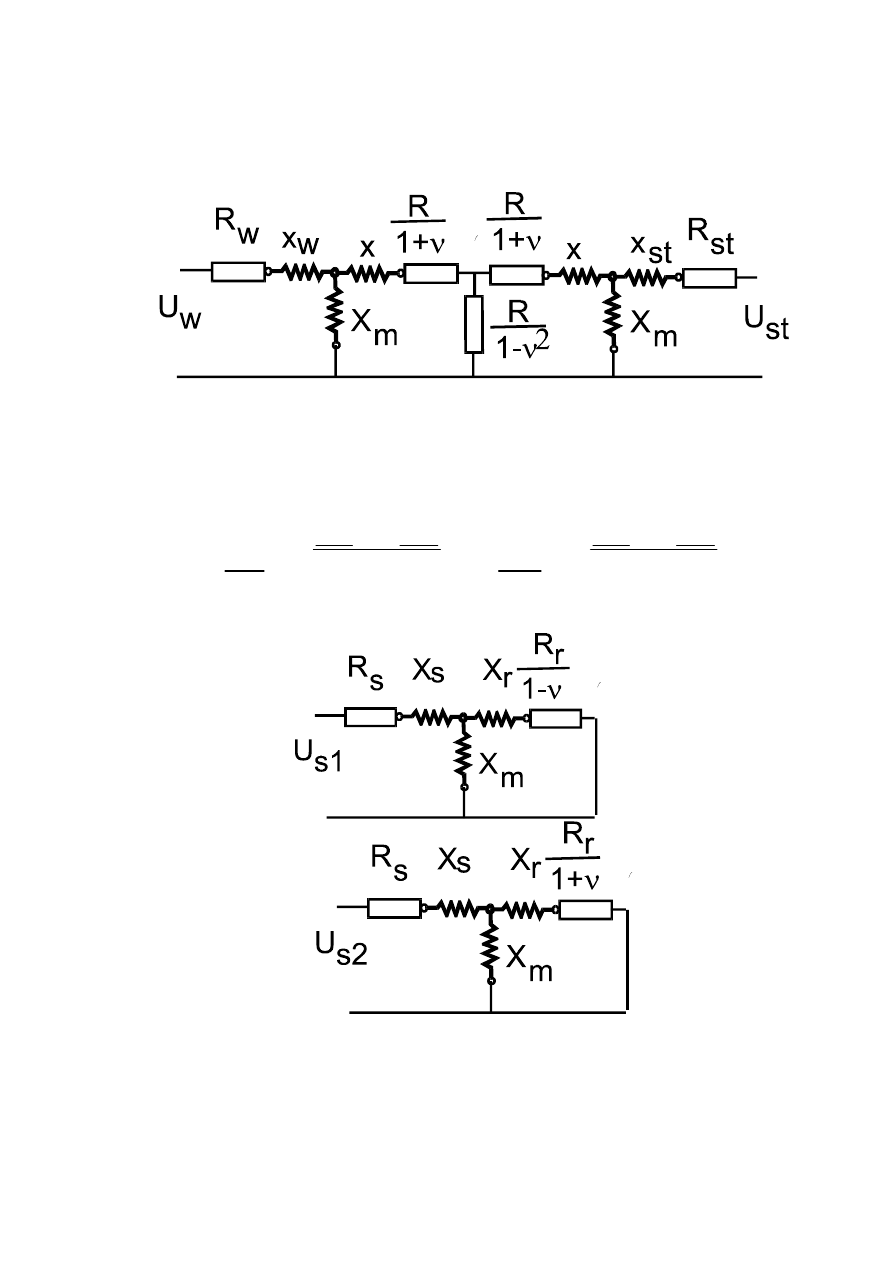
STAN USTALONY DWUFAZOWEGO SILNIKA WYKONAWCZEGO
W literaturze można spotkać schemat zastępczy silnika dwufazowego dla dowolnego sposobu
zasilania opierając się na równaniach dynamiki przekształconych dla sinusoidalnego zasilania.
Np. wg Kowalowskigo schemat zastępczy przyjmuje postać:
Innym sposobem analizy DSW w stanie ustalonym jest metoda składowych symetrycznych, w
której układ napięć zasilających rozkłada się na składową zgodną i przeciwną, dla których
schemat zastępczy jest analogiczny jak dla silnika indukcyjnego w stanie ustalonym. Przy
założeniu, że oba uzwojenia są identyczne składowe symetryczne można policzyć z zależności:
2
2
2
1
st
w
s
st
w
s
U
j
U
U
U
j
U
U
−
=
+
=
−
−
Schematy zastępcze dla składowych przyjmują postać (Rw=Rst=Rs):
Zwykle pomija się tu rezystancję odpowiedzialną za straty w żelazie. Rezystancja ta nie ma
odpowiednika w modelu matematycznym i dla silnika indukcyjnego oraz transformatora
wprowadzana w sposób „sztuczny”. Jej umiejscowienie w gałęzi poprzecznej jest związane
z przyjęciem założenia, że to strumień główny jest bezpośrednio związany ze stratami w żelazie.
W przypadku dużej impedancji wirnika i małych zmian impedancji DSW przy przejściu z od
stanu zwarcia do biegu jałowego można przyjąć, że straty te są stałe i zalezą od napięcia
zasilającego a nie od strumienia głównego. Stąd w schemacie zastępczym DSW można
-14-
całkowicie pominąć R
fe
.
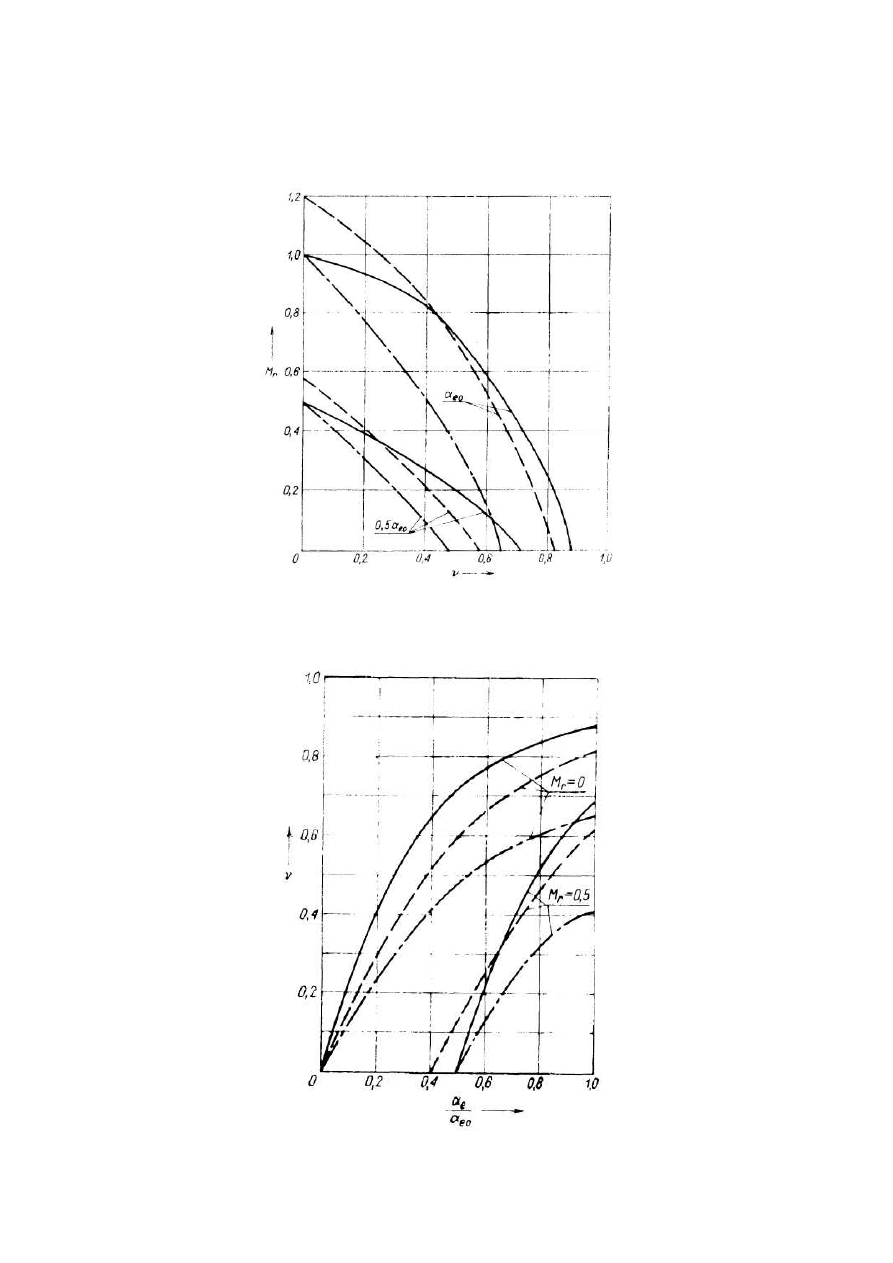
2.1.6 Charakterystyki
Sterowanie amplidudowo-fazowe:
linia ciągła-kondensator dobierany na pole kołowe
linia przerywana- na maksymalny moment rozruchowy
linia z kropką-warunek rezonansu napięć w stanie zwarcia
-15-
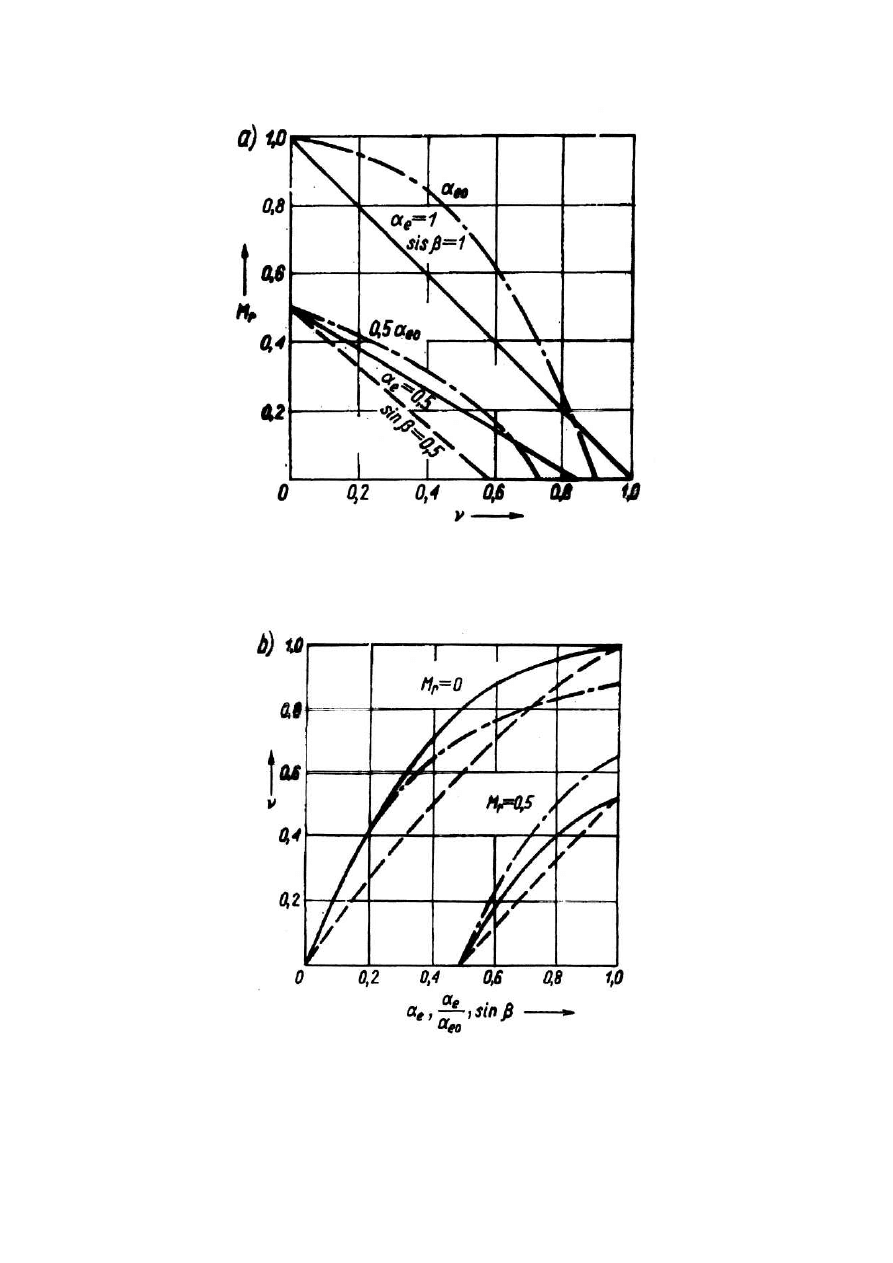
Porównanie charakterystyk: linia ciągła sterowanie
amplitudowe; linia przerywana-fazowe; linia z kropką -
amplitudowo-fazowe
-16-
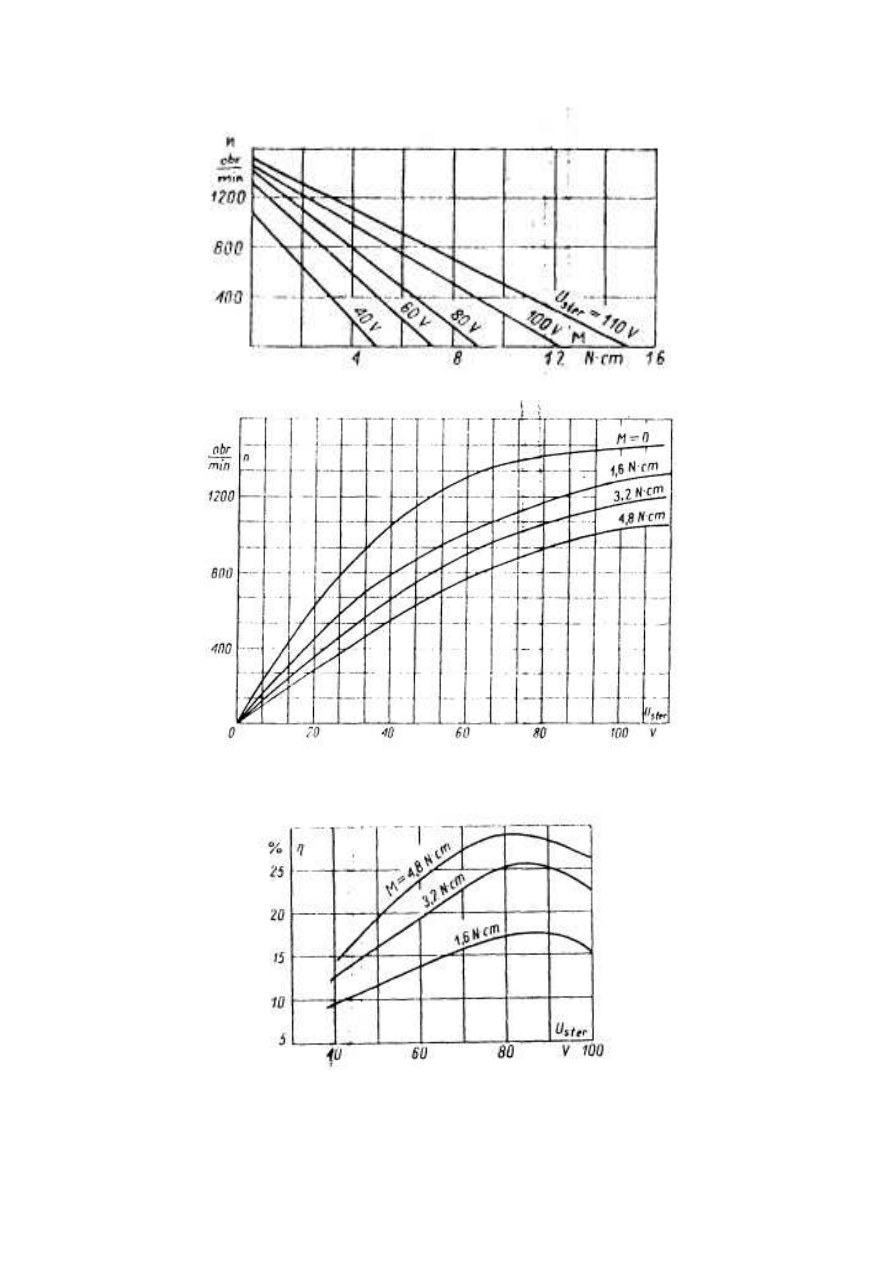
Charakterystyki obciążenia silnika typu SA-5T przy różnych napięciach sterujących
Charakterystyki regulacyjne silnika typu SA-5T przy różnych wartościach obciążeni
Charakterystyki sprawności silnika typu SA-5T przy różnych wartościach obciążenia
-17-

Idealna charakterystyka mechaniczna silnika dwufazowego jest linią prostą, którą można
opisać równaniem:
ω
⋅
−
=
F
M
M
r
gdzie F bywa nazywany współczynnikiem tłumienia wewnętrznego
Dla charakterystyk rzeczywistych określa się współczynnik nieliniowości, który jest
równy ok. 10..15%
Przy sterowaniu amplitudowym możemy przyjąć, że:
st
M
r
U
k
M
⋅
=
gdzie: k
M
– momentowy współczynnik sterowania
st
wzb
P
r
P
P
k
M
⋅
=
gdzie: k
P
– mocowy współczynnik sterowania
Napięcie rozruchowe- najmniejsze napięcie sterujące, jakie należy przyłożyć do silnika,
aby obracał się on z najmniejszą możliwą prędkością. Napięcie to zależy od momenty
reluktancyjnego oraz momentu tarcia suchego:
r
T
rel
n
st
st
M
M
M
U
U
+
=
min
Równanie dynamiki idealnego DSW:
Dzieląc przez F i uwzględniając zależność
st
M
r
U
k
M
⋅
=
otrzymamy:
st
o
U
k
F
M
dt
d
T
⋅
=
+
+
ω
ω
ω
ω
)
(
K
ω
- prędkościowy współczynnik sterowania
T- elektromechaniczna stała czasowa
-18-
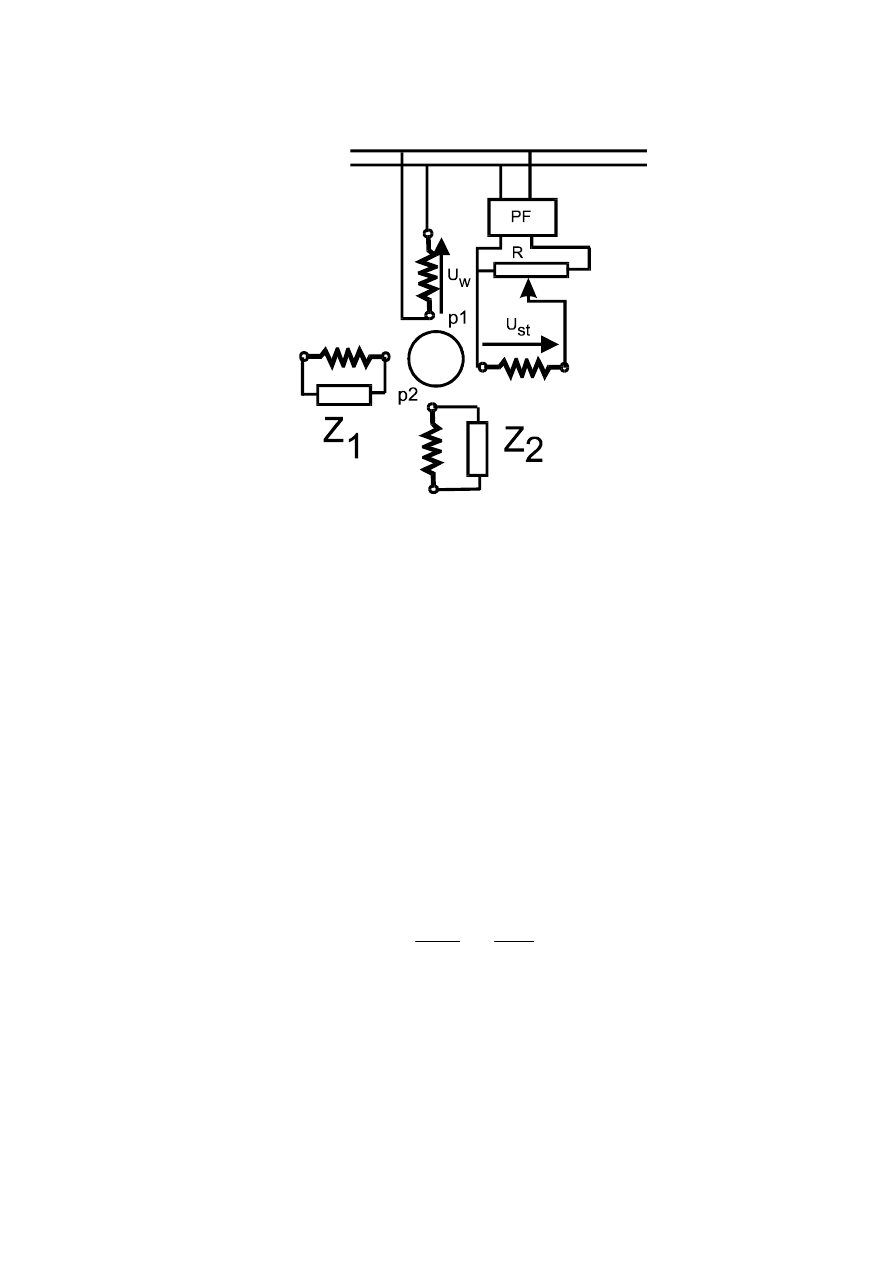
Silnik wykonawczy reduktorowy
Silnik ma dwie pary uzwojeń nawiniętych na stojanie o różnej liczbie par biegunów p
1
i p
2
.
Jedna z par uzwojeń jest zasilana na zasadzie takiej samej jak w silniku dwufazowym, tzn.
wytwarza pole o składowej zgodnej i pole składowej przeciwnej o zmiennych proporcjach
pomiędzy tymi polami. Rdzeń wirnika jest żłobkowany (żłobki otwarte) i nieuzwojony.
Zakłada się, że żłobkowanie stojana można pominąć (stojan „gładki”). Rozważania ogranicza
się do podstawowych składowych pola.
Przewodność magnetyczna (permeancja) szczeliny powietrznej:
λ
λ
λ
α ω
δ
r
or
r
t
=
+
−
1
2
cosŻ (
)
Wartość indukcji magnetycznej w szczelinie powietrznej jest iloczynem napięcia
magnetycznego oraz przewodności magnetycznej. Napięcie magnetyczne (dla składowej
zgodnej pola wirującego):
F
F
t p
n
=
−
cos(
)
ω
α
1
1
Ta składowa pola wiruje z prędkością:
ω
α
1
1
0
t p
−
=
Stąd po wykonaniu różniczkowania:
ω
α ω
=
=
d
dt
p
1
1
Indukcja w szczelinie:
B
F
r
δ
δ
µ λ
δ
=
0
0
/
-19-
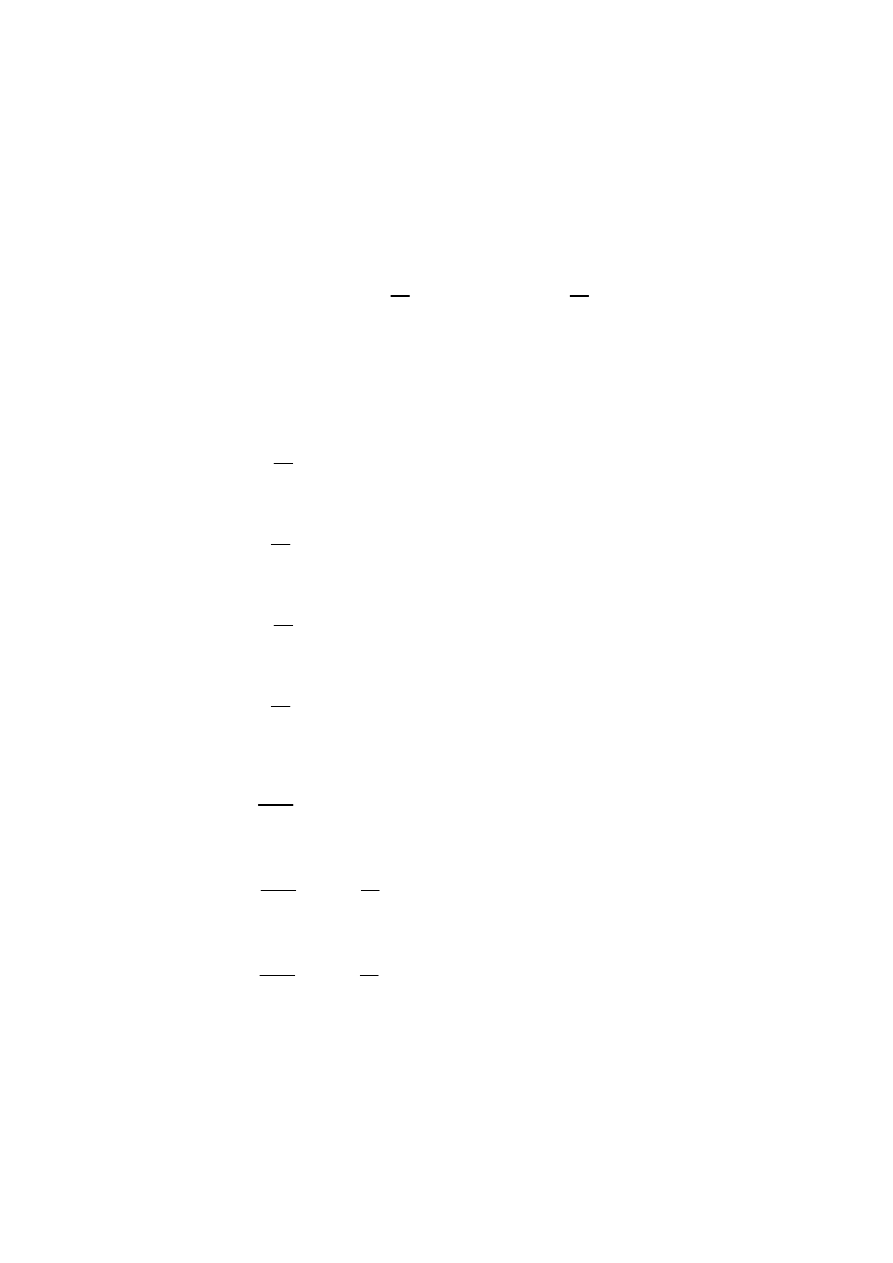
Stąd:
B
F
t
p
F
t
p
n
n
r
δ
t
µ
λ δ
ω
α
µ
λ δ
ω
α
α ω
=
−
+
−
−
0
0
0
1
1
0
1
0
1
1
2
/
cos(
)
/
cos(
) cosŻ (
)
Drugi składnik należy przekształcić korzystając z zależności trygonometrycznej:
cos
cos
cos(
)
cos(
)
α
β
α β
α
⋅
=
−
+
+
1
2
1
2
β
Otrzymamy:
cos(
) cosŻ (
)
cos(
Ż
Ż
)
cos(
Ż
Ż
)
cos[(
Ż
)
(
Ż ) )]
cos[(
Ż
)
(
Ż ) )]
ω
α
α ω
ω
α
α
ω
ω
α
α
ω
ω
ω
α
ω
ω
α
1
1
2
1
1
2
2
1
1
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
t p
t
t p
t
t p
t
t
p
t
p
r
r
r
r
r
−
+
=
−
−
+
+
−
+
−
=
+
−
+
+
−
−
−
=
+
=
+
Pole w szczelinie powietrznej ma zatem trzy składniki:
B
F
t p
B
F
t
p
B
F
t
p
n
n
r
n
r
1
0
0
0
1
1
2
0
0
0
1
2
1
2
3
0
0
0
1
2
1
2
1
2
1
2
=
−
=
+
−
=
−
−
+
−
µ
δ
λ
ω
α
µ
δ
λ
ω
ω
µ
δ
λ
ω
ω
cos(
)
cos[(
Ż
)
(
Ż ) )]
cos[(
Ż
)
(
Ż ) )]
α
α
Składnik B
1
związany jest z polem wzbudzającym wytworzonym bezpośrednio z
uzwojeniem o liczbie par biegunów p
1
. Dwa następne składniki są efektem żłobkowania
wirnika. Moment elektromagnetyczny może powstać w wyniku współdziałania któregoś ze
składników pola pod warunkiem iż liczba par biegunów tegoż pola będzie równa p
2
.
Przyjmijmy, że liczba żłobków wirnika jest równa:
-20-

Ż
2
1
2
=
+
p
p
W takiej sytuacji uzwojenie pierwsze jest „dopasowane” w sensie liczby par biegunów
do pierwszego składnika pola a uzwojenie drugie do trzeciego składnika pola, który można
wyrazić wzorem:
B
F
t p
n
r
3
0
0
0
1
2
1
2
=
−
2
+
µ
δ
λ
ω
ω
cos[(
Ż
)
)
α
]
Składnik ten wytwarza w uzwojeniu drugim s.em. o pulsacji:
ω
ω
ω
2
2
1
=
−
Ż
r
Po zwarciu uzwojenia drugiego popłyną w nim prądy wytwarzając pole o prędkości:
ω
ω
ω
ż
r
p
2
2
1
2
=
−
Ż
Prędkość synchroniczna jest wówczas, gdy częstotliwość prądu w drugim uzwojeniu
jest równa zeru, więc:
Ż
Ż
2
1
1
2
0
ω
ω
ω
ω
rs
rs
−
=
=
Współczynnik redukcji prędkości obrotowej jest równy w takiej sytuacji:
k
p
p
p
p
p
p
r
rs
=
=
=
+
= +
ω
ω
1
2
1
1
2
1
2
1
1
Ż
Prędkość wirowania silnika jest równa:
n
f
s
r
=
−
60
1
2
Ż
(
)
Silnik taki zasilany jest zwykle napięciem o częstotliwości 400
÷1000Hz, co powoduje
iż przy danej mocy silnik ma mniejsze gabaryty. Zwiększa się także trwałość maszyny
(mniejsza prędkość na wale maszyny).
(90% awarii silników to awarie łożysk). Zaletą jest także brak przekładni mechanicznej.
Wada: Bardzo droga technologia.
-21-
Document Outline
Wyszukiwarka
Podobne podstrony:
Silnik wykonawczy dwufazowy, Elektrotechnika, Rok 3, Maszyny elektryczne specjalne, specjalne
Sprawozdanie Silnik wykonawczy prądu stałego
silnik wykonawczy
2 Silnik wykonawczy prądu stałego XP
Silnik wykonawczy prądu stałego
Sprawozdanie Silnik wykonawczy prądu stałego
1997 07 Sterownik dwufazowych silników krokowych
WA Silnik wykonawczy wykresy
EA1 2 fazowe silniki wykonawcze
badanie silnika dwufazowego malej mocy
Badanie silnika dwufazowego małej mocy
Badanie silnika dwufazowego małej mocy 2
elektr lab WA, Silniki asynchroniczne dwufazowe
Silnik Dwufazowy
silniki prądu stałego
więcej podobnych podstron