Czwórniki RC i RL

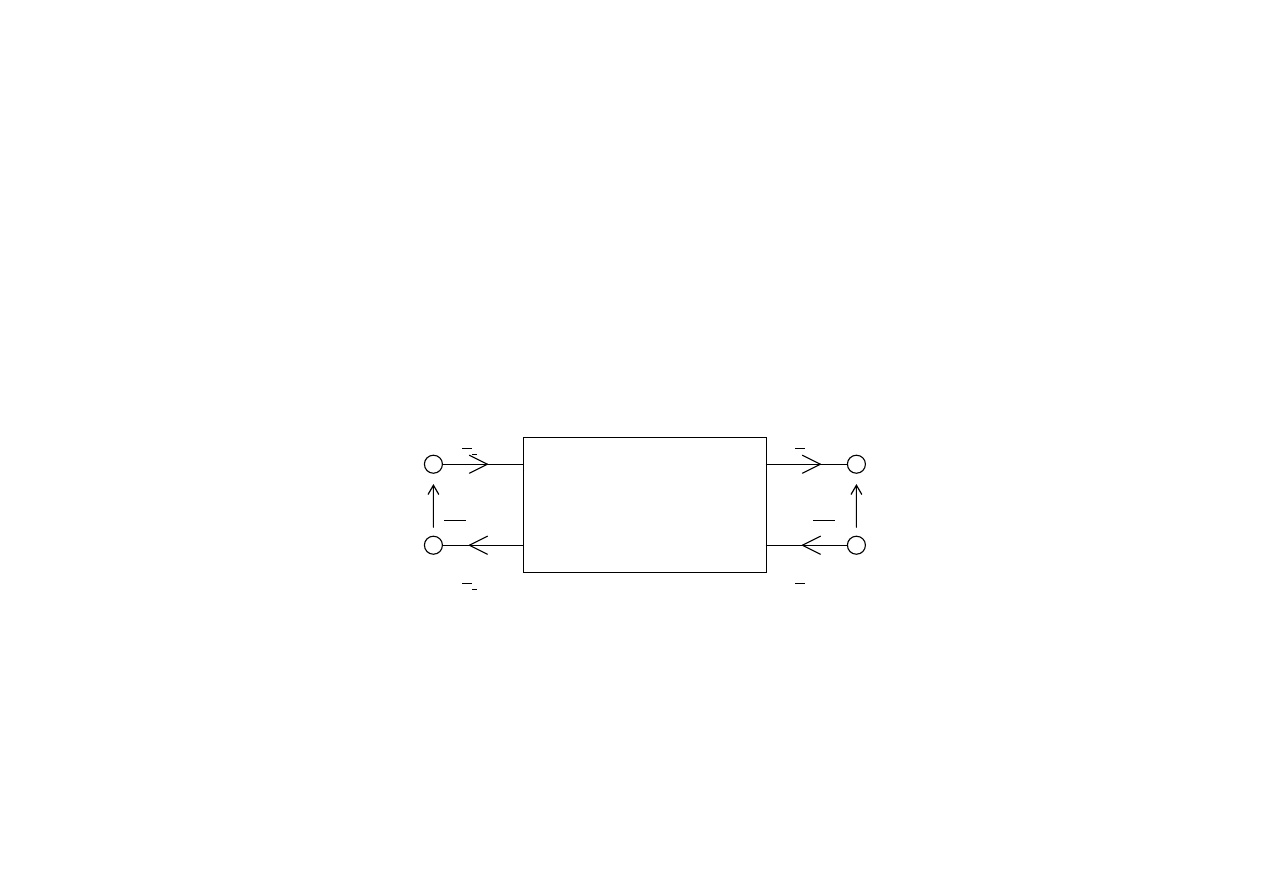
Czwórnikiem nazywamy układ mający cztery zaciski, a
dokładnie dwie pary uporządkowanych zacisków. Jedna z tych
par stanowi wejście, a druga wyjście czwórnika.

We

Wy

I

1

I

2

I

1

’

I

2

’

1

2

1’

2’

U

1

U

2

Klasyfikacja czwórników

Czwórniki można podzielić na:

1. liniowe i nieliniowe

2. symetryczne i niesymetryczne

3. odwracalne i nieodwracalne

4. pasywne i aktywne

Czwórnik liniowy występuje wtedy, gdy wszystkie elementy
wchodzące w jego skład są liniowe. Jeżeli czwórnik zawiera
chociaż

jeden element nieliniowy wówczas jest on

czwórnikiem nieliniowym.

Czwórnik jest symetryczny jeżeli po zamianie miejscami
wejścia z wyjściem nie zmieni się rozpływ prądów i rozkład
napięć w obwodzie dołączonym do wejścia i wyjścia
czwórnika.

Czwórnik odwracalny: jeżeli do zacisków wejściowych
doprowadzone zostanie idealne źródło napięcia E, które
wywoła przepływ prądu I w zwartym obwodzie wyjściowym,
to po przeniesieniu tego źródła do wyjścia, w zwartym
obwodzie wejściowym też popłynie prąd I.

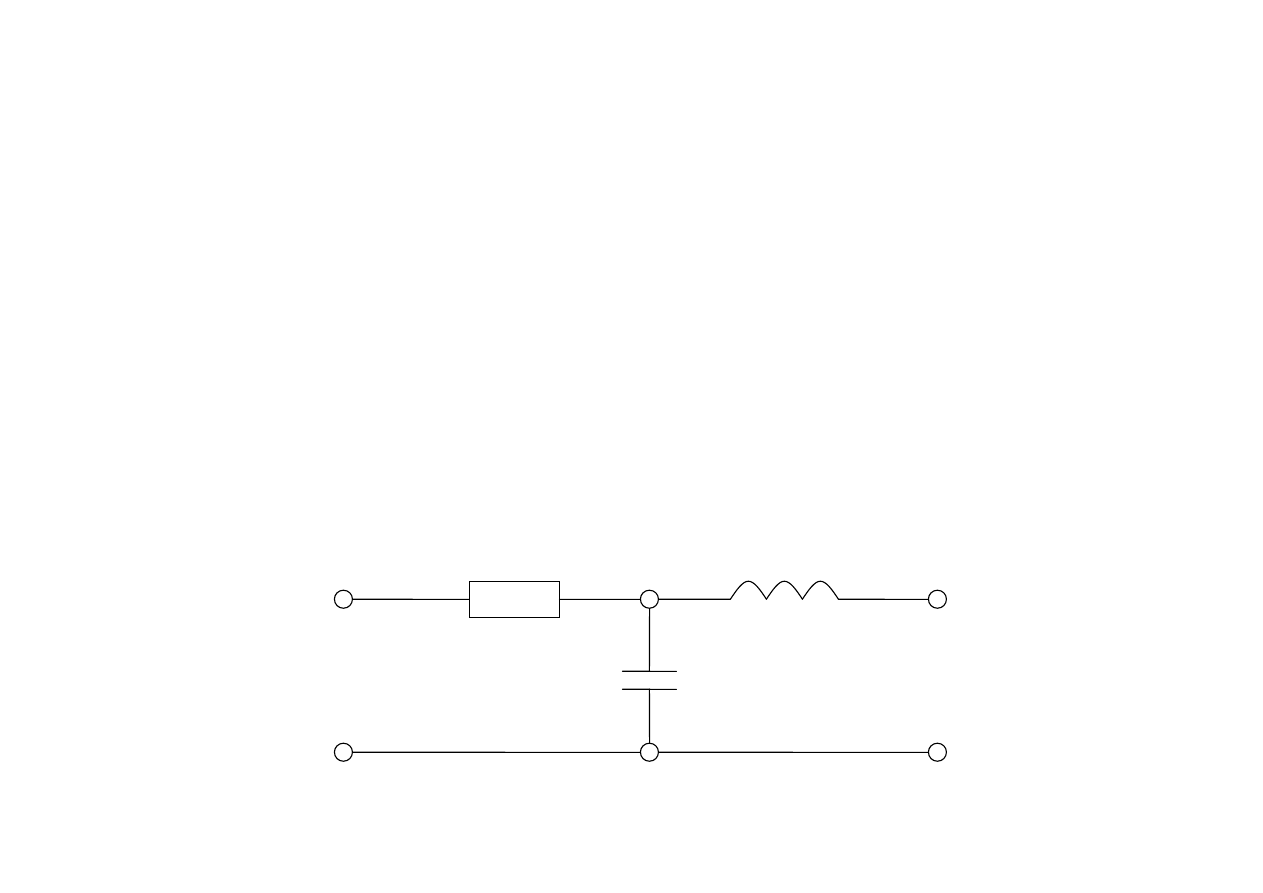
Czwórnik jest pasywny, jeżeli całkowita energia pobrana przez
elementy czwórnika po dołączeniu do jego zacisków źródła
energii, jest nieujemna, tzn. dodatnia lub równa zeru. Składa
się zazwyczaj z rezystorów, cewek i kondensatorów.

Czwórnik, który nie spełnia warunków podanych w definicji
czwórnika pasywnego, jest nazywany czwórnikiem aktywnym.
Charakteryzuje się on tym, że w jego schemacie zastępczym
występuje źródło sterowane lub niesterowane.

We

Wy

R

L

C

Równania czwórników

1. Postać impedancyjna:

U

1

= Z

11

I

1

+ Z

12

I

2

U

2

= Z

21

I

1

+ Z

22

I

2

2. Postać łańcuchowa:

U

1

= A U

2

+ B I

2

I

2

= C U

2

+ D I

2

3. Postać hybrydowa:

U

1

= h

11

I

1

+ h

12

U

2

I 2 = h

21

I

1

+ h

22

U

2

Stany pracy czwórnika

Wyróżnia się trzy stany pracy czwórnika. Są to:

1. Stan jałowy

2. Stan zwarcia

3. Stan obciążenia

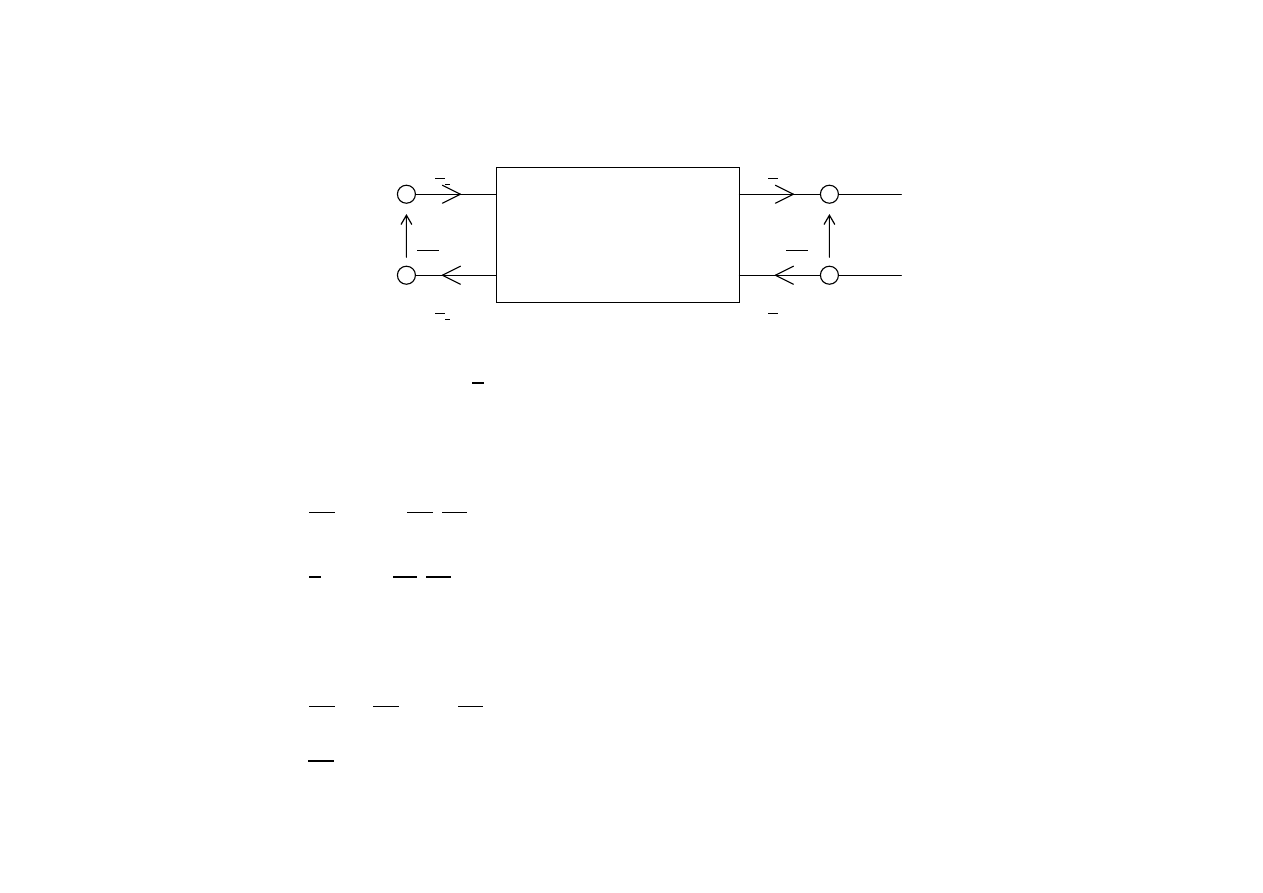
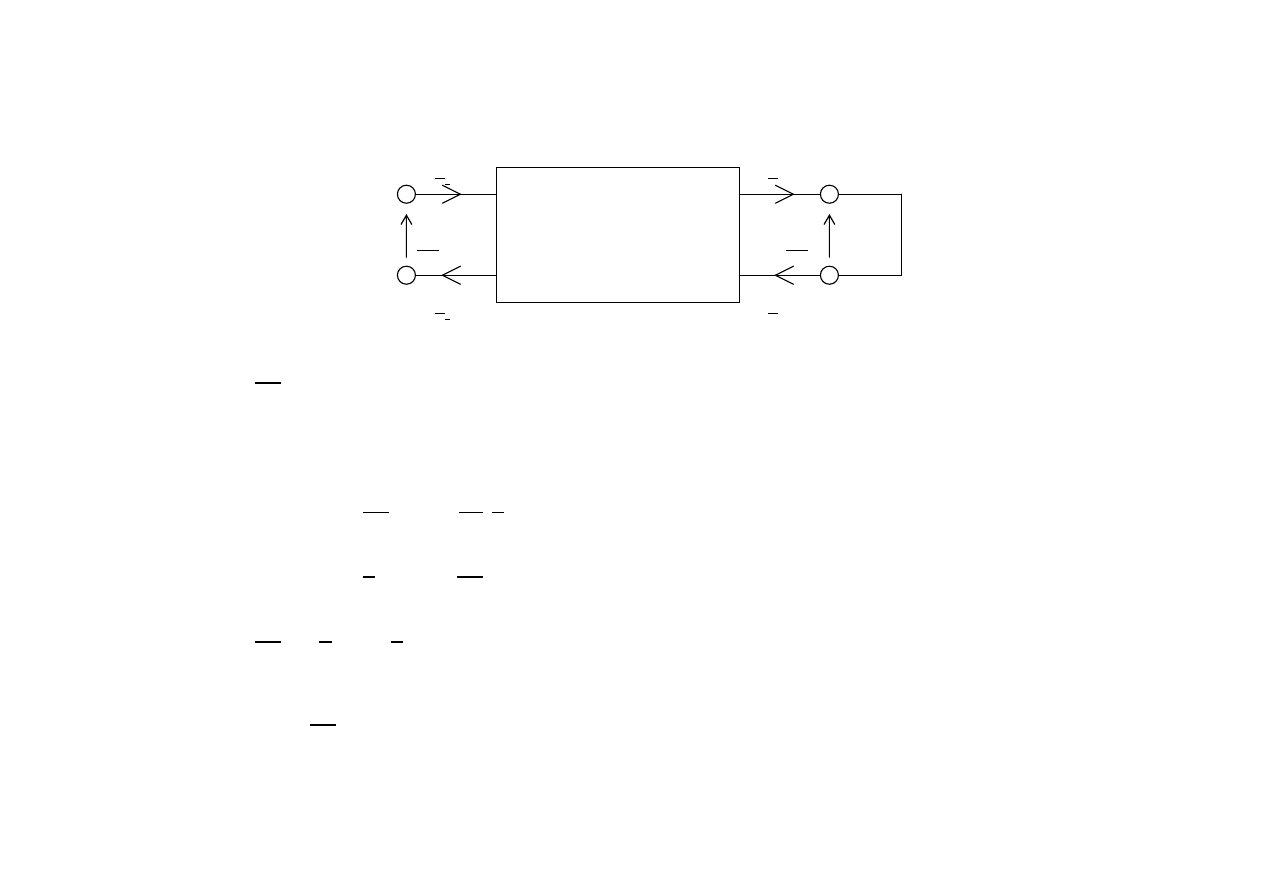
Stan jałowy

I

1

I

2

I

1

’

I

2

’

1

2

1’

2’

U

1

U

2

W stanie jałowym I

2

= 0

Równania mają postać:

U

1o

= A U

2o

I

1o

= C U

2o

Stąd:

A = U

1o

/ U

2o

Parametr A stanowi przekładnię napięciową czwórnika w stanie
jałowym.

Stan zwarcia

I

1

I

2

I

1

’

I

2

’

1

2

1’

2’

U

1

U

2

U

2

= 0

Równania mają postać:

U

1z

= B I

2z

I 1z = D I

2z

D = I

1z

/ I

2z

Parametr D jest przekładnią prądową czwórnika w stanie
zwarcia.

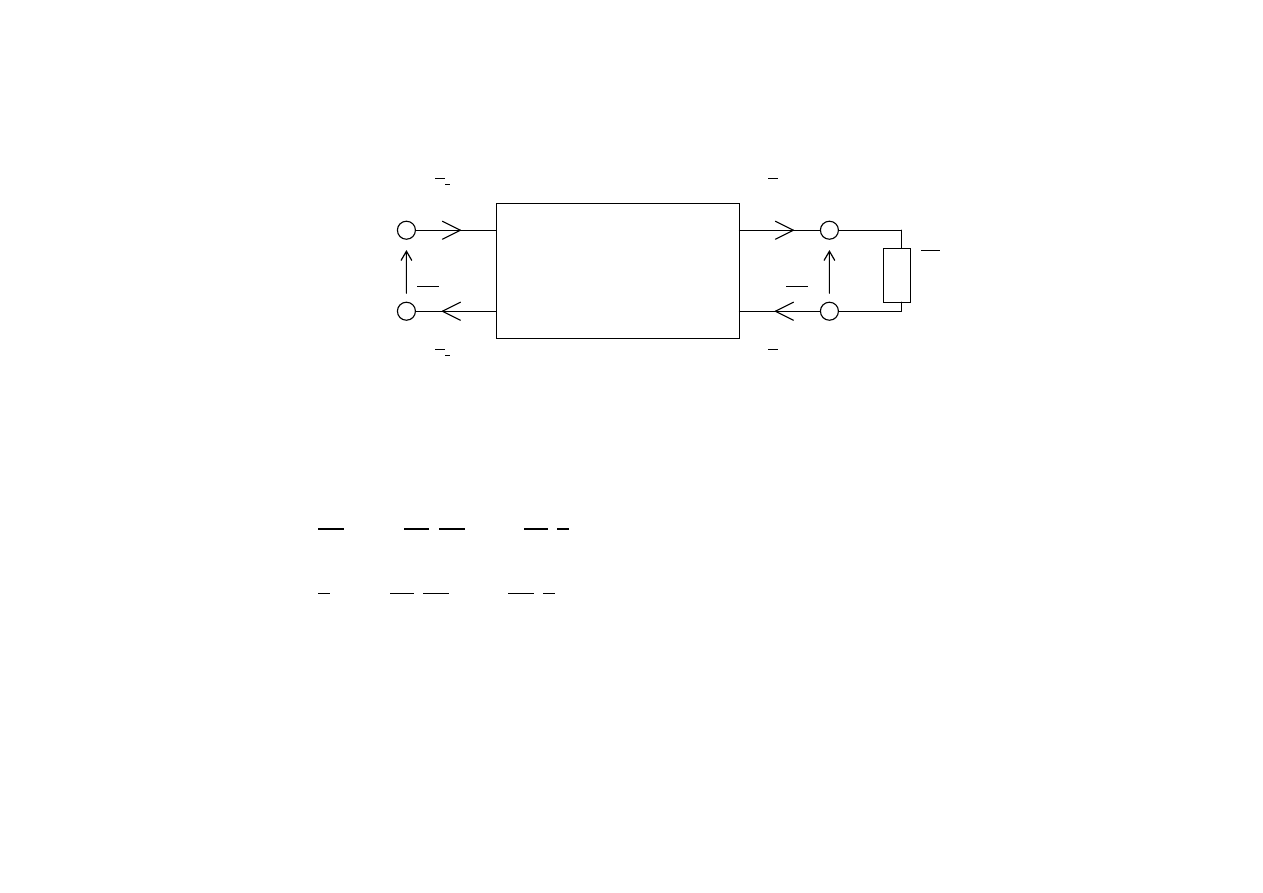
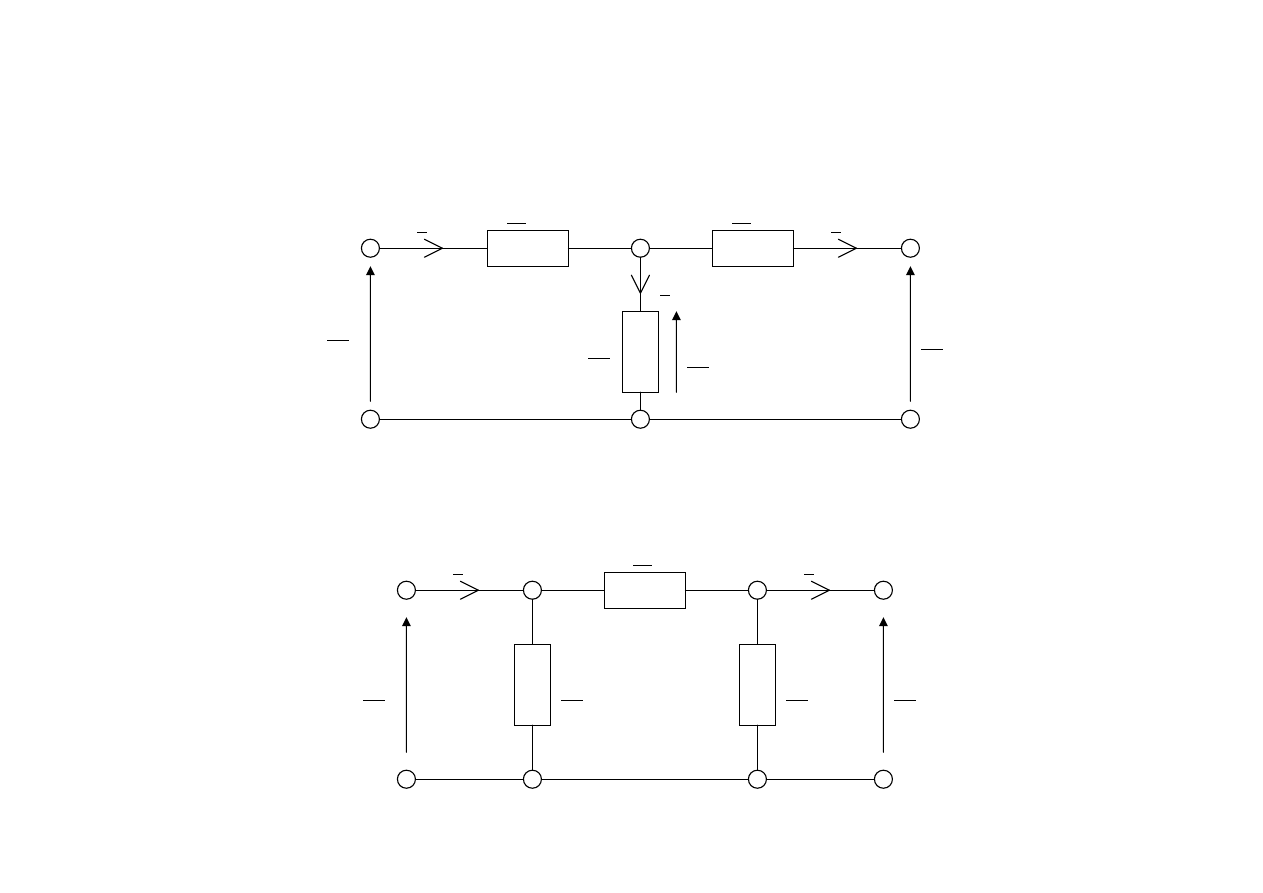
Stan obciążenia

I

1

I

2

I

1

’

I

2

’

1

2

1’

2’

U

1

U

2

Z

o

W stanie obciążenia równania wyglądają następująco:

U

1

= A U

2

+ B I

2

I

1

= C U

2

+ D I

2

Schematy zastępcze czwórników

U

1

U

1

U

2

U

2

I

1

I

2

I

1

I

2

I’

Z

1

Z

2

Z

Y

1

Y

2

Y

U’

Typu T

Typu Π

Stany nieustalone

Warunki początkowe

Stanem początkowym obwodu nazywa się stan, w którym
wszystkie napięcia i prądy w obwodzie są równe zeru.
Warunki początkowe są wtedy zerowe.

Komutacją nazywa się zmiany stanu w obwodzie zachodzące
w pewnej określonej chwili, spowodowane np. włączaniem
lub odłączaniem dodatkowej gałęzi do obwodu.

Z takim zjawiskiem związane są dwa prawa zwane prawami
komutacji.

Pierwsze prawo komutacji mówi, że prąd w obwodzie z
indukcyjnością nie może zmienić się „skokiem” i w chwili
tuż przed komutacją ma taką samą wartość jak w chwili tuż
po komutacji. Pierwsze prawo komutacji nazywane jest też
zasadą ciągłości prądu i strumienia magnetycznego w cewce.

Zgodnie z drugim prawem komutacji

napięcie na

kondensatorze nie może zmienić się „skokiem” i w chwili tuż
przed komutacją ma taką samą wartość jak w chwili tuż po
komutacji. Prawo to jest także nazywane zasadą ciągłości
napięcia i ładunku na pojemności.

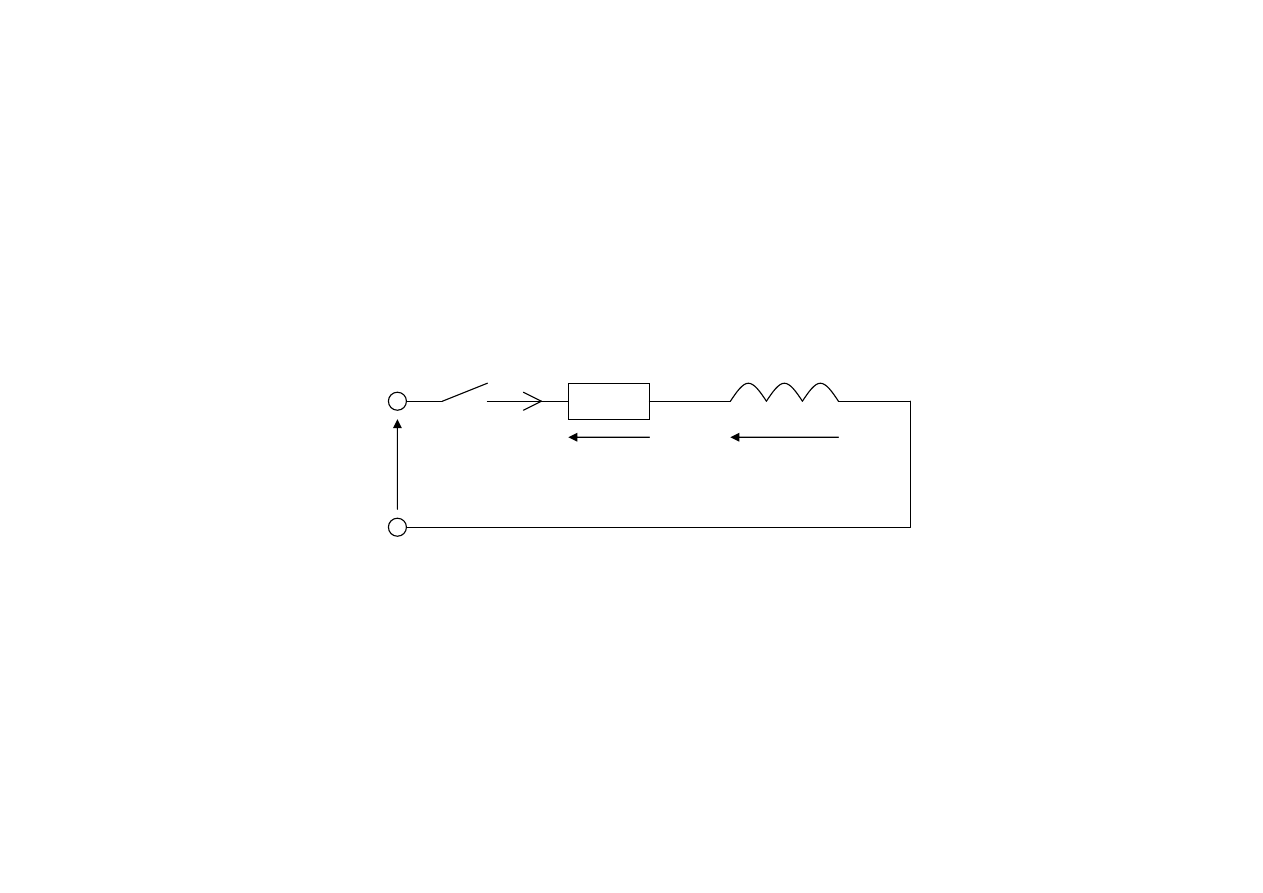
Stan nieustalony w dwójniku RL

Włączenie napięcia stałego

u

i

u

R

u

L

W

R

L

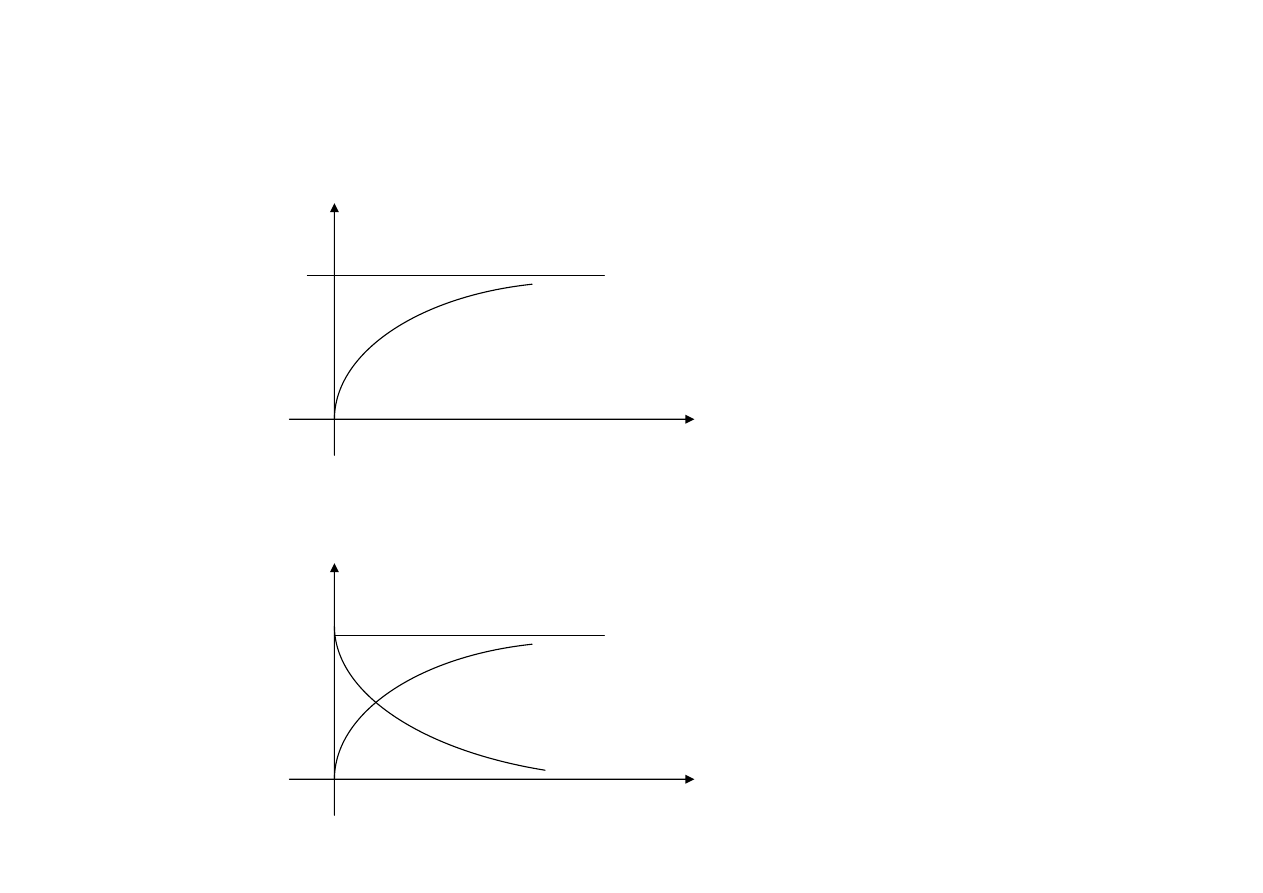
Przebiegi

i

t

i

U

R

u, u

R

, u

L

t

u

R

U

u

L

Prąd w funkcji czasu:

Napięcie na cewce i rezystorze w funkcji czasu:

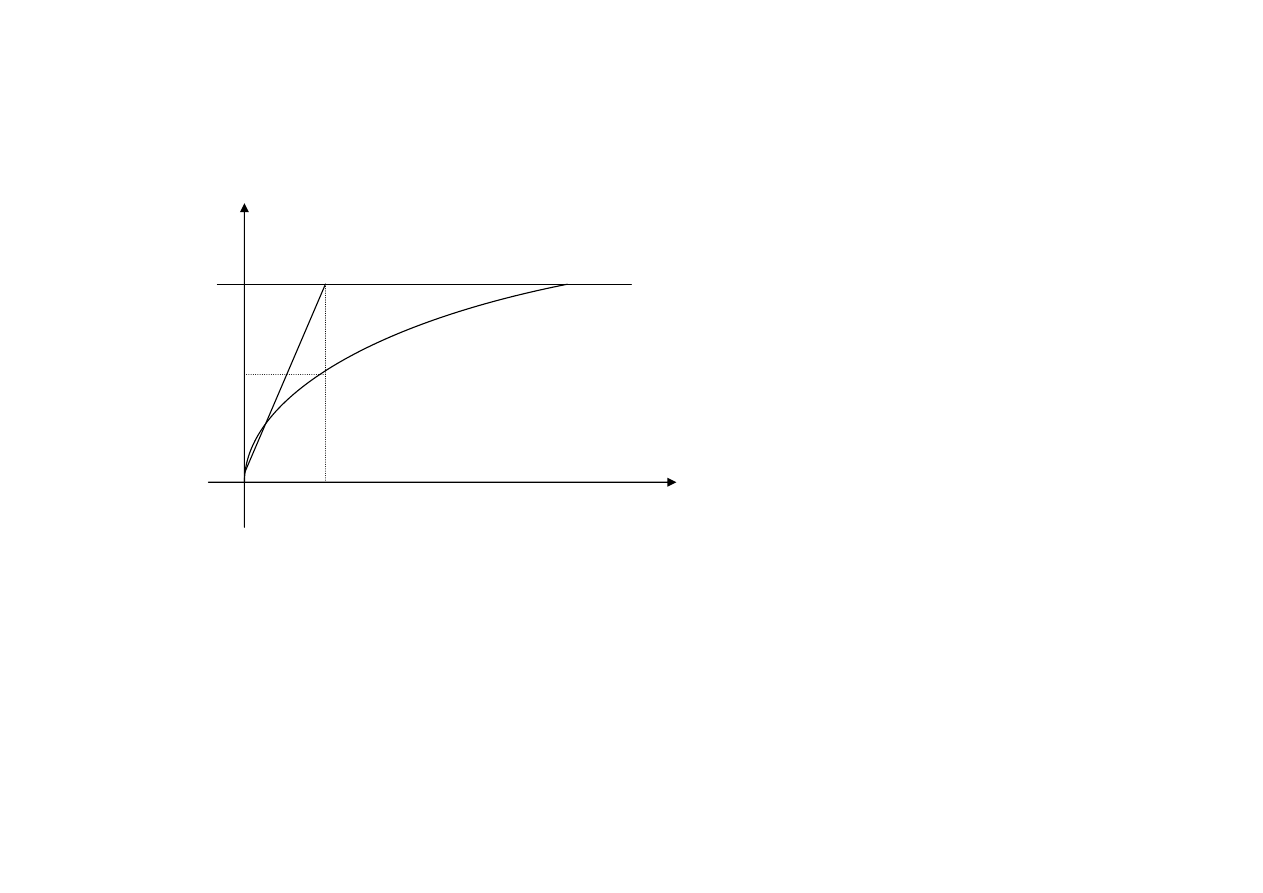
Sposoby określania stałej czasowej

i

t

U

R

τ

1. Metoda graficzna:

2. Stała czasowa jest to czas, po którym prąd w cewce
osiągnie wartość 0,63 i

ust.

(63% i

ust.

). Przyjmuje się, że

prąd ustalony będzie po czasie równym 4τ÷5τ.

3. Ze wzoru:

τ

= L / R [s]

0,63 i

ust.

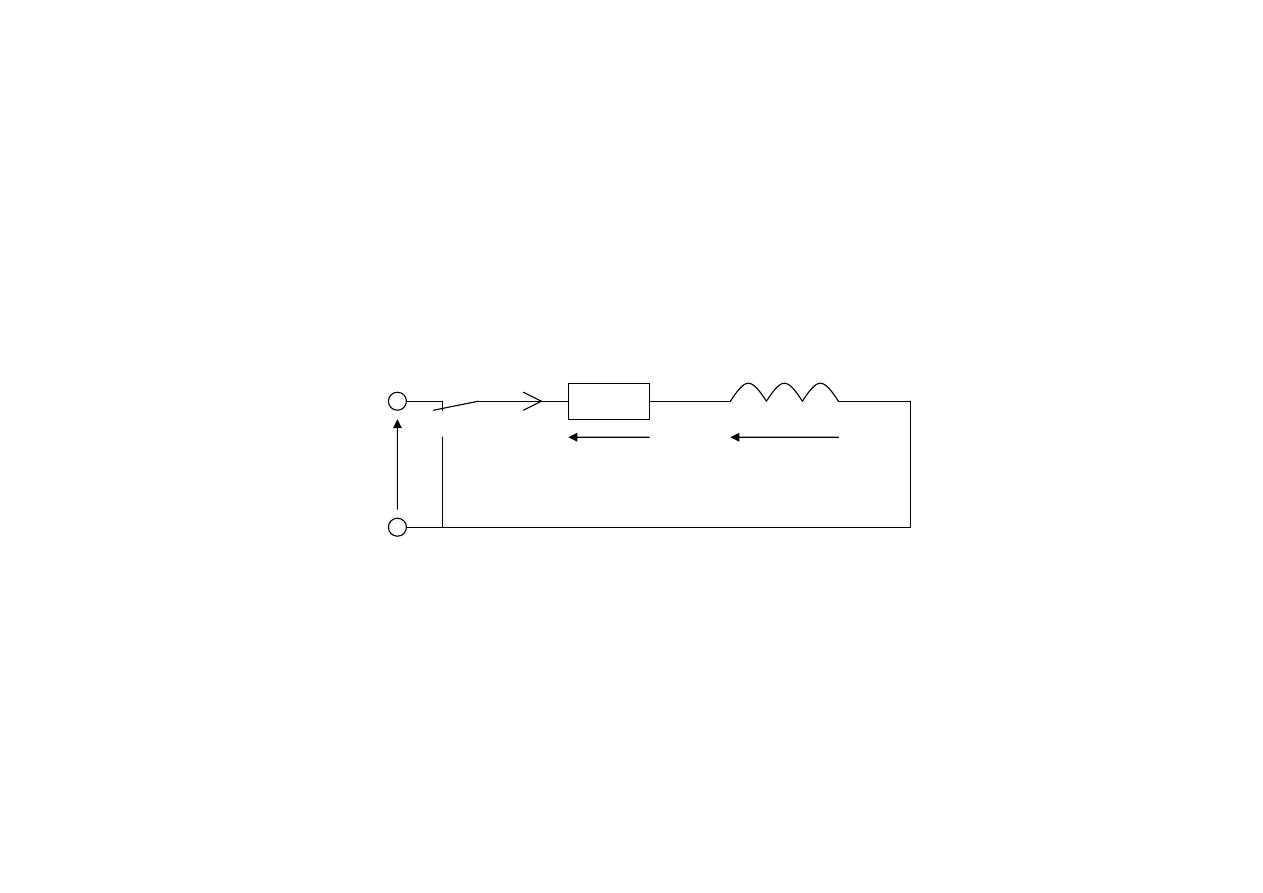
Zwarcie obwodu RL przy warunku początkowym
niezerowym

u

i

u

R

u

L

R

L

W

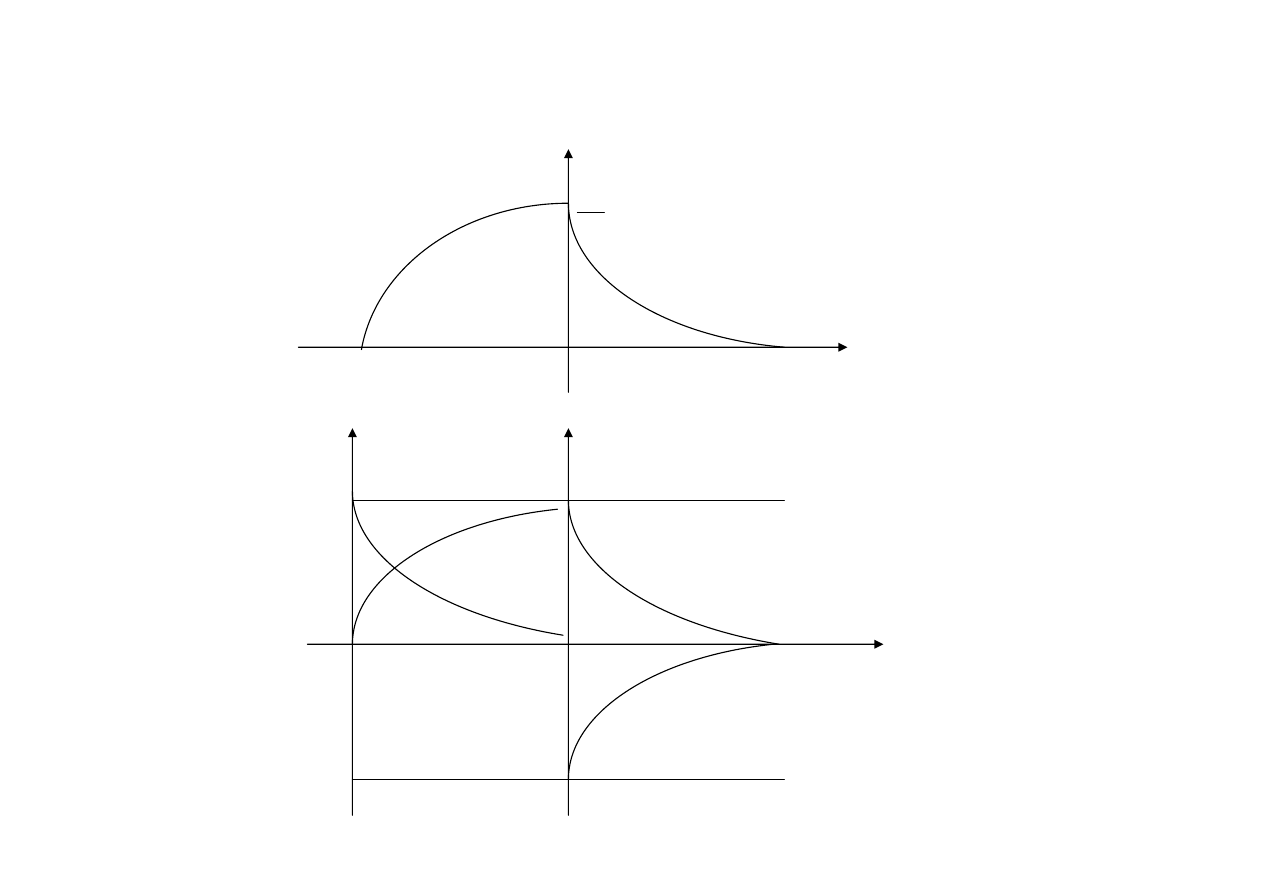
Przebiegi

i

t

U

R

u, u

R

, u

L

t

u

R

U

u

L

-U

u

R

u

L

Sposoby określania stałej czasowej

1. Metoda graficzna:

i

t

U

R

τ

0,37 i

ust.

2. Stała czasowa jest to czas, po którym prąd w cewce
osiągnie wartość 0,37 i

ust.

(37% i

ust.

). Przyjmuje się, że

prąd ustalony będzie po czasie równym 4τ÷5τ.

3. Ze wzoru:

τ

= L / R [s]

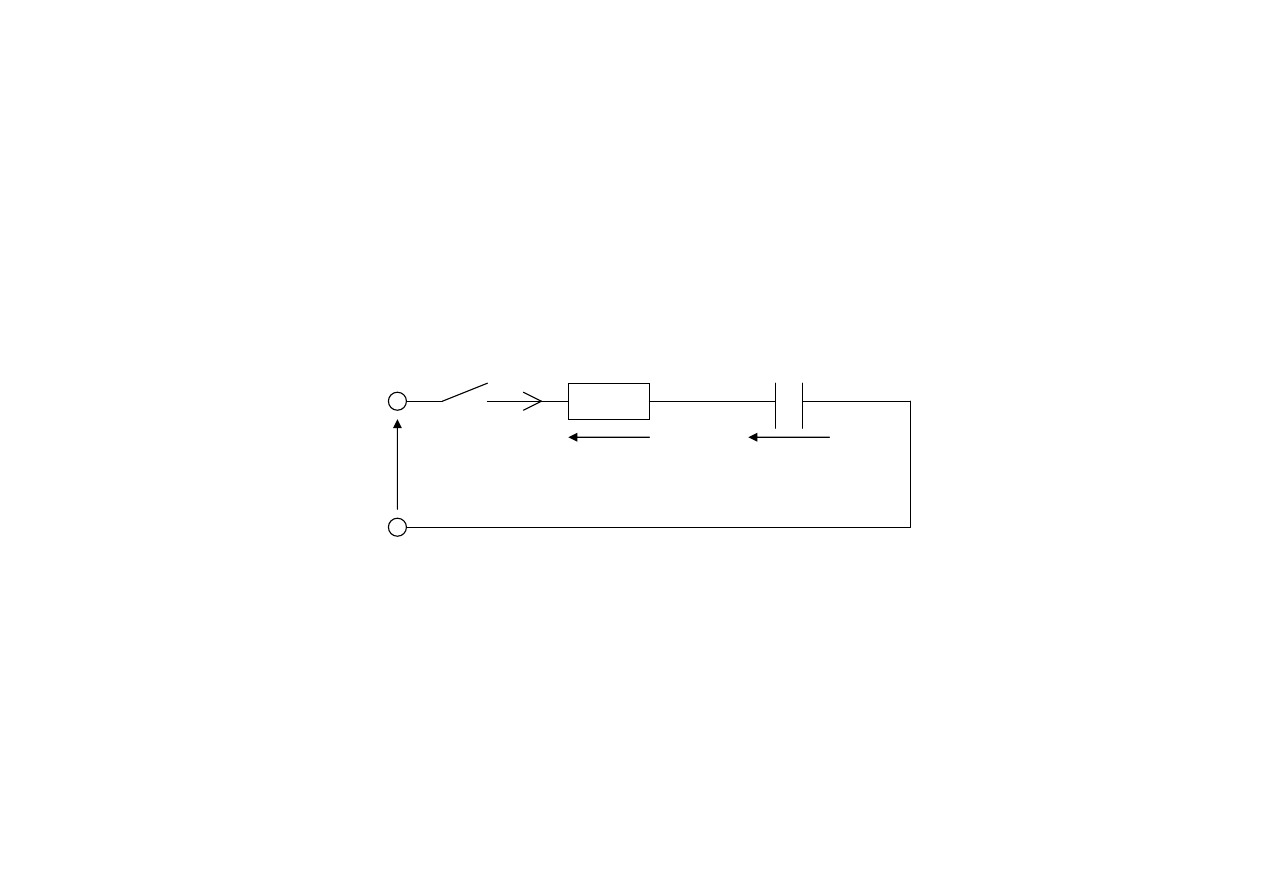
Stan nieustalony w dwójniku RC

Włączenie napięcia stałego

u

i

u

R

u

C

W

R

C

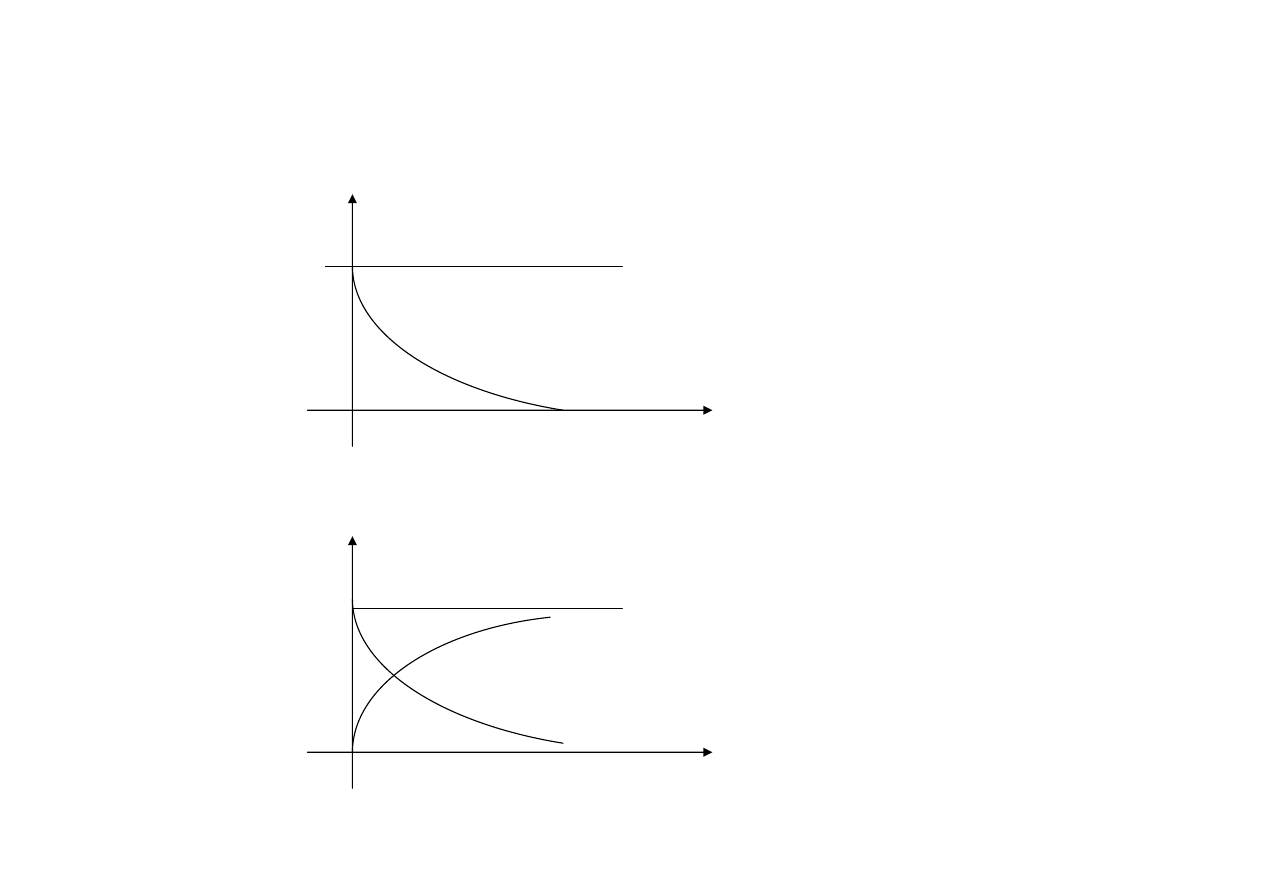
Przebiegi

i

t

i

U

R

u, u

R

, u

C

t

u

C

U

u

R

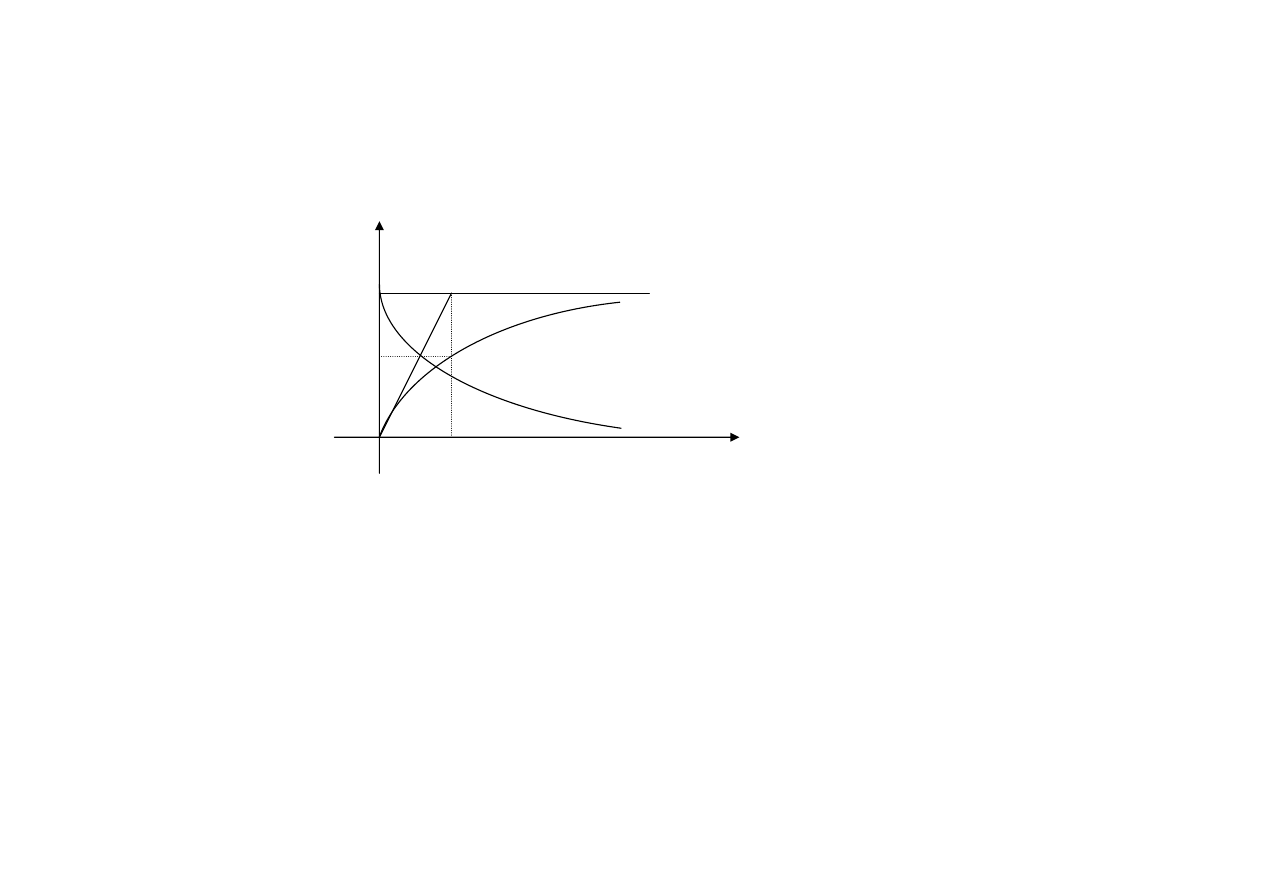
Sposoby określania stałej czasowej

1. Metoda graficzna:

u, u

R

, u

C

t

u

C

U

u

R

0,63 u

ust.

2. Stała czasowa jest to czas, po którym napięcie na
kondensatorze osiągnie wartość 0,63 u

ust.

(63% u

ust.

).

Przyjmuje się, że napięcie ustalone będzie po czasie
równym 4τ÷5τ.

3. Ze wzoru:

τ

= RC [s]

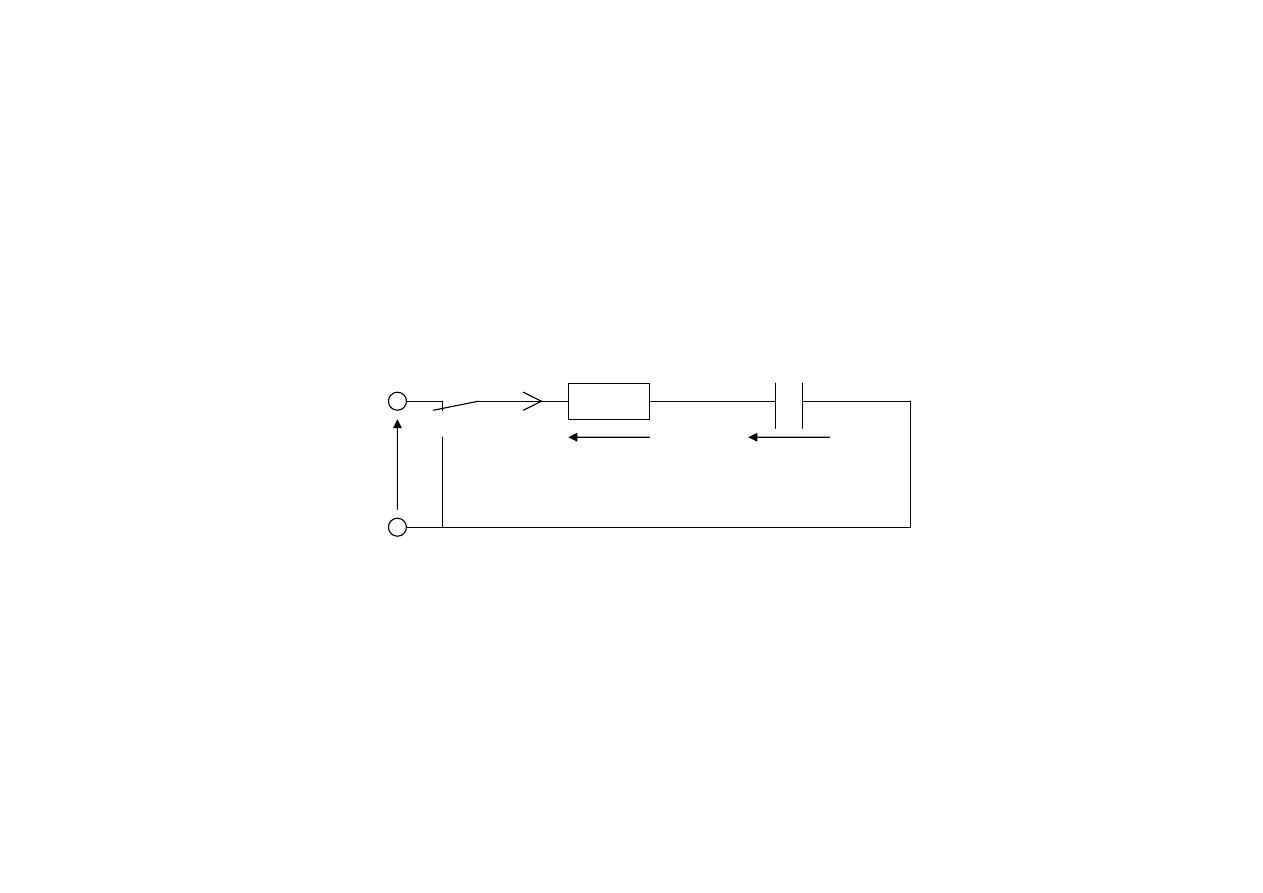
Zwarcie obwodu RL przy warunku początkowym
niezerowym

u

i

u

R

R

u

C

C

W

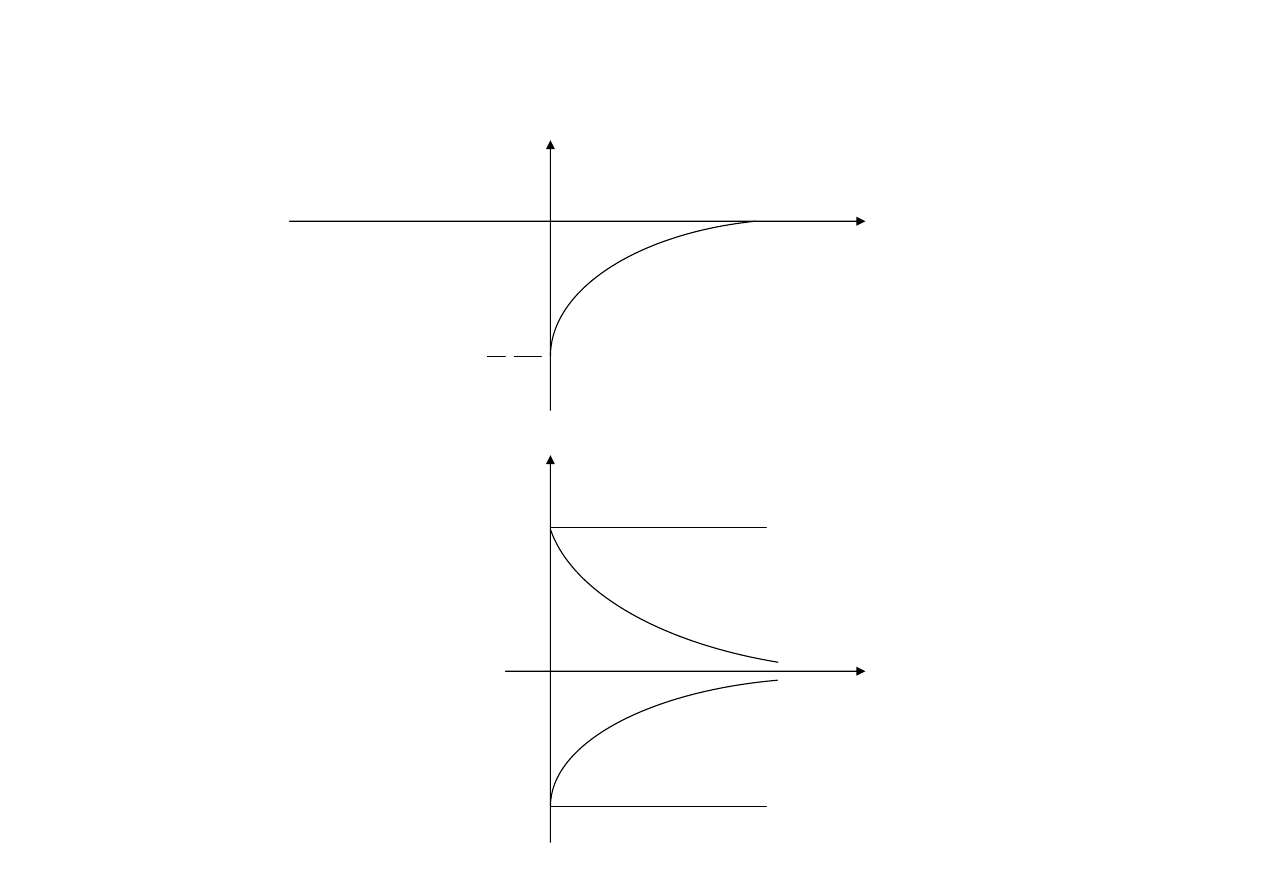
Przebiegi

t

i

U

R

u, u

R

, u

C

t

U

-U

u

C

u

R

t

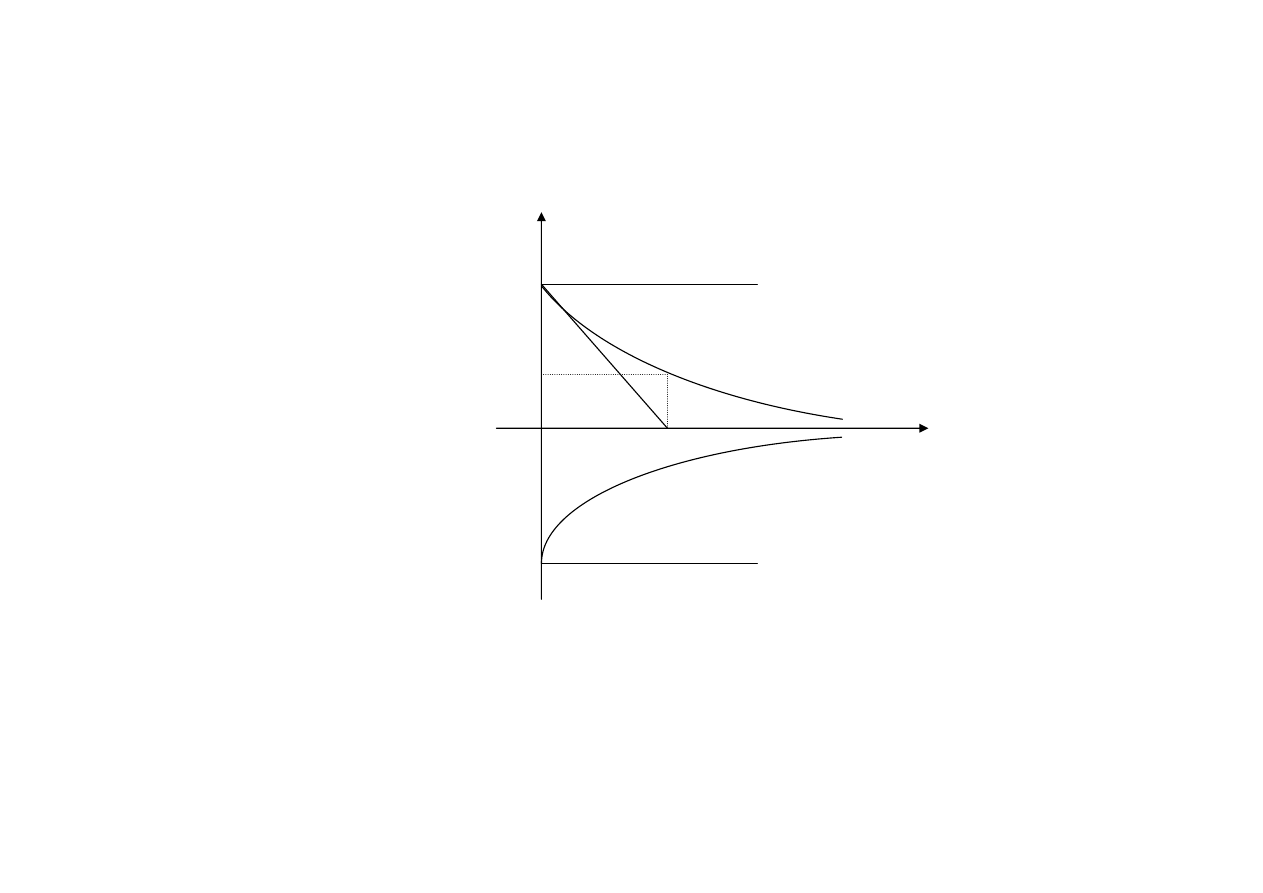
Sposoby określania stałej czasowej

1. Metoda graficzna:

u, u

R

, u

C

t

U

-U

u

C

u

R

0,37 u

ust.

2. Stała czasowa jest to czas, po którym napięcie na
kondensatorze osiągnie wartość 0,37 u

ust.

(37% u

ust.

).

Przyjmuje się, że napięcie ustalone będzie po czasie
równym 4τ÷5τ.

Przebiegi w czwórnikach RC

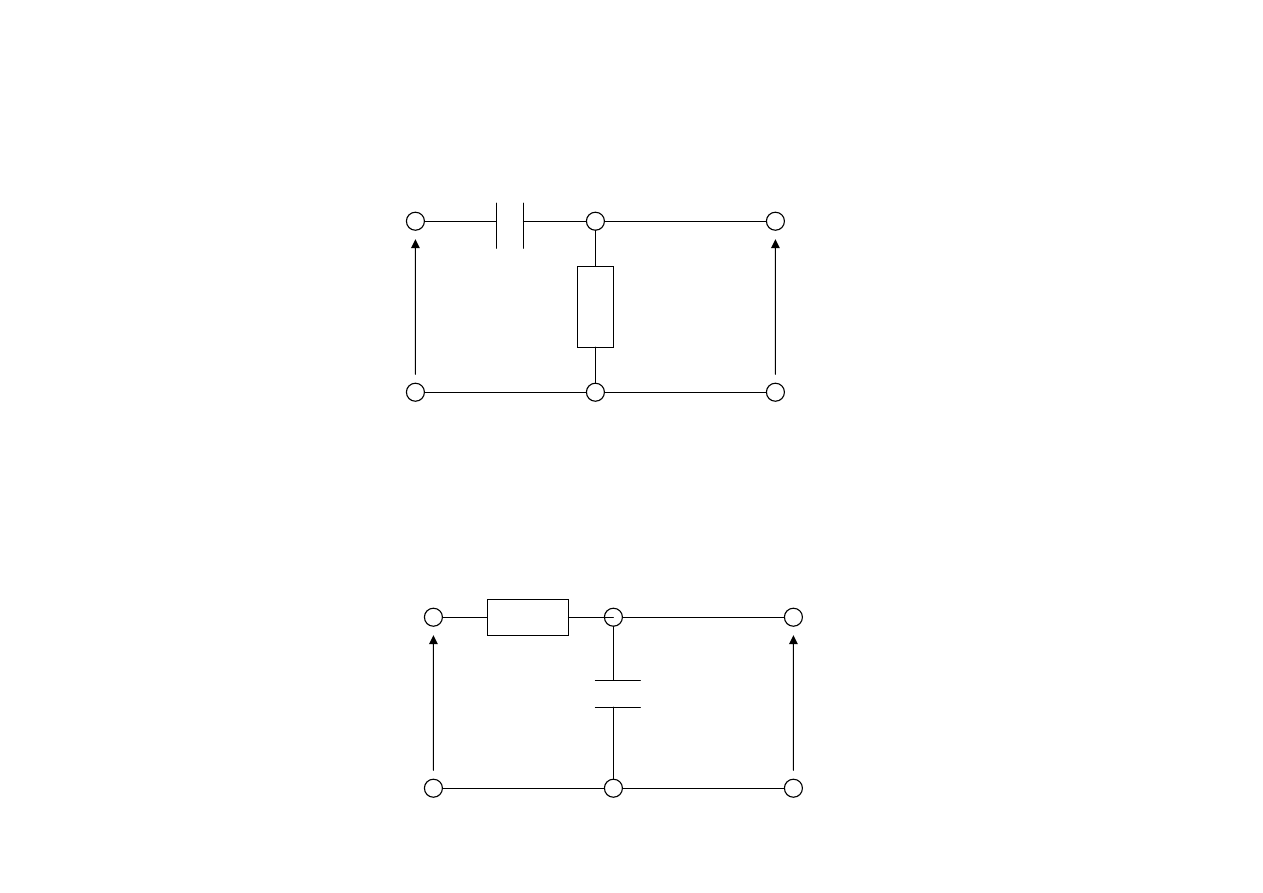
Układ różniczkujący

R

C

U

1

U

2

R

C

U

1

U

2

Układ całkujący

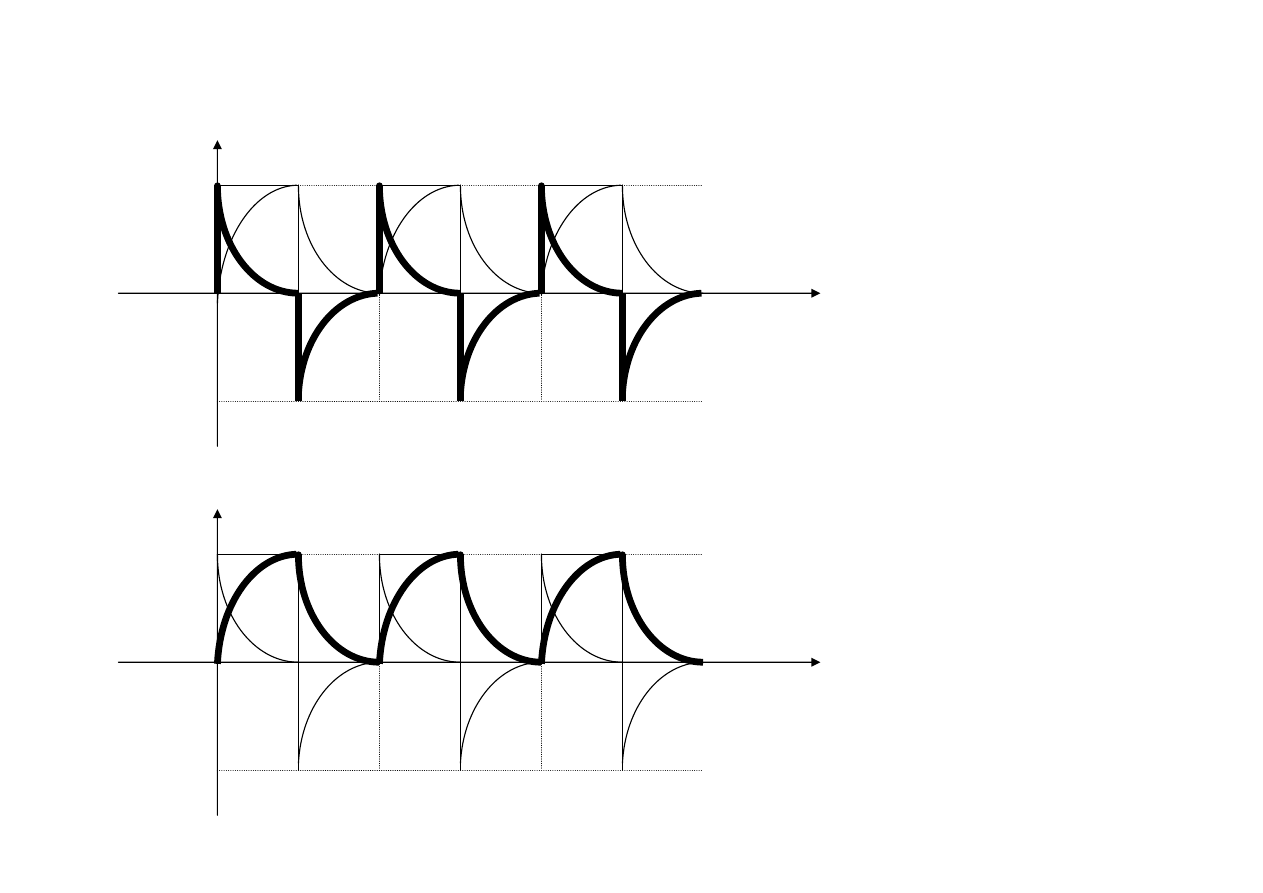
Wymuszenie prostokątne jednego znaku

u

C

u

R

u

C

u

R

Różniczkujący

Całkujący

u, u

R

, u

C

u, u

R

, u

C

t

t

U

U

-U

-U

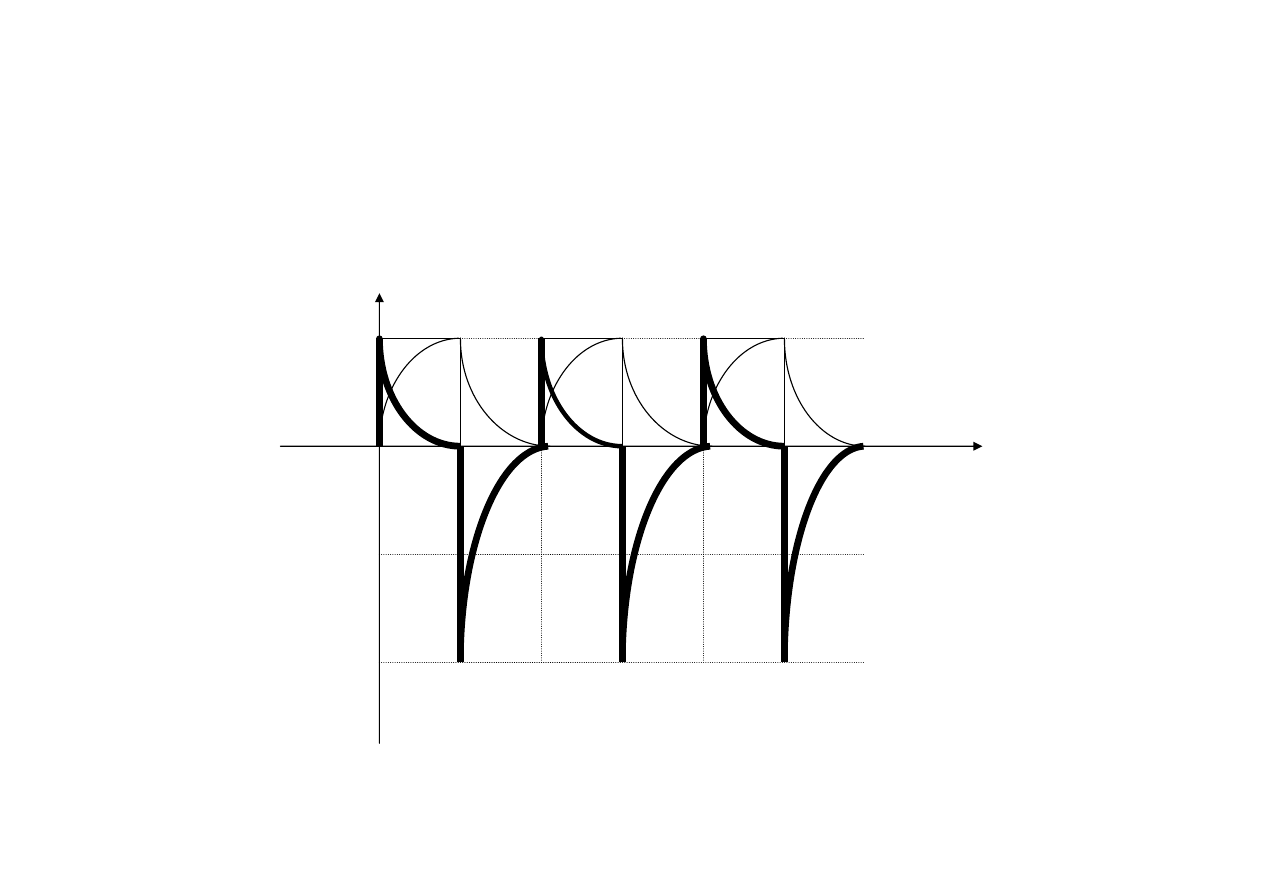
Wymuszenie prostokątne zmiennego znaku

Różniczkujący

u

C

u

R

u, u

R

, u

C

t

U

-U

-2U

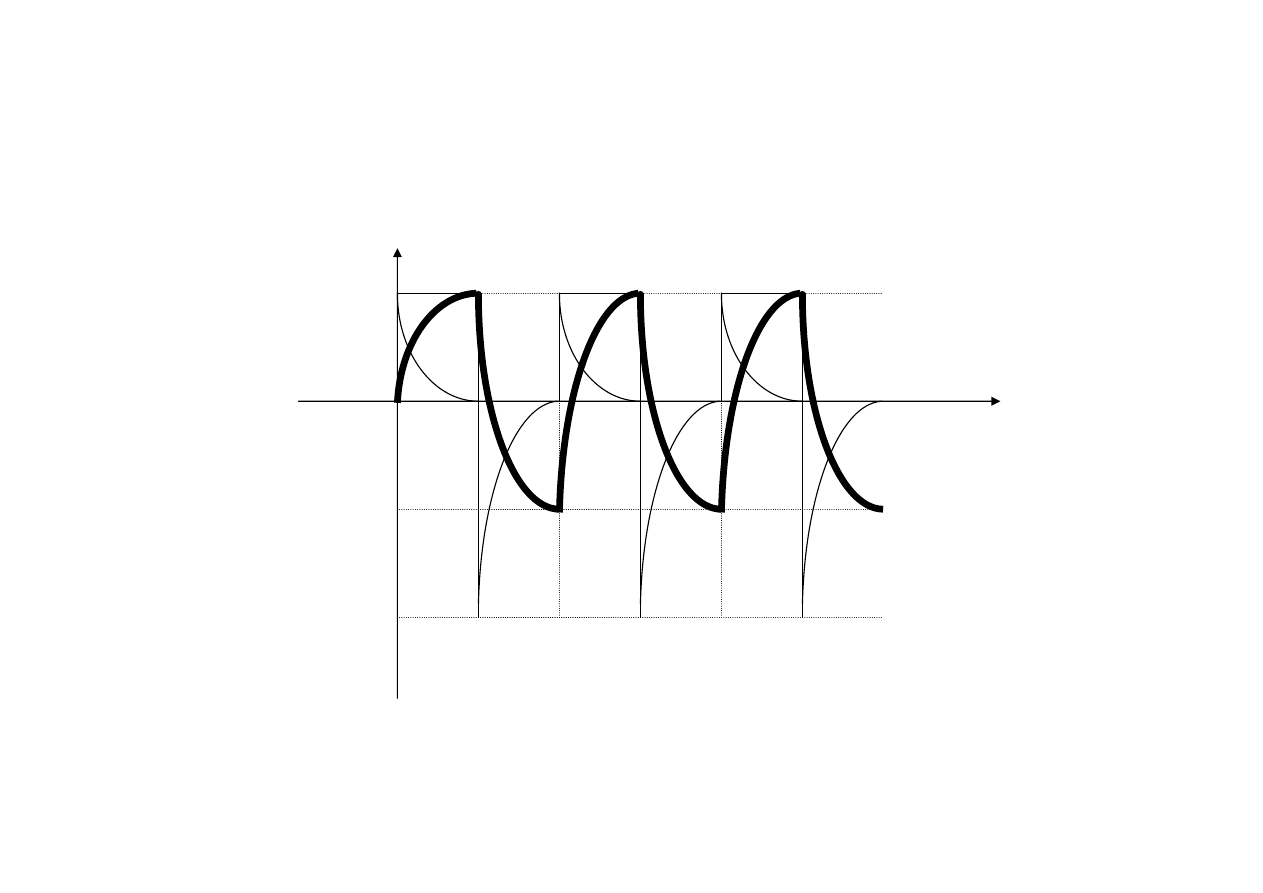
Całkujący

u

C

u

R

u, u

R

, u

C

t

U

-U

-2U

Filtry częstotliwościowe

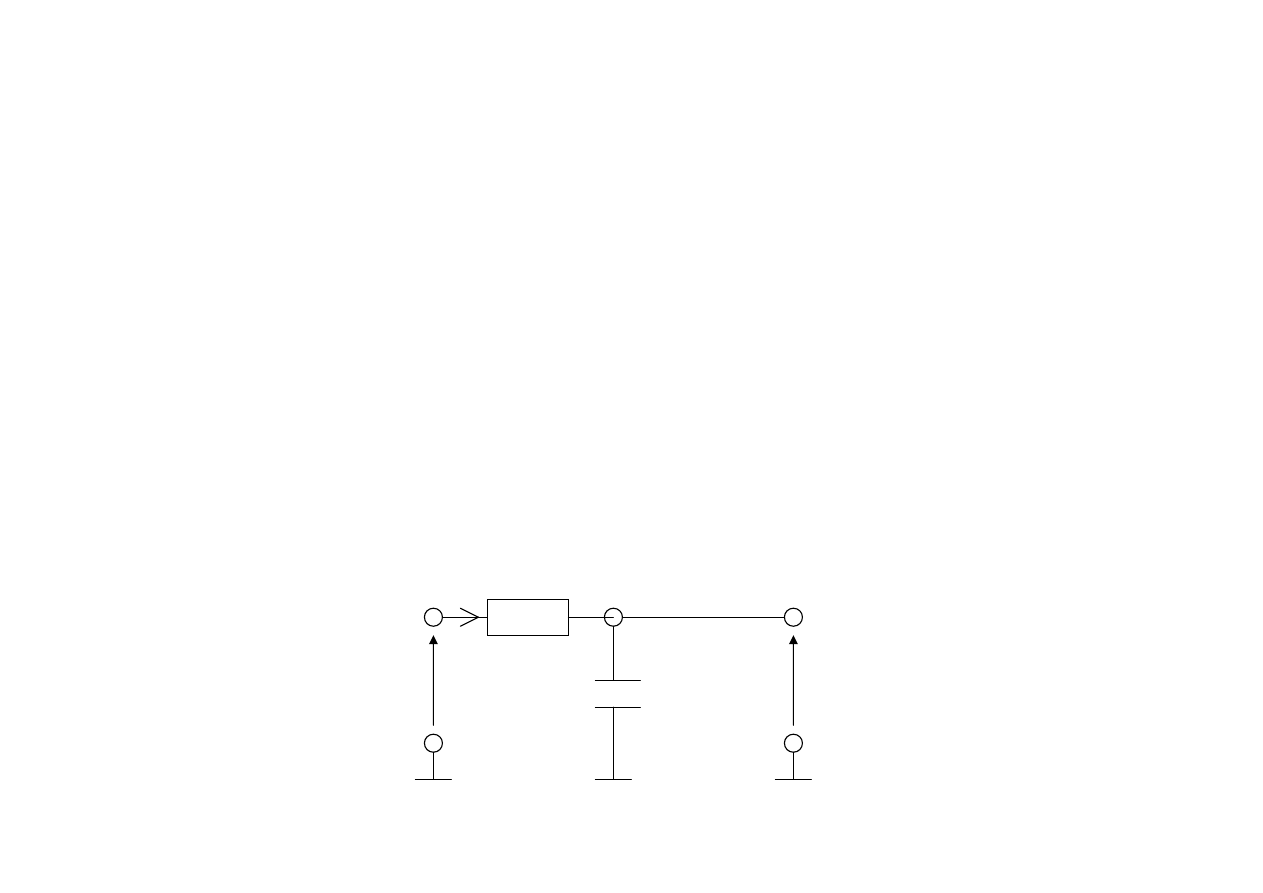
Filtr dolnoprzepustowy RC

Zadanie tego filtru polega na:

•

przenoszeniu, bez tłumienia, składowych widma
sygnału wejściowego leżących w dolnej jego
części

•

tłumieniu składowych widma sygnału
wejściowego leżących w górnej jego części

R

C

U

we

U

wy

I

we

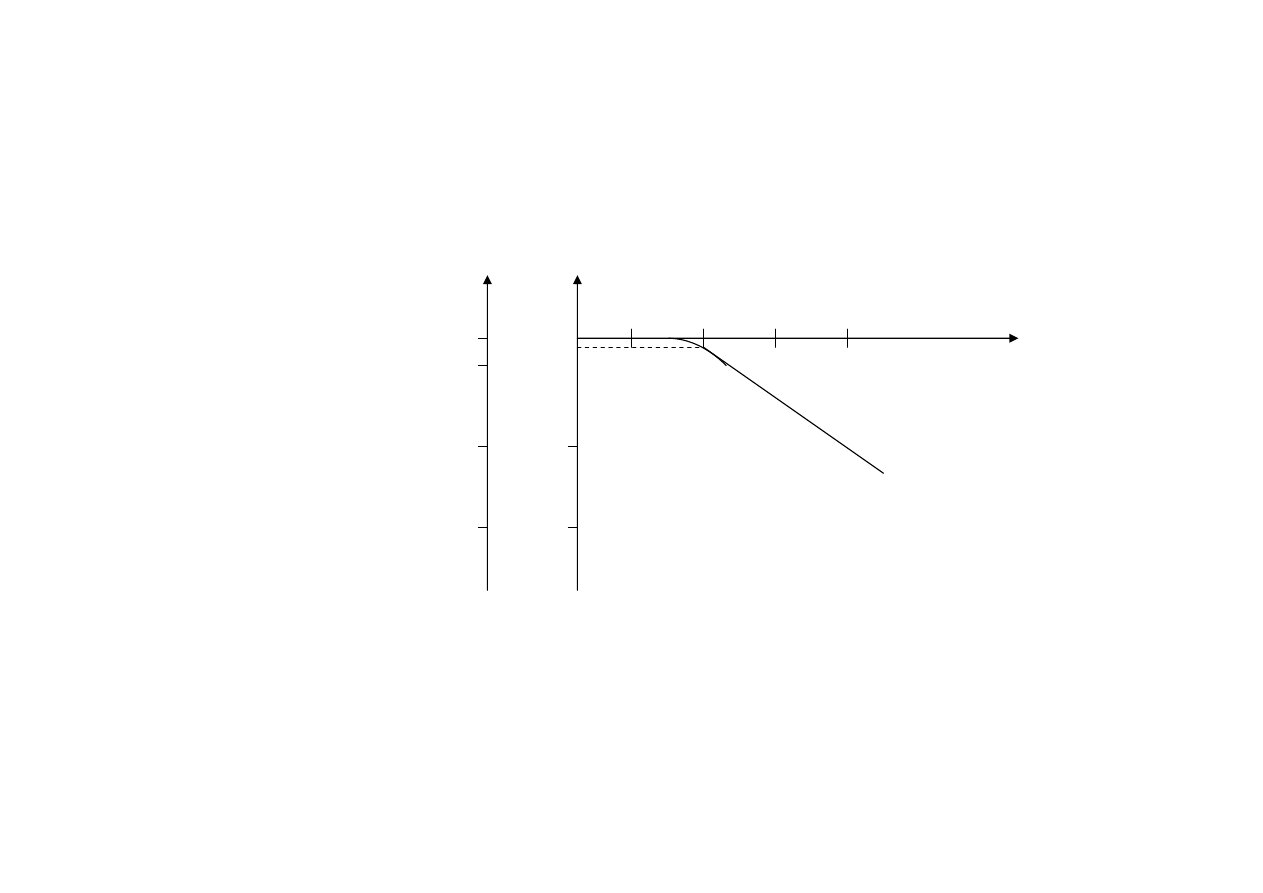
f

|k

u

|

|k

u

|

log

1

-20

-3

0

-40

0,01

0,1

0,707

0,1f

g

f

g

100f

g

10f

g

Charakterystyka amplitudowa

f

φ

arg(k

u

)= φ

0

-

π

/

4

-3

0

-90

o

-45

o

0,1f

g

f

g

100f

g

10f

g

-

π

/

2

Charakterystyka fazowa

Filtr dolnoprzepustowy jest czwórnikiem całkującym i
wprowadza ujemne przesunięcie fazowe, które dla f

g

wynosi –45

o

.

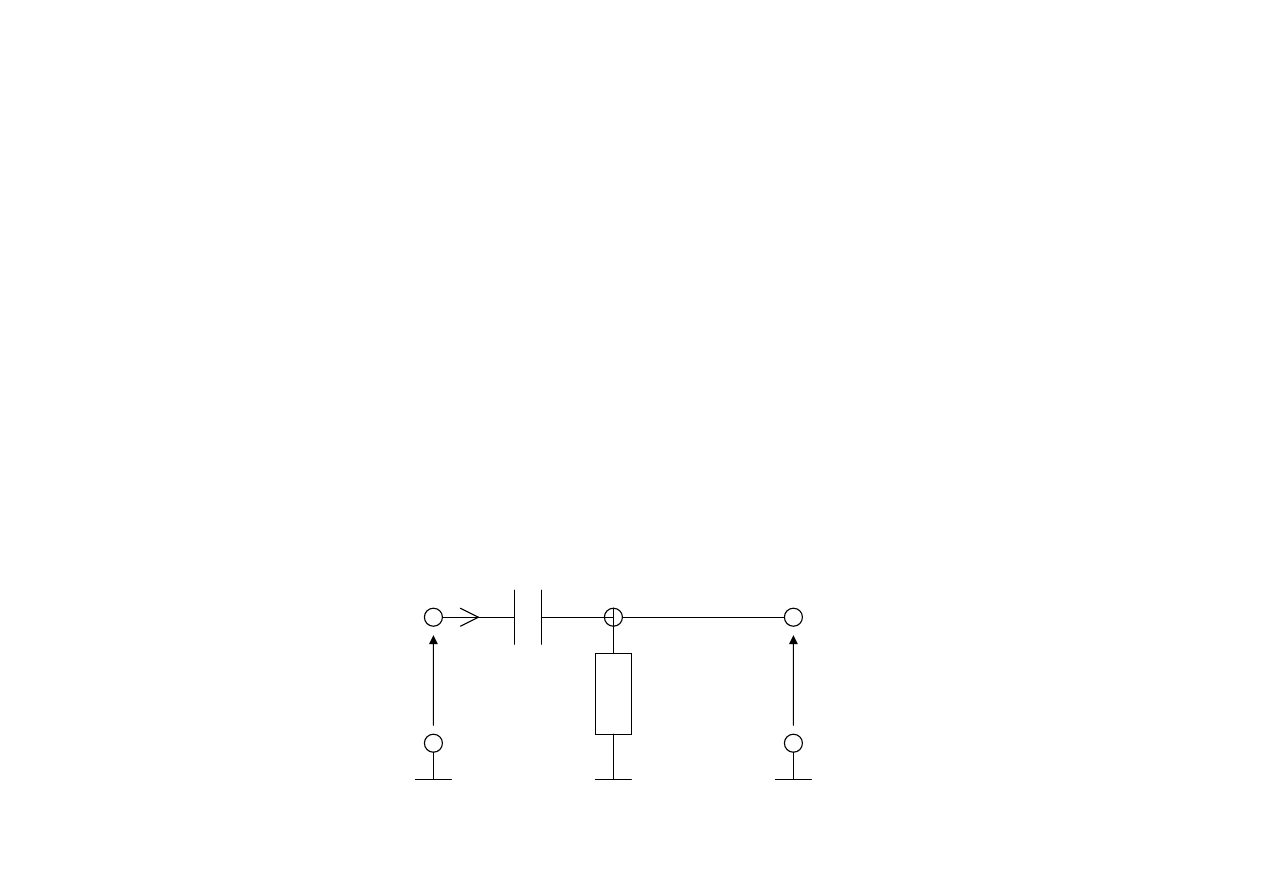
Filtr górnoprzepustowy RC

Zadanie tego filtru polega na:

•

przenoszeniu, bez tłumienia, składowych widma
sygnału wejściowego leżących w górnej jego
części

•

tłumieniu składowych widma sygnału
wejściowego leżących w dolnej jego części

R

C

U

we

U

wy

I

we

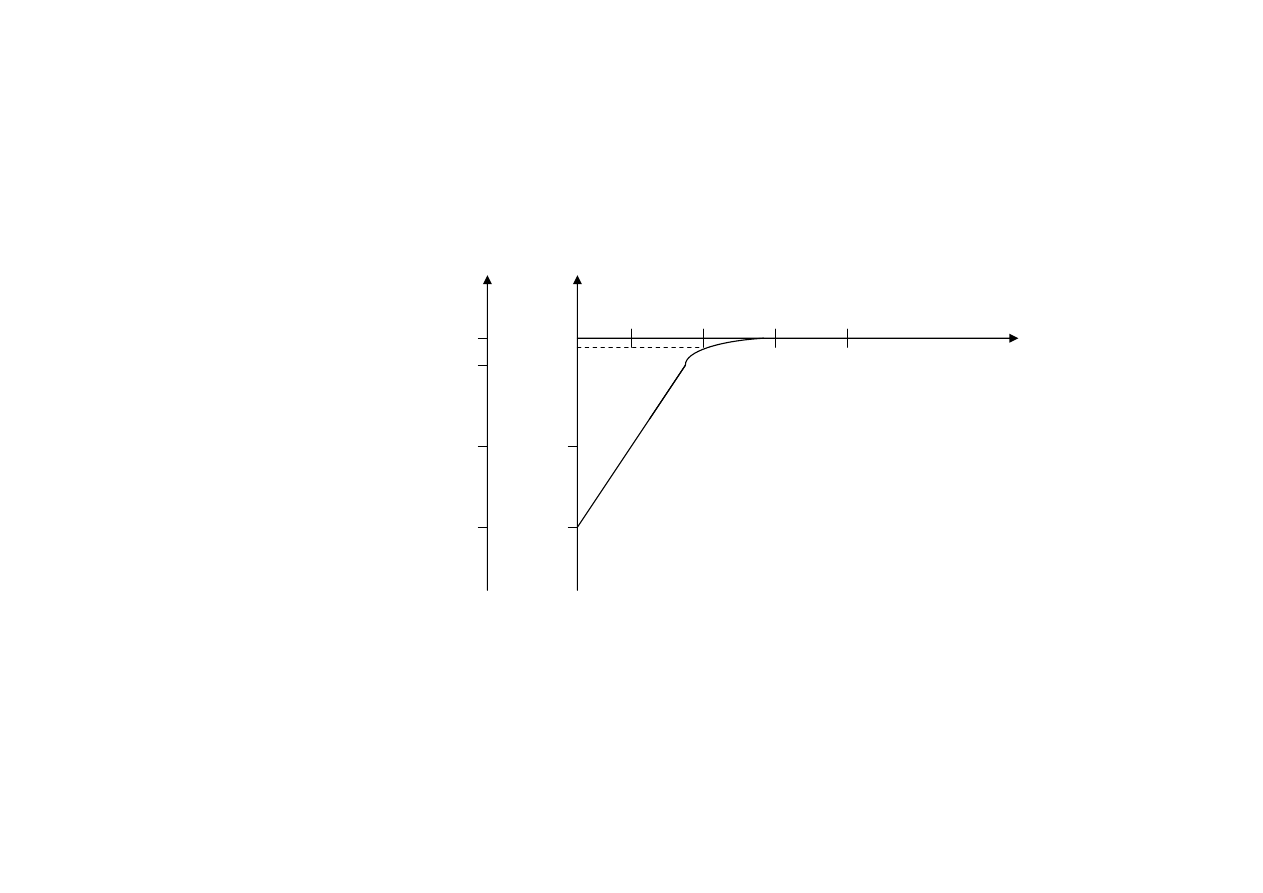
Charakterystyka amplitudowa

f

|k

u

|

|k

u

|

log

1

-20

-3

0

-40

0,01

0,1

0,707

0,1f

d

f

d

100f

d

10f

d

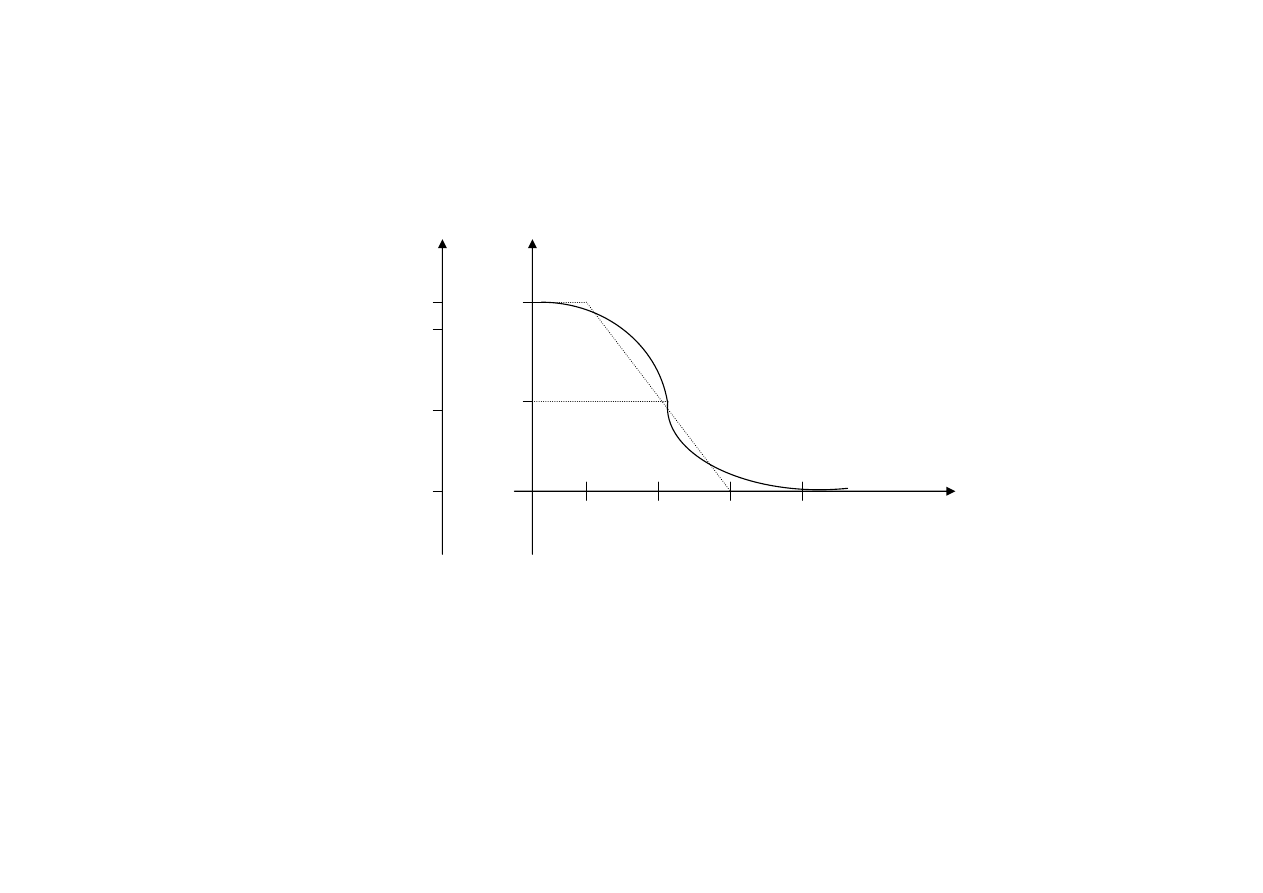
Charakterystyka fazowa

f

φ

arg(k

u

)= φ

0

-

π

/

4

-3

0

-90

o

-45

o

0,1f

d

f

d

100f

d

10f

d

-

π

/

2

Filtr górnoprzepustowy RC wprowadza przesunięcie
fazowe +45

o

.

Filtr środkowoprzepustowy

Zadanie tego filtru polega na:

•

przenoszeniu, bez tłumienia, składowych widma
sygnału wejściowego leżących w paśmie
przenoszenia

•

tłumieniu składowych widma sygnału
wejściowego leżących poza tym pasmem

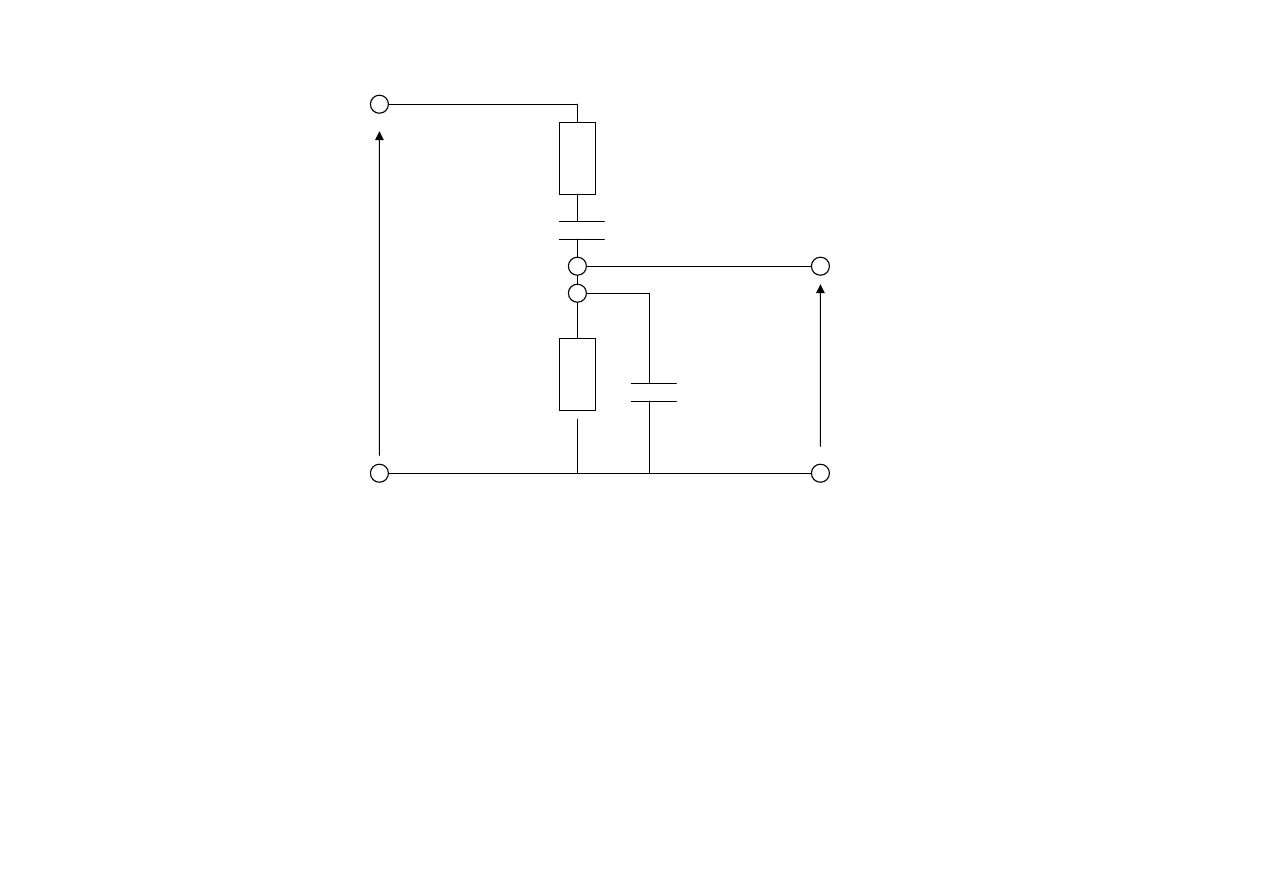
U

we

U

wy

R

R

C

C

Filtr środkowoprzepustowy nie wprowadza przesunięcia
fazowego.

Filtr środkowozaporowy

Zadanie tego filtru polega na:

•

tłumieniu składowych widma sygnału
wejściowego leżących w paśmie zaporowym

•

przenoszenie składowych części widma leżących
poza tym pasmem

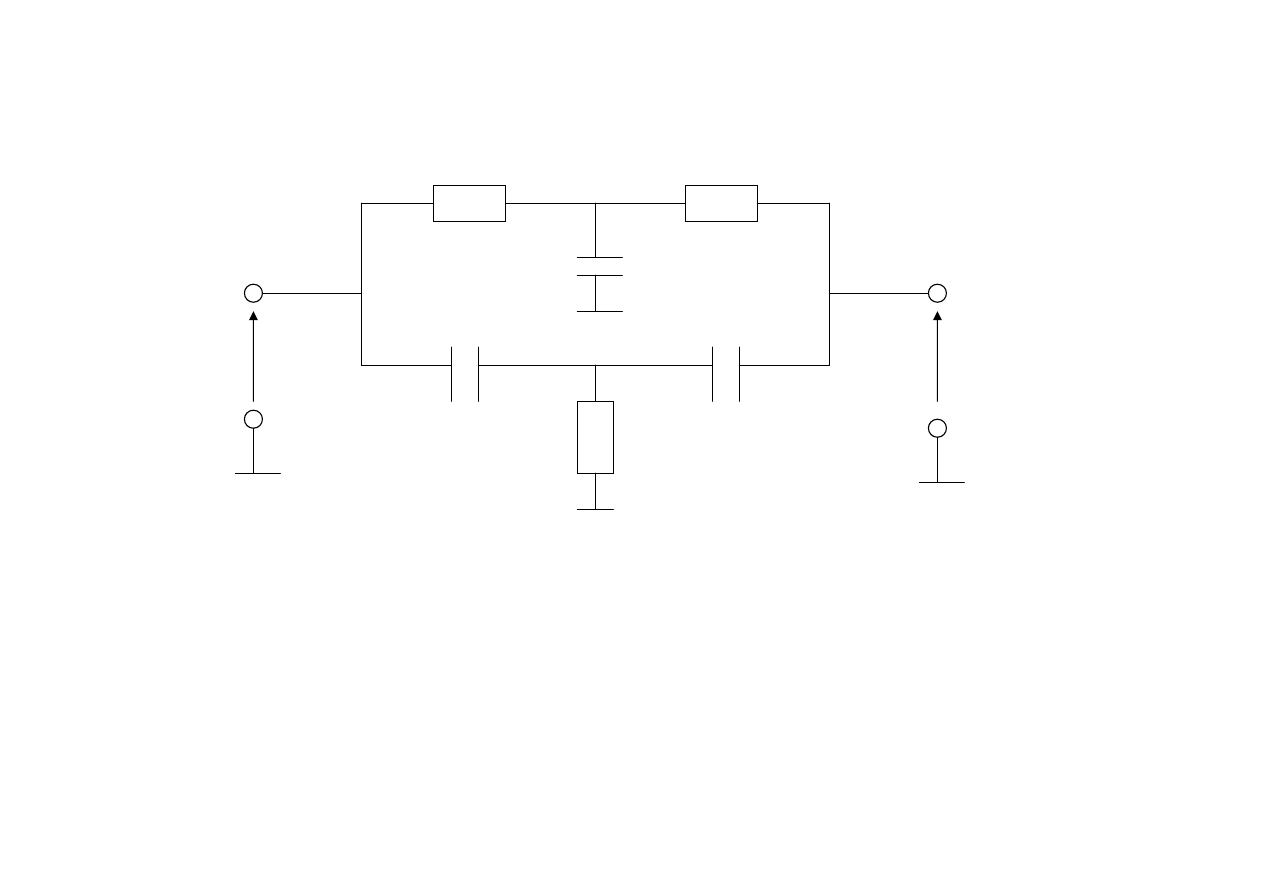
R

R

R/2

C

C

2C

U

we

U

wy