Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 1

PROJEKTOWANIE POŁĄCZEŃ ŚRUBOWYCH

wg PN-EN 1993 1-8

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 2

Częściowe współczynniki nośności dotyczące węzłów:

• PN-EN 1993-1-8
• EUROKOD 3: Projektowanie konstrukcji stalowych
• Częśd 1-8: Projektowanie węzłów

Norma

• projektowanie węzłów konstrukcji ze stali

S235, S275, S355

i

S460

• sprawdzenie nośności węzłów w warunkach

przeważająco statycznych

Zakres normy

• przekroju poprzeczenego

g

M0

= 1,0

• elementów przy ocenie ich stateczności

g

M1

= 1,0

• na rozerwanie przekrojów z otworami

g

M2

= 1,25

PN-EN 1993 1-1 - współczynniki nośności:

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 3

• śrub, nitów, sworzni, spoin, blach na docisk

g

M2

= 1,25

• śrub na poślizg w stanie granicznym nośności

g

M3

= 1,25

• śrub na poślizg w stanie granicznym użytkowania

g

M3,ser

= 1,1

• na docisk śrub z iniekcją

g

M4

= 1,0

• węzłów kratownic z kształtowników rurowych

g

M5

= 1,0

• sworzni w stanie granicznym użytkowania

g

M6,ser

= 1,0

• przy sprężaniu śrub o wysokiej wytrzymałości

g

M7

= 1,1

PN-EN 1993 1-8 - współczynniki nośności:

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 4

Nośnośd obliczeniowa śrub:

Klasy śrub wraz z parametrami wytrzymałościowymi (EC3-1-8-Tab.3.1):

Klasa śruby

4.6

4.8

5.6

5.8

6.8

8.8 10.9

f

yb

(N/mm

2

)

240 320 300 400 480 640 900

f

ub

(N/mm

2

)

400 400 500 500 600 800 1000

• A - pole przekroju trzpienia śruby przy rozciąganiu
• A

s

- pole przekroju czynnego rdzenia śruby przy rozciąganiu

• d - średnica trzpienia śruby
• d

0

- średnica otworu przejściowego na śrubę

• f

u

- wytrzymałośd na rozciąganie stali łączonego elementu

• f

ub

- wytrzymałośd na rozciąganie stali śruby

• f

y

- granica plastyczności stali łączonego elementu

• f

yb

- granica plastyczności stali śruby

• t - grubośd ścianki łączonego elementu

Oznaczenia:

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 5

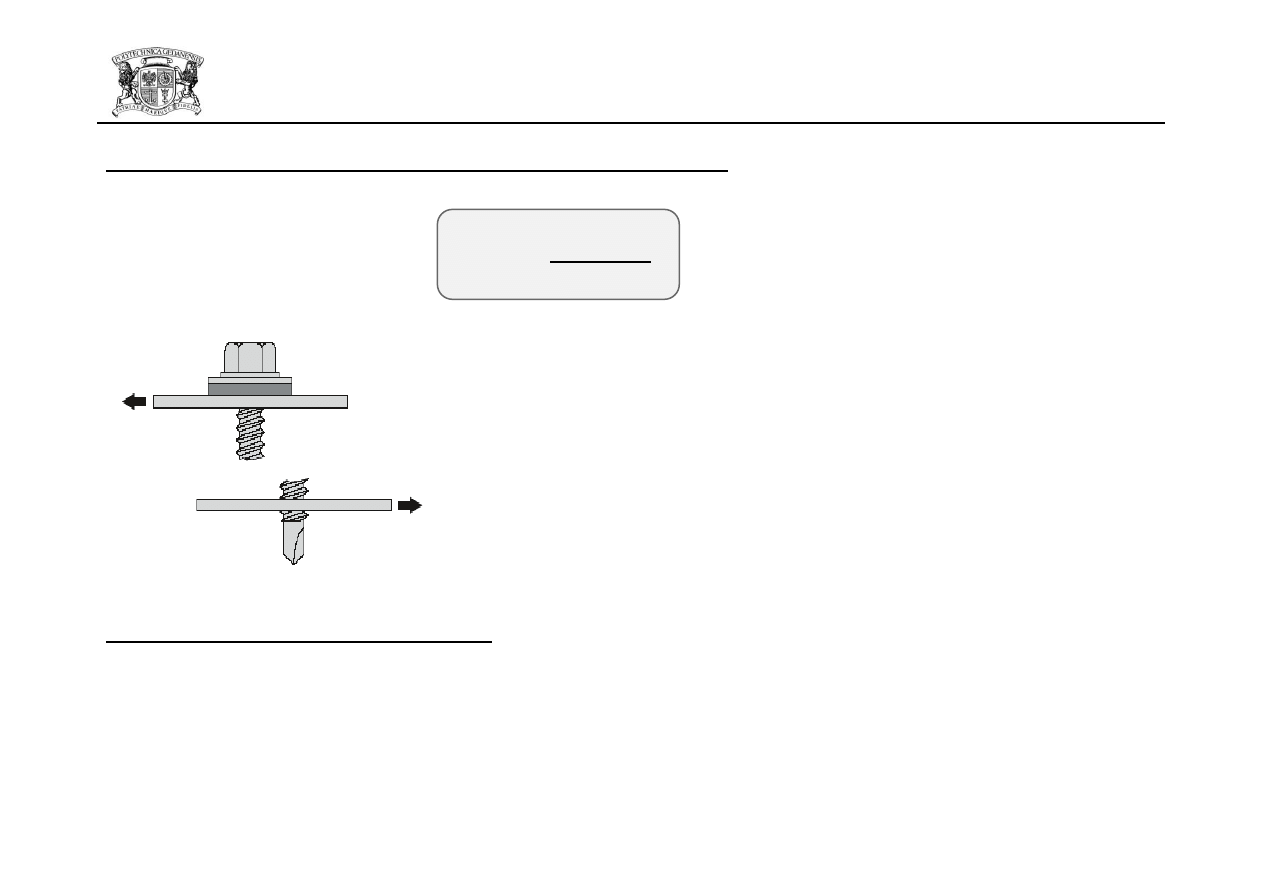
Obliczeniowa nośnośd śruby na rozciąganie:

𝐹

𝑡,𝑅𝑑

=

𝑘

2

𝑓

𝑢𝑏

𝐴

𝑠

𝛾

𝑀 2

(EC3-1-8-Tab.3.4)

gdzie:
k

2

= 0,9 – śruby z łbem sześciokątnym,

k

2

= 0,63 – śruby z łbem wpuszczanym.

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 6

Obliczeniowa nośnośd śruby na ścinanie w jednej płaszczyźnie:

𝐹

𝑣,𝑅𝑑

=

∝

𝑣

𝑓

𝑢𝑏

𝐴

𝑖

𝛾

𝑀2

(EC3-1-8-Tab.3.4)

Gdzie:



jeżeli płaszczyzna ścinania przechodzi przez gwintowaną częśd
śruby, A

i

jest polem przekroju czynnego śruby A

s

oraz:



v

= 0,6 – w przypadku klas 4.6, 5.6, 8.8.



v

= 0,5 – w przypadku klas 4.8, 5.8, 6.8, 10.9.



jeżeli płaszczyzna ścinania nie przechodzi przez gwintowaną częśd
śruby, A

i

jest polem przekroju trzpienia śruby oraz



v

= 0,6.

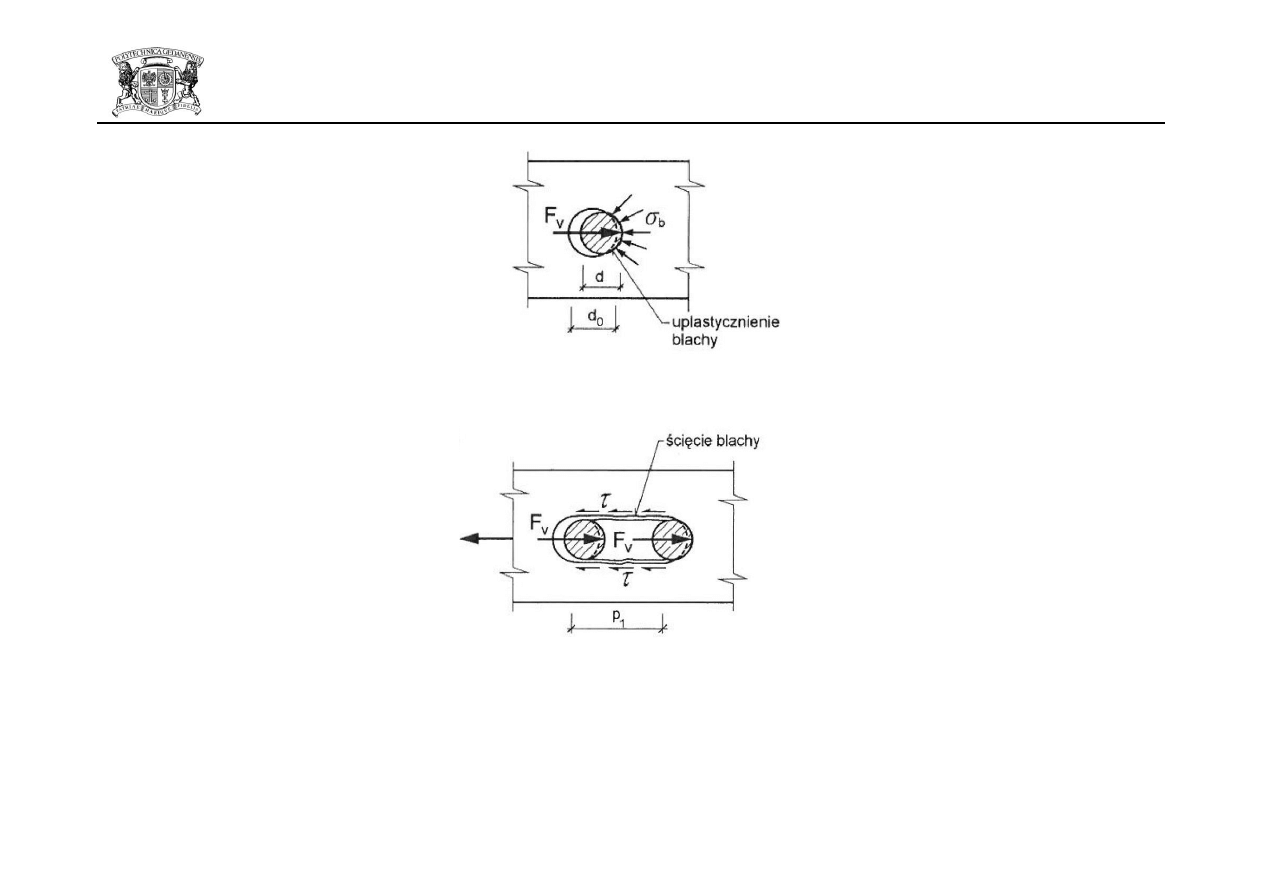
Obliczeniowa nośnośd śruby na docisk:

Obliczeniowa nośnośd śruby na docisk uwzględnia:
- wyczerpanie wytrzymałości z warunku na docisku trzpienia śruby do otworu (uplastycznienie blachy),

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 7

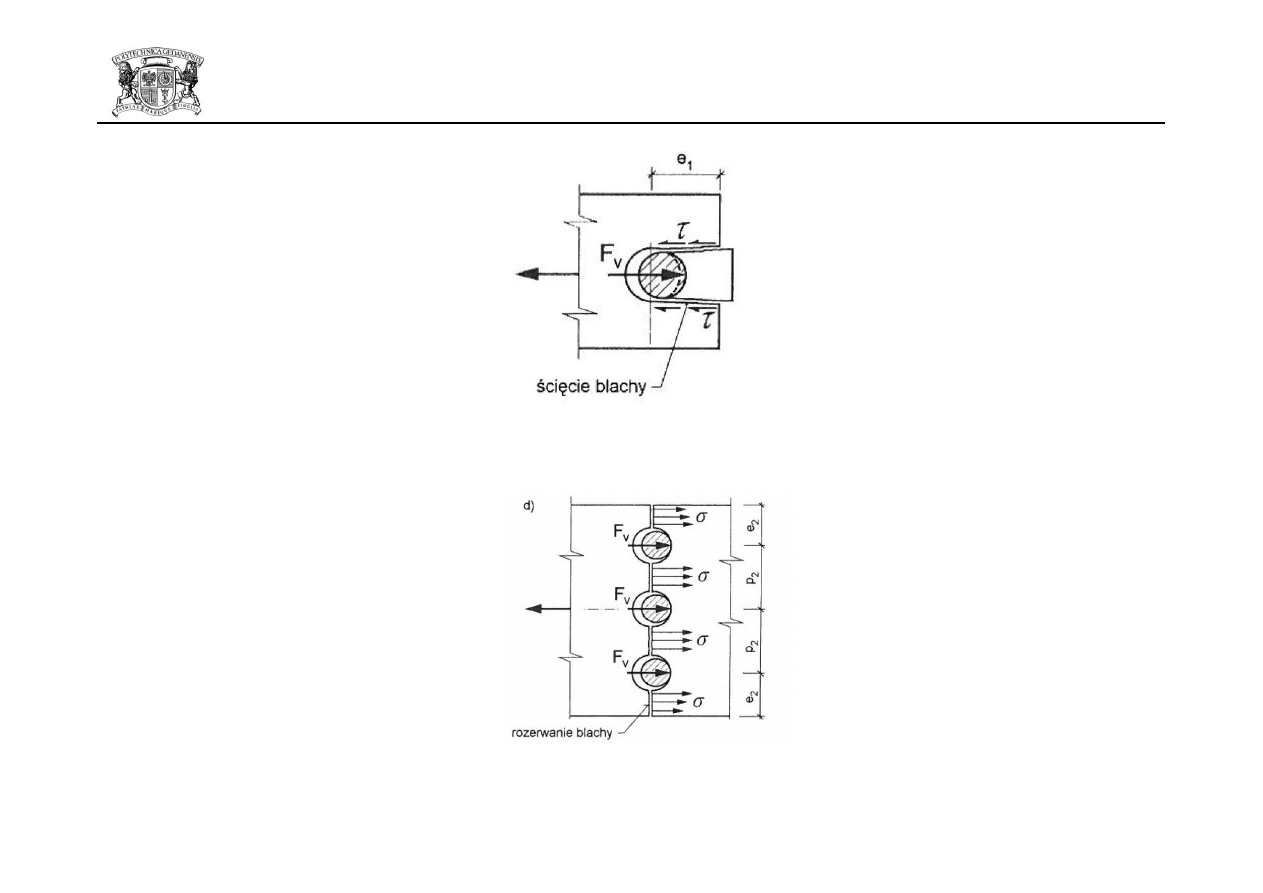
- możliwośd ścięcia blach między otworami na kierunku obciążenia,

- możliwośd ścięcia blach między otworem i brzegiem blachy na kierunku obciążenia,

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 8

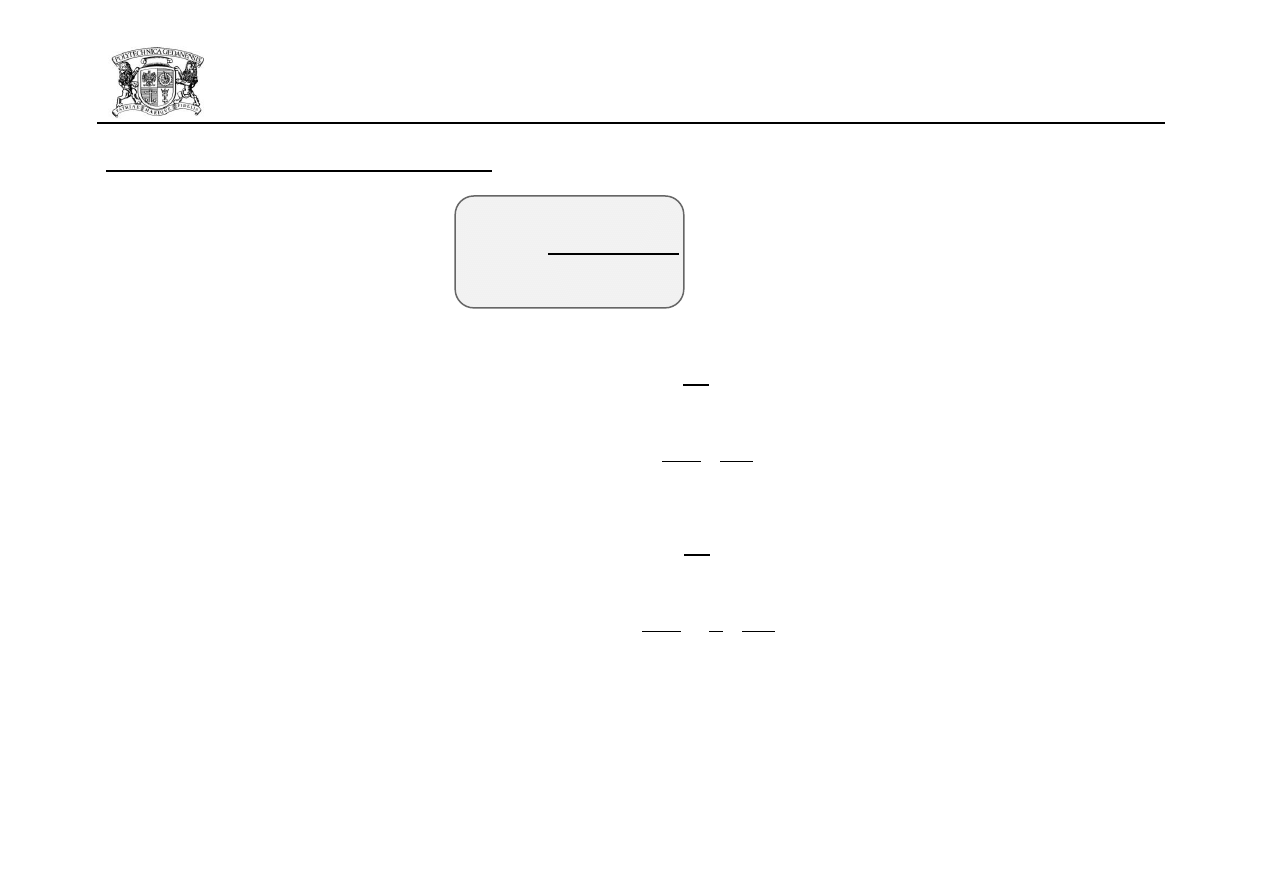
- możliwośd rozerwania blachy w kierunku prostopadłym do osi wytężenia.

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 9

Obliczeniowa nośnośd śruby na docisk:

𝐹

𝑏,𝑅𝑑,𝑖

=

𝑘

1,𝑖

∝

𝑏,𝑖

𝑓

𝑢

𝑑𝑡

𝛾

𝑀2

(EC3-1-8-Tab.3.4)

- dla śrub skrajnych:

𝑘

1,𝑠

= min 2,8

𝑒

2

𝑑

𝑜

− 1,7 ; 2,5

∝

𝑏,𝑠

= min

𝑒

1

3𝑑

𝑜

;

𝑓

𝑢𝑏

𝑓

𝑢

; 1.0

- dla śrub pośrednich:

𝑘

1,𝑝

= min 1,4

𝑝

2

𝑑

𝑜

− 1,7 ; 2,5

∝

𝑏,𝑝

= min

𝑝

1

3𝑑

𝑜

−

1
4

;

𝑓

𝑢𝑏

𝑓

𝑢

; 1.0

d

o

– średnica otworu na śrubę,

e

1

, e

2

, p

1

, p

2

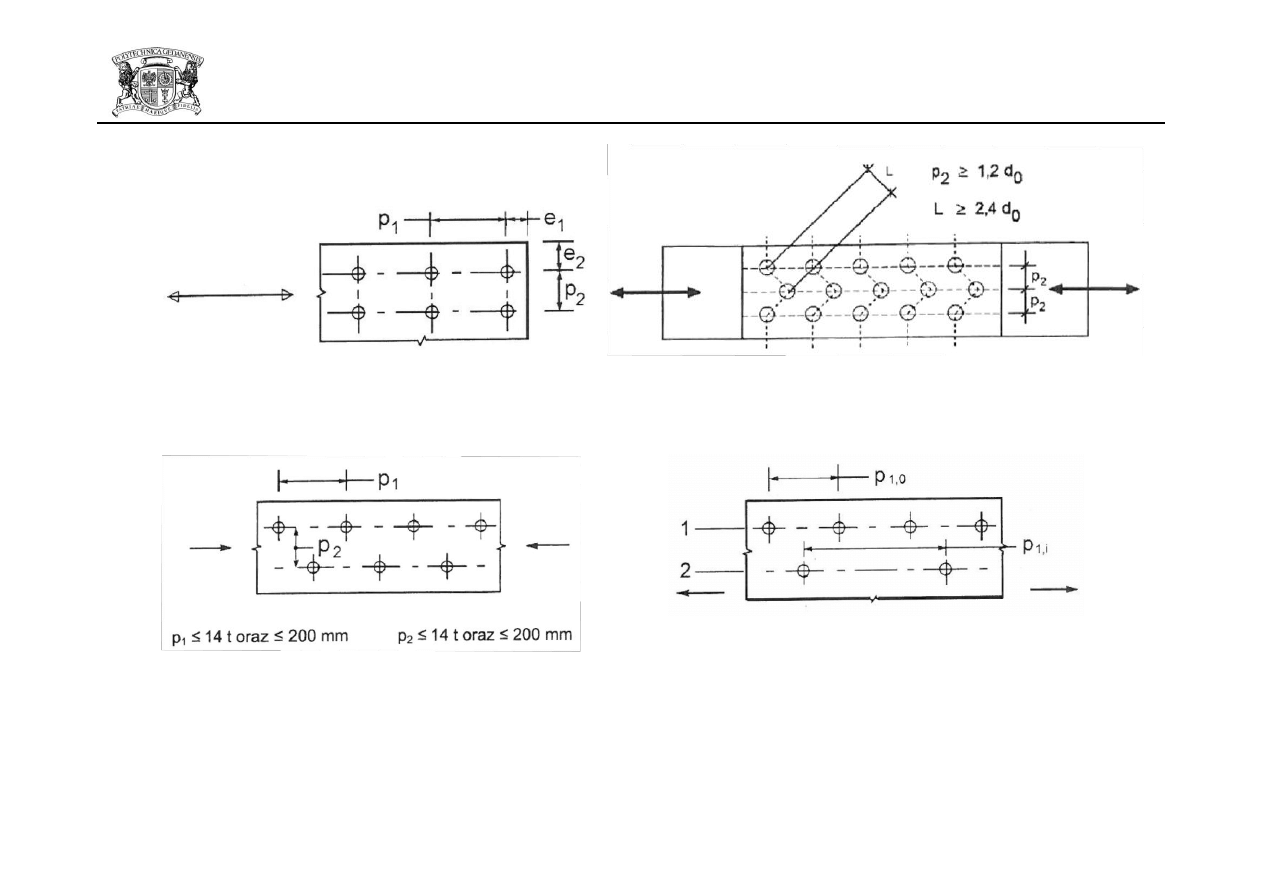
– wielkości określające rozmieszczenie śrub w połączeniu. Należy je określad z

uwzględnieniem kierunku działającej siły na podstawie EC3-1.8-Rys.3.1.

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 10

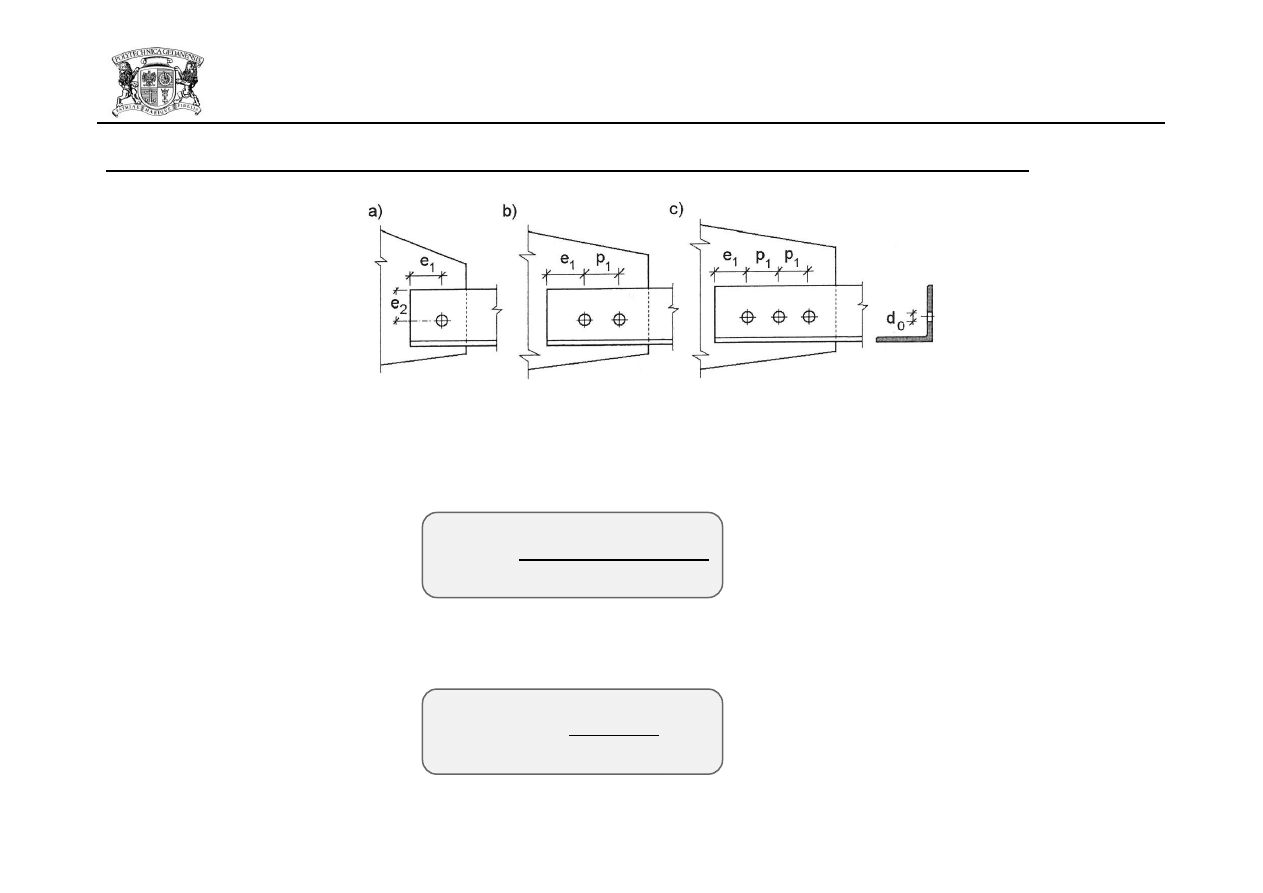
a) symbole rozstawów i długości brzegowych

b) symbole rozstawów w układzie przestawionym

c) rozstawy w układzie przestawionym w

elementach ściskanych

d) rozstawy w układzie przestawionym w elementach

rozciąganych

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 11

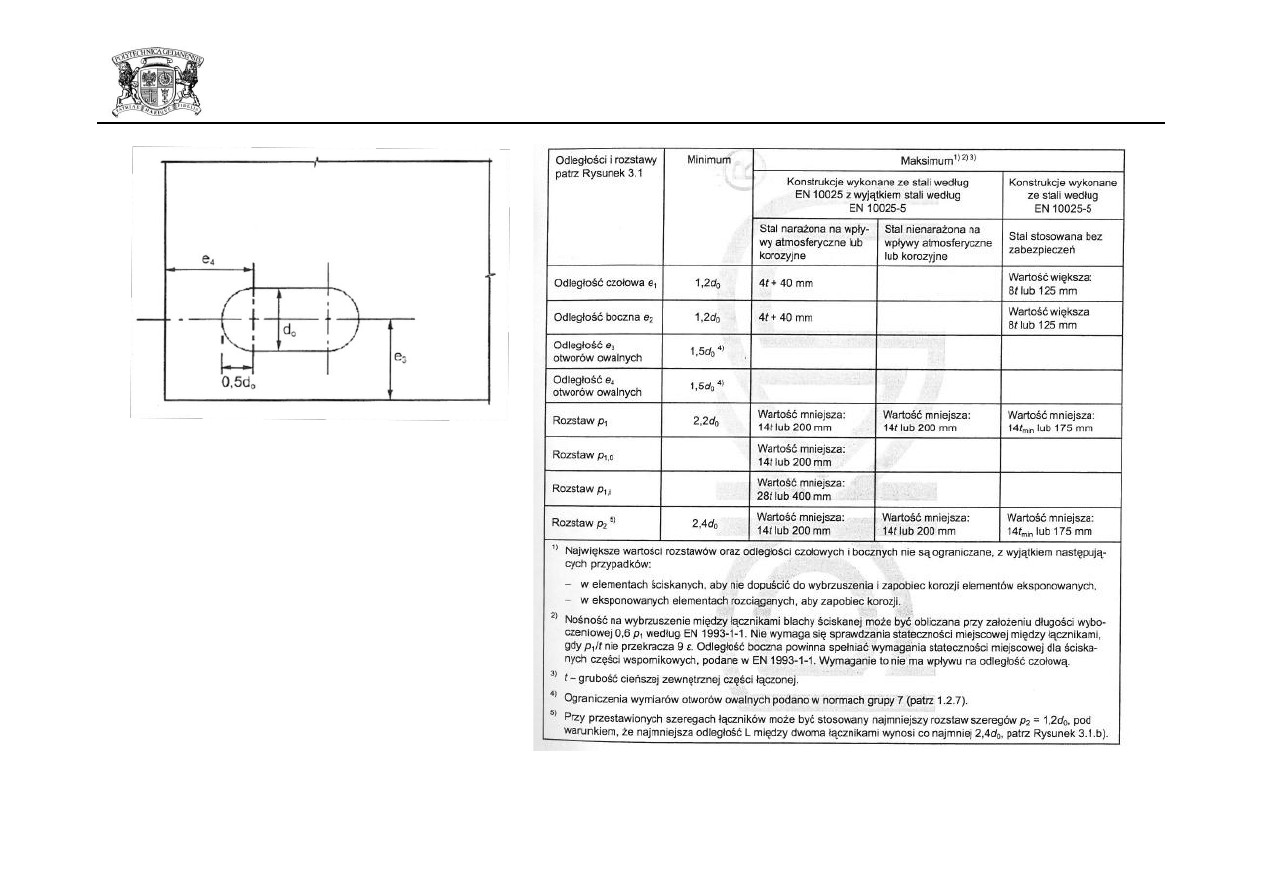
e) odległości czołowe i boczne w przypadku

otworów owalnych

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 12

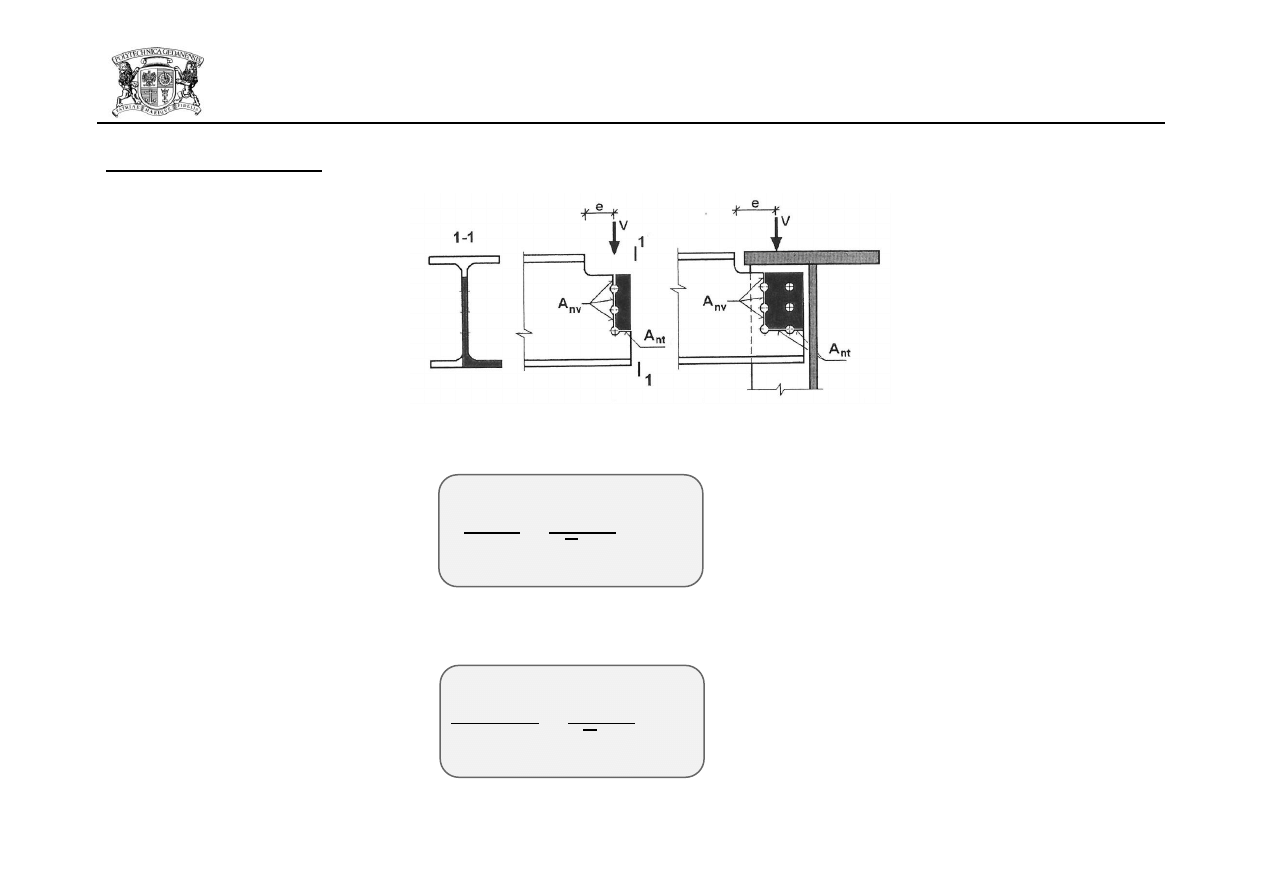
Rozerwanie blokowe:

- w przypadku symetrycznej grupy śrub obciążonej osiowo:

𝑓

𝑢

𝐴

𝑛𝑡

𝛾

𝑀2

+

𝑓

𝑦

𝐴

𝑛𝑣

3𝛾

𝑀0

≤ 1,0

(EC3-1-8-3.9)

- w przypadku grupy śrub obciążonej mimośrodowo:

0,5𝑓

𝑢

𝐴

𝑛𝑡

𝛾

𝑀2

+

𝑓

𝑦

𝐴

𝑛𝑣

3𝛾

𝑀0

≤ 1,0

(EC3-1-8-3.10)

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 13

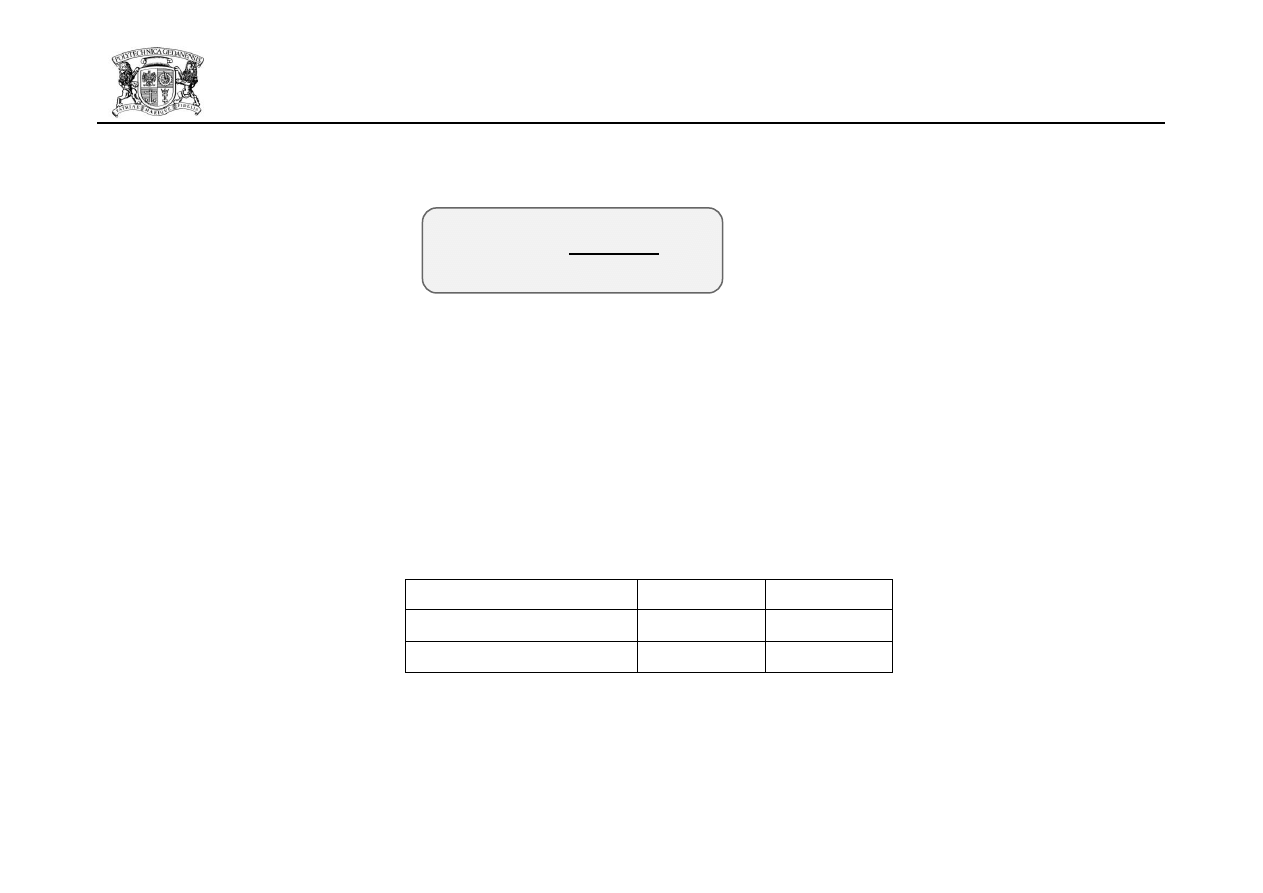
Kątowniki połączone jednym ramieniem i inne niesymetrycznie łączone elementy rozciągane

Nośnośd obliczeniowa elementu:

- przy jednej śrubie:

𝑁

𝑢,𝑅𝑑

=

2,0 𝑒

2

− 0,5𝑑

0

𝑡𝑓

𝑢

𝛾

𝑀2

(EC3-1-8-3.11)

- przy dwóch śrubach:

𝑁

𝑢,𝑅𝑑

=

𝛽

2

𝐴

𝑛𝑒𝑡

𝑓

𝑢

𝛾

𝑀2

(EC3-1-8-3.12)

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 14

- przy trzech lub większej ilości śrub:

𝑁

𝑢,𝑅𝑑

=

𝛽

3

𝐴

𝑛𝑒𝑡

𝑓

𝑢

𝛾

𝑀2

(EC3-1-8-3.13)

Gdzie:

A

net

– pole przekroju netto kątownika; dla kątowników nierównoramiennych łączonych węższym ramieniem,

A

net

- przyjmuje się równe polu przekroju netto zastępczego kątownika o szerokości obu ramion równej

szerokości ramienia węższego.



1

,



2

– współczynniki redukcyjne zależne od rozstawu p

1

, dla pośrednich wartości p

1

wartośd



i

można

interpolowad (i=1,2);

Rozstaw p

1

≤2,5d

o

≥5,0d

o

2 śruby



2

0,4

0,7

3 śruby lub więcej



3

0,5

0,7

EC3-1.8-Tab.3.8

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 15

Nośnośd grupy łączników

„Obliczeniową nośnośd grupy łączników można przyjmowad jako sumę nośności obliczeniowych pojedynczych
łączników na docisk F

b,Rd

pod warunkiem, że nośnośd obliczeniowa na ścinanie każdego łącznika F

V,Rd

jest nie

mniejsza od jego nośności obliczeniowej na docisk F

V,Rd

. Gdy ten warunek nie jest spełniony, obliczeniową

nośnośd grupy łączników oblicza się jako iloczyn liczby łączników i najmniejszej nośności obliczeniowej łącznika
w grupie.”

PN-EN 1993 1-8 pkt. 3.7

- dla F

v,Rdi

> F

b,Rdi

nośnośd grupy łączników:

𝐹

𝑣,𝑅𝑑

= 𝐹

𝑏,𝑅𝑑𝑖

𝑛

𝑏

𝑖

- w przeciwnym wypadku:

𝐹

𝑣,𝑅𝑑

= 𝑛

𝑏

𝐹

𝑅𝑑 ,𝑚𝑖𝑛𝑖

F

Rd,mini

= min (F

v,Rdi

, F

b,Rdi

)

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 16

Złącza długie

Jeśli odległośd osiowa L

j

między skrajnymi łącznikami mierzona w kierunku obciążenia, jest większa niż 15d, to

obliczeniową nośnośd na ścinanie wszystkich łączników F

V,Rd

redukuje się współczynnikiem



Lf

, określonym

wzorem:

𝛽

𝐿𝑓

= 1 −

𝐿

𝑗

− 15𝑑

200𝑑

𝑙𝑒𝑐𝑧 𝛽

𝐿𝑓

≤ 1,0 𝑜𝑟𝑎𝑧 𝛽

𝐿𝑓

≥ 0,75

Postanowienie to ,nie odnosi się do przypadków, w których siła rozkłada się równomiernie na całej długości
złącza, jak np. w przypadku siły ścinającej między środnikiem a pasem kształtownika.

Politechnika Gdaoska
Wydział Inżynierii Lądowej i Środowiska
Katedra Konstrukcji Metalowych i Zarządzania w Budownictwie

POŁĄCZENIA ŚRUBOWE

Strona

| 17

LITERATURA:

[1] A.Biegus. Obliczanie nośności śrub według PN-EN 1993-1-8. Inżynieria i Budownictwo nr 3/2008 str.113-

118.

*2+ A.Kozłowski, Z.Pisarek, S.Wierzbicki. Projektowanie zakładkowych połączeo śrubowych według PN-EN 1993-

1-1 i PN-EN 1993-1-8. Inżynieria i Budownictwo nr 9/2008 str. 496-500.

[3] J.Augustyn, J.Bródka, J.Łaguna. Obliczanie nośności śrub i połączeo zakładkowych według PN-90/B-03200.

Inżynieria i Budownictwo nr 6/91 str. 227-230.

*4+ J.Bródka, M.Broniewicz. Projektowanie konstrukcji stalowych zgodnie z eurokodem 3-1-1 wraz z

przykładami obliczeo. Wydawnictwo Politechniki Białostockiej. Białystok 2001.