
Mechanika ogólna
Mechanika ogólna
1
1
Wykład nr 9
Wykład nr 9
Kratownice
Kratownice –
– metoda Rittera.
metoda Rittera.
Przykład A
Przykład A –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
(z lewej)
(z lewej)
2 1
:
sin
0
l
A
Y
V
N
1
2 3
:
3
10
3
3
0
l
A
M
V
m
kN
m
N
m
:
3
3
0
l
M
H
m
N
m
2
2
3m
3
m
10kN
3,5m
20kN
R
B
V
A
H
A
a
b
A
B
1
2
3
4
N
A-1
N
1-A
N
2-1
N
1-2
N
2-3
N
3-2
2 1
6,154
8, 704
0, 707
kN
N
kN
2 3
6,154
10
16,154
N
kN
kN
kN
2
1
:
3
3
0
l
A
A
M
H
m
N
m
1
10
A
N
kN
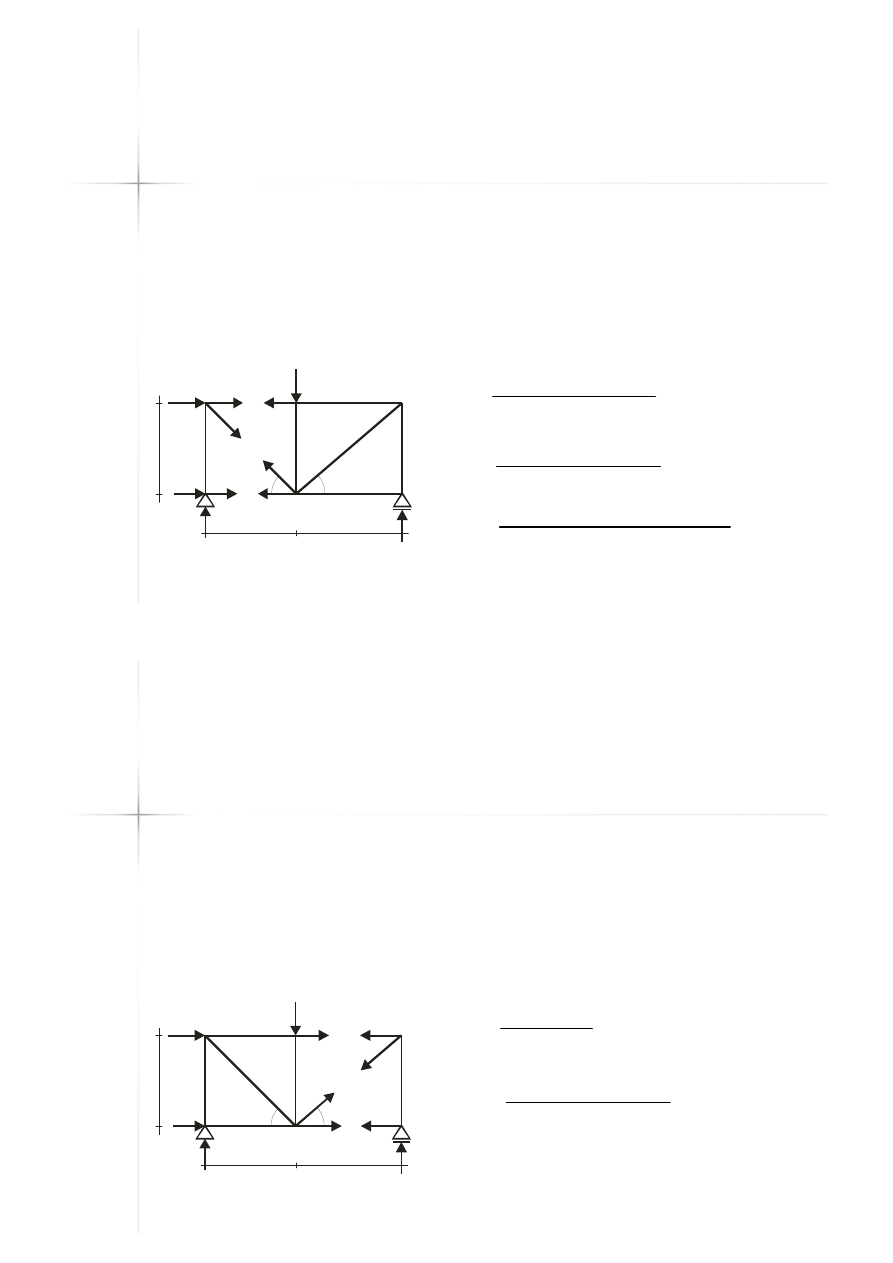
Przykład A
Przykład A –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
(z prawej)
(z prawej)
1 2
:
sin
20
0
p
B
Y
R
N
kN
1
3 2
:
3, 5
3
0
p
B
M
R
m
N
m
:
6, 5
3
20
3
0
p
M
R
m
N
m
kN
m
3
3
3m
3
m
10kN
3,5m
20kN
R
B
V
A
H
A
a
b
A
B
1
2
3
4
N
A-1
N
1-A
N
2-1
N
1-2
N
2-3
N
3-2
1 2
20
13,846
8, 704
0, 707
kN
kN
N
kN
3 2
13,846
3, 5
16,154
3
kN
m
N
kN
m
2
1
:
6, 5
3
20
3
0
p
B
A
M
R
m
N
m
kN
m
1
13,846 6,5
20
3
10
3
A
m
kN
m
N
kN
m
Przykład A
Przykład A –
– metoda
metoda
Rittera
Rittera –
– przekrój 2
przekrój 2
4 1
:
sin
0
p
B
Y
R
N
1
4 3
:
3, 5
3
0
p
B
M
R
m
N
m
:
3
0
p
M
N
m
4
4
3m
3
m
10kN
3,5m
20kN
R
B
V
A
H
A
a
b
A
B
1
2
3
4
N
3-4
N
4-3
N
4-1
N
1-4
N
1-B
N
B-1
4 1
13,846
21, 269
0, 651
kN
N
kN
4 3
13,846
3, 5
16,154
3
kN
m
N
kN
m
4
1
:
3
0
p
B
M
N
m
1
0
B
N
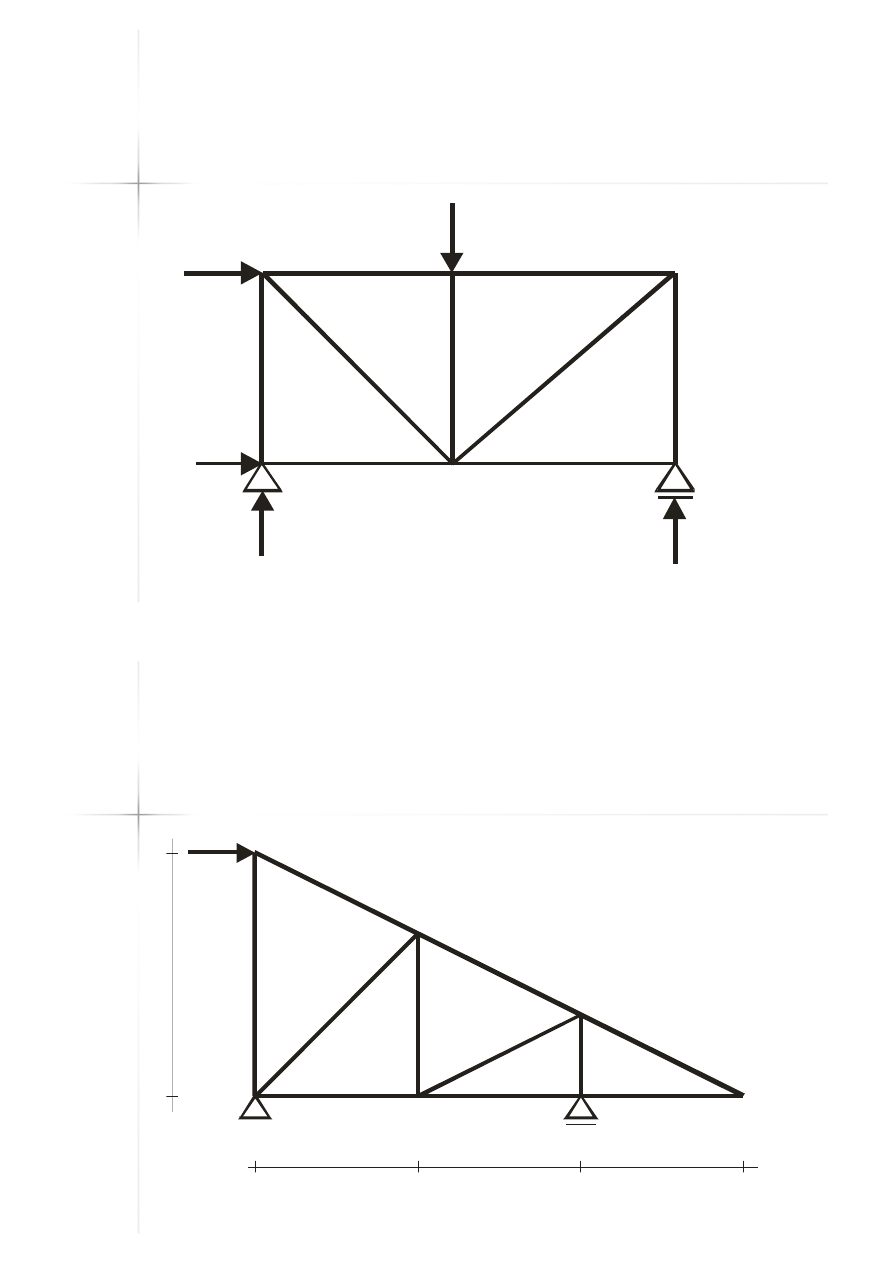
Przykład A
Przykład A –
– Wyniki:
Wyniki:
zestawienie sił
zestawienie sił
10kN
20kN
kN
-16,154kN
8
-16,154kN
5
5
13,846kN
6,154kN
-10kN
0
21
,2
69
kN
-1
3
,8
4
6
k
N
-2
0
k
N
-6
,1
5
4
k
N
8,7
04
kN
10kN
Przykład B
Przykład B –
– kratownica
kratownica
trójkątna
trójkątna
20kN
6
6
3m
4
,5
m
3m
3m
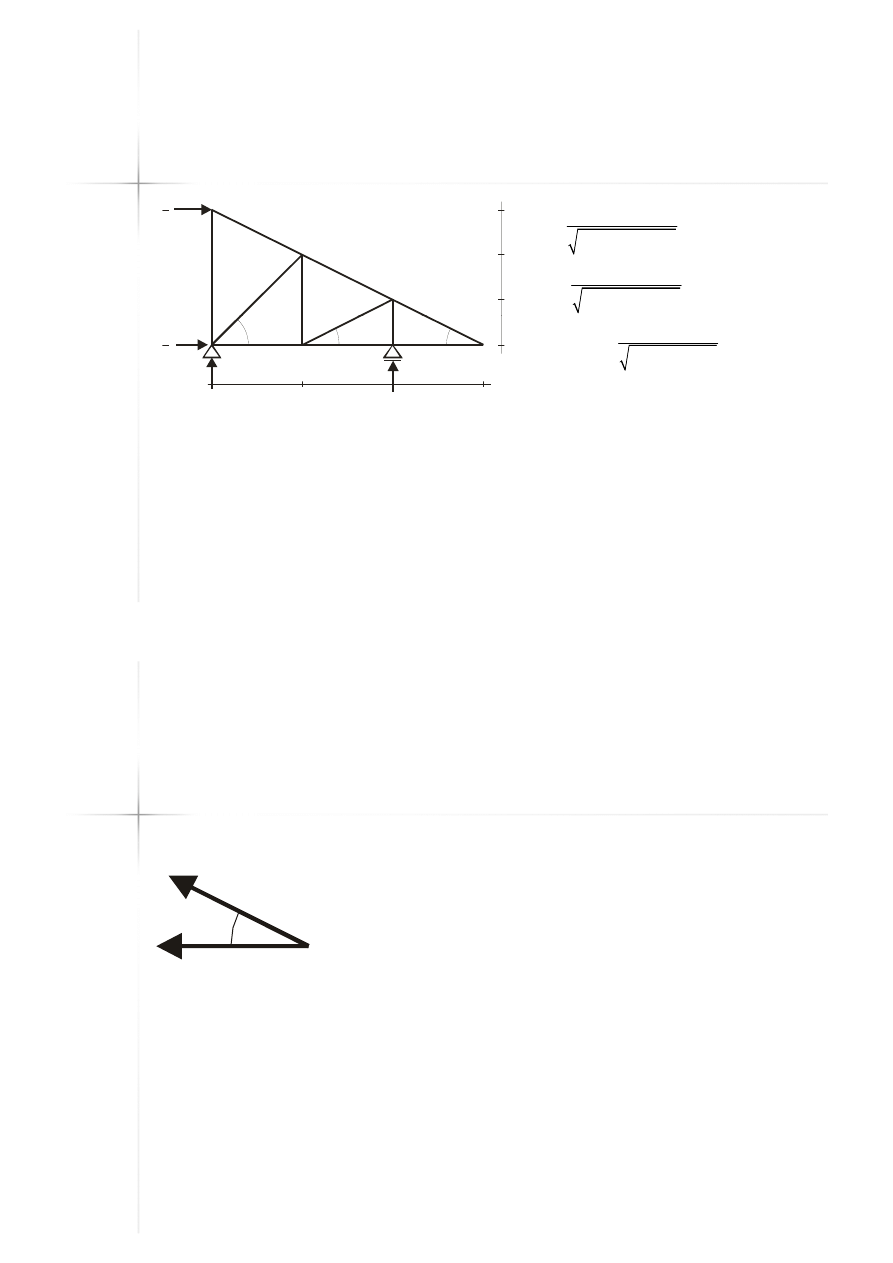
Przykład B
Przykład B –
– reakcje
reakcje
4
,5
m
20kN
1
,5
m
1
,5
m
m
3
4
5
2
2
1, 5
sin
0, 447
1, 5
3
m
m
m
2
2
3
cos
0,894
1, 5
3
m
m
m
7
7
R
B
V
A
H
A
3m
3m
3m
a
a
b
1
,5
m
A
B
1
2
:
20
0
A
X H
kN
:
0
A
B
Y V
R
:
6
20
4, 5
0
A
B
M
R
m
kN
m
2
2
3
sin
cos
0, 707
3
3
m
m
m
20
A
H
kN
15
A
V
kN
15
B
R
kN
Węzeł 2
Węzeł 2
2
N
2-3
2 3
:
sin
0
Y N
2 3
0
N
8
8
N
2-B
2
2 3
:
cos
0
B
X N
N
2
0
B
N
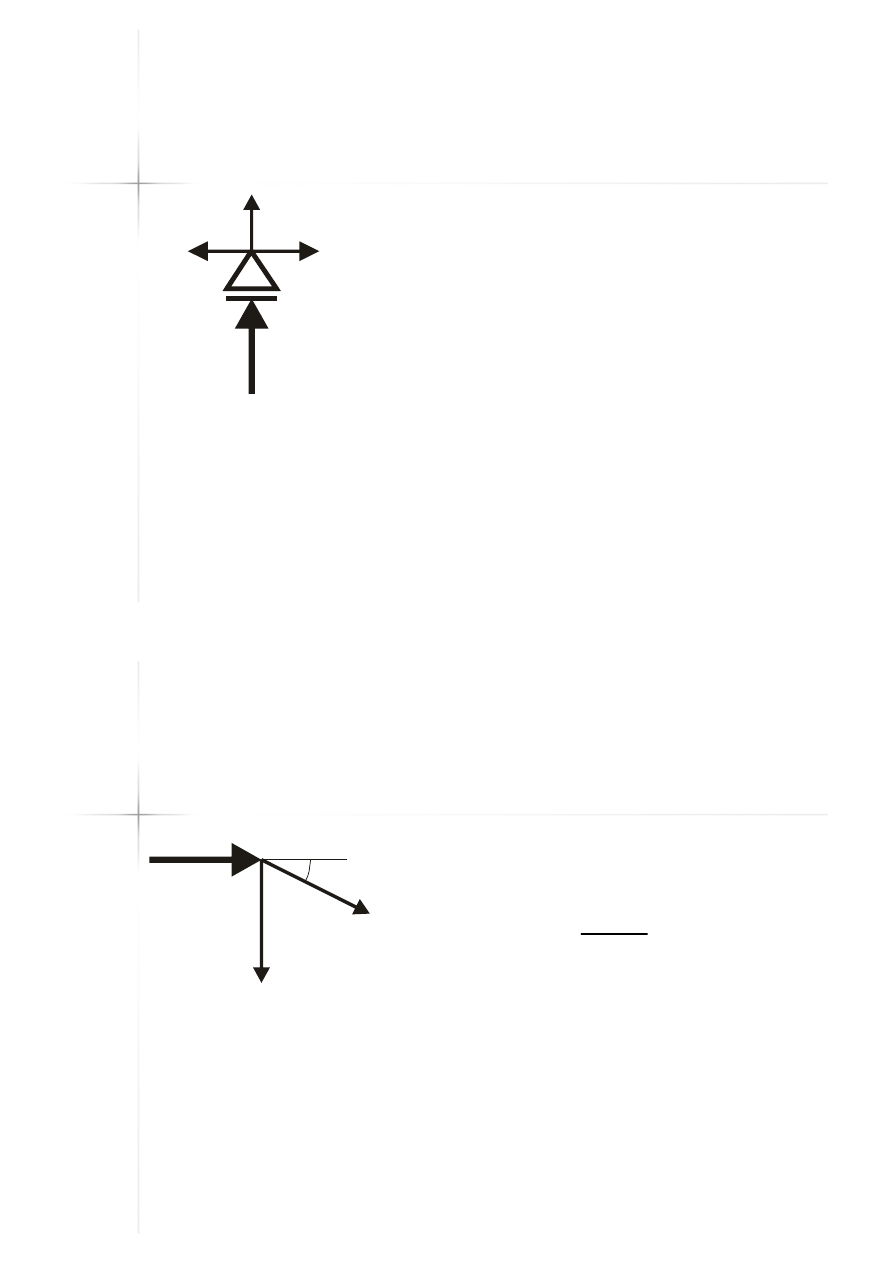
Węzeł B
Węzeł B
R
B
N
B-1
N
B-3
N
B-2
2
1
:
0
B
B
X N
N
1
0
B
N
9
9
R
B
3
:
0
B
B
Y R
N
3
15
B
N
kN
Węzeł 5
Węzeł 5
20kN 5
N
N
5-4
5 4
: 20
cos
0
X
kN
N
5 4
20
22, 371
0,894
kN
N
kN
10
10
N
5-A
5
5 4
:
sin
0
A
Y N
N
5 4
0,894
5
22, 371
0, 447
10
A
N
kN
kN
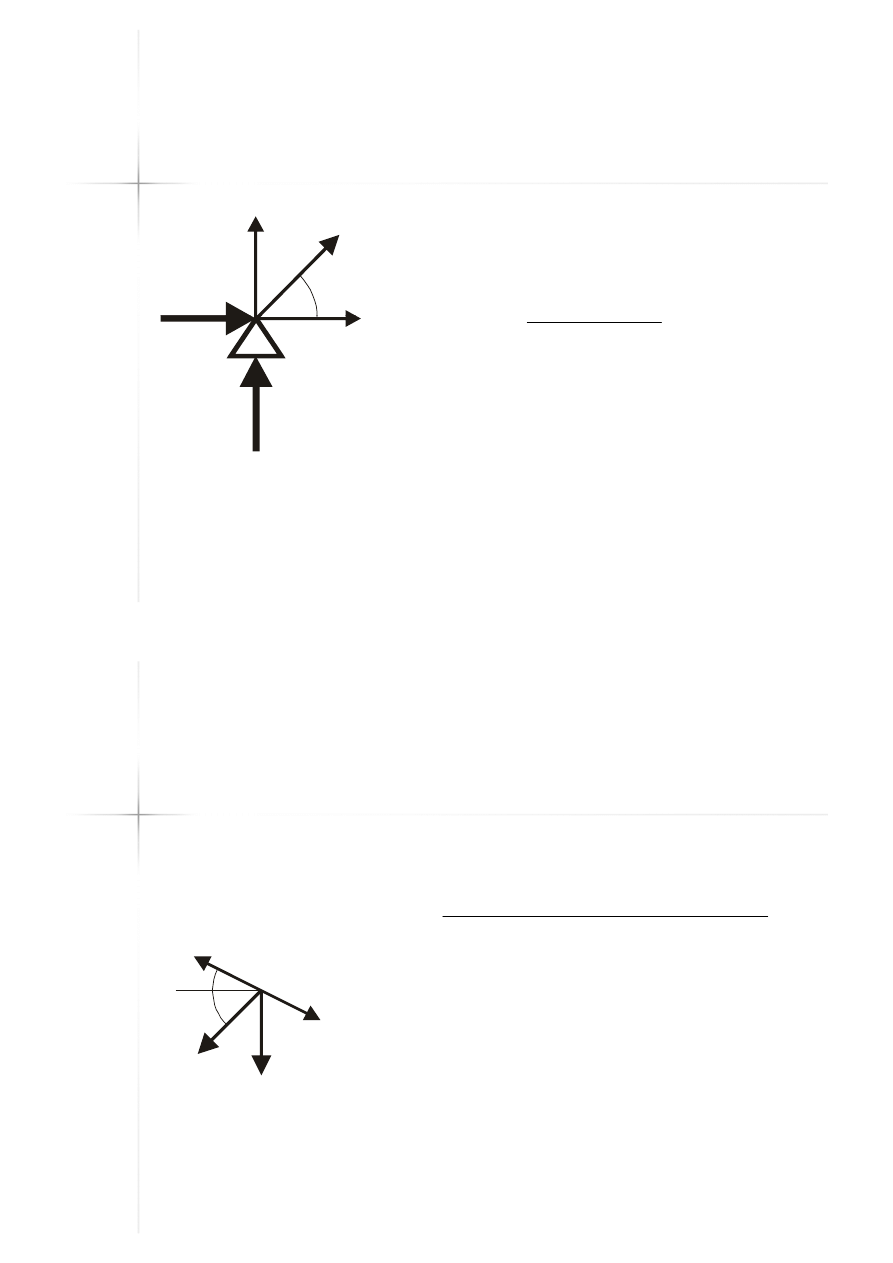
Węzeł A
Węzeł A
H
A
N
A-5
N
A-4
5
4
:
sin
0
A
A
A
Y N
N
V
10
15
7, 072
kN
kN
N
kN
11
11
V
A
N
A-1
1
4
:
cos
0
A
A
A
X N
N
H
1
20
7, 072
0, 707
15
A
N
kN
kN
kN
4
10
15
7, 072
0, 707
A
kN
kN
N
kN
Węzeł 4
Węzeł 4
N
4-5
4 3
4
4 5
:
cos
cos
cos
0
A
X N
N
N
4 3
7, 072
0, 707 22, 371
0,894
0,894
kN
kN
N
12
12
4
N
4-5
N
4-3
N
4-1
N
4-A
4 5
4
4 1
4 3
:
sin
sin
sin
0
A
Y N
N
N
N
16, 778kN
4 1
22, 371
0, 447 7, 072
0, 707 16, 778
0, 447
7, 5
N
kN
kN
kN
kN
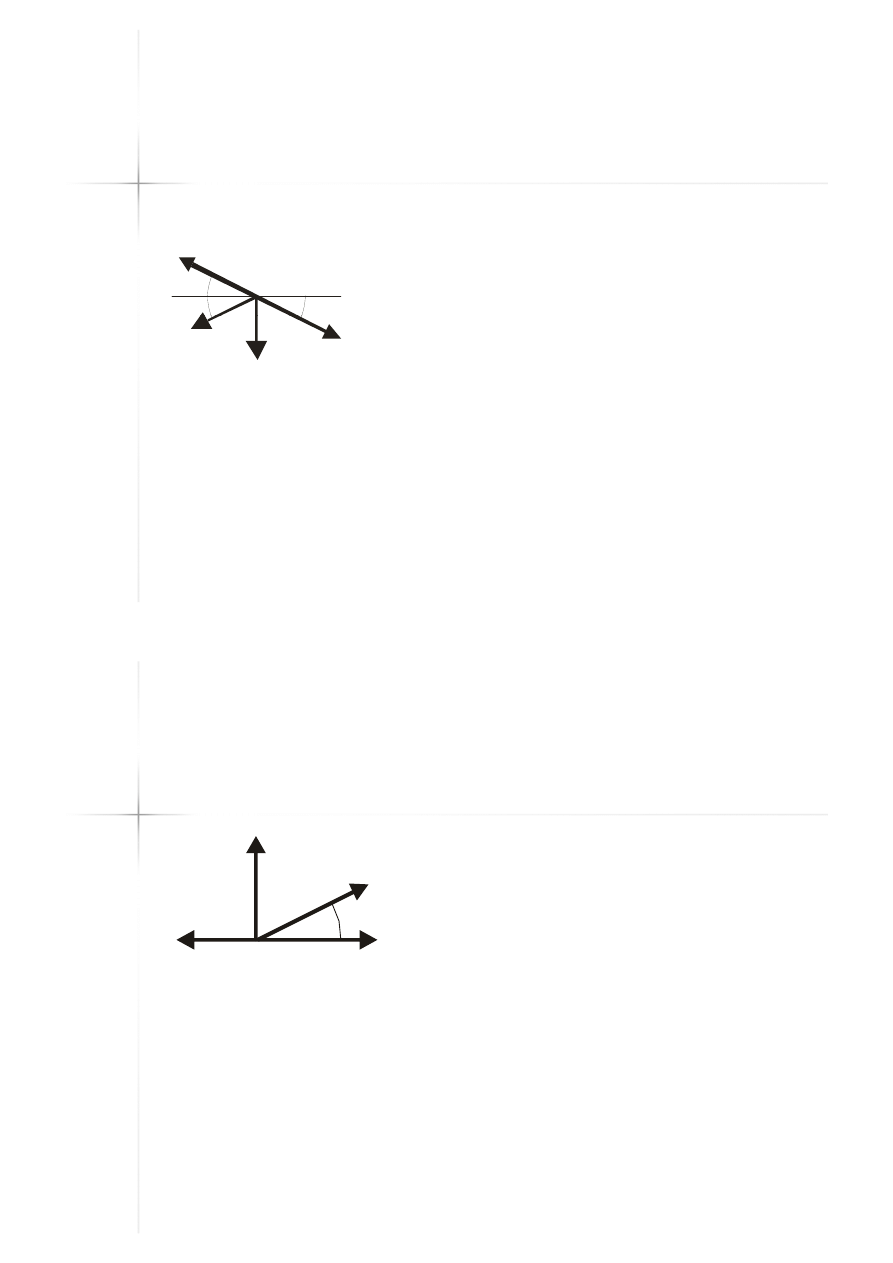
Węzeł 3
Węzeł 3
3
N
4-3
a
a
a
N
3 2
3 1
3 1
:
cos
cos
cos
0
X N
N
N
3 1
16, 778
N
kN
13
13
a
a
N
3-1
N
3-2
N
3-B
4 3
3
3 1
3 2
:
sin
sin
sin
16, 778
0, 447 16, 778
0, 447 15
0
B
Y N
N
N
N
kN
kN
kN
Sprawdzenie:
Sprawdzenie:
Węzeł 1
Węzeł 1
1
N
N
1-4
N
1-3
N
1 3
1
1
:
cos
16, 778
0,894 15
0
B
A
X N
N
N
kN
kN
Sprawdzenie:
Sprawdzenie:
14
14
1
N
1-A
N
1-B
16, 778
0,894 15
0
kN
kN
1 4
1 3
:
sin
7, 5
16, 778
0, 447
0
Y N
N
kN
kN
Sprawdzenie:
Sprawdzenie:
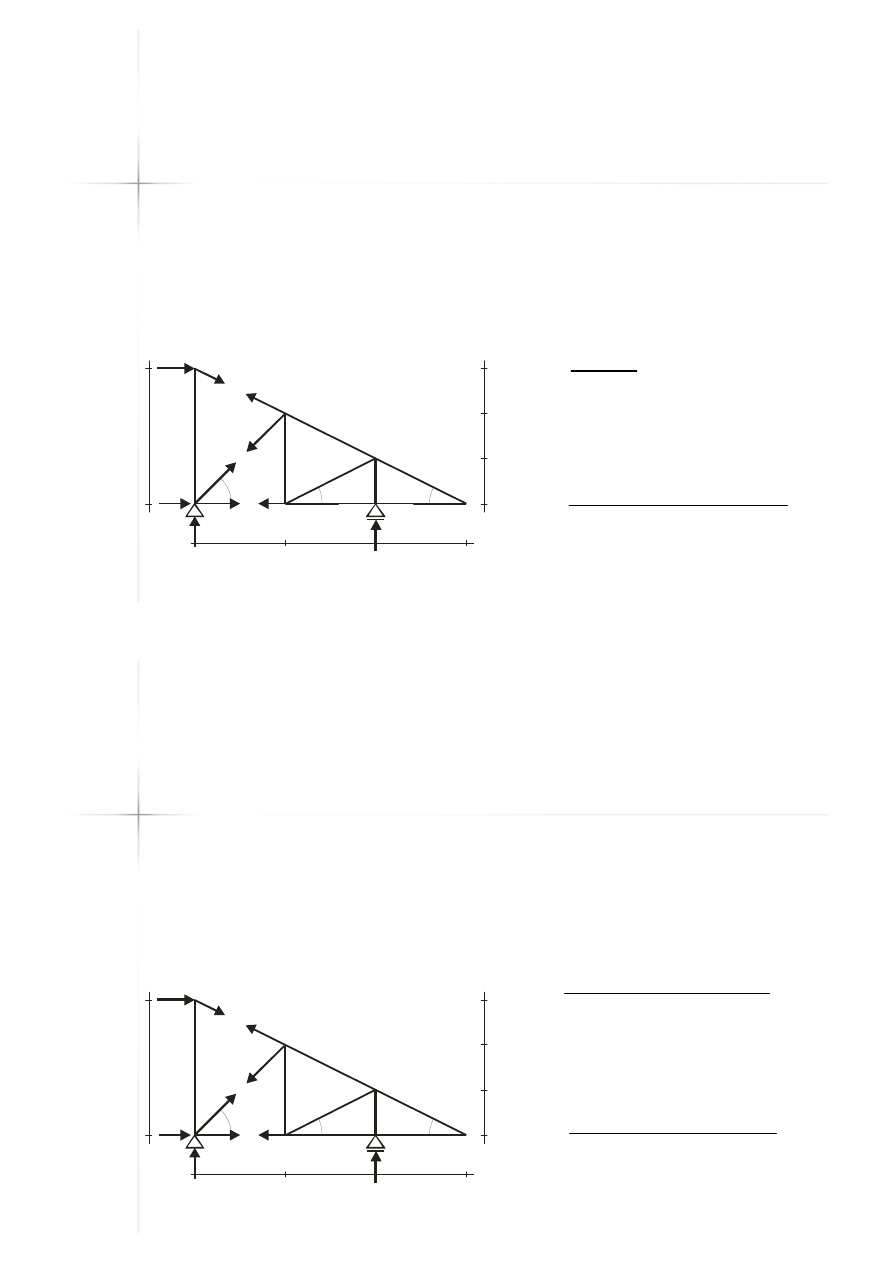
Przykład B
Przykład B –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
(z lewej)
(z lewej)
5 4
:
cos
4, 5
20
4, 5
0
l
A
M
N
m
kN
m
4
1
:
3
3
20
1, 5
3
0
l
A
A
A
M
V
m
H
m
kN
m
N
m
2
4
:
9
20
4, 5
sin
9
0
l
A
A
M
V
m
kN
m
N
m
15
15
R
B
V
A
H
A
3m
4
,5
m
20kN
3m
3m
a
a
b
1
,5
m
1
,5
m
1
,5
m
A
B
1
2
3
4
5
N
5-4
N
4-5
N
A-4
N
4-A
N
A-1
N
1-A
2
4
:
9
20
4, 5
sin
9
0
A
A
M
V
m
kN
m
N
m
5 4
20
22,371
0,894
kN
N
kN
1
15
20
10
15
A
N
kN
kN
kN
kN
4
15
9
20
4, 5
0, 707 9
7, 072
A
kN
m
kN
m
N
m
kN
Przykład B
Przykład B –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
(z prawej)
(z prawej)
4 5
4 5
:
cos
3
sin
3
6
0
p
A
B
M
N
m
N
m
R
m
4
1
:
3
3
0
p
B
A
M
R
m
N
m
2
4
4
:
3
sin
6
cos
3
0
p
B
A
A
M
R
m
N
m
N
m
16
16
R
B
V
A
H
A
3m
4
,5
m
20kN
3m
3m
a
a
b
1
,5
m
1
,5
m
1
,5
m
A
B
1
2
3
4
5
N
5-4
N
4-5
N
A-4
N
4-A
N
A-1
N
1-A
2
4
4
:
3
sin
6
cos
3
0
B
A
A
M
R
m
N
m
N
m
4 5
15
6
0,894 3
0, 447 3
22, 371
kN
m
N
m
m
kN
1
15
A
N
kN
4
15
3
0, 707 6
0, 707 3
7, 072
A
kN
m
N
m
m
kN
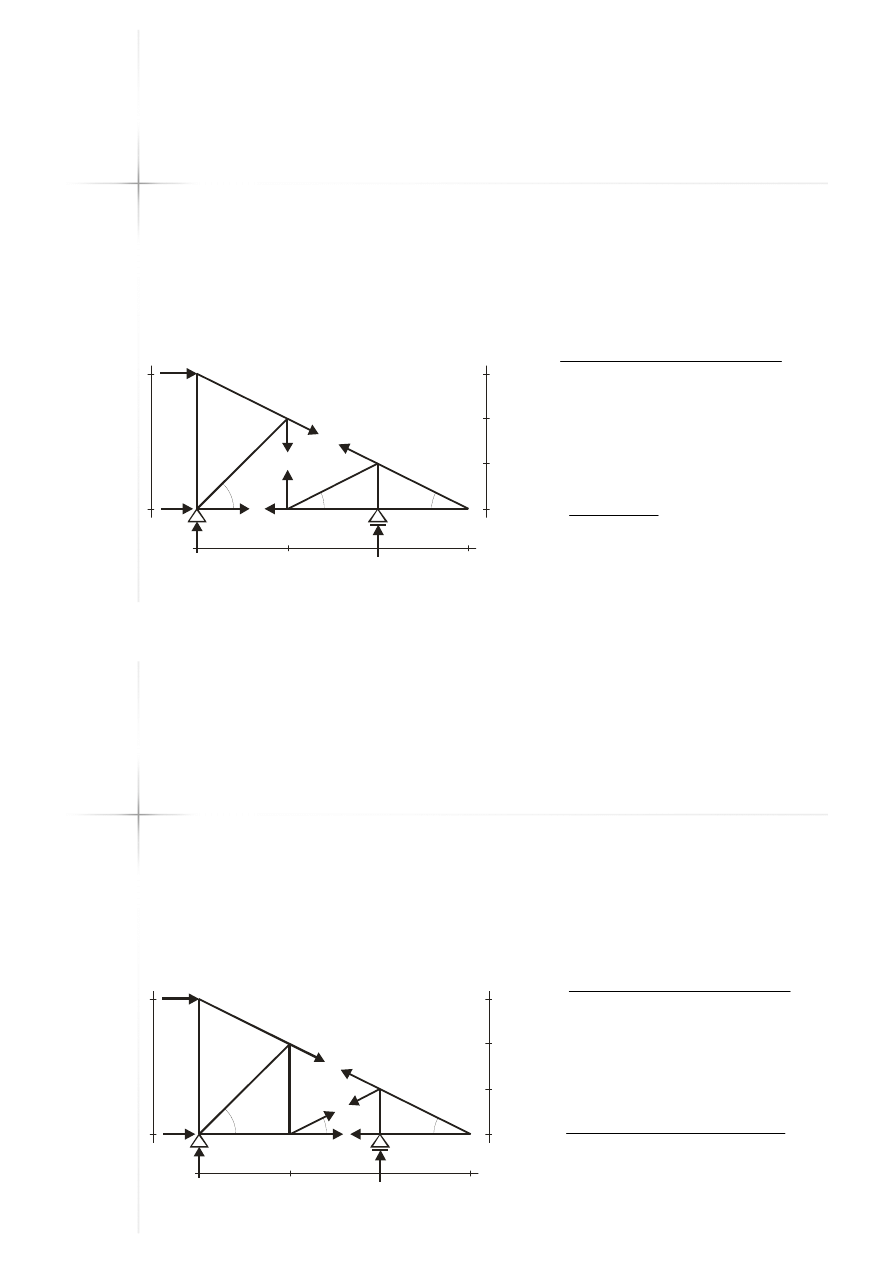
Przykład B
Przykład B –
– metoda
metoda
Rittera
Rittera –
– przekrój 2
przekrój 2
1
4 3
4 3
:
cos
1, 5
sin
3
3
0
p
B
M
N
m
N
m
R
m
4
1
:
3
3
0
p
B
A
M
R
m
N
m
2
1 4
:
3
6
0
p
B
M
R
m
N
m
17
17
R
B
V
A
H
A
3m
4
,5
m
20kN
3m
3m
a
a
b
1
,5
m
1
,5
m
1
,5
m
A
B
1
2
3
4
5
N
4-3
N
4-3
N
4-1
N
1-4
N
A-1
N
1-A
2
1 4
:
3
6
0
B
M
R
m
N
m
4 3
15
3
0,894 1, 5
0, 447 3
16, 779
kN
m
N
m
m
kN
1
15
A
N
kN
1 4
15
3
7, 5
6
kN
m
N
kN
m
Przykład B
Przykład B –
– metoda
metoda
Rittera
Rittera –
– przekrój 3
przekrój 3
1
4 3
4 3
:
cos
1, 5
sin
3
3
0
p
B
M
N
m
N
m
R
m
3
5 1
:
1, 5
0
p
M
N
m
2
1 3
:
9
20
4, 5
sin
6
0
l
A
M
V
m
kN
m
N
m
18
18
R
B
V
A
H
A
3m
4
,5
m
20kN
3m
3m
a
a
b
1
,5
m
1
,5
m
1
,5
m
A
B
1
2
3
4
5
N
4-3
N
4-3
N
1-3
N
3-1
N
1-B
N
B-1
2
1 3
:
9
20
4, 5
sin
6
0
A
M
V
m
kN
m
N
m
4 3
15
3
0,894 1, 5
0, 447 3
16, 779
kN
m
N
m
m
kN
5 1
0
N
1 3
15
9
20
4, 5
0, 447 6
16, 779
kN
m
kN
m
N
m
kN
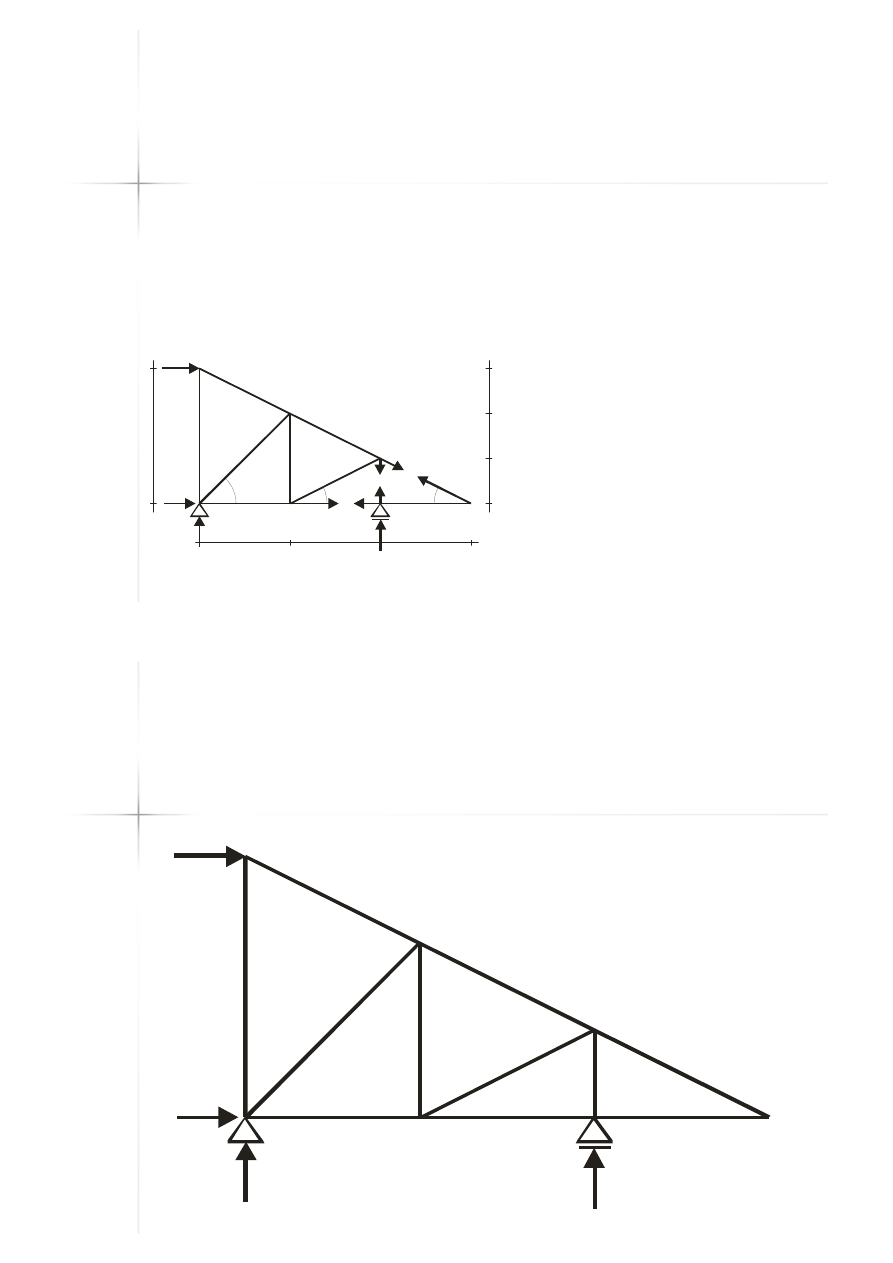
Przykład B
Przykład B –
– metoda
metoda
Rittera
Rittera –
– przekrój 4
przekrój 4
3
1
:
1, 5
0
p
B
M
N
m
2 3
:
sin
3
0
p
B
M
N
m
2
3
:
3
3
0
p
B
B
M
R
m
N
m
19
19
R
B
V
A
H
A
3m
4
,5
m
20kN
3m
3m
a
a
b
1
,5
m
1
,5
m
1
,5
m
A
B
1
2
3
4
5
N
3-2
N
2-3
N
3-B
N
B-3
N
B-1
N
1-B
2
3
:
3
3
0
B
B
M
R
m
N
m
1
0
B
N
2 3
0
N
3
15
B
N
kN
Przykład B
Przykład B –
– wyniki:
wyniki:
zestawienie sił
zestawienie sił
20kN
-22
,371
kN
-16
20
20
-20kN
-15kN
-16
,778
kN
0
15kN
0
16
,77
8kN
-1
5
k
N
-7
,5
kN
7,
07
2k
N
1
0
k
N
15kN
0
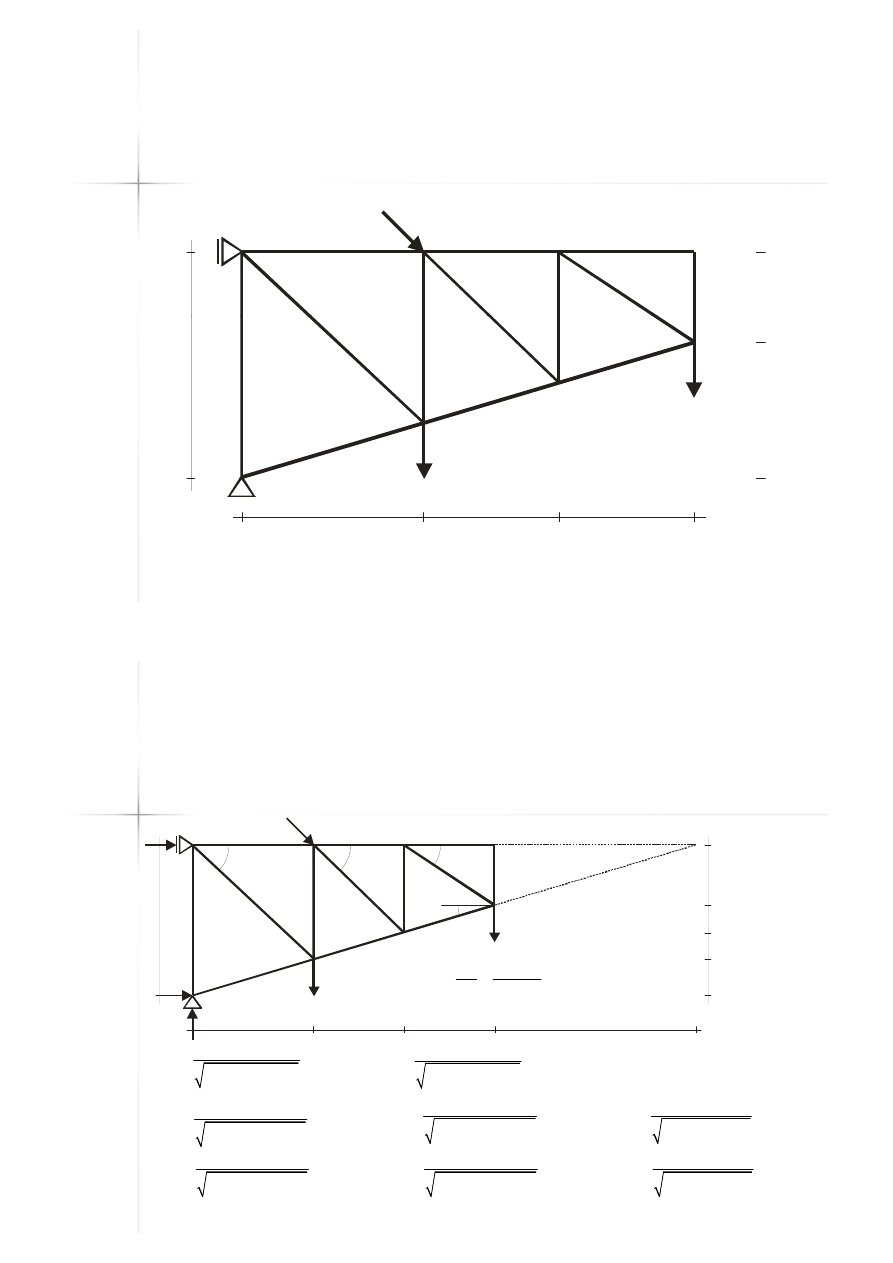
Przykład C
Przykład C –
– kratownica z
kratownica z
pasami zbieżnymi
pasami zbieżnymi
15kN
2
m
21
21
4m
5
m
10kN
3m
3m
20kN
3
m
Przykład C
Przykład C –
– wymiary
wymiary
5
m
10kN
15kN
R
B
B
1
2
3
4
5
6
0
,9
m
2
m
9
m
a
b
g
d
C
x
22
22
2
2
3
sin
0, 287
10
3
m
m
m
10
2
5
x
m
x
m
m
6, 667
x
m
2
2
10
cos
0, 958
10
3
m
m
m
2
2
3,8
sin
0, 689
3,8
4
m
m
m
2
2
4
cos
0, 725
3,8
4
m
m
m
2
2
2, 9
sin
0, 695
2, 9
3
m
m
m
2
2
3
cos
0, 719
2, 9
3
m
m
m
2
2
2
sin
0, 555
2
3
m
m
m
2
2
3
cos
0,832
2
3
m
m
m
4m
3m
3m
20kN
V
A
H
A
1
A
0
,9
1
,2
m
x
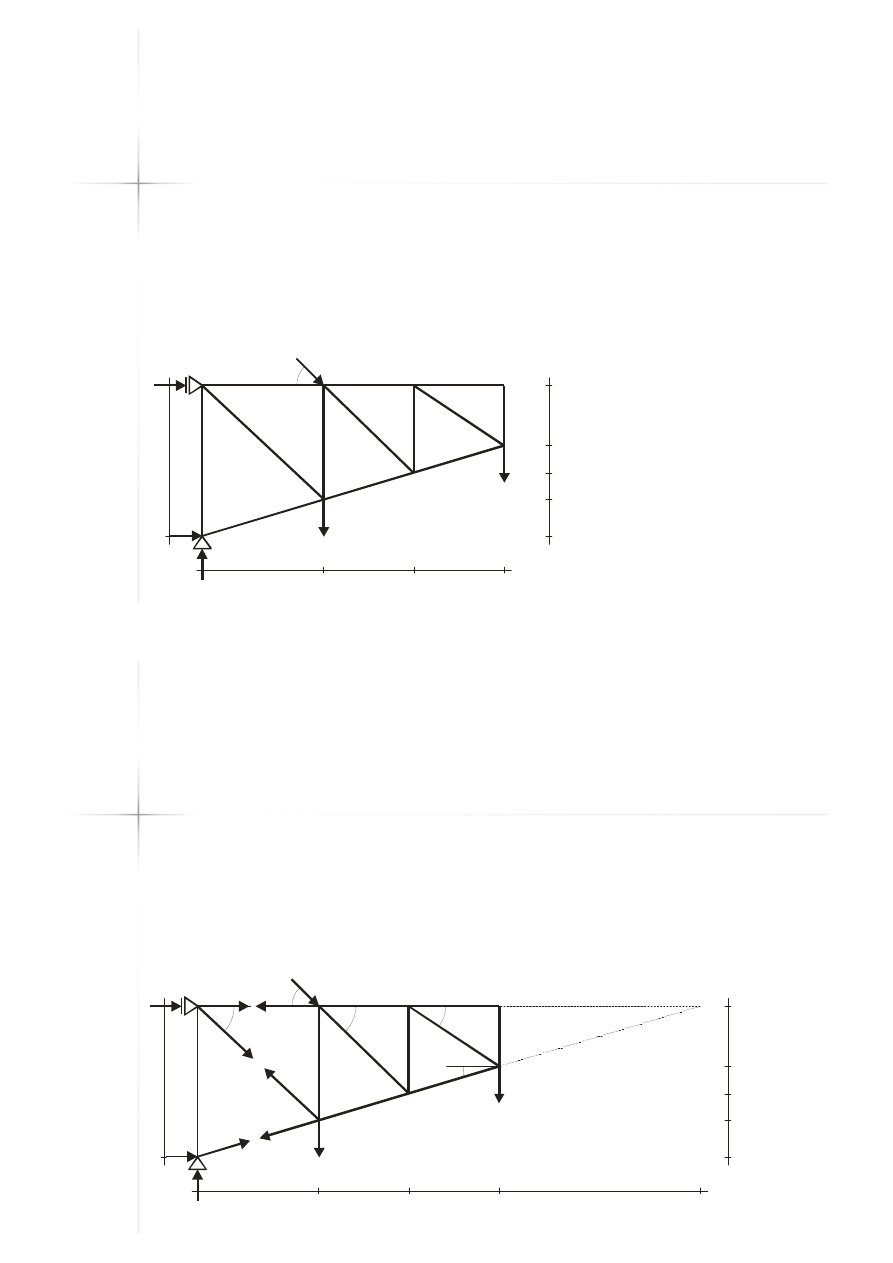
Przykład C
Przykład C -- reakcje
reakcje
:
15
cos
0
A
B
X H
R
kN
:
20
10
15
sin
0
A
Y V
kN
kN
kN
:
5
20
4
10
10
A
B
M
R
m
kN
m
kN
m
23
23
15
sin
4
15
cos
5
0
kN
m
kN
m
44, 340
A
H
kN
40, 425
A
V
kN
55,125
B
R
kN
4m
5
m
10kN
3m
3m
20kN
15kN
V
A
H
A
R
B
B
1
A
2
3
4
5
6
0
,9
m
2
m
0
,9
m
1
,2
m
g
Przykład C
Przykład C –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
1
4
:
3,8
15
cos
3,8
10
6
0
p
B
M
N
m
kN
m
kN
m
1
:
cos
5
5
0
l
B
A
A
M
N
m
H
m
1
:
16, 667
5
sin
16, 667
0
l
C
A
A
B
M
V
m
H
m
N
m
4
26, 574
B
N
kN
1
46, 284
A
N
kN
4
39, 366
B
N
kN
24
24
1
:
16, 667
5
sin
16, 667
0
C
A
A
B
M
V
m
H
m
N
m
4m
5
m
10kN
3m
3m
20kN
15kN
V
A
H
A
R
B
B
1
A
2
3
4
5
6
0
,9
m
2
m
0
,9
m
1
,2
m
N
4-3
N
B-4
N
4-B
N
B-1
N
1-B
N
1-A
N
A-1
a
b
g
d
C
6,667m
g
4
39, 366
B
N
kN
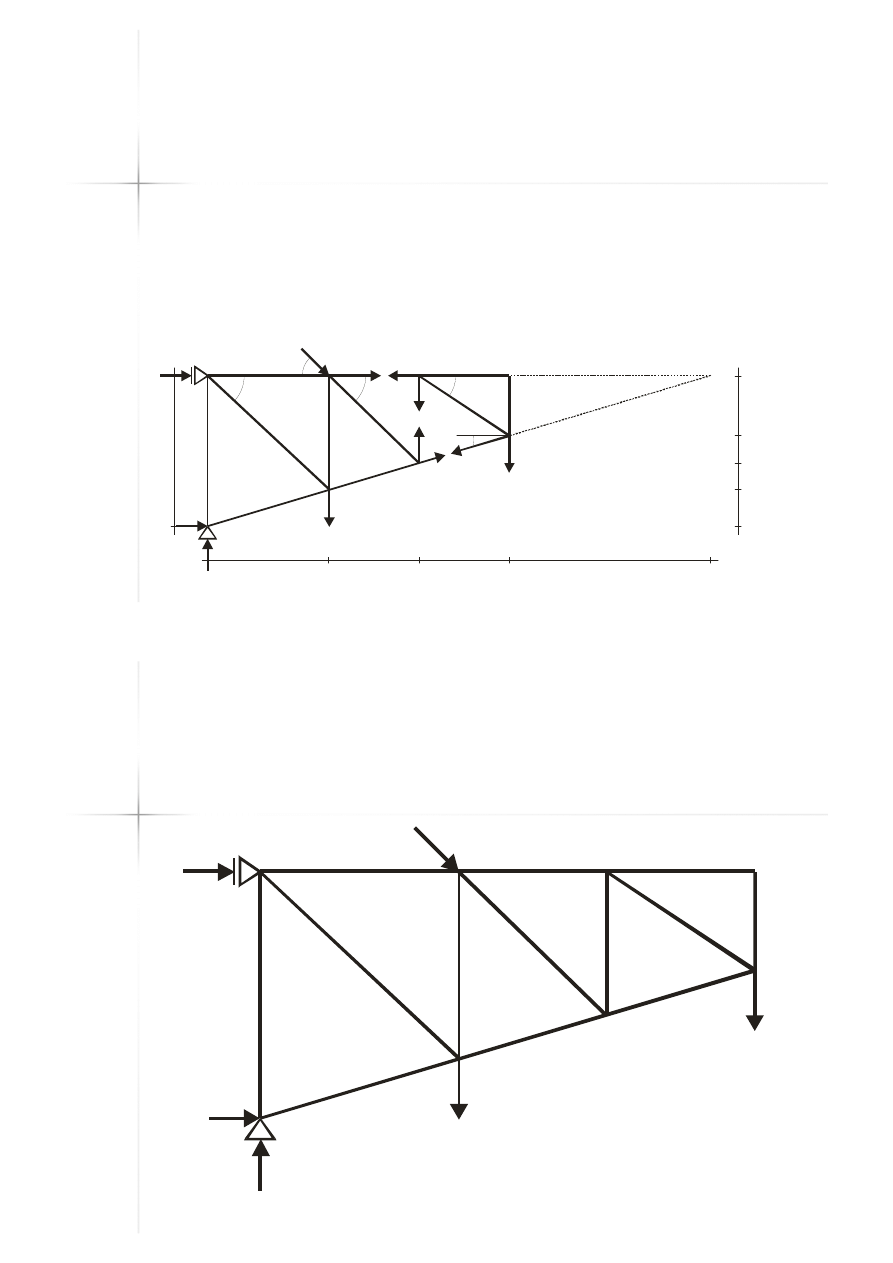
Przykład C
Przykład C –
– metoda
metoda
Rittera
Rittera –
– przekrój 2
przekrój 2
2
5 4
:
2, 9
10
3
0
p
M
N
m
kN
m
5
3 2
3 2
:
cos
2
sin
3
10
3
0
p
M
N
m
N
m
kN
m
5 2
:
9, 667
10
6, 667
0
p
C
M
N
m
kN
m
5 4
10, 345
N
kN
3 2
10,803
N
kN
5 2
6,897
N
kN
25
25
5 2
6,897
N
kN
4m
5
m
10kN
3m
3m
20kN
15kN
V
A
H
A
R
B
B
1
A
2
3
4
5
6
N
2-3
N
3-2
N
5-2
N
2-5
N
5-4
N
4-5
a
b
g
d
C
6,667m
g
0
,9
m
2
m
0
,9
m
1
,2
m
Przykład C
Przykład C –
– wyniki:
wyniki:
zestawienie sił
zestawienie sił
15kN
-55,125kN
26,574kN
10,345kN
0
8
9
k
N
8
9
7
k
N
0
39
,3
66
7
,57
3k
N
12,4
33k
N
26
26
10kN
20kN
40,425kN
44,340kN
-46,2
84kN
-16,4
85k
N
-10,
803
kN
-2
7
,1
2
3
k
N
-1
5
,6
8
-6
,8
36
6k
N
kN
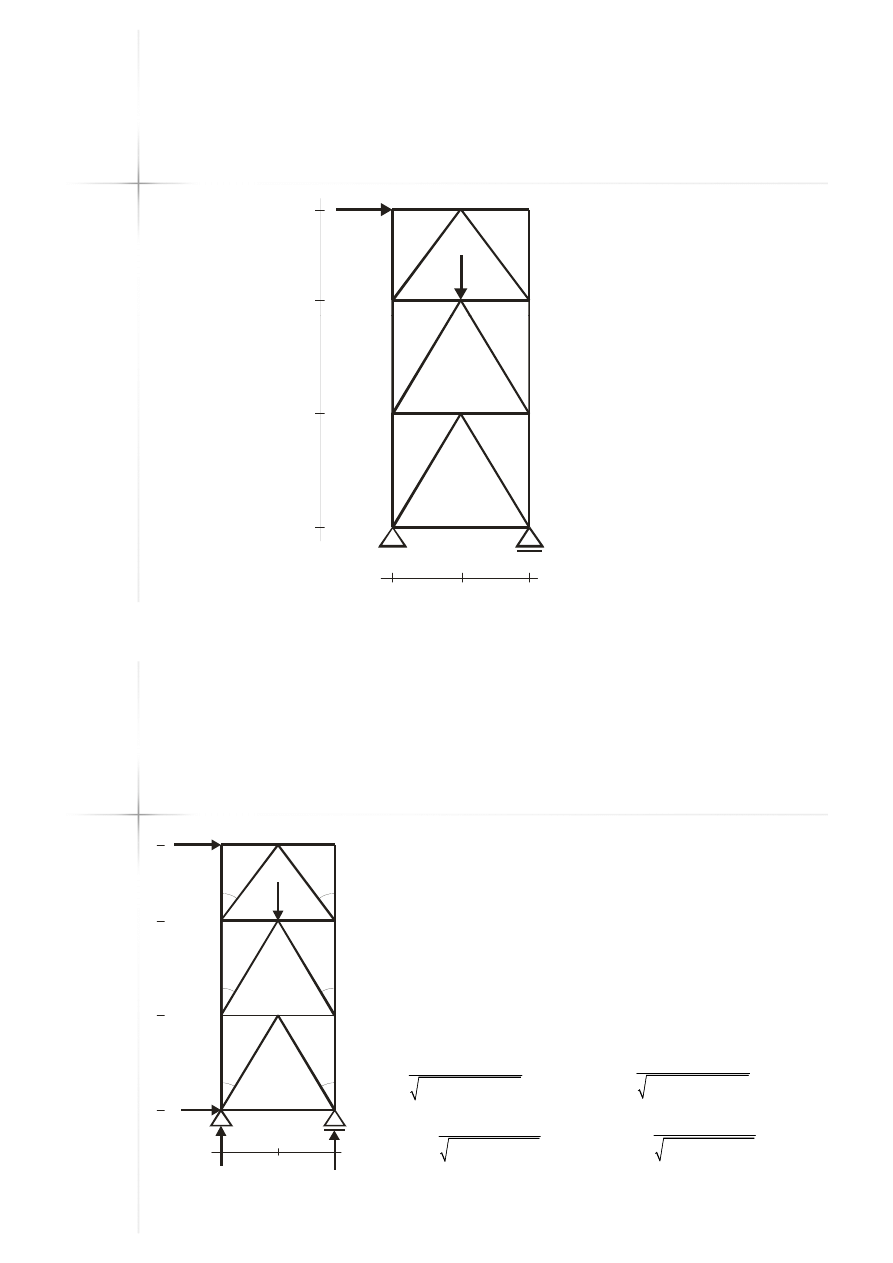
Przykład D
Przykład D –
– kratownica
kratownica
typu „K”
typu „K”
15kN
10kN
2
m
27
27
1,5m
2
,5
m
2
,5
m
1,5m
Przykład D
Przykład D –
– reakcje
reakcje
:
10
0
A
X H
kN
:
15
0
A
B
Y V
R
kN
:
3
15
1, 5
10
7
0
M
R
m
kN
m
kN
m
20
A
H
kN
15,833
A
V
kN
15kN
10kN
2
m
5
4
6
7
9
8
b
b
28
28
:
3
15
1, 5
10
7
0
A
B
M
R
m
kN
m
kN
m
30,833
B
R
kN
2
,5
m
2
,5
m
V
A
H
A
R
B
A
B
1
3
2
a
a
a
a
1,5m
1,5m
2
2
1, 5
sin
0, 514
1,5
2, 5
m
m
m
2
2
2, 5
cos
0,857
1, 5
2, 5
m
m
m
2
2
1,5
sin
0, 6
1, 5
2
m
m
m
2
2
2
cos
0,8
1, 5
2
m
m
m
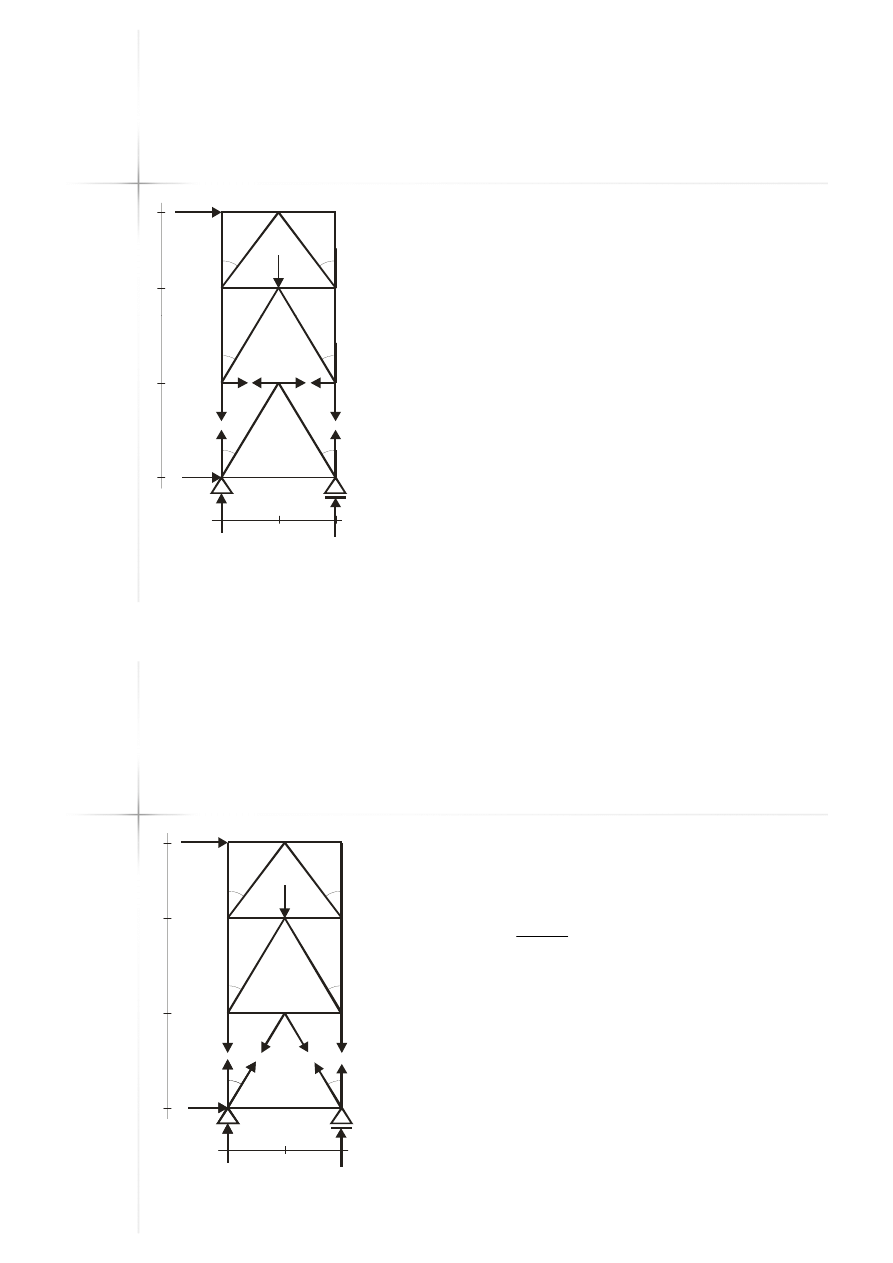
Przykład D
Przykład D –
– metoda
metoda
Rittera
Rittera –
– przekrój 1
przekrój 1
15kN
10kN
2
m
5
4
6
7
9
8
b
b
1
3
:
3
15
1, 5
10
4, 5
0
g
B
M
N
m
kN
m
kN
m
3
22, 500
B
N
kN
29
29
2
,5
m
2
,5
m
V
A
H
A
R
B
A
B
1
3
2
N
1-A
N
A-1
N
1-2
N
2-1
N
2-3
N
3-2
N
B-3
N
3-B
a
a
a
a
1,5m
1,5m
3
1
:
3
15
1, 5
10
4, 5
0
g
A
M
N
m
kN
m
kN
m
1
7, 500
A
N
kN
Przykład D
Przykład D –
– metoda
metoda
Rittera
Rittera –
– przekrój 2
przekrój 2
15kN
10kN
2
m
5
4
6
7
9
8
b
b
2
2
:
sin
sin
10
0
g
A
B
X
N
N
kN
2
2
10
sin
A
B
kN
N
N
30
30
2
,5
m
2
,5
m
H
A
R
B
A
B
1
3
2
N
2-A
N
2-B
N
A-2
N
B-2
a
a
a
a
N
1-A
N
3-B
N
A-1
N
B-3
V
A
H
A
A
N
A-2
a
N
A-1
1,5m
1,5m
2
2
sin
A
B
N
N
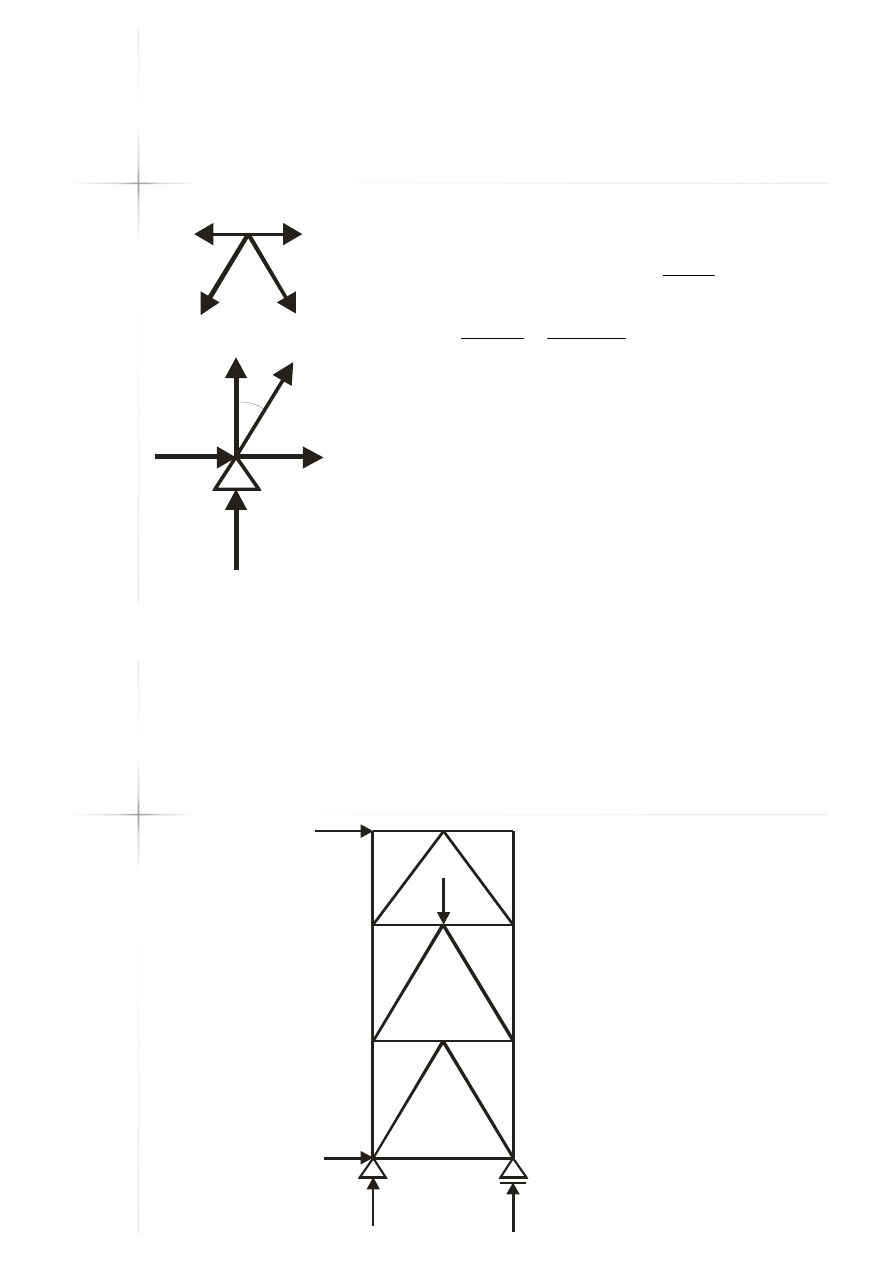
Przykład D
Przykład D –
– metoda
metoda
równoważenia węzłów
równoważenia węzłów
2
N
2-1
N
2-3
N
2-A
N
2-B
2
2
:
cos
cos
0
A
B
Y N
N
2
2
B
A
N
N
2
10
2
sin
A
kN
N
10
10
kN
kN
31
31
V
A
H
A
A
N
A-2
a
N
A-1
N
A-1
2
10
10
9, 728
2 sin
2 0, 514
A
kN
kN
N
kN
2
1
:
sin
0
A
A
A
X N
N
H
1
10
9, 728
0, 514
5
A
N
kN
kN
kN
2
9, 728
B
N
kN
Przykład D
Przykład D –
– wyniki:
wyniki:
zestawienie sił
zestawienie sił
15kN
10kN
-10kN
0
0
0
-5kN
5kN
-
8,
33
3k
N
-8
,3
3
3k
N
32
32
-15,833kN
-10kN
30,833kN
6
,6
6
7
k
N
-6
,6
6
7
k
N
-2
2
,5
kN
7
,5
k
N
-0,5kN
9,5kN
26,574kN
9
,7
2
8k
N
-9
,7
2
8k
N
0,
97
2
k
N
-1
8
,4
65
kN
Wyszukiwarka
Podobne podstrony:
Metoda Rittera
Kratownica Metoda Równoważenia Węzłów
Metoda Rittera
Kratownica Metoda Równoważenia WÄzÅów
Metoda Rittera
Mieczysław Wilk Metoda Rittera
Metoda Rittera
37 Kratownica typu K metoda przecięć Rittera
36 Kratownica typu N metoda przecięć Rittera
37 Kratownica typu K metoda przecięć Rittera
Metoda sił kratownica
Metoda sił, projekt-kratownica
Metoda sił projekt kratownica
Metoda sił ćwiczenie nr 2 kratownica statycznie niewyznaczalna
więcej podobnych podstron