P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

1 |

S t r o n a

METODA

SIŁ

KRATOWNICA

P

RZYKŁAD

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

2 |

S t r o n a

Obliczyć siły w prętach kratownicy oraz sporządzić wykres sił normalnych.
Rozwiązanie przeprowadzić w oparciu o metodę sił.

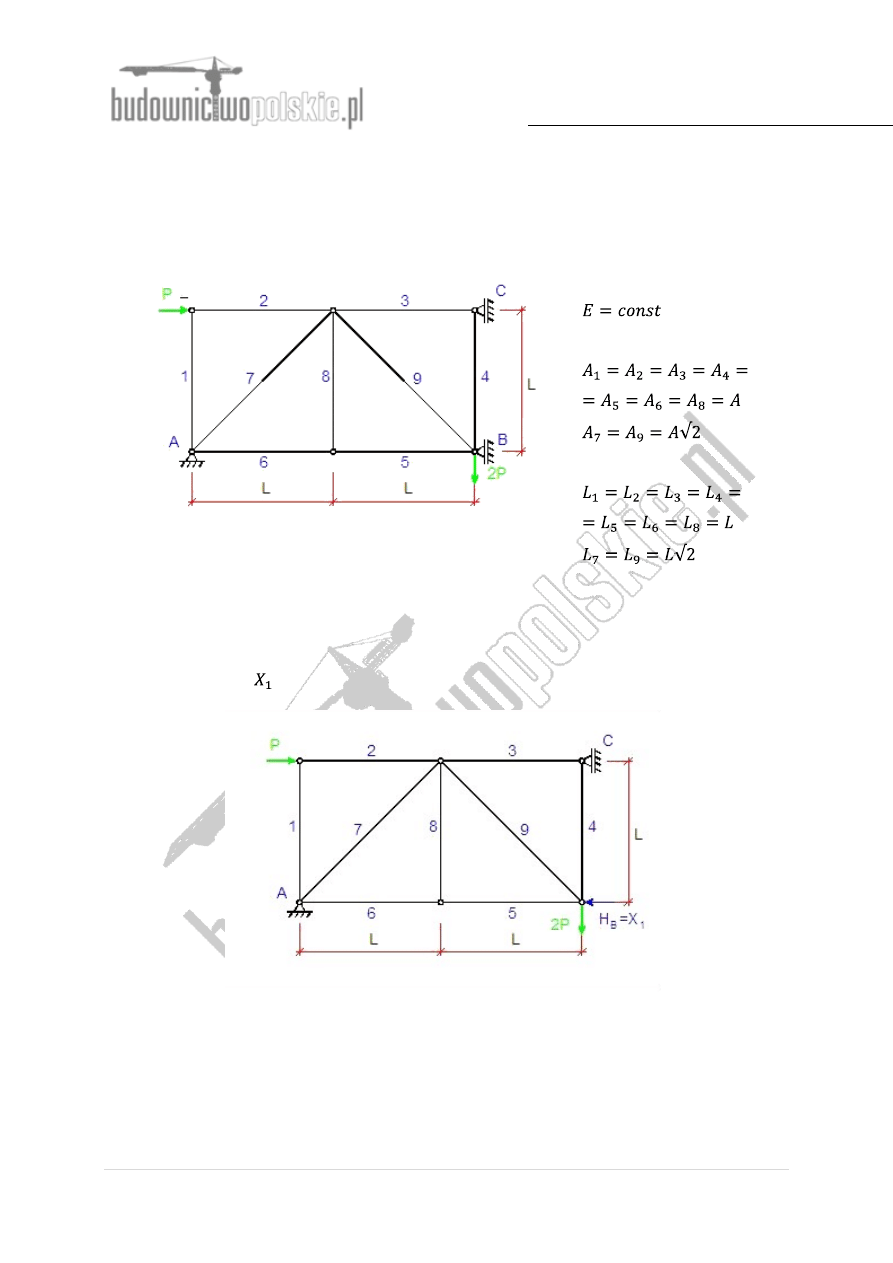
Rys.1 Schemat kratownicy

moduł Younga:

przekroje prętów:

długości prętów:

Kratownica przedstawiona na rys. 1 jest układem jednokrotnie statycznie niewyznaczalnym
zewnętrznie.

Przyjmujemy układ podstawowy usuwając nadliczbowy więz podporowy poziomy w punkcie
B zastępując go siłą

zgodnie z poniższym schematem:

Rys.2 Układ podstawowy

Sporządzamy wykresy sił normalnych dla przyjętego układu podstawowego (rys.2) kolejno
od obciążenia zewnętrznego i od obciążenia jednostkowego przyłożonego w miejscu i na
kierunku usuniętego więzu (rys. 3 i 4). Pręty ściskane oznaczono strzałkami zwróconymi do
węzłów, rozciągane – od węzłów.

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

3 |

S t r o n a

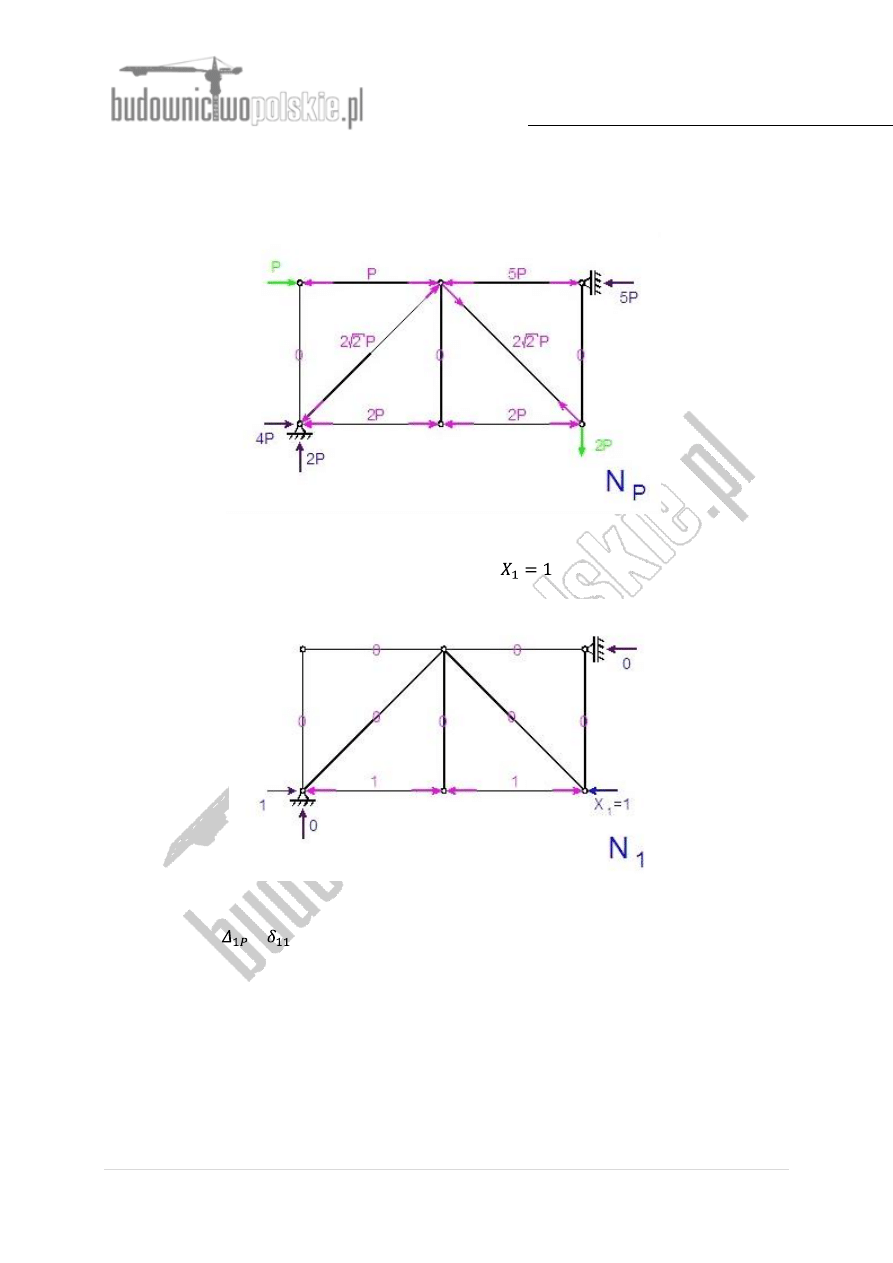
Wykres sił normalnych od obciążenia zewnętrznego dla układu podstawowego:

Rys.3 Wykres sił normalnych od obciążenia zewnętrznego dla układu podstawowego

Wykres sił normalnych od obciążenia jednostkowego

dla układu podstawowego:

Rys.4 Wykres sił normalnych od obciążenia jednostkowego X

1

=1 dla układu podstawowego

Współczynniki

i

(przemieszczenia od obciążenia zewnętrznego i siły jednostkowej,

gdzie pierwszy indeks oznacza miejsce, drugi przyczynę przemieszczenia) obliczamy na
podstawie wykresów sił normalnych dla poszczególnych stanów. Obliczenia wygodnie jest
przeprowadzić w tabeli, która zamieszczona została poniżej.

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

4 |

S t r o n a

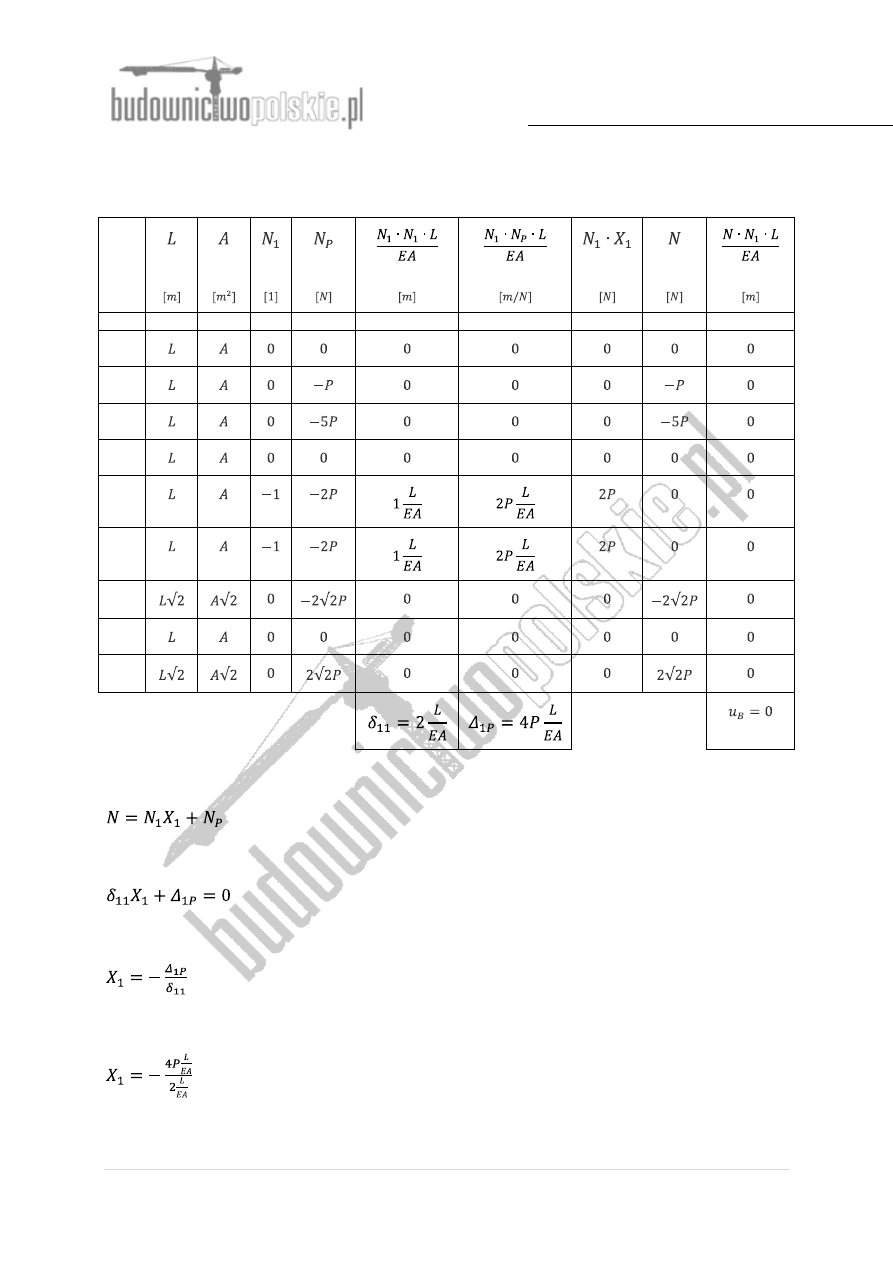
Tabela 1.

Nr

pręta

(5+8)

1

2

3

4

5

6

7

8

9

10

1

2

3

4

5

6

7

8

9

suma

suma

Wartości sił normalnych w kolumnie 9 Tabeli 1. zostały obliczone wg zależności:

Równanie kanoniczne metody sił:

Przekształcając mamy:

Po podstawieniu odpowiednich wartości z Tabeli 1 otrzymujemy:

skąd:

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

5 |

S t r o n a

Znak minus oznacza, że zwrot reakcji jest przeciwny do założonej przez nas siły

w

układzie podstawowym (rys. 2).

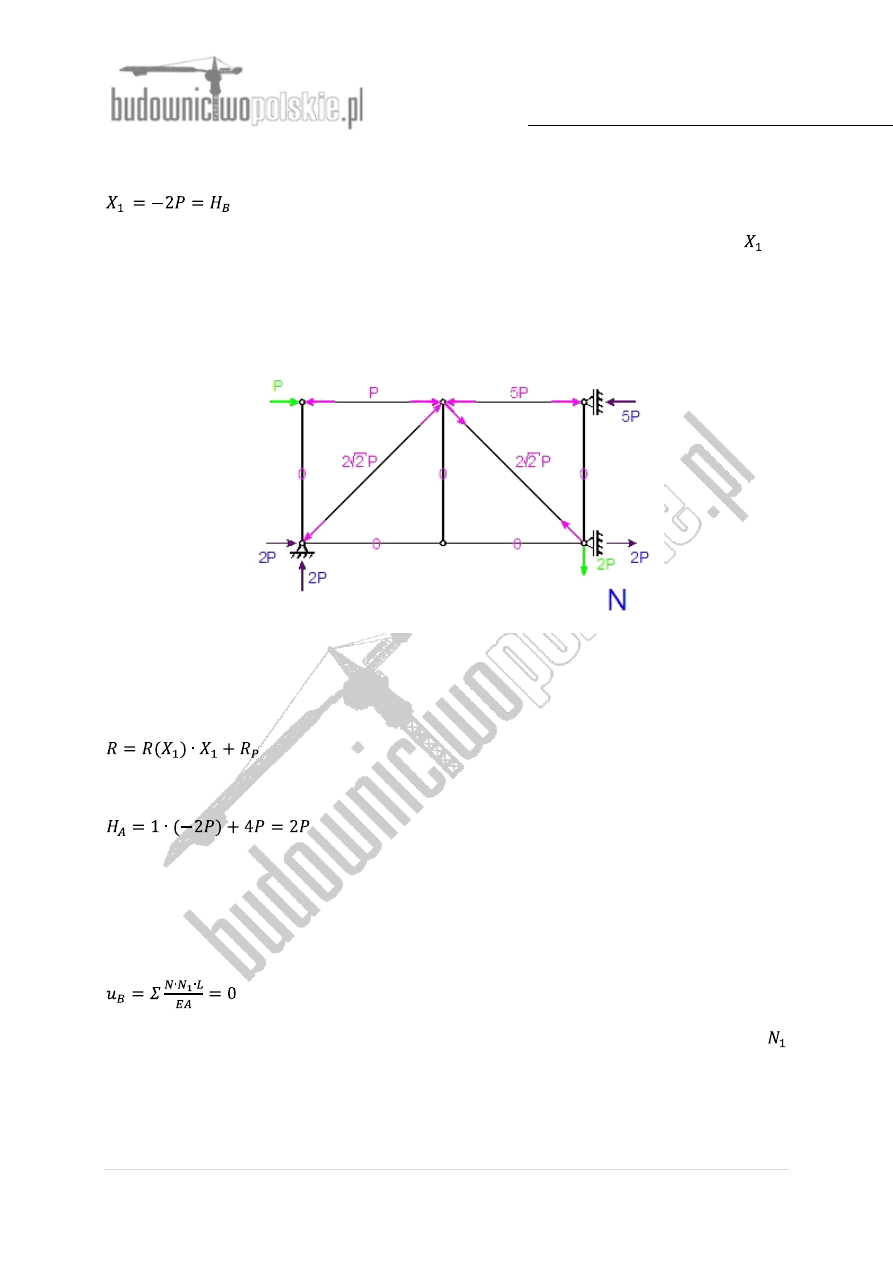
Ostatecznie wykres sił normalnych otrzymujemy przenosząc wartości sił dla poszczególnych
prętów z Tabeli 1 z kolumny 9:

Rys.5 Wykres sił normalnych

Reakcje w punktach podparcia wyznaczamy z warunków równowagi lub na podstawie zasady
superpozycji wg wzoru:

np.:

Na koniec wykonamy jeszcze sprawdzenie zgodności odkształceń.

Sprawdzenie to polega na obliczeniu przemieszczenia w miejscu, w którym wiemy ile

ono będzie wynosić. W tym celu obliczymy przemieszczenie poziome punktu B, które

powinno wynieść zero ponieważ znajdująca się tam podpora uniemożliwia przesunięcie.
Przemieszczenie wnosi (zgodnie z kolumną 10 tabeli 1):

Do obliczenia przemieszczenia poziomego w punkcie B wykorzystano wykres

(przemieszczenie obliczamy przykładając w miejscu i na jego kierunku jednostkową

siłę).

Przemieszczenie na podporze równe jest zero zatem kratownica została rozwiązana

prawidłowo.