Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

1

POLITECHNIKA POZNA

Ń

SKA

INSTYTUT KONSTRUKCJI BUDOWLANYCH
ZAKŁAD MECHANIKI BUDOWLI

Obliczanie układów statycznie niewyznaczalnych metoda

sił z wykorzystaniem symetrii i antysymetrii

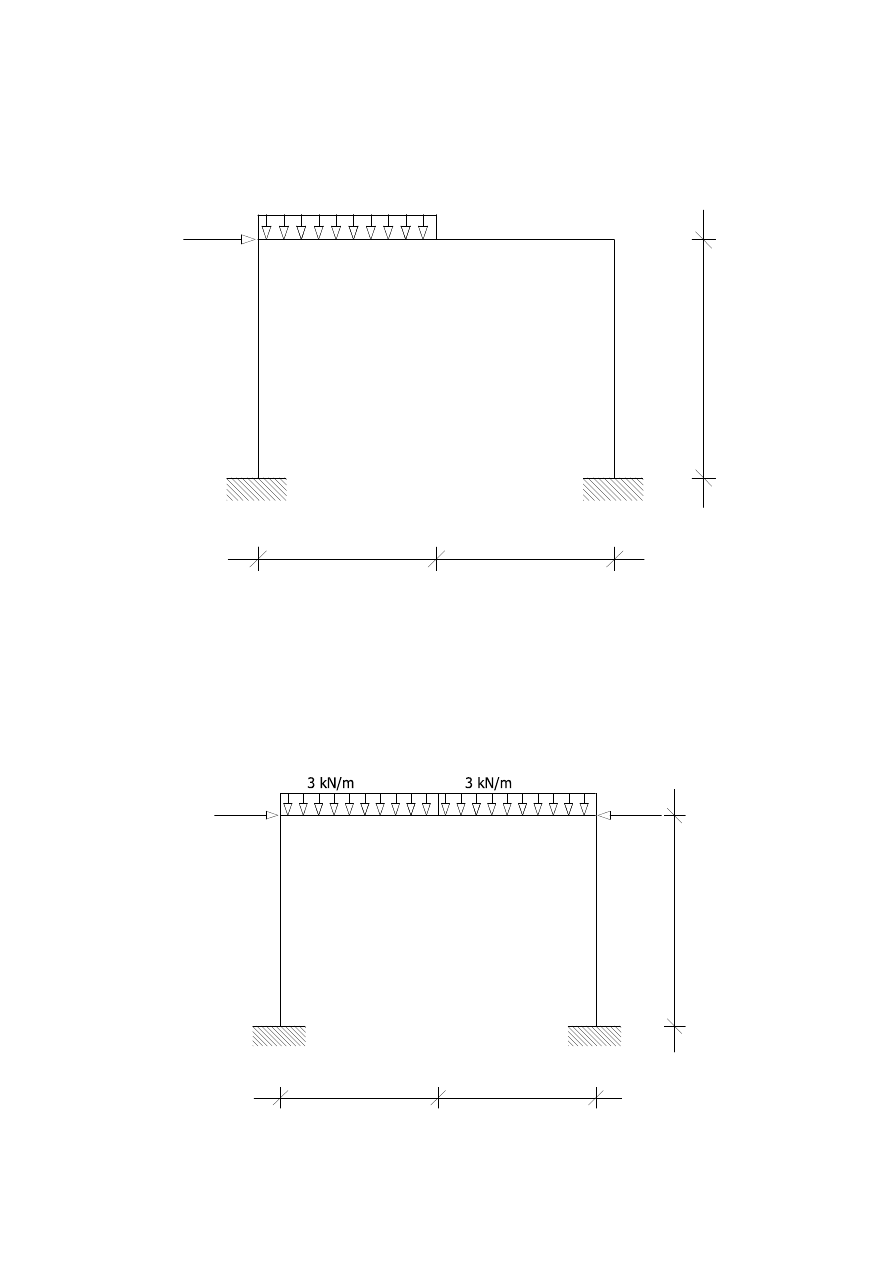
Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

2

6 kN/m

EI

10 kN

4

EI

3

3

2EI

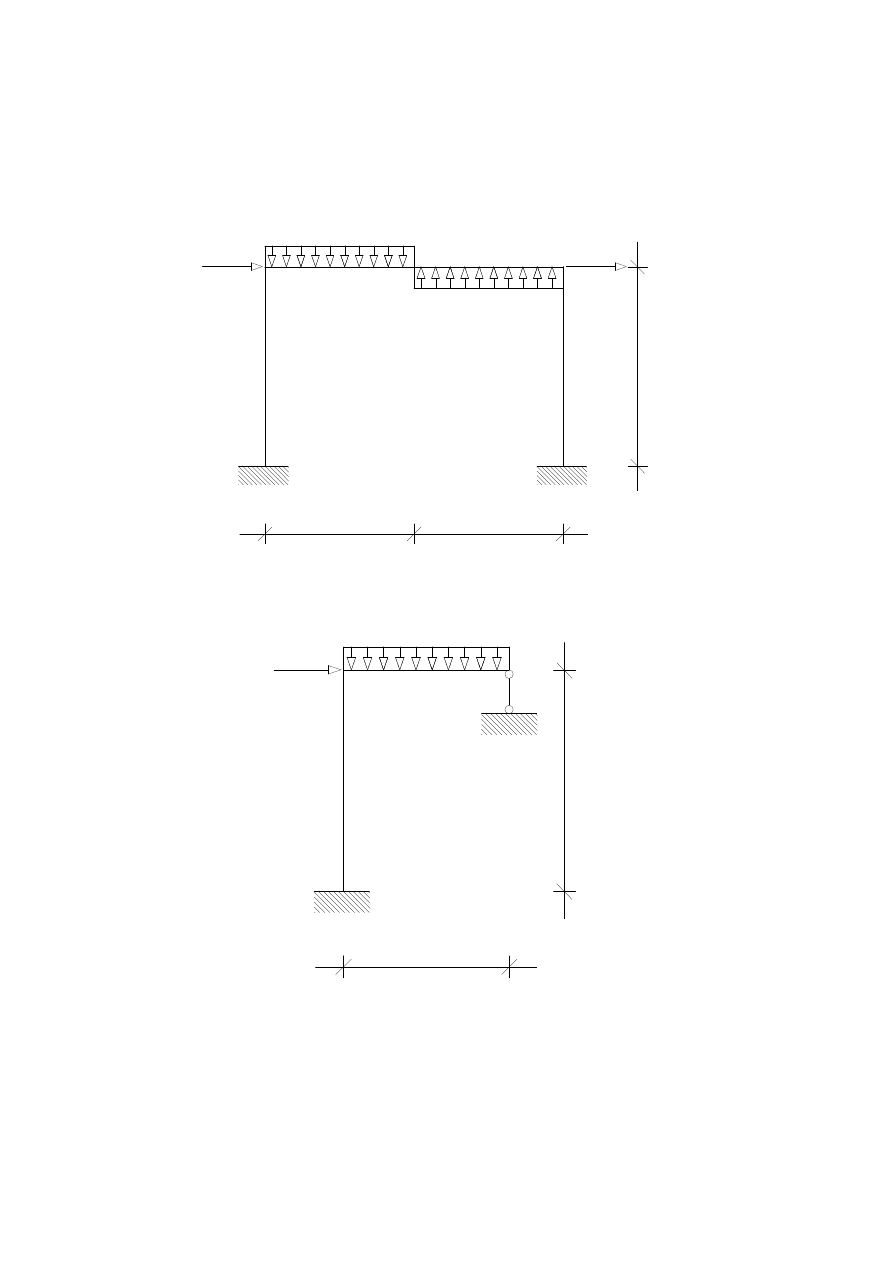
Ponieważ rama jest symetryczna, do obliczenia nadliczbowych niewiadomych

skorzystamy z symetrii i antysymetrii obciążenia zewnętrznego. W tym celu tworzymy dwa
oddzielne schematy obciążenia dające w sumie obciążenie dane pierwotnie. Jedno z nich jest
symetryczne, drugie antysymetryczne.

W przypadku obciążenia symetrycznego wykresy NORMALNEJ i MOMENTU są

symetryczne, a wykres TNĄCEJ - antysymetryczny.

EI

5 kN

4

EI

3

3

2EI

5 kN

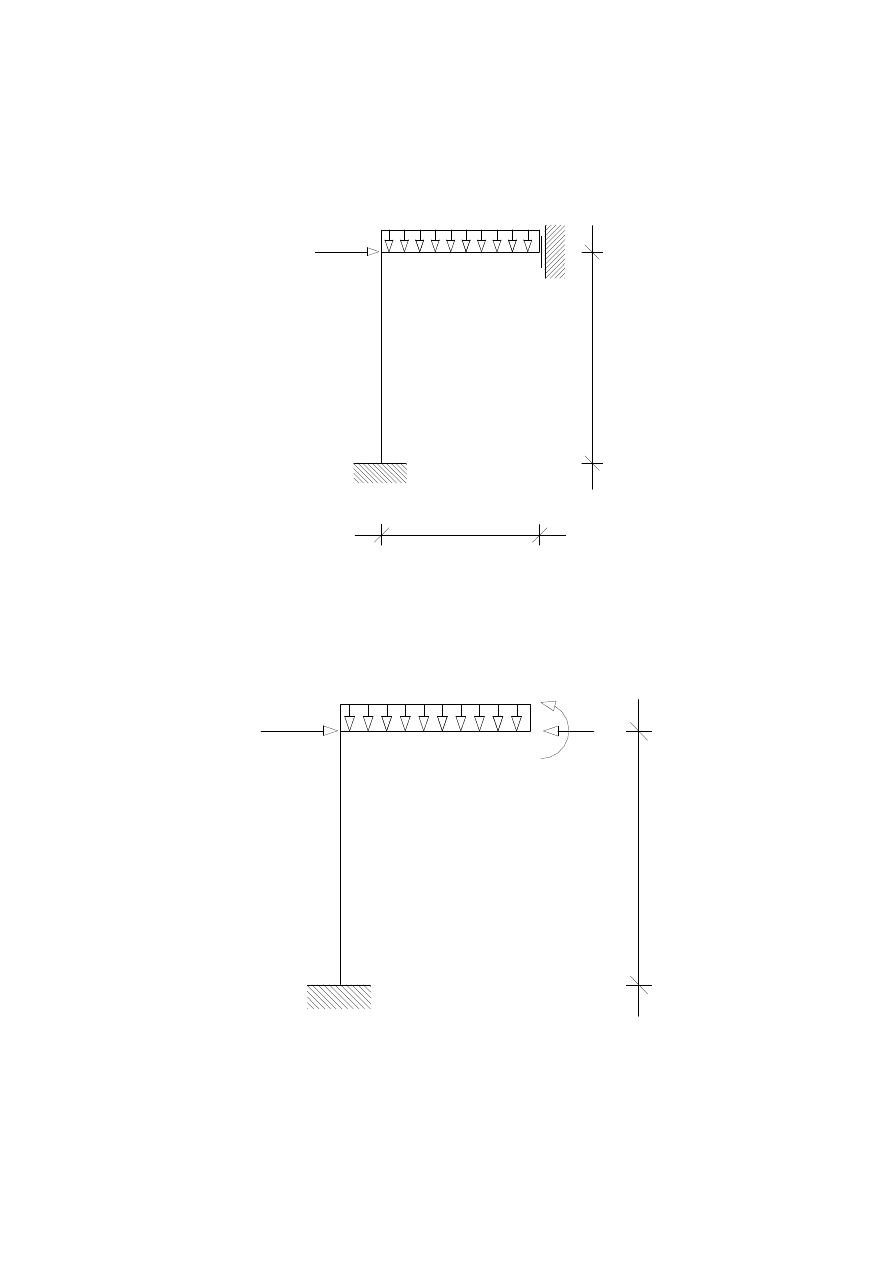
Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

3

Do obliczeń bierzemy połowę ramy.

3 kN/m

EI

5 kN

3

4

2EI

STOPIEŃ STATYCZNEJ NIEWYZNACZALNOŚCI

SSN=5-3=2

1.

PRZYJMUJĘ UKŁAD PODSTAWOWY

3 kN/m

EI

5 kN

2EI

X

1

X

2

4

WARUNKI

0

1

1

=

∆

0

1

2

=

∆

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

4

0

)

(

)

(

)

(

2

1

1

1

1

=

∆

+

∆

+

∆

X

X

P

0

)

(

)

(

)

(

2

2

1

2

2

=

∆

+

∆

+

∆

X

X

P

GDZIE:

1

11

1

1

)

(

X

X

δ

=

∆

2

12

2

1

)

(

X

X

δ

=

∆

PO PRZEKSZTAŁCENIU:

0

1

2

12

1

11

=

+

+

P

X

X

δ

δ

δ

0

2

2

22

1

21

=

+

+

P

X

X

δ

δ

δ

∫

∑

=

EI

M

M

k

i

ik

δ

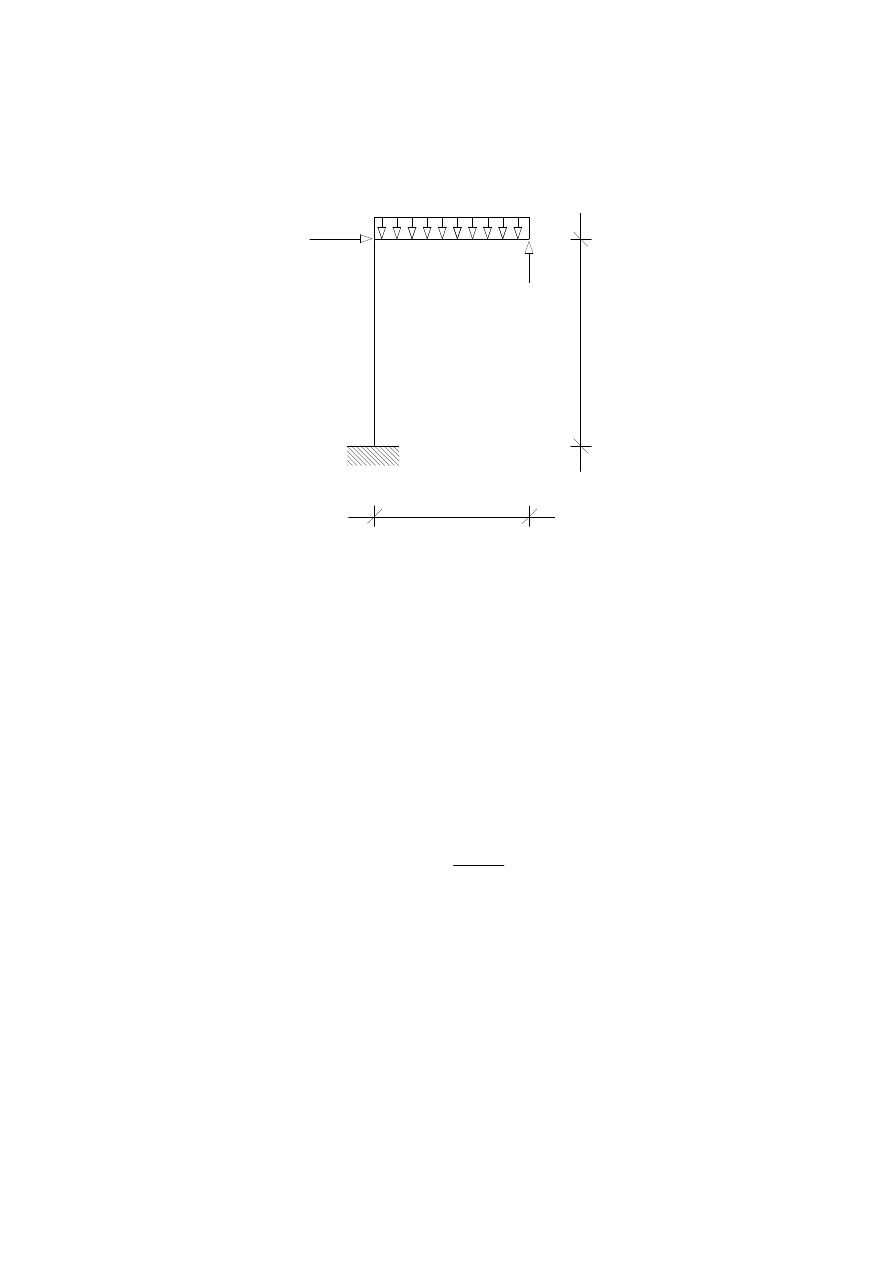
2.

STAN

1

1

=

X

H

A

R

A

M

A

A

EI

3

2EI

1

4

∑

:

X

1

=

A

H

∑

:

Y

0

=

A

R

∑

:

A

M

0

4

1

=

⋅

+

A

M

4

−

=

A

M

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

5

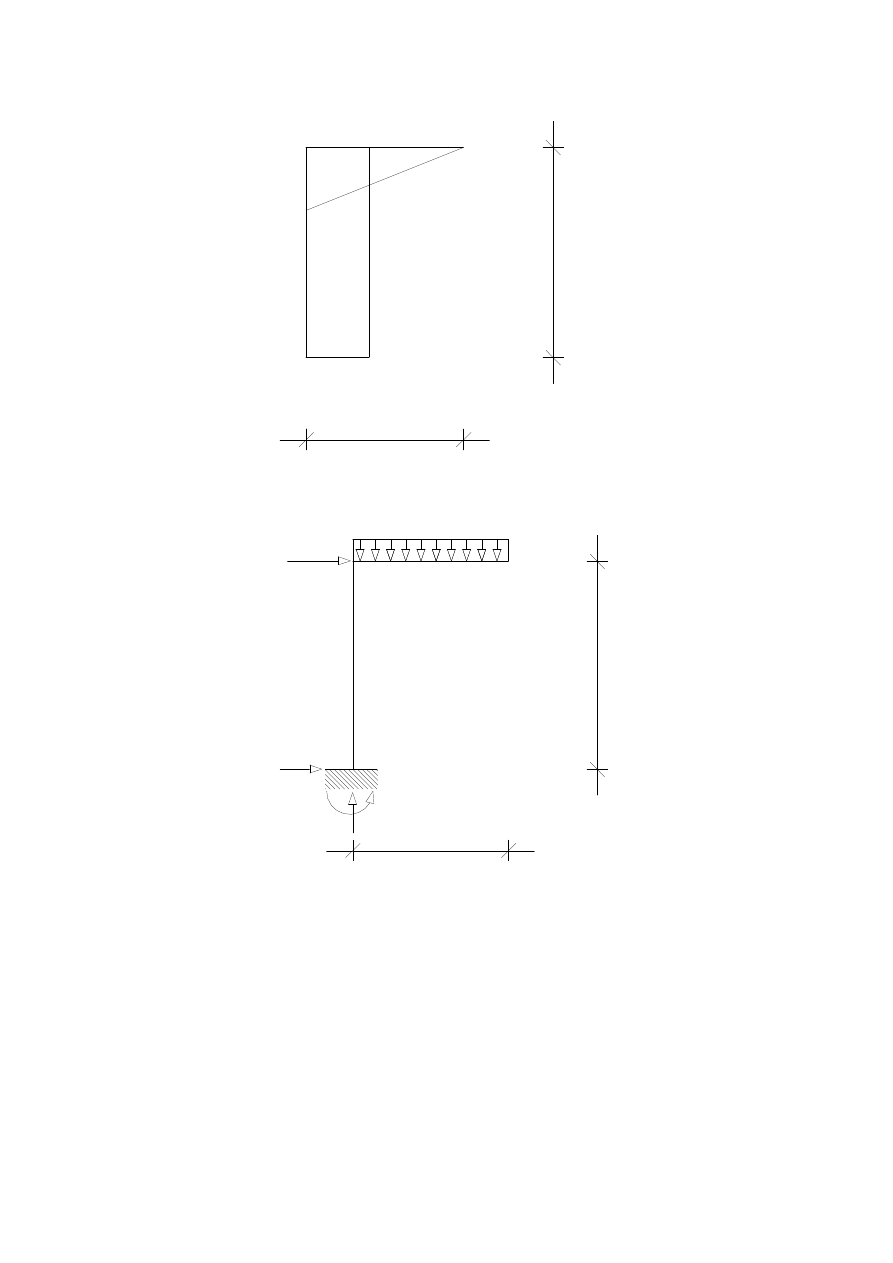
3.

WYKRES MOMENTU W STANIE

1

1

=

X

M

1

[m]

4

3

4

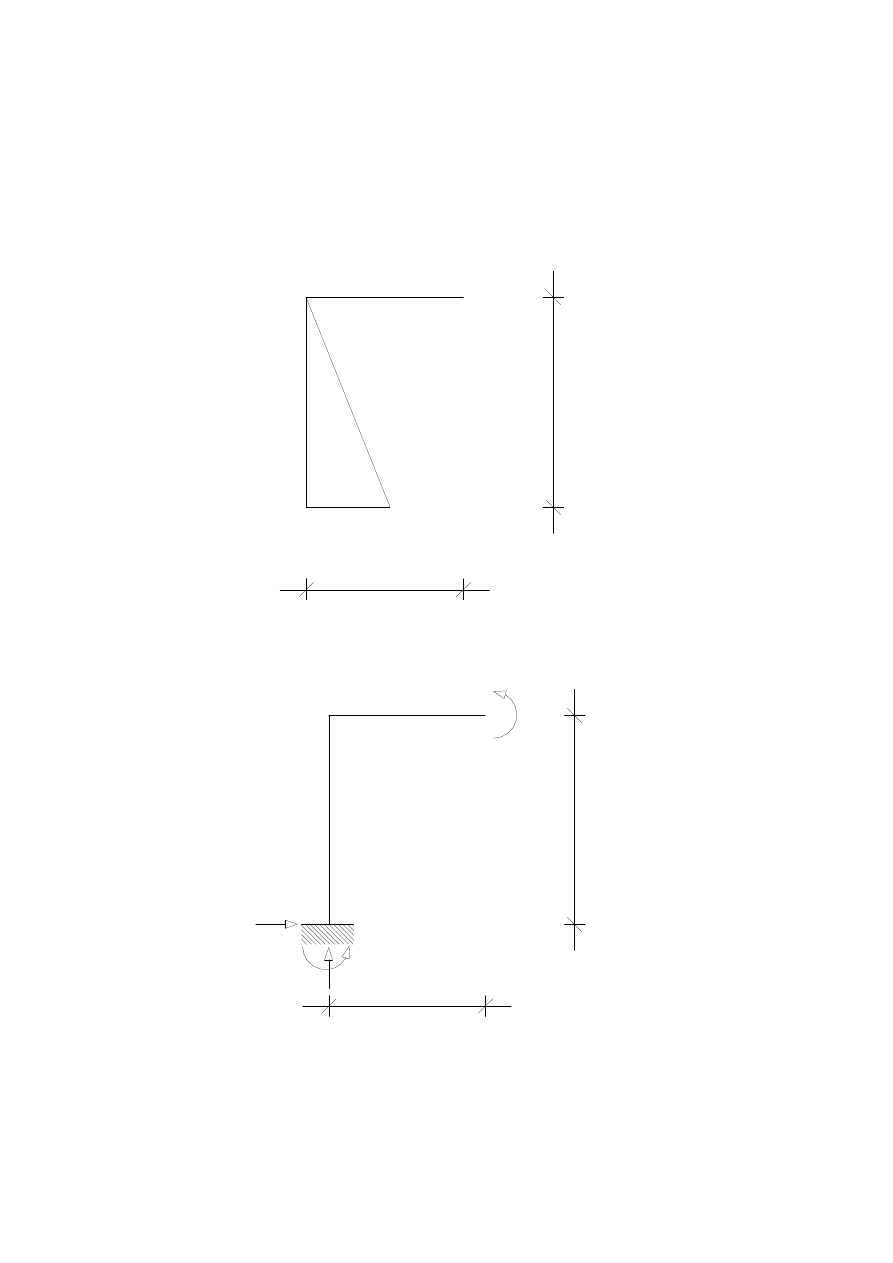
4.

STAN

1

2

=

X

H

A

R

A

M

A

A

EI

3

2EI

1

4

∑

:

X

0

=

A

H

∑

:

Y

0

=

A

R

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

6

∑

:

A

M

0

1

=

+

A

M

1

−

=

A

M

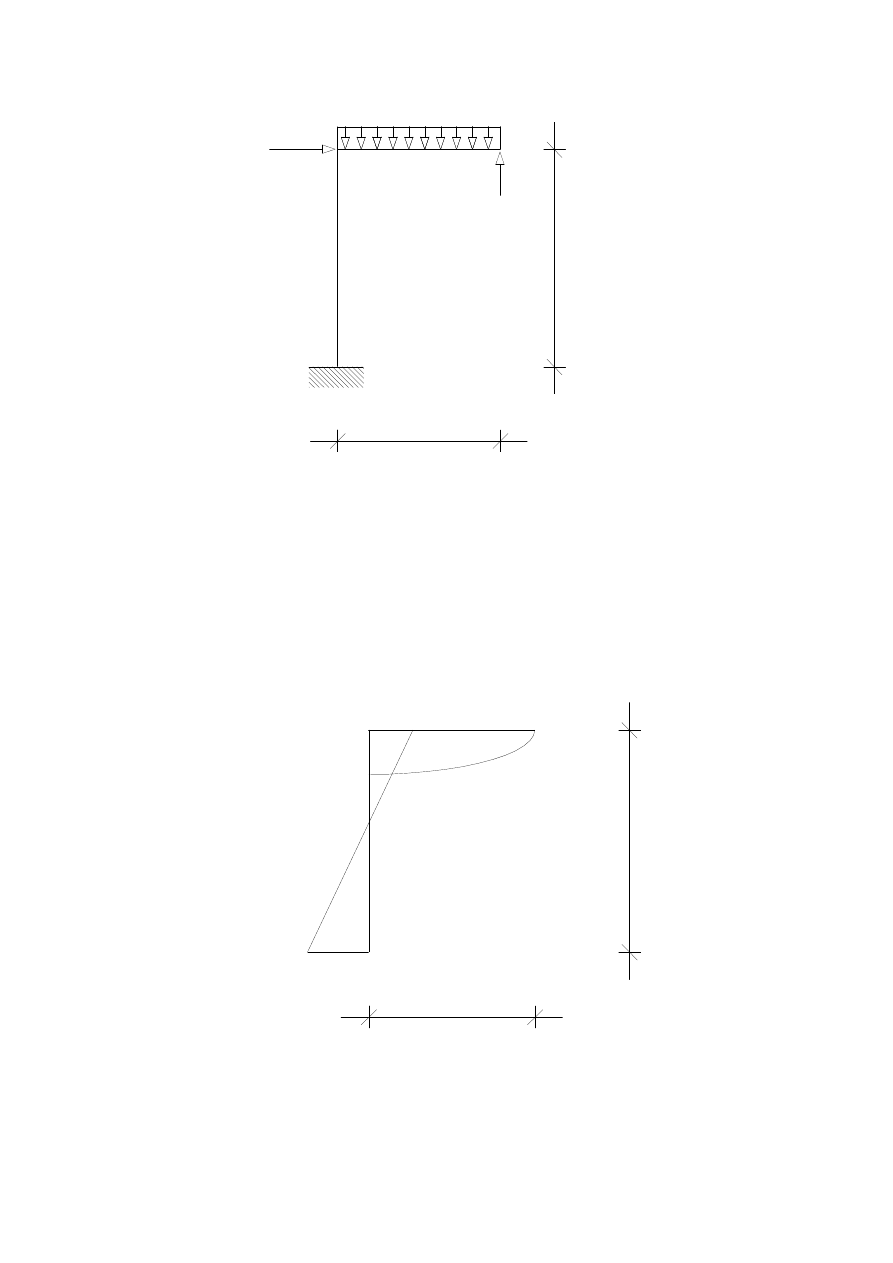
5.

WYKRES MOMENTU W STANIE

1

2

=

X

M

2

[m]

3

1

1

1

4

1

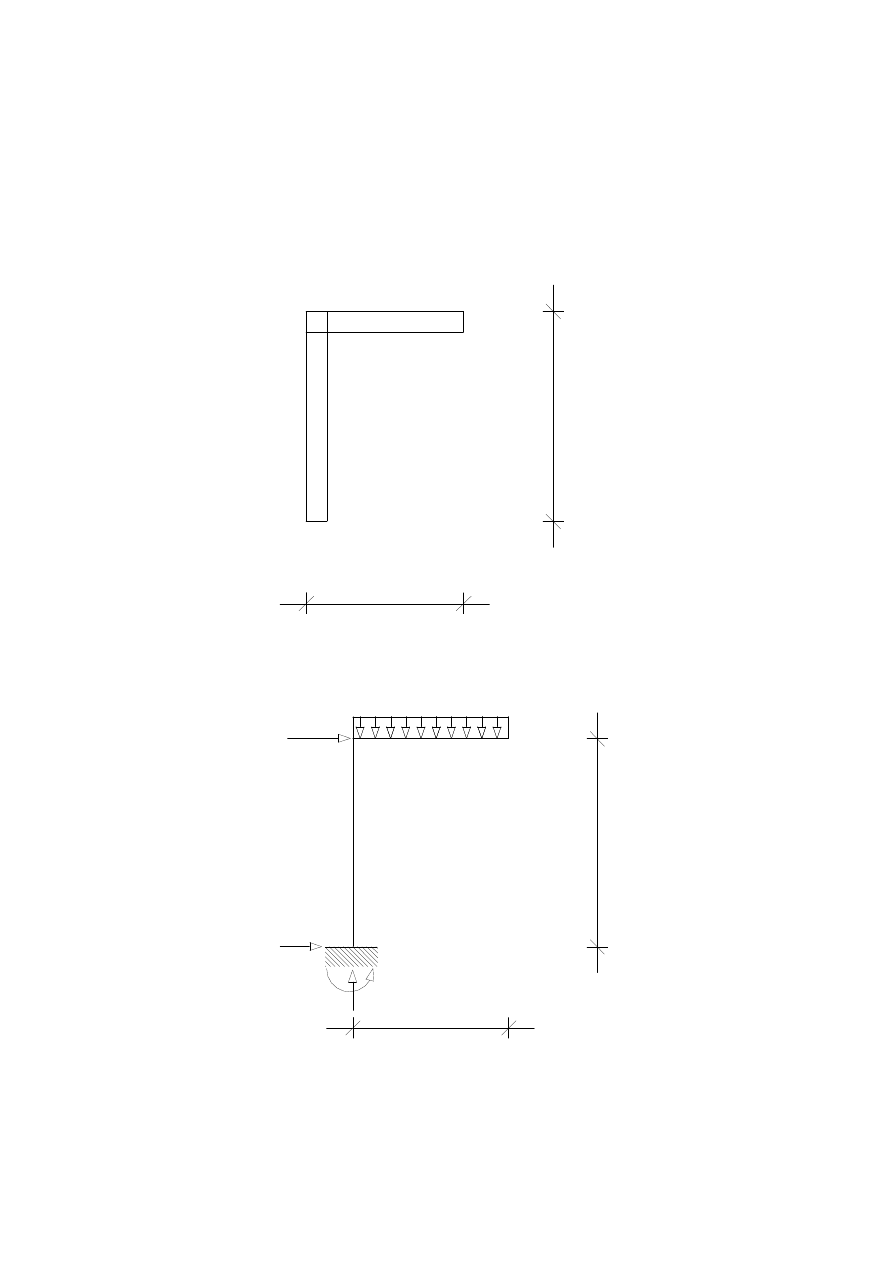
6.

STAN P

3 kN/m

H

A

R

A

M

A

A

EI

5 kN

3

2EI

4

∑

:

X

5

−

=

A

H

∑

:

Y

9

=

A

R

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

7

∑

:

A

M

0

4

5

5

,

1

3

3

=

⋅

−

⋅

⋅

−

A

M

5

,

33

=

A

M

7.

WYKRES MOMENTU W STANIE P

M

P

[kNm]

13,5

33,5

3

13,5

4

8.

WYZNACZANIE

δ

∫

∑

=

EI

M

M

k

i

ik

δ

Dla ułatwienia obliczeń korzystam również ze wzoru Mohra-Wiereszczagina

∫

⋅

=

B

A

S

dx

x

g

x

f

η

)

(

)

(

EI

EI

333

,

21

)

4

3

2

4

4

5

,

0

(

1

11

=

⋅

⋅

⋅

⋅

=

δ

EI

EI

EI

5

,

5

)

1

4

1

(

1

)

1

3

1

(

2

1

22

=

⋅

⋅

+

⋅

⋅

=

δ

EI

EI

8

)

1

4

4

5

,

0

(

1

12

=

⋅

⋅

⋅

=

δ

Zgodnie z twierdzeniem Maxwella

ki

ik

δ

δ

=

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

8

EI

8

21

12

=

=

δ

δ

EI

EI

P

664

,

214

)]

5

,

13

3

/

1

5

,

33

3

2

(

4

4

5

,

0

[

1

1

−

=

⋅

+

⋅

⋅

⋅

⋅

−

=

δ

EI

EI

EI

P

75

,

100

)

1

5

,

33

4

5

,

0

1

5

,

13

4

5

,

0

(

1

)

1

3

8

3

3

3

2

1

5

,

13

3

5

,

0

(

2

1

2

2

−

=

⋅

⋅

⋅

−

⋅

⋅

⋅

−

+

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

−

=

δ

WYZNACZANIE X

1

, X

2

0

75

,

100

5

,

5

8

0

664

,

214

8

333

,

21

2

1

2

1

=

−

+

=

−

+

EI

X

EI

X

EI

EI

X

EI

X

EI

]

[

11

,

8

]

[

017

,

7

2

1

kN

X

kN

X

=

=

5 kN

EI

2EI

3 kN/m

7,017

8,11

4

∑

:

X

kN

H

A

017

,

2

=

∑

:

Y

kN

R

A

9

=

∑

:

A

M

kNm

M

A

678

,

2

=

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

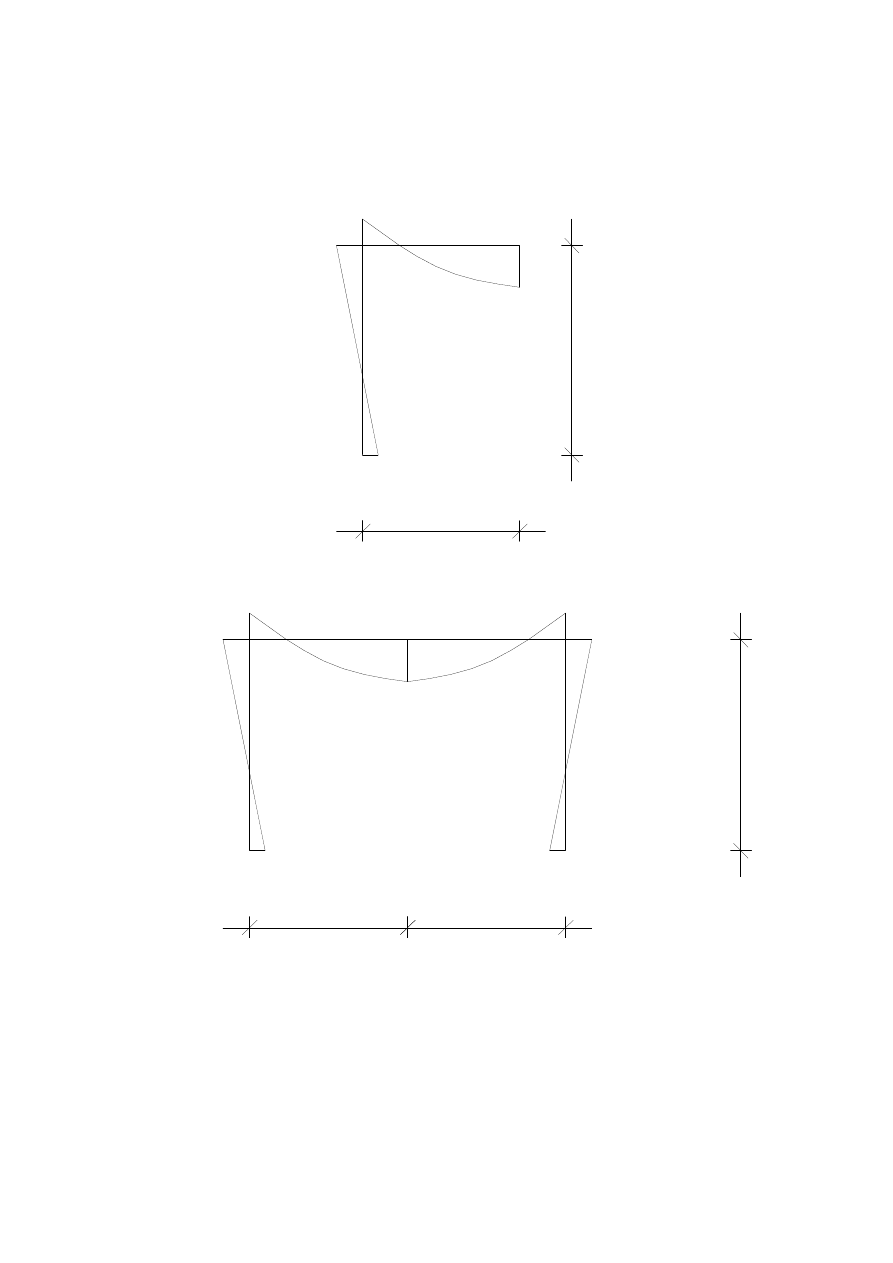
9

M

N

[kNm]

3

2,678

5,39

5,39

8,11

4

3

2,678

5,39

5,39

8,11

4

5,39

5,39

2,678

3

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

10

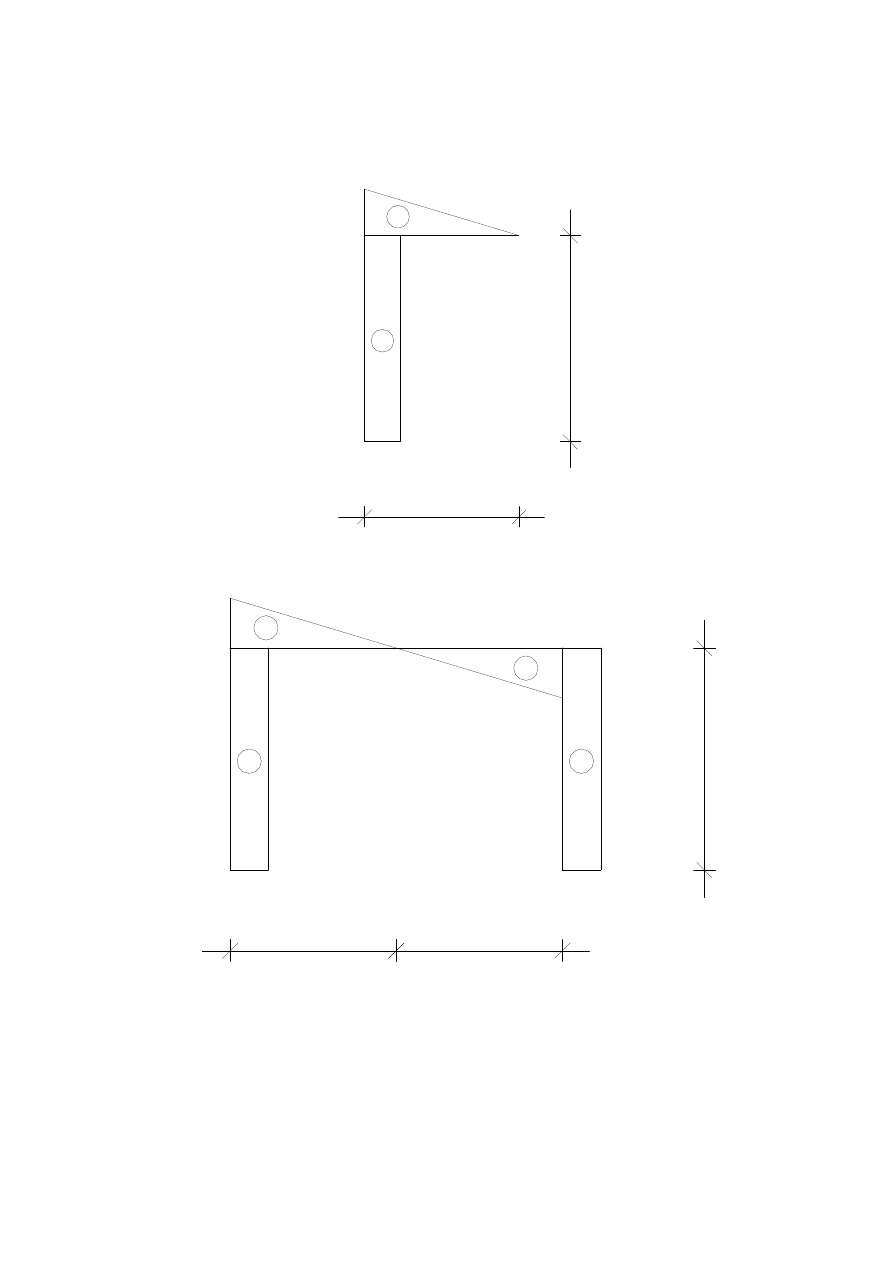
T

N

[kN]

7,017

3

-

4

7,017

9

+

7,017

3

-

7,017

4

9

+

-

+

7,017

7,017

9

3

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

11

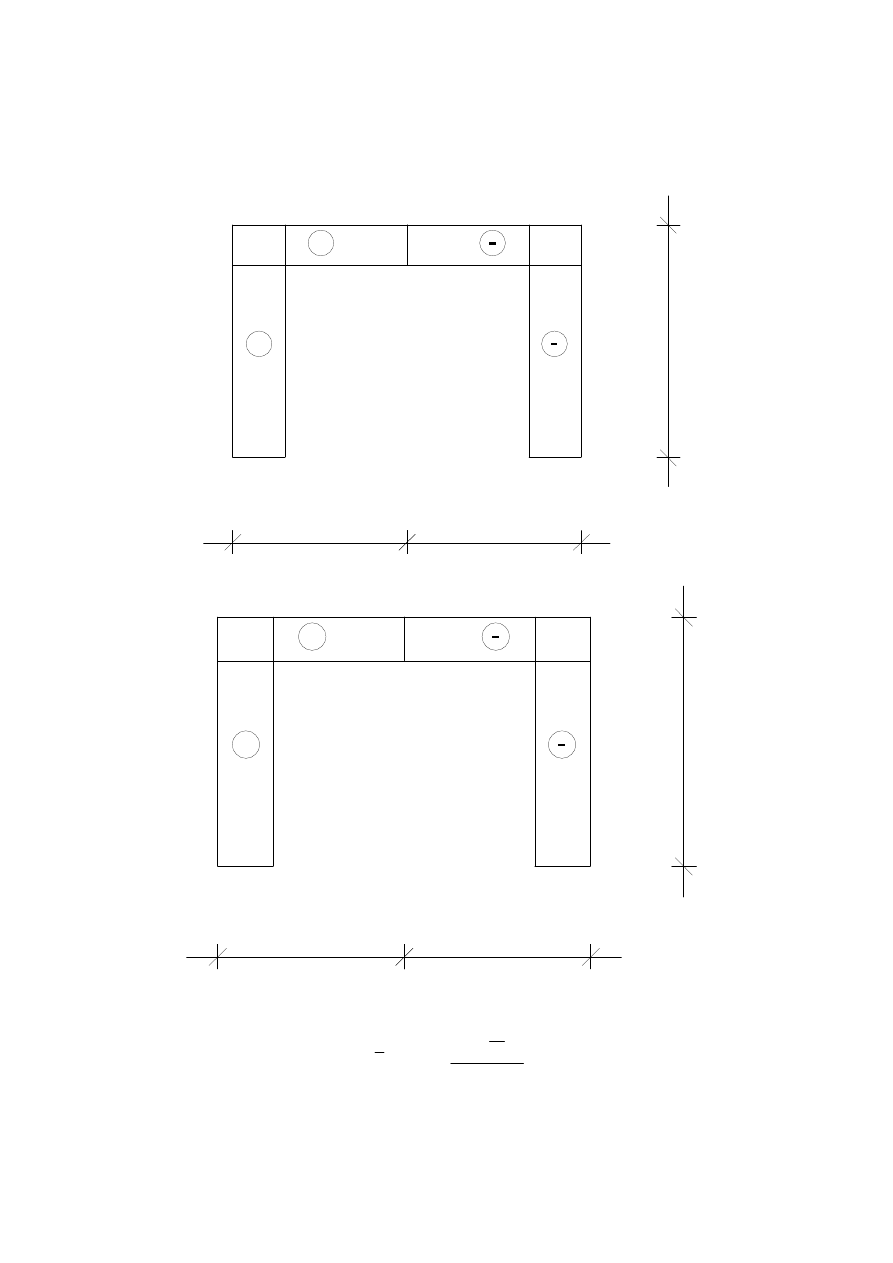
N

N

[kN]

4

3

7,017

-

7,017

9

9

-

7,017

9

9

3

3

7,017

-

7,017

4

9

9

-

7,017

9

9

3

9.

WYKONUJE SPRAWDZENIE KINEMATYCZNE

∫

∑

=

⋅

dx

EI

M

M

o

n

)

(

)

(

1

δ

W tym celu przyjmuję nowy układ podstawowy

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

12

2EI

3

EI

R

A

H

A

X

1

5 kN

3 kN/m

X

2

H

B

4

10.

STAN OBCIĄśENIA WIRTUALNEGO W NOWYM UKŁADZIE
PODSTAWOWYM

H

A

R

A

1

EI

3

2EI

4

H

B

∑

:

A

M

25

,

0

−

=

A

H

∑

:

Y

0

=

A

R

∑

:

X

25

,

0

−

=

B

H

11.

WYKRES MOMENTU W STANIE OBCIĄśENIA WIRTUALNEGO

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

13

M [m]

3

1

4

12.

OBLICZANIE ZEROWEGO PRZEMIESZCZENIA PUNKTU A

EI

EI

A

0178

,

0

]

1

3

2

678

,

2

4

2

1

)

1

3

1

(

39

,

5

4

5

,

0

[

1

1

1

=

⋅

⋅

⋅

⋅

−

⋅

⋅

⋅

⋅

=

⋅

ϕ

BŁĄD PROCENTOWY

0

%

49

,

0

%

100

)

5897

,

3

:

0178

,

0

(

≈

=

⋅

EI

EI

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

14

W przypadku obciążenia antysymetrycznego wykresy NORMALNEJ i MOMENTU

są antysymetryczne, a wykres TNĄCEJ - symetryczny.

EI

3

5 kN

3 kN/m

EI

4

3

2EI

3 kN/m

5 kN

Do obliczeń bierzemy połowę ramy.

3 kN/m

EI

5 kN

3

4

2EI

STOPIEŃ STATYCZNEJ NIEWYZNACZALNOŚCI

SSN=4-3=1

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

15

13.

PRZYJMUJĘ UKŁAD PODSTAWOWY

2EI

3

EI

5 kN

3 kN/m

4

X

1

WARUNKI

0

1

1

=

∆

0

)

(

)

(

1

1

1

=

∆

+

∆

X

P

GDZIE:

1

11

1

1

)

(

X

X

δ

=

∆

PO PRZEKSZTAŁCENIU:

0

1

1

11

=

+

P

X

δ

δ

∫

∑

=

EI

M

M

k

i

ik

δ

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

16

14.

STAN

1

1

=

X

3

R

A

H

A

M

A

A

EI

1

4

2EI

∑

:

X

0

=

A

H

∑

:

Y

1

−

=

A

R

∑

:

A

M

0

3

1

=

⋅

+

A

M

3

−

=

A

M

15.

WYKRES MOMENTU W STANIE

1

1

=

X

M

1

[m]

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

17

3

3

3

3

4

16.

STAN P

3 kN/m

H

A

R

A

M

A

A

EI

5 kN

3

2EI

4

∑

:

X

5

−

=

A

H

∑

:

Y

9

=

A

R

∑

:

A

M

0

4

5

5

,

1

3

3

=

⋅

−

⋅

⋅

−

A

M

5

,

33

=

A

M

17.

WYKRES MOMENTU W STANIE P

M

P

[kNm]

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

18

13,5

33,5

3

13,5

4

18.

WYZNACZANIE

δ

∫

∑

=

EI

M

M

k

i

ik

δ

Dla ułatwienia obliczeń korzystam również ze wzoru Mohra-Wiereszczagina

∫

⋅

=

B

A

S

dx

x

g

x

f

η

)

(

)

(

EI

EI

EI

5

,

40

)

3

4

3

(

1

)

3

3

/

2

3

3

5

,

0

(

2

1

11

=

⋅

⋅

+

⋅

⋅

⋅

⋅

=

δ

EI

EI

EI

P

1875

,

297

)

3

5

,

33

4

5

,

0

3

5

,

13

4

5

,

0

(

1

)

3

5

,

0

3

8

3

3

3

/

2

3

3

/

2

5

,

13

3

5

,

0

(

2

1

2

1

−

=

⋅

⋅

⋅

−

⋅

⋅

⋅

−

+

⋅

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

⋅

−

=

δ

WYZNACZANIE X

1

0

1875

,

297

5

,

40

1

=

−

EI

X

EI

]

[

338

,

7

1

kN

X

=

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

19

3 kN/m

EI

5 kN

3

4

2EI

7,338

∑

:

X

5

−

=

A

H

∑

:

Y

652

,

1

=

A

R

∑

:

A

M

486

,

11

=

A

M

19.

WYKRESY RAMY STATYCZNIE NIEWYZNACZALNEJ

M

N

[kNm]

11,486

3

8,514

8,514

4

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

20

T

N

[kN]

-

5

3

+

1,667

5

7,338

4

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

21

-

5

3

+

5

7,338

4

5

5

3

N

N

[kN]

3

1,667

-

1,667

4

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

22

3

1,667

-

1,667

4

1,667

1,667

3

20.

WYKONUJE SPRAWDZENIE KINEMATYCZNE

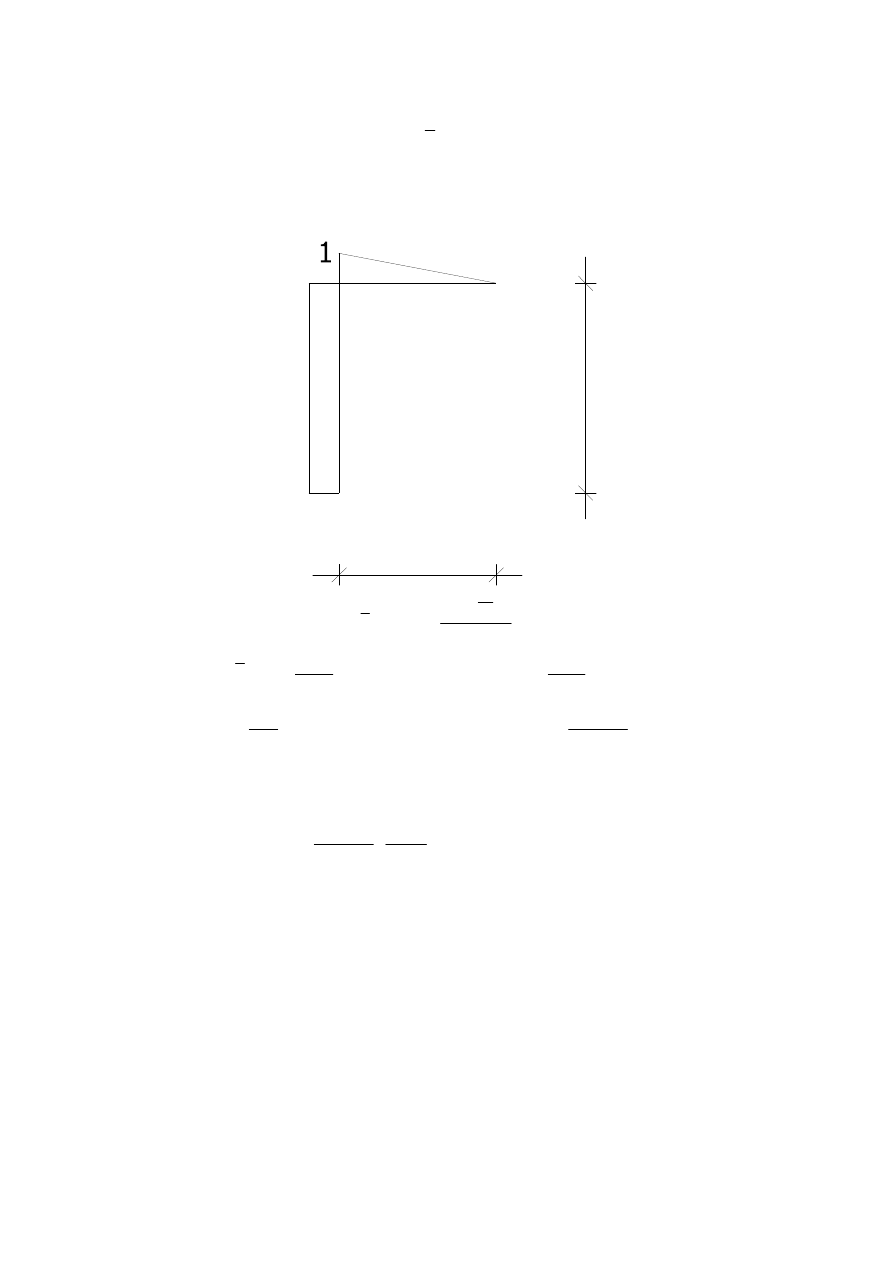
W tym celu przyjmuję nowy układ podstawowy

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

23

3 kN/m

H

A

R

A

X

1

A

EI

5 kN

3

4

R

B

2EI

21.

STAN OBCIĄśENIA WIRTUALNEGO W NOWYM UKŁADZIE
PODSTAWOWYM

H

A

R

A

1

A

EI

3

4

R

B

2EI

∑

:

X

0

=

B

H

∑

:

A

M

3

1

−

=

B

R

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

24

∑

:

Y

3

1

=

A

R

WYKRES MOMENTU W STANIE OBCIĄśENIA WIRTUALNEGO

M [m]

3

1

1

4

∑ ∫

=

⋅

m

o

n

dx

EI

M

M

)

(

)

(

1

δ

EI

EI

EI

A

00335

,

0

)

1

486

,

11

4

5

,

0

1

514

,

8

4

5

,

0

(

1

)

1

5

,

0

3

8

3

3

3

/

2

1

3

/

2

514

,

8

3

5

,

0

(

2

1

1

2

−

=

⋅

⋅

⋅

+

⋅

⋅

⋅

−

+

⋅

⋅

⋅

⋅

⋅

−

⋅

⋅

⋅

⋅

−

=

⋅

ϕ

BŁĄD PROCENTOWY

0

%

056

,

0

%

100

)

944

,

5

:

00335

,

0

(

≈

=

⋅

EI

EI

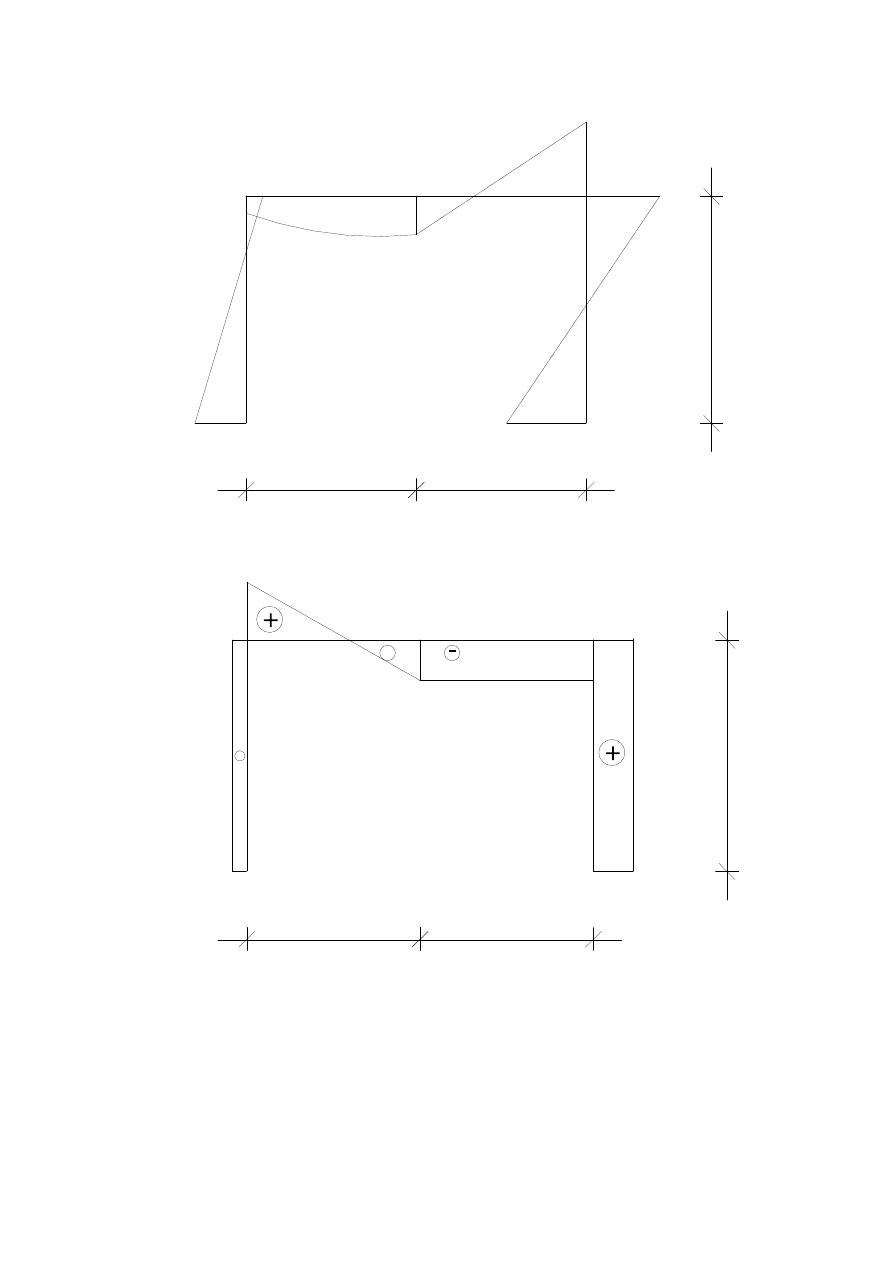
Wykresy w układzie statycznie niewyznaczalnym

M [kNm]

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

25

8,808

3

3,124

4

14,164

13,904

3

3,124

13,904

8,11

T [kN]

-

2,983

3

+

10,667

7,338

4

7,017

3

2,983

7,338

7,017

N [kN]

Hasan Qaraqish, Paweł Wasiniewski

Obliczanie układów statycznie niewyznaczalnych

Gr. 3 rok III

26

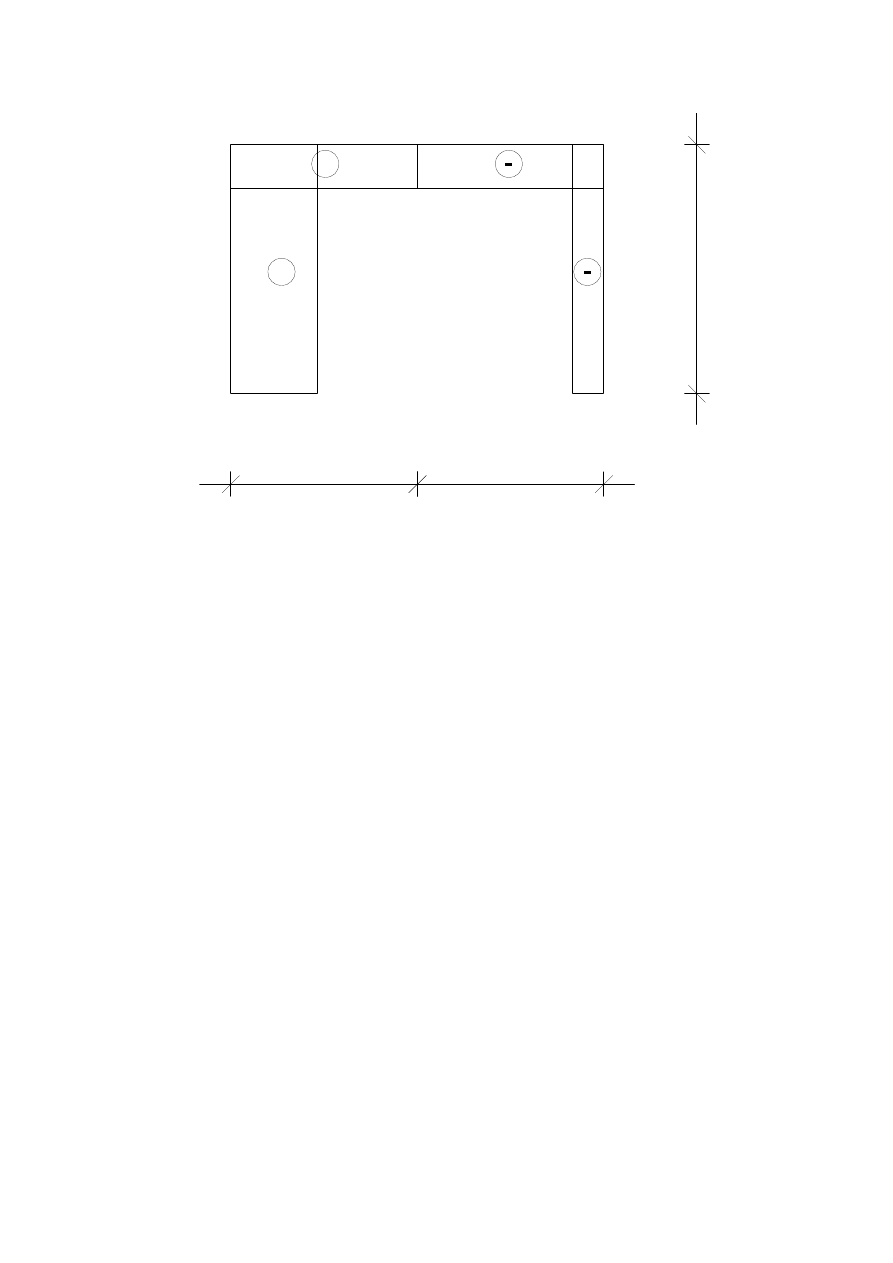
3

7,017

-

4

14

-

7,017

4

3

14

4

10,667

7,333