Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

1

POLITECHNIKA POZNAŃSKA
INSTYTUT KONSTRUKCJI BUDOWLANYCH
ZAKŁAD MECHANIKI BUDOWLI

ĆWICZENIE NR 1

OBLICZANIE RAMY PRZESTRZENNEJ METODĄ SIŁ

Agnieszka Sysak Gr. 3

2004-03-16

Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

2

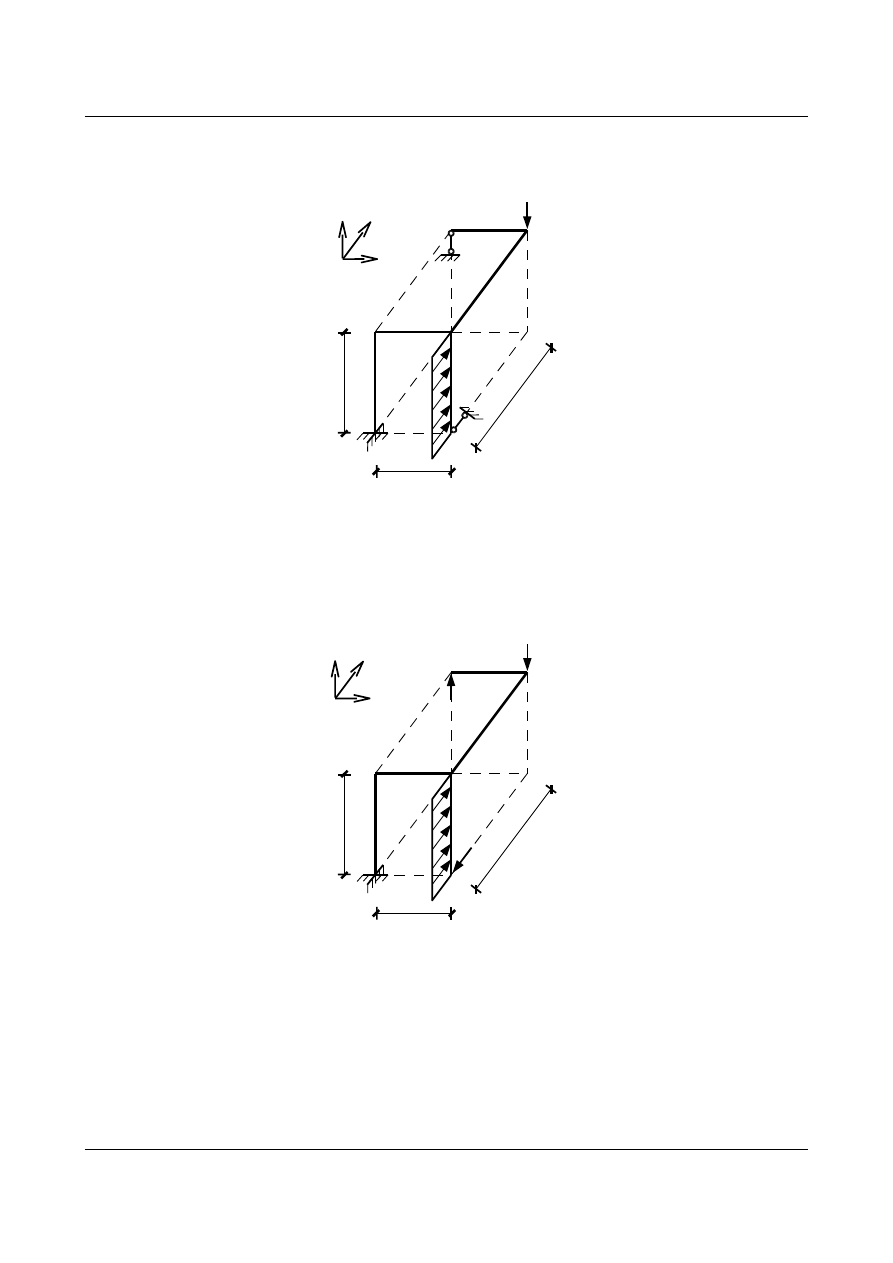
Dla ramy przestrzennej wyznaczyć wykresy sił wewnętrznych wywołanych zadanym obciążeniem.

Przyjąć, że rama składa się z prętów stalowych o przekroju kołowym (G=0,375E, J

s

=2J).

10 kN

5 kN/m

4,0

3,0

5,0

[m]

x

y

z

Układ jest statycznie niewyznaczalny dlatego określamy stopień statycznej niewyznaczalności i dobieramy
układ podstawowy.

SSN = 2

W celu rozwiązania zadania metodą sił przyjmujemy układ podstawowy

10 kN

5 kN/m

4,0

3,0

5,0

[m]

X

2

X

1

A

B

x

y

z

który musi spełniać warunki kinematycznej zgodności z układem wyjściowym. Oznacza to, że
przemieszczenie punktu A po kierunku osi y oraz przemieszczenie punktu B po kierunku osi z muszą być
równe zero.



A

y

=0



B

z

=0

Agnieszka Sysak Gr. 3

2004-03-16

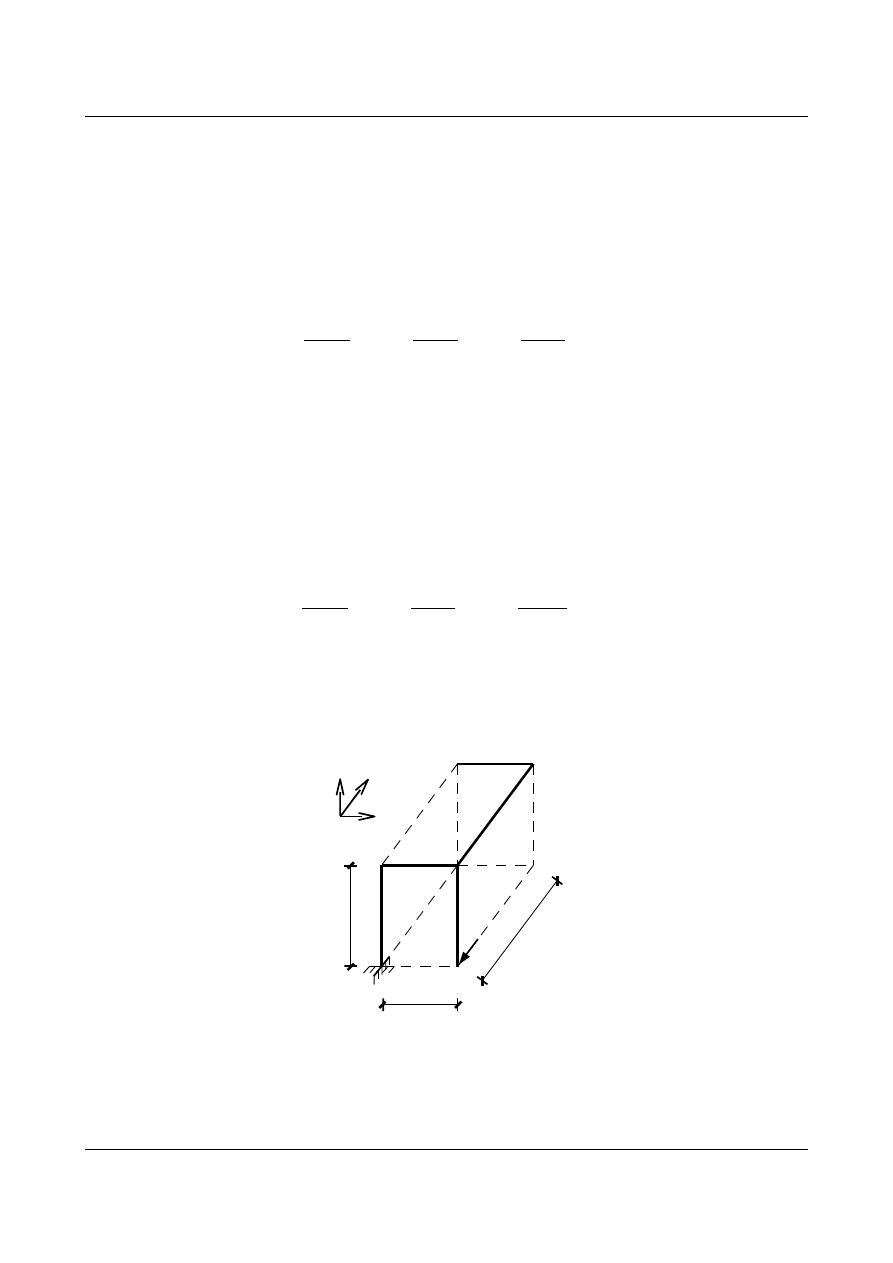
Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

3

Na powyższe przemieszczenia wpływ mają nadliczbowe siły X

i

oraz obciążenie zewnętrzne. Równania

kanoniczne przyjmą zatem postać:



A

y

=

11

⋅X

1



12

⋅X

2



1 P

=0



B

z

=

21

⋅X

1



22

⋅X

2



2 P

=0

Przemieszczenia w ramie przestrzennej obliczamy pomijając wpływ sił normalnych i tnących:



1 ⋅

ik

=

∑∫

M

i

y

M

k

y

EJ

y

dx

∑∫

M

i

z

M

k

z

EJ

z

dx

∑∫

M

i

s

M

k

s

GJ

s

dx

gdzie:

M

i

y

,

M

k

y

,

M

i

z

,

M

k

z

- momenty zginające liczone odpowiednio względem osi y i z,

M

i

s

,

M

k

s

- momenty skręcające liczone względem osi pręta,

J

s

- biegunowy moment bezwładności.

Ponieważ przekrój pręta jest kołowy to J

y

= J

z

=J. Podstawiając dane G i J

s

otrzymamy:



1 ⋅

ik

=

∑∫

M

i

y

M

k

y

EJ

dx

∑∫

M

i

z

M

k

z

EJ

dx

∑∫

M

i

s

M

k

s

0,75 EJ

dx

Kolejnym etapem jest wyznaczenie wartości momentów zginających i skręcających od sił

jednostkowych, przyłożonych kolejno w miejsca niewiadomych X

1

i X

2

, oraz od obciążenia zewnętrznego.

•

Stan od obciążenia X

1

= 1

4,0

3,0

5,0

[m]

X

1

=1

x

y

z

Agnieszka Sysak Gr. 3

2004-03-16

Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

4

4,0

3,0

5,0

[m]

4,0

3,0

5,0

[m]

x

x

y

y

z

z

M

1

[m]

M

s

1

[m]

4

4

3

_

-4

_

-3

•

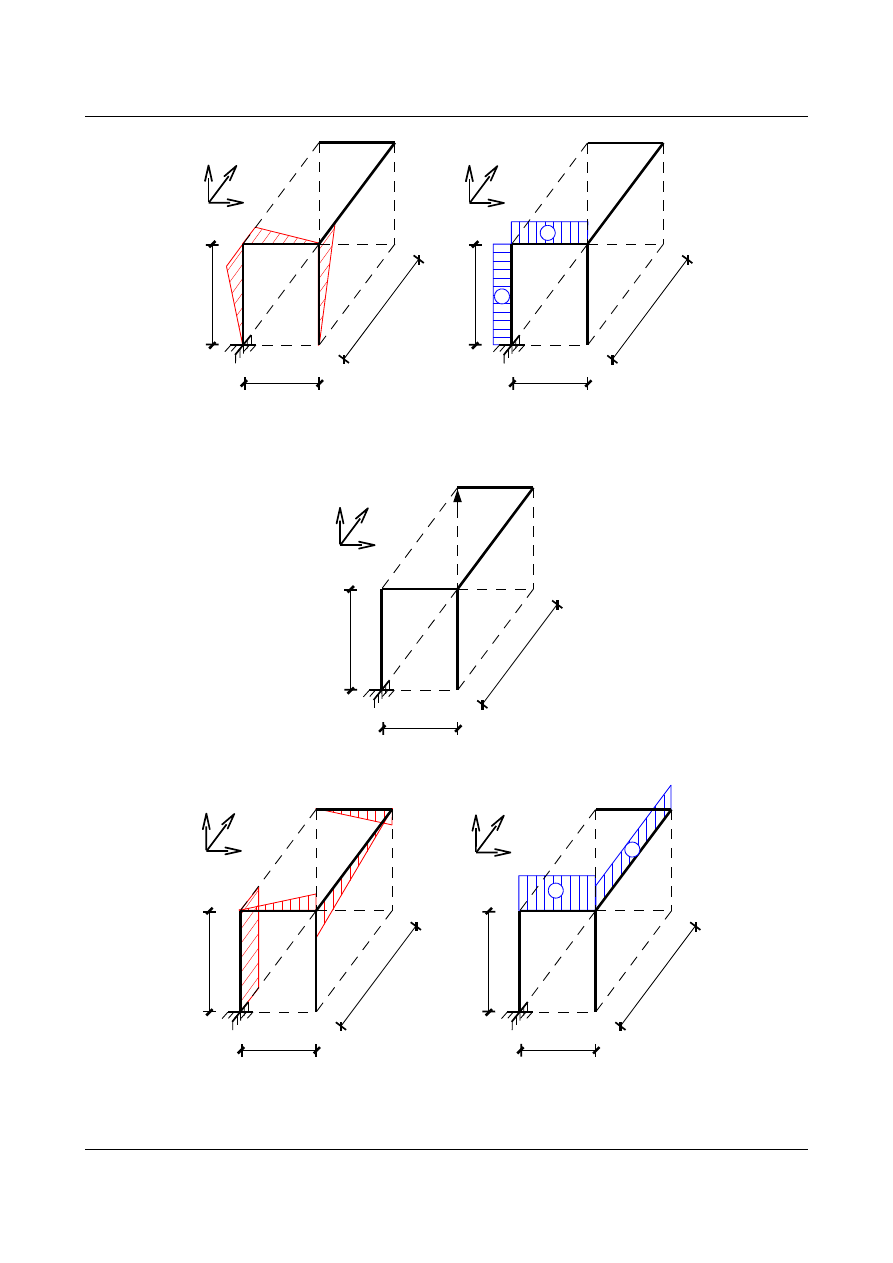
Stan od obciążenia X

2

= 1

4,0

3,0

5,0

[m]

x

y

z

X

2

=1

4,0

3,0

5,0

[m]

4,0

3,0

5,0

[m]

x

x

y

y

z

z

M

2

[m]

M

s

2

[m]

5

3

3

5

+

3

5

+

Agnieszka Sysak Gr. 3

2004-03-16

Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

5

•

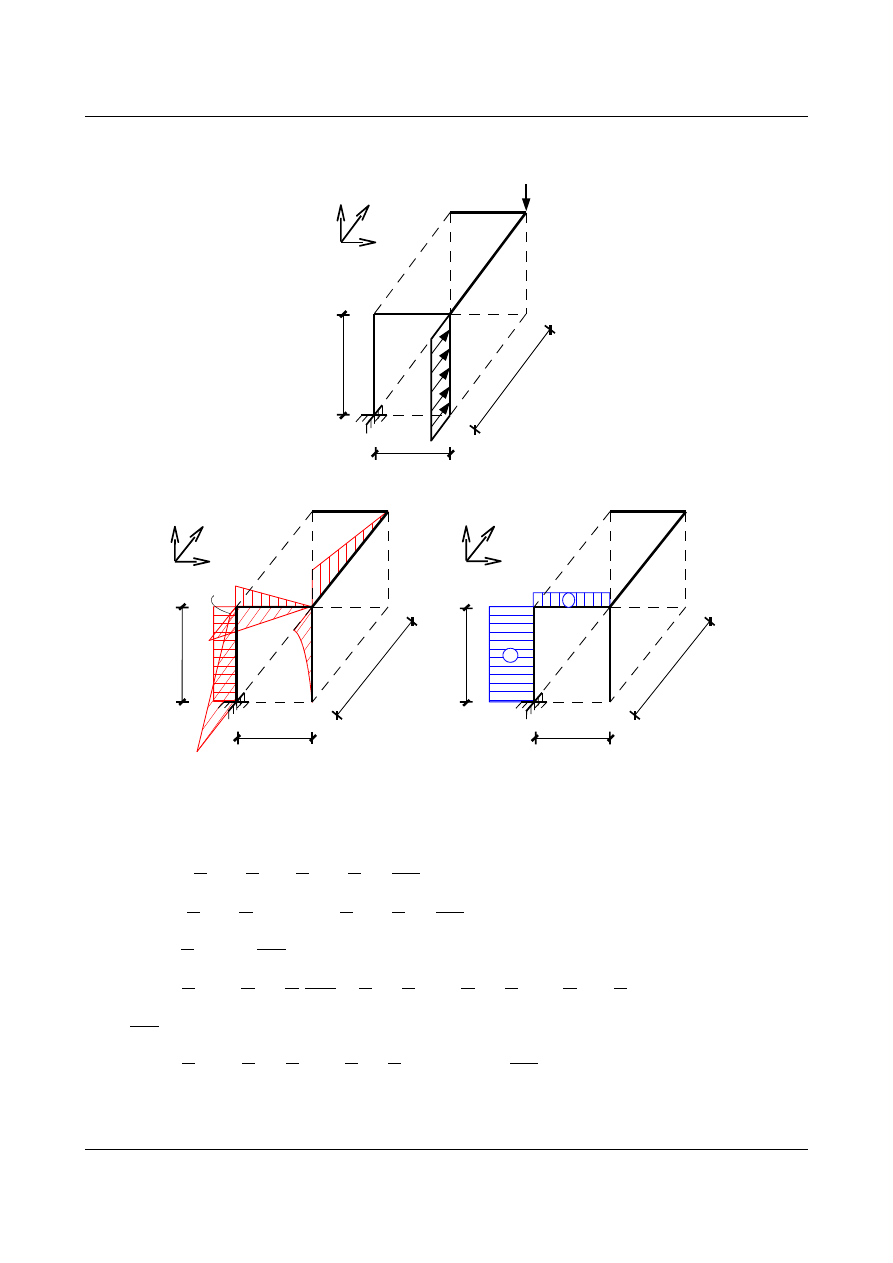
Stan od obciążenia P

10 kN

5 kN/m

4,0

3,0

5,0

[m]

x

y

z

4,0

3,0

5,0

[m]

4,0

3,0

5,0

[m]

x

x

y

y

z

z

M

0

P

[kNm]

M

s0

P

[kNm]

60

40

50

30

+

60

-10

_

30

90

10

Obliczamy potrzebne w równaniach kanonicznych przemieszczeniach korzystając z metody Wereszczagina
– Mohra:

EJ 

11

=2 ⋅



1

2

⋅4 ⋅4 ⋅

2
3

⋅4



1

2

⋅3 ⋅3 ⋅

2
3

⋅3 

1

0,75

⋅

[

−4 ⋅3 ⋅−4−3⋅4 ⋅−3

]

=163,6 

EJ 

22

=2 ⋅

1

2

⋅3 ⋅3 ⋅

2
3

⋅3 4 ⋅5 ⋅5 

1

2

⋅5 ⋅5 ⋅

2
3

⋅5 

1

0,75

⋅

[

5 ⋅3 ⋅5 3 ⋅5 ⋅3

]

=319,6 

EJ 

12

=−1

2

⋅4 ⋅4 ⋅5 

1

0,75

⋅−4⋅3 ⋅5 =−120,0

EJ 

1 P

=−1

2

⋅40 ⋅4 ⋅

2
3

⋅4 

2
3

⋅5

⋅4

2

8

⋅4 ⋅

1

2

⋅4 −

1

2

⋅60 ⋅3 ⋅

2
3

⋅3 

1

2

⋅4 ⋅4 ⋅



2
3

⋅10 

1
3

⋅90





 1

0,75

⋅[−4 ⋅3 ⋅−10−3 ⋅4 ⋅60]=−846,6 

EJ 

2 P

=−1

2

⋅50 ⋅5 ⋅

2

3

⋅5 

1

2

⋅30 ⋅3 ⋅

1

3

⋅3 −

1

2

⋅10 90⋅4 ⋅5 

1

0,75

⋅−10⋅3 ⋅5 =−1571,6 

Agnieszka Sysak Gr. 3

2004-03-16

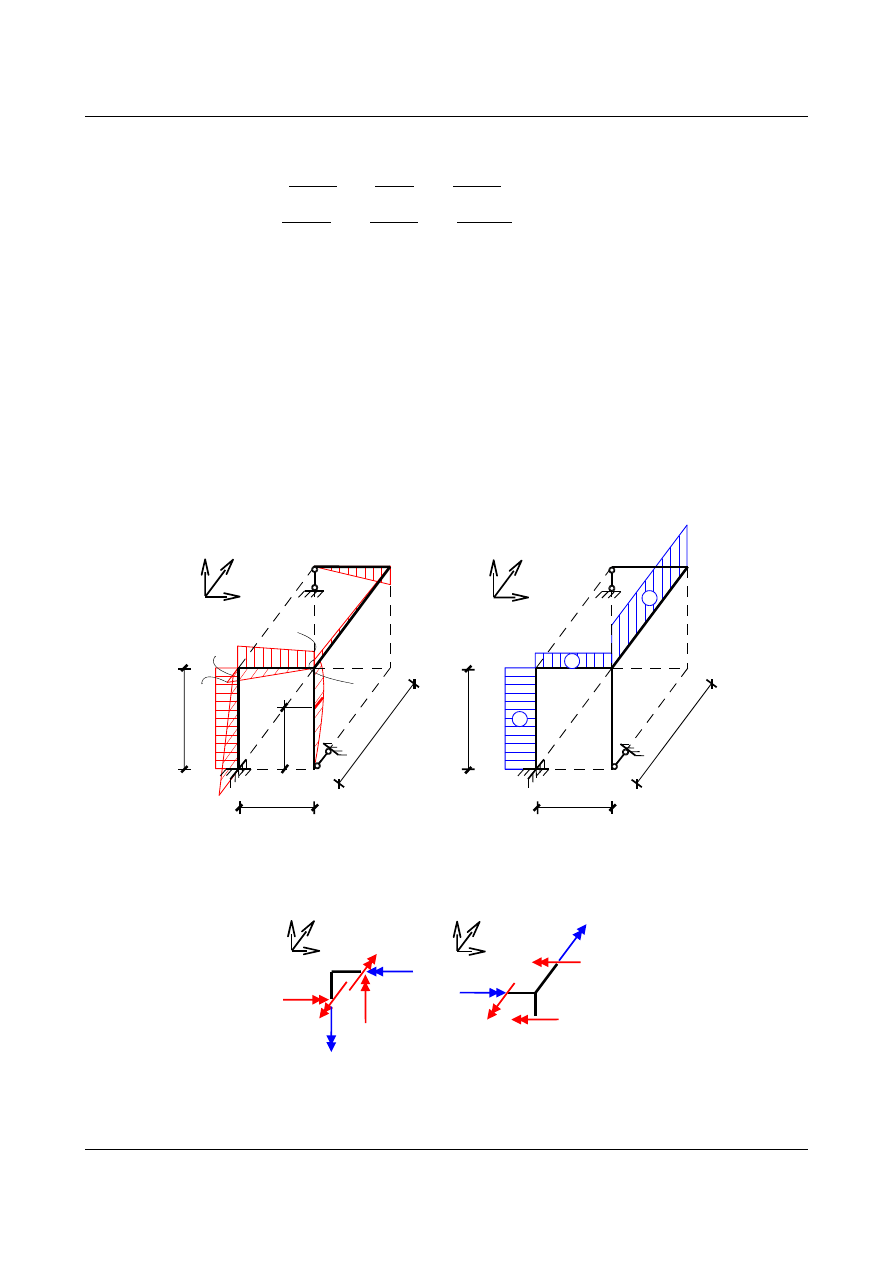
Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

6

Układ równań kanonicznych przyjmuje postać:

{

163,6 

EJ

⋅X

1

− 120,0

EJ

⋅X

2

− 846,

6 

EJ

=0

−120,0

EJ

⋅X

1

 319,

6 

EJ

⋅X

2

− 1571,

6 

EJ

=0

Z rozwiązania powyższego układu otrzymano następujące wyniki:

{

X

1

=12,111 [kN ]

X

2

=9,463 [kN ]

Wartości momentów zginających i skręcających w układzie niewyznaczalnym otrzymamy korzystając z
zasady superpozycji:

M

n

=M

P

0

M

1

⋅X

1

M

2

⋅X

2

M

sn

=M

s

P

0

M

1

s

⋅X

1

M

2

s

⋅X

2

4,0

3,0

5,0

[m]

4,0

3,0

5,0

[m]

x

x

y

y

z

z

M

(n)

[kNm]

M

s(n)

[kNm]

23,667

8,444

2,685

30

+

23,667

-11,129

_

30

42,685

11,129

+

28,389

28,389

28,389

14,399

2,42

•

Sprawdzenie równowagi w węzłach

x

x

y

y

z

z

23,667

30

11,129

30

11,129

8,444

2,685

28,389

28,389

11,129

23,667

Agnieszka Sysak Gr. 3

2004-03-16

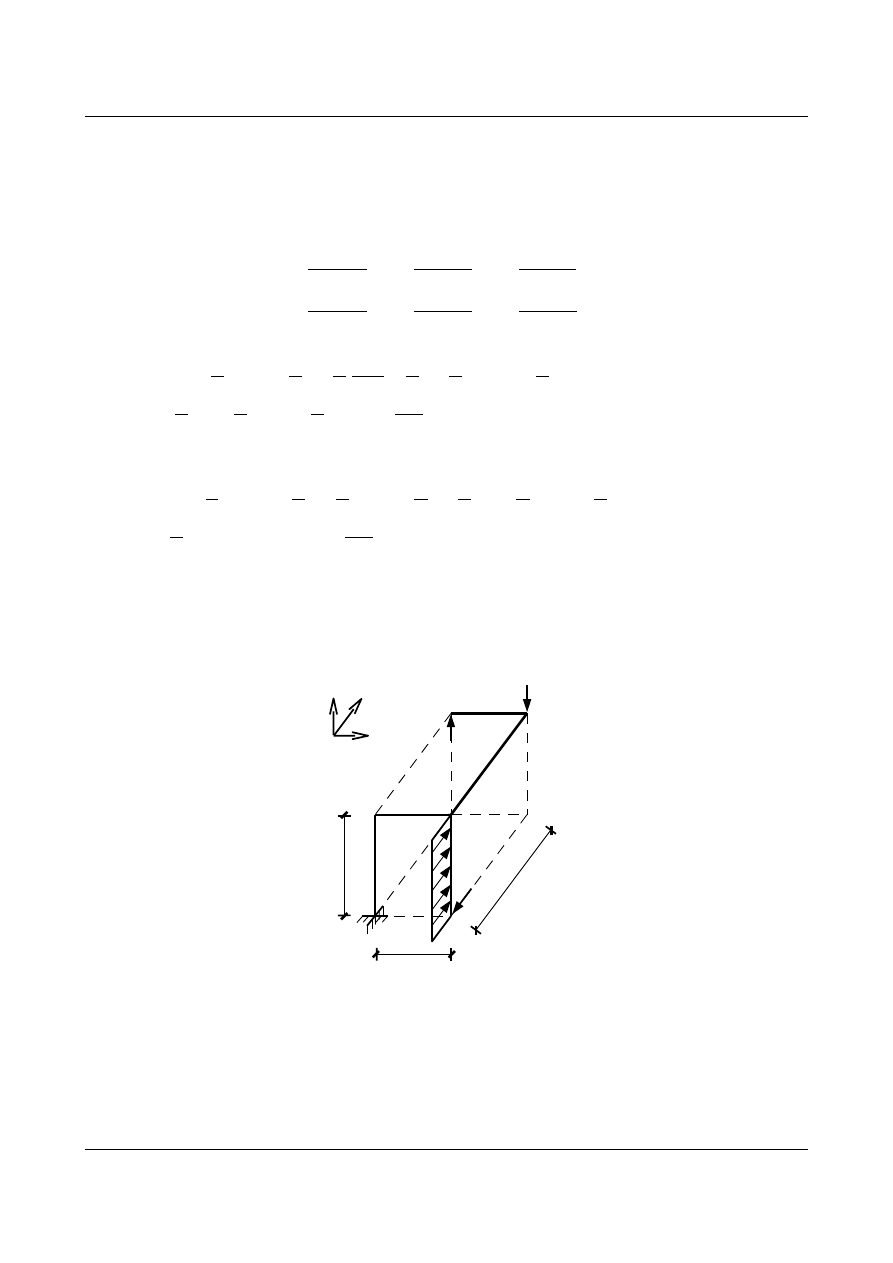
Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

7

•

Kontrola kinematyczna

W celu wykonania kontroli kinematycznej korzystamy z twierdzenia redukcyjnego. Do sprawdzenia przyjęto
układy podstawowe takie jak w stanach X

1

= 1 oraz X

2

= 1 z tą różnicą, że tym razem przyłożone siły

jedynkowe są siłami wirtualnymi.



1 ⋅

A

y

=

∑∫

M

1

y

M

y n

EJ



∑∫

M

1

z

M

z n

EJ



∑∫

M

1

s

M

sn

0,75 EJ



1 ⋅

B

z

=

∑∫

M

2

y

M

y n

EJ



∑∫

M

2

z

M

z n

EJ



∑∫

M

2

s

M

sn

0,75 EJ

EJ 

A

y

=1

2

⋅8,444 ⋅4 ⋅

2
3

⋅4 

2
3

⋅5

⋅4

2

8

⋅4 ⋅

1

2

⋅4 −

1

2

⋅3 ⋅23,667 ⋅

2
3

⋅3 

1

2

⋅4 ⋅4 ⋅



2
3

⋅11,129 

1
3

⋅42,685



 1

0,75

⋅−4 ⋅3 ⋅−11,129−3 ⋅4 ⋅23,667=

=200,548 −200,608 =−0,060 ≈0

EJ 

B

z

=1

2

⋅28,389 ⋅3 ⋅

2
3

⋅3 −

1

2

⋅2,685 ⋅5 ⋅

2
3

⋅5 

1

2

⋅3 ⋅3 ⋅



2
3

⋅28,389 

1
3

⋅30



−

−1

2

⋅11,129 42,685⋅4 ⋅5 

1

0,75

⋅3 ⋅5 ⋅28,389 −3 ⋅5 ⋅11,129=

=−345,181345,200=0,019 ≈0

Ponieważ przy obliczeniu przemieszczeń pominięto wpływ normalnych i tnących, wykresy te w układzie
niewyznaczalnym musimy wykonać rozwiązując układ od obliczonych nadliczbowych i obciążenia
zewnętrznego.

10 kN

5 kN/m

4,0

3,0

5,0

[m]

9,463 kN

12,111 kN

x

y

z

Agnieszka Sysak Gr. 3

2004-03-16

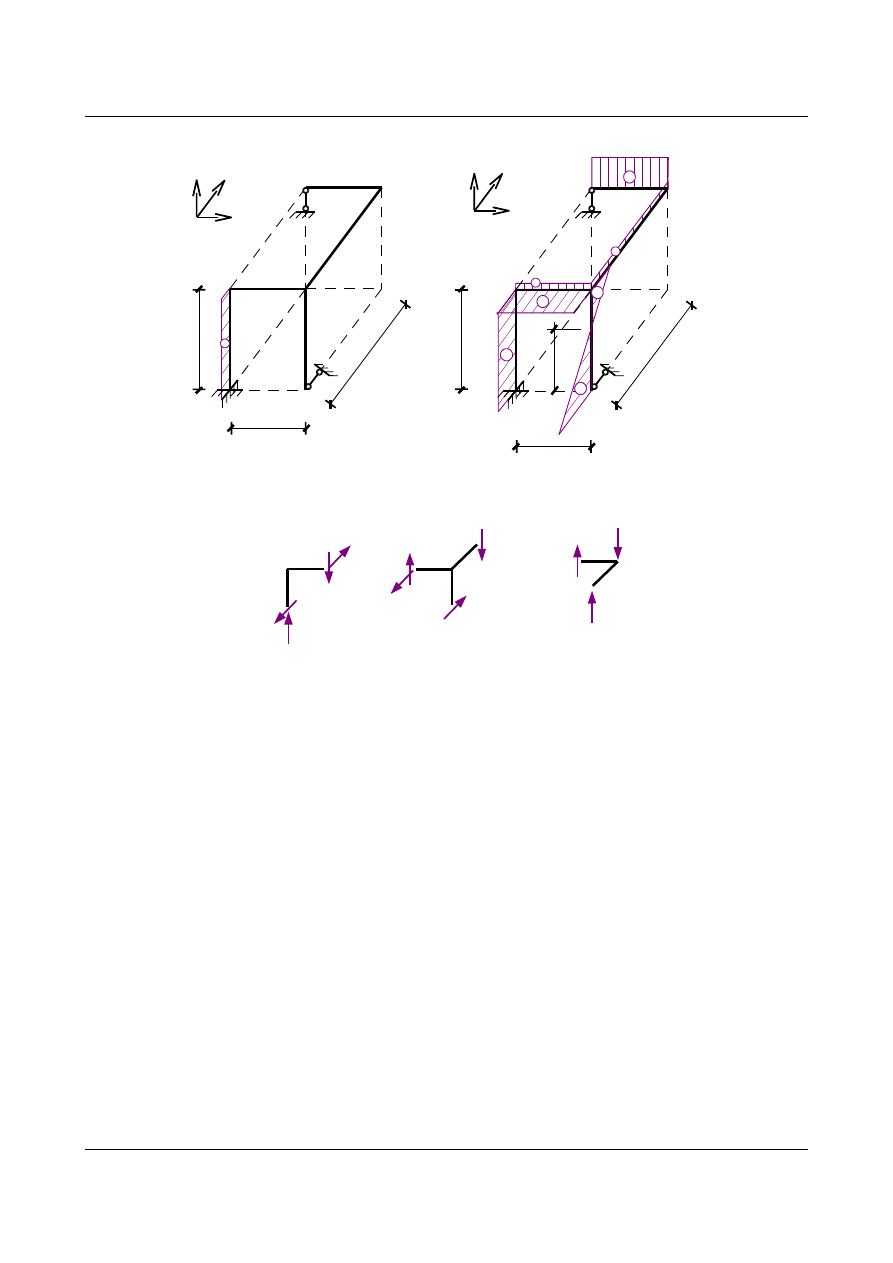
Część 1

OBLICZANIE RAMY PRZESTRZENNEJ MATODĄ SIŁ

8

4,0

3,0

5,0

[m]

4,0

3,0

5,0

[m]

x

x

y

y

z

z

N

(n)

[kN]

T

(n)

[kN]

-0,537

-9,463

_

_

-0,537

-0,537

7,889

+

7,889

+

_

_

-7,889

_

+

12,111

2,42

•

Sprawdzenie równowagi w węzłach

7,889

7,889

7,889

7,889

0,537

0,537

0,537

0,537

0,537

9,463

10,0

Agnieszka Sysak Gr. 3

2004-03-16