U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

1

O

BLICZANIE UKŁADÓW PRZESTRZENNYCH STATYCZNIE

NIEWYZNACZALNYCH METODĄ SIŁ

.

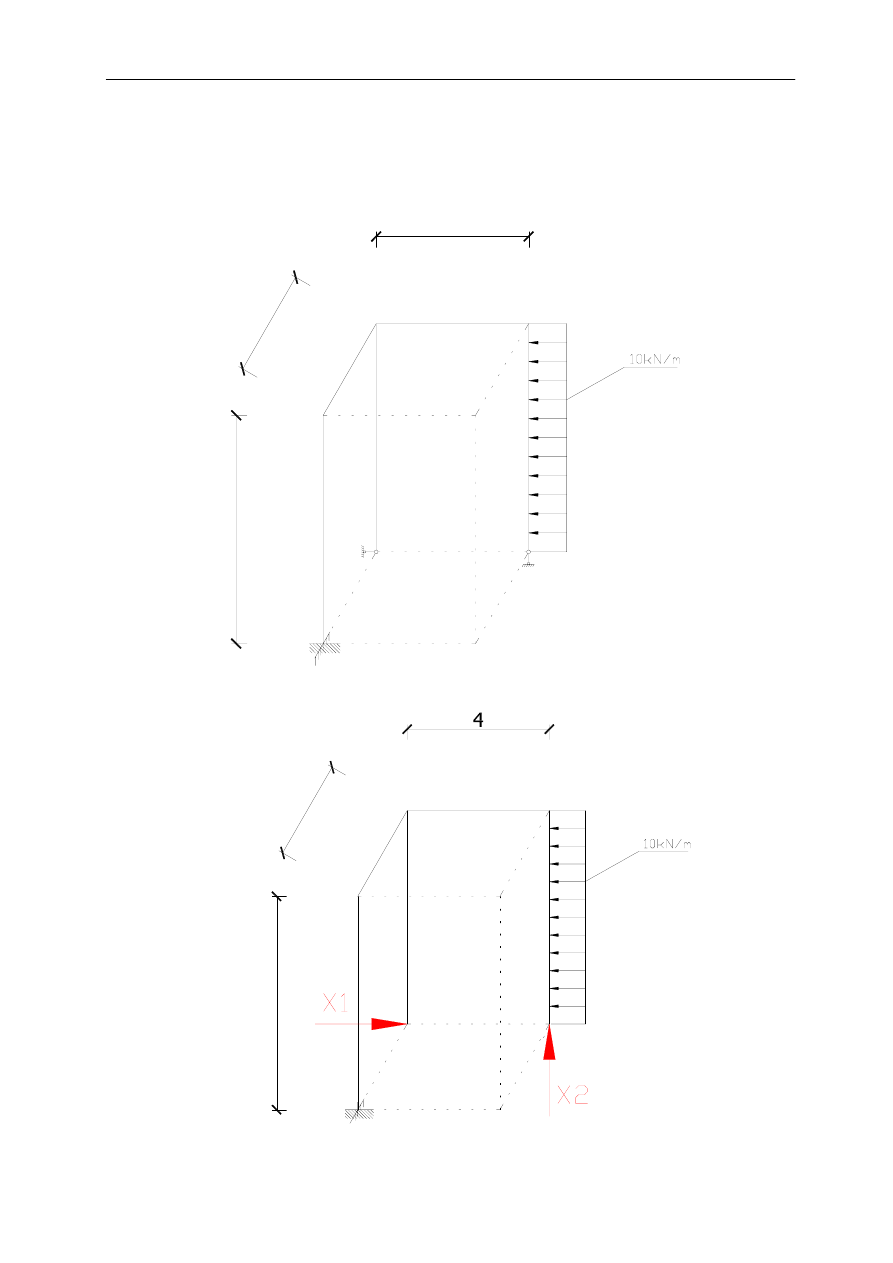
Zadana rama:

4

3

6

Dobieram układ podstawowy i zapisuję układ równań kanonicznych:

6

3

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

2







=

∆

+

⋅

+

⋅

=

∆

+

⋅

+

⋅

0

0

2

2

22

1

21

1

2

12

1

11

P

P

X

X

X

X

δ

δ

δ

δ

∫

∫

⋅

+

⋅

=

ds

EI

M

M

ds

EI

M

M

k

s

i

s

k

i

ik

δ

∫

∫

⋅

+

⋅

=

∆

ds

EI

M

M

ds

EI

M

M

k

s

i

s

i

P

iP

Parametry przekroju
rurowego

I

I

E

G

s

2

375

,

0

=

=

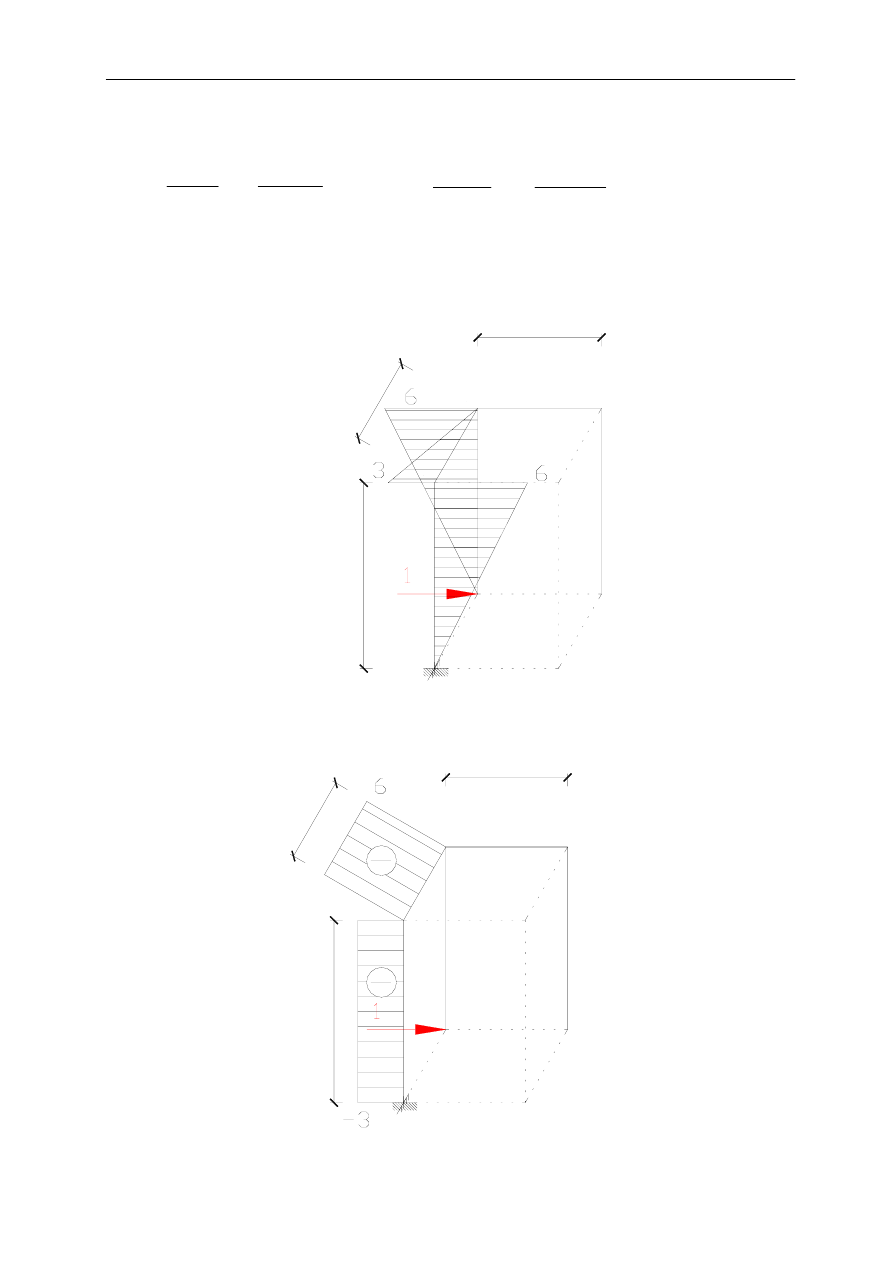
Rysuję wykresy momentów od poszczególnych sił jednostkowych:

M

1

[m]

6

4

3

M

s

1

[m]

3

6

4

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

3

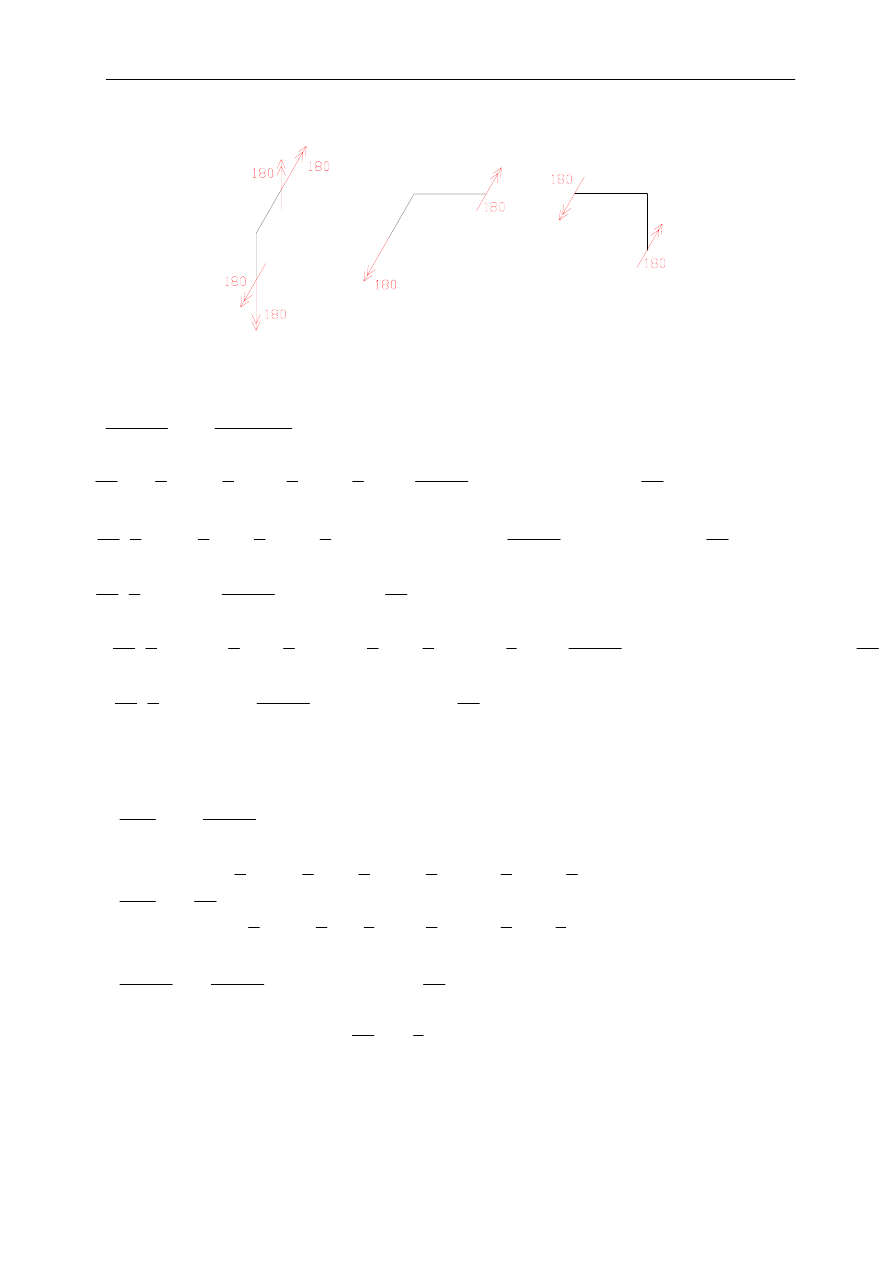
Równowaga węzłów:

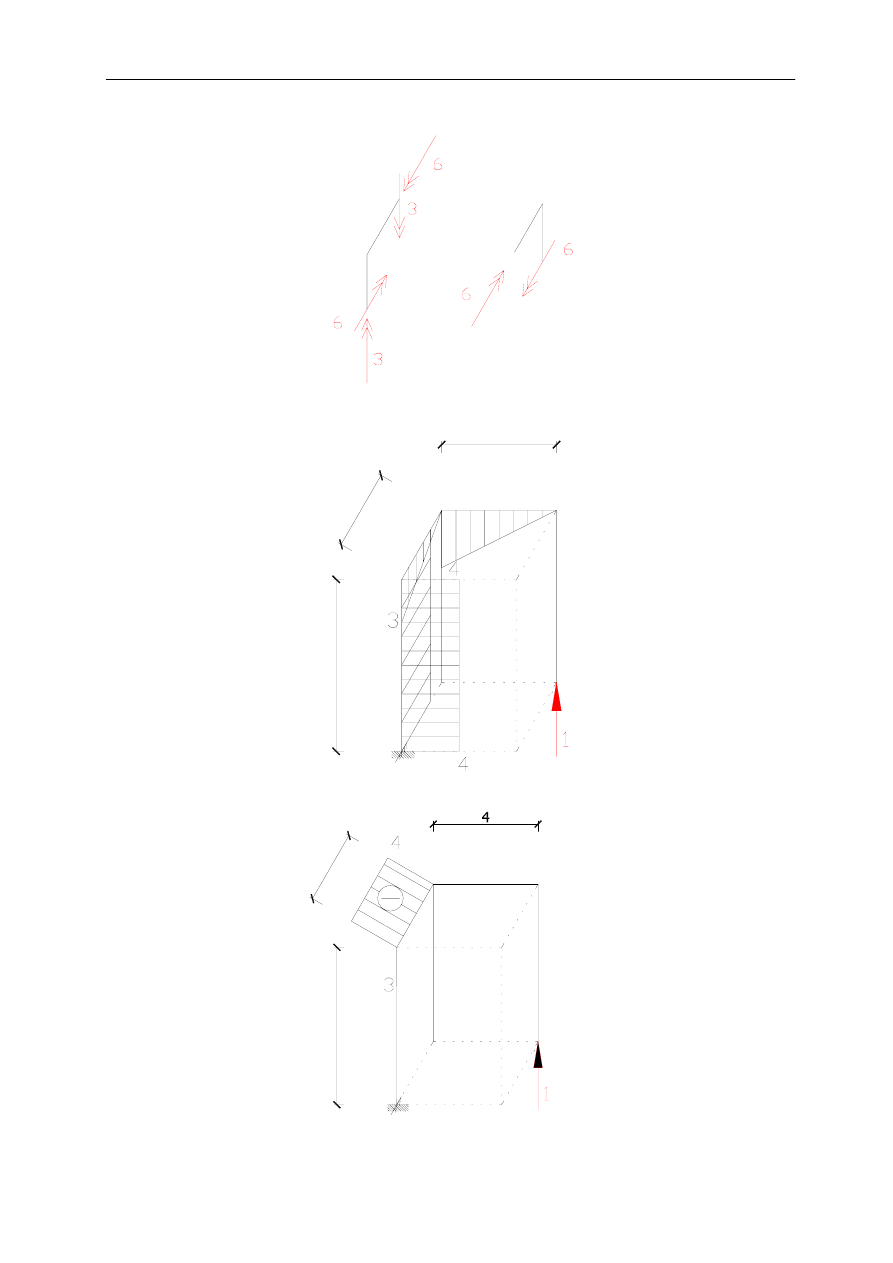
M

2

[m]

3

4

6

M

s

2

[m]

3

6

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

4

Równowaga węzłów:

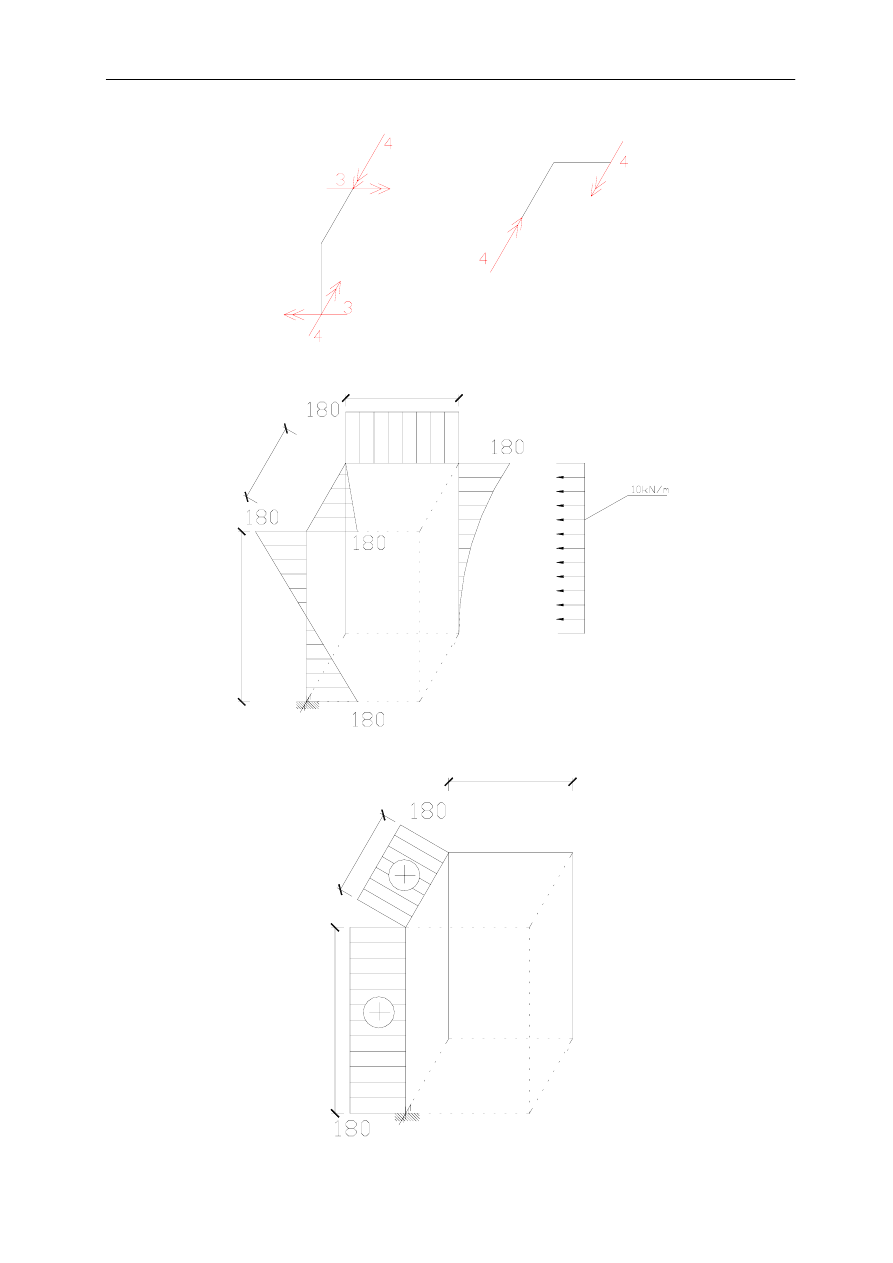
M

P

[kNm]

6

4

3

M

s

P

[kNm]

6

4

3

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

5

Równowaga węzłów:

Korzystając z metody Wereszczegina- Mohra całkowania iloczynu dwóch funkcji (w tym
jednej prostoliniowej) otrzymuje się:

[

]

[

]

[

]

[

]

[

]

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

EI

ds

EI

M

M

ds

EI

M

M

P

P

k

s

i

s

k

i

ik

1

4320

4

180

3

75

,

0

1

180

4

4

2

1

1

1

10260

180

3

6

180

3

6

75

,

0

1

6

3

1

180

6

2

1

6

3

2

180

6

2

1

3

3

2

180

3

2

1

1

1

168

4

3

6

75

,

0

1

4

6

6

2

1

1

1

)

3

(

3

,

244

4

4

3

75

,

0

1

3

3

6

4

4

6

3

3

2

3

3

2

1

4

3

2

4

4

2

1

1

1

369

3

3

6

6

3

6

75

,

0

1

3

3

2

3

3

2

1

6

3

2

6

6

2

1

2

1

2

1

12

22

11

⋅

−

=

⋅

⋅

−









⋅

⋅

⋅

−

=

∆

⋅

−

=

⋅

⋅

+

⋅

⋅

−























 ⋅

⋅

⋅

⋅

−











 ⋅

⋅

⋅

⋅

+











 ⋅

⋅

⋅

⋅

−

=

∆

⋅

=

⋅

⋅

+









⋅

⋅

⋅

=

⋅

=

⋅

⋅

+













⋅

⋅

+

⋅

⋅

+











 ⋅

⋅

⋅

⋅

+











 ⋅

⋅

⋅

⋅

=

⋅

=

⋅

⋅

+

⋅

⋅

+























 ⋅

⋅

⋅

⋅

+



















 ⋅

⋅

⋅

⋅

⋅

=

=

⋅

+

⋅

=

∫

∫

δ

δ

δ

δ

Sprawdzenie globalne delt:

[

]

3

1

949

1

472

1

3

3

6

10

10

3

75

,

0

1

75

,

0

)

3

(

3

,

477

4

3

1

10

3

2

6

10

2

1

10

3

1

4

3

2

6

4

2

1

3

3

6

3

3

2

3

3

2

1

2

6

3

2

6

6

2

1

4

3

2

4

4

2

1

1

75

,

0

22

21

12

11

2

2

2

2

⋅

=

+

+

+

=

⋅

=

⋅

⋅

+

⋅

⋅

⋅

=

=





































⋅

+

⋅

⋅

⋅

⋅

+













⋅

+

⋅

⋅

⋅

⋅

+

+

⋅

⋅

+











 ⋅

⋅

⋅

⋅

⋅

+











 ⋅

⋅

⋅

⋅

+











 ⋅

⋅

⋅

⋅

⋅

=

=

+

∑∑

∫

∫

∑∑

∫

∫

EI

EI

EI

ds

EI

M

EI

ds

EI

M

ds

EI

M

ds

EI

M

i

k

ik

S

S

S

i

k

ik

S

S

S

δ

δ

δ

δ

δ

δ

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

6

Mając dane wszystkie wielkości podstawiam je do układu równań i rozwiązuje go:









=

−

⋅

+

⋅

=

−

⋅

+

⋅

0

4320

3

1

244

168

0

10260

168

369

2

1

2

1

X

X

X

X

kN

X

kN

X

0925

,

2

7575

,

28

2

1

−

=

=

4

3

6

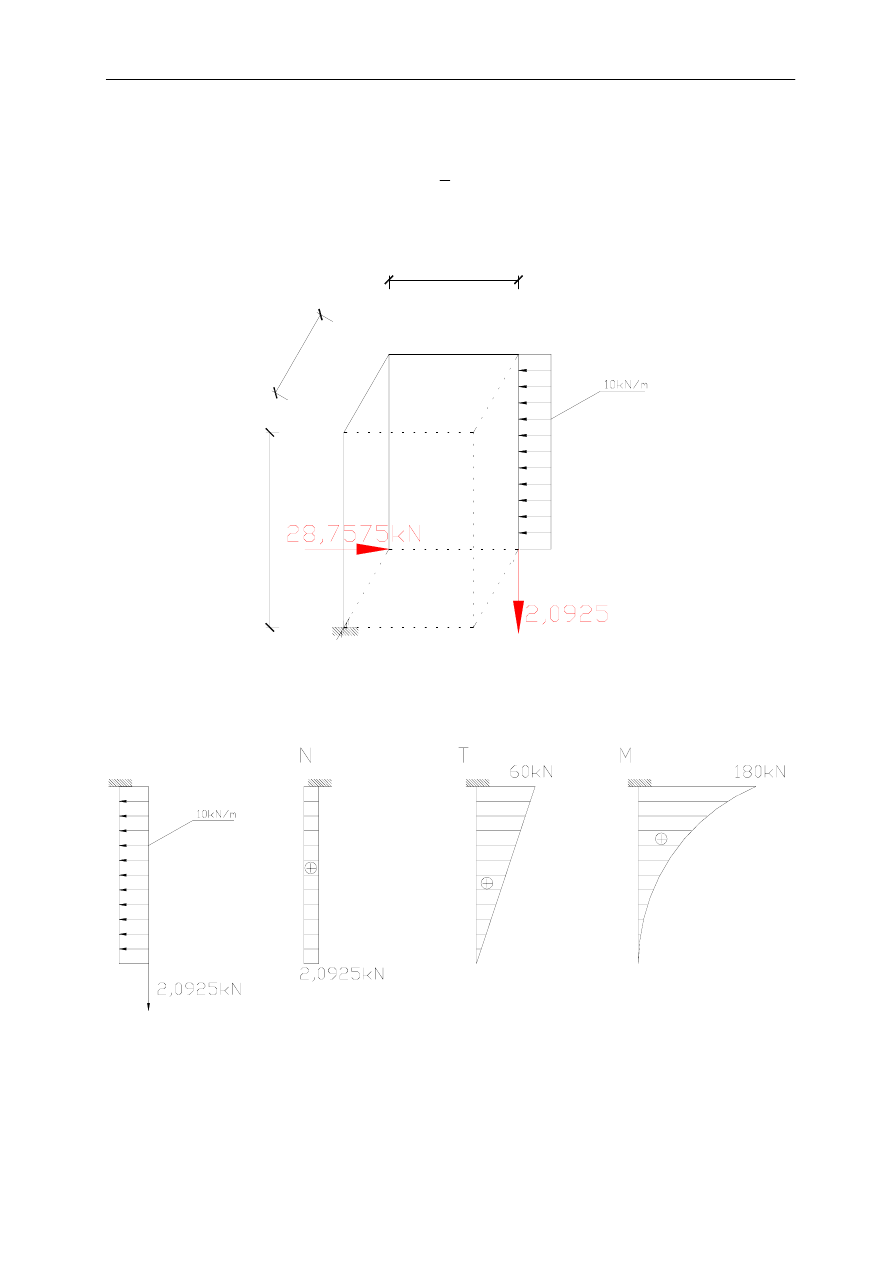
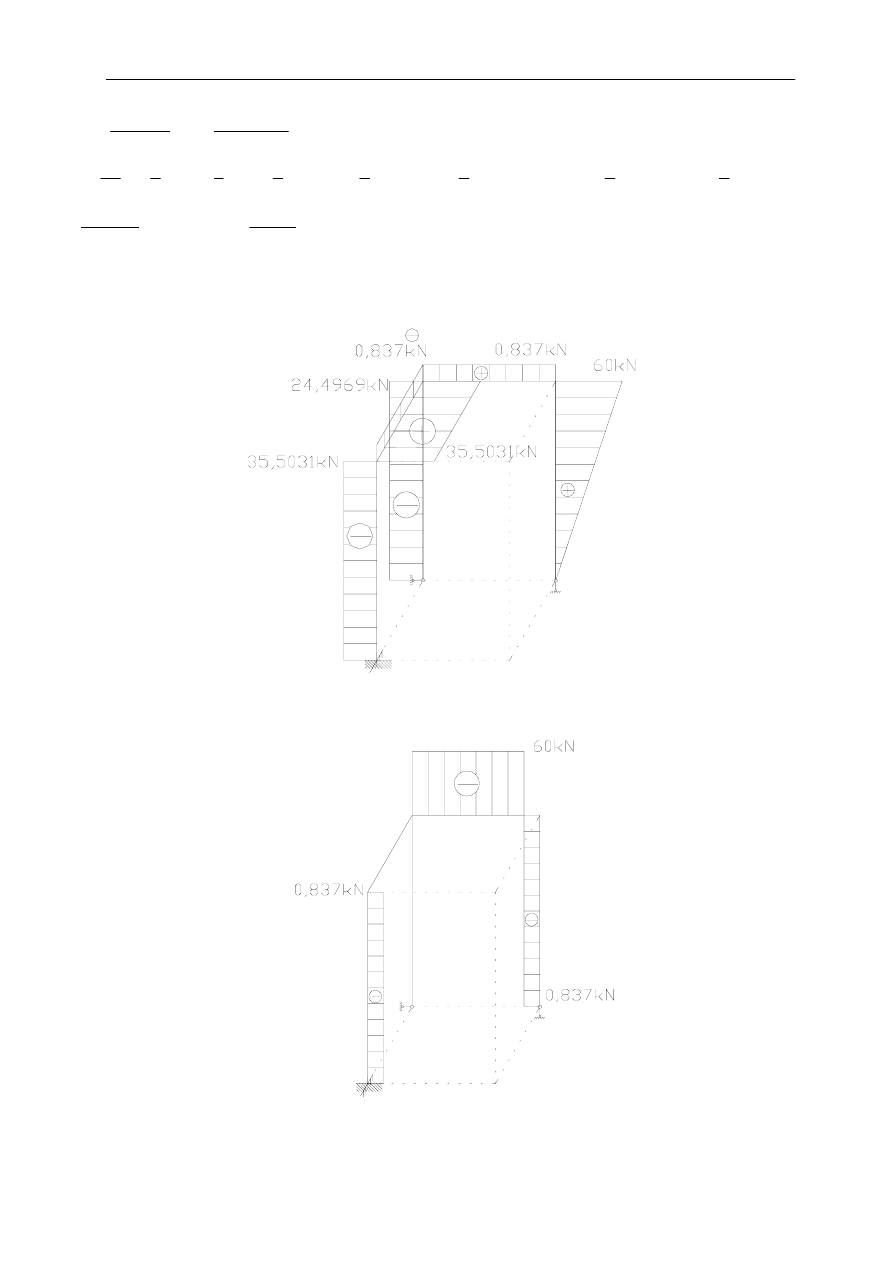
Siły występujące w poszczególnych prętach:

Pręt 1

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

7

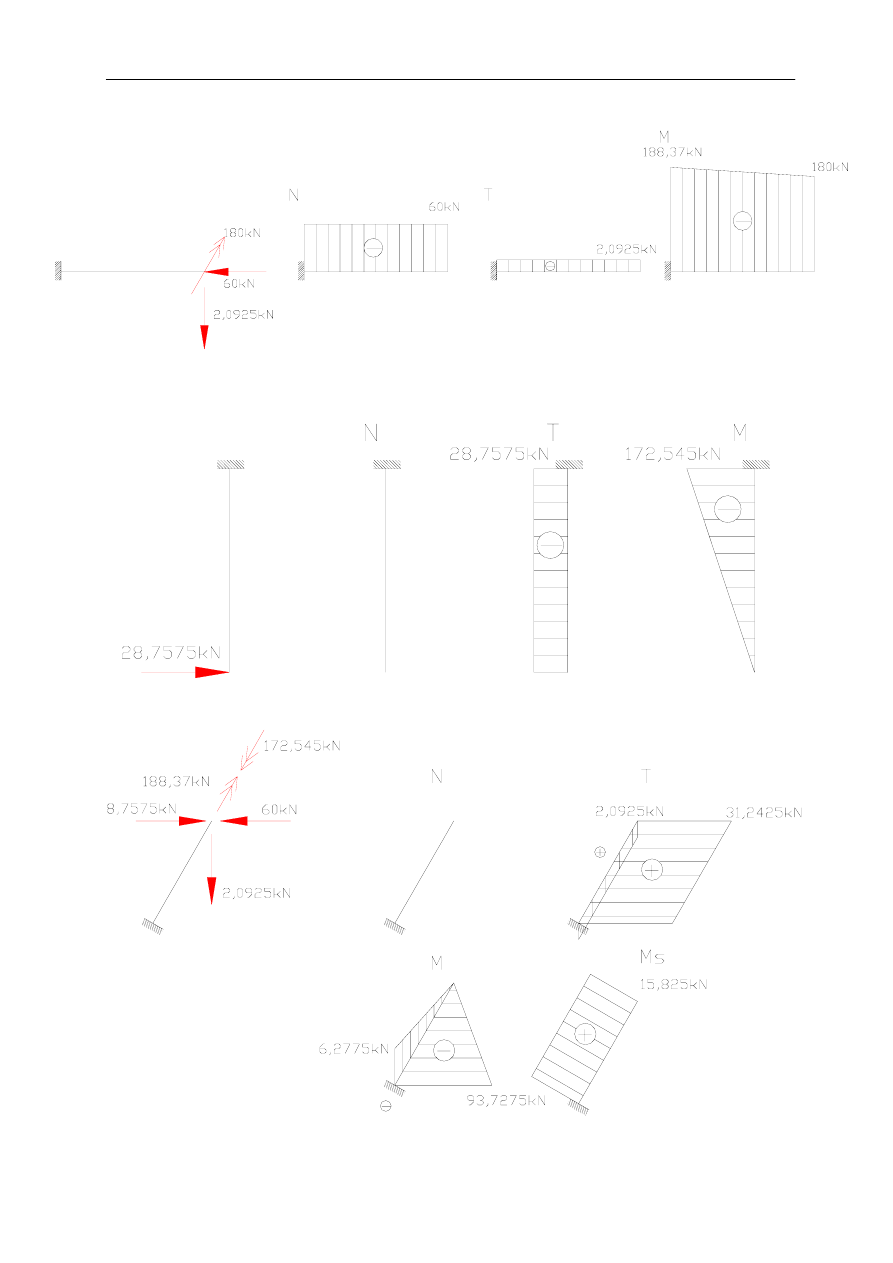
Pręt 2

Pręt 3

Pręt 4

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

8

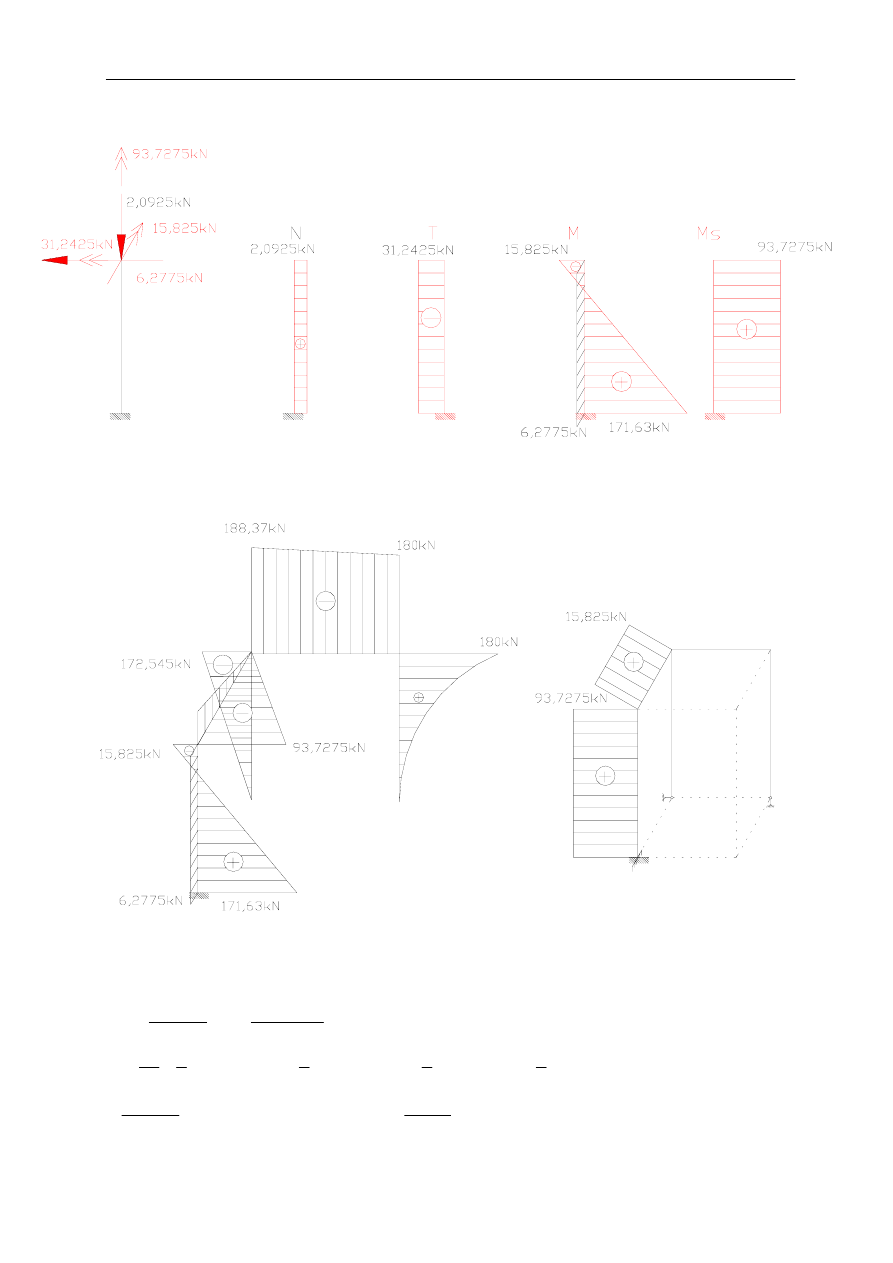
Pręt 5

Końcowy wykres momentów:
M

n

[kNm]

M

s

n

[kNm]

Kontrola kinematyczna:

[

]

EI

EI

EI

u

ds

EI

M

M

ds

EI

M

M

u

S

S

n

n

0225

,

0

825

,

15

3

6

3

6

7275

,

93

75

,

0

1

2

63

,

171

6

2

1

4

825

,

15

6

2

1

2

7275

,

93

3

2

1

4

545

,

172

6

2

1

1

1

1

1

1

=

⋅

⋅

−

⋅

⋅

−

⋅

⋅

+

+









⋅

⋅

⋅

+

⋅

⋅

⋅

−

⋅

⋅

⋅

−

⋅

⋅

⋅

⋅

=

⋅

+

⋅

=

∫

∫

U

KŁADY

P

RZESTRZENNE

Politechnika Poznańska Adam

Łodygowski ®

9

[

]

EI

EI

EI

u

ds

EI

M

M

ds

EI

M

M

u

S

S

n

n

0075

,

0

4

825

,

15

3

75

,

0

1

4

63

,

171

6

2

1

4

825

,

15

6

2

1

2775

,

6

3

6

3

3

2

2775

,

6

3

2

1

37

,

188

3

2

180

3

1

4

4

2

1

1

2

2

2

2

=

⋅

⋅

⋅

⋅

+

+













⋅

⋅

⋅

+

⋅

⋅

⋅

−

⋅

⋅

−











 ⋅

⋅

⋅

⋅

−













⋅

+

⋅

⋅

⋅

⋅

−

⋅

=

⋅

+

⋅

=

∫

∫

Końcowy wykres tnących:
T

n

[kN]

Końcowy wykres normalnych:
N

n

[kN]