Politechnika Poznanska

Wydział Budownictwa, Architektury i In

ż

ynierii

Ś

rodowiska

Konstrukcje Budowlane i In

ż

ynierskie, grupa 3

Projekt z Mechaniki Budowli
Projekt 1 - Rama przestrzenna

Prowadz

ą

cy

ć

wiczenia i konsultacje:

Dr in

ż

. Przemysław Litewka

Projekt wykonał:

Krystian Paczkowski

1

6kN/m

10kN

5kN

c

c

a

a

b

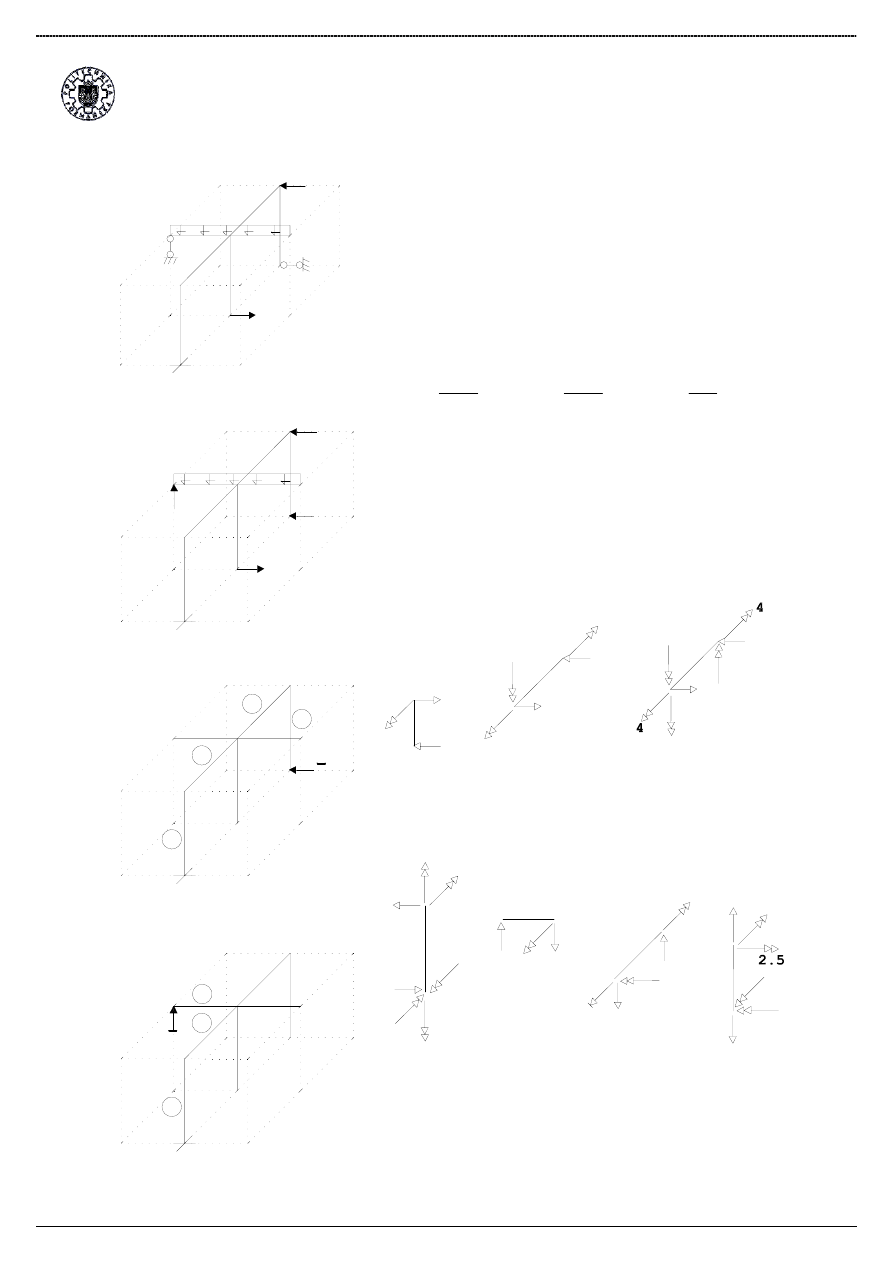
Układ podstawowy

6kN/m

10kN

5kN

c

c

a

a

b

X2

X1

Stan X1:

c

c

a

a

1

1

2

3

4

Stan X2:

c

c

a

a

1

1

2

3

Zadany przykład:

Dla przedstawionej ramy wyznaczy

ć

wykresy sił

wewn

ę

trznych wywołanych zadanym obci

ąż

eniem.

Przyj

ę

to,

ż

e rama składa si

ę

z pr

ę

tów stalowych o

przekroju kołowym (G=0.375E, I

s

=2I).

a=2,5 [m] b=4 [m] c=3 [m] SSN=2

Do oblicze

ń

poszczególnych współczynników

δ

ik

korzystam z

wzoru:

1

n

j

z

M

ix

M

kx

EI

x

⌠





⌡

d

∑

=

1

n

j

z

M

iy

M

ky

EI

y

⌠





⌡

d

∑

=

+

1

n

j

z

M

i

M

k

GI

s

⌠





⌡

d

∑

=

+

gdzie I

x

=I

y

=I ; GI

s

=0.375E * 2I= 0.75EI

Dobór układu podstawowego:

Równania kanoniczne:

δ

11

X

1

δ

12

X

2

+

δ

1P

+

0

:=

δ

21

X

1

δ

22

X

2

+

δ

2P

+

0

:=

Wyznaczenie warto

ś

ci momentów zginaj

ą

cych i skr

ę

caj

ą

cych

dla stanu X1:

1

1

4

1

1

4

4

2,5

1

1

2,5

2,5

2,5

Wyznaczenie warto

ś

ci momentów

zginaj

ą

cych i skr

ę

caj

ą

cych dla stanu X2:

Pr

ę

t 4: Pr

ę

t nr1: Pr

ę

t nr2: Pr

ę

t nr3:

4

4

4

1

1

5

5

1

1

3

1

4

3

1

2.5

3

1

1

2.5

3

Politechnika Poznanska

Wydział Budownictwa, Architektury i In

ż

ynierii

Ś

rodowiska

Konstrukcje Budowlane i In

ż

ynierskie, grupa 3

Projekt z Mechaniki Budowli
Projekt 1 - Rama przestrzenna

Prowadz

ą

cy

ć

wiczenia i konsultacje:

Dr in

ż

. Przemysław Litewka

Projekt wykonał:

Krystian Paczkowski

2

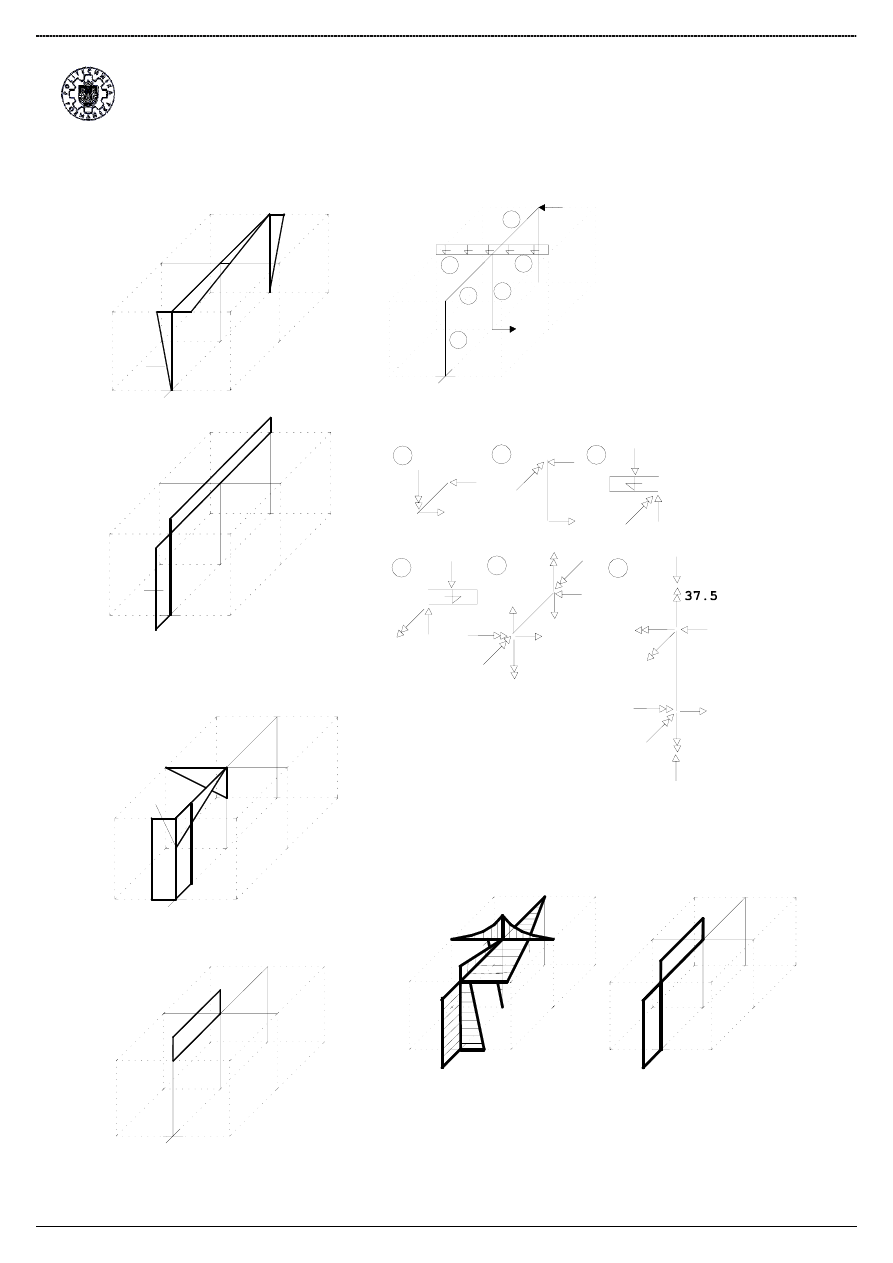
Wykresy dla stanu X1:

Momentów zginaj

ą

cych [m]:

4

4

2.5

5

Momentów skr

ę

caj

ą

cych [m]:

4

5

+

+

Wykresy dla stanu X2:

Momentów zginaj

ą

cych [m]:

3

3

2.5

2.5

Momentów skr

ę

caj

ą

cych [m]:

3

+

Stan P:

5kN

6kN/m

10kN

1

2

3

4

5

6

Wyznaczenie warto

ś

ci momentów zginaj

ą

cych i skr

ę

caj

ą

cych

dla stanu P:

1

10

25

10

2

5

20

5

3

18

6

18

27

4

18

18

27

6

5

5

20

20

36

36

5

25

37.5

6

36

20

90

36

40

90

37.5

5

90

5

Wykresy dla stanu P:

Momentów zginaj

ą

cych [kNm]: Momentów skr

ę

caj

ą

cych [kNm]:

90

90

90

20

27

25

20

20

-

40

37.5

+

37.5

Politechnika Poznanska

Wydział Budownictwa, Architektury i In

ż

ynierii

Ś

rodowiska

Konstrukcje Budowlane i In

ż

ynierskie, grupa 3

Projekt z Mechaniki Budowli
Projekt 1 - Rama przestrzenna

Prowadz

ą

cy

ć

wiczenia i konsultacje:

Dr in

ż

. Przemysław Litewka

Projekt wykonał:

Krystian Paczkowski

3

Obliczenia współczynników

:

EJ

δ

11

1

2

4

⋅

4

⋅

2

3

⋅

4

⋅

1

2

5

⋅

5

⋅

2

3

⋅

5

⋅

+

1

2

4

⋅

4

⋅

2

3

⋅

4

⋅

+

1

0.75

5

4

⋅

5

⋅

4

5

⋅

4

⋅

+

(

)

⋅

+

:=

EJ

δ

11

324.333

:=

EJ

δ

12

1

2

4

⋅

4

⋅

3

⋅

1

0.75

4

2.5

⋅

3

⋅

(

)

⋅

+

:=

EJ

δ

12

64

:=

EJ

δ

22

1

2

3

⋅

3

⋅

2

3

⋅

3

⋅

1

2

2.5

⋅

2.5

⋅

2

3

⋅

2.5

⋅

+

3

4

⋅

3

⋅

+

2.5

4

⋅

2.5

⋅

+

1

0.75

3

2.5

⋅

3

⋅

(

)

⋅

+

:=

EJ

δ

22

105.208

:=

EJ

δ

1P

1

2

20

4

⋅

2

−

3

4









⋅

1

2

40

4

⋅

1

−

3

4









⋅

+

1

2

25

2.5

⋅

2

3

2.5

1

3

5

+









+

1

2

37.5

2.5

⋅

2

3

5

1

3

2.5

+









+

1

2

2.5

25

⋅

2

3

2.5

⋅

+

:=

P

1

0.75

37.5

4

⋅

5

⋅

20

2.5

⋅

4

⋅

−

(

)

EJ

δ

1P

871.56249999999999999

:=

P

EJ

δ

2 P

⋅

1

2

20

40

+

(

)

⋅

4

⋅

3

−

(

)

⋅

90

4

⋅

2.5

−

⋅

+

1

2

2.5

⋅

90

⋅

2

−

3

2.5

⋅









⋅

+

1

2

27

⋅

3

⋅

2

−

3

3

⋅









⋅

+

2

3

6

3

2

⋅

8

⋅

3

⋅

1.5

⋅

+

1

0.75

20

−

2.5

⋅

3

⋅

(

)

+

:=

P

EJ

δ

2P

1708.2500000000000000

−

:=

P

Z czego wynika:

324.333

X

1

⋅

64

X

2

⋅

+

871.5625

−

:=

64

X

1

⋅

105.208

X

2

⋅

+

1708.25

:=

Z czego otrzymujemy:

X

1

6.69482

−

:=

X

2

20.3095

:=

[kN]

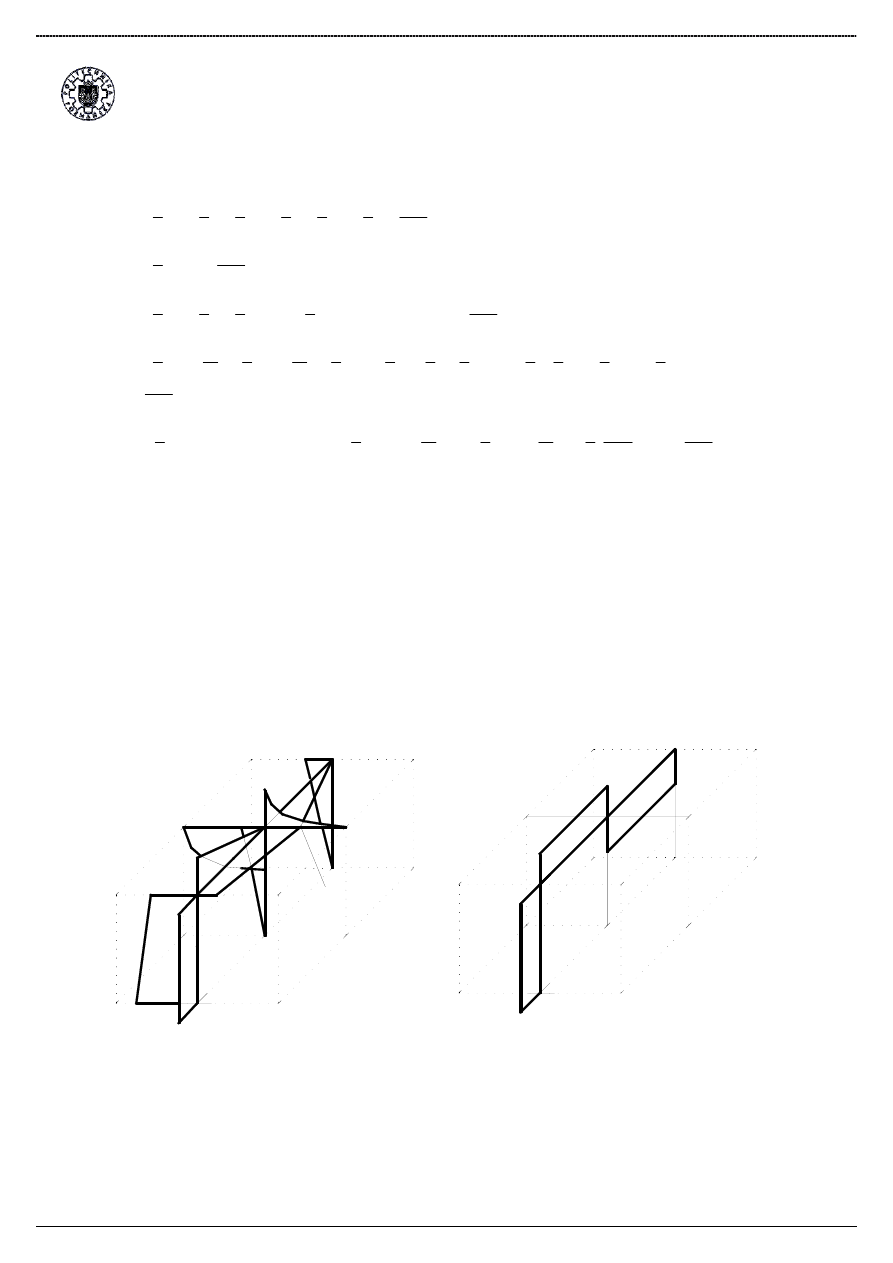
Korzystaj

ą

c z zasady superpozycji otrzymuj

ę

wykresy momentów rzeczywistych:

S

n

S

p

S

1

X

1

⋅

+

S

2

X

2

⋅

+

:=

Wykres momentów zginaj

ą

cych: Wykres momentów skr

ę

caj

ą

cych:

M[kNm]

[kNm]

20

33.929

20.929

14.149

26.779

27

+

+

-

4.0259

26.779

14.149

8.26295

4.0259

39.226

39.226

δ

ik

Politechnika Poznanska

Wydział Budownictwa, Architektury i In

ż

ynierii

Ś

rodowiska

Konstrukcje Budowlane i In

ż

ynierskie, grupa 3

Projekt z Mechaniki Budowli
Projekt 1 - Rama przestrzenna

Prowadz

ą

cy

ć

wiczenia i konsultacje:

Dr in

ż

. Przemysław Litewka

Projekt wykonał:

Krystian Paczkowski

4

Sprawdzenie kinematyczne:

Przyjmuje jako układ wirtualny,układ X1,przykładaj

ą

c w miejscu siły X1 sił

ę

wirtualn

ą

równ

ą

1.

1



δ

⋅

1

2

14.149

⋅

4

⋅

2

3

⋅

4

⋅

1

2

20.929

⋅

4

⋅

1

3

⋅

4

⋅

+

1

2

4.0259

⋅

2.5

⋅

2

3

5

⋅

1

3

2.5

⋅

+









⋅

+

1

2

8.26295

⋅

2.5

⋅

2.5

2

3

⋅

1

3

5

⋅

+









⋅

+

:=

1



δ

⋅

1

2

2.5

⋅

8.26295

⋅

2

3

⋅

2.5

⋅

1

2

26.779

⋅

4

⋅

2

−

3

4

⋅









⋅

+

1

0.75

4.0259

4

⋅

5

⋅

14.149

2.5

⋅

4

⋅

+

26.779

2.5

⋅

4

⋅

−

(

)

⋅

+

1



δ

⋅

1.9666666666666665

10

-2

⋅

EJ

:=

[m] Wynik jest bliski zeru zatem obliczenia uznaj

ę

za poprawne.

Bł

ą

d procentowy wynosi:

1



δ

⋅

61.06233333333333333

61.042666666666666665

−

+

:=

1.9666666666666665

10

-2

⋅

61.06233333333333333

3.221

10

4

−

×

=

Bł

ą

d jest < 0,1% zatem zakładam,

ż

e kontrola jest poprawna.

Kontrolne sprawdzenie dla drugiego układu wirtualnego, przyjmuj

ę

w miejscu siły X2 sił

ę

wirtualn

ą

równ

ą

1.

1



δ

⋅

1

2

3

⋅

33.929

⋅

2

3

⋅

3

⋅

2

3

6

3

2

⋅

8

⋅

3

⋅

1.5

⋅

+

1

2

2.5

⋅

39.226

⋅

2

3

⋅

2.5

−

(

)

⋅

+

39.226

4

⋅

2.5

−

(

)

⋅

+

:=

1



δ

⋅

1

2

14.149

20.929

+

(

)

⋅

4

⋅

3

⋅

1

0.75

14.149

2.5

⋅

3

⋅

(

)

⋅

+

1



δ

⋅

1.416666666666667

10

-2

⋅

EJ

:=

EJ

[m] Wynik jest bliski zeru, co jest potwierdzeniem poprawno

ś

ci

oblicze

ń

.

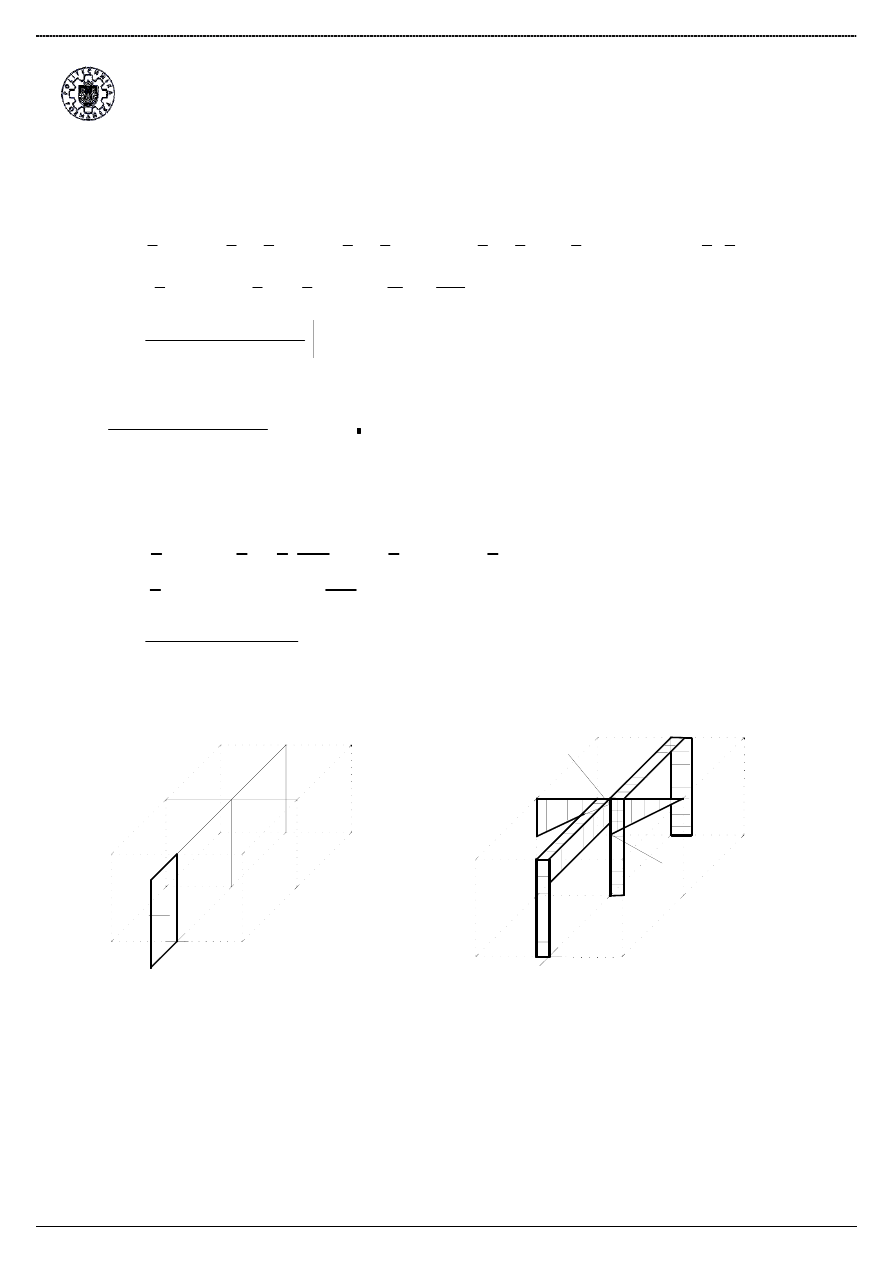
Wykres sil Normalnych wyst

ę

puj

ą

cych w ramie: Wykres sil Tn

ą

cych wyst

ę

puj

ą

cych w ramie:

-

15.6905

2.31

20.31

1.695

15.69

5

6.695

3.305

18

1.695

-

-

-

-

-

-

+

N[kN]

T[kN]