Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

1

POLITECHNIKA POZNAŃSKA
INSTYTUT KONSTRUKCJI BUDOWLANYCH
ZAKŁAD MECHANIKI BUDOWLI

ĆWICZENIE NR 3

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH

METODĄ SIŁ OD OSIADANIA PODPÓR I TEMPERATURY

Agnieszka Sysak Gr 3

2003-12-16

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

2

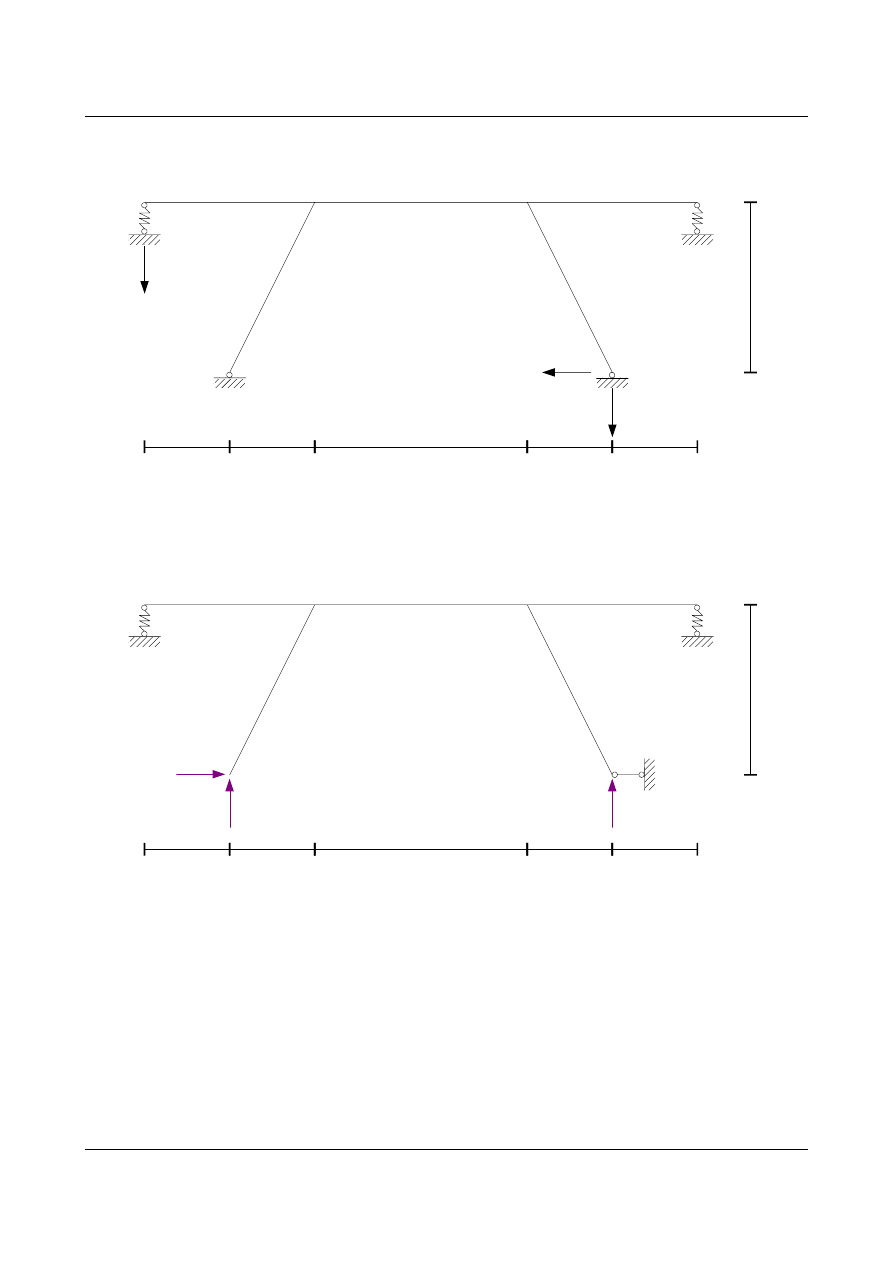
Osiadanie podpór

Obliczone wcześniej δ

11

, δ

12

, δ

13

, δ

22

, δ

23

, δ

33

zależą tylko od geometrii przyjętego do obliczeń układu, zatem

przyjmując układ podstawowy identyczny z układem podstawowym dla obliczeń od obciążeń zewnętrznych,
unikniemy ponownych obliczeń tych wartości i w przyjętym układzie podstawowym obliczamy jedynie
wartości δ

1∆

, δ

2∆

, δ

3∆

.

Układ podstawowy

Zapisujemy warunki kinematycznej zgodności przyjętego układu podstawowego z układem wyjściowym:

u

d

=

1

 X

1

⋅

11

 X

2

⋅

1 2

 X

3

⋅

1 3

=0

v

d

=

2 

 X

1

⋅

2 1

 X

2

⋅

2 2

 X

3

⋅

2 3

=0

v

c

=

3

 X

1

⋅

31

 X

2

⋅

3 2

 X

3

⋅

3 3

=0

Dzielimy na stany od poszczególnych obciążeń i obliczamy potrzebne przemieszczenia

=−

∑



R⋅

Agnieszka Sysak Gr 3

2003-12-16

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

0,003 m

0,002 m

0,005 m

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

X

1

X

2

X

3

A

B

C

D

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

3

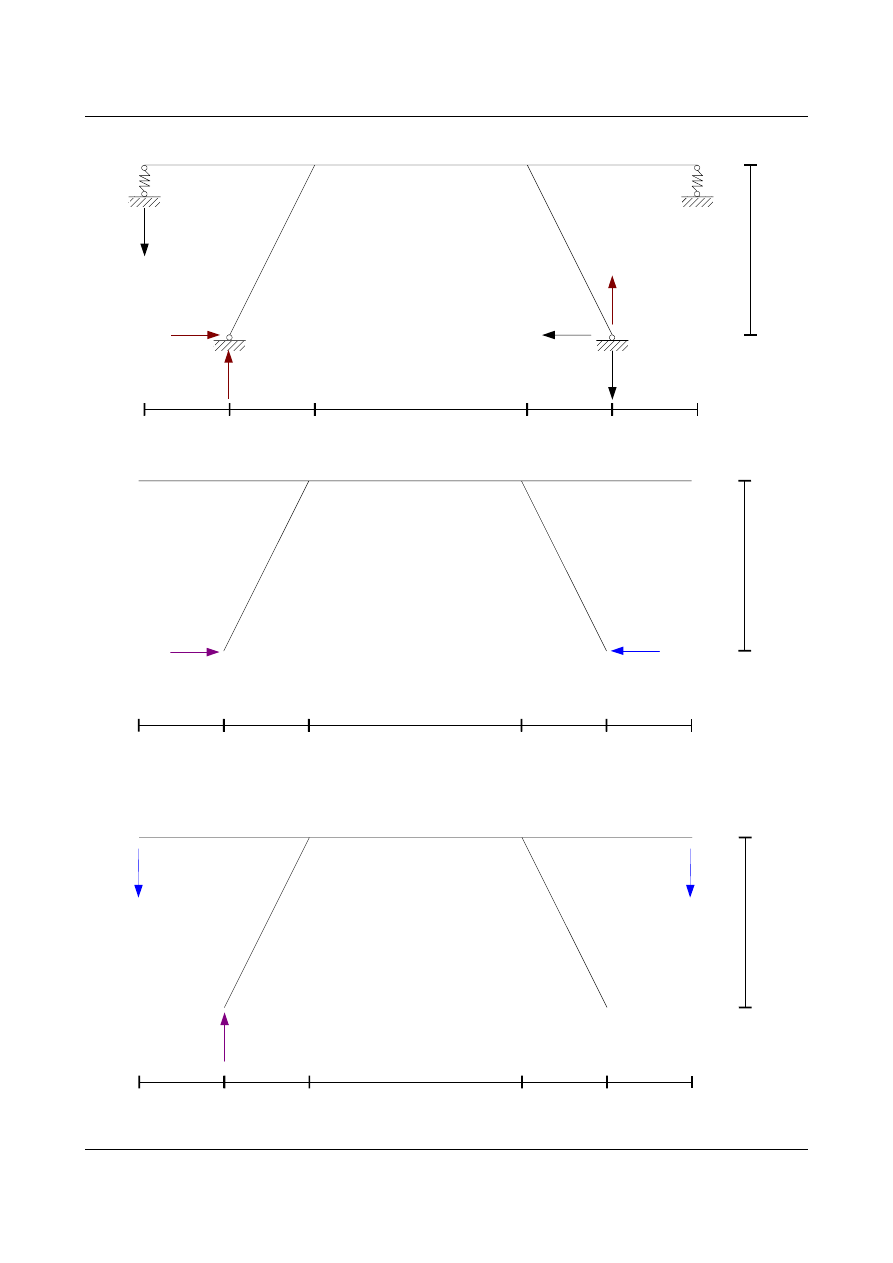
Szukane przemieszczenia w układzie podstawowym

•

Stan od obciążenia X

1



1 

=−1⋅0,005=−0,005000 [m]

•

Stan od obciążenia X

2



2 

=−0,846⋅0,003=−0,002538 [m]

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

X

1

=1

A

C

B

1 kN

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

0,003 m

0,002 m

0,005 m

δ

1∆

δ

2∆

δ

3∆

4

2

2

5

2

2

[m]

A

C

0,846 kN

0,154 kN

B

X

2

=1

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

4

•

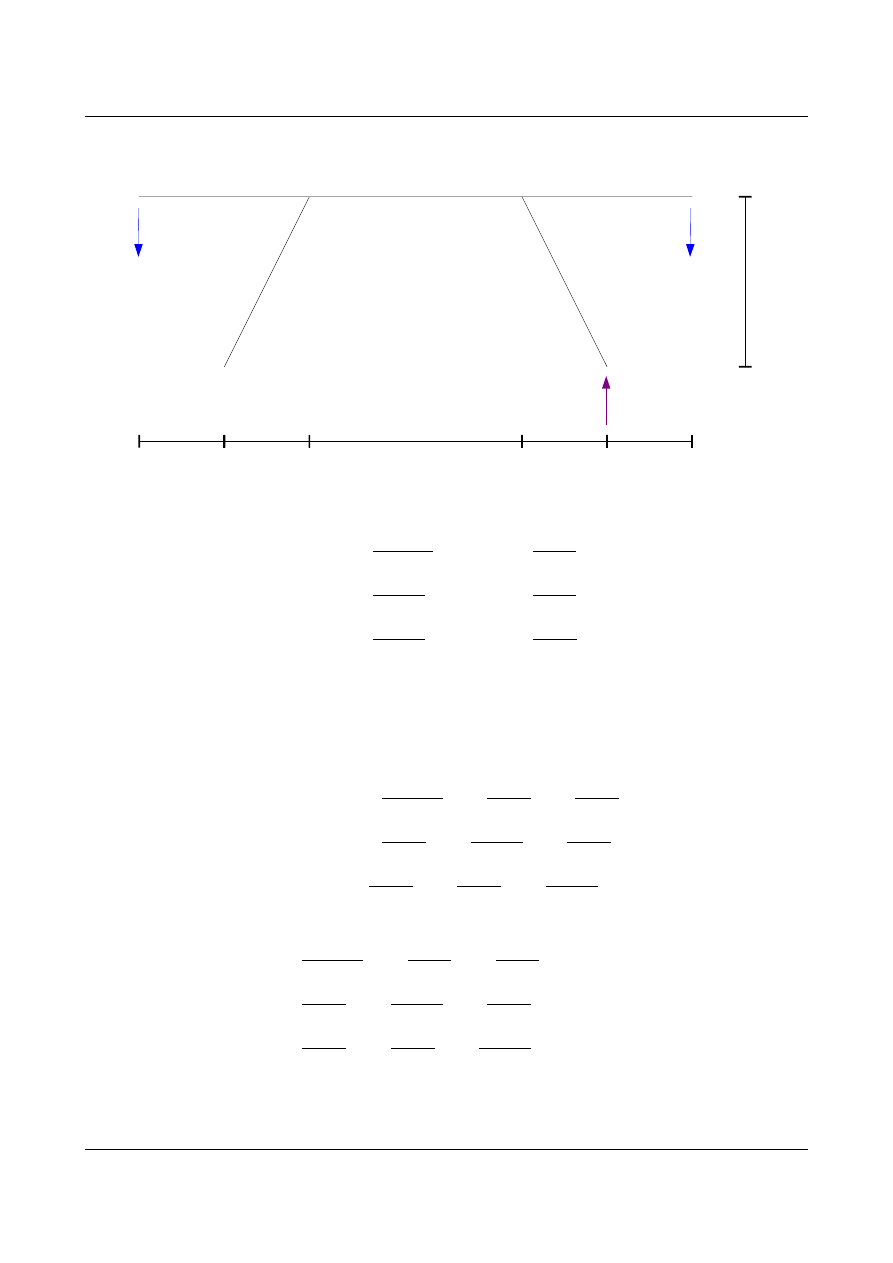
Stan od obciążenia X

3



3 

=−0,154⋅0,003−1⋅0,002=0,001538 [m]

Obliczone wcześniej przemieszczenia:



11

=105,303

EI



22

=25,543

EI



33

=25,543

EI



12

=

21

=2,474

EI



13

=

31

=2,474

EI



23

=

32

=8,986

EI

Dane fizyczne i geometryczne:

E = 205·10

6

[kN/m

2

]

I = 3060·10

-8

[m

4

]

Zapisujemy układ równań i obliczamy niewiadome X

1

, X

2

, X

3

{

−0,005000 X

1

⋅105,303

E I

 X

2

⋅2,474

E I

 X

3

⋅2,474

E I

=0

−0,002538 X

1

⋅2,474

E I

 X

2

⋅25,543

E I

 X

3

⋅8,986

E I

=0

0,001538 X

1

⋅2,474

E I

 X

2

⋅8,986

E I

 X

3

⋅25,543

E I

=0

{

X

1

⋅105,303

E I

 X

2

⋅2,474

E I

 X

3

⋅2,474

E I

=0,005000

X

1

⋅2,474

E I

 X

2

⋅25,543

E I

 X

3

⋅8,986

E I

=0,002538

X

1

⋅2,474

E I

 X

2

⋅8,986

E I

 X

3

⋅25,543

E I

=−0,001538

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

A

C

0,154 kN

0,846 kN

B

X

3

=1

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

5

{

X

1

=0,2946 [kN ]

X

2

=0,8419 [kN ]

X

3

=−0,7024 [kN ]

* obliczenia wykonano w programie Derive

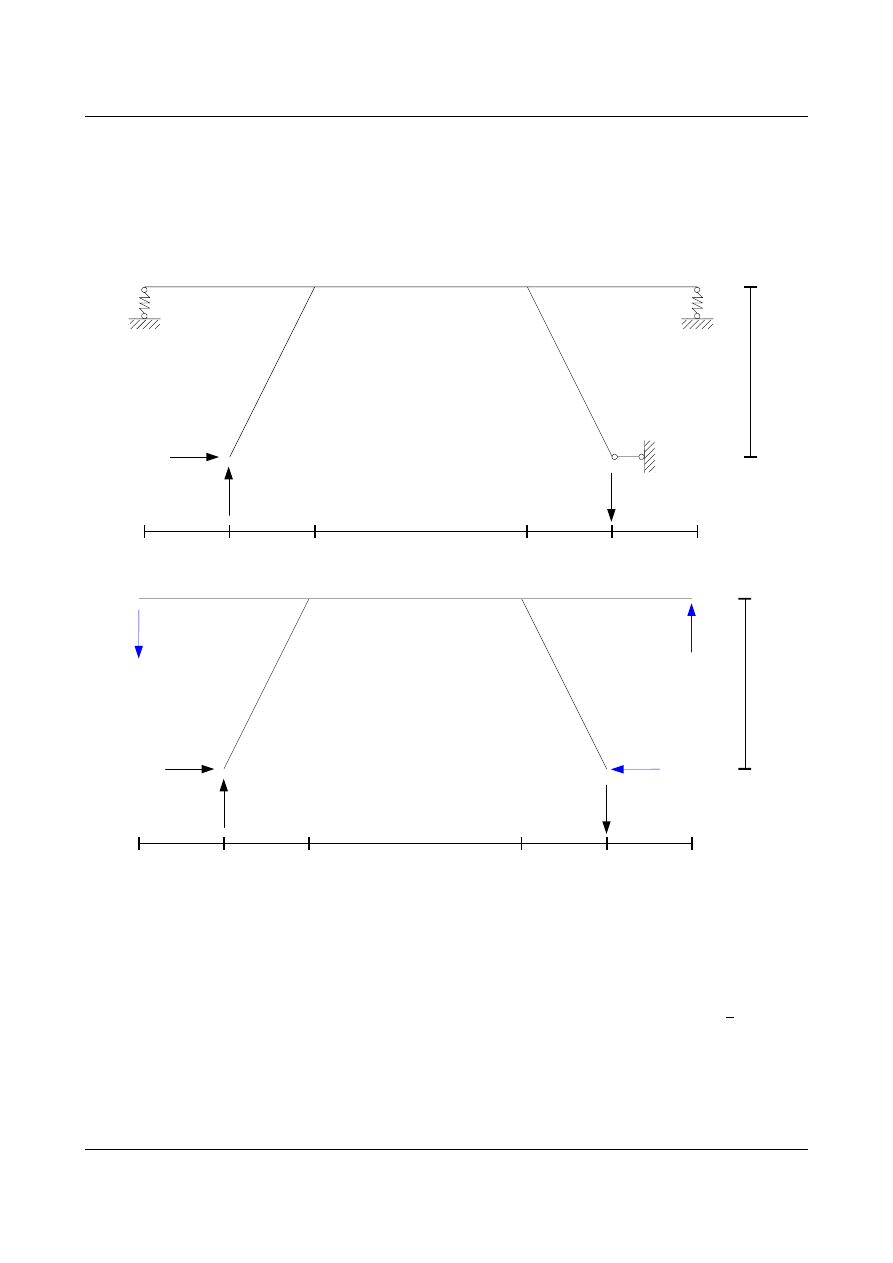
Zestawienie wyników

Obliczenie reakcji

∑

X :

0,2946−R

c

=0

⇒

R

c

=0,2946 [kN ]

∑

M

A

:

0,8419⋅2−0,7024⋅11R

b

⋅130,2946⋅4−R

c

⋅4=0

⇒

R

b

=0,4648 [kN ]

∑

M

B

:

−0,7024⋅20,8419⋅11−R

a

⋅13R

c

⋅4−0,2946⋅4=0

⇒

R

a

=0,6043[kN ]

∑

Y

spr

:

−R

a

R

b

0,8419−0,7024=−0,60430,46480,8419−0,7024=0

Agnieszka Sysak Gr 3

2003-12-16

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

A

B

C

D

0,2946 kN

0,8419 kN

0,7024 kN

4

2

2

5

2

2

[m]

R

c

R

a

R

b

A

B

C

D

0,2946 kN

0,8419 kN

0,7024 kN

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

6

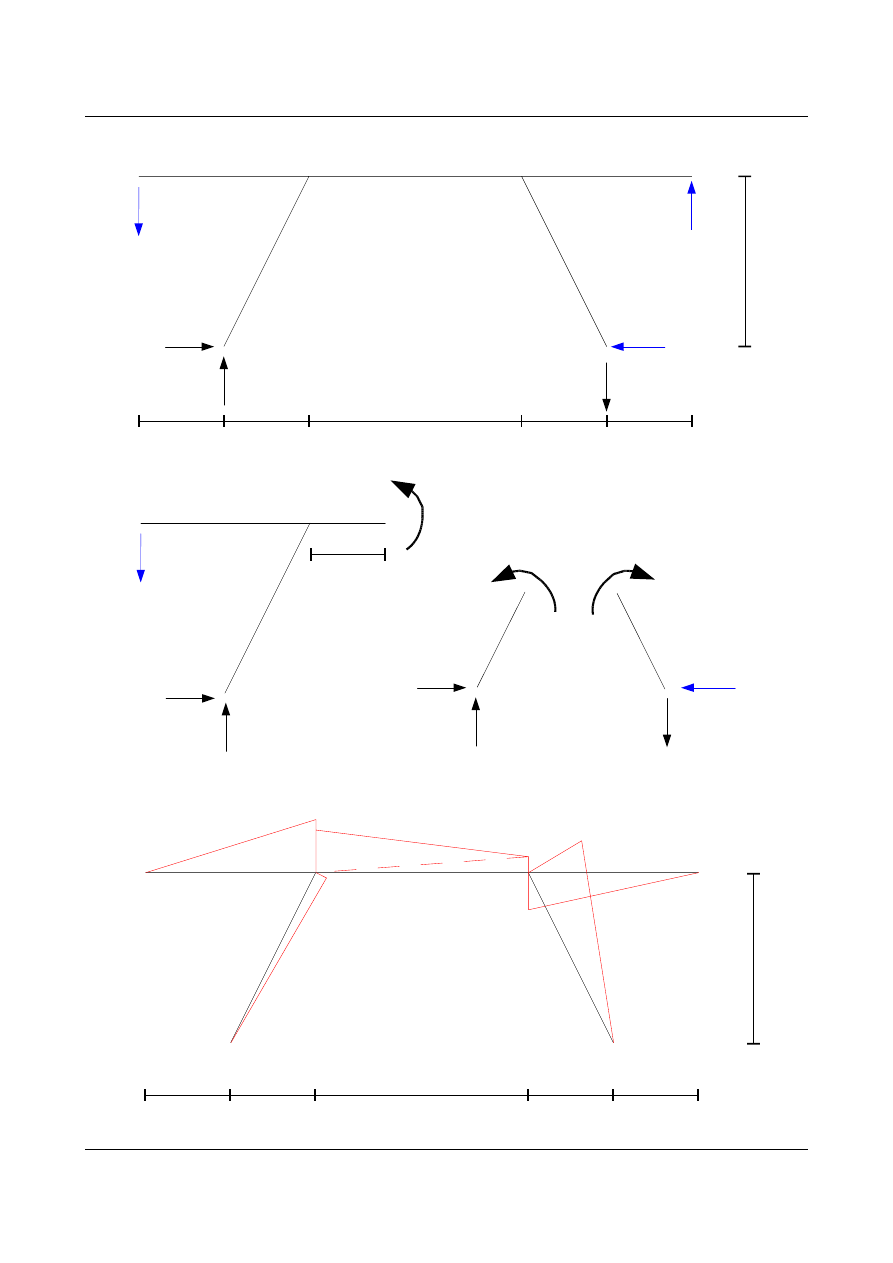
Zestawienie wyników reakcji

Rysunki pomocnicze do wykonania wykresu

Wykres momentów zginających

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

0,2946 kN

0,6043 kN

0,4648 kN

A

B

C

D

0,2946 kN

0,8419 kN

0,7024 kN

0,2946 kN

C

0,7024 kN

D

0,2946 kN

0,8419 kN

0,6043 kN

A

x

D

0,2946 kN

0,8419 kN

4

2

2

5

2

2

[m]

M

n

[kNm]

4,4172

1,9118

0,5054

0,7238

1,8592

2,5832

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

7

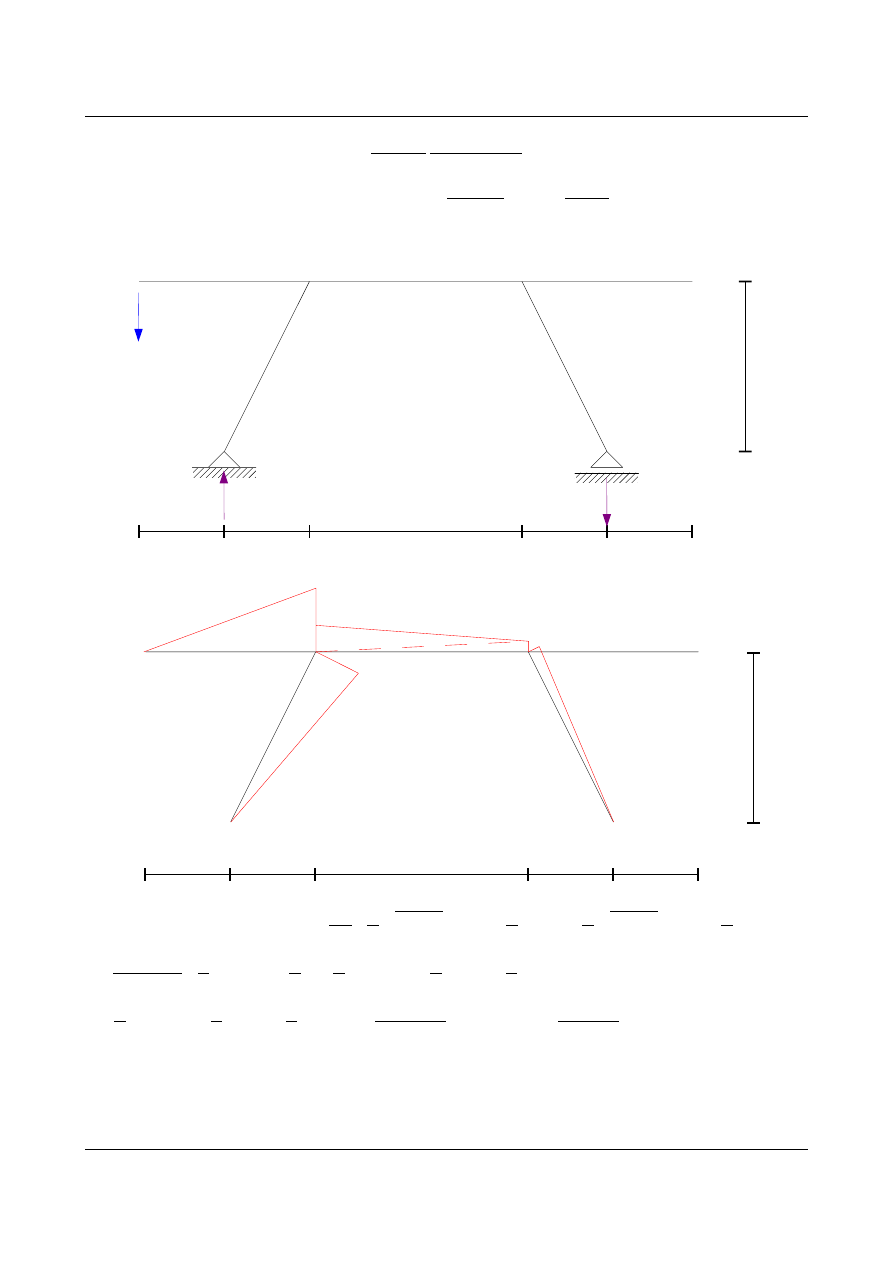
kontrola kinematyczna

1⋅=−

∑



R⋅

∑∫

M

n

⋅ 

M

0

EI

dx

∑

m

R

n

⋅

R

0

k

•

obliczenie zerowego przemieszczenia v

A

dla nowego układu podstawowego

wykres momentów zginających od jednostkowej siły w punkcie A

v

A

=−[1⋅0,0030,222⋅0,002]

1

EI

⋅



1

2

⋅



4

2

2

2

⋅0,5054⋅

2
3

⋅2,444

1

2

⋅



4

2

2

2

⋅2,5832⋅

2
3

⋅0,444





1

1,389⋅EI

⋅



1

2

⋅4⋅2,4172⋅

2
3

⋅4

1

2

⋅5⋅1,9118⋅

2
3

⋅1,556

1
3

⋅0,444

1

2

⋅5⋅0,7238⋅

2
3

⋅0,444

1
3

⋅1,556 



1

⋅0,6043

0,167⋅EI

=−0,003444

21,5993

EI

=

=−0,0034440,003443=−0,000001 [m]≈0

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

A

C

1

B

D

1,222

0,222

[ ī ]

4

2

2

5

2

2

[m]

M

1

0

[m]

4

1,556

2,444

0,444

0,444

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

8

•

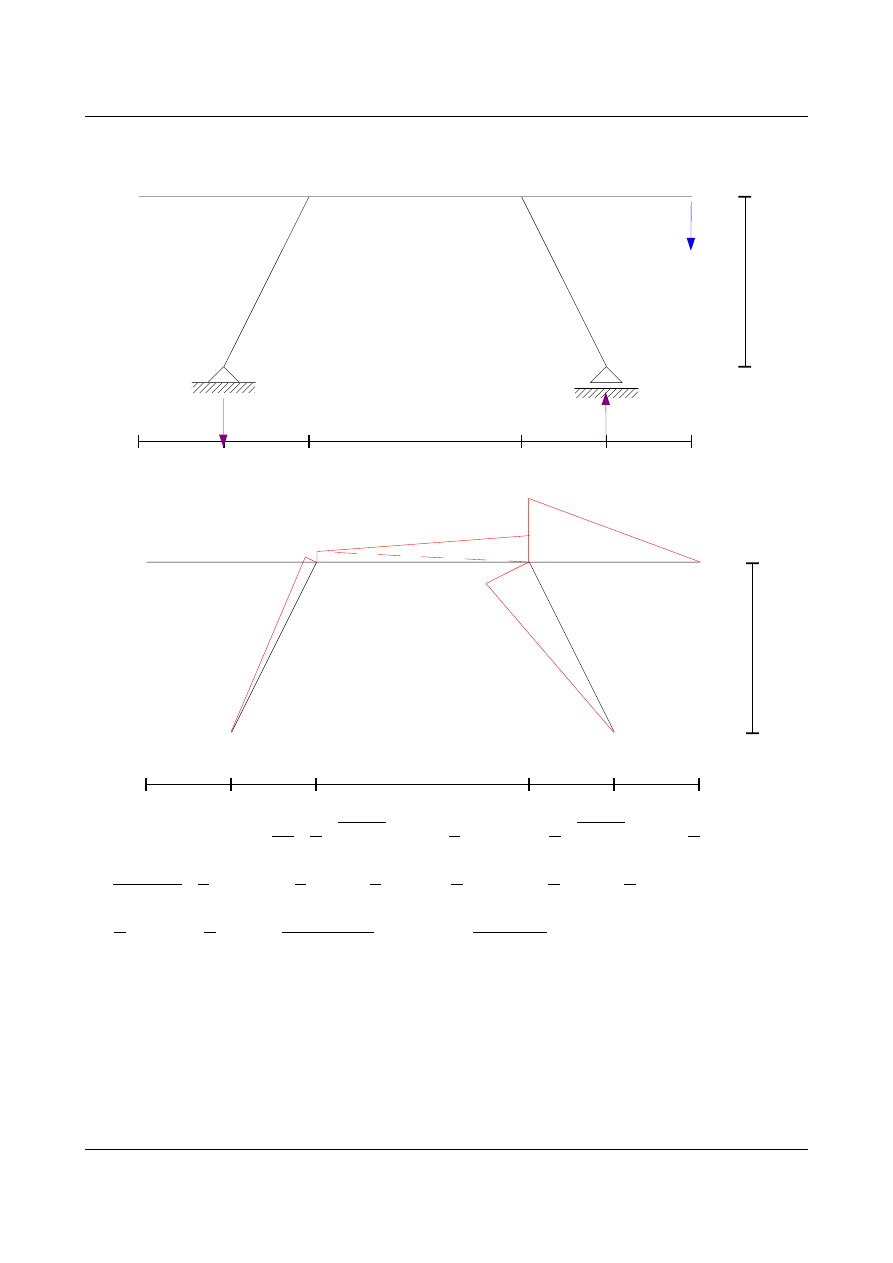
obliczenie zerowego przemieszczenia v

B

dla nowego układu podstawowego

wykres momentów zginających od jednostkowej siły w punkcie B

v

A

=−[−0,002⋅1,222]

1

EI

⋅



1

2

⋅



4

2

2

2

⋅0,5054⋅

2
3

⋅−0,444

1

2

⋅



4

2

2

2

⋅2,5832⋅

2
3

⋅−2,444





1

1,389⋅EI

⋅



1

2

⋅5⋅1,9118⋅

2
3

⋅0,444

1
3

⋅1,556 

1

2

⋅5⋅0,7238⋅

2
3

⋅1,556

1
3

⋅0,444

1

2

⋅4⋅1,8592⋅

2
3

⋅−4



1

⋅−0,4648

0,167⋅EI

=0,002444

−15,3263

EI

=

=0,002444−0,002443=0,000001 [m]≈0

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

A

C

1

B

D

1,222

0,222

[ ī ]

4

2

2

5

2

2

[m]

M

2

0

[m]

4

1,556

2,444

0,444

0,444

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

9

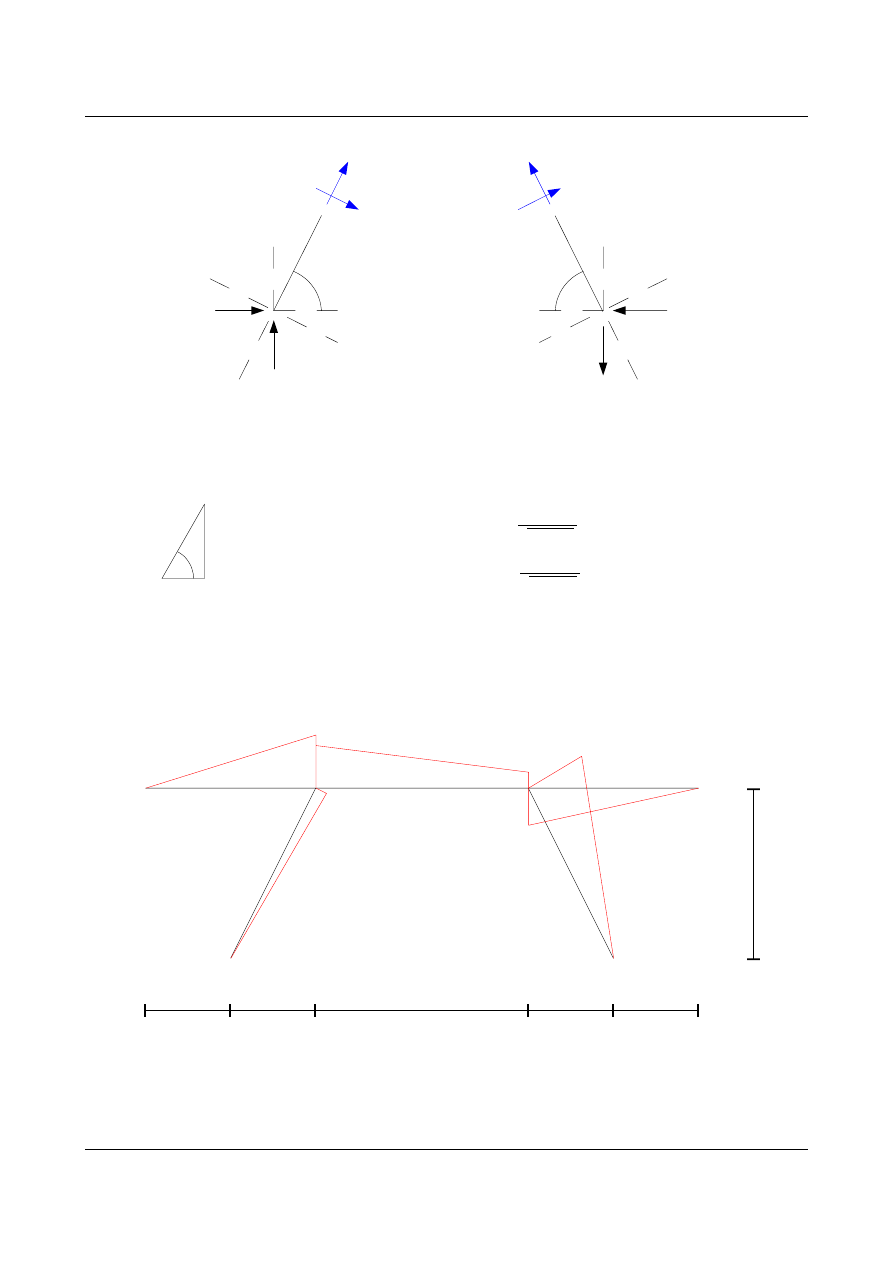
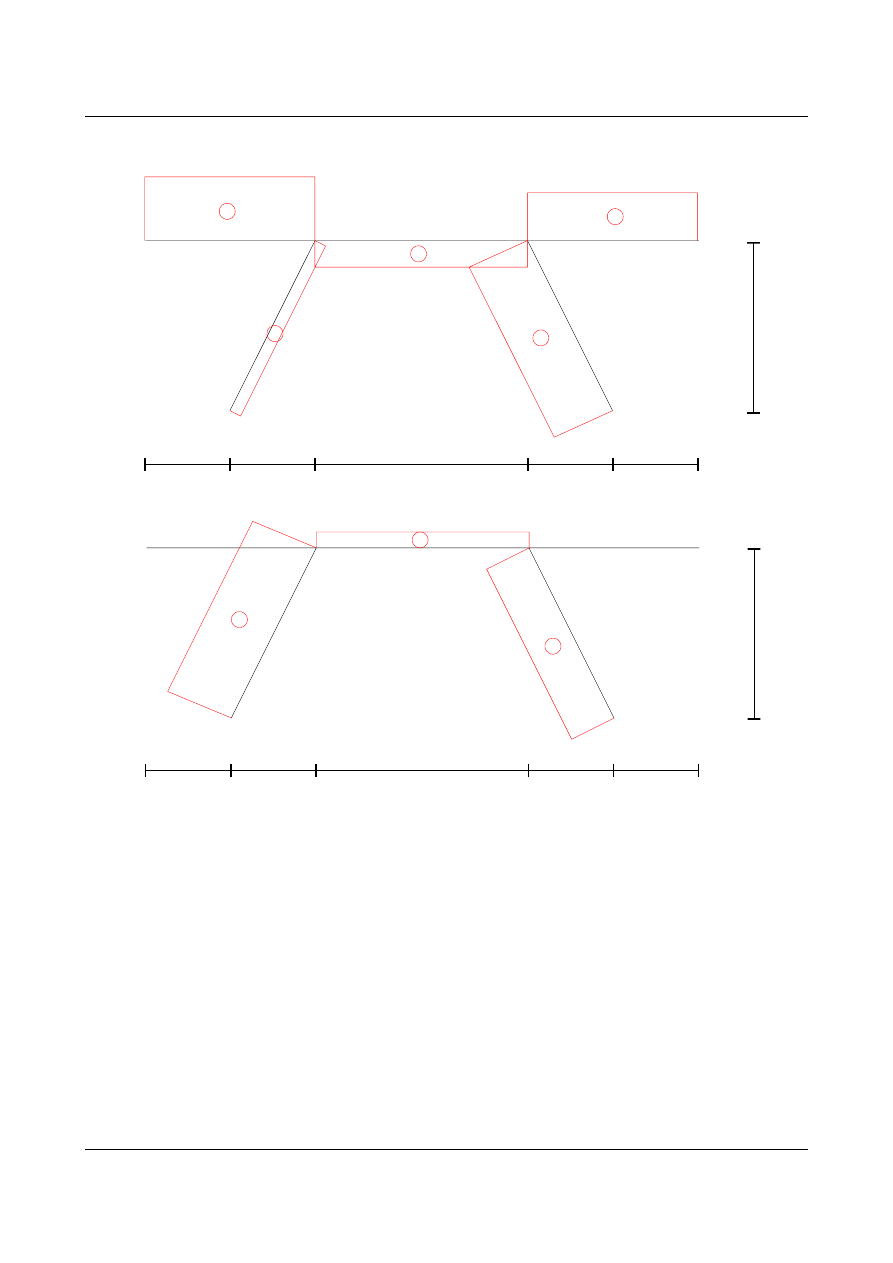
Rysunki i obliczenia pomocnicze

dla części pierwszej  I 

∑

∨:

N =−0,2946⋅cos−0,8419⋅sin

∑

∧:

T =−0,2946⋅sin0,8419⋅cos

dla części drugiej  II 

∑

∧:

N =0,7024⋅sin−0,2946⋅cos

∑

∨:

T =0,7024⋅cos0,2946⋅sin

sin=

4



4

2

2

2

=0,89443

cos=

2



4

2

2

2

=0,44721

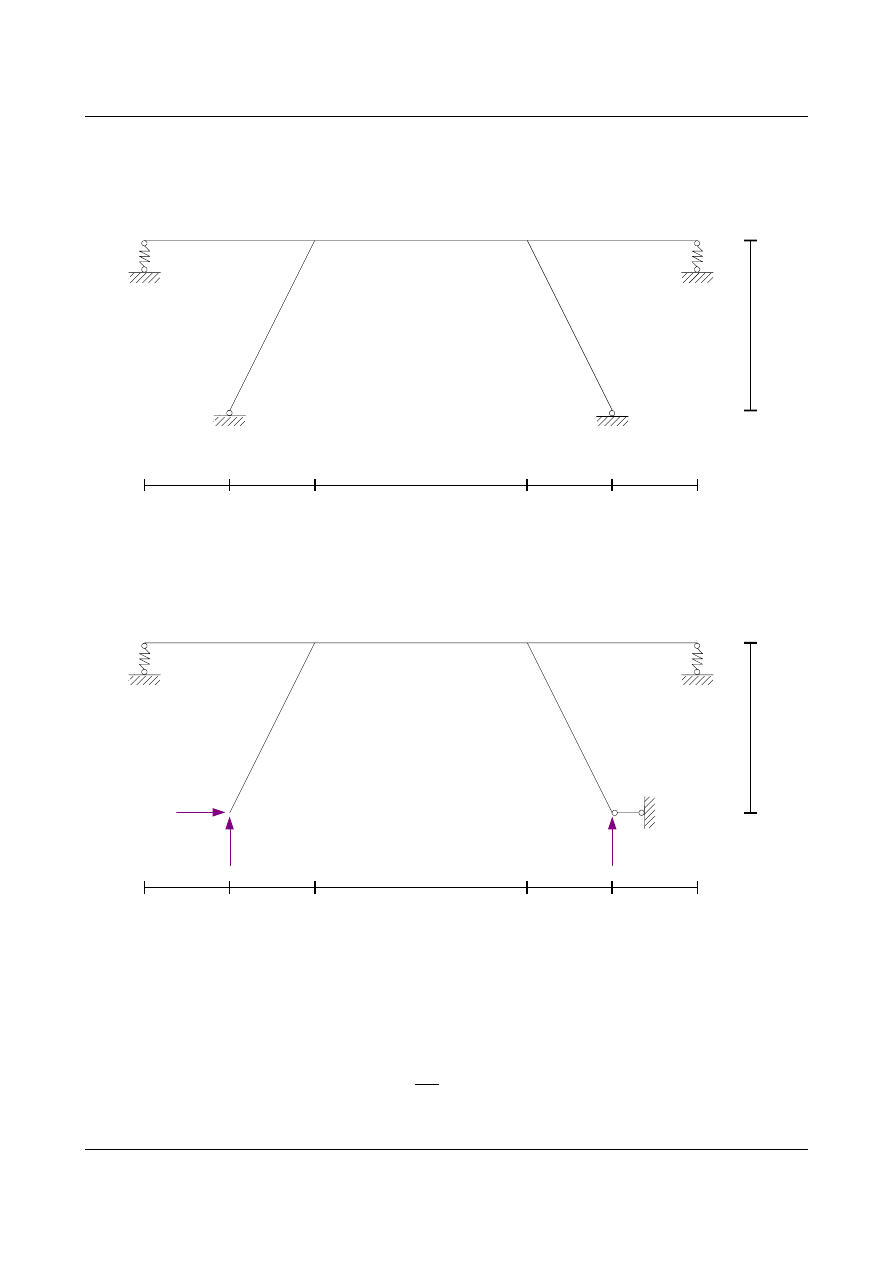
Wykresy sił wewnętrznych w układzie statycznie niewyznaczalnym

Agnieszka Sysak Gr 3

2003-12-16

2

4

φ

4

2

2

5

2

2

[m]

M

n

[kNm]

4,4172

1,9118

0,5054

0,7238

1,8592

2,5832

0,2946 kN

C

0,7024 kN

D

0,2946 kN

0,8419 kN

φ

φ

N

N

T

T

I

II

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

10

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

N

n

[kN]

-0,8848

0,4965

-0,2946

_

_

+

4

2

2

5

2

2

[m]

T

n

[kN]

0,1130

-0,4648

-0,6043

0,5776

0,2376

+

+

_

_

+

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

11

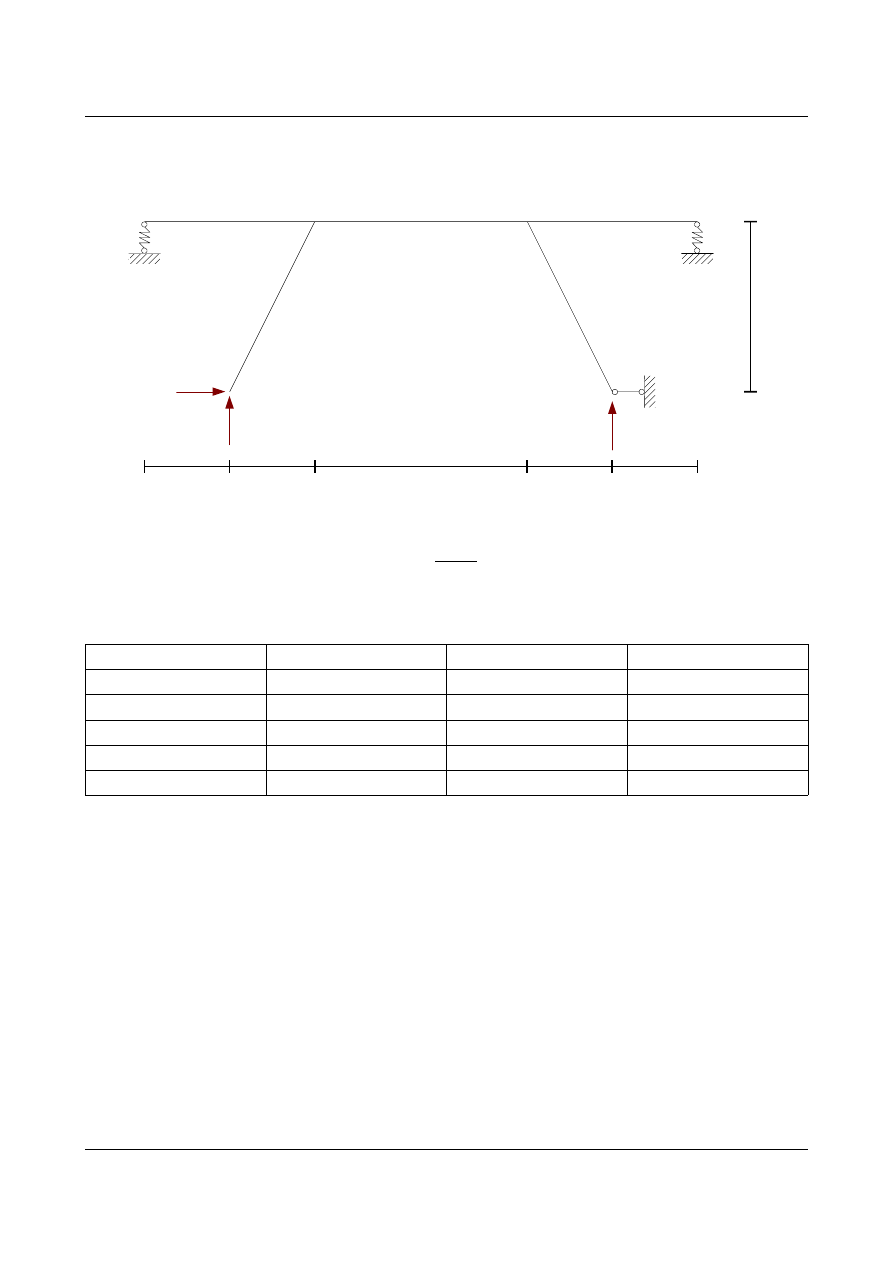
Temperatura

Obliczone wcześniej δ

11

, δ

12

, δ

13

, δ

22

, δ

23

, δ

33

zależą tylko od geometrii przyjętego do obliczeń układu, zatem

przyjmując układ podstawowy identyczny z układem podstawowym dla obliczeń od obciążeń zewnętrznych,
unikniemy ponownych obliczeń tych wartości i w przyjętym układzie podstawowym obliczamy jedynie
wartości δ

1T

, δ

2T

, δ

3T

.

Układ podstawowy

Zapisujemy warunki kinematycznej zgodności przyjętego układu podstawowego z układem wyjściowym:

u

d

=

1T

 X

1

⋅

11

 X

2

⋅

1 2

 X

3

⋅

1 3

=0

v

d

=

2T

 X

1

⋅

2 1

 X

2

⋅

2 2

 X

3

⋅

2 3

=0

v

c

=

3T

 X

1

⋅

31

 X

2

⋅

3 2

 X

3

⋅

3 3

=0

Dzielimy na stany od poszczególnych obciążeń i obliczamy potrzebne przemieszczenia

=

∑∫



M⋅

T

⋅

 t

h

dx

∑∫



N⋅

T

⋅t

0

dx

Agnieszka Sysak Gr 3

2003-12-16

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

-15

o

C

+20

o

C

+10

o

C

-10

o

C

t

m

= -25

o

C

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

X

1

X

2

X

3

A

B

C

D

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

12

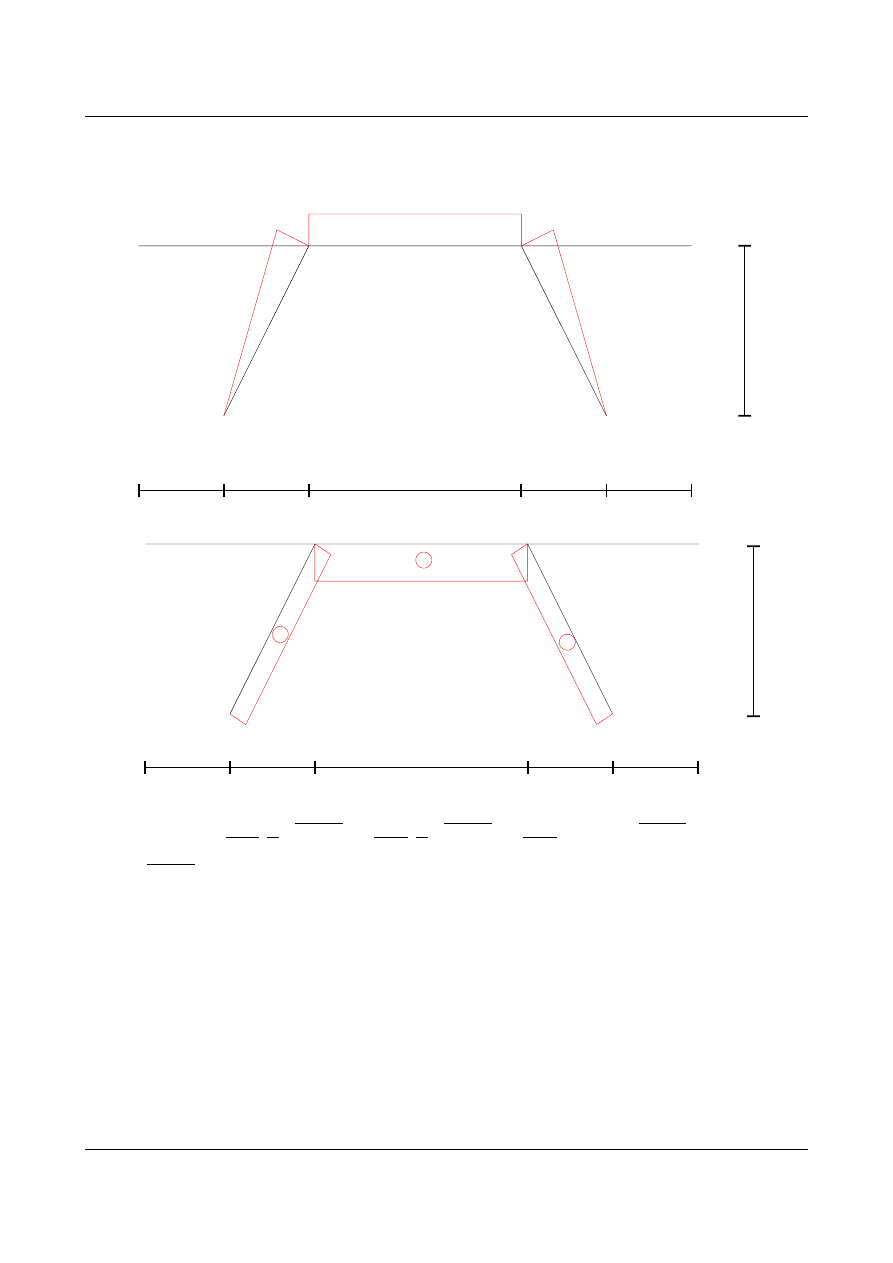
Szukane przemieszczenia w układzie podstawowym

 t=∣t

1

−t

2

∣

t

śr

=

t

1

t

2

2

t

0

=t

śr

−t

m

∆t [

o

C]

t

śr

[

o

C]

t

0

[

o

C]

AF

25

-2,5

-27,5

EF

35

2,5

-22,5

FB

5

-12,5

-37,5

DE

10

15

-10

CF

30

5

-20

Dane fizyczne i geometryczne:

I

1

→ h = 22 cm = 0,22m

I

2

→ h = 24 cm = 0,24m

I = 3060 · 10

-8

m

4

E = 205 · 10

6

kN/m

2

α

T

= 1,2 · 10

-5

1/

o

C

Agnieszka Sysak Gr 3

2003-12-16

δ

1T

δ

2T

δ

3T

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

-15

o

C

+20

o

C

+10

o

C

-10

o

C

t

m

= -25

o

C

A

E

D

F

C

B

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

13

•

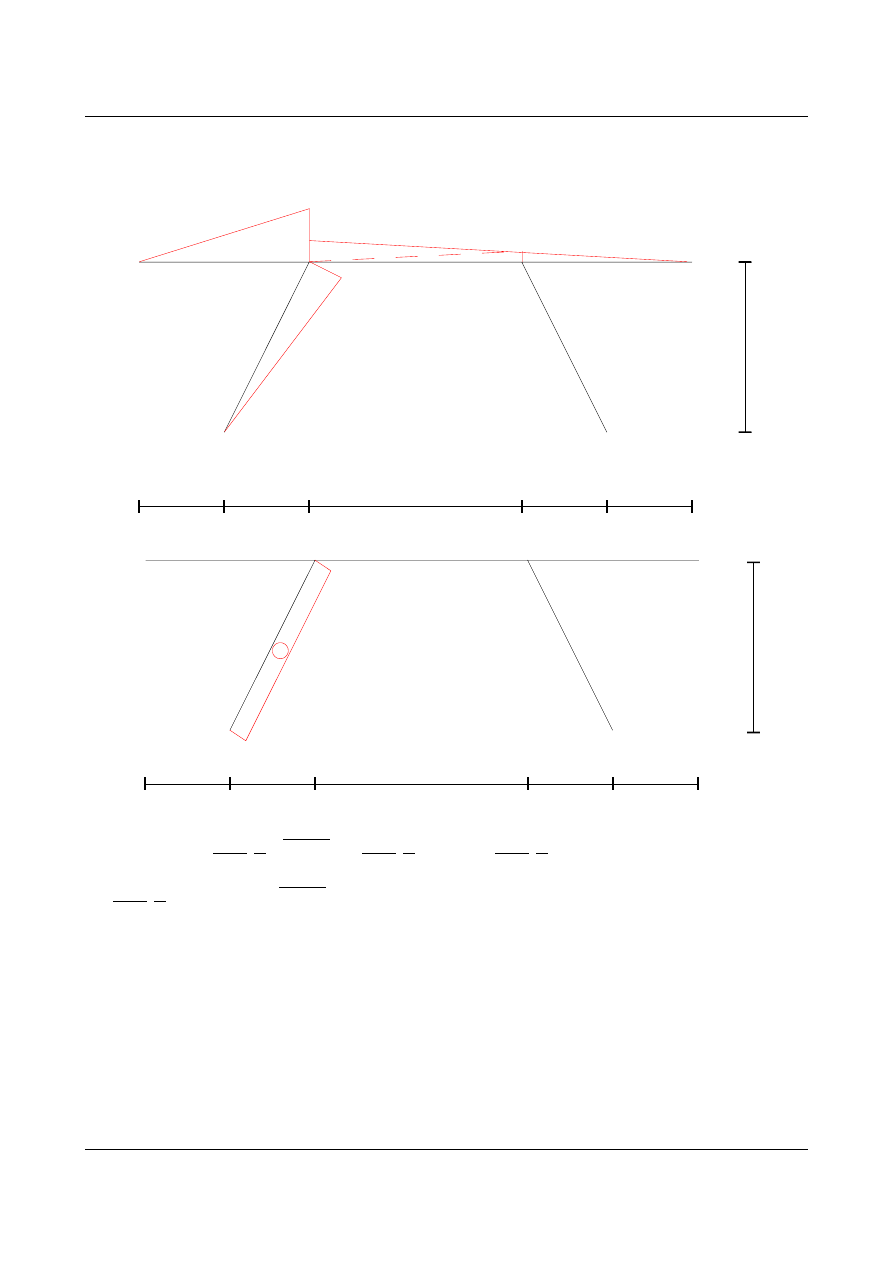
Stan od obciążenia X

1



1T

=1,2⋅10

−5

⋅



− 10

0,22

⋅1

2

⋅



4

2

2

2

⋅4−

30

0,22

⋅1

2

⋅



4

2

2

2

⋅4−

35

0,24

⋅5⋅4−10⋅



4

2

2

2

⋅−0,447 

−20⋅



4

2

2

2

⋅−0,447 −22,5⋅5⋅−1



=−0,052445 [m]

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

M

1

[m]

4

4

4

4

4

2

2

5

2

2

[m]

N

1

[kN]

-0,447

-1,0

_

_

_

-0,447

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

14

•

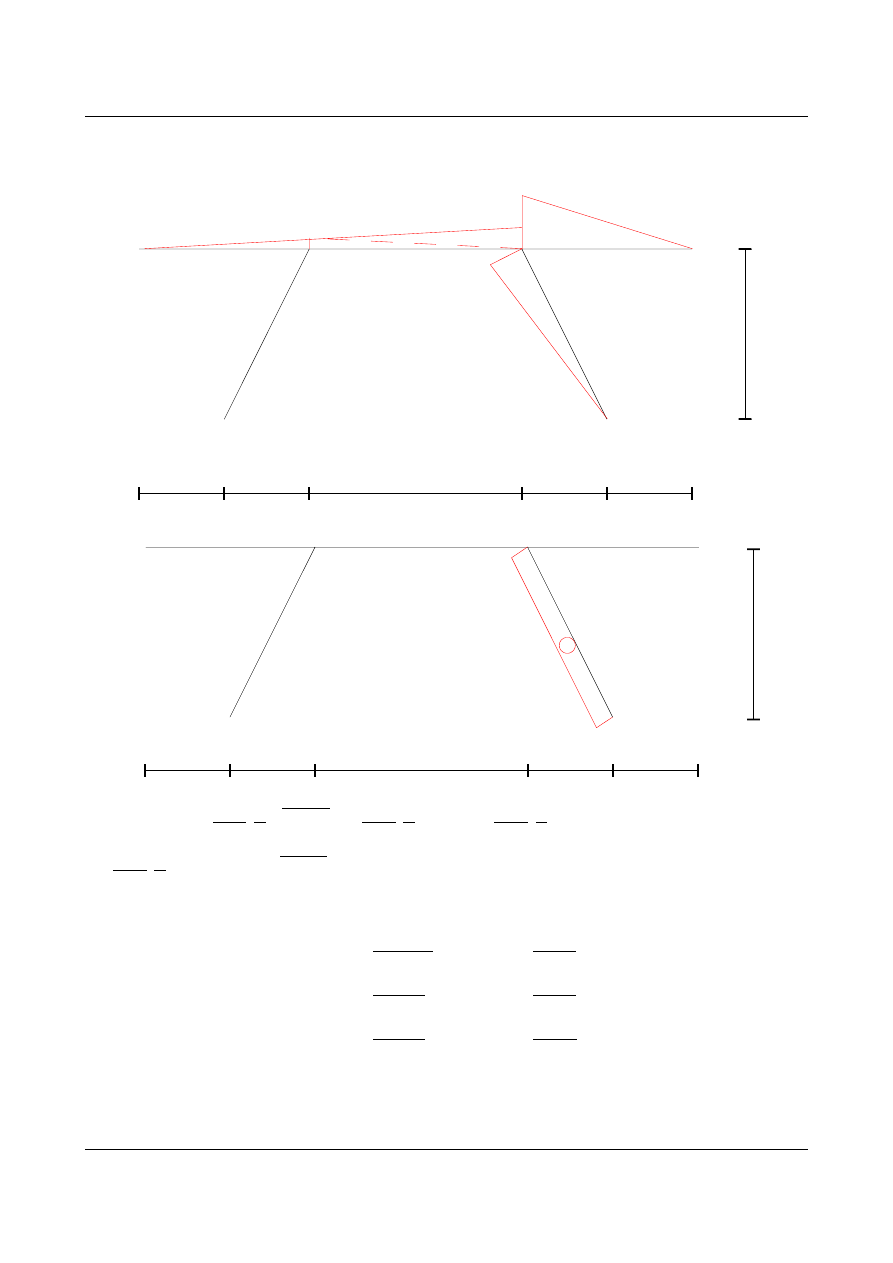
Stan od obciążenia X

2



2 T

=1,2⋅10

−5

⋅



10

0,22

⋅1

2

⋅



4

2

2

2

⋅2−

25

0,24

⋅1

2

⋅4⋅3,385−

35

0,24

⋅1

2

⋅5⋅1,3850,615

− 5

0,24

⋅1

2

⋅4⋅0,615−10⋅



4

2

2

2

⋅−0,894



=−0,014601 [m]

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

M

2

[m]

3,385

1,385

0,615

2

4

2

2

5

2

2

[m]

N

2

[kN]

-0,894

_

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

15

•

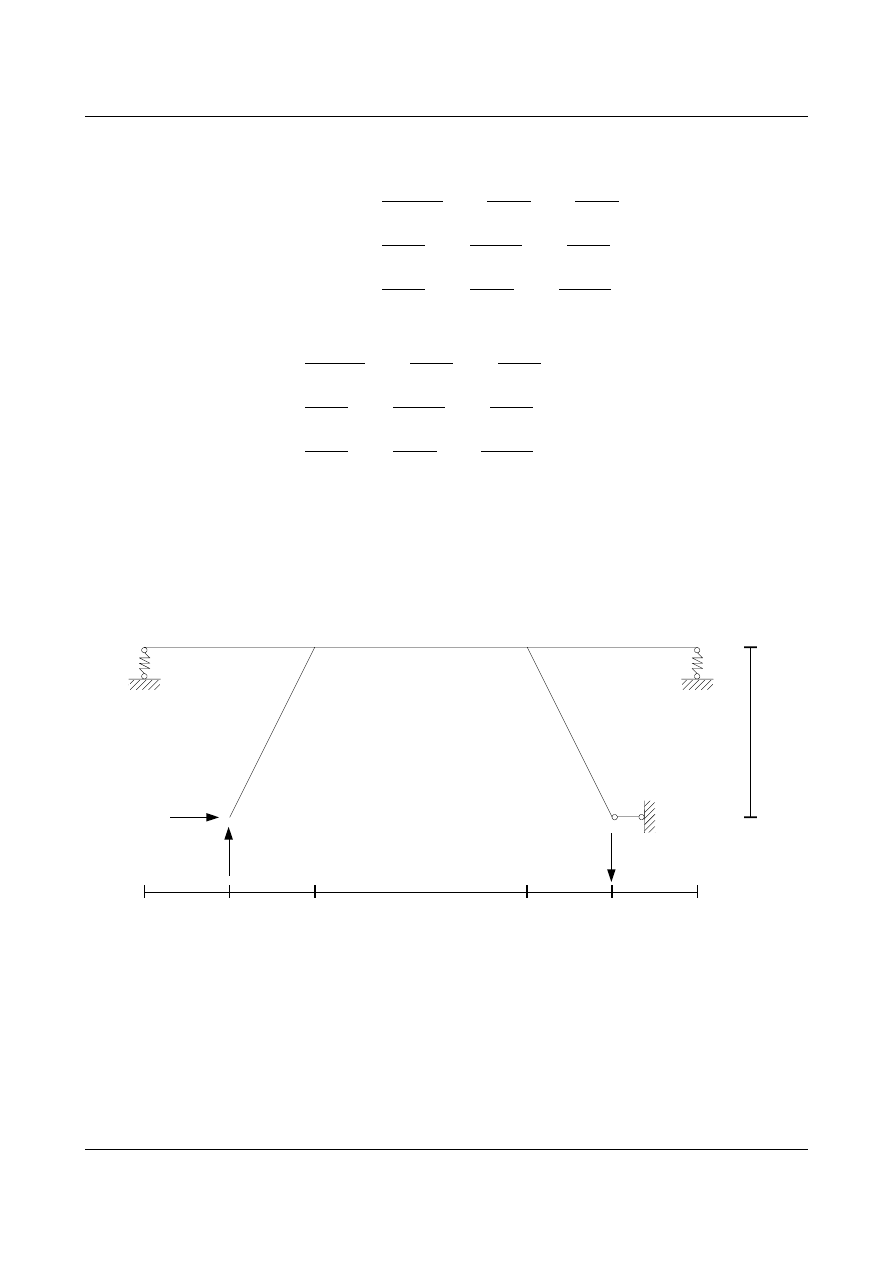
Stan od obciążenia X

3



3T

=1,2⋅10

−5

⋅



30

0,22

⋅1

2

⋅



4

2

2

2

⋅2−

25

0,24

⋅1

2

⋅4⋅0,615−

35

0,24

⋅1

2

⋅5⋅0,6151,385

− 5

0,24

⋅1

2

⋅4⋅3,385−20⋅



4

2

2

2

⋅−0,894



=−0,003702 [m]

Obliczone wcześniej przemieszczenia:



11

=105,303

EI



22

=25,543

EI



33

=25,543

EI



12

=

21

=2,474

EI



13

=

31

=2,474

EI



23

=

32

=8,986

EI

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

M

3

[m]

3,385

1,385

0,615

2

4

2

2

5

2

2

[m]

N

3

[kN]

-0,894

_

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

16

Zapisujemy układ równań i obliczamy niewiadome X

1

, X

2

, X

3

{

−0,052445 X

1

⋅105,303

E I

 X

2

⋅2,474

E I

 X

3

⋅2,474

E I

=0

−0,014601 X

1

⋅2,474

E I

 X

2

⋅25,543

E I

 X

3

⋅8,986

E I

=0

−0,003702 X

1

⋅2,474

E I

 X

2

⋅8,986

E I

 X

3

⋅25,543

E I

=0

{

X

1

⋅105,303

E I

 X

2

⋅2,474

E I

 X

3

⋅2,474

E I

=0,052445

X

1

⋅2,474

E I

 X

2

⋅25,543

E I

 X

3

⋅8,986

E I

=0,014601

X

1

⋅2,474

E I

 X

2

⋅8,986

E I

 X

3

⋅25,543

E I

=0,003702

{

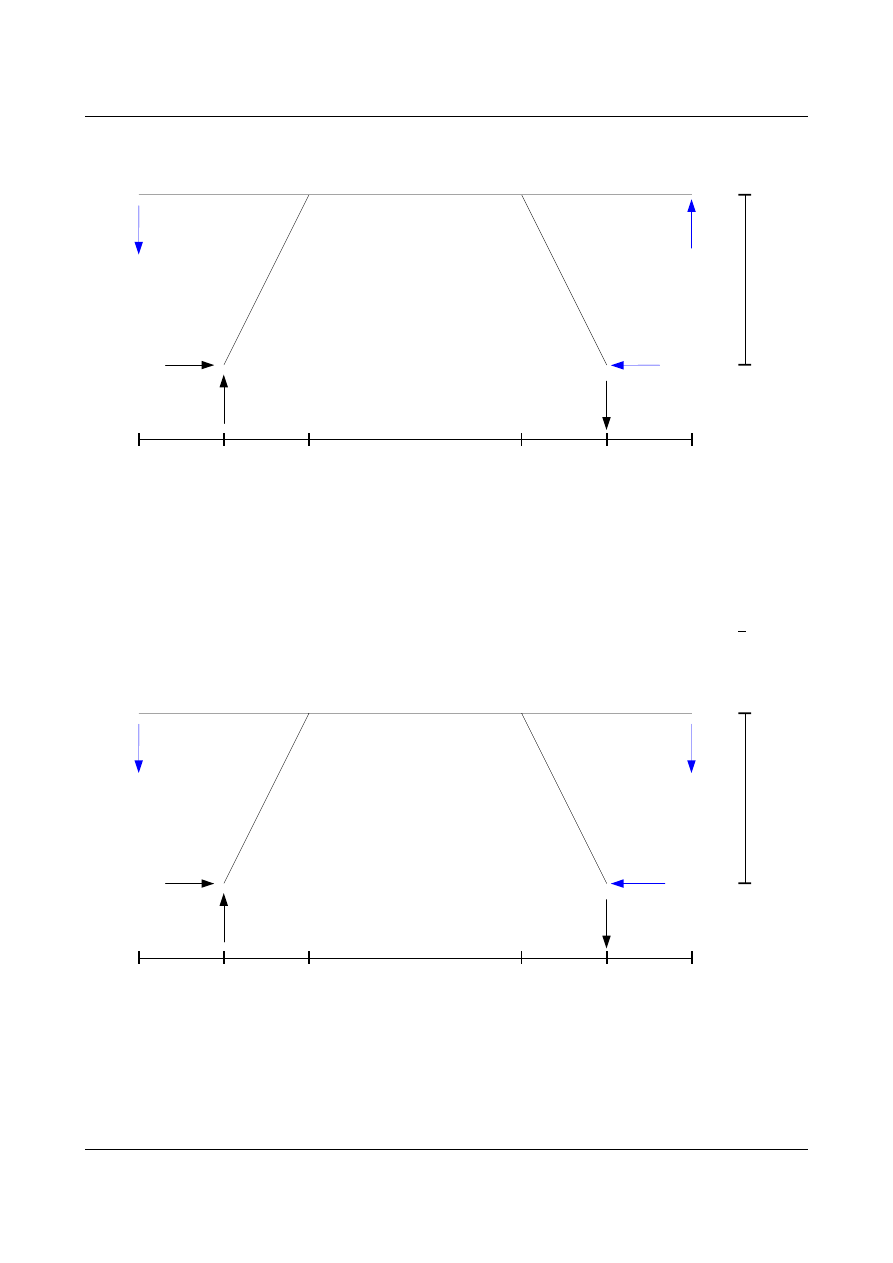
X

1

=3,0564 [kN ]

X

2

=3,5083 [kN ]

X

3

=−0,6211 [kN ]

* obliczenia wykonano w programie Derive

Zestawienie wyników

Agnieszka Sysak Gr 3

2003-12-16

k

k

I

2

I

2

I

2

I

1

I

1

4

2

2

5

2

2

[m]

A

B

C

D

3,0564 kN

3,5083 kN

0,6211 kN

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

17

Obliczenie reakcji

∑

X :

3,0564−R

c

=0

⇒

R

c

=3,0564 [kN ]

∑

M

A

:

3,5083⋅2−0,6211⋅11R

b

⋅133,0564⋅4−R

c

⋅4=0

⇒

R

b

=−0,0142[kN ]

∑

M

B

:

−0,6211⋅23,5083⋅11−R

a

⋅13R

c

⋅4−3,0564⋅4=0

⇒

R

a

=2,8730[kN ]

∑

Y

spr

:

−R

a

R

b

3,5083−0,6211=−2,8730−0,01423,5083−0,6211=0

Zestawienie wyników reakcji

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

R

c

R

a

R

b

A

B

C

D

3,0564 kN

3,5083 kN

0,6211 kN

4

2

2

5

2

2

[m]

3,0564 kN

2,8730 kN

0,0142 kN

A

B

C

D

3,0564 kN

3,5083 kN

0,6211 kN

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

18

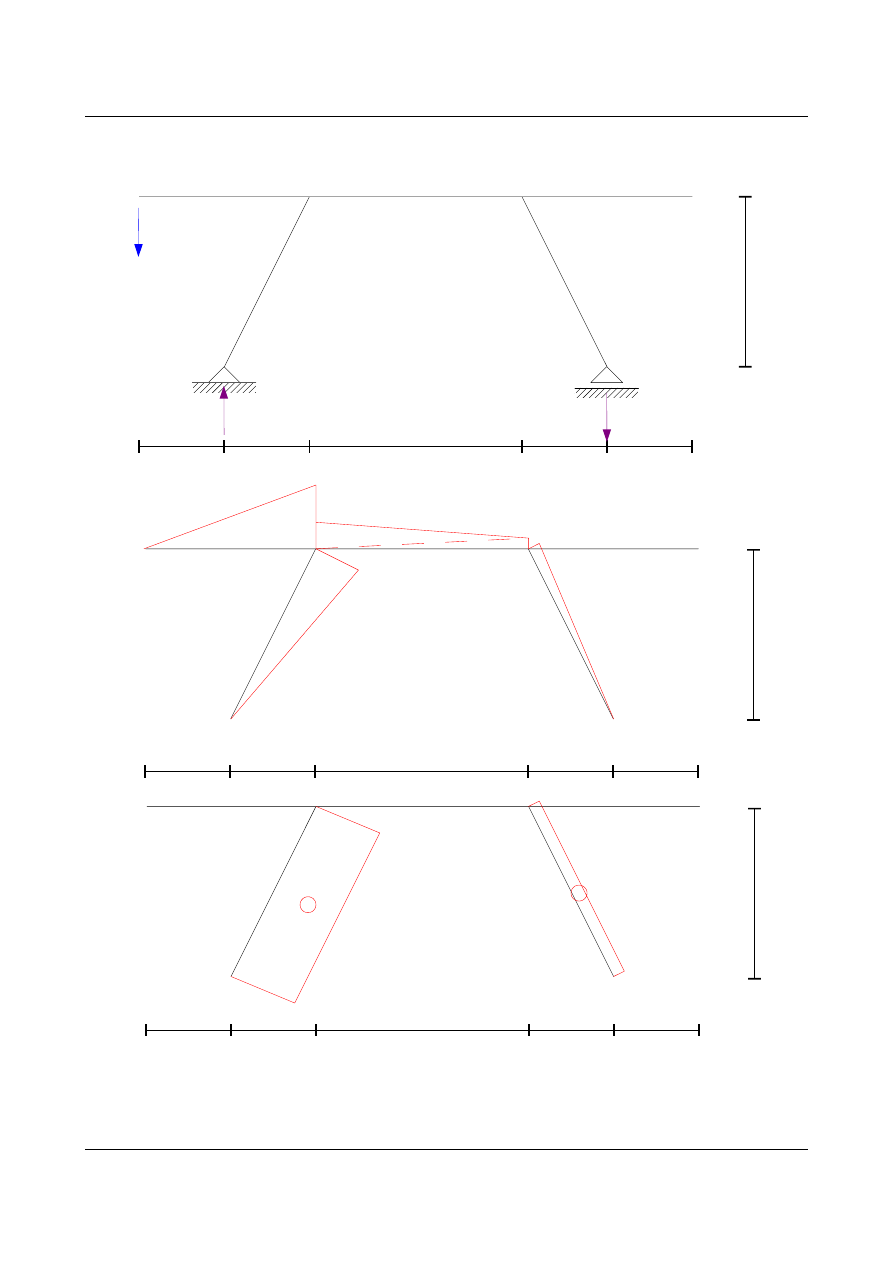
Rysunki pomocnicze do wykonania wykresu

Wykres momentów zginających

kontrola kinematyczna

1⋅=

∑∫



M⋅

T

⋅

 t

h

dx

∑∫



N⋅

T

⋅t

0

dx

∑∫

M

n

⋅ 

M

0

EI

dx

∑

m

R

n

⋅

R

0

k

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

M

n

[kNm]

11,4920

13,5246

5,2090

16,7010

0,0568 13,4678

3,0564 kN

C

0,6211 kN

D

3,0564 kN

3,5083 kN

2,8730 kN

A

x

D

3,0564 kN

3,5083 kN

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

19

•

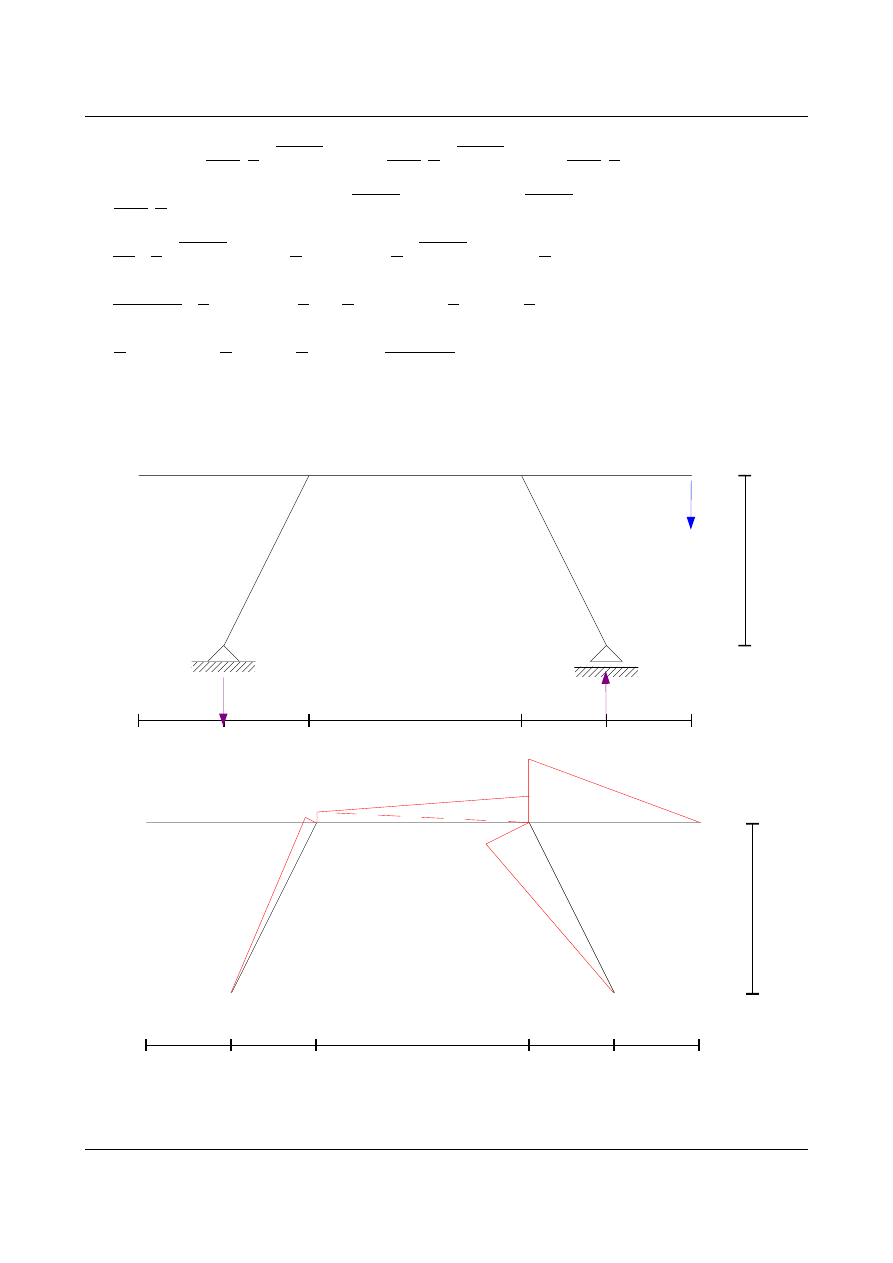
obliczenie zerowego przemieszczenia v

A

dla nowego układu podstawowego

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

A

C

1

B

D

1,222

0,222

[ 1 ]

4

2

2

5

2

2

[m]

M

1

0

[m]

4

1,556

2,444

0,444

0,444

4

2

2

5

2

2

[m]

N

1

0

[kN]

-1,093

_

+

0,199

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

20

v

A

=1,2⋅10

−5

⋅



10

0,22

⋅1

2

⋅



4

2

2

2

⋅2,444−

30

0,22

⋅1

2

⋅



4

2

2

2

⋅0,444−

25

0,24

⋅1

2

⋅4⋅4

− 35

0,24

⋅1

2

⋅1,5560,444⋅5−10 ⋅



4

2

2

2

⋅−1,093−20 ⋅



4

2

2

2

⋅0,199



 1

EI

⋅



1

2

⋅



4

2

2

2

⋅5,2090⋅

2
3

⋅−2,444

1

2

⋅



4

2

2

2

⋅13,4678⋅

2
3

⋅0,444





1

1,389⋅EI

⋅



1

2

⋅4⋅11,4920⋅

2
3

⋅4

1

2

⋅5⋅16,7010⋅

2
3

⋅1,556

1
3

⋅0,444

1

2

⋅5⋅13,5246⋅

1
3

⋅1,556

2
3

⋅0,444



1

⋅2,8730

0,167⋅EI

=

=−0,01702080,0170204=0,0000003 [m]≈0

•

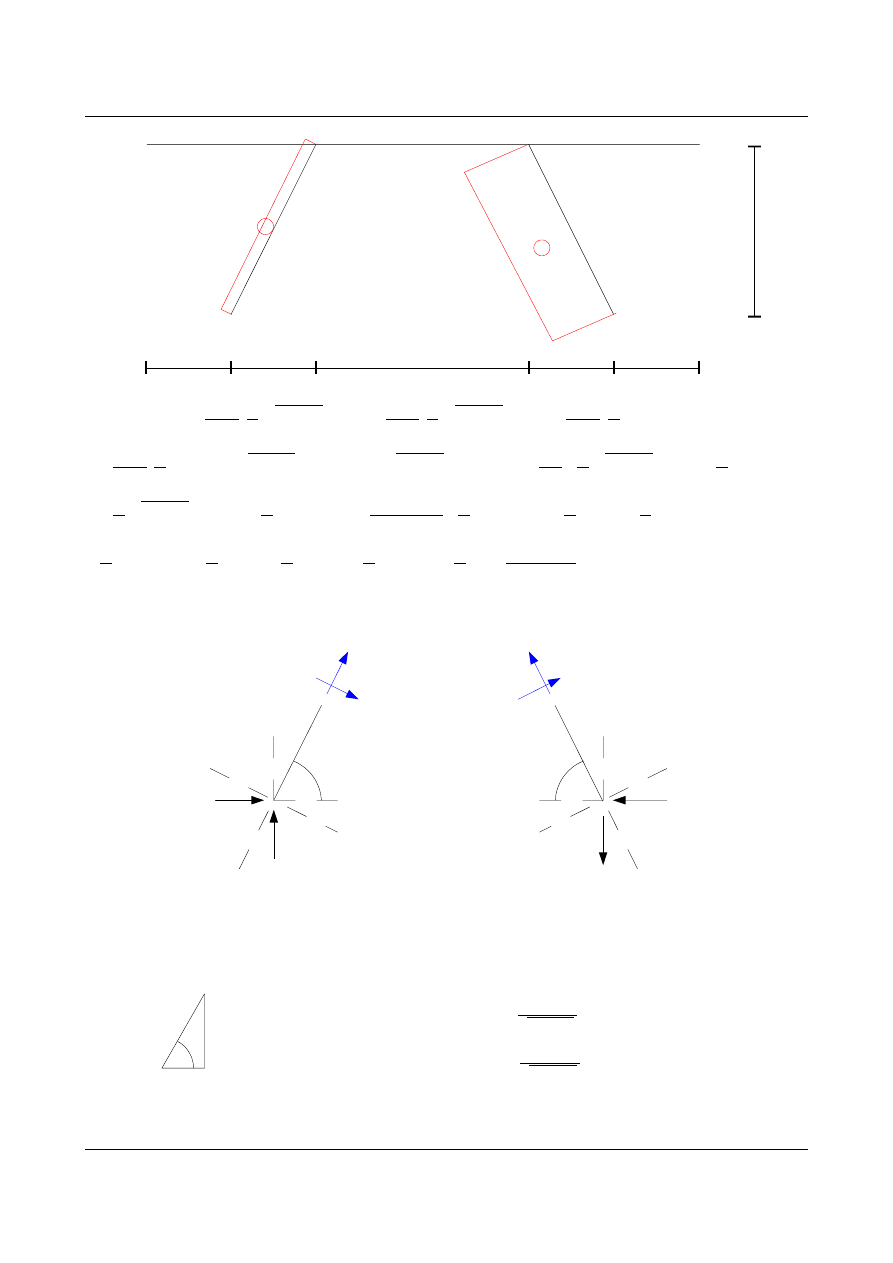
obliczenie zerowego przemieszczenia v

B

dla nowego układu podstawowego

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

A

C

1

B

D

1,222

0,222

[ 1 ]

4

2

2

5

2

2

[m]

M

2

0

[m]

4

1,556

2,444

0,444

0,444

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

21

v

B

=1,2⋅10

−5

⋅



−10

0,22

⋅1

2

⋅



4

2

2

2

⋅0,444

30

0,22

⋅1

2

⋅



4

2

2

2

⋅2,444−

35

0,24

⋅1

2

⋅0,4441,556 ⋅5

− 5

0,24

⋅1

2

⋅4⋅4−10⋅



4

2

2

2

⋅0,199−20 ⋅



4

2

2

2

⋅−1,093



 1

EI

⋅



1

2

⋅



4

2

2

2

⋅5,2090⋅

2
3

⋅0,444

1

2

⋅



4

2

2

4

⋅13,4678⋅

2
3

⋅−2,444





1

1,389 ⋅EI

⋅



1

2

⋅5⋅16,7010⋅

2
3

⋅0,444

1
3

⋅1,556 

1

2

⋅5⋅13,5246⋅

1
3

⋅0,444

2
3

⋅1,556 

1

2

⋅4⋅0,0568⋅

2
3

⋅4



1

⋅0,0142

0,167⋅EI

=

=−0,001282560,00128216=−0,0000004 [m]≈0

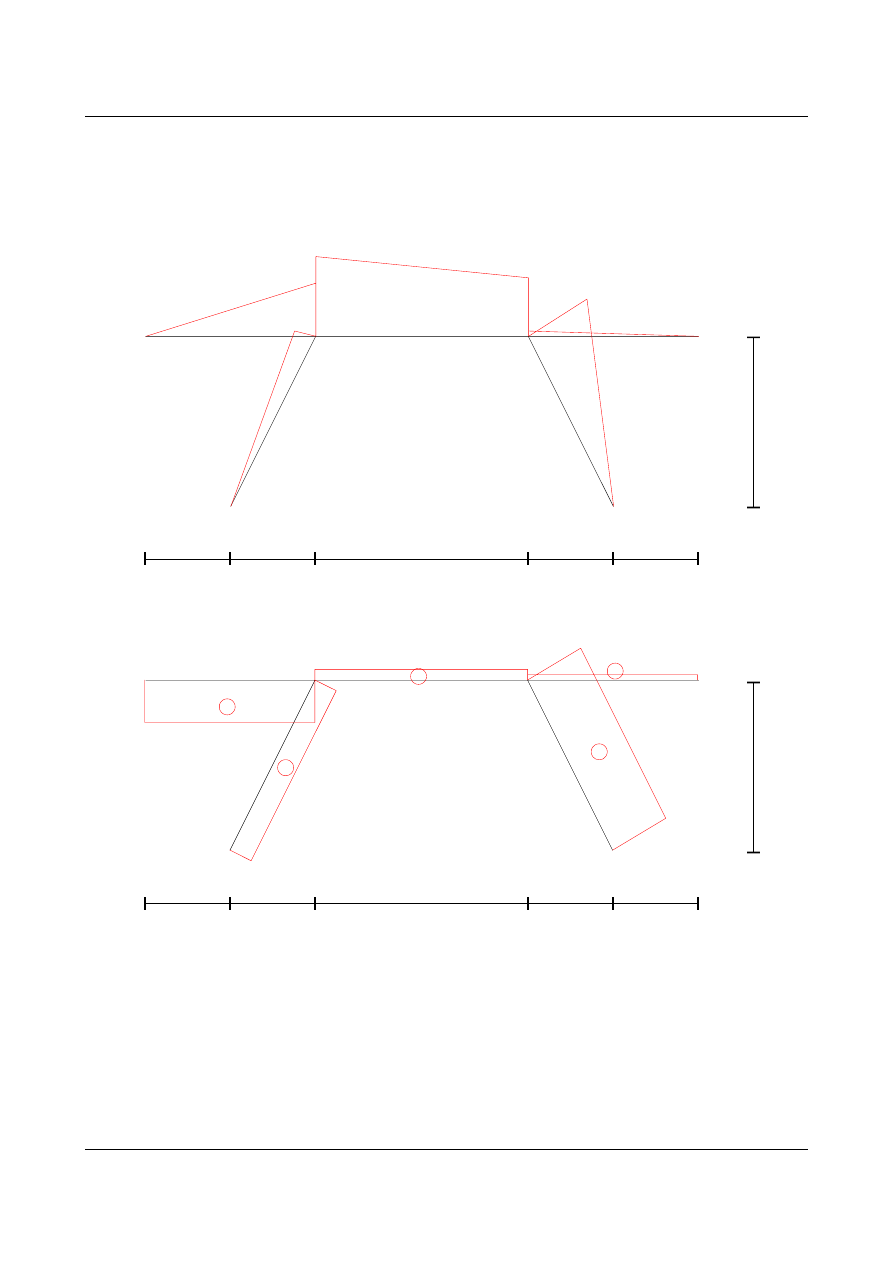
Rysunki i obliczenia pomocnicze

dla części pierwszej  I 

∑

∨:

N =−3,0564⋅cos−3,5083⋅sin

∑

∧:

T =−3,0564⋅sin3,5083⋅cos

dla części drugiej  II 

∑

∧:

N =0,6211⋅sin−3,0564⋅cos

∑

∨:

T =0,6211⋅cos3,0564⋅sin

sin=

4



4

2

2

2

=0,89443

cos=

2



4

2

2

2

=0,44721

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

N

2

0

[kN]

-1,093

_

+

0,199

2

4

φ

3,0564 kN

C

0,6211 kN

D

3,0564 kN

3,5083kN

φ

φ

N

N

T

T

I

II

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

22

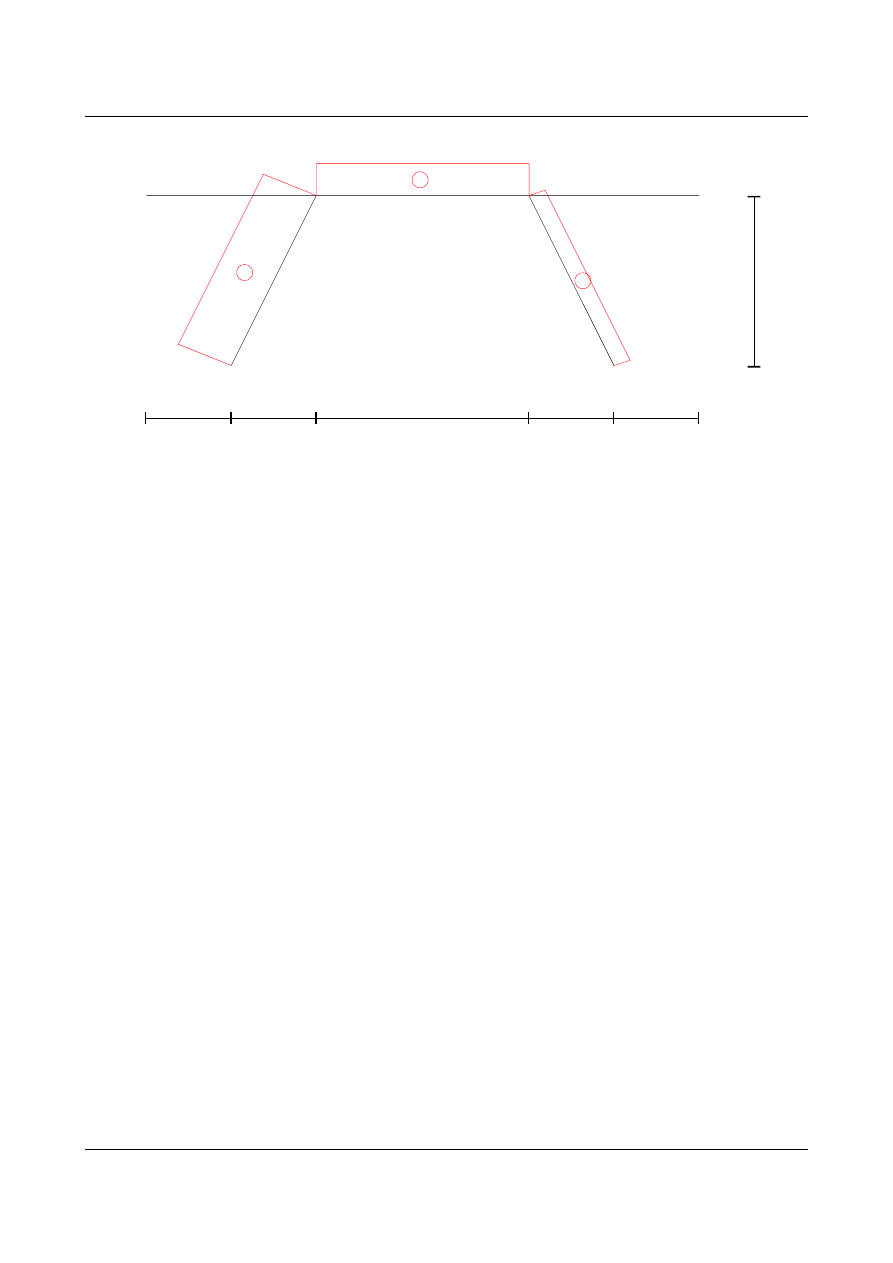
Wykresy sił wewnętrznych w układzie statycznie niewyznaczalnym

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

M

n

[kNm]

11,4920

13,5246

5,2090

16,7010

0,0568 13,4678

4

2

2

5

2

2

[m]

T

n

[kN]

-1,1648

0,0142

-2,8730

3,0115

0,6353

+

+

_

_

+

Część 2

OBLICZANIE UKŁADÓW STATYCZNIE NIEWYZNACZALNYCH METODĄ SIŁ

23

Agnieszka Sysak Gr 3

2003-12-16

4

2

2

5

2

2

[m]

N

n

[kN]

-4,5048

-0,8113

-3,0564

_

_

_