Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli

Układy statycznie niewyznaczalne - metoda sił, obliczanie przemieszczeń

Zad.1

II rok studiów zawodowych zaocznych /2003

Anita Kaczor

1

Zad.1. Dla zadanej ramy statycznie niewyznaczalnej:

a) wyznaczyć wykresy sił wewnętrznych korzystając z metody sił.
b) obliczyć przemieszczenie poziome pktu D.
c) obliczyć obrót pktu C.

Zad.1a)

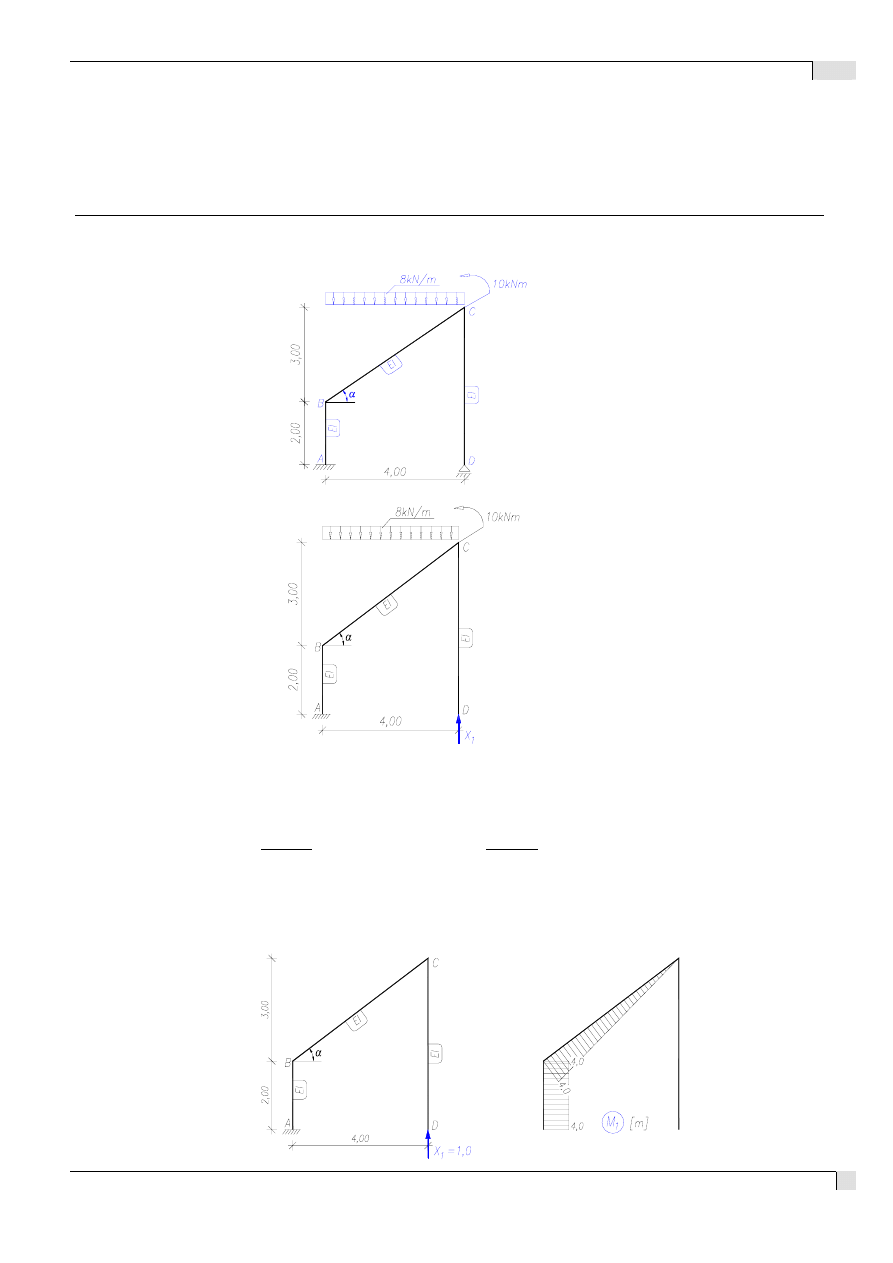
1. Schemat konstrukcji:

SSN=1;

EI=const
E=205Gpa;

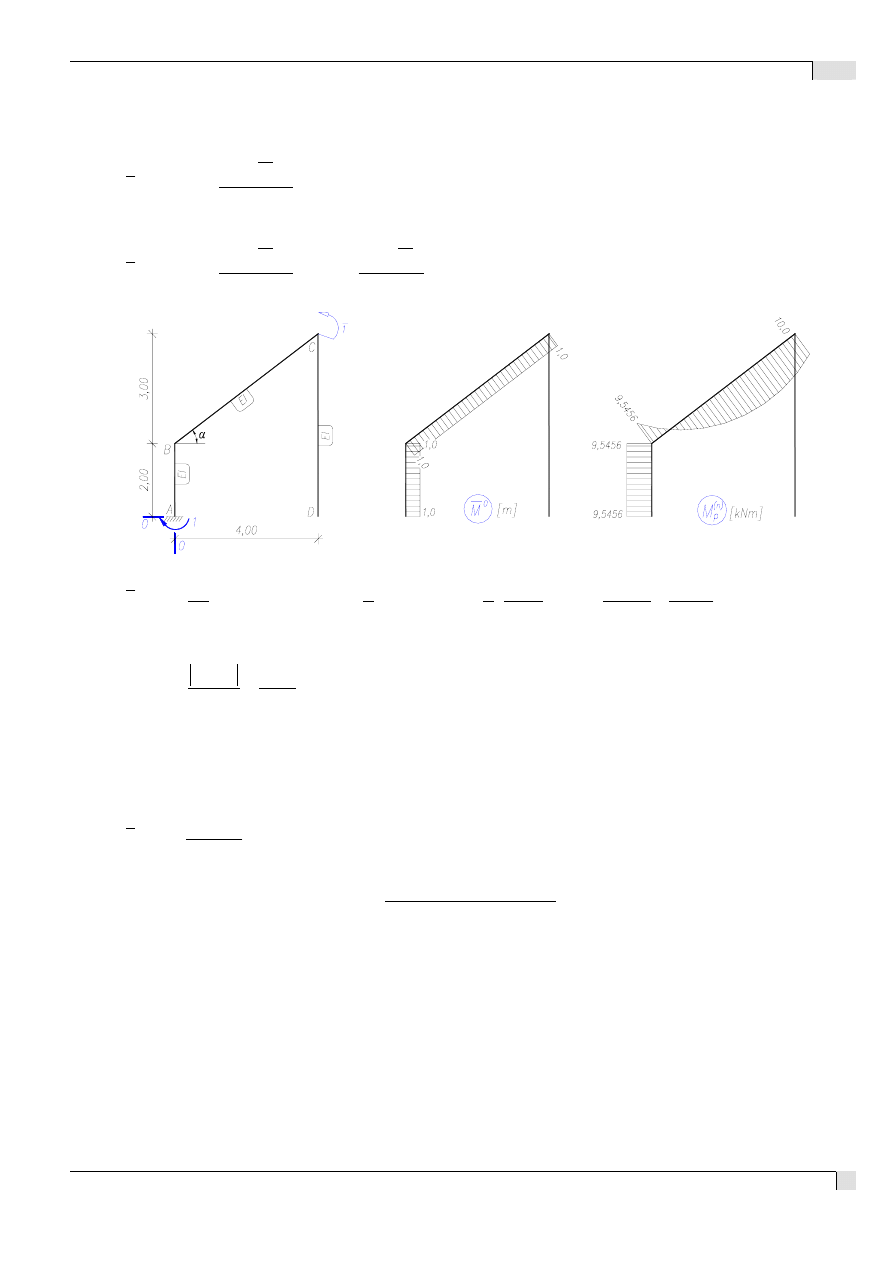
2. Układ podstawowy:

Układ spełnia warunki
statycznej wyznaczalności
i geometrycznej niezmienności.

3. Układ równań kanonicznych:

δ

11

· X

1

+ δ

1P

= 0

gdzie: współczynniki δ

ik

, δ

iP

:

∑∫

=

δ

l

k

i

ik

dx

EI

M

M

0

;

∑∫

=

δ

l

P

i

iP

dx

EI

M

M

0

;

gdzie: M

i

– momenty zginające od obciążenia siłą jednostkową X

i

=1,0 (w ukł. podst.)

M

p

– momenty zginające od obciążenia zewnętrznego (w ukł. podst.)

3.1. Stan X

1

= 1:

Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli

Układy statycznie niewyznaczalne - metoda sił, obliczanie przemieszczeń

Zad.1

II rok studiów zawodowych zaocznych /2003

Anita Kaczor

2

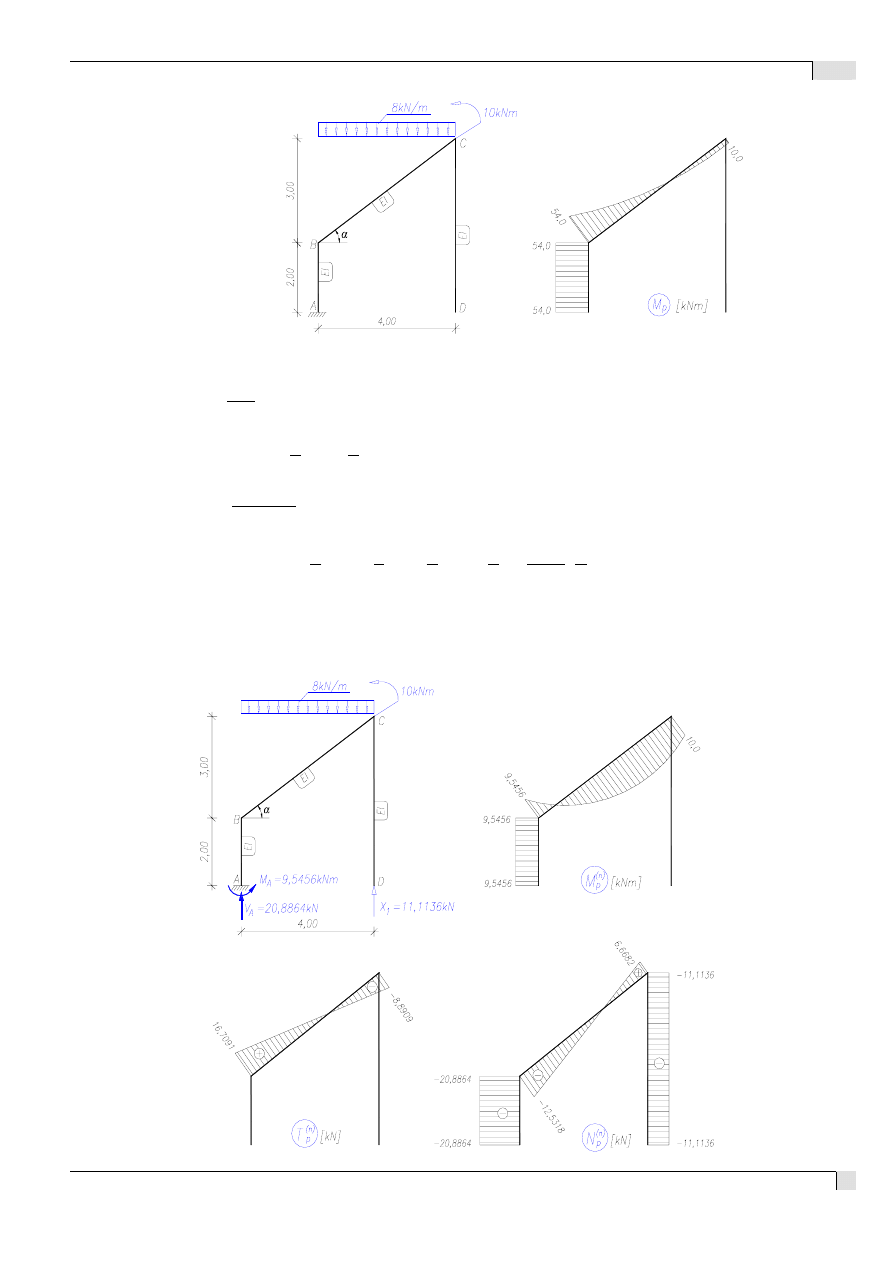
3.2. Stan „P”:

3.3. Obliczenie współczynników δ

ik

, δ

iP

∑∫

=

δ

l

dx

EI

M

0

2

1

11

3

11

)

6

(

,

58

4

3

2

5

4

2

1

4

4

2

m

EI

=

⋅

⋅

⋅

⋅

+

⋅

⋅

=

δ

⋅

∑∫

⋅

=

δ

l

p

P

dx

EI

M

M

0

1

1

3

2

1

652

4

2

1

8

4

8

5

3

2

)

54

3

2

10

3

1

(

5

4

2

1

54

4

2

kNm

EI

P

−

=

⋅

⋅

⋅

⋅

⋅

+

⋅

−

⋅

⋅

⋅

⋅

+

⋅

⋅

−

=

δ

⋅

3.4. Rozwiązanie układu równań kanonicznych:

58,(6)/EI · X

1

– 652/EI = 0

⇒ X

1

= 11,1136 kN

4. Wykresy sił wewnętrznych w ramie:

Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli

Układy statycznie niewyznaczalne - metoda sił, obliczanie przemieszczeń

Zad.1

II rok studiów zawodowych zaocznych /2003

Anita Kaczor

3

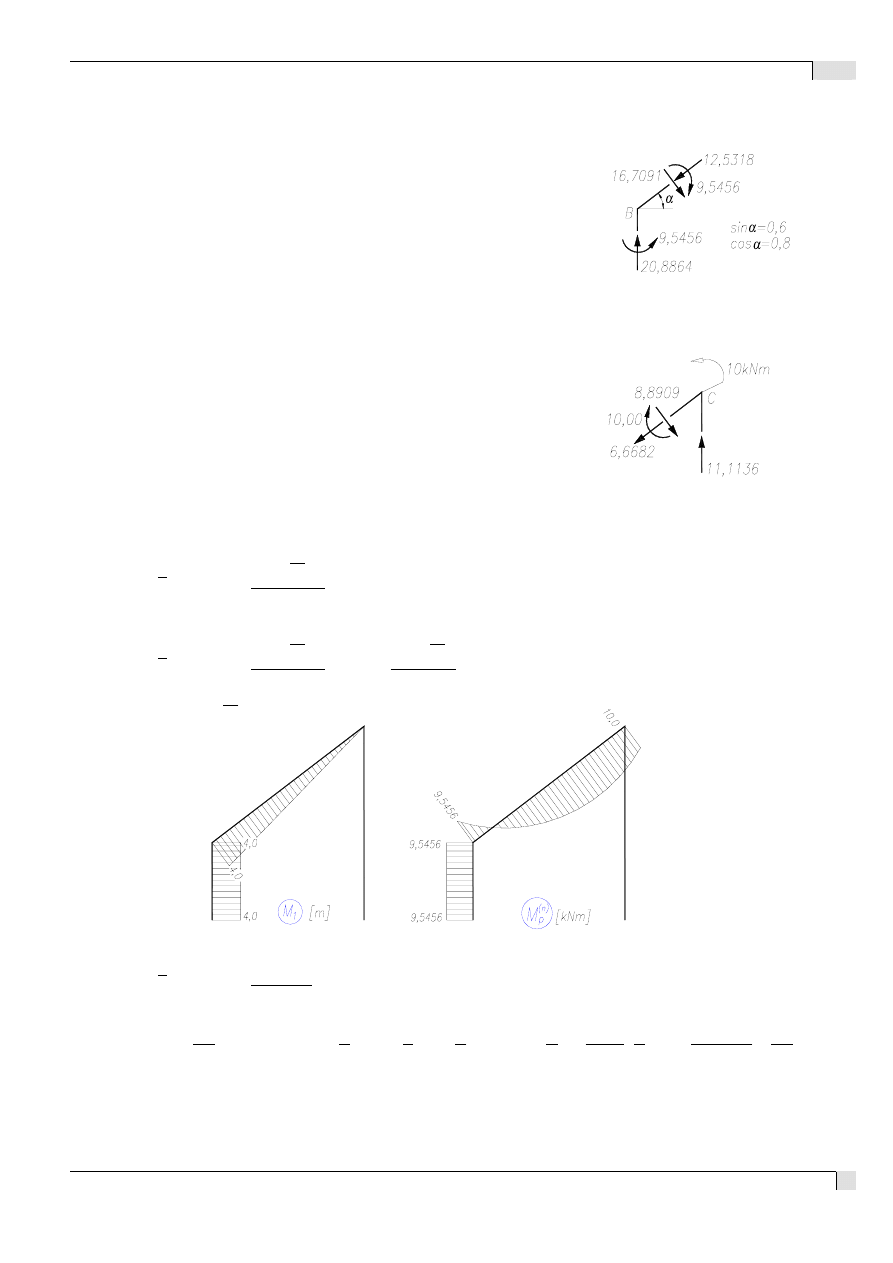
5. Kontrola poprawności obliczeń.

5.1. Kontrola statyczna.

- spr. równowagi węzła B:

∑X = 0:

-12,5318cosα + 16,7091sinα = 0

0 = 0

∑Y = 0

-12,5318sinα - 16,7091cosα + 20,8864 = 0

0 = 0

∑M = 0

9,5456 – 9,5456 = 0

0 = 0

- spr. równowagi węzła C:

∑X = 0:

-6,6682cosα + 8,8909sinα = 0

0 = 0

∑Y = 0

11,1136 – 6,6682sin

α

- 8,8909cos

α

= 0

0 = 0

∑M = 0

10 – 10 = 0

0 = 0

5.2. Kontrola kinematyczna.

- przemieszczenie pionowe pktu D:

∑∫

=

ν

⋅

l

n

n

p

D

dx

EI

M

M

0

)

(

)

(

1

- zgodnie z tw. redukcyjnym:

∑∫

∑∫

=

=

ν

⋅

l

n

p

l

n

n

p

D

dx

EI

M

M

dx

EI

M

M

0

0

)

(

0

)

(

)

(

1

- ponieważ

1

0

M

M

=

:

=

=

ν

⋅

∑∫

l

n

p

D

dx

EI

M

M

0

1

)

(

1

0

1

0021

,

0

4

2

1

8

4

8

5

3

2

)

5456

,

9

3

2

10

3

1

(

4

5

2

1

5456

,

9

4

2

1

2

≅

<

−

=













⋅

⋅

⋅

⋅

⋅

+

⋅

−

⋅

⋅

⋅

⋅

+

⋅

⋅

−

=

EI

EI

EI

Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli

Układy statycznie niewyznaczalne - metoda sił, obliczanie przemieszczeń

Zad.1

II rok studiów zawodowych zaocznych /2003

Anita Kaczor

4

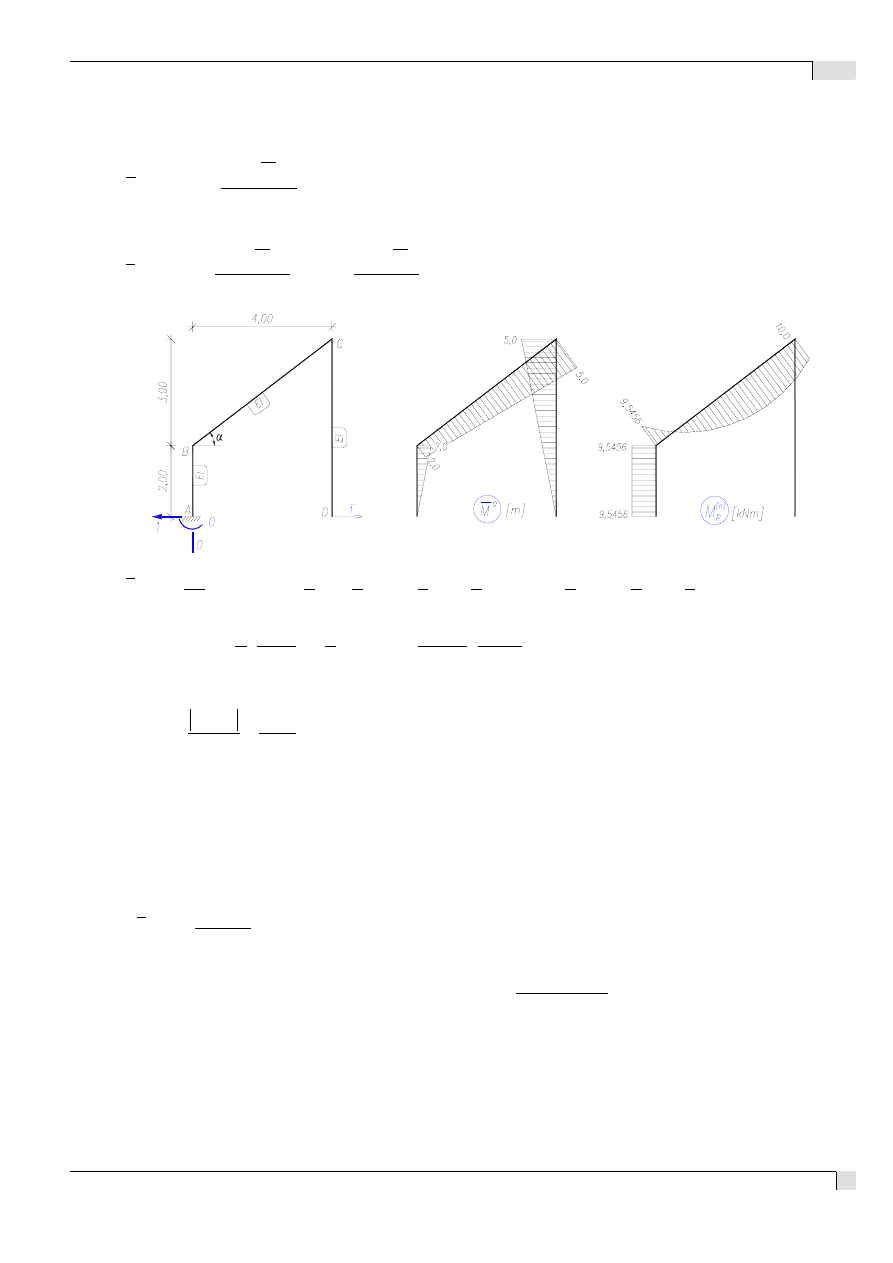
Zad.1b)

Przemieszczenie poziome punktu D (pomijamy wpływ sił tnących i normalnych):

∑∫

=

δ

⋅

l

n

n

p

h

D

dx

EI

M

M

0

)

(

)

(

1

Skorzystamy z tw. redukcyjnego i wyznaczonego w Zad.1. wykresu momentów zginających:

∑∫

∑∫

=

=

δ

⋅

l

n

p

l

n

n

p

h

D

dx

EI

M

M

dx

EI

M

M

0

0

)

(

0

)

(

)

(

1







+













⋅

−

⋅

⋅

⋅

⋅

+













⋅

−

⋅

⋅

⋅

⋅

+

⋅

⋅

⋅

−

=

δ

⋅

5456

,

9

3

1

10

3

2

5

5

2

1

5456

,

9

3

2

10

3

1

2

5

2

1

2

2

1

5456

,

9

2

1

1

EI

h

D

(

)













=







+

⋅

⋅

⋅

⋅

⋅

+

EI

kNm

EI

3

2

98

,

195

5

2

2

1

5

8

4

8

3

2

Wymiarowanie przekroju:

3

51

,

46

5

,

21

1000

cm

M

w

x

ekstr

potrz

x

=

=

σ

=

Przyjęto I160: w

x

=117cm

3

;

I

x

=935cm

4

;

I

y

=117cm

4

;

E=205Gpa;

EI = 935·10

-8

·205·10

6

= 1916,75 kNm

2

cm

m

h

D

2

,

10

102

,

0

75

,

1916

98

,

195

1

=

=

=

δ

⋅

Przemieszczenie poziome punktu D (dla I160)

wynosi:

cm

h

D

2

,

10

=

δ

Politechnika Poznańska ► Instytut Konstrukcji Budowlanych ► Zakład Mechaniki Budowli

Układy statycznie niewyznaczalne - metoda sił, obliczanie przemieszczeń

Zad.1

II rok studiów zawodowych zaocznych /2003

Anita Kaczor

5

Zad.1c)

Kąt obrotu punktu C (pomijamy wpływ sił tnących i normalnych):

∑∫

=

ϕ

⋅

l

n

n

p

C

dx

EI

M

M

0

)

(

)

(

1

Skorzystamy z tw. redukcyjnego i wyznaczonego w Zad.1. wykresu momentów zginających:

∑∫

∑∫

=

=

ϕ

⋅

l

n

p

l

n

n

p

C

dx

EI

M

M

dx

EI

M

M

0

0

)

(

0

)

(

)

(

1

(

)













=













⋅

⋅

⋅

⋅

+

−

⋅

⋅

+

⋅

⋅

−

=

ϕ

⋅

EI

kNm

EI

EI

C

2

2

378

,

35

1

5

8

4

8

3

2

5456

,

9

10

2

1

1

5

5456

,

9

1

2

1

1

Wymiarowanie przekroju:

3

51

,

46

5

,

21

1000

cm

M

w

x

ekstr

potrz

x

=

=

σ

=

Przyjęto I160: w

x

=117cm

3

;

I

x

=935cm

4

;

I

y

=117cm

4

;

E=205Gpa;

o

06

,

1

0184

,

0

75

,

1916

378

,

35

1

=

=

=

ϕ

⋅

rad

C

Kąt obrotu pktu C (dla I160)

wynosi:

o

06

,

1

0184

,

0

=

=

ϕ

rad

C