ZAKŁAD STATYKI I BEZPIECZE

Ń

STWA BUDOWLI

INSTYTUT IN

Ż

YNIERII L

Ą

DOWEJ

POLITECHNIKA WROCŁAWSKA

© 2000 dr in

ż

. Stanisław BIERNAT

[e-mail]

KONSTRUKCJA ZAŁAMANA

W PLANIE - METODA SIŁ

S

S

P

P

I

I

S

S

T

T

R

R

E

E

Ś

Ś

C

C

I

I

1.

PRZYJ

ĘCIE UKŁADÓW WSPÓŁRZĘDNYCH

.............................................................................. 2

2.

OBLICZENIE STOPNIA STATYCZNEJ NIEWYZNACZALNO

ŚCI

I DOBRANIE UKŁADU

PODSTAWOWEGO METODY SIŁ

........................................................................................................... 3

3.

BUDOWA UKŁADU RÓWNA

Ń METODY SIŁ

.............................................................................. 4

3.1 Posta

ć ogólna układu równań metody sił ................................................................... 4

3.2 Obliczenie współczynników układu równa

ń............................................................... 4

4.

OBLICZENIE RZECZYWISTYCH SIŁ PRZEKROJOWYCH

...................................................... 9

5.

ROZWI

ĄZANIE RUSZTU Z WYKORZYSTANIEM PROGRAMU STRAINS

........................... 10

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 2

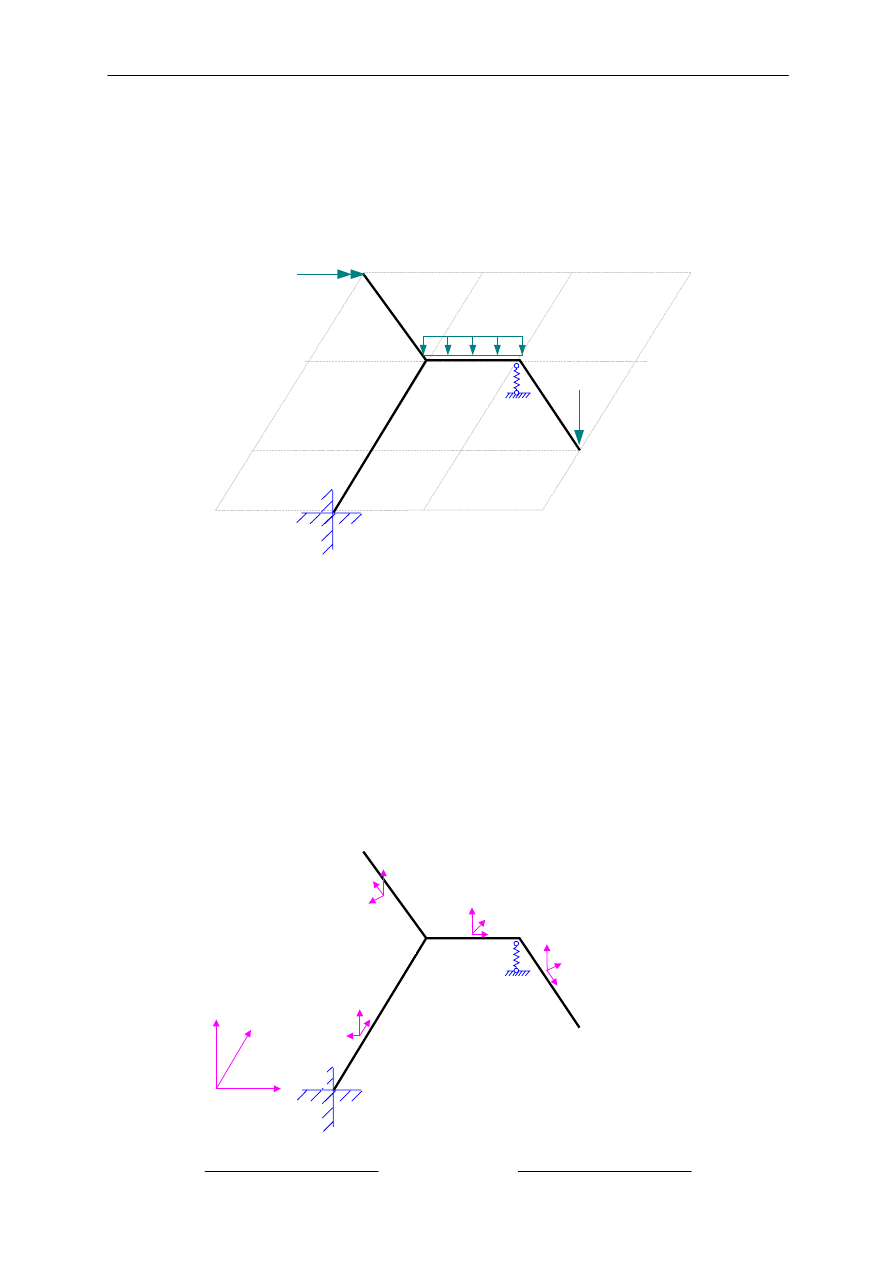
ZADANIE:

Stosuj

ąc metodę sił rozwiązać konstrukcję załamaną w planie o schemacie i

obci

ążeniu jak na rysunku.

P=12 kN

q=4 kN/m. M=24 kNm

k=8 EI

y

/m

3

GI

x

=0.5EI

y

k

q

P

M

4 m

4 m

3 m

3 m

3 m

2 m

1EI

1EI

1EI

2EI

1.

PRZYJ

ĘCIE UKŁADÓW WSPÓŁRZĘDNYCH

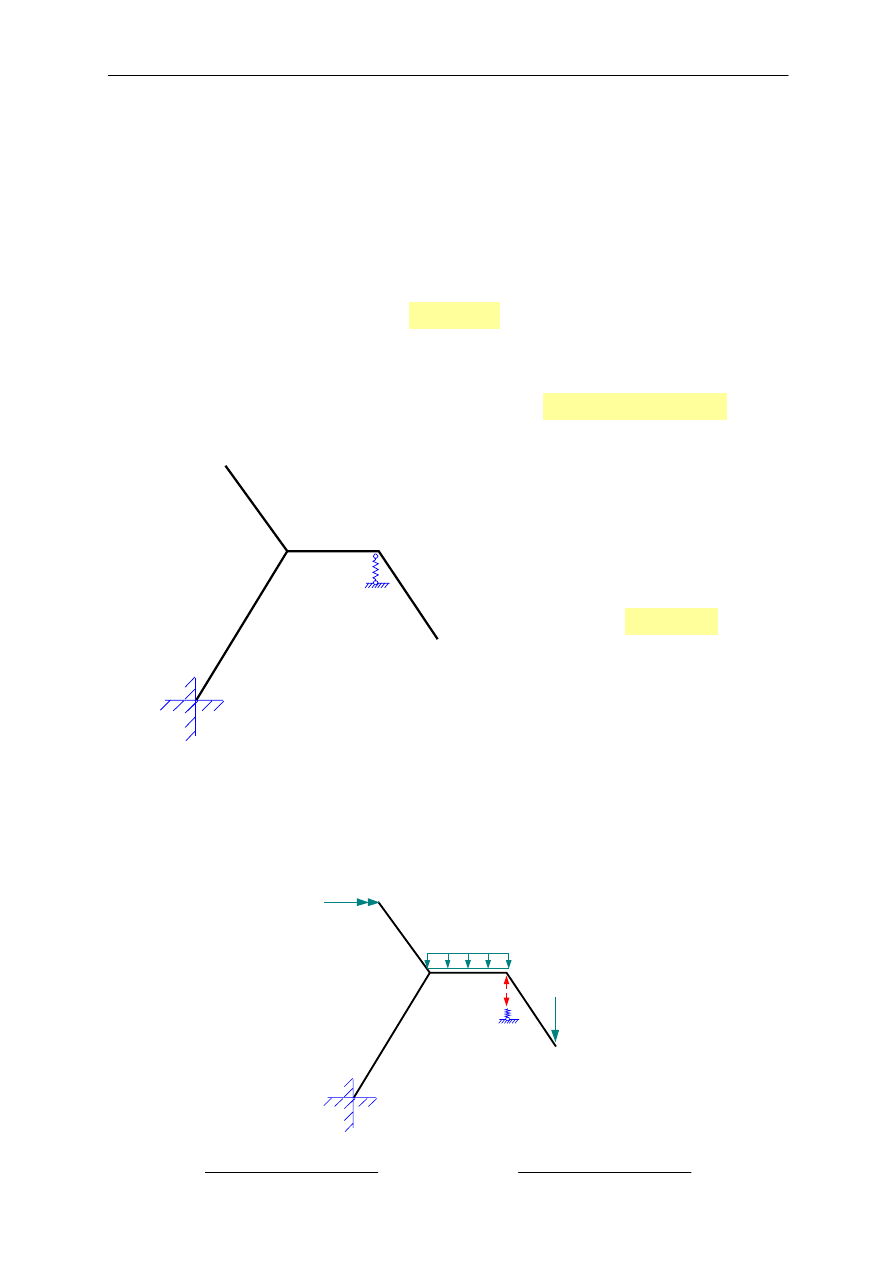
Przy rozwi

ązywaniu przestrzennych układów konstrukcyjnych niezbędne jest przyjęcie

globalnego układu współrz

ędnych dla całego układu (przyjęto prawoskrętny układ osi XYZ

tak jak w programie STRAINS - o

ś Z do góry) oraz lokalnych układów współrzędnych dla

poszczególnych elementów (pr

ętów). Przyjmujemy prawoskrętne układy współrzędnych z osią

lokaln

ą x będącą osią pręta oraz z osią z do góry (tak jak STRAINS), lokalne układy

współrz

ędnych jak i numerację węzłów pokazano na rysunku poniżej.

UWAGA - chc

ąc uzyskać te same układy współrzędnych lokalnych w STRAINS trzeba podawać dla prętów

odpowiednio w

ęzły początkowy i końcowy - wyznaczające kierunek przyjętej dla pręta osi lokalnej

x (pr

ęty : 1-2, 1-B, B-3, A-1)

k

A

B

1

2

3

X

Y

Z

x

y

z

x

y

z

x

y

z

x

y

z

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 3

2. OBLICZENIE STOPNIA STATYCZNEJ NIEWYZNACZALNO

ŚCI

I DOBRANIE UKŁADU PODSTAWOWEGO METODY SIŁ

Konstrukcje załamane w planie (wszystkie pr

ęty leżą w jednej płaszczyźnie) poddane działaniu

obci

ążeń pionowych lub wektorów momentów leżących w płaszczyźnie konstrukcji są

szczególnym przypadkiem konstrukcji przestrzennych. Z sze

ściu sił występujących w układach

przestrzennych sił przekrojowych (N

x

, T

y

, T

z

, M

x

, M

y

, M

z

) niezerowe siły wewn

ętrzne to (T

z

,

M

x

, M

y

). Stopie

ń statycznej niewyznaczalności w takich układach liczymy podobnie jak dla

płaskich układów pr

ętowych ze wzoru:

t

e

n

h

⋅

−

=

3

,

gdzie e jest liczb

ą więzi elementarnych , a t jest liczbą tarcz układu.

Liczba tarcz w układzie t=1, oraz e=4 wi

ęzi elementarne.

1

1

3

4

3

=

⋅

−

=

⋅

−

=

t

e

n

h

A wi

ęc

układ jest jednokrotnie statycznie niewyznaczalny. Na rysunku poni

żej zaznaczono więzi

elementarne.

k

e=3

e=1

Na podporze A wyst

ępują trzy więzi

(pomijamy wi

ęzi w których siły są z

zało

żenia zerowe Ty, Nx, Mz) oraz w

punkcie

B

wyst

ępuje jedna więź

pionowa (spr

ężysta).

UWAGA - rozpatruj

ąc zadanie jako pełny

układ przestrzenny

t

e

n

h

⋅

−

=

6

i wtedy na

podporze A wyst

ępuje komplet e=6 więzi oraz

na podporze B wyst

ępuje e=1 więź pionowa.

A wi

ęc także n

h

=1

Układ podstawowy metody sił pokazany na rysunku poni

żej przyjęto rozcinając więź sprężystą

w punkcie B - uwidoczniono nadliczbow

ą niewiadomą metody sił X

1

. Taki układ podstawowy

jest w tym zadaniu wygodny, gdy

ż do określenia sił wewnętrznych na wszystkich czterech

pr

ętach nie potrzebujemy wartości reakcji podporowych w punkcie A.

k

q

P

M

X

1

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 4

3. BUDOWA UKŁADU RÓWNA

Ń METODY SIŁ

3.1 Posta

ć ogólna układu równań metody sił

Poniewa

ż w zadaniu n

h

=1 układ równa

ń redukuje się do jednego równania :

0

1

1

11

=

∆

+

F

X

δ

3.2 Obliczenie współczynników układu równa

ń

Współczynniki przy niewiadomych układu równa

ń obliczymy ze wzoru Maxwella-Mohra

(uwzgl

ędniając wpływ momentów zginających M

y

,skr

ęcających M

x

oraz wi

ęzi sprężystych -

wpływ sił tn

ących T

z

na rozwi

ązanie pomijamy gdyż w belkach smukłych jest on niewielki)

å

åò

åò

+

+

=

n

n

j

n

i

n

p

x

j

x

i

x

p

y

j

y

i

y

ij

k

R

R

ds

GI

M

M

ds

EI

M

M

δ

wyrazy wolne od obci

ążeń siłami ze wzoru

å

åò

åò

+

+

=

∆

n

n

F

n

i

n

p

x

F

x

i

x

p

y

F

y

i

y

F

i

k

R

R

ds

GI

M

M

ds

EI

M

M

gdzie

F

y

i

y

M

M ,

,

F

x

i

x

M

M ,

s

ą odpowiednio momentami zginającymi i skręcającymi w

układzie podstawowym wywołanymi odpowiednio siłami hiperstatycznymi

1

=

i

X

oraz

obci

ążeniem danym,

F

n

i

n

R

R ,

s

ą siłami w n-tej więzi sprężystej wywołanymi odpowiednio

siłami hiperstatycznymi

1

=

i

X

oraz obci

ążeniem danym,

n

k

jest sztywno

ścią n-tej więzi

spr

ężystej.

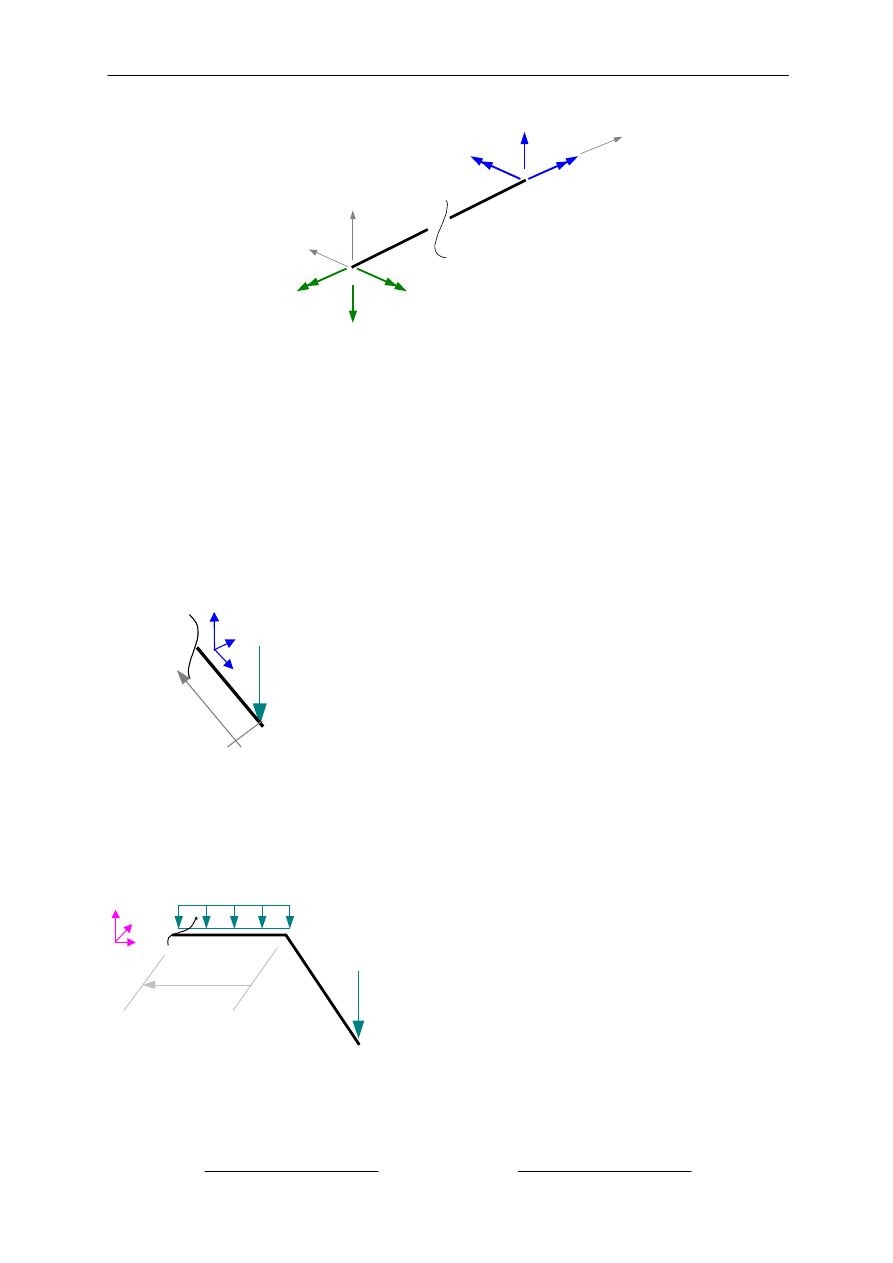
3.2.1 Definicja znakowania sił przekrojowych.

Uwaga: Momenty zginaj

ące odkładamy zawsze po stronie włókien rozciąganych, znaki wynikają z przyjętych

lokalnych układów współrz

ędnych, a definicja znakowania jest pokazana na rysunku i jest następująca : jeśli w

przyj

ętym lokalnym układzie osi :

równowa

żymy obciążenia po stronie związanej z początkiem p pręta to

dodatnie siły przekrojowe maj

ą zwroty przeciwne do osi

równowa

żymy obciążenia po stronie związanej z końcem k pręta to

dodatnie siły przekrojowe maj

ą zwroty zgodne z osiami.

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 5

x

z

y

p

k

T

z

T

z

M

y

M

y

M

x

M

x

Wniosek - dobrze tak ustali

ć zwroty osi lokalnych x w obliczeniach ręcznych, żeby zawsze

korzysta

ć z

definicji drugiej

(tak te

ż uczyniono w tym zadaniu).

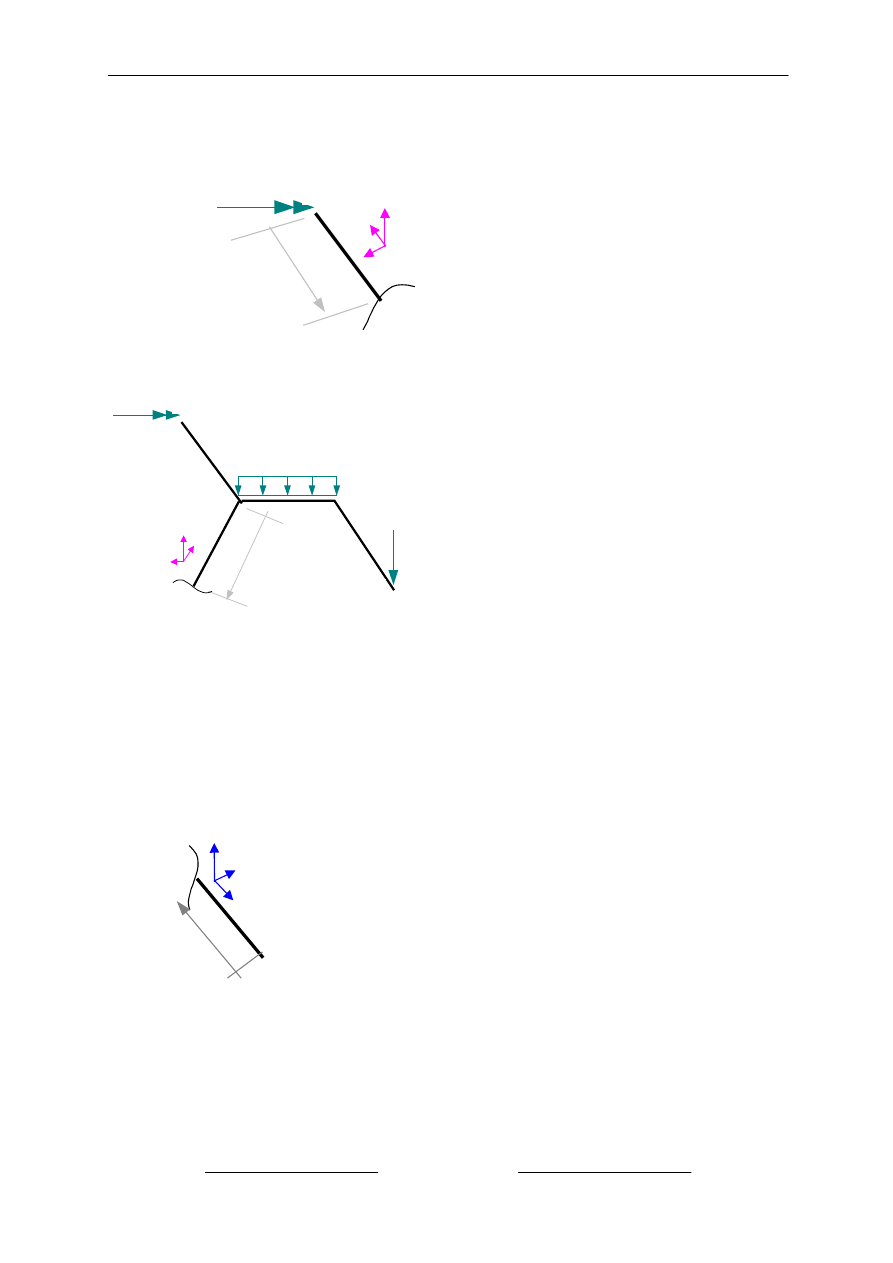
3.2.2

Rozwi

ązanie układu podstawowego od obciążenia zewnętrznego.

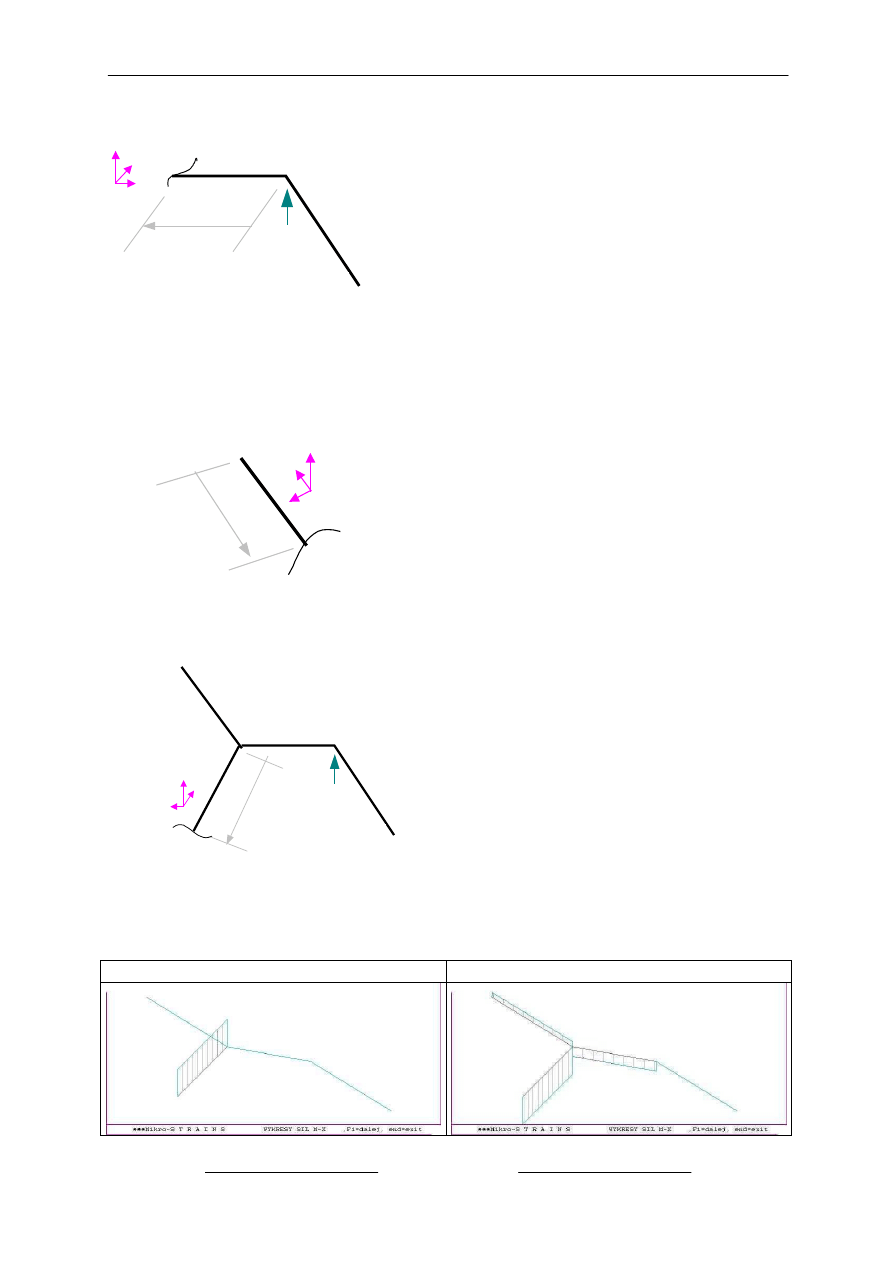
Na pr

ętach kolejno sporządzamy wykresy sił przekrojowych :

−

=

3-B

("od ko

ńca" -

definicja druga -

a wi

ęc osie lokalne wyznaczają dodatnie zwroty sił)

P

3

Mx

My

Tz

x

5

0

≤

≤

x

M

y

(x)= + Px

=

0 ... 60 kNm

(rozci

ąga włókna górne)

M

x

(x)= 0

T

z

(x)= -P = -12 kN = const

−

=

B-1

("od ko

ńca" -

definicja druga -

a wi

ęc osie lokalne wyznaczają dodatnie zwroty sił)

q

P

B

3

x

2

Mx

My

Tz

3

0

2

≤

≤

x

M

y

(x

2

)= + P(4+x

2

)+0.5qx

2

2

=

= 48

.... 70.5 .... 102 kNm

(rozci

ąga włókna górne)

M

x

(x

2

)= +P*3 = 36 kNm

T

z

(x

2

)= -P - qx

2

= -12 ... -24 kN

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 6

−

=

2-1

("od ko

ńca" -

definicja druga

)

M

2

x

4

Mx

My

Tz

5

0

4

≤

≤

x

M

y

(x

4

)= -0.6 M = -14.4 kNm

(rozci

ąga włókna dolne)

M

x

(x

4

)= -0.8 M. = -19.2 kNm

T

z

(x

4

)= 0

−

=

1-A

(od ko

ńca -

definicja druga

)

q

P

M

B

1

2

3

Mx

My

Tz

x

5

5

0

5

≤

≤

x

M

y

(x

5

) = -M. + 3q x

5

- P(3-x

3

) =

= -60 ... 60 kNm

(dla x

5

=0 rozci

ąga włókna dolne)

M

x

(x

5

)= +3q * 1.5 + 7P = 102 kNm

T

z

(x

5

)= -P - 3q = -24 kN

3.2.3

Rozwi

ązanie układu podstawowego od obciążenia nadliczbową X

1

.

Na pr

ętach kolejno sporządzamy wykresy sił przekrojowych :

−

=

3-B

("od ko

ńca" -

definicja druga -

a wi

ęc osie lokalne wyznaczają dodatnie zwroty sił)

3

Mx

My

Tz

x

Brak obci

ążeń po prawej stronie przekroju stąd

5

0

≤

≤

x

M

y

1

(x)= 0

M

x

1

(x)= 0

T

z

1

(x)= 0

−

=

B-1

("od ko

ńca" -

definicja druga -

a wi

ęc osie lokalne wyznaczają dodatnie zwroty sił)

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 7

X

1

B

3

x

2

Mx

My

Tz

3

0

2

≤

≤

x

M

y

1

(x

2

)= - 1 x

2

(rozci

ąga włókna dolne)

M

x

1

(x

2

)= 0 = const

T

z

1

(x

2

)= +1 = const

−

=

2-1

("od ko

ńca" -

definicja druga

)

2

x

4

Mx

My

Tz

Brak obci

ążeń po lewej stronie przekroju stąd

5

0

4

≤

≤

x

M

y

1

(x

4

)= 0

M

x

1

(x

4

)= 0

T

z

1

(x

4

)= 0

−

=

1-A

(od ko

ńca -

definicja druga

)

B

1

2

3

Mx

My

Tz

x

5

X

1

5

0

5

≤

≤

x

M

y

1

(x

5

)= -1 x

5

(rozci

ąga włókna dolne)

M

x

1

(x

5

)= -3

T

z

1

(x

5

)= +1

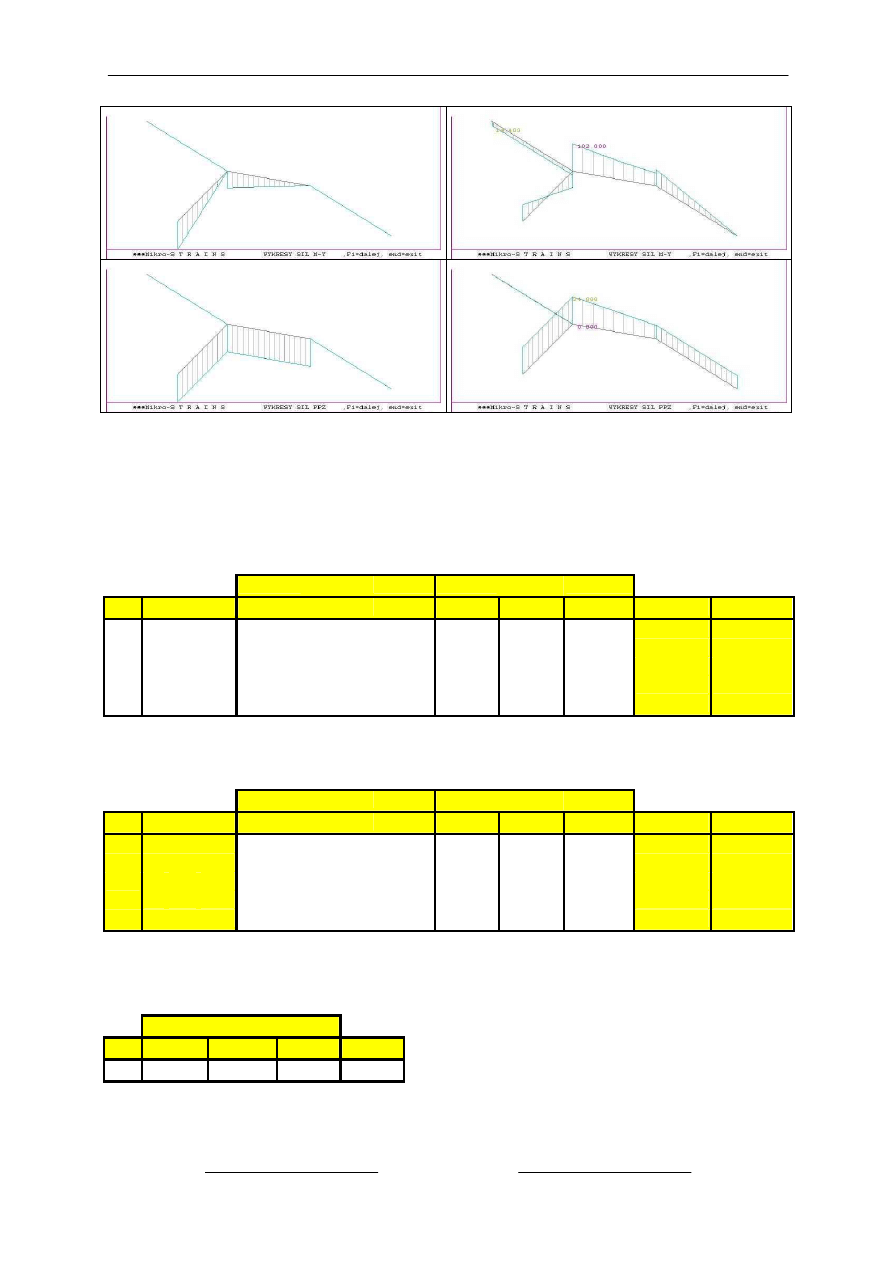
Wykresy momentów momentów skr

ęcających Mx, zginających My, i sił tnących Tz, uzyskane

z programu STRAINS przedstawiono na rysunku poni

żej dla obu stanów obciążenia :

stan X1 =1

stan obci

ążenia

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 8

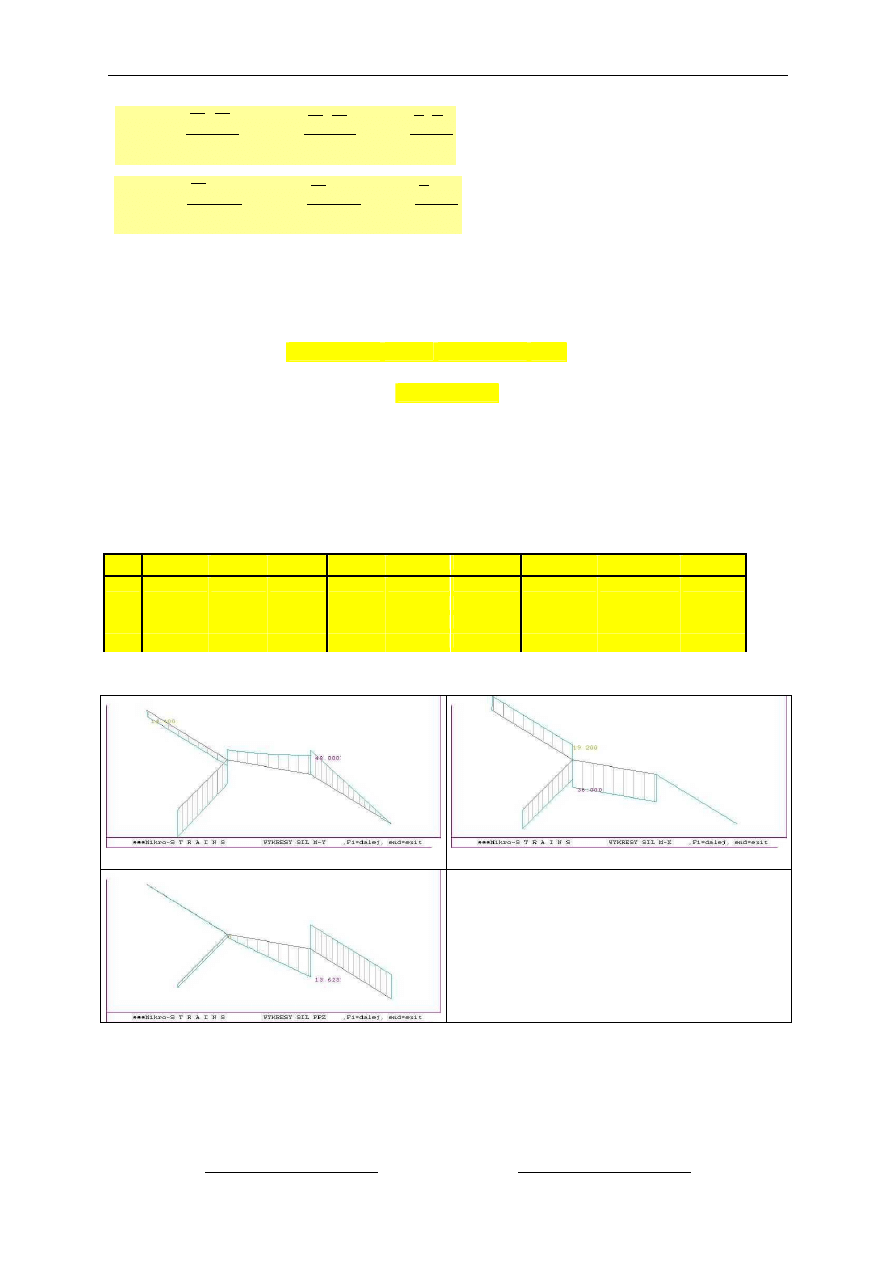
3.2.4 Obliczenie współczynników macierzy podatno

ści i wyrazów wolnych

W tym przykładzie skorzystamy ze wzoru uproszczonego całkowania Simpsona i wzoru
Maxwella-Mohra automatyzuj

ąc obliczenia za pomocą tabeli z programu EXCEL

- uwzgl

ędnienie odkształcalności giętnej

My1

My0

ij

L

EI

GJ

a

b

c

A

B

C

d11

d10

A1

5

1

0,5

-5

-2,5

0

60

0

-60

41,667

-250

1B

3

2

1

-3

-1,5

0

102

70,5

48

4,500

-182,25

B3

5

1

0,5

0

0

0

60

30

0

0,000

0

12

5

1

0,5

0

0

0

-14,4

-14,4

-14,4

0,000

0

suma

46,167

-432,250

- uwzgl

ędnienie odkształcalności skrętnej

Mx1

Mx0

ij

L

EI

GJ

a

b

c

A

B

B

d11

d10

A1

5

1

0,5

-3

-3

-3

102

102

102

90,000

-3060

1B

3

2

1

0

0

0

36

36

36

0,000

0

B3

5

1

0,5

0

0

0

0

0

0

0,000

0

12

5

1

0,5

0

0

0

-19,2

-19,2

-19,2

0,000

0

90,000

-3060,0

- uwzgl

ędnienie sprężystości podpory B

Reakcja w spr

ęż

ynie

k

∆

R1

R0

d11

d10

8

1

0

0,125

0

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 9

å

åò

åò

+

+

=

n

n

j

n

i

n

p

s

j

x

i

x

p

y

j

y

i

y

ij

k

R

R

ds

GI

M

M

ds

EI

M

M

δ

= 1/EI (46.167 + 90 + 0.125 ) =

136.292/EI

å

åò

åò

+

+

=

∆

n

n

F

n

i

n

p

s

F

x

i

x

p

y

F

y

i

y

F

i

k

R

R

ds

GI

M

M

ds

EI

M

M

= 1/EI (-432.25 - 3060 + 0 ) =

-3492.25/EI

3.2.5 Posta

ć szczegółowa równania metody sił

136,292

X1

-3492,250

= 0

X1 =

25,623 kN

4. OBLICZENIE RZECZYWISTYCH SIŁ PRZEKROJOWYCH

Rzeczywiste momenty zginaj

ące, momenty skręcające oraz siły tnące obliczymy wykorzystując

zasad

ę superpozycji. Pod spodem podano wartości sił na początku i na końcu pręta.

ij

My

Mx

Tz

A1

-68,117

-60,000

25,130

25,130

1,623

1,623

1B

25,130

32,065

48,000

36,000

36,000

1,623

13,623

B3

60,000

0,000

0,000

0,000

-12,000

-12,000

12

-14,400

-14,400

-19,200

-19,200

0,000

0,000

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 10

5. ROZWI

ĄZANIE RUSZTU Z WYKORZYSTANIEM PROGRAMU STRAINS

W ramach laboratorium wszystkie dane do programu zostan

ą przygotowane w pliku

tekstowym przy u

życiu języka problemowo zorientowanego, którego interpreter jest częścią

składow

ą systemu STRAINS. Plik użytkownika składa się z rozkazów, w których wyróżnić

mo

żna nazwę rozkazu, a po niej ewentualne parametry. Wszystkie rozkazy mogą być użyte w

formie pełnej lub skróconej. Wydruk pod spodem prezentuje obie formy; tzn. np. zamiennie do
słowa inicjuj

ącego START można użyć słowa ST - co zostało zaakcentowane dużymi literami

- STart, nie oznacza to rozró

żniania małych i dużych liter przez program. Wszystkie rozkazy w

wydruku zaprezentowano w tej konwencji i od u

żytkownika zależy czy chce stosować notację

pełn

ą czy skróconą. Omówienie pełnej składni jest w tym miejscu niecelowe i odsyłam

zainteresowanych do instrukcji STRAINSa, a na podstawie przykładu i kilku komentarzy po
prawej stronie wszystkie dane mo

żna przygotować poprzez analogię.

Uwaga: W systemie STRAINS po znaku

średnika umieszcza się komentarze, co jest wygodne do czasowego

wył

ączania niektórych linii - tak jak zrobiono to poniżej.

Poni

żej zamieszczono wydruk zbioru danych dla powyższego przykładu, który należy dla

własnego zadania przygotowa

ć za pomocą dowolnego edytora tekstowego (np. NOTATNIK

w Windows).

STart 'KONSTRUKCJA ZALAMANA W PLANIE '
TYP RaMaPrzestrzenna
Wezly 5
ELementy 4
WSPolrzedne
1 4 0 0
2 4 5 0
3 7 5 0
4 11 2 0
5 0 8 0
TOPologia
1 1 2
2 2 3
3 3 4
4 2 5
WezlyPosrednie 1 2
Materialy

E V A IZ BETA WSZystkie 1 0.3 100000 1 0
IX IY 2 WarTosci 2.6 2 PoZostale 1.3 1

PoDPory
1 ZamocowaNY
3 ZamocowanySPrezyscie z 8
OPisOBciazenia 'zewnetrzne'
WeZlowe 4 z -12
PRostokatne 2 z -4
MomenT 4 x 24 WZGledne 1
;OPisOBciazenia 'wirtualne'
;WZ 3 z 1
WYNiki
OBLicz
STop

liczba w

ę

złów

liczba elementów

WP ilo

ść

pr

ę

t

ZNY = we wszystkich kier.
ZSP kierunek sztywno

ść

WZ w

ę

zeł kierunek warto

ść

PR pr

ę

t kierunek warto

ść

MT pr

ę

t kierunek warto

ść

wzgl

ę

dne poło

ż

enie

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 11

Szerszego komentarza wymaga blok "Materialy". W zadaniu mamy zdefiniowan

ą zależność

α

=

S

Y

GI

EI

,

gdzie

α

=2. Korzystaj

ąc z zależności

)

1

(

2

ν

+

=

G

E

dostajemy :

α

ν

=

+

S

Y

I

I

)

1

(

2

czyli

α

ν

Y

S

I

I

)

1

(

2

+

=

a wi

ęc przyjmując jakąś wartość

ν

(0.3 w zadaniu) oraz znaj

ąc

α

i I

y

da si

ę policzyć I

S

.

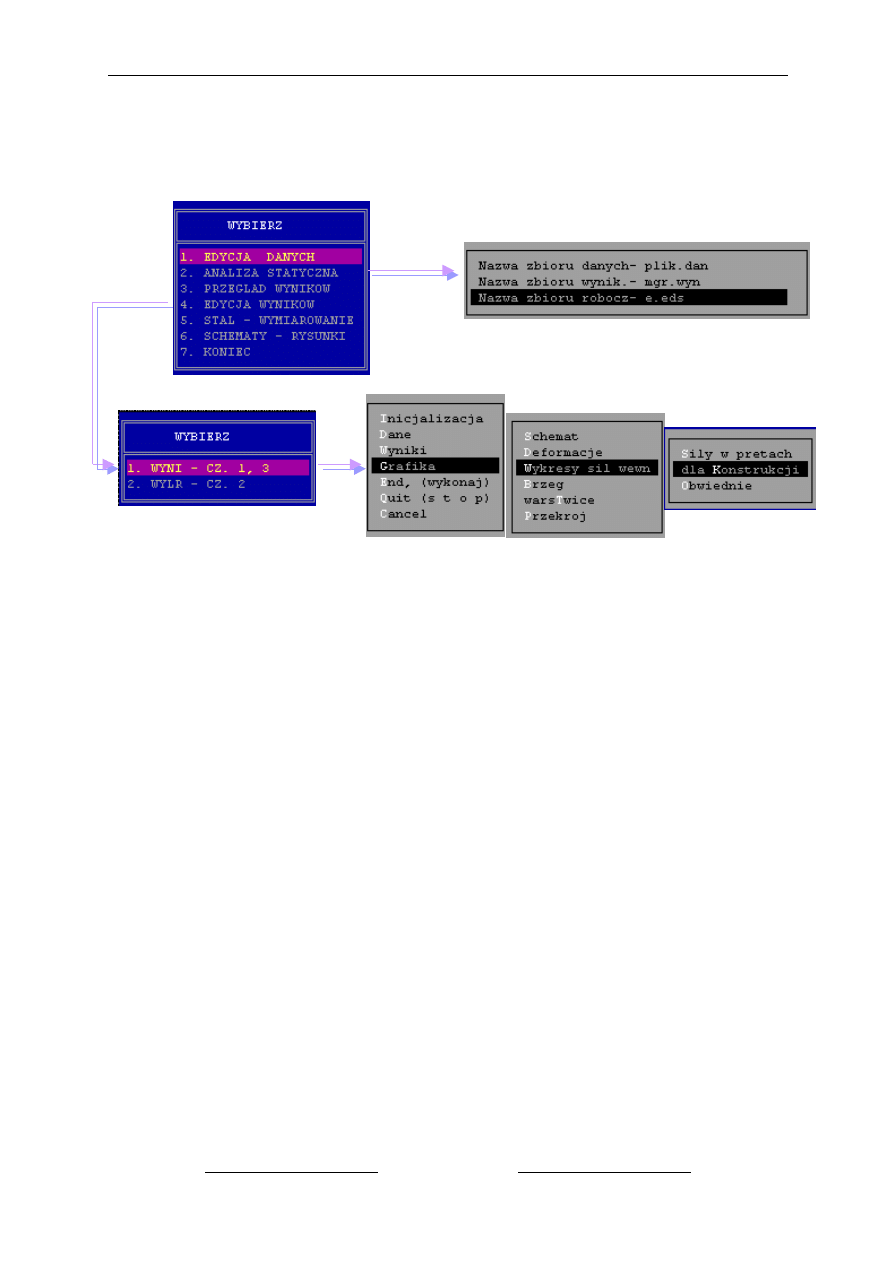
Pod spodem zamieszczono wyselekcjonowane wyniki dla zadania (rzeczywiste warto

ści

przemieszcze

ń, sił przekrojowych i reakcji).

UWAGA !!! W systemie STRAINS stosowana jest odwrotna do stosowanej na wykładzie i

ćwiczeniach umowa

znakowania sił przekrojowych, co oznacza

że wszystkie siły przekrojowe z pliku wynikowego powinny mieć

przeciwne znaki do sił wyznaczanych "r

ęcznie".

Na czerwono zaznaczono reakcj

ę w podporze sprężystej - wartość niewiadomej X

1

metody sił.

Podobnie dla wyników z układu podstawowego da si

ę odczytać wartości wyrazów równania

kanonicznego metody sił korzystaj

ąc z definicji, a więc jako przemieszczenia na odpowiednim

kierunku od odpowiednich zestawów obci

ążeń.

Pełny model przestrzenny zastosowany w zadaniu potwierdza :
-

zerowe przemieszczenia w płaszczy

źnie konstrukcji UX UY

-

zerowe obroty w płaszczy

źnie konstrukcji FIZ

-

zerowe siły osiowe (podłu

żne) PX

-

zerowe siły tn

ące (poprzeczne) PY

-

zerowe momenty działaj

ące w płaszczyźnie konstrukcji MZ

-

poprawno

ść wykresów sporządzonych ręcznie

5. WYNIKI PRZEMIESZCZENIA

WEZEL NR

UX

UY

UZ

FIX

FIY

FIZ

1

.00000

.00000

.00000

.00000

.00000

.00000

2

.00000

.00000

817.63987

320.29200

251.29930

.00000

3

.00000

.00000

-3.20292

428.29200

301.64680

.00000

4

.00000

.00000

-2994.66581

518.29200

421.64680

.00000

5

.00000

.00000

2963.71295

517.09200

193.69930

.00000

SILY I MOMENTY

PRET NR

WEZEL

SILA PODL.PX

SILA POPRZ.PY

SILA POPRZ.PZ

MOMENT SKR.MX

MOM. ZGIN.MY

MOM. ZGIN.MZ

1

1

.0000

.00000

-1.62336

-25.12993

68.11678

.00000

2

.0000

.00000

-1.62336

-25.12993

60.00000

.00000

2

2

.0000

.00000

-1.62336

-36.00000

-25.12993

.00000

.500

.0000

.00000

-7.62336

-36.00000

-32.06496

.00000

3

.0000

.00000

-13.62336

-36.00000

-48.00000

.00000

3

3

.0000

.00000

12.00000

.00000

-60.00000

.00000

4

.0000

.00000

12.00000

.00000

.00000

.00000

4

2

.0000

.00000

.00000

19.20000

14.40000

.00000

5

.0000

.00000

.00000

.00000

.00000

.00000

REAKCJE
WEZEL NR

X

Y

Z

XY

XZ

YZ

1

.00000

.00000

-1.62336

.00000

-25.12993

-68.11678

3

25.62336

KONTROLA ROWNOWAGI

KIERUNEK

OBCIAZENIA

REAKCJE

X

.00000

.00000

Y

.00000

.00000

Z

-24.00000

24.00000

YZ

-60.00000

60.00000

XZ

198.00000

-198.00000

XY

.00000

.00000

KONIEC OBLICZEN

WBLiW statyka sem. V

Konstrukcja załamana w planie – metoda sił – przykład

strona 12

Z przygotowanym w ramach laboratorium zbiorem tekstowym w programie STRAINS
korzystamy z nast

ępującej ścieżki MENU

Bardziej szczegółowy opis edycji wyników w ramach laboratorium.