Sprawozdanie Mateusz Łubiarz gr. 13

Zagadnieniem którym zajmowaliśmy sie na laboratoriach dotyczących metod numerycznych była metoda
Eurela (w tym przypadku jawnej ) , która miała podać przybliżona wartość równania różniczkowego
pierwszego rzędu :

Kod programu

a=0;

b=10;

y(1)=1;

g(1)=1;

n=50;

h=(abs(b-a))/n;

t=a:h:b;

w=length(t);

for

i=1:w-1

y(i+1)=y(i)+h*(-y(i)+t(i));

g(i+1)=2*exp(-t(i+1))+t(i+1)-1;

end

for

j=1:w

e(j)=(abs(g(j)-y(j)))/g(j);

end

y1(1)=1;

kroki=100;

for

k=7:kroki

h1(k-6)=(abs(a-b))/k;

t1=a:h1(k-6):b;

w1=length(t1);

for

i=1:w1-1

y1(i+1)=y1(i)+h1(k-6)*(-y1(i)+t1(i));

End

roz(k-6)=y1(w1-1);

End

n1=7:1:kroki;

subplot(3,1,1);
plot(t,y,

'b-+'

,t,g,

'g-*'

);

xlabel(

'Czas'

);

ylabel(

'Wartość'

);

title(

'Wykres rozwiązania numerycznego i analitycznego'

);

grid;
subplot(3,1,2);

plot(t,e,

'r-o'

);

xlabel(

'Czas'

);

ylabel(

'Wartość błędu względnego'

);

czasu'

);

title(

'Zależność błędu względnego od

grid;
subplot(3,1,3);

plot(n1,roz,

'r-'

);

xlabel(

'Ilość przedziałów'

);

ylabel(

'Wartość funkcji'

);

title(

'Zależność wartości funkcji w chwili t=10 od ilości

przedziałów n'

);

grid;


Wykresy

Wnioski :

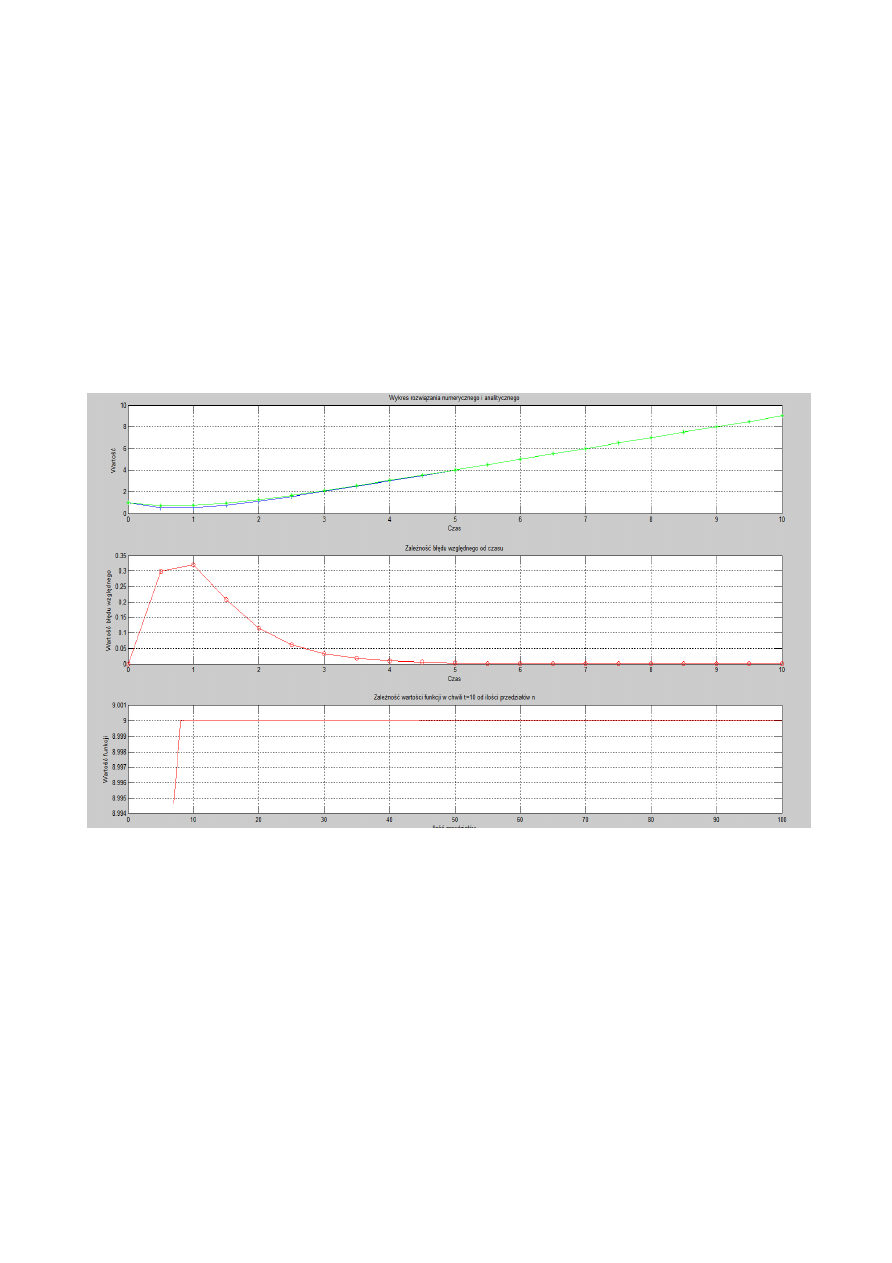
Wykresy rozwiazan metody Eurela oraz metody analitycznej odbiegaja od siebie , mozna to
zmienić zwiększając liczbę kroków . Wykres błędu wzglednego od czasu pokazuje ze najwieszka
wartość błedu jest w czasie 1 sec .
Wartość funkcji w dla czasu t od ilości przedziałów po ilości przedziałów równej 8 staje sie
jednowarosciowa i przyjmuje wartość 9 .