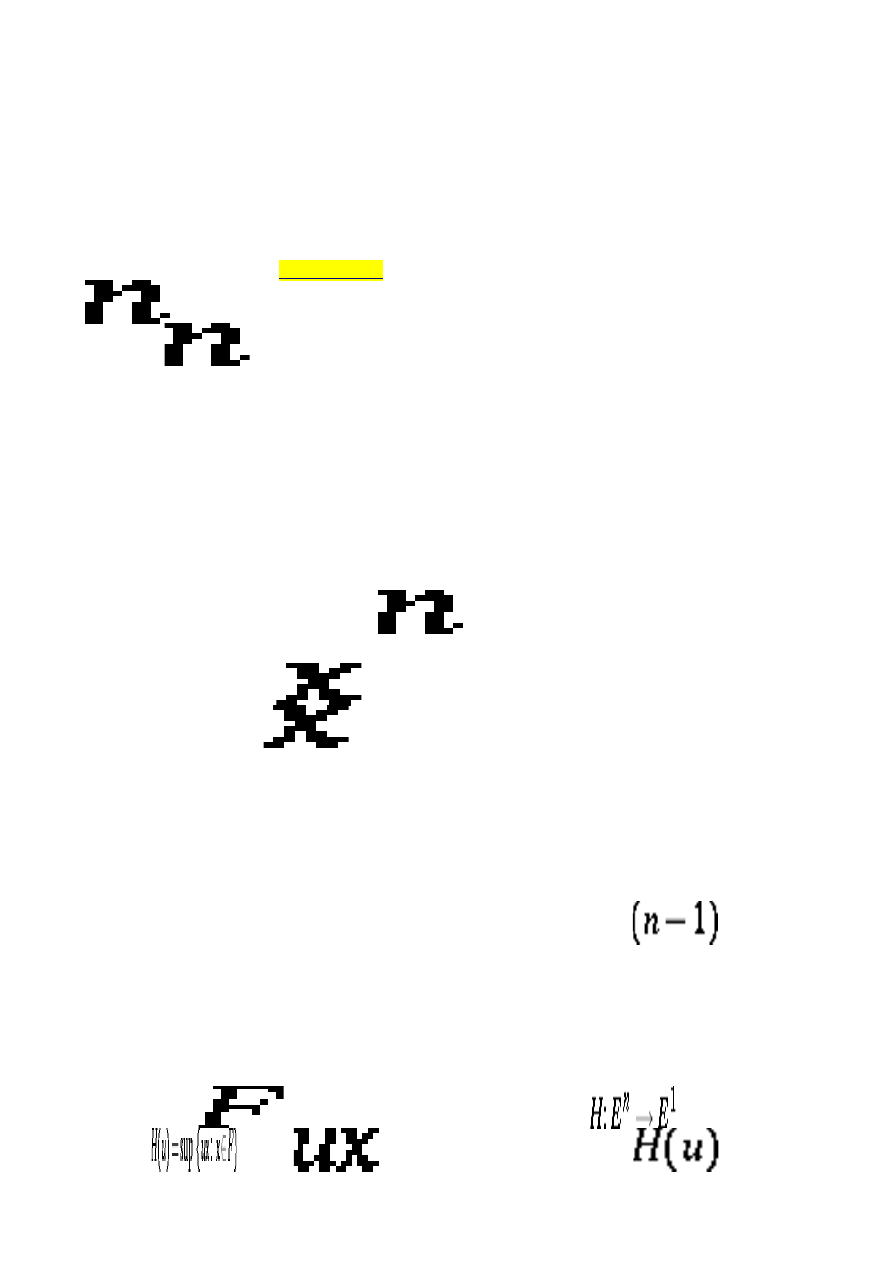
Convex set
in a Euclidean or in another vector space
A set containing with two arbitrary points all points of the segment connecting these points. The
intersection of any family of convex sets is itself a convex set.
The smallest dimension of a plane (i.e. affine subspace) containing a given convex set is called the
dimension of that set. The closure of a convex set (i.e. the result of adding to the convex set all its
boundary points) yields a convex set of the same dimension. The principal subject of the theory of
convex sets is the study of
convex bodies
, which are finite (i.e. bounded) convex sets of dimension
. If boundedness is not stipulated, one speaks of infinite convex bodies, and if the
dimension
is not stipulated, one speaks of degenerate convex bodies or of convex
bodies of lower dimension.
A convex body is homeomorphic to a closed ball. An infinite convex body not containing straight
lines is homeomorphic to a half-space, while those containing a straight line are cylinders with a
convex (possibly, infinite) cross-section.
Through each point of the boundary of a convex set there passes at least one hyperplane such that
the convex set lies in one of the two closed half-spaces defined by this hyperplane. Such
hyperplanes and such half-spaces are called supporting for this set at the given point of the
boundary. A closed convex set is the intersection of its supporting half-spaces. The intersection of a
finite number of closed half-spaces is a convex polyhedron. The faces of a convex body are its
intersections with the supporting hyperplanes. A face is a convex body of lower dimension. The
convex body is considered to be its own
-dimensional face. As distinct from a
polyhedron, a face of a face need not be a face of the initial convex body.
With each boundary point
of a convex body is connected: an open tangent cone, filled
by the rays issuing from
and passing through interior points of the convex body; the
closed tangent cone, which is its closure; and the surface tangent cone which is its boundary. The
two first-mentioned cones are convex.
The points of the boundary of a convex body are classified by the minimal dimension of the faces to
which they belong, and also by the dimension of the set of supporting hyperplanes at the point. The
points of zero-dimensional faces are called exposed points. Extremal points of a convex body are
points which are not interior to any segment belonging to that convex body. The problem of the
possible abundance of points and of the set of directions of faces of various types is being studied.
For instance, the points with a non-unique supporting hyperplane have zero
-
dimensional area on the boundary; the directions of the segments lying on the boundary have
measure zero among all directions in space.
Each point not belonging to a convex body is strictly separated from it by a hyperplane such that
this point and the convex body are in distinct open half-spaces. Two non-intersecting convex sets
are separated by a hyperplane, leaving them in different closed half-spaces. This separation property
is retained in the case of convex sets in infinite-dimensional vector spaces.
A convex body
has associated with it its support function
, defined by the
equation
, where
is the scalar product. The function
is
positively homogeneous of the first degree:
for
, and is convex:
All functions with these two properties are support functions for some unique convex body.
Specifying the support function is one of the principal methods of specifying a convex body.
If the coordinate origin is located inside a convex body, one introduces a distance function
, which, for
, is defined by the equation
under the assumption that
. This is also a positively homogeneous convex function of
the first degree, defining
. Two convex bodies are called polar (or dual) with respect to
each other if the support function of one is the distance function of the other. The existence of dual
convex bodies is connected with the self-duality of
.
If a convex body
is symmetric with respect to the coordinate origin, the function
is a metric. This is the metric of the Minkowski space (of a finite-dimensional Banach
space),
playing the role of the unit ball. In a similar manner, the unit ball in an infinite-
dimensional Banach space is a convex set. The properties of the space are connected with the
geometry of this ball, in particular with the presence of points of different types on its boundary
[3]
.
A convex body may be given as the
convex hull
of the points on its boundary or of some of these
points.
There are a number of criteria permitting one to conclude whether or not a set (or any one set from
some family) is convex. For instance, if a
-smooth closed surface in
has
non-negative Gaussian curvature at all of its points, this surface is the boundary of a convex body;
if the intersection of a compact set
in
with any plane which leaves
in one half-space is simply connected,
is convex
[4]
.
There are many ways of introducing a metric on a set of convex bodies including degenerate convex
bodies but not the empty convex body. The Hausdorff metric is the one most commonly used (cf.
Convex sets, metric space of
). In this metric each convex body can be approximated by convex
polyhedra, and also by convex bodies defined by
, where
is a polynomial in
the coordinates, and which have positive principal curvatures at all points on the boundary.
A convex body always has a finite volume (in the sense of Jordan), which is identical with its
-dimensional Lebesgue measure. The boundary of a convex body has finite
-
dimensional area, and the various ways of introducing an area in such a case are equivalent. The
volume and the area of the boundary depend continuously (in the Hausdorff metric) on the convex
body.
Mixed-volume theory
is connected with the study of the dependence of the volume of a linear
combination
of convex bodies on the coefficients
. Mixed volumes include
not only the volume and the area of the boundary, but also many other functionals connected with
convex bodies
[5]
, such as
-dimensional volumes of projections in different directions
on
-dimensional planes and their average values. The principal results of this theory are
various inequalities between mixed volumes, including the classical isoperimetric inequality (cf.
Isoperimetric inequality, classical
).
Convex bodies are related to several simple figures. Thus, each convex body has a unique largest
(with respect to volume) inscribed and a smallest circumscribed ellipsoid
[6]
. Criteria have been
found to characterize the balls, ellipsoids and centrally symmetric bodies among other convex
bodies
[1]
,
[2]
. Theorems on families of convex sets form a special subject of the theory of convex
sets
[6]
.
The importance of the theory of convex sets lies in the illustrative nature of its methods and results
and in the fact that they are general and independent of analytic requirements of smoothness (non-
smooth convex bodies often represent solutions of extremal problems).
References
[1] T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934)
[2] F. Valentine, "Convex sets" , McGraw-Hill (1964)
[3] M.M. Day, "Normed linear spaces" , Springer (1958)
[4] Yu.D. Burago, V.A. Zalgaller, "Sufficient conditions of convexity" J. Soviet Math. , 16 : 3
(1978) pp. 395–434 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. , 45 (1974) pp.
3–53
[5] H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)
[6] L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" , Proc. Symp. Pure
Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180
Yu.D. Burago
V.A. Zalgaller
Comments
The polar set of a convex set in
is defined directly by
. The support function of is then also defined by
, and similarly the distance function is given by
. Given the distance function
, the corresponding closed convex
set is defined by
.
References
[a1] H.G. Eggleston, "Convexity" , Cambridge Univ. Press (1969)