C04 - RACHUNEK PRAWDOPODOBIE STWA - Zadania do oddania

Parametr k = liczba trzycyfrowa, dwie ostatnie cyfry to dwie ostatnie cyfry numeru indeksu,

pierwsza cyfra to pierwsza cyfra liczby liter pierwszego imienia.

Poszczególne zadania oddajemy na oddzielnych kartkach!

Zadanie 1

Niech P(A) = 0,0007

⋅k, P(B) = 0,0008⋅k, P(A∪B) = 0,0009⋅k.

Oblicz: a)

)

(

B

A

P

∩

, b)

)

(

B

A

P

∩

′

, c)

)

(

B

A

P

′

∩

′

, d)

)

(

B

A

P

∪

′

, e)

)

(

B

A

P

′

∪

′

.

Zadanie 2

Z przedziału <-k, k> wybrano losowo liczby b, c. Obliczy prawdopodobie stwo, e równanie

0

25

,

0

2

=

+

+

c

bx

kx

ma pierwiastki rzeczywiste.

Zadanie 3

W skrzyni jest k detali wyprodukowanych w zakładzie A, 2k detali wyprodukowanych

w zakładzie B i 5k detali wyprodukowanych w zakładzie C. Wadliwo produkcji

poszczególnych zakładów wynosi odpowiednio: 0,01k%, 0,05k % i 0,02k %.

a)

Obliczy prawdopodobie stwo, e losowo wybrany detal oka e si dobry,

b)

Wylosowany detal okazał si wadliwy jakie jest prawdopodobie stwo, e wyprodukował

go zakład B?

Zadanie 4

Zmienna losowa X ma rozkład okre lony funkcj prawdopodobie stwa:

x

k

– 1

0

0,01k

p

k

k

1

,

0

1

k

k

1

,

0

3

1

,

0

−

k

1

,

0

2

a) wyznaczy dystrybuant tej zmiennej losowej i naszkicowa jej wykres,
b) obliczy P(X > 0), P(X

≥ 0), P(X < 1), P(|X| ≥ 1),

c) obliczy EX, D

2

X.

Zadanie 5.
X jest zmienn losow o g sto ci

+

+

∪

−

−

−

−

∈

=

x

innych

dla

k

k

k

k

x

dla

c

x

f

0

]

4

01

,

0

;

2

01

,

0

[

]

1

01

,

0

;

2

01

,

0

[

)

(

a)

wyznaczy c,

b)

wyznaczy dystrybuant ,

c)

obliczy

(

)

3

01

,

0

5

,

1

01

,

0

+

≤

≤

−

−

k

X

k

P

i zinterpretowa na wykresie g sto ci,

d)

wyznacz x, aby

(

)

25

,

0

=

≥ x

X

P

,

e)

obliczy EX, D

2

X

f)

Y = -2X + 1. Oblicz EY, D

2

Y.

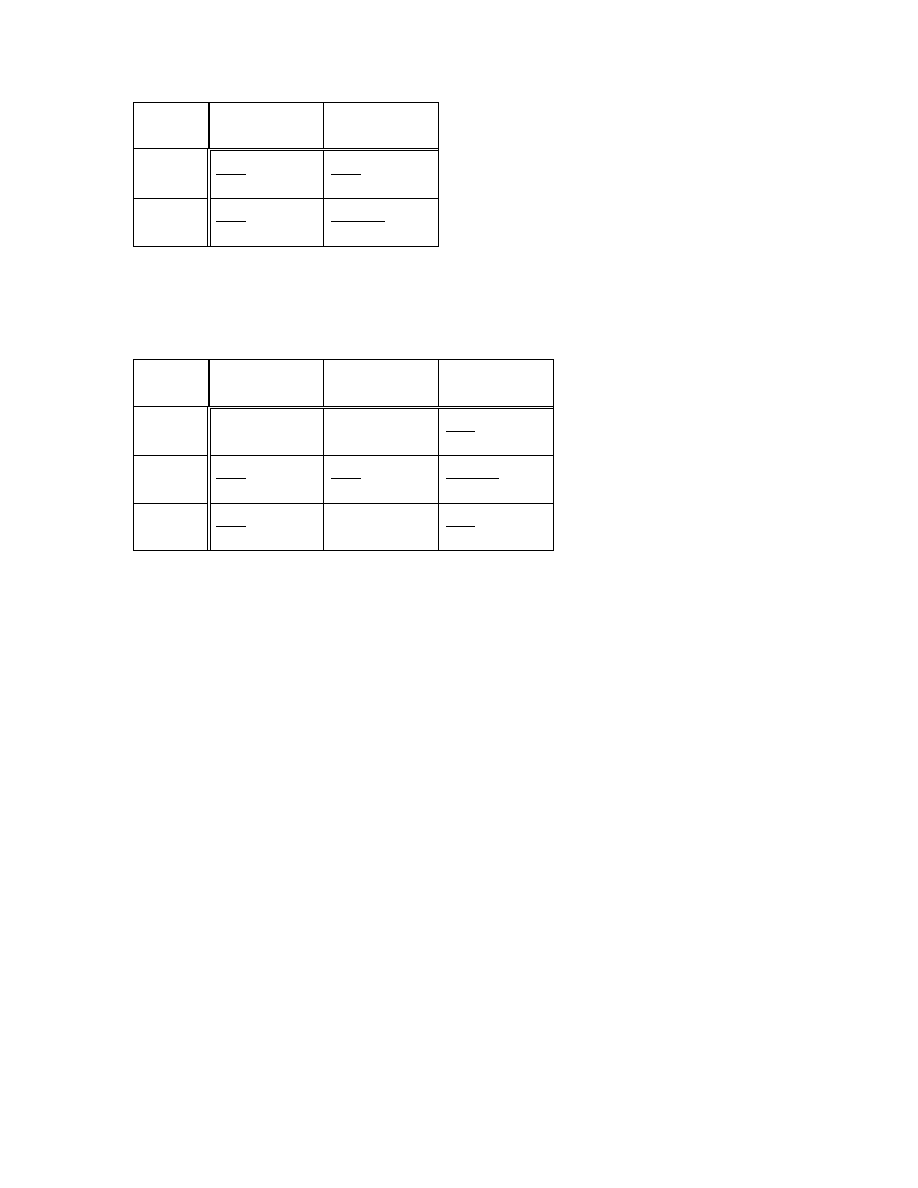
Zadanie 6

Zmienna losowa (X, Y) ma rozkład okre lony tabel :
Y
X

-1

0

1

k

1

,

0

1

k

1

,

0

2

0

k

1

,

0

1

k

k

1

,

0

4

1

,

0

−

a) Wyznaczy macierz kowariancji,
b) Obliczy współczynnik korelacji mi dzy tymi zmiennymi.
c) Czy X, Y s skorelowane? Czy X, Y s niezale ne?
Zadanie 7
Zmienna losowa (X, Y) ma rozkład okre lony tabel :
Y
X

0

1

2

-1

0

0

k

1

,

0

1

0

k

1

,

0

2

k

1

,

0

2

k

k

1

,

0

8

1

,

0

−

1

k

1

,

0

2

0

k

1

,

0

1

a)

wyznaczy F(1; 2),

b)

obliczy

(

)

1

|

|

;

1

|

|

≤

≥

Y

X

P

,

c) Wyznacz rozkład zmiennej losowej X.
d) Wyznacz rozkład zmiennej losowej Y.
e)

wyznacz rozkładów warunkowych

1

|

=

Y

X

;

0

|

=

X

Y

,

f) Obliczy współczynnik korelacji mi dzy tymi zmiennymi.
g) Czy X, Y s skorelowane? Czy X, Y s niezale ne?

Zadanie 8

Zmienna losowa (X, Y) ma macierz kowariancji:

−

−

=

16

005

,

0

005

,

0

4

k

k

K

Ile wynosi współczynnik korelacji mi dzy X i Y?

Zadanie 9

Zmienne losowe X

1

, X

2

s niezale ne. Wiadomo, e D

2

X

1

= k, D

2

X

2

= 2k.

Niech Y = X

1

- 2X

2

, Z = X

1

+ X

2

.

Ile wynosi współczynnik korelacji mi dzy Y i Z?

Zadanie 10.

Zmienna losowa X ma g sto

<

≥

⋅

=

⋅

−

0

0

0

01

,

0

)

(

01

,

0

x

dla

x

dla

ke

x

f

kx

a) wyznaczy jej funkcj charakterystyczn ,
b) za pomoc funkcji charakterystycznej obliczy

EX, D

2

X, współczynnik asymetrii i kurtoz .

Zadanie 11.

(X, Y ) jest zmienn losow o g sto ci

+

∈

∈

=

)

,

(

0

]

01

,

0

1

;

[

],

1

;

0

[

)

,

(

y

x

k

x

y

x

c

y

x

f

innych

dla

dla

a)

wyznaczy c,

b)

wyznaczy F(0,001

⋅⋅⋅⋅

k; 0,0005

⋅⋅⋅⋅

k),

c)

obliczy

(

)

1

|

|

;

1

001

,

0

≤

≤

≤

Y

X

k

P

i zinterpretowa na wykresie g sto ci,

d)

wyznacz g sto ci rozkładów warunkowych

1

|

=

Y

X

;

5

,

0

|

=

X

Y

,

e)

obliczy cov(X, Y), czy X, Y s nieskorelowane?

f)

czy X, Y s niezale ne?

Zadanie 12.

(X, Y ) jest zmienn losow o g sto ci

∉

∈

=

D

y

x

D

y

x

c

y

x

f

)

,

(

0

)

,

(

)

,

(

dla

dla

gdzie D jest trójk tem o wierzchołkach (-0,01k; 0); (0; -0,01k); (-0,01k; -0,01k).

a)

wyznaczy c,

b)

wyznaczy F(0,0),

c)

obliczy EX, EY, cov(X, Y). Czy X, Y s nieskorelowane?

d)

wyznacz prost regresji Y wzgl dem X,

Zadanie 13.

Prawdopodobie stwo wygrania nagrody na loterii wynosi

0,0001

⋅⋅⋅⋅

k

. Korzystaj c z przybli enia

Poissona wyznaczy prawdopodobie stwo, e w ród 1000 osób graj cych na tej loterii:

a) adna nie wygra,

b) wygraj 2 osoby,

c) wygraj co najmniej 3 osoby,

Zadanie 14.

Zmienna losowa X ma rozkład N(– k; 0,1

⋅k).

Obliczy :

a)

P(X > – 0,9

⋅k),

b)

P(X < – 0,95

⋅k),

c)

)

15

,

0

(

k

k

X

P

<

+

Otrzymane wyniki zinterpretowa na wykresie g sto ci.

Zadanie 15.

Zmienna losowa X ma rozkład N(– k; 0,01

⋅k).

Wyznaczy x aby:

a)

P(X > x) = 0,98,

b)

P(X < x) = 0,01,

c)

05

,

0

)

(

=

>

+

x

k

X

P

.

Otrzymane wyniki zinterpretowa na wykresie g sto ci.

Nale y odda co najmniej 10 zada .

L.Kowalski, 23.02.2005