KONKURENCJA

DOSKONAŁA

KONKURENCJA

DOSKONAŁA

dr Sylwia Machowska

Definicja

• Konkurencja doskonała jest modelem

teoretycznym opisuj

ą

cym jedn

ą

z form

konkurencji na rynku; cech

ą

charakterystyczn

ą

konkurencji doskonałej

w odró

ż

nieniu od innych jej form jest

przekonanie zarówno kupuj

ą

cych jak i

sprzedaj

ą

cych,

ż

e ich indywidualne

decyzje nie maj

ą

wpływu na cen

ę

rynkow

ą

.

KONKURENCJA DOSKONAŁA

KONKURENCJA DOSKONAŁA

Teoretyczna konstrukcja modelu
konkurencji doskonałej, lub rynku
doskonale konkurencyjnego opiera si

ę

na czterech podstawowych
zało

ż

eniach:

KONKURENCJA DOSKONAŁA

KONKURENCJA DOSKONAŁA

zało

ż

enie o jednorodno

ś

ci produktu

Produkty ka

ż

dego z producentów s

ą

identyczne. Ka

ż

dy z wielu producentów

sprzedaje dokładnie taki sam produkt.
Równocze

ś

nie kupuj

ą

cy traktuj

ą

i oceniaj

ą

produkty oferowane przez wielu
producentów jako identyczne.

•

zało

ż

enie o swobodzie wej

ś

cia i

wyj

ś

cia z bran

ż

y

Nie istniej

ą ż

adne bariery wej

ś

cia ani

wyj

ś

cia z bran

ż

y; dzi

ę

ki temu przy

wi

ę

kszym zapotrzebowaniu ze strony

kupuj

ą

cych producenci b

ę

d

ą

mogli

swobodnie rozpocz

ąć

dodatkow

ą

produkcj

ę

, zwi

ę

kszaj

ą

c tym samym

poda

ż

, a przy zmniejszonym

zapotrzebowaniu wycofa

ć

si

ę

nie

ponosz

ą

c dodatkowych strat.

•

du

ż

a liczba sprzedaj

ą

cych i

kupuj

ą

cych

Rynek składa si

ę

z wielu producentów

(sprzedaj

ą

cych) i z wielu kupuj

ą

cych.

Udział ka

ż

dego producenta w globalnej

poda

ż

y oraz udział ka

ż

dego kupuj

ą

cego

w globalnym popycie s

ą

stosunkowo

niewielkie.

•

zało

ż

enie doskonałej informacji o

rynku

Wszyscy sprzedaj

ą

cy i kupuj

ą

cy

posiadaj

ą

pełn

ą

informacj

ę

o produkcie i

jego cenie, zarówno w danym momencie
jak i w przyszło

ś

ci.

Zgodnie z tym zało

ż

eniem nie wyst

ę

puje

niepewno

ść

i ryzyko. Dlatego producent

zawsze mo

ż

e okre

ś

li

ć

rozmiary produkcji

maksymalizuj

ą

ce zysk a kupuj

ą

cy

zawsze mo

ż

e okre

ś

li

ć

wielko

ść

swojego

popytu.

Czynnik czasu

Czynnik czasu

• Czynnik czasu:

– krótki okres czasu: rozmiary przedsi

ę

biorstwa

s

ą

stałe, wielko

ść

produkcji zmienia si

ę

wraz

ze zmianami wykorzystania czynników
zmiennych

– długi okres: zmieniaj

ą

si

ę

rozmiary

przedsi

ę

biorstwa w zale

ż

no

ś

ci od kosztów

produkcji oraz od sytuacji rynkowej, zmienia
si

ę

liczba przedsi

ę

biorstw w gał

ę

zi

RÓWNOWAGA RYNKOWA W

KRÓTKIM OKRESIE CZASU

RÓWNOWAGA RYNKOWA W

KRÓTKIM OKRESIE CZASU

• Na rynku doskonale konkurencyjnym cena

jest wielko

ś

ci

ą

dan

ą

, zarówno dla

producenta jak i dla konsumenta. Cen

ę

równowagi rynkowej P

e

obowi

ą

zuj

ą

c

ą

podmioty gospodarcze wyznacza punkt
przeci

ę

cia si

ę

krzywej popytu rynkowego z

krzyw

ą

poda

ż

y rynkowej. Punkt przeci

ę

cia

si

ę

obydwu krzywych wyznacza

równocze

ś

nie wielko

ść

równowagi Xe.

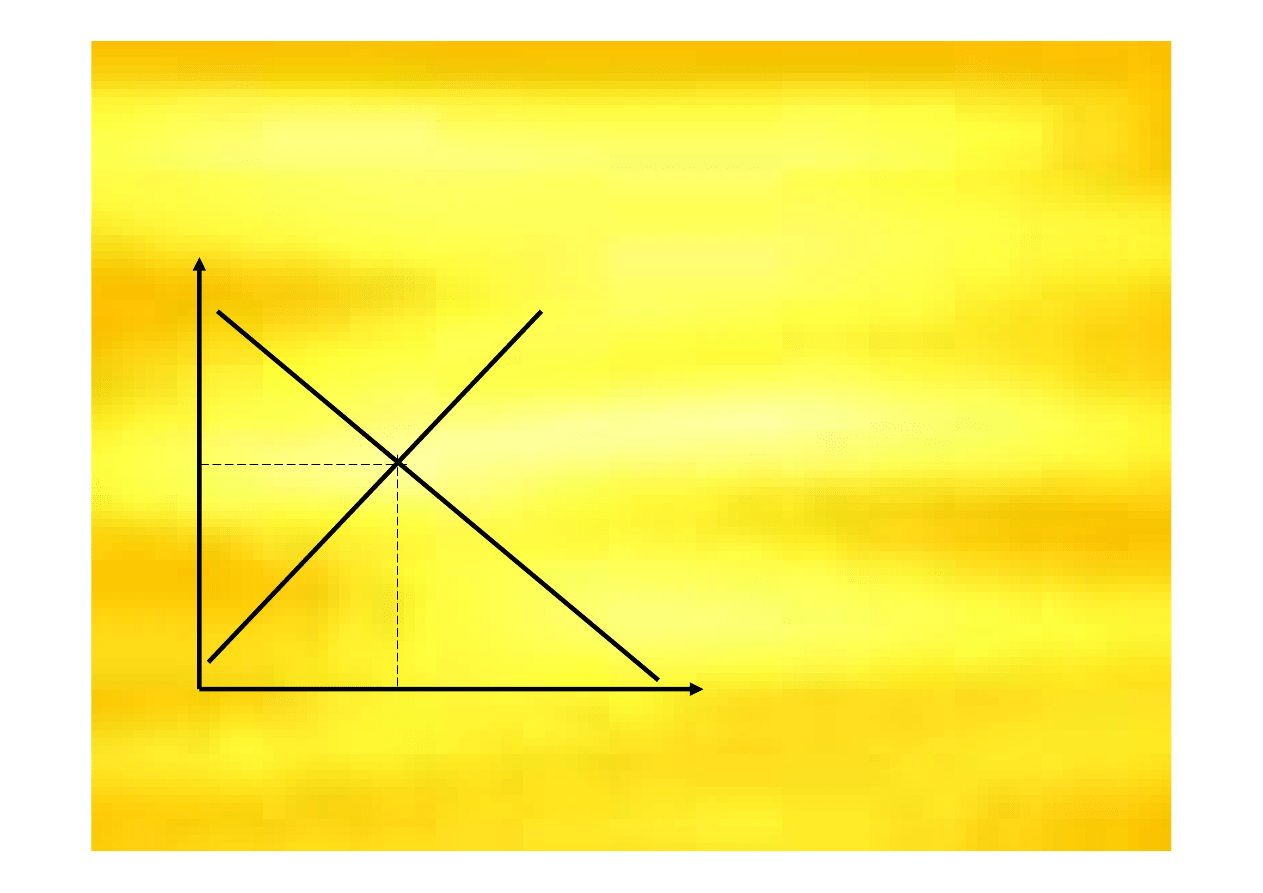
Rynek doskonale konkurencyjny w

krótkim okresie

Rynek doskonale konkurencyjny w

krótkim okresie

Punkt równowagi rynkowej
(punkt E) znajduje si

ę

zarówno na krzywej popytu
rynkowego, jak i na krzywej
poda

ż

y rynkowej, a

wielko

ść

zgłaszanego

popytu jest równa wielko

ś

ci

oferowanej produktu (Xe).
W punkcie równowagi
nast

ę

puje maksymalizacja

zadowolenia wszystkich
konsumentów oraz
maksymalizacja zysków
wszystkich przedsi

ę

biorstw.

S

D

Pe

Xe

E

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie

• Krzywa popytu na wyrób firmy jest

doskonale elastyczna (Edp = -

∞

) co

wynika z bardzo małego udziału na rynku.

• Zmiany wielko

ś

ci produkcji firmy b

ę

d

ą

miały tak nikły wpływ na cen

ę

,

ż

e mo

ż

na

go uzna

ć

za zerowy.

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie

• Przedsi

ę

biorstwo działaj

ą

ce w warunkach

konkurencji doskonałej d

ąż

y do

maksymalizacji zysku, zarówno do
maksymalizacji zysku dodatniego, jak i do
minimalizacji wyniku ujemnego.

CENA, PRZYCHÓD CAŁKOWITY,

PRZECI

Ę

TNY I MARGINALNY

CENA, PRZYCHÓD CAŁKOWITY,

PRZECI

Ę

TNY I MARGINALNY

• Dla przedsi

ę

biorstwa znajduj

ą

cego si

ę

na

rynku doskonale konkurencyjnym cena
jest równa przychodowi przeci

ę

tnemu oraz

przychodowi marginalnemu. Jednocze

ś

nie

jest to krzywa popytu producenta.

P = AR = MR = d

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie –

krzywa popytu

Przedsi

ę

biorstwo doskonale

konkurencyjne w krótkim okresie –

krzywa popytu

d= P = AR = MR

X

j.p

j.p. – jednostki pieni

ęż

ne

X – wielko

ść

produkcji

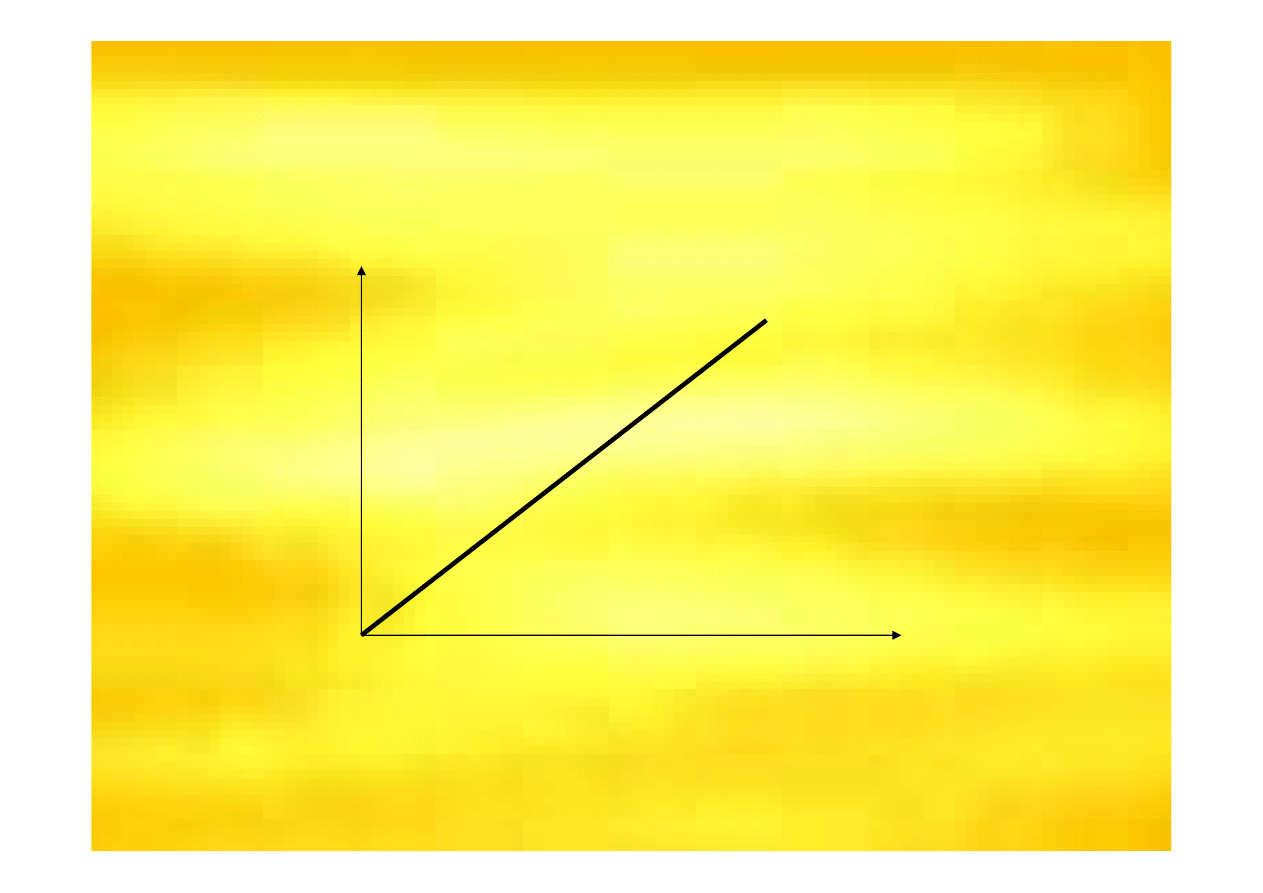
Krzywa przychodu całkowitego

przedsi

ę

biorstwa

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

X

TR

TR

TR – przychód całkowity

X – wielko

ść

produkcji

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

X

TR

TR

TR – przychód całkowity

X – wielko

ść

produkcji

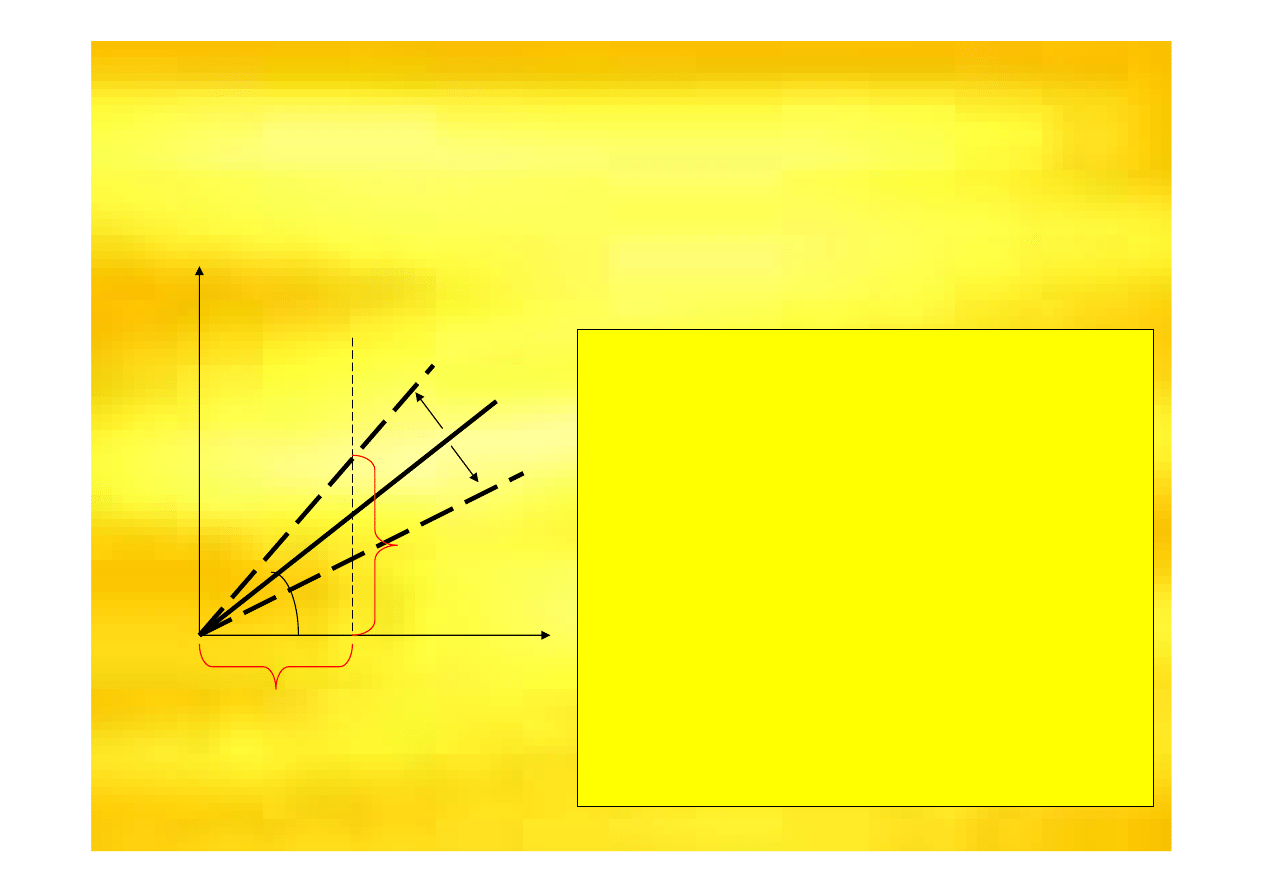
α

X

Krzywa przychodu
całkowitego nachylona
jest pod k

ą

tem

α

,

którego tg

α

= TR/X = P,

a wi

ę

c warto

ść

nachylenia TR
wyznacza P.

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

Krzywa przychodu całkowitego

przedsi

ę

biorstwa

X

TR

TR

TR – przychód całkowity

X – wielko

ść

produkcji

α

X

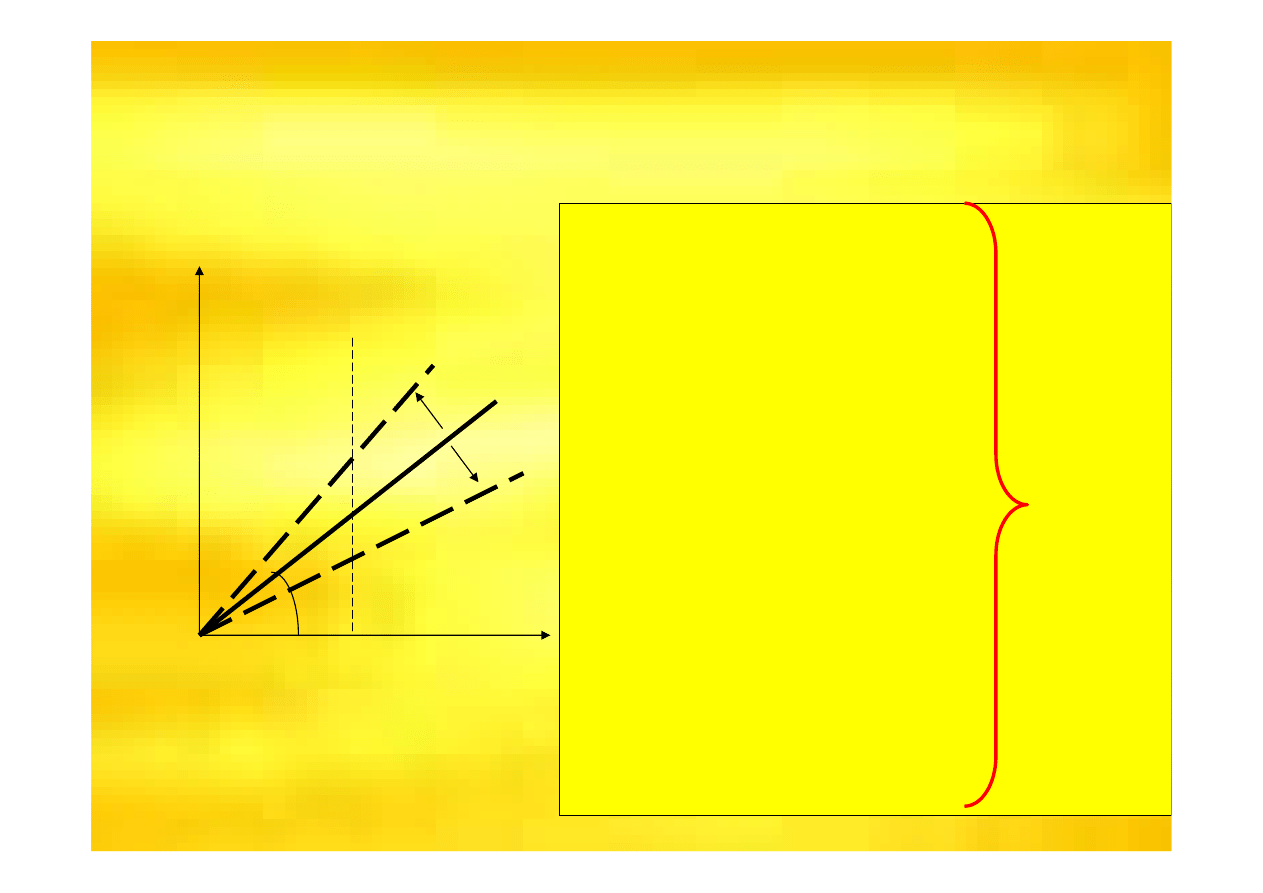
Je

ż

eli wi

ę

c cena

danego dobra
maleje to linia
przychodu obraca
si

ę

w prawo od

pocz

ą

tku układu

współrz

ę

dnych.

Je

ś

li cena ro

ś

nie to

linia przychodu
obraca si

ę

w lewo.

Oczywi

ś

cie

dla danej
wielko

ś

ci

produkcji

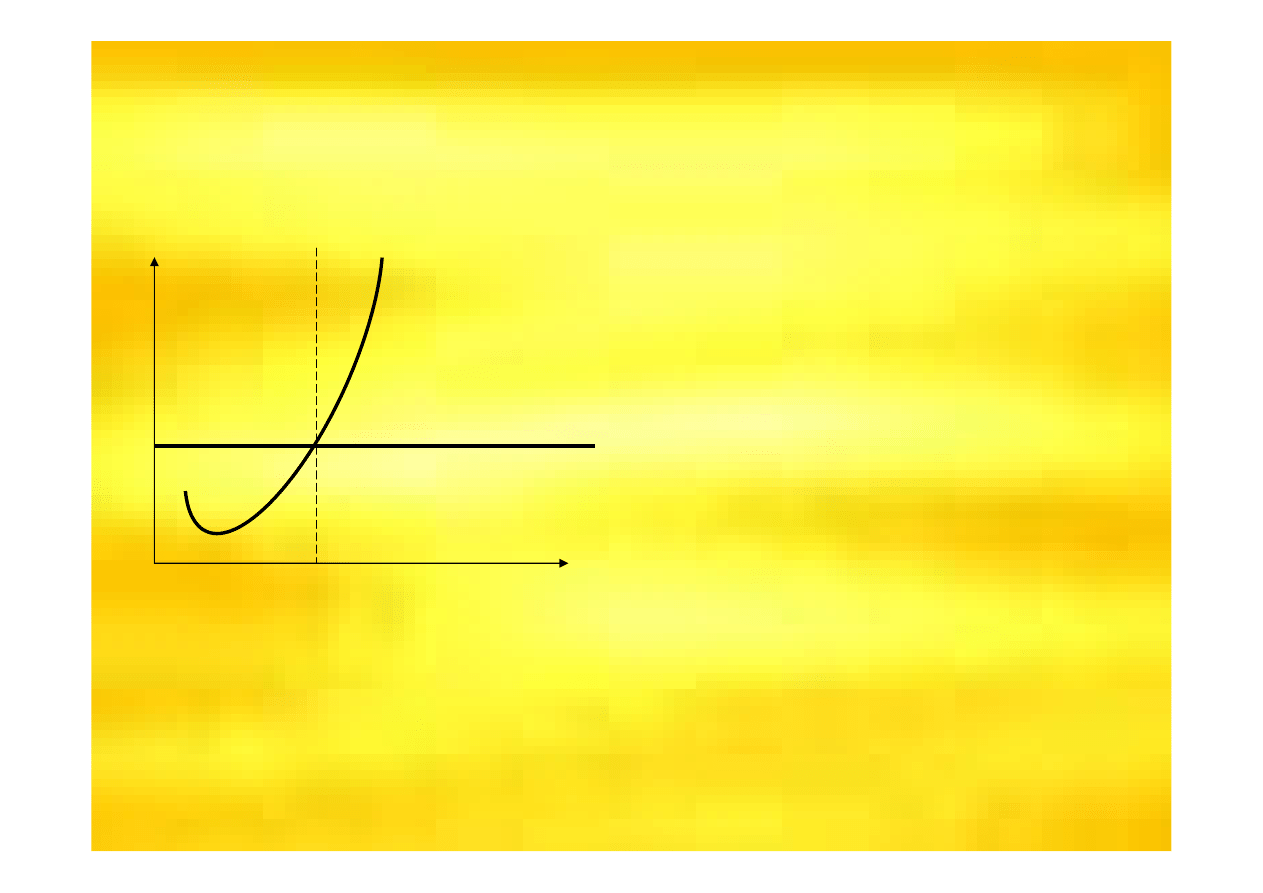
RÓWNOWAGA W KRÓTKIM

OKRESIE CZASU

RÓWNOWAGA W KRÓTKIM

OKRESIE CZASU

Podejmuj

ą

c decyzje

dotycz

ą

ce rozmiarów

produkcji firma kieruje
si

ę

kryterium

maksymalizacji zysków
a

ś

ci

ś

lej optymalizacji

wyniku
ekonomicznego, które
wymaga zrównania
przychodu kra

ń

cowego

z kosztem kra

ń

cowym.

MC= MR

MC= MR

d= P =

MR

= AR

X

j.p

MC

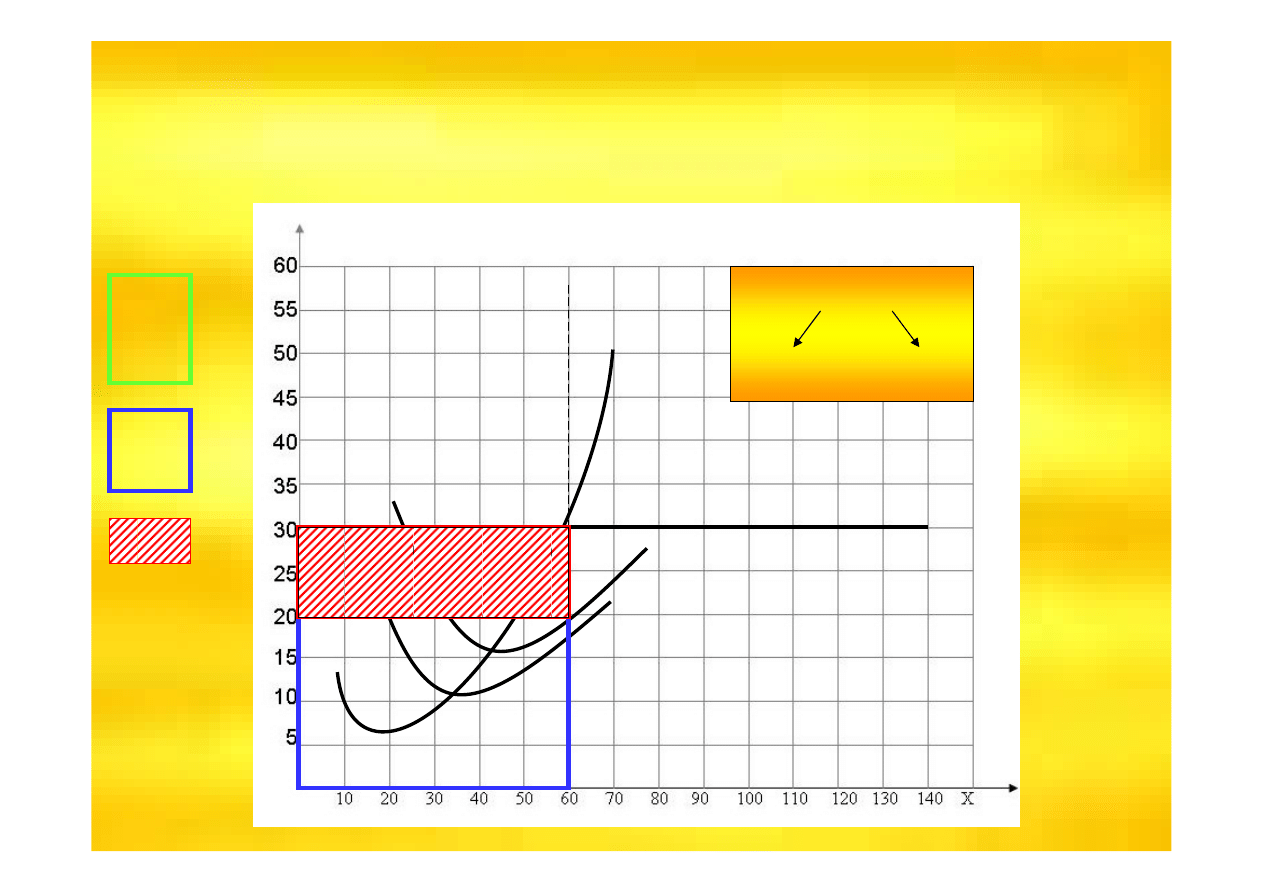
Wynik ekonomiczny w przedsi

ę

biorstwie

doskonale konkurencyjnym

Wynik ekonomiczny w przedsi

ę

biorstwie

doskonale konkurencyjnym

d= P = AR = MR

ATC

AVC

j.p.

MC

Poniewa

ż

TR>TC

wynikiem jest zysk
ekonomiczny

TR

TC

zysk

WE = TR - TC

P•X

ATC•X

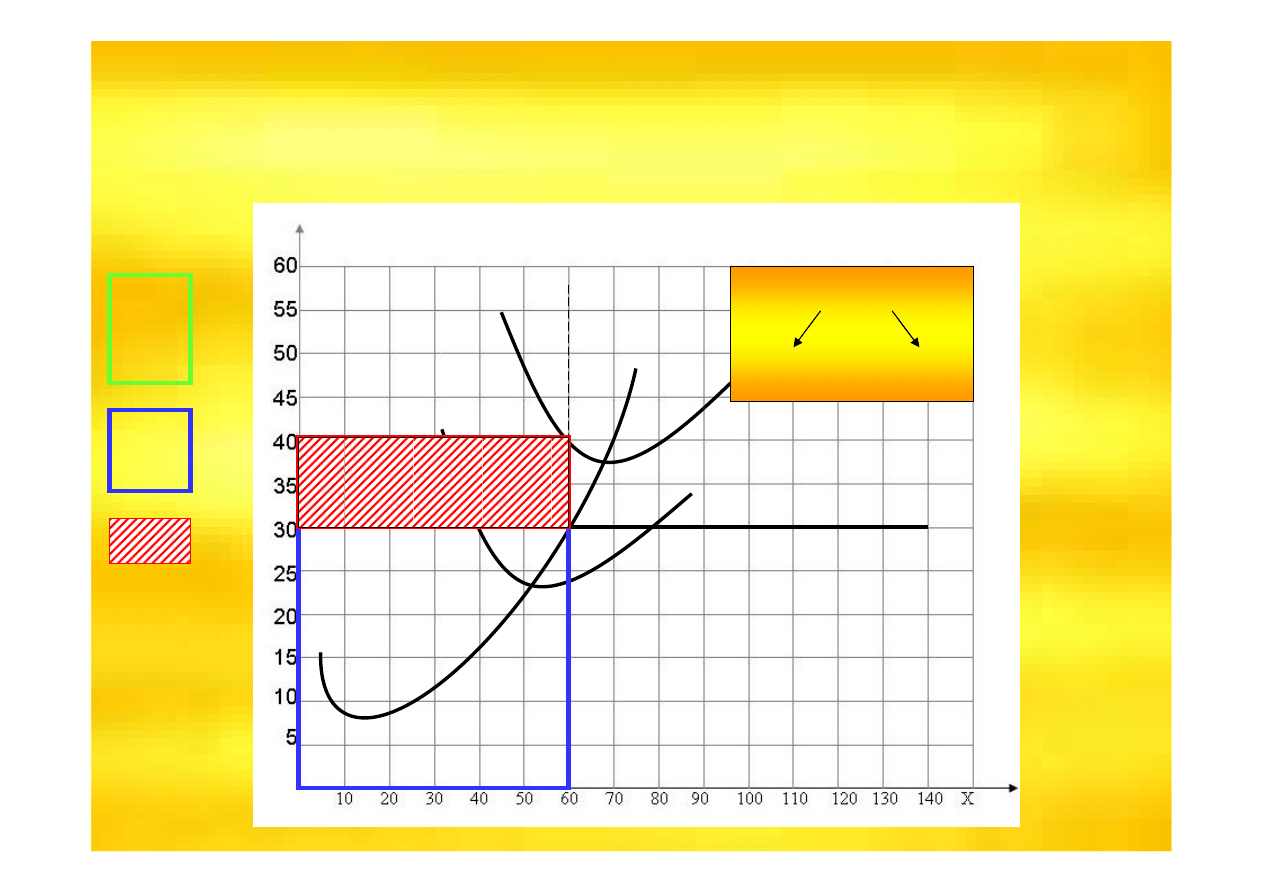
Wynik ekonomiczny w przedsi

ę

biorstwie

doskonale konkurencyjnym

Wynik ekonomiczny w przedsi

ę

biorstwie

doskonale konkurencyjnym

d= P = AR = MR

ATC

AVC

j.p.

MC

Poniewa

ż

TC>TR

wynikiem jest
strata

TR

TC

strata

WE = TR - TC

P•X

ATC•X

Jest to strata z kontynuacj

ą

produkcji poniewa

ż

P>AVC

Optymalizacja wyniku

ekonomicznego

Optymalizacja wyniku

ekonomicznego

• Ile produkowa

ć

,

ż

eby wynik finansowy

przedsi

ę

biorstwa był maksymalny

(optymalny)?

• Rozmiary produkcji, przy których wynik

finansowy przedsi

ę

biorstwa jest

maksymalny (optymalny), to

optimum

produkcyjne.

Optimum produkcyjne

Optimum produkcyjne

Optimum produkcyjne przedsi

ę

biorstwa

osi

ą

gane jest wtedy, gdy

koszt kra

ń

cowy zrównuje si

ę

z

przychodem kra

ń

cowym.

MC= MR

Optimum produkcyjne przedsi

ę

biorstwa

osi

ą

gane jest wtedy, gdy

koszt kra

ń

cowy zrównuje si

ę

z

przychodem kra

ń

cowym.

MC= MR

Odpowied

ź

na pytanie: ile produkowa

ć

,

ż

eby wynik

finansowy przedsi

ę

biorstwa był optymalny?

Co to jest wynik optymalny?

Co to jest wynik optymalny?

NAJWI

Ę

KSZY Z

MO

ś

LIWYCH

NAJMNIEJSZA Z

MO

ś

LIWYCH

ZYSK

STRATA

MAKSYMALIZACJA

ZYSKU

MINIMALIZACJA

STRATY

Optymalny czyli najlepszy z mo

ż

liwych

w danych warunkach.

Czy wi

ę

ksza produkcja = wi

ę

ksze

zyski?

Czy wi

ę

ksza produkcja = wi

ę

ksze

zyski?

• Czy zwi

ę

kszanie rozmiarów produkcji

idzie w parze ze zwi

ę

kszaniem zysków?

Wynik finansowy = przychody – koszty

• Wi

ę

ksza produkcja to wi

ę

ksze

przychody (cho

ć

nie zawsze!), ale te

ż

wi

ę

ksze koszty.

-55

175

120

12

-30

151

121

11

-9

129

120

10

6

111

117

9

17

95

112

8

24

81

105

7

27

69

96

6

26

59

85

5

21

51

72

4

13

44

57

3

4

36

40

2

-4

25

21

1

-10

10

0

0

Wynik

finansowy

(zł/tydzie

ń

)

Koszty

całkowite

(zł/tydzie

ń

)

Przychód

(zł/tydzie

ń

)

Produkcja

i sprzeda

ż

(szt./tydzie

ń

)

24

22

18

16

14

12

10

8

7

8

11

15

-

Koszt

Koszt

kra

kra

ń

ń

cowy

cowy

-1

1

3

5

7

9

11

13

15

17

19

21

-

Przych

Przych

ó

ó

d

d

kra

kra

ń

ń

cowy

cowy

-55

175

120

12

-30

151

121

11

-9

129

120

10

6

111

117

9

17

95

112

8

24

81

105

7

27

69

96

6

26

59

85

5

21

51

72

4

13

44

57

3

4

36

40

2

-4

25

21

1

-10

10

0

0

Wynik finansowy

(zł/tydzie

ń

)

Koszty

całkowite

(zł/tydzie

ń

)

Przychód

(zł/tydzie

ń

)

Produkcja

i sprzeda

ż

(szt./tydzie

ń

)

Analiza kra

ń

cowa (marginalna)

Analiza kra

ń

cowa (marginalna)

• Analiza kra

ń

cowa

nale

ż

y do najcz

ęś

ciej

wykorzystywanych metod analizy
mikroekonomicznej. Polega ona na badaniu
efektów zwi

ę

kszania badanej zmiennej o

jednostk

ę

(np. o 1 sztuk

ę

, 1 zł, 1 kg itp.).

• W polu naszego zainteresowania b

ę

dzie

le

ż

ał przychód kra

ń

cowy (MR) i koszt

kra

ń

cowy (MC).

Decyzje produkcyjne w krótkim

okresie

Decyzje produkcyjne w krótkim

okresie

Przedsi

ę

biorstwo

zmniejsza produkcj

ę

P<MC

Cena ni

ż

sza od kosztów

kra

ń

cowych

Optymalna wielko

ść

produkcji (produkcja nie
ulega zmianie)

P=MC

Cena równa kosztom
kra

ń

cowym

Przedsi

ę

biorstwo

zwi

ę

ksza produkcj

ę

P>MC

Cena przekracza koszty
kra

ń

cowe

Decyzje przedsi

ę

biorstwa

Kryterium decyzyjne

Jak to działa?

Jak to działa?

Jak to działa?

d= P = AR = MR

ATC

AVC

j.p.

MC

Poniewa

ż

TR>TC

wynikiem jest zysk
ekonomiczny

TR

TC

zysk

WE = TR - TC

P•X

ATC•X

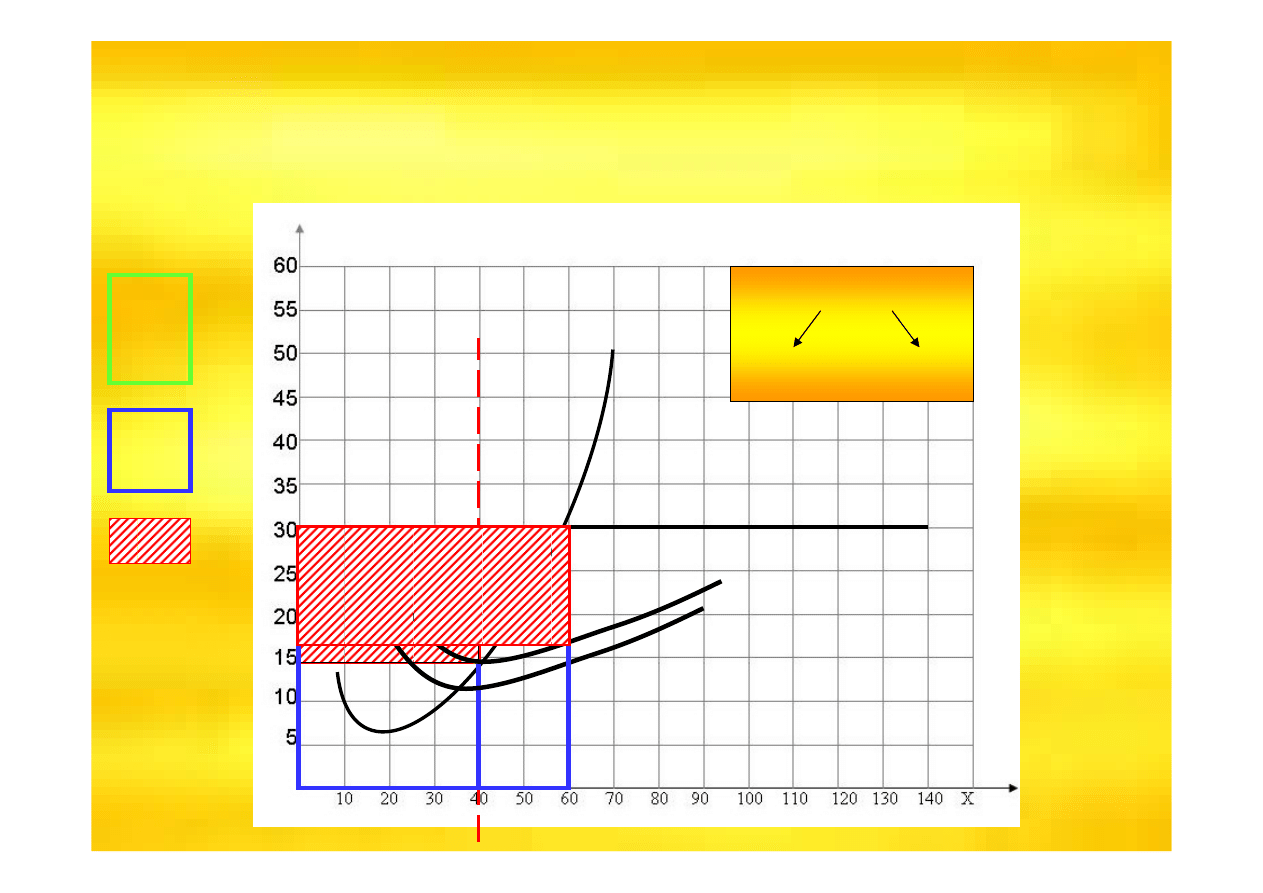
Czy ten zysk jest maksymalny ?

NIE

A KIEDY JEST?

Wynik ekonomiczny w przedsi

ę

biorstwie doskonale konkurencyjnym

d= P = AR = MR

ATC

AVC

j.p.

MC

Poniewa

ż

TC>TR

wynikiem jest
STRATA Z
KONTYNUACJ

Ą

PRODUKCJI

TR

TC

STRATA

WE = TR - TC

P•X

ATC•X

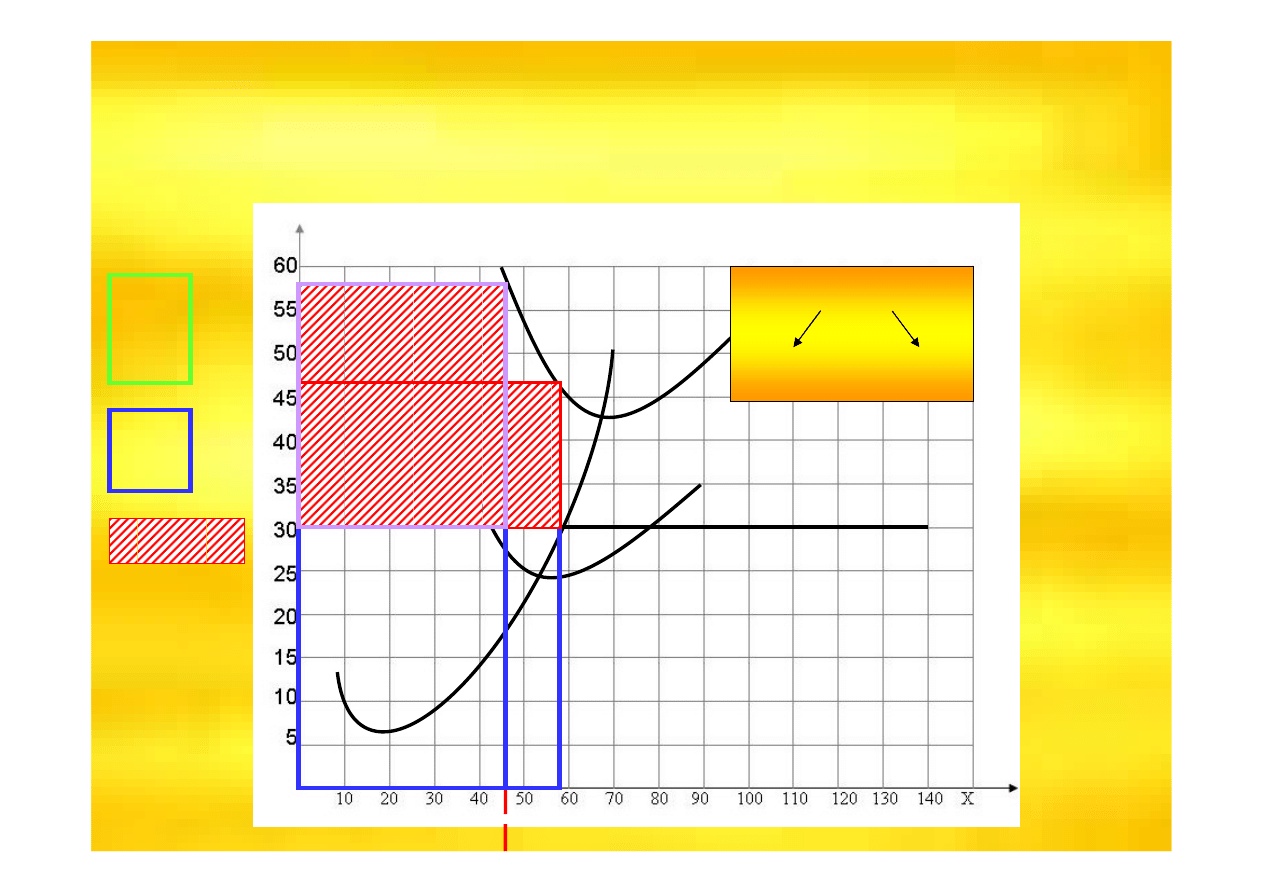
CZY MO

ś

NA CO

Ś

ZROBI

Ć

BY

T

Ą

STRAT

Ę

ZMNIEJSZY

Ć

?

TAK

Wynik ekonomiczny w uk

Wynik ekonomiczny w uk

ł

ł

adzie

adzie

wielko

wielko

ś

ś

ci ca

ci ca

ł

ł

kowitych

kowitych

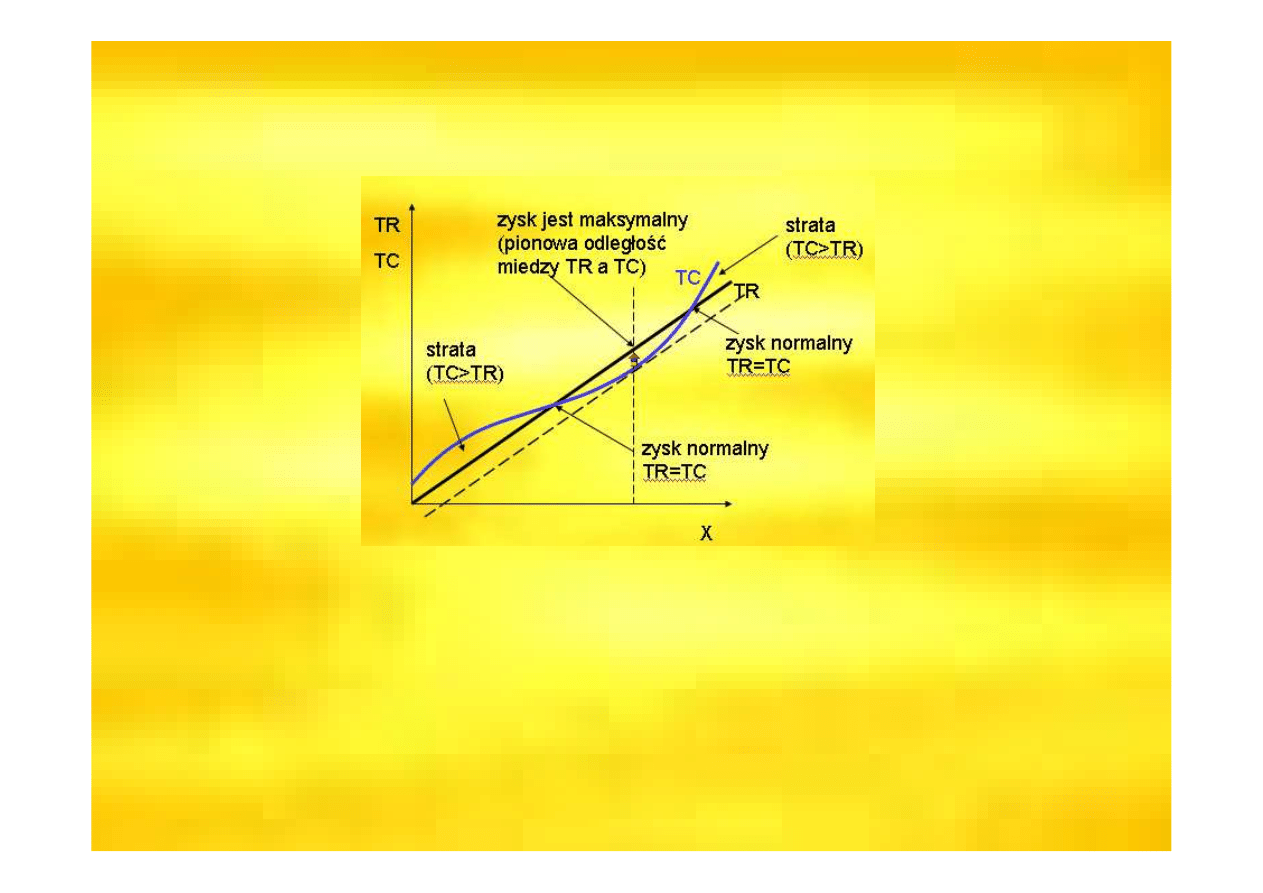
Analizuj

ą

c przebieg krzywej kosztu

całkowitego i linii przychodu całkowitego,

mo

ż

emy stwierdzi

ć

,

ż

e przy danym koszcie

wytworzenia okre

ś

lonej ilo

ś

ci produktu:

Wynik ekonomiczny w układzie

wielko

ś

ci całkowitych

1. Mo

ż

liwo

ś

ci uzyskania zysku zale

żą

od

poło

ż

enia linii przychodu całkowitego, gdy

TR>TC to wynik ekonomiczny >0 (zysk),
je

ś

li za

ś

TR<TC to wynik ekonomiczny < 0

(strata). Przedział ilo

ś

ci produkcji

zapewniaj

ą

cej zysk jest wyznaczony przez

punkty przeci

ę

cia linii przychodu

całkowitego i krzywej kosztu całkowitego.

2. Maksymalny zysk lub minimaln

ą

strat

ę

firma

uzyskuje tylko przy okre

ś

lonej wielko

ś

ci

produkcji, któr

ą

wyznacza warunek MC=MR.

Warunek ten jest uzasadniony
geometrycznie równoległo

ś

ci

ą

linii przychodu

całkowitego i stycznej do krzywej kosztu
całkowitego, a wi

ę

c obie proste maj

ą

tak

ą

sam

ą

warto

ść

nachylenia wzgl

ę

dem osi X.

Warto

ść

nachylenia dla linii przychodu

całkowitego wyznacza cena (równa MR

w konkurencji doskonałej), natomiast dla

stycznej do krzywej kosztu całkowitego

koszt marginalny (kra

ń

cowy).

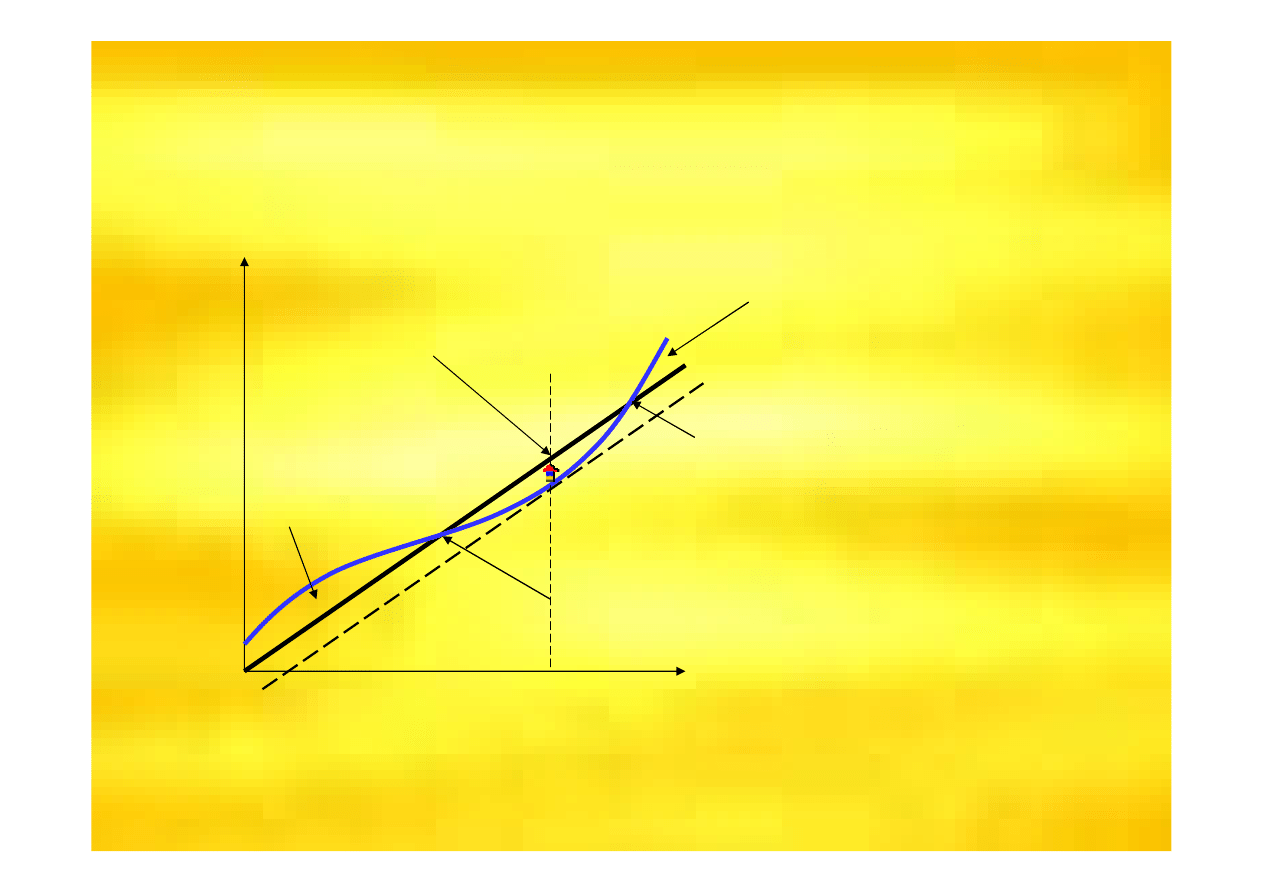
Wynik ekonomiczny w układzie

wielko

ś

ci całkowitych

X

TR

TC

TR

TC

zysk jest maksymalny
(pionowa odległo

ść

miedzy TR a TC)

strata
(TC>TR)

strata
(TC>TR)

zysk normalny
TR=TC

zysk normalny
TR=TC

Warunki maksymalizacji zysku

ekonomicznego

(analiza formalna)

• Funkcja zysku:

π

(x) = TR(x) – TC(x)

• Funkcja maksymalizacji zysku:

max

π

(x) = max [TR(x) – TC(x)]

TC = f (X)
f‘ (X)=

∆

TC/

∆

X = MC

TR = f (X)
f‘ (X) =

∆

TR/

∆

X = MR

• Aby

π

(x) było maksymalne pierwsza

pochodna funkcji zysku musi by

ć

równa zero.

π

'(x) = [TR(x) – TC(x)]' = 0

zatem: TR'(x) = TC'(x)

• W przypadku ci

ą

głych i

ró

ż

niczkowalnych funkcji przychodu

całkowitego i kosztu całkowitego
powy

ż

sze równanie jest równowa

ż

ne

formule:

MR(x) = MC(x)

• MC = MR przedstawia warunek konieczny istnienia

ekstremum funkcji zysku. Jego spełnienie nie
wystarczy jednak, by stwierdzi

ć

o jakie ekstremum

chodzi. Interesuje nas wył

ą

cznie maksimum (chodzi

przecie

ż

o maksymalizacj

ę

zysku), musimy posłu

ż

y

ć

si

ę

warunkiem drugiego rz

ę

du wskazuj

ą

cym na jego

istnienie:

• Wzór przedstawia warunek wystarczaj

ą

cy

maksymalizacji funkcji zysku firmy doskonale
konkurencyjnej. Dotyczy on drugiej pochodnej funkcji
zysku, która w przypadku wielko

ś

ci X ,

maksymalizuj

ą

cej zysk, musi by

ć

ujemna.

0

2

2

2

2

2

2

〈

−

=

Π

x

d

TC

d

dx

TR

d

dx

d

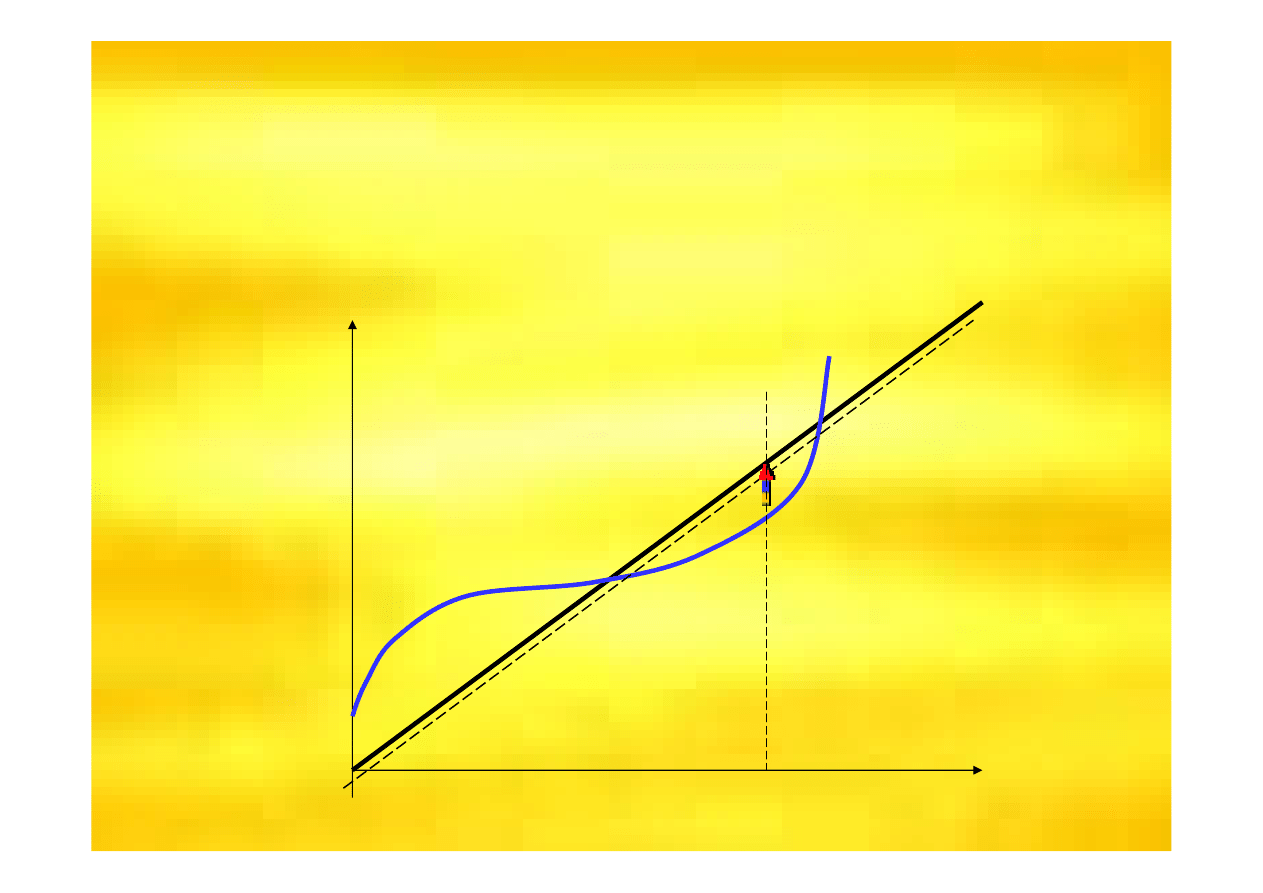
Analiza wyniku ekonomicznego na wielko

ś

ciach całkowitych

zysk maksymalny

Analiza wyniku ekonomicznego na wielko

Analiza wyniku ekonomicznego na wielko

ś

ś

ciach ca

ciach ca

ł

ł

kowitych

kowitych

zysk maksymalny

X

TC

TR

TR

TC

X

Zysk normalny

Zysk normalny

X

TC

TR

TR

TC

X

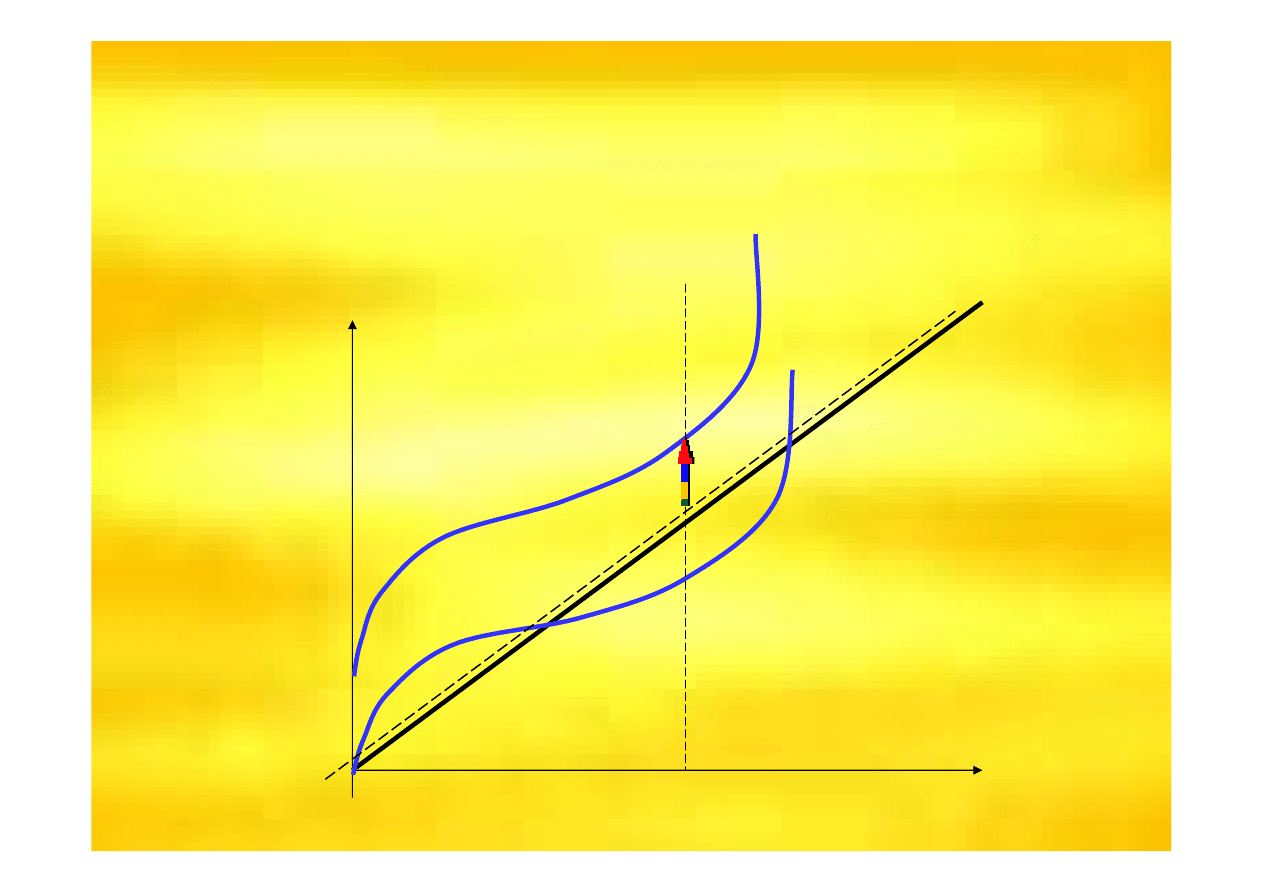
Strata minimalna z kontynuacj

ą

produkcji

Strata minimalna z kontynuacj

ą

produkcji

X

TC

TVC

TR

TR

TC

TVC

X

Strata zawieszenie produkcji

Strata zawieszenie produkcji

X

TC

TVC

TR

TR

TC

TVC

Strata na granicy

(punkt zamkni

ę

cia)

Strata na granicy

(punkt zamkni

ę

cia)

TC

TVC

TR

X

TR

TC

TVC

X

Uwaga!

• Wynik ekonomiczny analizowany na

układzie wielko

ś

ci całkowitych jest

odcinkiem (pionow

ą

odległo

ś

ci

ą

mi

ę

dzy

krzywymi).

Analiza optymalizacji wyniku

ekonomicznego na wielko

ś

ciach

przeci

ę

tnych

Analiza optymalizacji wyniku

ekonomicznego na wielko

ś

ciach

przeci

ę

tnych

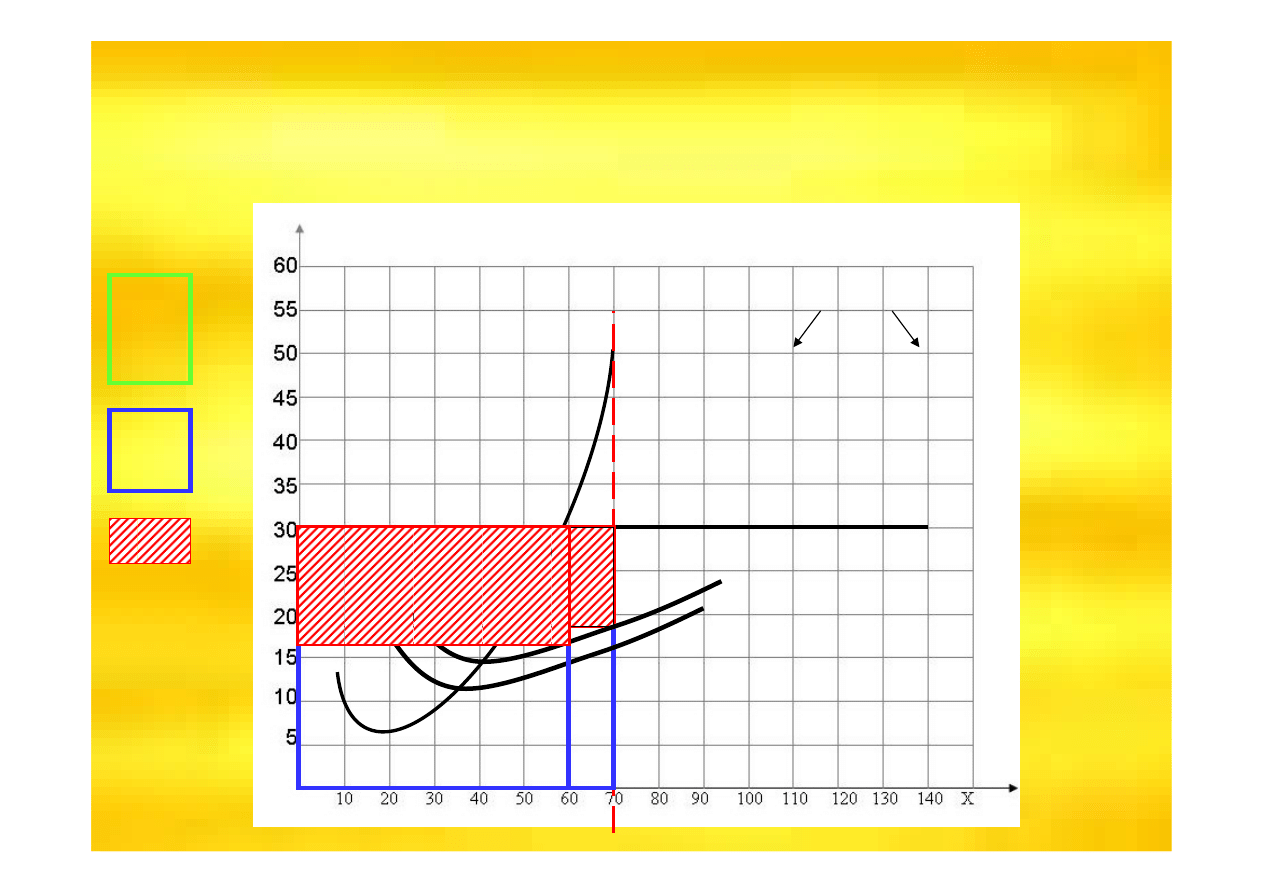
Jak to działa?

d= P = AR = MR

ATC

AVC

j.p.

MC

Poniewa

ż

TR>TC

wynikiem jest zysk
ekonomiczny

TR

TC

zysk

WE = TR - TC

P•X

ATC•X

Maksymalizacja zysku

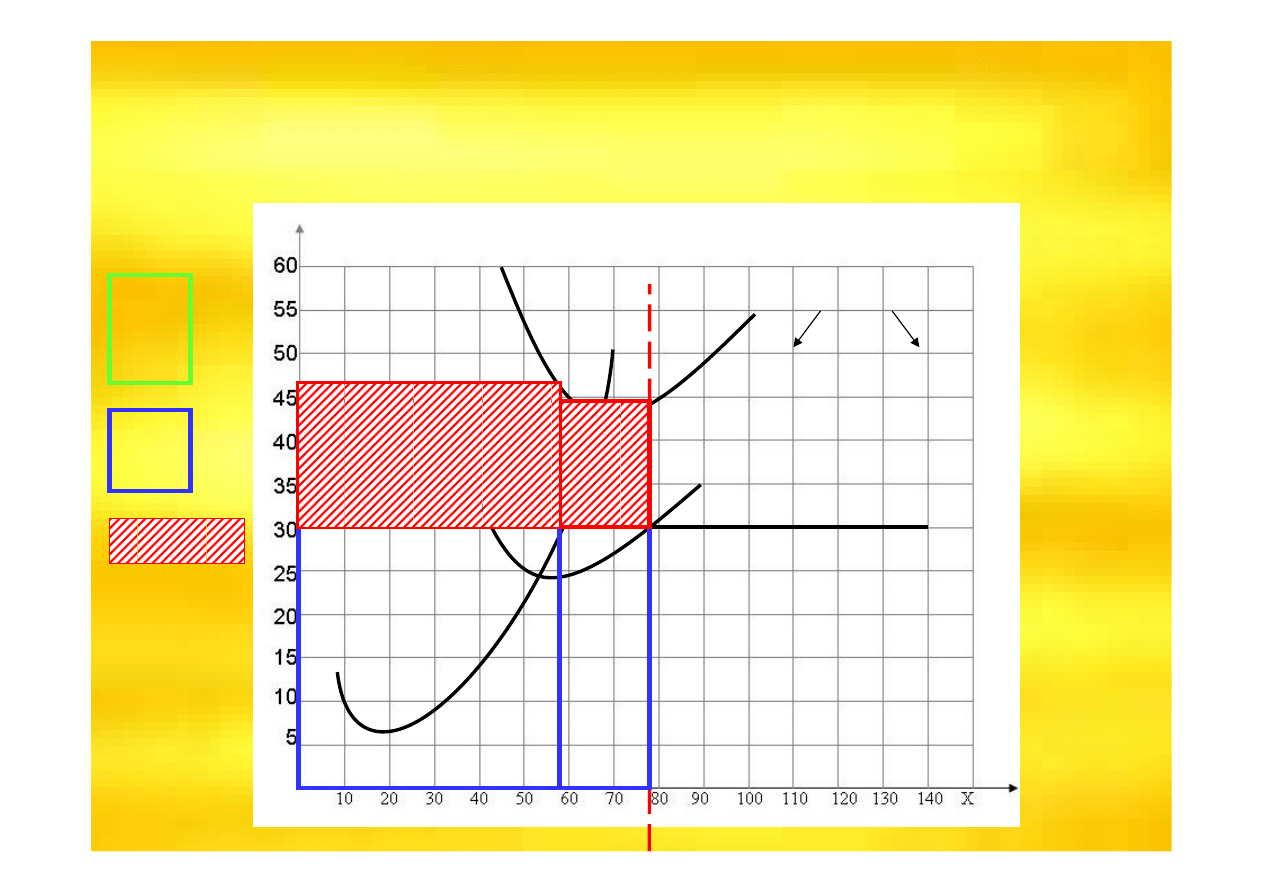
d= P = AR = MR

ATC

AVC

j.p.

MC

wynikiem jest
STRATA Z
KONTYNUACJ

Ą

PRODUKCJI

TR

TC

STRATA

WE = TR - TC

P•X

ATC•X

Minimalizacja straty

Minimalizacja straty

Uwaga !

• Wynik ekonomiczny analizowany na

układzie wielko

ś

ci przeci

ę

tnych jest polem

prostok

ą

ta, podobnie jak przychód

całkowity i koszty całkowite.

Zadanie

Zakładamy,

ż

e cena rynkowa dobra X jest

niezale

ż

na od wielko

ś

ci poda

ż

y realizowanej

przez producenta. Wykorzystuj

ą

c krzywe

wielko

ś

ci przeci

ę

tnych i kra

ń

cowych, zilustruj

graficznie sytuacje ekonomiczne w których
producent:

1. Osi

ą

ga zysk ekonomiczny;

2. Osi

ą

ga zysk normalny;

3. Ponosi strat

ę

ekonomiczn

ą

uzasadniaj

ą

c

ą

kontynuacj

ę

produkcji;

4. Ponosi strat

ę

ekonomiczn

ą

uzasadniaj

ą

c

ą

;

zaprzestanie produkcji.

5. Znajduje si

ę

w punkcie zamkni

ę

cia;

Osi

ą

ga zysk ekonomiczny

X

X

d=AR=MR=P

MC

ATC

d=AR=MR=P

MC

ATC

Osi

ą

ga zysk normalny;

Osi

ą

ga zysk normalny

X

X

d=AR=MR=P

MC

ATC

d=AR=MR=P

MC

ATC

Ponosi strat

ę

ekonomiczn

ą

uzasadniaj

ą

c

ą

kontynuacj

ę

produkcji

X

X

d=AR=MR=P

MC

ATC

d=AR=MR=P

MC

ATC

AVC

AVC

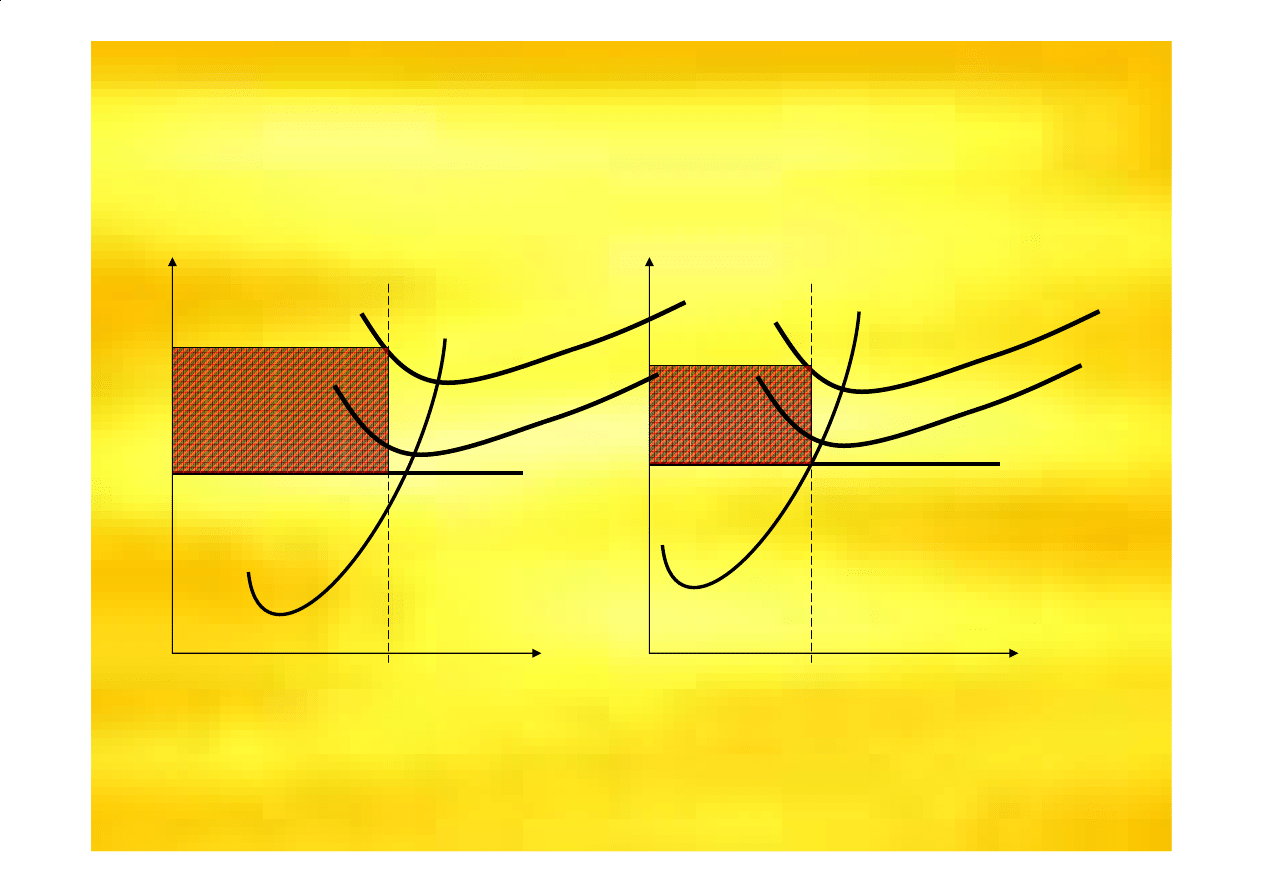
Ponosi strat

ę

ekonomiczn

ą

uzasadniaj

ą

c

ą

zaprzestanie produkcji

X

X

d=AR=MR=P

MC

ATC

d=AR=MR=P

MC

ATC

AVC

AVC

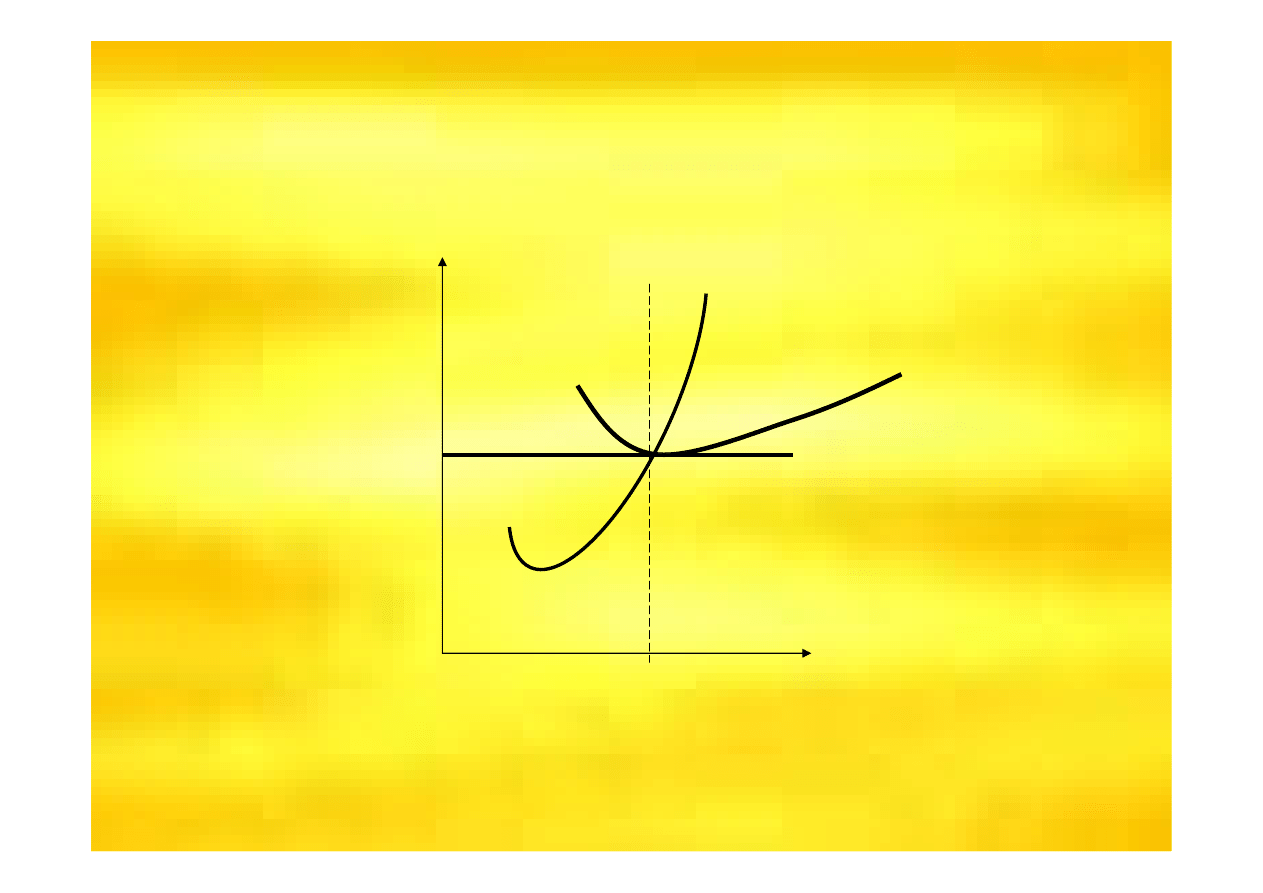
Osi

ą

ga zysk normalny;

Znajduje si

ę

w punkcie zamkni

ę

cia;

X

d=AR=MR=P

MC

AVC

Zadanie

• Podane tabele dotycz

ą

sytuacji

ekonomicznej konkurentów doskonałych.

• Uzupełnij brakuj

ą

ce dane.

• Zilustruj sytuacj

ę

ekonomiczna producenta

na układzie wielko

ś

ci kra

ń

cowych i

przeci

ę

tnych.

• Okre

ś

l kierunek zmian wielko

ś

ci produkcji.

Zadanie

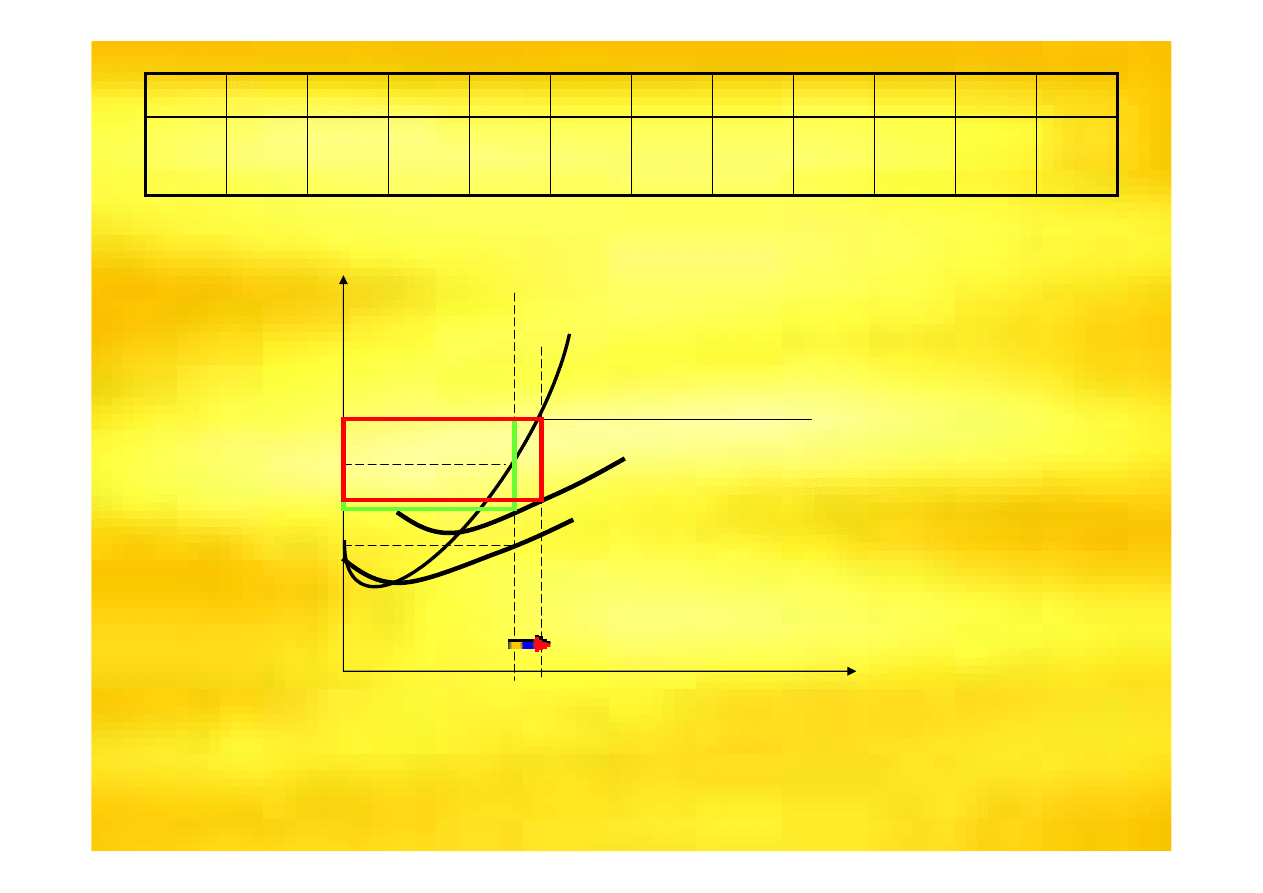
8

1

6

56

80

10

WE

MC

AFC

AVC

ATC

TVC

TFC

TC

TR

X

MR

P

7

24

8

10

8

48

X

d=AR=MR=P

10

8

8

MC

7

ATC

6

AVC

Co zrobi

ć ż

eby

zmaksymalizowa

ć

ten

zysk?

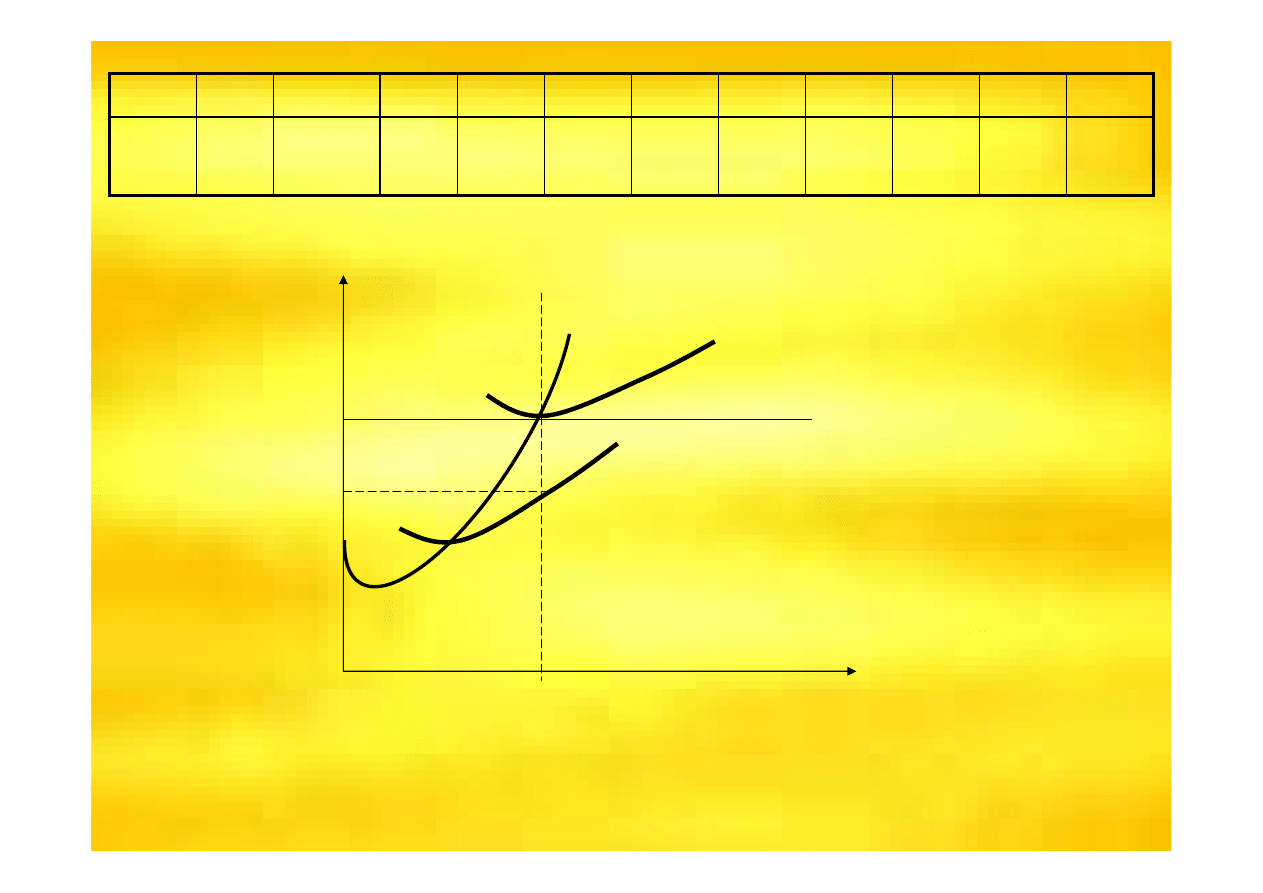
50

min

500

100

50

50

WE

MC

AFC

AVC

ATC

TVC

TFC

TC

TR

X

MR

P

X

d=AR=MR=P

50

100

MC

45

ATC

AVC

5000

50

5

5000

4500

45

0

Uzyskali

ś

my zysk

normalny w stanie
równowagi wi

ę

c produkcj

ę

pozostawiamy bez zmian.

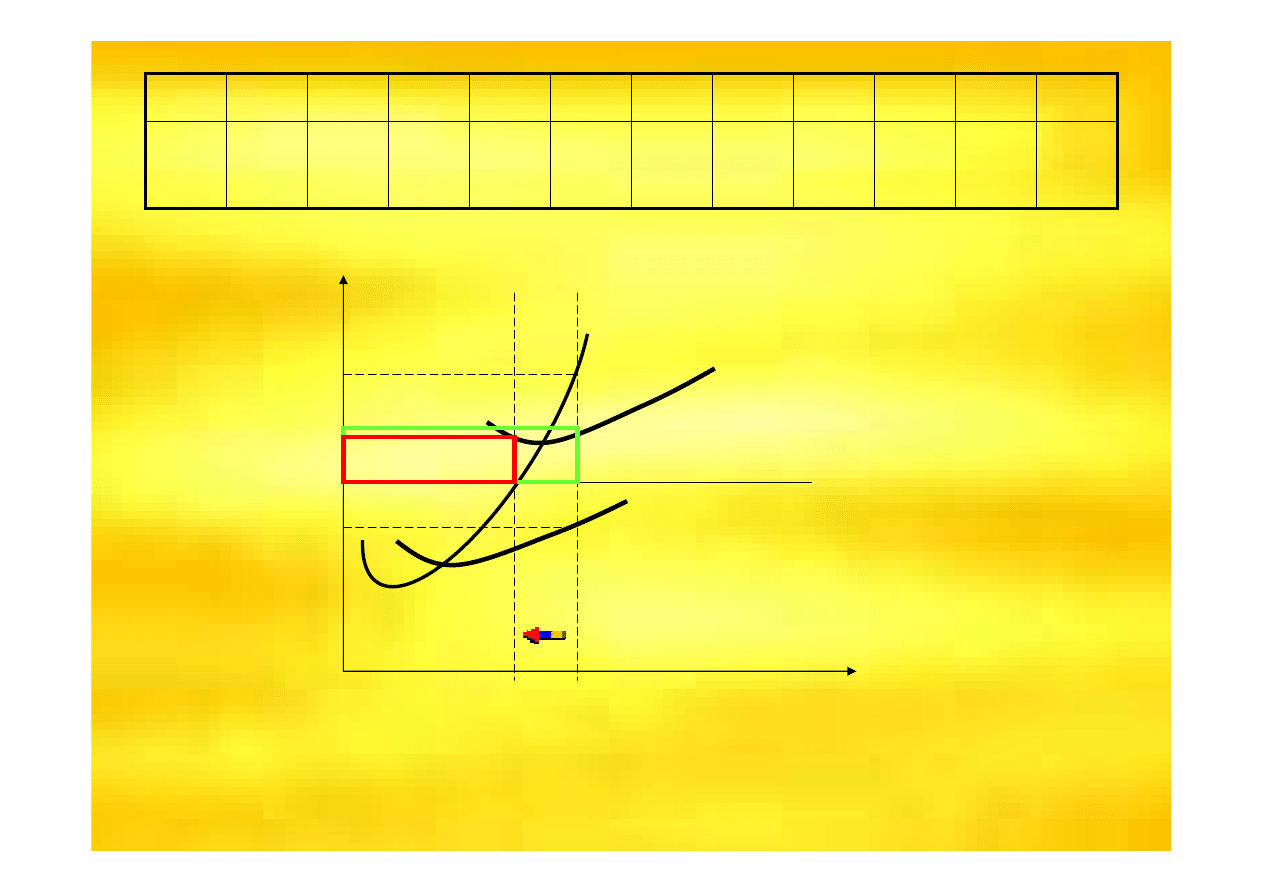
100

25

400

300

60

60

WE

MC

AFC

AVC

ATC

TVC

TFC

TC

TR

X

MR

P

5

-100

125

80

275

55

X

d=AR=MR=P

5

60

100

MC

ATC

80

55

AVC

Co zrobi

ć

z t

ą

strat

ą

?

DZI

Ę

KUJ

Ę

ZA UWAG

Ę