% AISDT : podstawy programowania w rodowisku MATLAB

% Rozpocz cie ( MATLAB, cd) i zako czenie pracy w MATLABie (exit);

% Okna: komend, historii, przestrzeni roboczej, katalogu bie cego

% Szukanie informacji o programie i jego funkcjach: help, lookfor, okno MATLAB Help

% Edytor : wbudowany do MATLABa (uruchamianie: komenda edit lub File->New-> M-File)

% Orientacja macierzowa rodowiska (przy czym UWAGA:

macierze indeksowane s od 1, nie od zera

!)

% Elementami macierzy mog by liczby lub struktury

A=[1,2,3;4,5,6] % macierz 2 wiersze x 3 kolumny ; elementy wiersza rozdzielone przecinkami lub spacjami , rednik

oznacza koniec wiersza

size(A) % rozmiar A; wynik : ans 2 3 ; ans - nazwa zmiennej zawieraj cej wynik ostatniej operacji .

clear(A) % usuwanie z pami ci zmiennej A; clear bez parametrów usuwa wszystkie zmienne (i funkcje).

s1= struct('pole1',[],'pole2',2,'pole3',rand(5)); % inicjalizacja struktury o 3 polach. Warto ka dego pola jest macierz ;

mo e by równie macierz pust - warto niezdefiniowana, albo macierz o wymiarach 1x1- skalar.

% Odwołania do elementu macierzy

a=A(2,3) % Przy odwołaniu do elementu macierzy u ywane s

nawiasy okr głe!

Rozró niane s małe i du e litery.

a1=A(1,:)

% do zmiennej a1 zapisany pierwszy wiersz macierzy A

a2=A(:,2)

% zmienna a2 - druga kolumna macierzy A

b=s1.pole2

% do zmiennej b przypisana zostaje warto 'pole2' struktury s1 (tu: b=2).

A=A(2,3) % Instrukcja podstawienia powoduje aktualizacj rozmiaru obiektu (tu: zmniejszenie A do wymiaru 1x1)

% Mo liwo dynamicznej zmiany rozmiarów macierzy bez konieczno ci wcze niejszej deklaracji (np. przez

podstawienie nieistniej cego elementu)

A(4,5)=10 % Takie podstawienie powoduje zwi kszenie rozmiarów A (i wyzerowanie niezdefiniowanych elementów)

S(5)=struct('key',5,'value',[0:4]) % S5 - tablica struktur. Je li ju istniała to musiała mie zdefiniowane pola 'key' i 'value',

je li nie istniała to zostaje utworzona 5-elementowa tablica struktur zawieraj cych takie pola, przy czym: dla i=1...4

s(i).key i s(i).value nie maj przypisanych warto ci, s(5).key=5 s(5).value= [0 1 2 3 4]

S=[S,s1] - powi kszenie tablicy struktur S o jedn pozycj zwieraj c struktur s1 (s1 dopisane na ko cu S)

% Nie mo na si odwoła do elementu spoza aktualnego zakresu indeksów macierzy

a=A(6,7) % pojawia si informacja o bł dzie: ??? Index exceeds matrix dimensions.

% Przydatne kreatory tablic

A=zeros(3);

% Macierz 3x3 z zerami; rednik na ko cu blokuje wy wietlanie wyniku operacji na ekranie

B=rand(3)

% Macierz 3x3 z liczbami pseudolosowymi z przedziału (0.0,1.0),wektor tworzy si przez: rand(n,1)

C=ones(10,1)

% Macierz 10x1 z jedynkami

N=linspace(0,1,11) % wektor wierszowy (1x11) liczb równo rozło onych w przedziale <0.0,1.0> tzn. : 0 0.1 0.2 .... 0.9 1

M=0:0.1:1

% wektor wierszowy (tu: M=N) utworzony z ci gu liczb od 0 do 1 z krokiem 0.1: 0 0.1 0.2 0.3 ... 0.9 1

% Działania matematyczne + - * / * .* ./ .* ‘ ^

A=[ 1, 2; 3, 4 ]; B=[1,2; 2,1];

A+B

B-A

A*B

B*A

A^2

% mno enie macierzowe A*A

A.*B, A.^2

% mno enie element po elemencie

B./A

% dzielenie element po elemencie

AT=A’ % transpozycja macierzy A

% Układy równa A*x=b (lewe dzielenie \)

b=sum(A,2)

% Wektor b tworzony jest z sum wierszy macierzy A

x=A\b

% Rozwi zanie układu A*x=B

format long; x % wy wietla x z dok. 15 cyfr, powrót do 5 cyfr: format short

% Proste wykresy (patrz help do funkcji: plot, semilogx, semilogy, loglog)

x=linspace(-2,2,21); y1=x; y2=x.^2; y3=x.^3; y4=x.^4;

plot(x,y1,’b-o’,x,y2,’r-x’); xlabel(‘x’); ylabel('warto ci funkcji'); title(‘Pierwsze wykresy’);

pause % zatrzymanie programu (potrzebne przy pracy z m-plikiem), dalsze dział. po wci ni ciu dowolnego klawisza

hold on

% wł czenie dodawania nowych wykresów do bie cego okna wykresów

plot(x,y3,’-v’,x,y4,’-s’); hold off % po hold off nowy wykres b dzie rysowany w uprzednio wyczyszczonym oknie

legend(‘y=x’,’y=x^2’,’y=x^3’,’y=x^4’)

% opis wykresów

grid on % dodanie siatki, grid off -usuni cie siatki

figure % dodanie nowego okna wykresów o kolejnym (pierwszym wolnym) numerze

% Skrypty i funkcje

Skrypty

, to pliki tekstowe o rozszerzeniu m b d M, zawieraj ce polecenia i instrukcje MATLABa. Skrypty nie pobieraj

adnych argumentów wej ciowych, ani nie zwracaj argumentów wyj ciowych; działaj na zmiennych głównej przestrzeni

roboczej (workspace). Skrypt uruchamia si podaj c jego nazw (bez rozszerzenia) w wierszu polece MATLABa b d w

innym skrypcie. Uruchamiany skrypt musi by w bie cym katalogu lub na cie ce poszukiwa interpretera (path).

Funkcja

- m-plik o postaci:

function [ lista_parametrów_wyj ciowych ]=nazwa_funkcji( lista_parametrów_wej ciowych )

% NAZWA_FUNKCJI - krótka instrukcja u ycia (dla polecenia help nazwa_funkcji)

Ciało funkcji

=

4

3

2

1

A

,

=

1

2

2

1

B

,

=

∗

10

11

4

5

B

A

,

=

∗

4

6

4

1

.

B

A

,

=

4

/

1

3

/

2

1

1

/

.

A

B

,

=

4

2

3

1

AT

=

4

3

2

1

A

=

7

3

b

=

0000

.

1

0000

.

1

x

Funkcje akceptuj parametry wej ciowe. W trakcie oblicze działaj na parametrach wej ciowych i zmiennych

utworzonych we własnej przestrzeni roboczej, niedost pnej z wiersza polece . Funkcja mo e wyznacza warto ci

parametrów wyj ciowych – zwracanych do nadrz dnej przestrzeni roboczej (w której kontek cie wywołano funkcj ).

Uwaga: zmienne w funkcji s z definicji lokalne. Dost p do tych zmiennych z przestrzeni roboczej zapewnia deklaracja

global (trzeba jej u y w 2 miejscach: zarówno w funkcji, jak i w wołaj cym funkcj skrypcie)

Przykład 1: skrypt mno cy dwie kwadratowe macierze

losowe o zadanym rozmiarze zwracaj cy ilo mno e i

dodawa

%%%%%% plik

mul_check.m

- to jest skrypt %%%%%

n=5;

[a, m] =

mul_fun

(n);

fprintf(1,'liczba_dodawa =%g, liczba mno e =%g',a,m);

% formatowany komunikat na ekranie

%%%%% plik

mul_fun.m

- to jest funkcja %%%%%%

function [t1, t2] =

mul_fun

(n)

A=rand(n); B=rand(n);

N_add=0; N_mul=0; % warto ci pocz tkowe

for k1=1:n

for k2=1:n

s=0.0;

for k3=1:n

s=s+A(k1,k3)*B(k3,k2);

N_add=N_add+1;N_mul=N_mul+1;

end

D(k1,k2)=s;

end

end

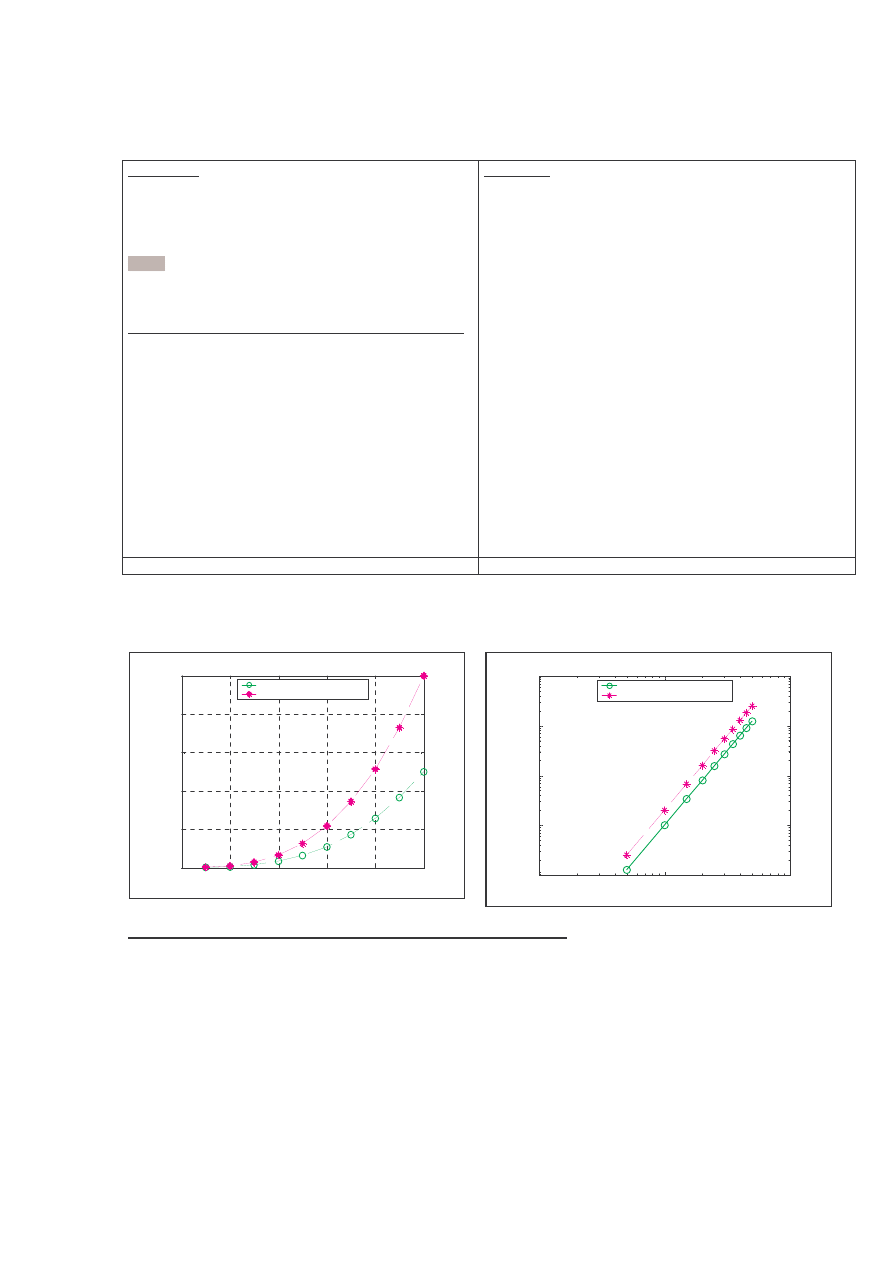
Przykład 2: badanie zło ono ci obliczeniowej mno enia

macierzy (same mno enia lub mno enia i dodawania

ł cznie)

%%%%%% plik

mul_test.m

- (skrypt) %%%%%

clear;

N=5:5:50; % lub: N=linspace(5,50,10);

% p tla dla ró nych wymiarów macierzy

for i=1:size(N,2)

[a(i), am(i) ]= mul_fun(N(i));

end;

% Wykresy

figure(1); hold off;

plot(N,a,'g-o',N,a+am,'m--*'); legend ('dodawania', 'ł cznie');

xlabel('rozmiar macierzy'); ylabel('liczba oper. domin.');

title('Zło ono obliczeniowa mno enia macierzy'); grid on

figure(2); hold off; % ten sam rys. w skali logarytmicznej

loglog(N,a,'g-o',N,a+am,'m--*'); legend ('dodawania',

'ł cznie');

xlabel('rozmiar macierzy'); ylabel('liczba oper. domin.');

title('Zło ono obliczeniowa mno enia macierzy')

%% WYNIKI poni ej

%% PROSZ wiadomie obejrze wykres funkcji pot gowej

w skali logarytmicznej !

Uwaga! Prosz zwróci uwag na sposób wywołania funkcji zwracaj cej wi cej ni 1 par. wyj ciowy. Aby uzyska

warto ci wszystkich parametrów zwracanych przez funkcj , KONIECZNIE przed znakiem '=' musi wyst pi nawias

kwadratowy z list zmiennych, do których podstawione zostan obliczone warto ci.

Uwaga do uwagi - oczywi cie zmienna oznacza macierz, nawet bardzo długi wektor jest jedn zmienn !

Kilka praktycznie u ytecznych uwag o programowaniu w MATLABie

1. Operatory MATLABa (help ops): porównania ( == , ~= , < , > , <= , >= ), logiczne ( |, &, ~ ), arytmetyczne

(standardowe oraz specyficzne dla MATLABA \, .* , .^, ./)

2. Ka da instrukcja warunkowe (if , switch) i tworz ca p tle (for, while,) musi by zako czona przez end

3.

rednik na ko cu linijki nie jest obowi zkowy, je li wyst puje, to wynik operacji nie jest wy wietlany na ekranie

4. Działaj cy program mo na przerwa przez ^C

5. W przypadku bł du programu nale y czyta komunikaty na ekranie!

6. Nale y u ywa funkcji, zwłaszcza wbudowanych, gdy tylko to jest mo liwe (istotnie przy piesza działanie programu!)

- w szczególno ci min, max, (mog zwraca równie indeks ekstremum), sum, linspace

7. Uruchamianiu programu sprzyja testowanie go etapami, w szczególno ci:

a) dobrze jest sprawdzi działanie funkcji jako skryptu (z wykomentowan 1-sz linijk ) - zapewnia to łatwy

dost p do wszystkich (w skrypcie globalnych) zmiennych

b) do testowania nale y u ywa danych o małych rozmiarach, dla których znane jest prawidłowe rozwi zanie

8. Je eli w zadaniu wymagany jest wykres, to najpierw nale y (najcz ciej w p tli w której zmienia si rozmiar zadania)

wygenerowa potrzebne dane, a potem zaj si grafik . Je li wyniki s zapisane nie po kolei - np. znajduj si w

wektorze res na pozycjach 2,4,6 9 (czyli res=[0 d1 0 d2 0 d3 0 0 d4] ), to te łatwo je wykre li :

a) albo wprost wypisuj c indeksy: plot( [2,4,6,9] , res( [2,4,6,9] ) )

b) albo definiuj c wektor pomocniczy: nx=[2,4,6,9]; plot(nx , res(nx) )

10

0

10

1

10

2

10

2

10

3

10

4

10

5

10

6

rozmiar macierzy

lic

zb

a

o

p

e

ra

cj

i d

o

m

in

uj

cy

ch

zło ono

obliczeniowa mno enia macierzy

dodawania
dodawania i mno enia ł cznie

0

10

20

30

40

50

0

0.5

1

1.5

2

2.5

x 10

5

rozmiar macierzy

lic

zb

a

o

p

e

ra

cj

i d

o

m

in

uj

cy

ch

Zło ono obliczeniowa mno enia macierzy

dodawania
dodawania i mno enia ł cznie