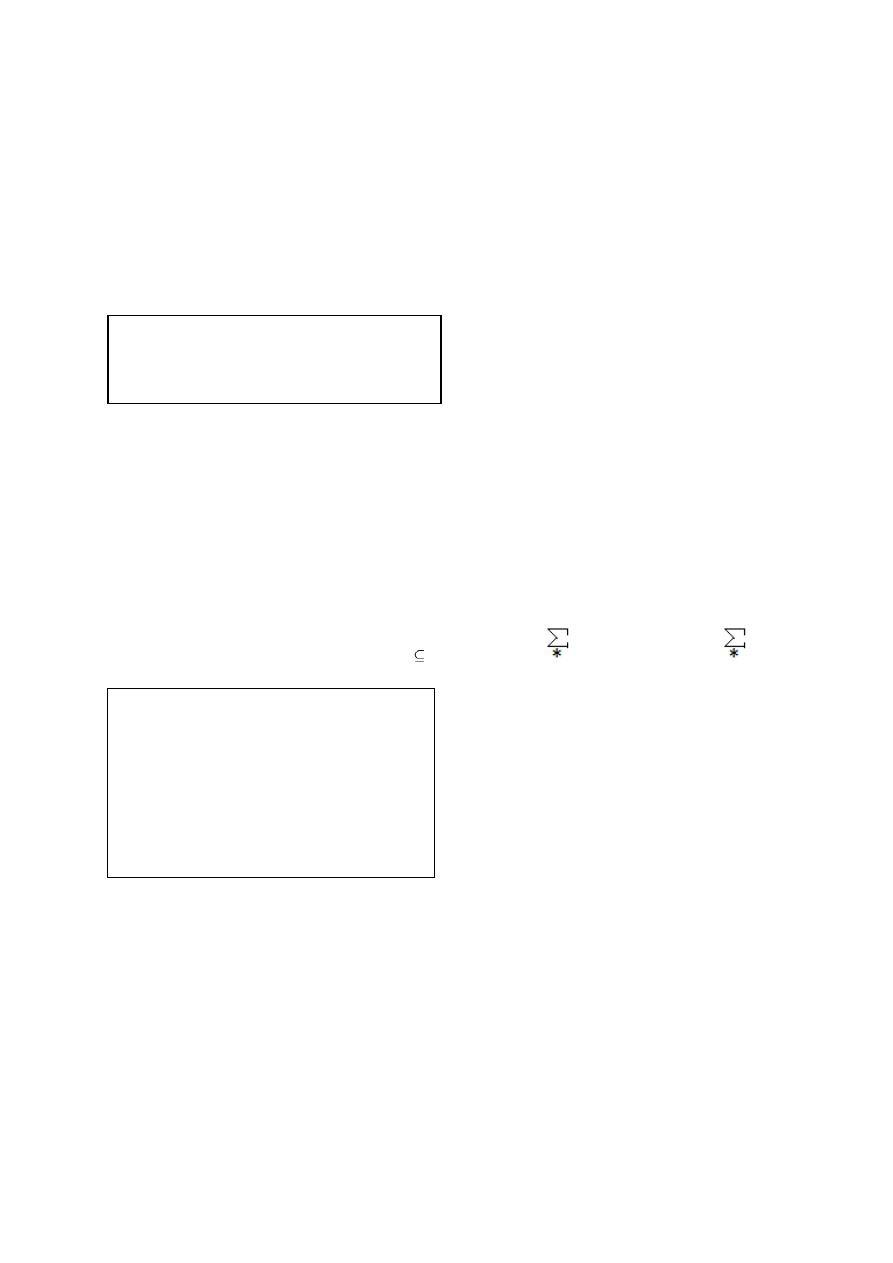
PAA Termin pierwszy

26 stycznia 2011

Cz1

1. Spójny graf planarny G zapisano w postaci macierzy sąsiedztwa wierzchołków. Naszkicuj algorytm 1-

absolutnie aproksymacyjny dla znajdowania maksymalnej kliki w G i oszacuj jego złożonośd
obliczeniową.

2. Dany jest graf G. Naszkicuj program lgs(G), który zwraca liczbę gwiazd spinających zawartych w G.

Oszacuj precyzyjnie jego złożonośd, w przypadku gdy G zapisany jest w postaci:
a) macierzy sąsiedztwa wierzchołków
b) listy sąsiadów
c) pęków wyjściowych

3. Podaj za pomocą wzoru liczbę kroków i za pomocą ϴ(*) złożonośd obliczeniową następującego

funkcji określonej dla liczb naturalnych n:

4. Na płaszczyznę rzucono n prostych. Niech R9n) oznacza największą możliwą liczbę regionów

(ograniczonych lub nie) powstałych w ten sposób, np. R(0) = 1, R(1) = 2. Wiadomo, że R(n) = xR(n-
1)+yn. Ustal wartośd x i y. Oszacuj tempo wzrostu R(n). Podaj wartośd R(4).

Cz2

1. Ty masz 100-wierzchołkowy graf hamiltonowski G zapisany w postaci macierzy sąsiedztwa

wierzchołków A(G) i bardzo Ci zależy na tym, aby stwierdzid, czy graf zawiera klikę K

10

lub większą,

gdyż możesz za to uzyskad 25 punktów. Ja mam program, który rozwiązuje problem jak na wejściu
poda się macierz sąsiedztwa wierzchołków grafu niehamiltonowskiego. Jak przerobisz macierz A(G),
byś mógł skorzystad z mojego programu? Napisz algorytm i oszacuj jego złożonośd obliczeniową.

2. Następujący algorytm rozwiązuje optymalizacyjną wersję problemu suma podzbioru w sposób 2-

aproksymacyjny, tzn. znajduje podzbiór A’ A takie, że k/2 ≤

a

i

przy ograniczeniu

a

i

≤ k

(* do sumy -> i:a

i

є A’)

a) oszacuj złożonośd
b) podaj przykład danych I(tu jest i), dla których F

0

(I) ~= 2F

ss*

(I)

c) niech SS będzie algorytmem SS*, z którego usunięto instrukcję (*). Pokaż, że nie istnieje stała
Ɛ<∞ taka, że SS jest algorytmem Ɛ-aproksymacyjnym

3. Zaprojektuj algorytm wielomianowy dla wyznaczania indeksy chromatycznego danego grafy G,

zapisanego w postaci macierzy sąsiedztwa wierzchołków, który jest 4/3-aproksymacyjny.
Udowodnij, że dla tego problemu nie istnieje schemat FPTAS, chyba, że P=NP.

4. Udowodnij, że problem pakowania pudełek (dany jest zbiór przedmiotów o znanych wielkościach

a

1

… a

n

oraz rozmiar pudełek l(tu jest el); należy zminimalizowad liczbę pudełek koniecznych do

zapakowania wszystkich przedmiotów) jest NP-trudny.

int fun(n) {

if(n==1) return 1;

else return fun(fun(n-1))+1; }

SS*(A,n,k) {

(*) uporządkuj zbiór A nierosnąco;

b=0;

for(i=1 to n)

if(b+A[i]≤k) b+= A[i];

write(b); {tj. F

ss*

(1)}

}