1

Zadania – część IV. Skrypty i funkcje

1.

Korzystając ze strategii m-plików wykonać poniższy skrypt. Zinterpretować uzyskane rysunki.

% Rysowanie walca
t(1:20)=5;
[X,Y,Z] = cylinder(t);
subplot(2,2,1); mesh(X)
subplot(2,2,2); mesh(Y)
subplot(2,2,3); mesh(Z)
subplot(2,2,4); mesh(X,Y,Z)

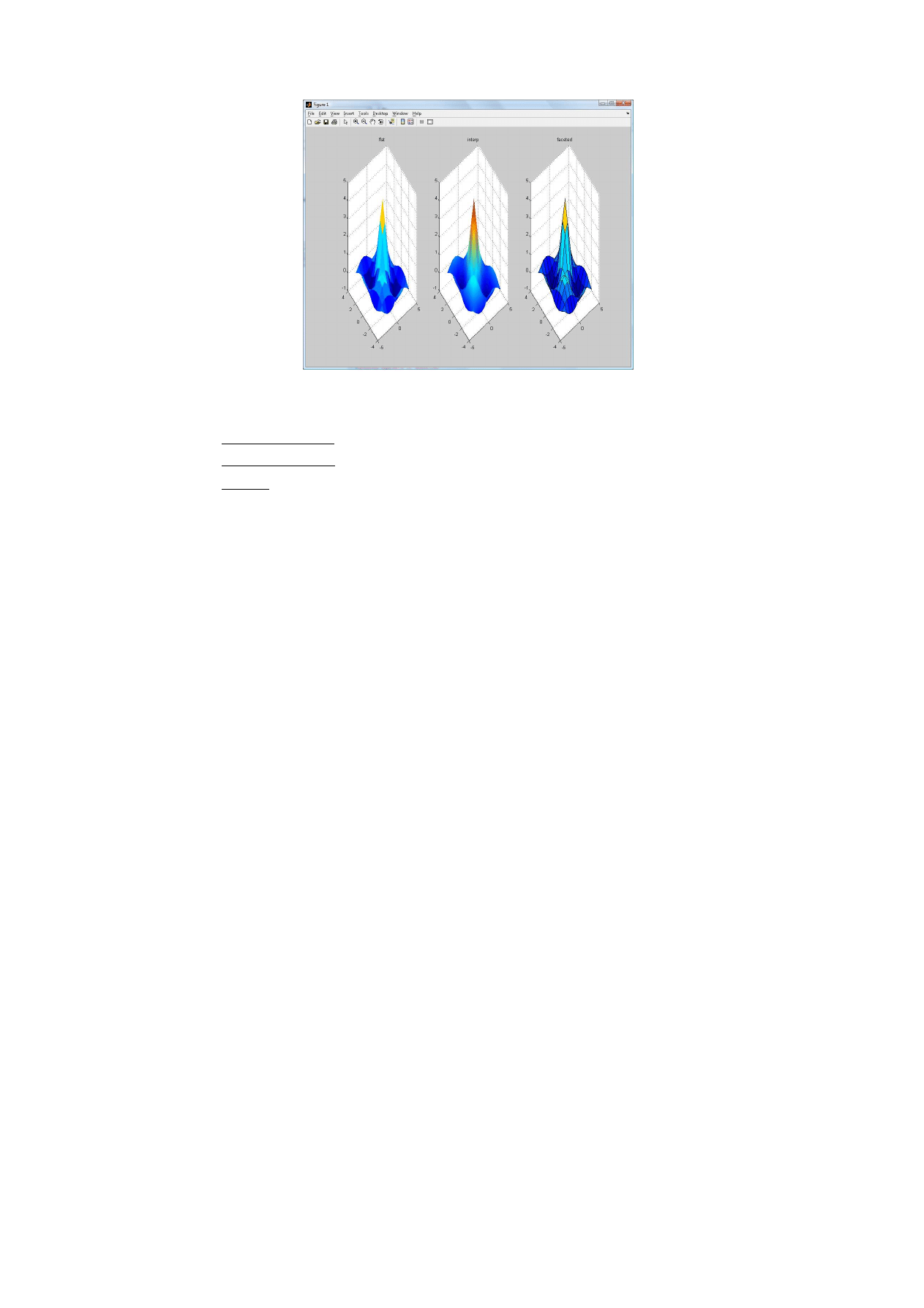
2. Wykreślone powierzchnie można poddać cieniowaniu używając funkcji:

shading flat

shading interp

shading faceted

Poniższy skrypt rysuje powierzchnię i używa cieniowania

flat

. Dokończyć ten skrypt wykorzystując do

cieniowania tej samej powierzchni parametry

interp

i

faceted

. Te nowe rysunki wyświetlić w kolejnych

układach współrzędnych (

subplot(1,3,2)

oraz

subplot(1,3,3)

).

% Skrypt rysuje powierzchnie poddane cieniowaniu
clf;
[x,y]=meshgrid(-3.5:0.7:3.5);
z=sin(x).*sin(y)+4*exp(-(x-0.5).^2-(y-0.5).^2);

%Wykres w trybie flat
subplot(1,3,1)
surf(x,y,z)
shading flat
title(‘flat’)

…………..

2

3. Napisać funkcję minmax, która działa według poniższej specyfikacji:

- parametry wejściowe: wektor a o długości 100, zawierający liczby losowe z przedziału (0,1)

- parametry wyjściowe: wartość minimalna i maksymalna spośród elementów a, suma elementów a

- działanie: obliczenie wartości minimalnej, maksymalnej oraz sumy elementów wektora a.

Następnie przetestować działanie napisanej funkcji dla kilku różnych wektorów wejściowych. W

każdym przypadku sprawdzić wartości obliczonych parametrów.

4. Napisać skrypt, który po wprowadzeniu współrzędnych dwóch punktów (x1,y1) oraz (x2,y2) obliczy

współczynnik kierunkowy oraz wyraz wolny prostej y=ax+b, a następnie wypisze tę informację w

postaci:

Prosta y=ax+b

Podczas pisania skryptu wykorzystać funkcje wbudowane input oraz disp.