
MATHEMATICAL FORMULA
Quadratic Formula
• The roots of the quadratic equation
are
0
2
=
+
+
c
bx
ax
a
ac
b
b
x
x
2
4
,
2
2
1
−
±
−
=
Trigonometric Identities
1.
( )
x
x
sin
sin
−
=
−
2.
( )
x
x
cos
cos
=
−
3.
x
x
x
cos
sin
tan
=
4.
x
x
tan
1
cot
=
5.
x
x
sin
1
csc
=
6.
x
x
cos
1
sec
=
7.
(
)
x
x
o
cos
90
sin
±
=
±
8.
(
)
x
x
o
sin
90
cos
m
=
±
9.
(
)
x
x
o
sin
180
sin
−
=
±
10.
(
)
x
x
o
cos
180
cos
−
=
±
11.
1
sin
cos
2
2
=
+
x
x
12.
x
x
2
2
sec
tan
1
=
+
13.
x
x
2
2
csc
1
cot
=
+
14.
(
)
y
x
y
x
y
x
sin
cos
cos
sin
sin
±
=
±
15.
(
)
y
x
y
x
y
x
sin
sin
cos
cos
cos
m
=
±
16.
(
)
y
x
y
x
y
x
tan
tan
1
tan
tan
tan
m
±
=
±
17.
x
x
x
cos
sin
2
2
sin
=
18.
1
cos
2
sin
2
1
sin
cos
2
cos
2
2
2
2
−
=
−
=
−
=
x
x
x
x
x
19.
x
x
x
2
tan
1
tan
2
2
tan
−
=
20.
(
)
x
x
2
cos
1
2
1
sin
2
−
=
21.
(
)
x
x
2
cos
1
2
1
cos
2
+
=
22.
(
)
(
[
]
y
x
y
x
y
x
+
−
−
=
cos
cos
2
1
sin
sin
)
23.
(
)
(
[
]
y
x
y
x
y
x
+
+
−
=
cos
cos
2
1
cos
cos
)
24.
(
)
(
[
]
y
x
y
x
y
x
+
+
−
=
sin
sin
2
1
cos
sin
)
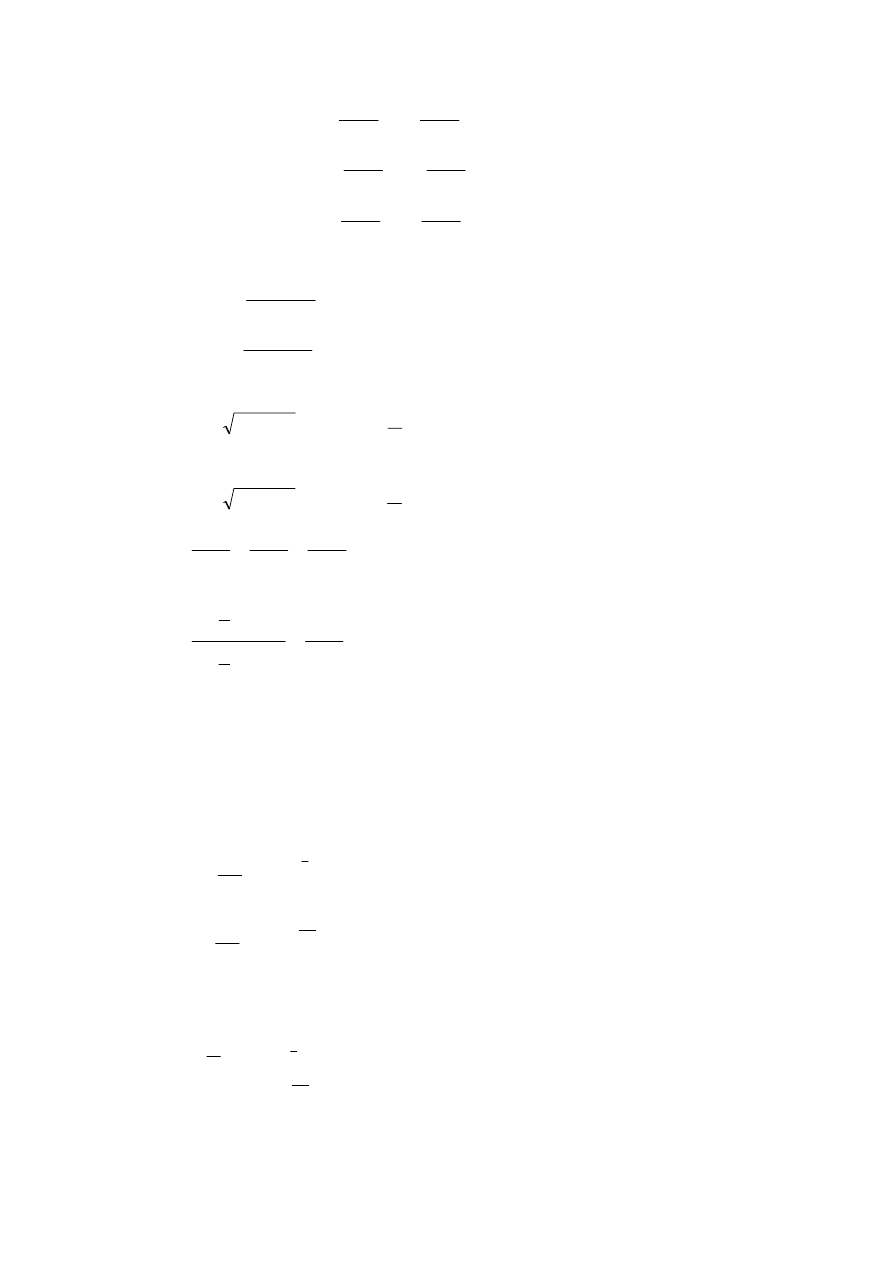
25.
⎟
⎠
⎞
⎜
⎝
⎛ ±
⎟
⎠
⎞
⎜
⎝
⎛
=
±
2
sin
2
cos
2
sin
sin
y
x
y
x
y
x
m
26.
⎟
⎠
⎞
⎜
⎝
⎛ −
⎟
⎠
⎞
⎜
⎝
⎛ +
=
+
2
cos
2
cos
2
cos
cos
y
x
y
x
y
x
27.
⎟
⎠
⎞
⎜
⎝
⎛ −
⎟
⎠
⎞
⎜
⎝
⎛ +
=
−
2
sin
2
sin
2
cos
cos
y
x
y
x
y
x
28.
; Euler’s Theorem
x
j
x
e
jx
sin
cos
±
=
±
29.
2
cos
jx
jx
e
e
x
−
+
=
30.
j
e
e
x
jx
jx
2
sin
−
−
=
31.
(
)
A
B
B
A
R
x
R
x
B
x
A
1
2
2
tan
,
cos
sin
cos
−
=
+
=
=
±
θ
θ
m
32.
(
)
B
A
B
A
R
x
R
x
B
x
A
1
2
2
tan
,
sin
sin
cos
−
=
+
=
±
=
±
θ
θ
33.
C
b
B
b
A
a
sin
sin
sin
=
=
(law of sinus)
34.
(law of cosinus)
A
bc
c
b
a
cos
2
2
2
2
−
+
=
35.
(
)
(
)
b
a
b
a
B
A
B
A
+
−
=
+
−
2
1
tan
2
1
tan
(law of tangents)
Values of cosine, sine and exponential functions
1.
( )
n
n
1
cos
−
=
π
2.
0
sin
=
π
n
3.
1
2
cos
=
π
n
4.
0
2
sin
=
π
n
5.
( )
⎪⎩
⎪
⎨
⎧
=
=
−
=
odd
n
even
n
n
n
;
0
;
1
2
cos
2
π
6.
( )
⎪⎩
⎪
⎨
⎧
=
=
−
=
−
even
n
odd
n
n
n
;
0
;
1
2
sin
2
1
π
7.
( )
n
jn
e
1
−
=
π
8.
1
2
=
π
n
j
e
9.
( )
( )
⎪⎩
⎪
⎨
⎧
=
−
=
−
=
−
odd
n
j
even
n
e
n
n
n
j
;
1
;
1
2
1
2
2
π
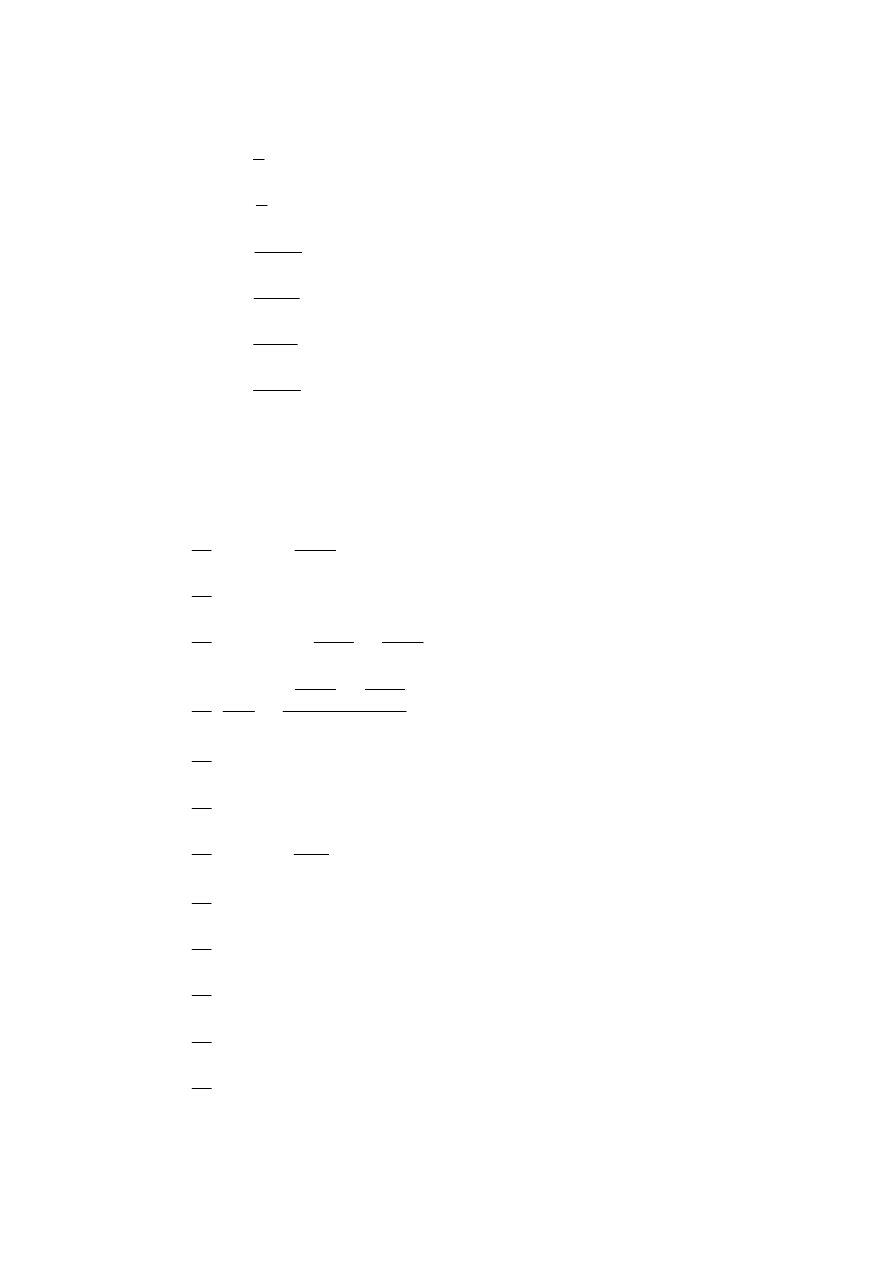
Hyperbolic Functions
1.
(
)
x
x
e
e
x
−
−
=
2
1
sinh
2.
(
)
x
x
e
e
x
−
+
=
2
1
cosh
3.
x
x
x
cosh
sinh
tanh
=
4.
x
x
tanh
1
coth
=
5.
x
hx
sinh
1
csc
=
6.
x
hx
cosh
1
sec
=
7.
(
)
y
x
y
x
y
x
sinh
cosh
cosh
sinh
sinh
±
=
±
8.
(
)
y
x
y
x
y
x
sinh
sinh
cosh
cosh
cosh
±
=
±
Differentiation
1.
( )
(
)
( )
dx
x
du
a
x
au
dx
d
=
2.
( )
(
)
( ) ( )
(
)
1
−
′
=
n
n
x
f
x
f
n
x
f
dx
d
3.
( ) ( )
(
)
( )
( )
dx
x
du
v
dx
x
dv
u
x
v
x
u
dx
d
+
=
4.
( )
( )
( )
( )
2
v
dx
x
dv
u
dx
x
du
v
x
v
x
u
dx
d
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
5.
( )
( )
( )
( )
a
x
f
a
a
dx
d
x
f
x
f
ln
′
=
6.
( )
( )
( )
( )
x
f
e
e
dx
d
x
f
x
f
′
=
7.
( )
(
)
( ) ( )
x
f
x
f
x
f
dx
d
′
=
1
ln
8.
( )
(
)
( )
( )
x
f
x
f
x
f
dx
d
cos
sin
′
=
9.
( )
(
)
( )
x
f
x
f
x
f
dx
d
sin
cos
′
−
=
( )
10.
( )
(
)
( )
( )
x
f
x
f
x
f
dx
d
2
sec
tan
′
=
11.
( )
(
)
( )
( )
( )
x
f
x
f
x
f
x
f
dx
d
cot
csc
csc
′
−
=
12.
( )
(
)
( )
( )
( )
x
f
x
f
x
f
x
f
dx
d
tan
sec
sec
′
=

13.
( )
(
)
( )
x
f
x
f
x
f
dx
d
2
csc
cot
′
−
=
( )
14.
( )
(
)
( )
( )
[
]
2
1
1
sin
x
f
x
f
x
f
dx
d
−
′
=
−
15.
( )
(
)
( )
( )
[
]
2
1
1
cos
x
f
x
f
x
f
dx
d
−
′
−
=
−
16.
( )
(
)
( )
( )
[
]
2
1
1
tan
x
f
x
f
x
f
dx
d
+
′
=
−
17.
( )
(
)
( )
( ) ( )
[
]
1
csc
2
1
−
′
−
=
−
x
f
x
f
x
f
x
f
dx
d
18.
( )
(
)
( )
( ) ( )
[
]
1
sec
2
1
−
′
=
−
x
f
x
f
x
f
x
f
dx
d
19.
( )
(
)
( )
( )
[
]
2
1
1
cot
x
f
x
f
x
f
dx
d
+
′
−
=
−
Indefinite Integration
1.
c
ax
dx
a
+
=
∫
2.
( )
( ) ( )
( )
du
u
v
x
v
x
u
dv
x
u
∫
∫
−
=
; Integration by parts
3.
1
,
1
1
−
≠
+
+
=
∫
+
n
c
n
x
dx
x
n
n
4.
∫
+
=
−
c
x
dx
x
ln
1
5.
c
a
a
dx
a
x
x
+
=
∫
ln
6.
c
e
dx
e
x
x
+
=
∫
7.
∫
+
−
=
c
x
x
x
dx
x
ln
ln
8.
c
x
dx
x
+
−
=
∫
cos
sin
9.
∫
+
=
c
x
dx
x
sin
cos
10.
(
)
∫
+
−
=
c
x
dx
x
cos
ln
tan
11.
(
)
∫
+
−
=
c
x
x
dx
x
cot
csc
ln
csc
12.
(
)
∫
+
+
=
c
x
x
dx
x
tan
sec
ln
sec
13.
(
)
∫
+
=
c
x
dx
x
sin
ln
cot
14.
c
x
x
x
dx
x
+
−
+
=
−
−
∫
2
1
1
1
sin
sin
15.
c
x
x
x
dx
x
+
−
−
=
−
−
∫
2
1
1
1
cos
cos
16.
(
)
c
x
x
x
dx
x
+
+
−
=
−
−
∫
2
1
1
1
ln
2
1
tan
tan

17.
c
x
x
x
x
x
dx
x
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
=
−
−
∫
2
1
1
1
1
ln
csc
csc
18.
c
x
x
x
x
x
dx
x
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
−
=
−
−
∫
2
1
1
1
1
ln
sec
sec
19.
(
)
c
x
x
x
dx
x
+
+
+
=
−
−
∫
2
1
1
1
ln
2
1
tan
cot
20.
b
a
c
b
a
x
b
a
b
a
x
b
a
dx
bx
ax
≠
+
+
+
−
−
−
=
∫
,
)
(
2
)
sin(
)
(
2
)
sin(
sin
sin
21.
b
a
c
b
a
x
b
a
b
a
x
b
a
dx
bx
ax
≠
+
+
+
+
−
−
=
∫
,
)
(
2
)
sin(
)
(
2
)
sin(
cos
cos
22.
b
a
c
b
a
x
b
a
b
a
x
b
a
dx
bx
ax
≠
+
+
+
−
−
−
−
=
∫
,
)
(
2
)
cos(
)
(
2
)
cos(
cos
sin
23.
c
a
ax
x
dx
ax
+
−
=
∫
4
2
sin
2
sin
2
24.
c
a
ax
x
dx
ax
+
+
=
∫
4
2
sin
2
cos
2
25.
∫
∫
−
+
−
=
dx
x
x
m
x
x
dx
x
x
m
m
m
cos
cos
sin
1
26.
∫
∫
−
−
=
dx
x
x
m
x
x
dx
x
x
m
m
m
sin
sin
cos
1
27.
∫
∫
−
−
=
dx
e
x
a
m
a
e
x
dx
e
x
ax
m
ax
m
ax
m
1
28.
c
b
a
bx
be
bx
ae
dx
bx
e
ax
ax
ax
+
+
−
=
∫
2
2
cos
sin
sin
29.
c
b
a
bx
be
bx
ae
dx
bx
e
ax
ax
ax
+
+
+
=
∫
2
2
sin
cos
cos
Definite Integration
1.
∫
=
π
2
0
0
sin
dx
ax
2.
∫
=
π
2
0
0
cos
dx
ax
3.
∫
=
π
π
0
2
2
sin
dx
ax
4.
∫
=
π
π
0
2
2
cos
dx
ax
5.
∫
⎪⎩
⎪
⎨
⎧
=
≠
=
π
π
0
;
2
1
;
0
sin
sin
n
m
n
m
dx
nx
mx
6.
∫
⎪⎩
⎪
⎨
⎧
=
≠
=
π
π
0
;
2
1
;
0
cos
cos
n
m
n
m
dx
nx
mx

7.
∫
⎪⎩
⎪
⎨
⎧
=
+
−
=
+
=
π
0
2
2
;
2
;
0
cos
sin
odd
n
m
n
m
m
even
n
m
dx
nx
mx
8.
∫
∞
⎪
⎪
⎩
⎪
⎪
⎨
⎧
<
−
=
>
=
0
0
;
2
0
;
0
0
;
2
sin
a
a
a
dx
x
ax
π
π
9.
0
;
2
0
2
2
>
=
+
∫
∞
a
dx
x
a
a
π
10.
0
;
sin
0
2
2
>
+
=
∫
∞
−
a
b
a
b
dx
bx
e
ax
11.
0
;
cos
0
2
2
>
+
=
∫
∞
−
a
b
a
a
dx
bx
e
ax
L’Hopital Rule
If
, then
( ) ( )
0
0
0
=
= h
f
( )
( )
( )
( )
x
h
x
f
x
x
h
x
f
x
′
′
→
=
→
0
lim
0
lim
Limit
1.
590452354
7182818284
.
2
1
1
lim
=
⎟
⎠
⎞
⎜
⎝
⎛ +
∞
→
=
x
x
x
e
2.
1
)
sin(
0
lim
=
→
x
x
x
Complex Number
jy
x
z
+
=
Rectangular form
θ
/
r
z
=
Polar form
θ
j
re
z
=
Exponential form
x
y
y
x
r
r
y
r
x
1
2
2
tan
,
sin
,
cos
−
=
+
=
=
=
θ
θ
θ

Power Series
Taylor Series
(
)
( )
( )
( )
( )
( )
n
n
x
n
a
f
x
a
f
x
a
f
x
a
f
a
f
a
x
f
!
......
!
3
!
2
3
2
+
′′′
+
′′
+
′
+
=
+
Maclaurin’s Series
( )
( )
( )
( )
( )
( )
n
n
x
n
f
x
f
x
f
x
f
f
x
f
!
0
......
!
3
0
!
2
0
0
0
3
2
+
′′′
+
′′
+
′
+
=
Binomial Series
(
)
(
)
(
)(
)
.....
!
3
2
1
!
2
1
1
1
3
2
+
−
−
+
−
+
+
=
+
x
n
n
n
x
n
n
nx
x
n
Standard Series
1.
9
7
5
3
!
9
1
!
7
1
!
5
1
!
3
1
sin
x
x
x
x
x
x
+
−
+
−
=
2.
8
6
4
2
!
8
1
!
6
1
!
4
1
!
2
1
1
cos
x
x
x
x
x
+
−
+
−
=
3.
9
7
5
3
!
9
7936
!
7
272
!
5
16
!
3
2
tan
x
x
x
x
x
x
+
+
+
+
=
4.
9
7
5
3
93555
2
4725
1
945
2
45
1
3
1
1
cot
x
x
x
x
x
x
x
−
−
−
−
−
=
5.
9
7
5
3
3421440
73
604800
127
15120
31
360
7
6
1
1
csc
x
x
x
x
x
x
x
+
+
+
+
+
=
6.
8
6
4
2
8064
277
720
61
24
5
2
1
1
sec
x
x
x
x
x
+
+
+
+
=
7.
(
)
9
8
7
6
5
4
3
2
9
1
8
1
7
1
6
1
5
1
4
1
3
1
2
1
1
ln
x
x
x
x
x
x
x
x
x
x
+
−
+
−
+
−
+
−
=
+
8.
9
8
7
6
5
4
3
2
!
9
1
!
8
1
!
7
1
!
6
1
!
5
1
!
4
1
!
3
1
!
2
1
1
x
x
x
x
x
x
x
x
x
e
x
+
+
+
+
+
+
+
+
+
=
Wyszukiwarka
Podobne podstrony:
adresowanie kopert i formularze
Formułowanie strategii marketingowej
(ebook PDF)Shannon A Mathematical Theory Of Communication RXK2WIS2ZEJTDZ75G7VI3OC6ZO2P57GO3E27QNQ
Formularz zmian w funduszach LeoLife
Mathematics HL P1 May 1995
Mathematics HL May 2004 TZ1 P1
Metastock Formule X Trading System fixed
Mathematics HL May 2003 P1
MGLab Formularz VIII 4
Brittish Mathematical Olympiad(2003)
Mathematics HL November 2008P3 Sets
MGLab Formularz III 2
Mathematics HL Nov 2002 P1 $
MGLab Formularz VIII 3
Formularze i raporty
formularz PPK Magnusson 2010, ELSA
więcej podobnych podstron