Iloczyn kartezjański i relacje binarne

Wstęp

2

1. Para uporządkowana i iloczyn kartezjański zbiorów

3

2. Relacje binarne

7

3. Rodzaje relacji binarnych

14

Bibliografia

18

2

Wstęp

Moduł czwarty przedstawi podstawowe pojęcia teorii mnogości potrzebne między
innymi do opisu i modelowania systemów informatycznych.

Temat pierwszy dotyczy pojęcia pary uporządkowanej oraz definicji iloczynu kar-
tezjańskiego zbiorów. Zostaną omówione i — w większości — udowodnione pod-
stawowe własności iloczynu kartezjańskiego.

Temat drugi zaprezentuje pojęcie relacji binarnej, reprezentacji graficznej relacji
i działań na relacjach wraz z ich podstawowymi własnościami.

W temacie trzecim zawarte są definicje własności relacji binarnych, przykłady oraz
zależności między nimi.

3

1. Para uporządkowana

i iloczyn kartezjański zbiorów

Para uporządkowana

i

iloczyn kartezjański

zbiorów

są podstawowymi pojęciami nauki

o zbiorach, na których opiera się pojęcie relacji.

Para uporządkowana (a, b) to dowolny, złożony z dwóch elementów obiekt, speł-
niający poniższe założenia:



jeśli a ≠ b , to (a, b) ≠ (b, a).



jeśli (a, b) = (c, d), to a = c oraz b = d.

Jeżeli (a, b) jest parą uporządkowaną, to element a nazywamy

poprzednikiem pary

,

zaś element b

następnikiem pary

.

Jedną z popularniejszych definicji pary uporządkowanej podał w 1920 roku polski
matematyk Kazimierz Kuratowski: (a, b) =

df.

{{a}, {a, b}}. Łatwo można udowod-

nić, że tak zdefiniowana —

za pomocą pojęcia zbioru — para uporządkowana speł-

nia podane wyżej wymagania.

Pojęcie pary uporządkowanej służy do zdefiniowania pojęcia iloczynu kartezjań-
skiego zbiorów. Niech A oraz B będą dowolnymi zbiorami. Iloczynem kartezjań-
skim zbiorów A i B nazywamy zbiór wszystkich takich par uporządkowanych
(a, b), że a ∈ A oraz b ∈ B. Iloczyn kartezjański zbiorów A oraz B oznaczamy sym-
bolem A × B.

Rozważmy zbiory A = {1, 2, 3} oraz B = {a, b}. Iloczynem kartezjańskim tych
zbiorów jest, zgodnie z definicją, zbiór wszystkich par uporządkowanych (a, b) ta-
kich, że a ∈ A oraz b ∈ B. Mamy zatem A × B = {(1, a), (2, a), (3, a), (1, b),
(2, b), (3, b)}.

Jeżeli zbiór A ma n elementów, a zbiór B ma k elementów, to iloczyn kartezjański
A × B ma n ⋅ k elementów.

Przykład 1

Znanym przykładem iloczynu kartezjańskiego jest płaszczyzna, rozumiana jako
zbiór punktów o współrzędnych rzeczywistych.

Twierdzenie 1

Zachodzą następujące własności dla iloczynu kartezjańskiego:

(a)

(A × B ≠ B × A) ⇔ (A ≠ B ∧ A ≠ ∅ ∧ B ≠ ∅),

(b)

(A × B = B × A) ⇔ (A = B ∨ A = ∅ ∨ B = ∅),

(c)

A × (B ∪ C) = (A × B) ∪ (A × C) (iloczyn kartezjański jest rozdzielny względem
sumy zbiorów),

(d)

A × (B ∩ C) = (A × B) ∩ (A × C) (iloczyn kartezjański jest rozdzielny względem
iloczynu zbiorów),

(e)

A × (B – C) = (A × B) – (A × C) (iloczyn kartezjański jest rozdzielny względem
różnicy zbiorów),

4

(f)

A × B ≠ ∅ ⇔ (A ≠ ∅ ∧ B ≠ ∅)

(g)

A × B = ∅ ⇔ (A = ∅ ∨ B = ∅),

(h)

A × ∅ = ∅,

(i)

∅ × A = ∅,

(j)

∅ × ∅ = ∅.

Dowód (c)

Aby udowodnić powyższą równość, musimy — zgodnie z definicją równości zbio-
rów — wykazać prawdziwość następującego warunku:

∀

x

(x ∈ A × (B ∪ C) ⇔ x ∈ (A × B) ∪ (A × C))

Niech x będzie dowolne. Rozpatrzmy dwa przypadki: albo x nie jest parą uporządko-
waną, albo x jest parą uporządkowaną. W pierwszym przypadku równoważność jest
oczywista (obie strony fałszywe, obiekt niebędący parą uporządkowaną nie może
należeć do iloczynu kartezjańskiego).

Jeśli zaś x = (a, b), to:

L : x ∈ A × (B ∪ C) ⇔

1

(a, b) ∈ A × (B ∪ C) ⇔

2

a ∈ A ∧ b ∈ (B ∪ C) ⇔

3

⇔ a ∈ A ∧ (b ∈ B ∨ b ∈

C) ⇔

4

(a ∈ A ∧ b ∈ B) ∨ (a ∈ A ∧ b ∈

C) ⇔

⇔ (a, b) ∈ (A × B) ∨ (a, b) ∈ (A × C) ⇔

⇔ x ∈ (A × B) ∨ x ∈ (A × C) ⇔ x ∈ (A × B) ∪ (A × C) : P

Dowód (e)

Mamy wykazać, że ∀

x

(x ∈ A × (B – C) ⇔ x ∈ (A × B) – (A × C)).

Niech x będzie dowolne. Rozpatrzmy dwa przypadki: albo x nie jest parą uporząd-
kowaną, albo x jest parą uporządkowaną.

W pierwszym przypadku równoważność jest oczywista.

W drugim przypadku, jeśli x = (a, b), to:

L : x ∈ A × (B – C) ⇔

5

(a, b) ∈ A × (B – C) ⇔

6

a ∈ A ∧ b ∈ (B – C) ⇔

7

⇔ a ∈ A ∧ (b ∈ B ∧ b ∉ C) (*)

P : x ∈ (A × B) – (A × C) ⇔ x ∈ (A × B) ∧ x ∉ (A × C) ⇔

⇔ (a, b) ∈ (A × B) ∧ (a, b) ∉ (A × C) ⇔ (a, b) ∈ (A × B) ∧ ¬[ (a, b) ∈ (A × C) ] ⇔

⇔ (a ∈ A ∧ b ∈ B) ∧ ¬(a ∈ A ∧ b ∈ C) ⇔ (a ∈ A ∧ b ∈ B) ∧ (¬(a ∈ A) ∨ ¬(b ∈ C)) ⇔

⇔ (a ∈ A ∧ b ∈ B ∧ ¬(a∈ A)) ∨ (a ∈ A ∧ b ∈ B ∧ ¬(b ∈ C)) ⇔

8

⇔ a ∈ A ∧ (b ∈ B ∧ b ∉ C) (*)

1

Ponieważ założyliśmy, że x = (a, b).

2

Z definicji iloczynu kartezjańskiego.

3

Definicja sumy zbiorów.

4

Prawo rozdzielności koniunkcji względem alternatywy.

5

Ponieważ założyliśmy, że x = (a, b).

6

Z definicji iloczynu kartezjańskiego.

7

Definicja różnicy zbiorów.

8

Lewy składnik alternatywy jest fałszywy, zatem alternatywa ta jest równoważna pozosta-

łemu składnikowi.

5

W rezultacie rozpisanie obu stron równoważności dało ten sam wynik (*), zatem
L ⇔ P, czyli:

x ∈ A × (B – C) ⇔ x ∈ (A × B) – (A × C).

Dowód (h)

Mamy wykazać, że ∀

x

(x ∈ A × ∅ ⇔ x ∈ ∅).

Niech x będzie dowolne. Rozpatrzmy dwa przypadki: albo x nie jest parą uporząd-
kowaną, albo x jest parą uporządkowaną. W pierwszym przypadku równoważność
jest oczywista.

W drugim przypadku, gdy x = (a, b), mamy:

L : x ∈ A × ∅ ⇔ (a, b) ∈ A × ∅ ⇔ a ∈ A ∧ b ∈ ∅ ⇔

9

x ∈ ∅ : P

Twierdzenie 2

W ogólnym przypadku nie zachodzą następujące własności iloczynu kartezjańskiego:
(a)

A ∪ (B × C) = (A ∪ B) × (A ∪ C),

(b)

A ∩ (B × C) = (A ∩ B) × (A ∩ C),

(c)

A – (B × C) = (A – B) × (A – C).

Dowód (a)

Pokażemy, że dla zbiorów A = B = C = R nie zachodzi równość z podpunktu (a).

Mamy:

L = R ∪ (R × R).

Zbiór ten to suma zbioru liczb rzeczywistych oraz zbioru par uporządkowanych,
których elementami są liczby rzeczywiste.

Mamy na przykład 1 ∈ R, co natychmiast daje 1 ∈ R ∪ (R × R).

Rozważmy stronę prawą równości. Mamy:

P = (R ∪ R) × (R ∪ R) = R × R.

Oczywiście, do tego zbioru należą tylko odpowiednie pary uporządkowane, a za-
tem 1 ∉ R × R.

Pokazaliśmy istnienie elementu, który należy do lewej strony równości, a nie nale-
ży do prawej, zatem zbiory powyższe nie są równe.

Dowód (b)

Pokażemy, że dla zbiorów A = B = C = R nie zachodzi równość z podpunktu (b).
Mamy:

P = (R ∩ R) × (R ∩ R) = R × R.

Oczywiście R × R ≠ ∅.

9

Ta równoważność jest prawdziwa, gdyż ma obie strony fałszywe (nic nie może należeć do

zbioru pustego).

6

L = R ∩ (R × R)

Zbiór ten to iloczyn dwóch rozłącznych zbiorów (R to zbiór liczb rzeczywistych,
a R × R to zbiór par uporządkowanych), zatem jest on równy zbiorowi pustemu.

Mamy:

P ≠ ∅ oraz L = ∅.

Oczywiście L ≠ P.

7

2. Relacje binarne

Na co dzień często dokonujemy porównań między pewnymi rzeczami, osobami,
zjawiskami (elementami danego zbioru lub danych zbiorów). Mówimy, że czło-
wiek A jest wyższy od człowieka B, produkt C jest tańszy od produktu D, liczba x
jest mniejsza od liczby y. Zauważamy więc (abstrahujemy z rzeczywistości) pewne
związki (zależności) między pewnymi obiektami. Zależności takie matematyka na-
zywa relacjami.

Relacje są również jednym z podstawowych narzędzi stosowanych w informatyce
między innymi do opisu (modelowania, charakteryzowania, specyfikacji) własno-
ści szeroko pojętych różnych systemów informatycznych, a przez to również syste-
mów oprogramowania.

Przykład 2

Rozważmy zależność między żołnierzami w jednostce wojskowej, nazy-
waną relacją „bycia podwładnym”.

Niech P = {K,

C,

S,

A, B,

D} będzie patrolem wojskowym, gdzie:

K — kapitan,

C — chorąży,
S — sierżant,

A,

B,

D — szeregowi.

Oczywiste, że A jest podwładnym S, S jest podwładnym C i tak dalej. Za-
uważmy, że jeżeli zastanowimy się nad reprezentacją graficzną zależności
między elementami zbioru P, łatwo można narysować następujący dia-
gram (rysunek 1).

Nietrudno zauważyć, że każdą z elementarnych relacji między żołnierza-
mi patrolu P można reprezentować (specyfikować) przez odpowiednią parę upo-
rządkowaną. Mamy zatem pary: (A, S),

(A, C),

(A, K),

(B, S),

(B, C),

(B, K),

(D, S),

(D, C),

(D, K),

(S, C),

(S, K),

(C, K).

Możemy więc powiedzieć, że relację „bycia podwładnym” określa pewien zbiór par
uporządkowanych. Zauważmy również, że ten zbiór jest podzbiorem iloczynu kar-
tezjańskiego P

× P, przy czym jest to tylko jego podzbiór właściwy (różny od całe-

go iloczynu P × P).

Jak widać, relacje dwuargumentowe, czyli zachodzące między dwoma elementami,
można definiować jako pewne zbiory par uporządkowanych.

Relacją

określoną na iloczynie kartezjańskim A × B nazwiemy zatem dowolny pod-

zbiór tego iloczynu kartezjańskiego.

Relacją binarną

określoną na zbiorze A nazywamy dowolny podzbiór iloczynu kar-

tezjańskiego A × A.

Jeżeli przyjmujemy taką definicję, to łatwo zauważyć, że elementami niepustych re-
lacji binarnych są pary uporządkowane.

K

C

S

B

A D

K

C

S

B

A D

K

C

S

B

A D

K

C

S

B

A D

Rysunek 1

K

C

S

B

A D

K

C

S

B

A D

K

C

S

B

A D

K

C

S

B

A D

8

Relacje binarne określone na zbiorze A oznaczać będziemy symbolem

δ (δ ⊆ A × A). Fakt należenia pary uporządkowanej (a, b) do relacji δ
będziemy oznaczać przez (a, b) ∈ δ. Zamiennie będziemy też używali
zapisu „a δ b” (element a jest w relacji δ z elementem b).

Nietrudno zauważyć, że skończone relacje binarne można łatwo inter-
pretować graficznie jako zbiór (graf) odpowiednich przejść (tranzycji)
między elementami odpowiedniego zbioru.

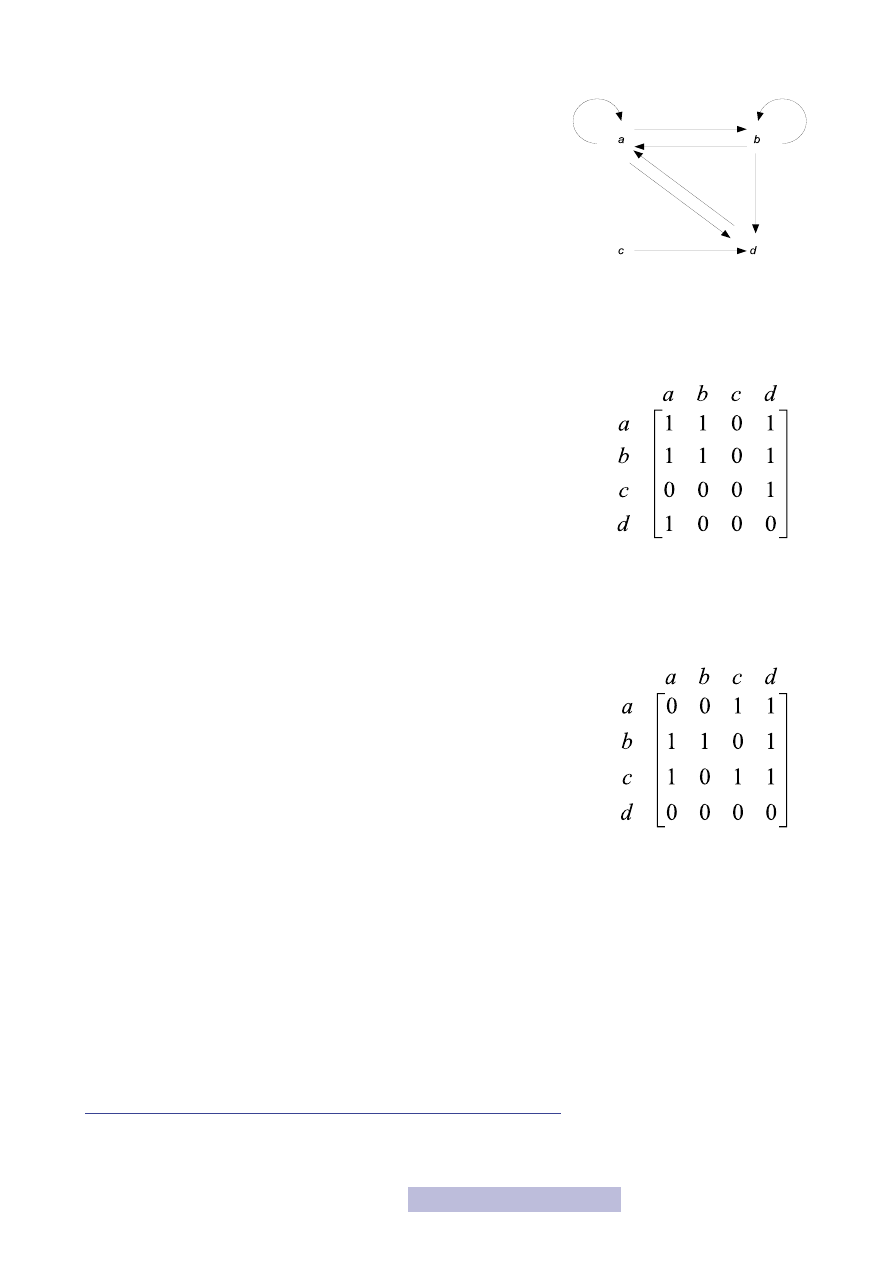
Przykład 3

Rozważmy zbiór A = {a, b, c, d} i określoną na nim relację:

δ = {(a, a), (b, b), (a, b), (b, a), (c, d), (a, d), (d, a), (b, d)}.

Reprezentacja graficzna tej relacji jest przedstawiona na rysunku 2.

Oczywiste jest, że odpowiedni zbiór par uporządkowanych (relacja) deter-
minuje dokładnie jeden graf. Zachodzi również własność odwrotna: każdy
graf determinuje dokładnie jedną relację (odpowiedni zbiór par uporząd-
kowanych).

Relacje skończone reprezentować można również za pomocą macierzy,
wpisując w polach o odpowiednich współrzędnych jedynkę (jeżeli relacja
zachodzi między danymi współrzędnymi macierzy) lub zero (gdy relacja
nie zachodzi).

Relację z poprzedniego przykładu reprezentować można jako następującą
macierz (rysunek 3).

Oczywiste jest również w tym przypadku, że odpowiedni zbiór par uporząd-
kowanych (relacja) determinuje dokładnie jedną macierz (z dokładnością do
kolejności ustawienia elementów-współrzędnych) oraz każda macierz deter-
minuje dokładnie jedną relację (odpowiedni zbiór par uporządkowanych).

Przykład 4

Rozważmy macierz przedstawioną na rysunku 4.

Reprezentuje ona oczywiście relację:

δ = {(a, c), (a, d), (b, a), (b, b), (b, d), (c, a), (c, c), (c, d)}.

Niech δ ⊆ X

× Y będzie relacją dwuargumentową na zbiorach X, Y.

Dziedziną relacji

δ, oznaczaną przez D(δ), nazywamy zbiór wszystkich poprzedni-

ków par należących do relacji δ.

D(δ) = {x ∈

X : ∃

y∈Y

(x, y) ∈ δ}

10

.

Przeciwdziedziną relacji

δ, oznaczaną przez D*(δ), nazywamy zbiór wszystkich na-

stępników par należących do relacji δ.

D*(δ) = {y ∈ Y : ∃

x∈X

(x, y) ∈ δ}

11

.

10

W innej formie D(δ) = {x ∈ X : ∃

y

∈

Y

x δ y}.

11

Inaczej D*(δ) = {y ∈ Y : ∃

x∈X

x δ y}.

a b

c d

0

0

0

1

1

0

0

0

1

0

1

1

1

0

1

1

d

c

b

a

d

c

b

a

0

0

0

0

1

1

0

1

1

0

1

1

1

1

0

0

d

c

b

a

d

c

b

a

Rysunek 2

Rysunek 3

Rysunek 4

9

Niżej zdefiniujemy podstawowe operacje na relacjach binarnych: sumę, iloczyn,
konwers i złożenie (superpozycję relacji).

Niech A oraz B będą dowolnymi zbiorami. Niech δ

1

będzie dowolną relacją okre-

śloną na zbiorze A (δ

1

⊆ A × A), zaś δ

2

będzie dowolną relacją określoną na zbiorze

B (δ

2

⊆ B × B).

Zauważmy, że A ⊆ A ∪ B oraz B ⊆ A ∪ B.

Możemy zatem stwierdzić, że zarówno δ

1

⊆ (A ∪ B) × (A ∪ B), jak i δ

2

⊆ (A ∪ B)

× (A ∪ B). Możemy teraz dla danych relacji δ

1

oraz δ

2

zdefiniować

sumę

oraz

iloczyn

tych relacji.

Relację (δ

1

∪ δ

2

) określoną na zbiorze A ∪ B ((δ

1

∪ δ

2

)

⊆ (A ∪ B)

× (A ∪ B)) speł-

niającą zależność:

a (δ

1

∪ δ

2

) b ⇔ a δ

1

b ∨ a δ

2

b,

nazywamy

sumą relacji

δ

1

oraz δ

2

.

Inaczej możemy zapisać:

(δ

1

∪ δ

2

) =

df.

{(a, b) ∈ (A ∪ B) × (A ∪ B) : (a, b) ∈ δ

1

∨ (a, b) ∈ δ

2

}.

Relację (δ

1

∩ δ

2

) określoną na zbiorze A ∪ B ((δ

1

∩ δ

2

)

⊆ (A ∪ B) × (A ∪ B)), speł-

niającą zależność:

a (δ

1

∩ δ

2

) b ⇔ a δ

1

b ∧ a δ

2

b,

nazywamy

iloczynem relacji

δ

1

oraz δ

2

.

Inaczej możemy zapisać:

(δ

1

∩ δ

2

) =

df.

{(a, b) ∈ (A ∪ B) × (A ∪ B) : (a, b) ∈ δ

1

∧ (a, b) ∈ δ

2

}.

Zauważmy, że jeżeli zbiór A ∩ B jest pusty, to i relacja (δ

1

∩ δ

2

) jest zbiorem

pustym.

Przykład 5

Relację „≤”, określoną na zbiorze liczb naturalnych, możemy traktować jako sumę
relacji „<” oraz relacji „=” określonych odpowiednio na zbiorze liczb naturalnych
(bo x ≤ y ⇔ x < y ∨ x = y).

Relację „=”, określoną na zbiorze liczb naturalnych, możemy traktować jako ilo-
czyn relacji „≤” oraz relacji „≥” określonych odpowiednio na zbiorze liczb natural-
nych (bo x = y ⇔ x ≤ y ∧ x ≥ y).

Zachodzą następujące własności dotyczące dziedziny i przeciwdziedziny sumy
i iloczynu relacji.

Twierdzenie 3

Dla dowolnych relacji δ

1

, δ

2

⊆ A × B:

(a)

D (δ

1

∪ δ

2

) = D(δ

1

) ∪ D(δ

2

),

(b)

D*(δ

1

∪ δ

2

) = D*(δ

1

) ∪ D*(δ

2

),

(c)

D(δ

1

∩ δ

2

) ⊆ D(δ

1

) ∩ D(δ

2

),

(d)

D*(δ

1

∩ δ

2

) ⊆ D*(δ

1

) ∩ D*(δ

2

).

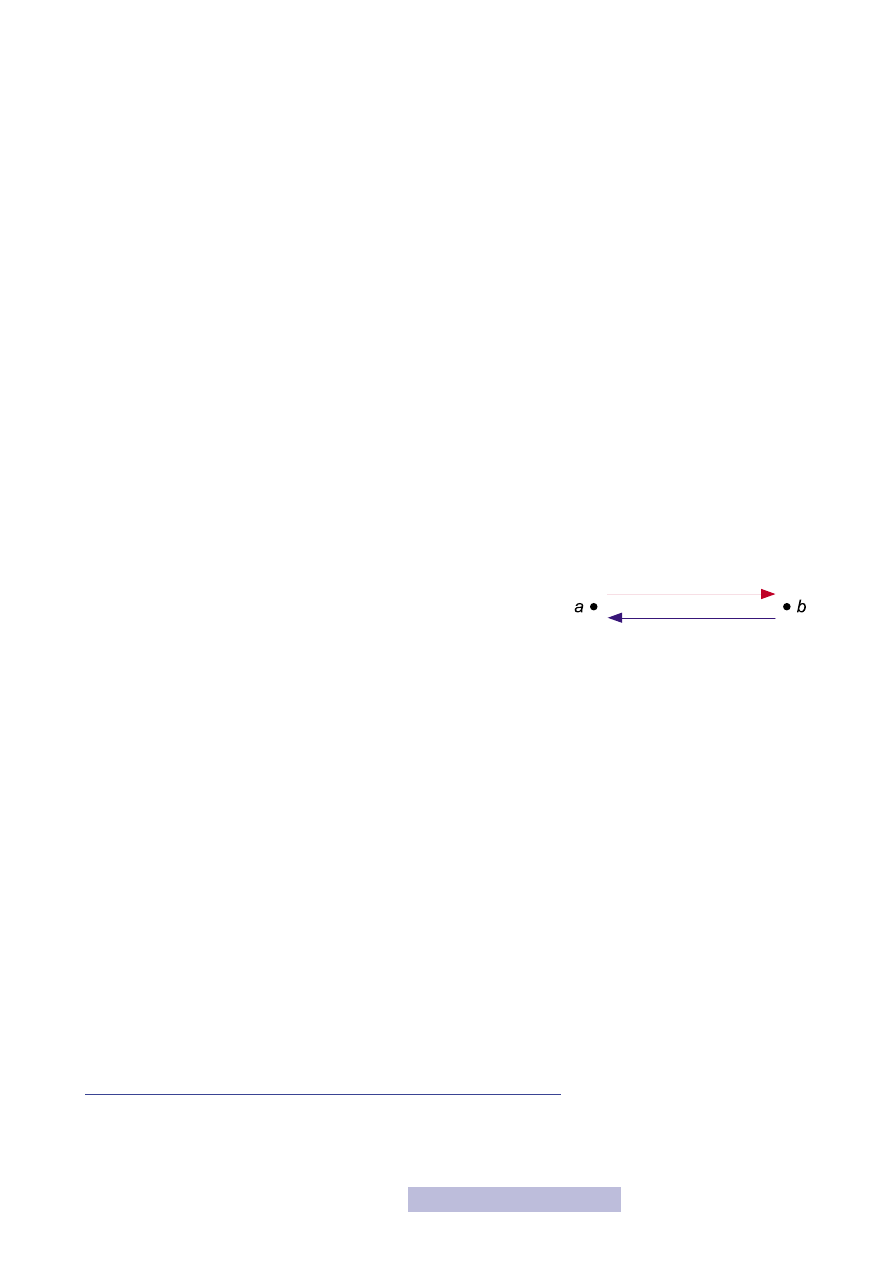
10

Szkic dowodu (a)

x ∈ D(δ

1

∪ δ

2

) ⇔ ∃

y∈B

(x, y) ∈ (δ

1

∪

δ

2

) ⇔ ∃

y∈B

(x δ

1

y ∨ x δ

2

y) ⇔

⇔ ∃

y∈B

x δ

1

y ∨ ∃

y∈B

x δ

2

y ⇔ x ∈ D(δ

1

) ∨ x ∈ D(δ

2

) ⇔

⇔ x ∈ D(δ

1

) ∪ D(δ

2

).

Stąd:

x ∈ D(δ

1

∪ δ

2

) ⇔ x ∈ D(δ

1

) ∪ D(δ

2

).

Szkic dowodu (c)

x

∈ D(δ

1

∩ δ

2

) ⇔ ∃

y∈B

(x, y) ∈ (δ

1

∩

δ

2

) ⇔ ∃

y∈B

(x δ

1

y ∧ x δ

2

y) ⇒

12

⇒ ∃

y∈B

x δ

1

y ∧ ∃

y∈B

x δ

2

y ⇔ x ∈ D(δ

1

) ∧ x ∈ D(δ

2

) ⇔

⇔ x ∈ D(δ

1

) ∩ D(δ

2

).

Stąd:

x

∈ D(δ

1

∩ δ

2

) ⇒ x

∈ D(δ

1

) ∩ D(δ

2

).

Rozważmy relację δ określoną na zbiorze A(δ

⊆ A × A).

Relację δ

–1

określoną na zbiorze A, spełniającą zależność:

a δ

–1

b ⇔ b δ a

13

nazywamy

konwersem (odwrotnością) relacji

δ.

Inaczej możemy zapisać:

δ

–1

=

df.

{(a, b) ∈ A × A : (b, a) ∈ δ}.

Interpretację graficzną konwersu relacji przedstawia rysunek 5.

Przykład 6

Relacją odwrotną do relacji „< ”, określonej na zbiorze liczb naturalnych, jest relacja
„>” (określona na tym samym zbiorze), zachodzi bowiem zależność y < x ⇔ x > y
(możemy też zapisać („<”)

–1

= „>”).

Relacją odwrotną do relacji „być żoną”, określonej na zbiorze ludzi, jest relacja „być
mężem”, określona na tym samym zbiorze, zachodzi bowiem zależność: „x jest
żoną y” ⇔ „y jest mężem x”.

Twierdzenie 4

Dla dowolnych relacji δ, δ

1

, δ

2

⊆ A × B jest:

(a)

(a, b) ∉ δ

–1

⇔ (b, a) ∉ δ,

(b)

D(δ

–1

) = D*(δ) (dziedzina konwersu jest równa przeciwdziedzinie danej relacji),

(c)

D*(δ

–1

) = D(δ) (przeciwdziedzina konwersu jest równa dziedzinie danej relacji),

(d)

(δ

–1

)

–1

= δ (konwers konwersu jest równy danej relacji),

(e)

(δ ’)

–1

= (δ

–1

)‘ (dopełnienie konwersu równe jest konwersowi dopełnienia),

12

Korzystamy z odpowiedniego prawa rozkładu kwantyfikatora szczegółowego względem

koniunkcji: ∃

x

[

Φ(x) ∧ Ψ(x)] ⇒ ∃

x

Φ(x) ∧ ∃

x

Ψ(x).

13

Inaczej: (a, b)

∈ δ

–1

⇔

(

b

, a)

∈

δ

.

Rysunek 5

d -1

d

a b

δ

δ

–1

11

(f)

(δ

1

∪ δ

2

)

–1

= δ

1

–1

∪ δ

2

–1

(konwers sumy relacji równy jest sumie konwersów),

(g)

(δ

1

∩ δ

2

)

–1

= δ

1

–1

∩ δ

2

–1

(konwers iloczynu relacji równy jest iloczynowi kon-

wersów).

Dowód (d)

Trzeba wykazać, że ∀

x

(x

∈ (δ

–1

)

–1

⇔ x

∈ δ).

Niech x będzie dowolny. Rozpatrzmy dwa przypadki: albo x nie jest parą uporząd-
kowaną, albo x jest parą uporządkowaną. W pierwszym przypadku równoważność
jest oczywista.

W drugim przypadku, jeśli x = (a, b), to:

L : x

∈ (δ

–1

)

–1

⇔ (a, b) ∈ (δ

–1

)

–1

⇔ (b, a) ∈ (δ

–1

) ⇔ (a, b) ∈ δ ⇔ x ∈ δ : P

Szkic dowodu (e)

L

:

x

∈ (δ’)

–1

⇔ (a, b) ∈ (δ’)

–1

⇔ (b, a) ∈ δ’ ⇔ (b, a) ∉ δ ⇔

⇔ (a, b) ∉ δ

–1

⇔ (a, b) ∈ (δ

–1

)’ ⇔ x ∈ (δ

–1

)’ : P

Szkic dowodu (f)

L :

x

∈ (δ

1

∪ δ

2

)

–1

⇔ (a, b) ∈ (δ

1

∪ δ

2

)

–1

⇔ (b, a) ∈ (δ

1

∪ δ

2

)

⇔

⇔ (b, a) ∈ δ

1

∨ (b, a) ∈ δ

2

⇔ (a, b) ∈ δ

1

–1

∨ (a, b) ∈ δ

2

–1

⇔

⇔ (a, b) ∈ δ

1

–1

∪ δ

2

–1

⇔ x ∈ δ

1

–1

∪ δ

2

–1

: P

Szkic dowodu (g)

L : x ∈ (δ

1

∩ δ

2

)

–1

⇔ (a, b) ∈ (δ

1

∩ δ

2

)

–1

⇔ (b, a) ∈ (δ

1

∩ δ

2

)

⇔

⇔ (b, a) ∈ δ

1

∧ (b, a) ∈ δ

2

⇔ (a, b) ∈ δ

1

–1

∧ (a, b) ∈ δ

2

–1

⇔

⇔ (a, b) ∈ δ

1

–1

∩ δ

2

–1

⇔ x ∈ δ

1

–1

∩ δ

2

–1

: P

Niech δ

1

⊆ A

× B oraz δ

2

⊆ B

× C.

Złożeniem relacji (superpozycją)

δ

1

oraz δ

2

nazywamy relację (δ

2

ο δ

1

) ⊆ A

× C taką, że:

a (δ

2

ο δ

1

) c ⇔ ∃

b∈B

(a δ

1

b ∧ b δ

2

c)

14

.

Symbolicznie:

δ

2

ο δ

1

= {(a, c) ∈ A × C : ∃

b∈B

[(a, b) ∈ δ

1

∧ (b, c) ∈ δ

2

]}.

Interpretację graficzną superpozycji relacji przedstawia rysunek 6.

Zachodzą poniższe własności operacji złożenia relacji.

14

Zwróćmy uwagę na „odwrotną notację”. Jeżeli a δ

1

b ∧ b δ

2

c, to powiemy, że a jest w re-

lacji (δ

2

ο

δ

1

) z elementem c.

12

Twierdzenie 5

Dla dowolnych relacji δ

1

, δ

2

, δ

3

⊆ A × A spełnione są warunki:

(a)

(δ

2

ο δ

1

)

–1

= δ

1

–1

ο δ

2

–1

,

(b)

δ

3

ο (δ

2

ο δ

1

) = (δ

3

ο δ

2

) ο δ

1

(operacja superpozycji relacji jest

łączna),

(c)

D*(δ

1

) = D(δ

2

) ⇒ D(δ

2

ο δ

1

) = D(δ

1

),

(d)

D*(δ

1

) = D(δ

2

) ⇒ D*(δ

2

ο δ

1

) = D*(δ

2

).

Dowód (a)

Trzeba pokazać, że ∀

x

(x

∈ (δ

2

ο δ

1

)

–1

⇔ x ∈ (δ

1

–1

ο δ

2

–1

)).

Niech x będzie dowolny. Rozpatrzmy dwa przypadki: albo x nie jest parą uporząd-
kowaną, albo x jest parą uporządkowaną. W pierwszym przypadku równoważność
jest oczywista.

W drugim przypadku mamy dla pewnej pary (a, b) : x = (a, b).

L : x ∈ (δ

2

ο δ

1

)

–1

⇔ (a, b) ∈ (δ

2

ο δ

1

)

–1

⇔ (b, a) ∈ δ

2

ο δ

1

⇔

⇔ ∃

c

(b δ

1

c ∧ c δ

2

a) ⇔ ∃

c

(c δ

1

–1

b ∧ a δ

2

–1

c) ⇔

⇔ ∃

c

(a δ

2

–1

c ∧ c δ

1

–1

b) ⇔ (a, b) ∈ δ

1

–1

ο δ

2

–1

⇔ x ∈ δ

1

–1

ο δ

2

–1

: P

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

δ

2

–1

δ

1

–1

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

Finalnie:

x

∈ (δ

2

ο δ

1

)

–1

⇔ x

∈ (δ

1

–1

ο δ

2

–1

).

Intuicję graficzną dowodu przedstawia rysunek 7.

Szkic dowodu (c)

Załóżmy, że

D*(δ

1

) = D(δ

2

).

L : a ∈ D(δ

2

ο δ

1

) ⇔ ∃

c

a(δ

2

ο δ

1

)c ⇔

⇔ ∃

c

∃

b

(a δ

1

b ∧ b δ

2

c) ⇒ ∃

c

∃

b

(a δ

1

b) ∧ ∃

c

∃

b

(b δ

2

c) ⇔

⇔ ∃

b

(a δ

1

b) ∧ ∃

c

(b δ

2

c) ⇒ ∃

b

(a δ

1

b) ⇔ a ∈ D(δ

1

) : P

Rysunek 6

Rysunek 7

d

1

d

2

a b

c

d

2

d

1

o

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

d

1

d

2

a c

b

d

2

d

1

o

d

1

–1

a c

b

d

2

-1

d

2

d

1

o

( )

-1

d

2-1

d

1-1

o

=

13

Finalnie:

a ∈ D(δ

2

ο δ

1

) ⇒ a ∈ D(δ

1

), zatem D(δ

2

ο δ

1

) ⊆ D(δ

1

).

P : a ∈ D(δ

1

) ⇔ ∃

b

(b ∈ D*(δ

1

) ∧ aδ

1

b) ⇔

⇔

15

∃

b

(b ∈ D(δ

2

) ∧ a δ

1

b) ⇒ ∃

b

(aδ

1

b ∧ ∃

c

bδ

2

c) ⇔

⇔ ∃

c

∃

b

(aδ

1

b ∧ bδ

2

c) ⇔ ∃

c

a(δ

2

ο δ

1

)c ⇔ a ∈ D(δ

2

ο δ

1

) : L

Zatem a ∈ D(δ

1

) ⇒ a ∈ D(δ

2

ο δ

1

), czyli D(δ

1

) ⊆ D(δ

2

ο δ

1

).

Finalnie — przy założeniu, że D*(δ

1

) = D(δ

2

) — mamy D(δ

1

) = D(δ

2

ο δ

1

).

15

Wykorzystujemy tutaj założenie, że D*(

δ

1

) = D(

δ

2

).

14

3. Rodzaje relacji binarnych

Podamy teraz różne rodzaje

relacji binarnych.

Rozważmy dowolną relację δ określoną na zbiorze A (δ

⊆ A

× A).

1.

Jeżeli każdy element zbioru A jest w relacji sam ze sobą, to powiemy, że rela-
cja δ jest

zwrotna

. Można to zapisać symbolicznie:

Relacja δ jest zwrotna wtw, gdy ∀

x∈A

(x δ x)

16

.

Przykład 7

Przykładem relacji zwrotnej jest relacja równoległości prostych na płaszczyź-
nie: każda prosta jest równoległa do samej siebie.

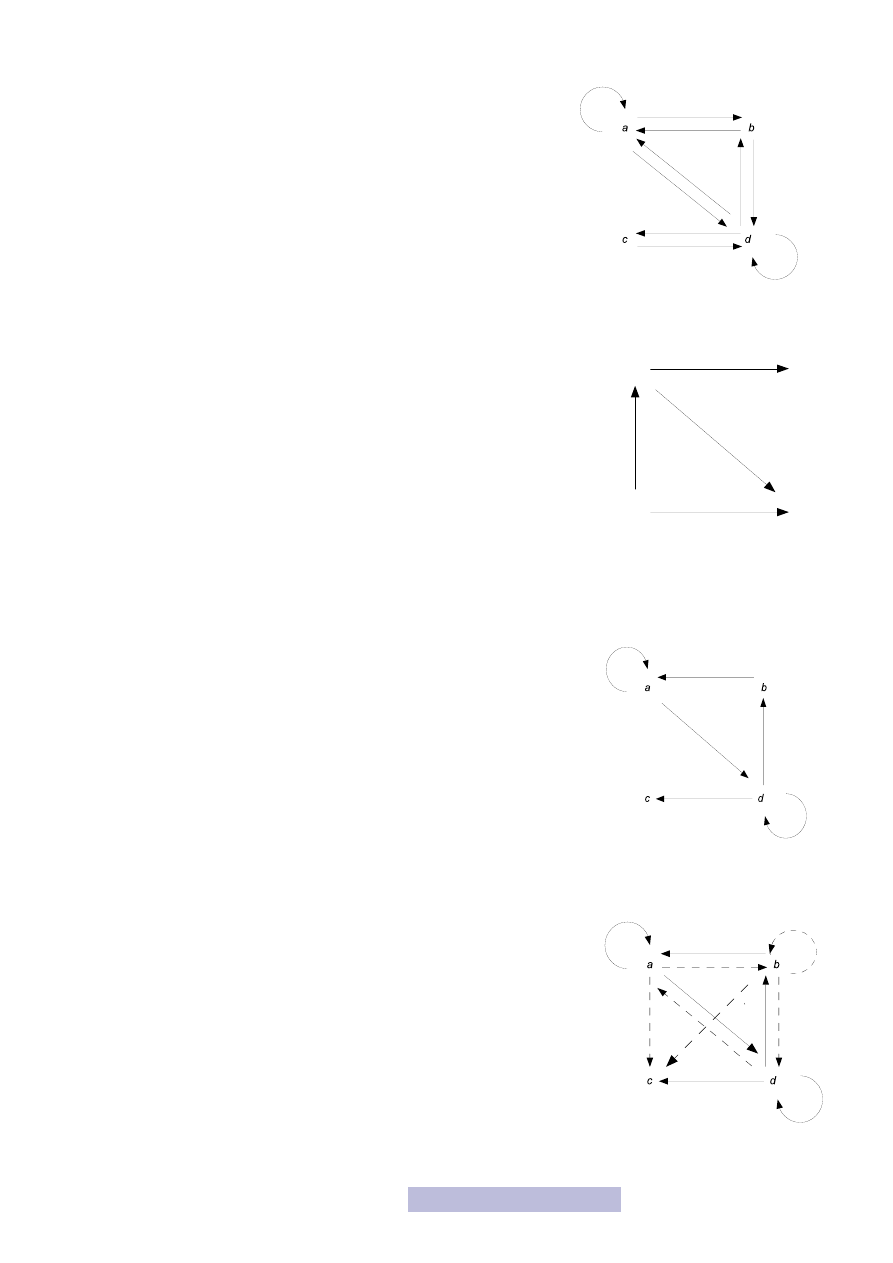
W reprezentacji graficznej relacja jest zwrotna, jeżeli z każdego elementu istnieje
przejście (tranzycja) do niego samego (tzw. tranzycja identycznościowa) (rysunek
8). Inne tranzycje nie mają tu znaczenia.

W reprezentacji macierzowej relacja jest zwrotna, jeżeli na głównej przekątnej są same
jedynki. Macierz dla powyższej relacji została przedstawiona na rysunku 9.

2.

Jeżeli żaden element zbioru A nie jest w relacji sam ze sobą, to powiemy, że rela-
cja δ jest

przeciwzwrotna

. Można to zapisać symbolicznie:

Relacja δ jest przeciwzwrotna wtw, gdy ∀

x∈A

¬(x δ x)

17

.

Przykład 8

Przykładem relacji przeciwzwrotnej jest relacja prostopadłości prostych na płasz-
czyźnie: żadna prosta nie jest prostopadła do samej siebie.

W reprezentacji graficznej relacja jest przeciwzwrotna, jeżeli żaden element zbio-
ru nie ma tranzycji do samego siebie (rysunek 10). Inne tranzycje nie mają zna-
czenia.

3.

Jeżeli dla każdych dwóch elementów x i y zbioru A z faktu, że element x jest
w relacji z elementem y wynika, że również y jest w relacji z x, to powiemy, że
relacja δ jest

symetryczna.

Symbolicznie:

Relacja

δ jest symetryczna wtw, gdy ∀

x,y∈A

(x δ y ⇒ y δ x).

Przykład 9

Przykładem relacji symetrycznej jest także relacja równoległości prostych na płasz-
czyźnie: jeżeli prosta p jest równoległa do prostej q, to prosta q jest również rów-
noległa do prostej p.

16

Inaczej ∀

x∈A

(x, x) ∈ δ.

17

Inaczej ∀

x∈A

(x, x)∉ δ.

a b

c d

Rysunek 8

Rysunek 9

a b

c d

Rysunek 10

1

0

0

0

1

1

0

0

1

0

1

0

1

0

1

1

d

c

b

a

d

c

b

a

1 1 0 1
0 1 0 1
0 0 1 1
0 0 0 1

15

W reprezentacji graficznej relacja jest symetryczna, jeżeli każda tranzycja
ma tranzycję przeciwną (rysunek 11).

4.

Jeżeli dla każdych dwóch elementów x i y zbioru A z faktu, że element x
jest w relacji z elementem y wynika, że y nie jest w relacji z x, to powie-
my, że relacja δ jest

asymetryczna.

Symbolicznie:

Relacja

δ jest asymetryczna wtw, gdy ∀

x,y∈A

[x

δ y ⇒ ¬(y

δ x)].

Przykład 10

Przykładem relacji asymetrycznej jest relacja mniejszości liczb rzeczywi-
stych: jeżeli liczba x jest mniejsza od liczby y, to liczba y nie jest mniejsza od
liczby x.

W reprezentacji graficznej relacja jest asymetryczna, jeżeli żadna tranzycja
nie ma tranzycji przeciwnej, nie ma też tranzycji identycznościowych (rysu-
nek 12).

5.

Jeżeli dla każdych dwóch elementów

x i y zbioru A, z faktu, że element x jest

w relacji z elementem y oraz y jest w relacji z x, wynika, że elementy x i y są
identyczne, to powiemy, że relacja δ jest

antysymetryczna.

Symbolicznie:

Relacja

δ jest antysymetryczna wtw, gdy ∀

x, y ∈ A

[(x δ y ∧ y δ x) ⇒ x = y].

Przykład 11

Przykładem relacji antysymetrycznej jest relacja „mniejsze lub równe”
określona na liczbach rzeczywistych: jeżeli liczba x jest mniejsza lub rów-
na od liczby y oraz y jest mniejsze lub równe od x, to wynika z tego, że
x = y.

W reprezentacji graficznej relacja jest antysymetryczna, jeżeli żadna tranzy-
cja nie ma tranzycji przeciwnej. Tranzycje identycznościowe są dopuszczalne
(rysunek 13).

6.

Jeżeli dla każdych trzech elementów x, y i z

zbioru A, z faktu, że element

x jest w relacji z elementem y oraz y jest w relacji z elementem z wyni-
ka, że element x jest w relacji z elementem z, to powiemy, że relacja δ jest

przechodnia.

Symbolicznie:

Relacja

δ jest przechodnia wtw, gdy ∀

x,y,z∈A

[(x δ y ∧ y δ z) ⇒ x δ z].

Przykład 12

Przykładem relacji przechodniej jest relacja równoległości prostych na
płaszczyźnie: jeżeli prosta p jest równoległa do prostej q oraz prosta q jest
równoległa do prostej s, to prosta p jest również równoległa do prostej s.

a b

c d

Rysunek 11

a b

c d

Rysunek 12

a b

c d

Rysunek 13

Rysunek 14

a b

c d

a b

c d

a b

c d

a

b

c

d

a

b

c

d

a

b

c

d

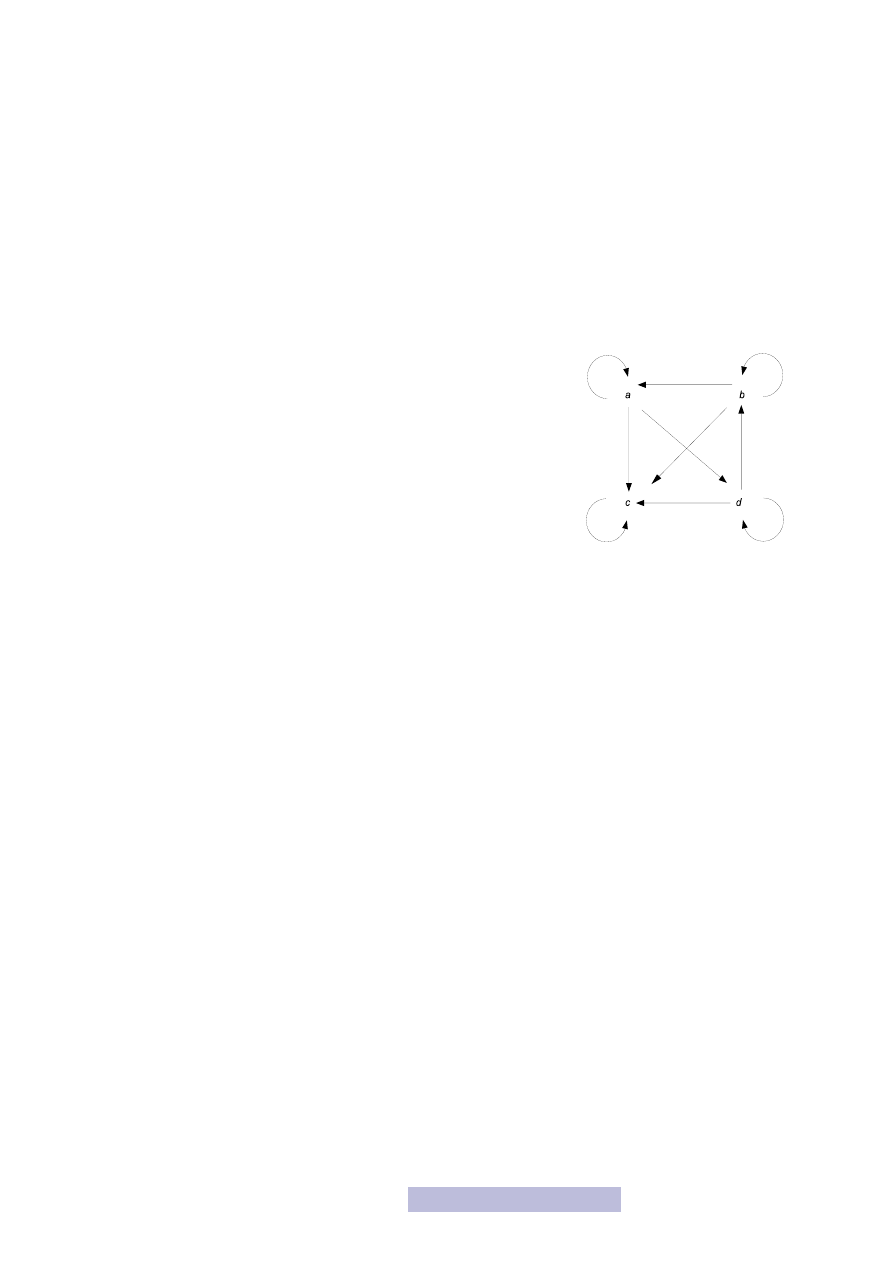
16

Na rysunku 14 pokazana jest reprezentacja graficzna relacji przechodniej. Rysunek
powstał z rysunku 13 przez dodanie odpowiednich (przerywanych) tranzycji, tak
aby finalna relacja spełniała warunek przechodniości.

7.

Jeżeli dla każdych dwóch elementów x i y zbioru A, element x jest w relacji
z elementem y lub y jest w relacji z elementem x, to powiemy, że relacja δ jest

spójna.

Można to zapisać symbolicznie:

Relacja

δ jest spójna wtw, gdy ∀

x,y∈A

(x δ

y ∨ y δ x).

Przykład 13

Przykładem relacji spójnej jest relacja „mniejsze lub równe” określona na
zbiorze liczb rzeczywistych: dla dowolnych dwóch liczb rzeczywistych x
i y liczba x jest mniejsza lub równa od liczby y lub liczba y jest mniejsza
lub równa od liczby x.

W reprezentacji graficznej relacja jest spójna, jeżeli między dwoma do-
wolnymi elementami istnieje co najmniej jedna tranzycja (w dowolną
stronę). Wszystkie tranzycje identycznościowe są również konieczne
(rysunek 15).

Oznaczmy przez id(A) relację identyczności na zbiorze A. Symbolicznie:

id(A) = {(x, x) : x

∈ A}

.

Twierdzenie 6

Niech δ ⊆ A × A będzie relacją niepustą. Zachodzą następujące własności:
(a)

δ jest zwrotna wtedy i tylko wtedy, gdy id(A) ⊆ δ,

(b)

δ jest przeciwzwrotna wtedy i tylko wtedy, gdy id(A) ∩ δ = ∅,

(c)

δ jest symetryczna wtedy i tylko wtedy, gdy δ = δ

-1

,

(d)

δ jest przechodnia wtedy i tylko wtedy, gdy δ ο δ ⊆ δ.

Dowód (a)

Należy wykazać, że jeżeli relacja δ jest zwrotna, to id(A) ⊆ δ, oraz odwrotnie — że
jeżeli relacja δ spełnia własność id(A) ⊆ δ, to jest zwrotna.

⇒

Jeśli relacja jest zwrotna, to na podstawie definicji mamy: ∀

x∈A

(x δ x). Zatem dla

dowolnego elementu x ze zbioru A mamy (x δ x), czyli (x, x) ∈ δ, zatem id(A) ⊆ δ.

⇐

Załóżmy, że id(A) ⊆ δ. Dla dowolnego x ∈ A mamy: (x, x) ∈ δ, czyli relacja jest
zwrotna.

Rysunek 15

a b

c d

a b

c d

a b

c d

a b

c d

a b

c d

17

Szkic dowodu (b)

⇒

Załóżmy nie wprost, że id(A) ∩ δ ≠ ∅. Dla pewnej pary (x

1

, x

1

) mamy (x

1

, x

1

) ∈ δ,

czyli x

1

δ x

1

. Otrzymujemy sprzeczność.

⇐

Załóżmy nie wprost, że id(A) ∩ δ = ∅ oraz to, że relacja nie jest przeciwzwrotna.
Mamy dla pewnej pary: x

1

δ x

1

, czyli (x

1

, x

1

) ∈ δ. Zatem id(A) ∩ δ ≠ ∅. Otrzymuje-

my sprzeczność.

Szkic dowodu (c)

⇒

Załóżmy, że relacja δ jest symetryczna. Niech (x, y) ∈ δ, mamy x δ y. Z własności
symetrii otrzymujemy y δ x, czyli (y, x) ∈ δ. Zatem (x, y) ∈ δ

-1

. Mamy δ ⊆ δ

-1

. In-

kluzji odwrotnej dowodzi się analogicznie.

⇐

Załóżmy, że δ = δ

-1

.

Niech (x, y) ∈ δ, wtedy z założenia (x, y) ∈ δ

-1

, czyli (y, x) ∈ δ.

Szkic dowodu (d)

⇒

Załóżmy, że δ jest przechodnia. Niech (x, y) ∈ δ ο δ, mamy x (δ ο δ) y. Z własno-
ści złożenia relacji dla pewnego z mamy (x δ z ∧ z δ y). Z założonej przechodniości
mamy x δ y, czyli (x, y) ∈ δ. A więc δ ο δ ⊆ δ.

⇐

Załóżmy, że δ ο δ ⊆ δ. Niech x δ y oraz y δ z. Wtedy x(δ ο δ) z, a więc (x, z) ∈ δ ο δ.
Z założenia (x, z) ∈ δ, czyli x δ z. Relacja δ jest więc przechodnia.

Twierdzenie 7

Prawdziwe są następujące własności niepustych relacji binarnych:
(a)

zwrotność i przeciwzwrotność wykluczają się wzajemnie,

(b)

symetria i asymetria wykluczają się wzajemnie,

(c)

każda relacja asymetryczna jest antysymetryczna,

(d)

każda relacja spójna jest zwrotna,

(e)

żadna relacja zwrotna nie jest asymetryczna.

Twierdzenie 8

Prawdziwe są następujące własności charakteryzujące związki między działaniami
na relacjach a ich rodzajami:



suma i iloczyn dwóch relacji zwrotnych jest relacją zwrotną,



suma i iloczyn dwóch relacji symetrycznych jest relacją symetryczną,



suma i iloczyn dwóch relacji spójnych jest relacją spójną.

18

Bibliografia

1. Gubareni N., 2001: Logika dla studentów, Wydawnictwo Politechniki

Częstochowskiej.

2. Kuratowski K., 2004: Wstęp do teorii mnogości i topologii, PWN, Warszawa.

3. Kuratowski K., Mostowski A., 1978: Teoria mnogości, PWN, Warszawa.

4. Marek W., Onyszkiewicz J., 2003: Elementy logiki i teorii mnogości

w zadaniach, PWN, Warszawa.

5. Rasiowa H., 2004: Wstęp do matematyki współczesnej, PWN, Warszawa.

6. Słupecki J., Hałkowska K., Piróg-Rzepecka K., 1994: Logika i teoria mnogości,

Warszawa.

Bibliografia stron WWW

7. Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego.

Witryna internetowa. http://www.mimuw.edu.pl/~tiuryn/skrypt-98.ps.gz, stan
z 21.09.2005 (J. Tiuryn, Wstęp do teorii mnogości i logiki).