dr Dymitr Słezion

1

Matematyka

Temat 4

ILOCZYN KARTEZJAŃSKI, PRZESTRZEŃ R

n

Przy opisie zbioru kolejność wymienianych elementów nie jest istotna i każdy element wymieniamy tylko

jeden raz. Bardzo często zachodzi potrzeba rozważania układów elementów danego zbioru, w których kolejność

wymienianych elementów jest istotna i elementy mogą się powtarzać.

D

EFINICJA

4.1 (para uporządkowana, układ uporządkowany elementów).

1. Parą uporządkowaną elementów niepustego zbioru nazywamy układ (a, b), w którym a jest elementem

pierwszym, natomiast b jest elementem drugim.

2. Układem uporządkowanym n-elementowym z elementów niepustego zbioru nazywamy układ postaci

)

,

,

,

,

(

3

2

1

n

a

a

a

a

K

,

w którym a

k

, k = 1, 2, ... , n, znajduje się na pozycji o numerze k.

3. Równość układów uporządkowanych definiujemy następująco:

.

;

,

,

2

,

1

)]

,

,

,

(

)

,

,

,

[(

2

1

2

1

k

k

df

n

n

b

a

n

k

b

b

b

a

a

a

=

=

∀

⇔

=

K

K

K

♦

D

EFINICJA

4.2 (iloczyn kartezjański).

1. Iloczynem (produktem) kartezjańskim zbiorów A oraz B nazywamy zbiór

A

×

B

df

=

{(a, b) : a

∈

A, b

∈

B}.

2. Iloczyn kartezjański

n

A

A

A

×

×

×

K

2

1

definiujemy następująco:

}.

,

,

,

:

)

,

,

,

{(

2

2

1

1

2

1

2

1

n

n

n

df

n

A

a

A

a

A

a

a

a

a

A

A

A

∈

∈

∈

=

×

×

×

K

K

K

♦

P

RZYKŁAD

4.1 (iloczyny kartezjańskie zbiorów skończonych).

Dla zbiorów A = {5, 2}, B = {b, a, d}, C = {2} mamy:

a) A

×

B = {(5, b), (5, a), (5, d), (2, b), (2, a), (2, d)},

B

×

A = {(b, 5), (b, 2), (a, 5), (a, 2), (d, 5), (d, 2)},

b) A

×

B

×

C = {(5, b, 2), (5, a, 2), (5, d, 2), (2, b, 2), (2, a, 2), (2, d, 2)},

♦

Z Def. 4.1 i 4.2 otrzymujemy (patrz Prz. 4.1)

W

NIOSEK

4.1 (nieprzemienność iloczynu kartezjańskiego).

Iloczyn kartezjański nie jest działaniem przemiennym: A

×

B

≠

B

×

A. Analogicznie dla iloczynu kartezjań-

skiego więcej niż dwóch zbiorów.

♦

U

MOWA

4.1 (potęga kartezjańska zbioru).

Dla danego zbioru A oraz n

∈

N stosujemy następujące oznaczenia i nazewnictwo:

,

n

oz

czynników

n

A

A

A

A

=

×

×

×

−

4

4 3

4

4 2

1

K

n-ta potęga kartezjańska zbioru A.

♦

Szczególne znaczenie mają potęgi kartezjańskie zbioru liczb rzeczywistych R.

dr Dymitr Słezion

2

Matematyka

U

MOWA

4.2 (przestrzeń rzeczywista n-wymiarowa

n

R ).

Zbiór

}

,

,

2

,

1

,

:

)

,

,

,

{(

2

1

n

i

x

x

x

x

i

n

czynników

n

n

K

K

4

4 3

4

4 2

1

K

=

∈

=

×

×

×

=

−

R

R

R

R

R

nazywamy n-wymiarową przestrzenią arytmetyczną albo przestrzenią rzeczywistą n-wymiarową. Element

n

n

x

x

x

R

∈

)

,

,

,

(

2

1

K

nazywamy punktem tej przestrzeni, a liczby

n

x

x

x

,

,

,

2

1

K

współrzędnymi tego punktu.

Będziemy stosowali oznaczenia:

.

)

,

,

,

(

)

,

,

,

(

2

1

2

1

n

n

n

x

x

x

x

x

x

X

X

R

∈

=

=

K

K

Punkt O(0,0,...,0) nazywamy punktem początkowym przestrzeni

.

n

R

♦

Dla n = 1, 2, 3 przestrzeniom

R

R

=

1

,

2

R

i

3

R możemy nadać realną interpretację geometryczną. W tych

przypadkach zamiast numeracji współrzędnych punktu wygodniej jest używać różnych liter, najczęściej x, y, z.

U

WAGA

4.1 (interpretacja geometryczna przestrzeni

3

2

1

,

,

R

R

R

).

1. Obrazem geometrycznym przestrzeni jednowymiarowej

R

R

=

1

jest oś liczbowa Ox.

2. Obrazem geometrycznym przestrzeni dwuwymiarowej

2

R

jest płaszczyzna z kartezjańskim układem

współrzędnych. pisy: X = X(x, y) = (x, y).

3. Obrazem geometrycznym przestrzeni trójwymiarowej

3

R

jest otaczająca nas „realna przestrzeń” z karte-

zjańskim układem współrzędnych, który, analogicznie jak w przypadku

,

2

R

tworzą trzy wzajemnie prostopadłe

osie liczbowe Ox, Oy, Oz, o identycznej jednostce i wspólnym punkcie O.

Każdej trójce liczb

3

)

,

,

(

R

∈

z

y

x

odpowiada więc jeden punkt X przestrzeni Oxyz i odwrotnie, każdemu punk-

towi X przestrzeni Oxyz odpowiada jedna trójka liczb (x, y, z), które nazywamy współrzędnymi tego punktu.

Stosujemy zapisy: X = X(x, y, z) = (x, y, z).

♦

P

RZYKŁAD

4.2 (interpretacja geometryczna iloczynów kartezjańskich).

Z Uw. 4.1 wynika, że ilustracją geometryczną iloczynu kartezjańskiego dwóch (trzech) zbiorów liczbowych

będzie odpowiedni zbiór płaszczyzny Oxy (przestrzeni realnej Oxyz).

A = {

−

2, 1},

B = {2, 1};

A

×

B = {(

−

2, 2), (

−

2, 1), (1, 2), (1, 1)},

Rys. 4.1.

C = R,

D = {

−

1, 2};

C

×

D = {(x, y): x

∈

R, y

∈

{

−

1,2}},

Rys. 4.2.

(

−

2,2)

Oy

Oy

Ox

(x,2)

(x,

−

1)

1

2

2

−

1

1

(1,2)

(1,1)

1

O

(

−

2,1)

1

−

2

Ox

O

Rys. 4.1

Rys. 4.2

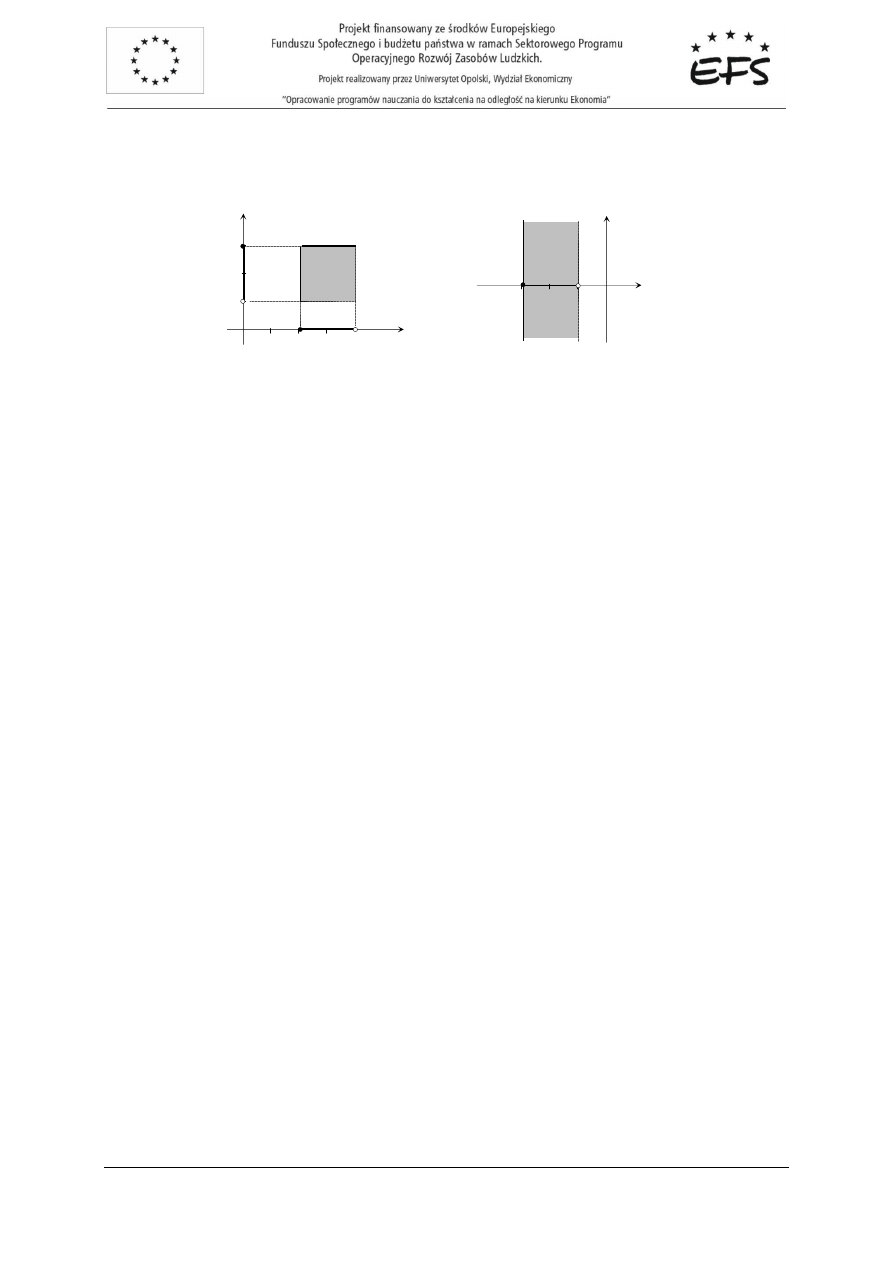
dr Dymitr Słezion

3

Matematyka

E = 〈

2

;4),

F =

(

1;3〉 ;

E

×

F = {(x, y): x

∈

〈

2

;4), y

∈

(1;3〉},

Rys. 4.3.

G = 〈

−3

;

−

1),

H = R ;

G

×

H = {(x, y): x

∈

〈

−3

;

−

1),

y

∈

R},

Rys. 4.4.

♦

Z

ADANIA

4

4.1. Dane są zbiory: A = {1}, B = {

−

2, 3}, C =

(−3

;1〉, D = 〈2;4〉

.

a) Zapisać definicje i podać ilustracje graficzne zbiorów: A

×

B, B

×

A, B

×

C, C

×

B, A

×

D, A

2

, B

2

, C

2

, D

×

R, R

×

B,

R

×{

0

}

, {0}

×

R.

b) Zapisać definicje i podać (opisać) ilustracje graficzne zbiorów: R

×

R

×{

0

}

, R

×

{0}

×

R, {0}

×

R

×

R, R

×{

0

}×{

0

}

,

{0}

×

R

×

{0},

{

0

}×{

0

}×

R, A

×

B

×

R, C

×

D

×

R, {0}

×

C

×

D.

Odpowiedzi, wskazówki.

4.1. a) A

×

B = {(x, y): x

∈

{1}, y

∈

{-2, 3}} = {(1, -2), (1, 3)},

},

4

;

2

,

1

;

3

(

:

)

,

{(

〉

〈

∈

〉

−

∈

=

×

y

x

y

x

D

C

)},

1

,

1

{(

}}

1

{

,

:

)

,

{(

2

=

∈

=

×

=

y

x

y

x

A

A

A

}

0

,

:

)

,

{(

}

0

{

=

∈

=

×

y

x

y

x

R

R

- oś Ox, {0}

×

R – oś Oy.

b)

}

0

,

,

:

)

,

,

{(

}

0

{

=

∈

=

×

×

z

y

x

z

y

x

R

R

R

−

Oxy, R

×

{0}

×

R

−

Oxz, {0}

×

R

×

R

−

Oyz,

}

0

,

:

)

,

,

{(

}

0

{

}

0

{

=

=

∈

=

×

×

z

y

x

z

y

x

R

R

−

Ox, {0}

×

R

×

{0}

−

Oy,

{

0

}×{

0

}×

R

−

Oz.

W

YMAGANE WIADOMOŚCI I UMIEJĘTNOŚCI

1. Definicje układu uporządkowanego elementów i iloczynu kartezjańskiegoi zbiorów.

2. Potęga kartezjańska zbioru, przestrzeń R

n

.

3. Wyznaczanie iloczynów kartezjańskich zbiorów liczbowych i ich ilustracja graficzna.

4. Zapisy osi układu współrzędnych w R

2

i R

3

oraz płaszczyzn układu współrzędnych w R

3

za pomocą iloczy-

nów kartezjańskich.

Ox

−

1

−

3

O

3

1

O

4

2

Ox

Oy

Oy

Rys. 4.3

Rys. 4.4