Logika i teoria mnogości/Wykład 5: Para
uporządkowana, iloczyn kartezjański, relacje,
domykanie relacji, relacja równoważności, rozkłady
zbiorów

From Studia Informatyczne

< Logika i teoria mnogości

Spis treści

1 Para uporządkowana
2 Iloczyn kartezjański
3 Relacje

3.1 Operacje na relacjach:

4 Relacje równoważności

4.1 Rozkłady zbiorów
4.2 Domykanie relacji

Para uporządkowana

Bardzo często będziemy chcieli mieć do czynienia ze zbiorem, który niesie w sobie informację o dwóch innych
zbiorach, informację tak trafnie zakodowaną, aby można było odzyskać z niej każdą z jego składowych. Do tego celu
wprowadzimy zbiór nazywany parą uporządkowaną dwóch innych zbiorów.

D

EFINICJA

1.1.

Niech oraz będą zbiorami. Przez parę uporządkowaną

rozumiemy zbiór

Parę uporządkowaną można zdefiniować inaczej na wiele sposobów. Chodzi jednak o to, aby ze zbioru, który jest
parą, można było odzyskać jednoznacznie każdą z jego składowych. Tak więc moglibyśmy zaakceptować każdą inną
inną definicję pod warunkiem, że będzie spełnione następujące twierdzenie:

T

WIERDZENIE

1.2.

Dla dowolnych zbiorów

zachodzi:

D

OWÓD

Dowód przeprowadzimy tylko ze strony lewej do prawej, bo w odwrotnym kierunku jest to fakt oczywisty. Niech
zatem dwie pary

i

będą równe. Ponieważ

, więc

. Mamy zatem

lub

. W pierwszym przypadku

, ale w drugim również jest tak, mamy bowiem, że

. Pierwszą

część twierdzenia mamy za sobą, bo już wiemy, że pierwsze współrzędne równych par są równe.

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

1 of 8

2012-03-28 17:45

Następnie przeprowadzamy dowód przez przypadki. Jeżeli jest tak, że

, to

. Zatem

, co daje, że

, a zatem

. W przeciwnym przypadku, gdy

mamy,

że

. Daje to dwie możliwości albo

, co nie może mieć miejsca, bo mielibyśmy,

że

albo zaś

. To drugie prowadzi do naszej tezy

.

Ć

WICZENIE

1.3

Dla każdej pary

udowodnij, że

Ć

WICZENIE

1.4

Udowodnij, że dla dowolnej pary uporządkowanej zbiór

jest pusty, gdy współrzędne par są różne, a w przeciwnym przypadku jest zbiorem jednoelementowym zawierającym
współrzędną pary .

Ć

WICZENIE

1.5

Pokaż, że z każdej pary można otrzymać jej drugą współrzędną, posługując się jedynie parą , mnogościowymi
operacjami

oraz stałą .

Iloczyn kartezjański

Zanim wprowadzimy definicję zbioru wszystkich par uporządkowanych elementów dwóch zbiorów (zwanego dalej
iloczynem kartezjańskim), należy nam się krótkie wprowadzenie. Otóż niech

oraz

. Łatwo zauważyć,

że zarówno

, jak i

są podzbiorami

. Zatem

oraz

. Więc

, co daje, że

.

Istnienie i konstrukcja iloczynu kartezjańskiego zostało dokładnie omówione w dodatkowym rozdziale "Iloczyn
kartezjański i aksjomat wyróżniania" . Proponuję przestudiowanie dodatkowego rozdziału dopiero po zapoznaniu się z
rozdziałami wcześniejszymi, pomimo braku precyzji w następnej definicji.

D

EFINICJA

2.1.

Niech

będą zbiorami. Iloczynem kartezjańskim (produktem)

nazywamy zbiór

Będziemy używać specjalnej notacji na zbiór

.

Ć

WICZENIE

2.2

Pokaż następujące elementarne własności iloczynu kartezjańskiego:

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

2 of 8

2012-03-28 17:45

Ć

WICZENIE

2.3

Produkt kartezjański jest monotoniczny ze względu na każdą współrzędną osobno, to znaczy:

Ć

WICZENIE

2.4

Sprawdź, czy dla dowolnych zbiorów

, prawdziwa jest następująca implikacja:

Relacje

D

EFINICJA

3.1.

Relacją nazywamy każdy podzbiór iloczynu

.

Operacje na relacjach:

D

EFINICJA

3.2.

Niech

oraz

.

Ć

WICZENIE

3.3

Niech relacja

oraz

. Pokazać elementarne własności operacji na relacjach:

Ć

WICZENIE

3.4

Niech relacja

oraz

. Pokaż własności:

Ć

WICZENIE

3.5

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

3 of 8

2012-03-28 17:45

Podaj przykład relacji, dla których poniższa równość nie jest prawdziwa.

Ć

WICZENIE

3.6

Udowodnij, że zbiór jest relacją wtedy i tylko wtedy, gdy

Relacje równoważności

W tym podrozdziale poznamy ważną klasę (zbiór) relacji zwaną klasą relacji równoważności(w innych podręcznikach
mogą się państwo spotkać z nazwą relacja abstrakcji). Relacje takie będą służyły do definiowania pojęć
abstrakcyjnych, o czym przekonamy się w wielu miejscach tego i innych wykładów. Bardzo dobrym ćwiczeniem
pokazującym abstrakcyjne metody definiowania pojęć będzie wykład 8, w którym zaprzęgniemy relacje abstrakcji do
definiowania liczb.

Rozpoczynamy rozdział od koniecznej definicji.

D

EFINICJA

4.1.

Dla zbioru definiujemy relację

jako

.

D

EFINICJA

4.2.

Relację

nazywamy relacją równoważnością o polu , jeżeli:

zawiera relacje

(zwrotność ),

(symetria ),

(przechodniość ).

Ć

WICZENIE

4.3

Pokazać, że definicje zwrotności, symetryczności i przechodniości relacji o polu są odpowiednio równoważne
następującym własnościom:

,

,

.

D

EFINICJA

4.4.

Niech będzie relacją równoważności o polu . Klasą równoważności elementu

jest zbiór

D

EFINICJA

4.5.

Zbiór klas równoważności relacji będący elementem zbioru

oznaczamy przez

.

T

WIERDZENIE

4.6.

Niech będzie relacją równoważności o polu . Następujące warunki są równoważne:

,

1.

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

4 of 8

2012-03-28 17:45

,

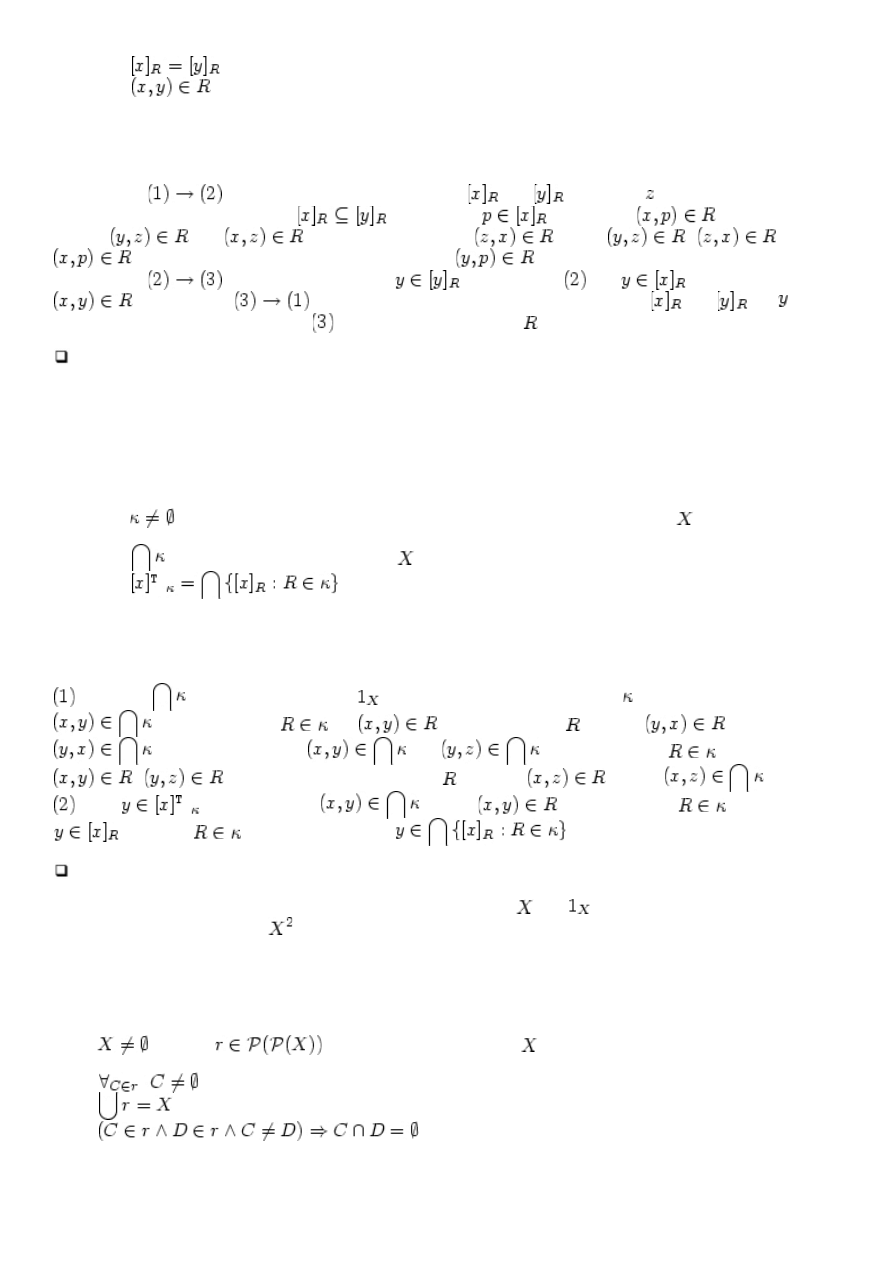
2.

.

3.

D

OWÓD

Pokażemy, że

. Niech wspólny element dwóch klas

oraz

nazywa się . Ze względu na pełną

symetrię tezy wystarczy pokazać, że

. Niech zatem

. Mamy więc

. Z założenia jest

również

oraz

. Z symetrii otrzymujemy

. Zatem

i

i

. Natychmiast z przechodniości otrzymujemy, że

.

Pokażemy, że

. Ze zwrotności mamy, że

, co z założenia

daje

, a to tłumaczy się na

. Pokażemy, że

. Wystarczy pokazać, że wspólnym elementem klas

oraz

jest . Dla

pierwszej z nich wynika to z założenia

, a dla drugiej ze zwrotności .

W następnym twierdzeniu zobaczymy, jak rodzina relacji równoważności jest odporna na przecinanie. Pokażemy
mianowicie, że przecięcie dowolnej liczby relacji równoważności jest nadal relacją równoważności.

T

WIERDZENIE

4.7.

Niech

będzie pewną rodziną (zbiorem) relacji równoważności o tym samym polu . Mamy że:

jest relacją równoważności o polu ,

1.

.

2.

D

OWÓD

Zwrotność

jest oczywista, ponieważ

zawiera się w każdej relacji rodziny . Symetria. Weźmy

. Dla każdej relacji

jest

. Z symetrii każdej jest więc

, co daje

. Przechodniość. Niech

oraz

. Dla każdej relacji

jest więc

i

. Z przechodniości każdej relacji mamy, że

, co daje

.

Niech

. Mamy zatem, że

, co daje

dla każdej relacji

. To zaś daje, że

dla każdej

, co jest równoważne z

.

W szczególności przecięcie wszystkich relacji równoważności o polu daje

. Jest ona najsilniejszą relacją

równoważności. Najsłabszą jest

.

Rozkłady zbiorów

D

EFINICJA

4.8.

Niech

. Rodzinę

nazywamy rozkładem zbioru , gdy:

,

1.

,

2.

.

3.

L

EMAT

4.9.

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

5 of 8

2012-03-28 17:45

Dla relacji równoważności o polu zbiór

jest rozkładem .

D

OWÓD

Każda klasa jest niepusta, bo zawiera element, który ją wyznacza.

, bo każda klasa jest

podzbiorem . Odwrotnie każdy

.

Dwie klasy, gdy są różne, muszą być rozłączne co

udowodniliśmy w twierdzeniu 4.6 (patrz twierdzenie 4.6.).

D

EFINICJA

4.10.

Niech będzie rozkładem zbioru . Definiujemy relacje

następująco:

wtw

L

EMAT

4.11.

Dla rozkładu

relacja

jest:

równoważnością,

1.
2.

D

OWÓD

Relacja

jest zwrotna, każdy bowiem

musi leżeć w pewnym zbiorze rozkładu . Symetria

nie

wymaga dowodu. Przechodniość

. Niech

i

. Istnieją zatem dwa zbiory i rozkładu

takie, że

oraz

. Przecięcie i jest więc niepuste, zatem

, co daje tezę

.

Inkluzja w prawo . Niech

. Klasa jest zatem wyznaczona przez pewien element taki, że

. Niech

będzie zbiorem rozkładu , do którego należy . Łatwo wykazać, że

. Inkluzja w

lewo . Niech

. jest niepusty, więc istnieje

. Klasa

.

Ć

WICZENIE

4.12

Niech będzie niepustym zbiorem oraz niech

. Zdefiniujemy relację

następująco:

dla dowolnych zbiorów

mamy

(

oznacza różnicę symetryczną zbiorów, czyli

). Udowodnij, że relacja jest

relacją równoważności.

Ć

WICZENIE

4.13

Udowodnij, że dla relacji równoważności

na zbiorze , relacja

jest relacją równoważności wtedy i tylko

wtedy, gdy

Podaj przykłady relacji równoważności

takich, że

jest relacją równoważności oraz

i

.

Domykanie relacji

W praktyce matematycznej często potrzebne jest rozważanie domknięć relacji ze względu na wiele przeróżnych
własności. W podrozdziale tym dokonamy charakteryzacji domknięć. Pokażemy między innymi, kiedy takie
domykanie jest możliwe.

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

6 of 8

2012-03-28 17:45

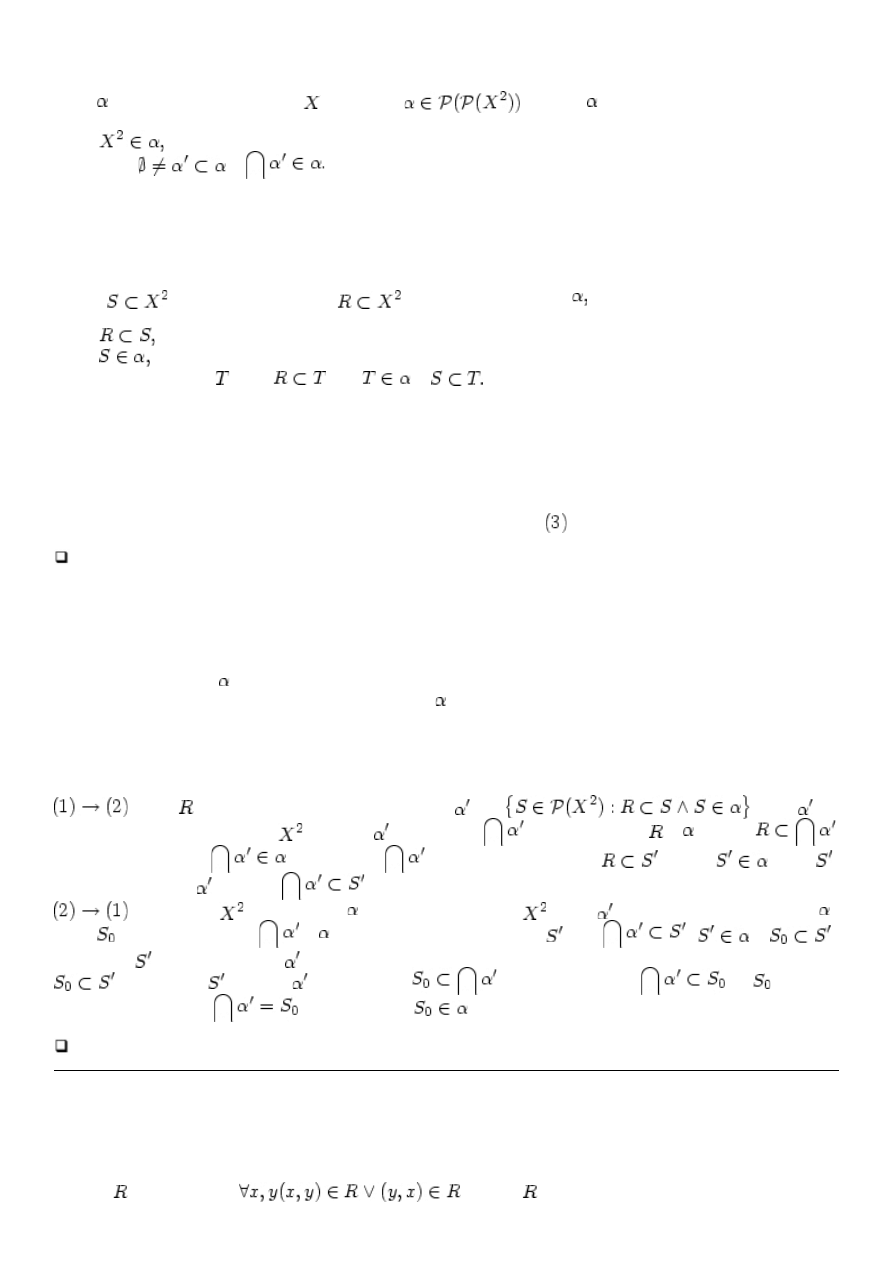
D

EFINICJA

4.14.

Niech będzie rodziną relacji o polu , czyli niech

. Rodzina jest zamknięta na przecięcia, gdy:

1.

jeżeli

to

2.

Poniżej podamy definicję domknięcia relacji w pewnej klasie (zbiorze) relacji. Definiujemy intuicyjnie najmniejszą
relację zawierającą daną należącą do klasy.

D

EFINICJA

4.15.

Relacja

jest domknięciem relacji

w klasie (zbiorze) relacji gdy:

1.
2.

dla każdej relacji jeżeli

oraz

to

3.

L

EMAT

4.16.

Domknięcie relacji (w dowolnej klasie), jeżeli istnieje, to jest jedyne.

D

OWÓD

Gdyby istniały dwa domknięcia pewnej relacji, to ze względu na warunek

wzajemnie by się zawierały.

T

WIERDZENIE

4.17.

Następujące warunki są równoważne:

Klasa relacji jest domknięta na przecięcia.

1.

Każda relacja ma domknięcie w klasie relacji .

2.

D

OWÓD

. Niech będzie relacją. Utwórzmy zbiór relacji jako

. Takie nie

jest puste, bowiem relacja totalna

należy do . Pokażmy, że

jest domknięciem w . Istotnie

. Z założenia mamy też

. Minimalność

stwierdzamy przez: niech

takie że

. Takie

musi leżeć w zbiorze , jest więc

.

. Po pierwsze

leży w zbiorze , bo wystarczy domknąć

. Niech będzie niepustym podzbiorem .

Niech będzie domknięciem

w . Wiemy, że dla dowolnej relacji , o ile

i

to

.

Połóżmy za dowolny element z . Założenia implikacji pozostają automatycznie spełnione, jest więc tak, że

dla dowolnej wyjętej z . W takim razie

. Ponieważ mamy też

, bo było

domknięciem, jest więc

, a to oznacza, że

.

Ć

WICZENIE

4.18

Pokazać jak wyglądają domknięcia w klasie relacji, zwrotnych, symetrycznych i przechodnich.

Pokazać, stosując twierdzenie 4.17 (patrz twierdzenie 4.17.), że nie istnieje domknięcie spójne ani antysymetryczne.
(Relacja jest spójna, gdy

. Relacja jest antysymetryczna, gdy z faktu, że

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

7 of 8

2012-03-28 17:45

oraz

, da się pokazać, że

).

Ć

WICZENIE

4.19

Dla relacji niech

,

,

oznaczają odpowiednio zwrotne, symetryczne, przechodnie domknięcie relacji .

Czy prawdą jest, że:

dla dowolnej relacji relacja

jest relacją równoważności,

1.

dla dowolnej relacji zachodzi

2.

W każdym z powyższych przypadków proszę podać dowód lub kontrprzykład.

Źródło: "http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogo%C5%9Bci/Wyk%C5
%82ad_5:_Para_uporz%C4%85dkowana%2C_iloczyn_kartezja
%C5%84ski%2C_relacje%2C_domykanie_relacji%2C_relacja_r%C3%B3wnowa%C5%BCno%C5%9Bci%2C_rozk
%C5%82ady_zbior%C3%B3w"

Tę stronę ostatnio zmodyfikowano o 19:48, 16 wrz 2006;

Logika i teoria mnogości/Wykład 5: Para uporządkowana, iloczyn kart...

http://wazniak.mimuw.edu.pl/index.php?title=Logika_i_teoria_mnogoś...

8 of 8

2012-03-28 17:45