1

T.3

A

.

POMIARY

PARAMETRÓW

PRĄDU

PRZEMIENNEGO

PRZYRZĄDAMI

ANALOGOWYMI

1. Błędy przypadkowe

Z uwagi na fakt, że wyniku pomiaru obarczonego błędem przypadkowym nie da się przewidzieć,

przyjmuje się, że jest on zmienną losową (najczęściej ciągłą). W procesie pomiaru zmienna ta
przyjmuje tylko jedną konkretną wartość; z określonym prawdopodobieństwem możliwe są jednak
również wartości inne. Ze względu na potwierdzone doświadczalnie założenia mówiące, że przy
odpowiednio dużej liczbie pomiarów (n > 30):



błędy równe co do wartości bezwzględnej, ale o przeciwnych znakach zdarzają się jednako-
wo często,



prawdopodobieństwo wystąpienia błędu dodatniego równe jest prawdopodobieństwu wystą-
pienia błędu ujemnego,



częstość występowania błędów małych jest większa niż błędów dużych,



błędy są zdarzeniami niezależnymi,

zmienna losowa X tworząca wynik pomiaru charakteryzuje się ściśle określonym rozkładem funkcji
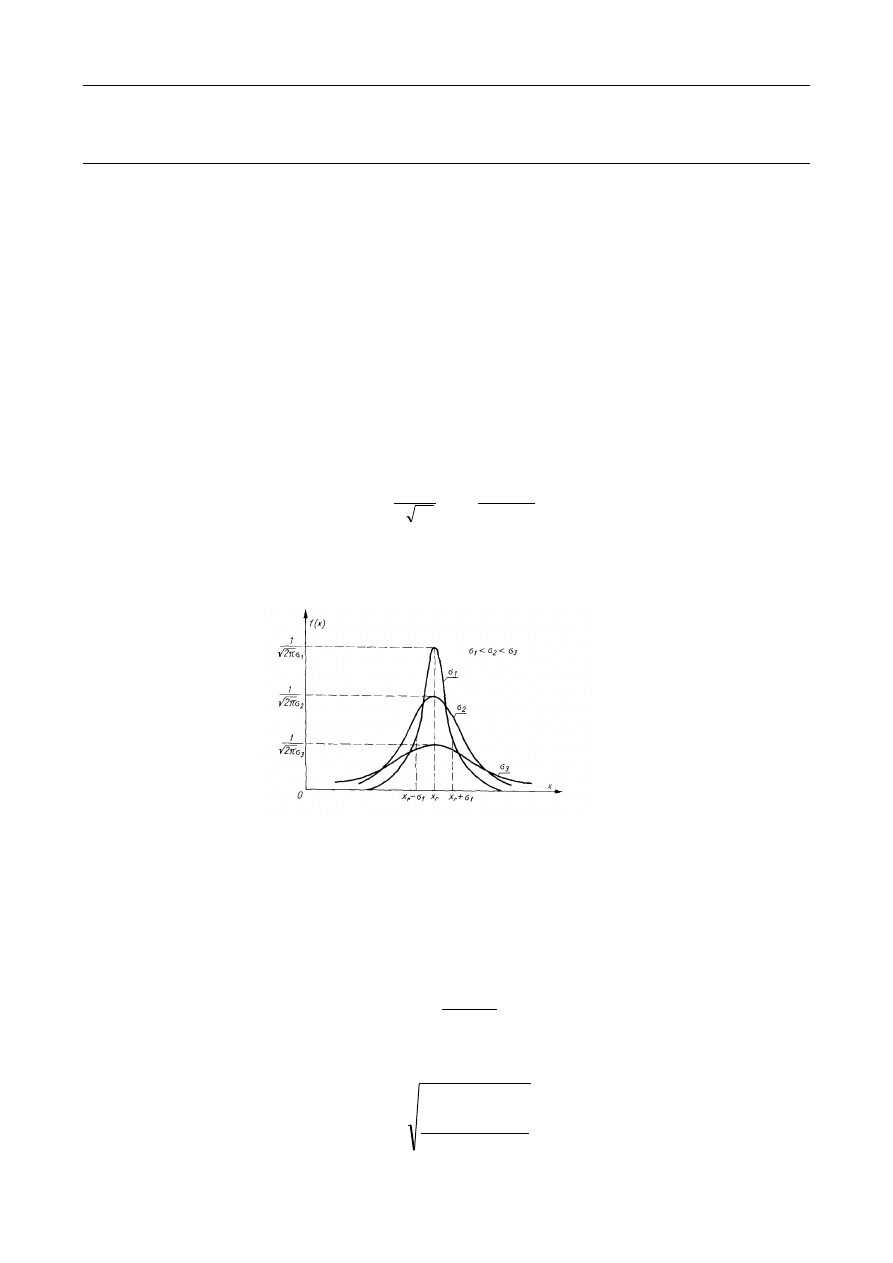
gęstości prawdopodobieństwa, zwanym rozkładem Gaussa (rys. 1):

 



























2

2

2

exp

2

1







r

x

x

x

f

w którym jako x

r

traktuje się wartość rzeczywistą wartości mierzonej. Parametr



> 0 jest miarą

rozrzutu wartości tak określonej zmiennej losowej i nosi nazwę odchylenia standardowego.

Podczas wykonywania pomiarów wartość rzeczywista x

r

wielkości mierzonej nie jest znana, ale

można wykazać, ze jej wartością najbardziej prawdopodobną ze statystycznego punktu widzenia
jest średnia arytmetyczna serii n pomiarów:

n

X

X

n

i

i

s







1

Drugi parametr rozkładu zmiennej losowej jako wyniku pomiaru, odchylenie standardowe



, przy

dostatecznie dużej liczbie pomiarów n > 30 może być wyznaczony ze wzoru:





1

1

2











n

X

x

n

i

s

i



Rys. 1. Przykłady funkcji Gaussa.

2

jako średni kwadratowy błąd pojedynczego pomiaru. Oczywiście samą średnią arytmetyczną X

s

serii pomiarów można też traktować jako zmienną losową (licząc średnie z kilku serii pomiarowych
uzyskuje się różniące się wartości). Teoria prawdopodobieństwa stwierdza, że odchylenie standar-
dowe średniej (średni kwadratowy błąd średniej) jest

n

razy mniejszy od odchylenia standardowe-

go pojedynczego pomiaru:









1

1

2















n

n

X

x

X

n

i

s

i

s

sp

s



Powyższy parametr jako miara rozrzutu średniej ma istotny sens fizyczny, gdyż wyznacza praw-

dopodobieństwo z jakim wartość rzeczywista x

r

zawiera się w przedziale (X

s



t



s

, X

s

+ t



s

).

Przedział ten nosi nazwę przedziału ufności, a prawdopodobieństwo mu odpowiadające nazywa

się poziomem ufności.

Charakterystycznymi przedziałami ufności i odpowiadającymi im poziomami ufności są:

dla t = 1

P(X

s





s

< x

r

< X

s

+



s

) = 0,6826,

dla t = 2

P(X

s



2



s

< x

r

< X

s

+ 2



s

) = 0,9546,

dla t = 3

P(X

s



3



s

< x

r

< X

s

+ 3



s

) = 0,9974.

Przedział



3



s

oznacza więc, że wystąpi w nim 99.74% wszystkich wyników obarczonych błę-

dami przypadkowymi. Prawdopodobieństwo wystąpienia błędu przypadkowego o module więk-
szym niż 3



s

jest więc bardzo małe. Przedział:

s

sp

s

gp

X

X









3

jest granicznym błędem przypadkowym wartości średniej, zwanym też granicznym przedzia-
łem ufności. Należy jednak pamiętać, że zależność na



sp

X

s

jest słuszna pod warunkiem dużej licz-

by powtórzeń pomiarów (teoretycznie n





). Przy liczbie pomiarów n = 3



20 wynik pomiaru

jako zmienna losowa ma rozkład Studenta. Rozkład ten jest szerszy i bardziej spłaszczony od roz-
kładu Gaussa – rys. 2.

Zależy on jednak od liczby pomiarów i przy n > 30 przyjmuje praktycznie kształt krzywej Gaus-

sa. Przy wyznaczaniu przedziału ufności z rozkładu Studenta korzysta się z odpowiednich tablic lub
stosuje się przybliżenie w postaci skorygowanego wzoru na



sp

X

s

rozkładu Gaussa:



’

sp

X

s

= k’



sp

X

s

gdzie:

1

1

1

'







n

k

Zależność na



gp

X

s

pozostaje bez zmian.

Rys. 2. Postać rozkładu Gaussa (1) i Studenta (2)

przy ustalonej liczbie pomiarów k.

3

2. Błędy w pomiarach pośrednich

W eksperymentach pomiarowych spotkać można dwa rodzaje pomiarów:
- pomiar bezpośredni, gdy wartość wielkości mierzonej jest określona na podstawie wskazania

jednego przyrządu;

- pomiar pośredni, gdy wyznaczana wielkość Y jest funkcją kilku innych wielkości pomocni-

czych X

i

:

Y = f(X

1

, X

2

,..., X

n

).

Rozważmy ten drugi rodzaj pomiarów.
Chcemy wiedzieć, jakim błędem wypadkowym



Y będzie obciążona wielkość Y, przy znanych

błędach wielkości pośrednich X

i

. Najczęściej stosowaną metodą szacowania tego błędu, zarówno w

odniesieniu do błędów systematycznych i przypadkowych, jest wykorzystanie pewnej tożsamości
matematycznej zwanej rozwinięciem funkcji w szereg Taylora. Ograniczając się do funkcji dwu
zmiennych powyższe rozwinięcie ma postać:









.

,

,

2

2

1

1

2

1

2

2

1

1

X

X

Y

X

X

Y

X

X

Y

X

X

X

X

Y

Y

Y



































gdzie



X

1

i



X

2

są przyrostami X

1

i X

2

a

n

n

n

n

X

Y

X

Y

2

1

/

i

/









są tzw. pochodnymi cząstkowymi Y

względem X

1

i X

2

. Oznacza to, że

n

n

X

Y

1

/





jest wynikiem różniczkowania Y względem X

1

przy

ustalonym X

2

, a

n

n

X

Y

2

/





to wynik różniczkowania Y względem X

2

przy ustalonym X

1

. Obie po-

chodne obliczane są w punkcie (X

1

, X

2

). Stąd błąd bezwzględny:

2

2

1

1

X

X

Y

X

X

Y

Y



















a błąd względny:

.

2

2

1

1

Y

X

X

Y

Y

X

X

Y

Y

Y

Y























W przypadku, gdy wielkości pomocniczych określonych z błędami jest więcej, korzysta się z

rozwinięcia w szereg Taylora funkcji kilku zmiennych. Błąd bezwzględny pomiaru wielkości Y
można wówczas przedstawić w następujący sposób:

n

n

X

X

Y

X

X

Y

X

X

Y

Y





























...

2

2

1

1

Pouczające jest wyznaczenie tego błędu dla dwu elementarnych pomiarów pośrednich. Jeżeli np.





2

1

2

1

,

X

X

X

X

Y





to obie pochodne cząstkowe:

1

2

1













X

Y

X

Y

Wówczas:



Y





X

1

+



X

2

I drugi przykład – jeżeli:





2

1

2

1

,

X

X

X

X

Y





to pochodne cząstkowe mają postać:

1

2

2

1

i

X

X

Y

X

X

Y













A zatem błąd bezwzględny wynosi:

2

1

1

2

X

X

X

X

Y















a błąd względny:

4

2

1

2

2

1

1

2

1

2

1

2

1

1

2

2

1

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

Y

Y

Y

Y













































Uzyskaliśmy więc dwie proste reguły wyznaczania błędów w pomiarach pośrednich:

1) błąd bezwzględny sumy kilku wielkości jest sumą błędów bezwzględnych każdej z nich;
2) błąd względny iloczynu kilku wielkości jest sumą błędów względnych każdej z nich.

Według wzoru określającego tzw. model propagacji (przenoszenia) błędów, możliwe jest wyzna-
czenie błędu dla dowolnej zależności funkcyjnej. Przykłady najczęściej spotykane przedstawia po-
niższa tabela:

Tabela: Przykłady propagacji błędów.

Funkcja

Sposób propagacji

błędu

y = ax



Y = a



X

y = ax, X

śr



0



y =



x

y = x

a

, X

śr



0



y = a



x

y = e

x

, Y

śr



0



y =



X

y = lnx , X

śr

> 0



Y =



x

y = x

1

+ x

2



Y =



X

1

+



X

2

y = x

1

- x

2



Y =



X

1

+



X

2

y = x

1



x

2



Y =



X

1

+



X

2

y = x

1

/ x

2



Y =



X

1

+



X

2







n

i

i

i

x

a

y

1











n

i

i

i

x

a

y

1







n

i

a

i

i

x

y

1







n

i

i

i

x

a

y

1





Dotychczas zakładaliśmy, że błędy wielkości pomocniczych



X

1

,



X

2

,...,



X

n

są dokładnie zna-

ne. W praktyce pomiarowej sytuacja taka jednak nigdy nie występuje. Analizując błędy przypad-
kowe, można zapisać:













,

...

2

2

1

1

1

1

nr

n

n

r

r

r

X

X

X

Y

X

X

X

Y

X

X

X

Y

Y

Y





























w której indeks „r” odnosi się do wartości oczekiwanych a Y, X

1

, X

2

,..., X

n

są zmiennymi losowymi

(można za nie podstawić wartości uzyskane w serii pomiarowej). Można wykazać, że odchylenie
średnie kwadratowe średniej arytmetycznej



sp

Y

s

wyraża się zależnością:













.

]

...

[

2

1

2

2

2

2

2

2

2

1

2

1

ns

sp

n

s

sp

s

sp

s

sp

X

X

Y

X

X

Y

X

X

Y

Y































































W przypadku błędów systematycznych konkretne wartości błędów wielkości pomocniczych

również nie są znane. Znane są za to granice, w których te błędy są zawarte. W takich wypadkach
oblicza się ekstremalną możliwą wartość błędu pomiaru pośredniego, związaną z przyjęciem przez
wszystkie jego składniki tego samego znaku. Jest to tzw. błąd najgorszego przypadku lub błąd gra-
niczny pomiaru pośredniego i opisuje się go następująco:

.

...

...

2

2

1

1

ns

sp

n

s

sp

s

sp

g

X

X

Y

X

X

Y

X

X

Y

Y































Jeżeli jednak wielkość mierzona zależy od wielu wielkości pomocniczych, to istnieje wówczas

bardzo małe prawdopodobieństwo takiego zdarzenia, że ich błędy systematyczne będą przyjmowały
wartości graniczne i niekorzystny układ znaków. Takie liczenie błędów prowadzi więc do wyniku
zawyżonego. Przy założeniu wzajemnej niezależności błędów wielkości pomocniczych można wy-

5

kazać, że błąd pomiaru pośredniego można obliczać tak, jak błąd przypadkowy. Bezwzględny błąd
graniczny pomiaru pośredniego oblicza się wtedy ze wzoru:













,

]

...

[

2

1

2

2

2

2

2

2

2

1

2

1

ns

g

n

s

g

s

g

g

X

X

Y

X

X

Y

X

X

Y

Y































































gdzie



g

X

i

jest błędem granicznym pomiaru wielkości X

i

.

3. Zasady tworzenia wykresów

Wykresy sporządzanych zależności powinny być wykonane estetycznie, ręcznie przy pomocy

krzywików lub w postaci wydruków na standardowych rozmiarach papierów. Wykresy wykonane
ręcznie muszą być nanoszone na papier milimetrowy a wydruki komputerowe można robić na pa-
pierze gładkim.

Każdy wykres powinien być zaopatrzony w opis zależności funkcyjnej oraz informację w jakich

warunkach był „zdejmowany”. Osie wykresów powinny być oznaczone, tzn. powinny zawierać
informację jakie wielkość są na nich odłożone oraz w jakich jednostkach są wykreślone ich warto-
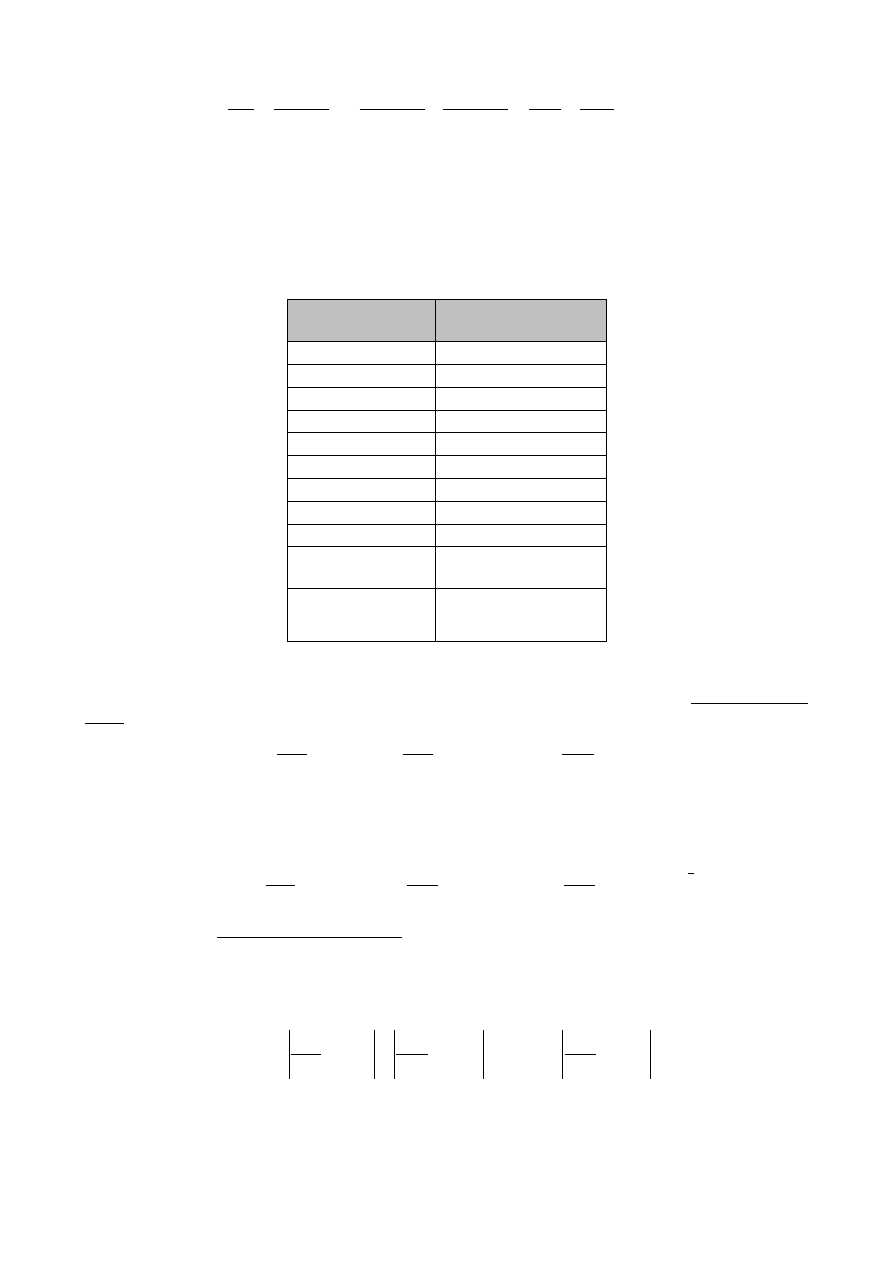
ści. Jeżeli na danym wykresie naniesiono kilka krzywych to należy je wykreślić różnymi kolorami
lub przy pomocy symboli np.



, o, x,



, itp. Wykres taki zawsze powinien być jednoznaczny – opis

poszczególnych krzywych należy zawrzeć pod rysunkiem lub w legendzie – rys. 3.

Rys.3. Przykład wykresu

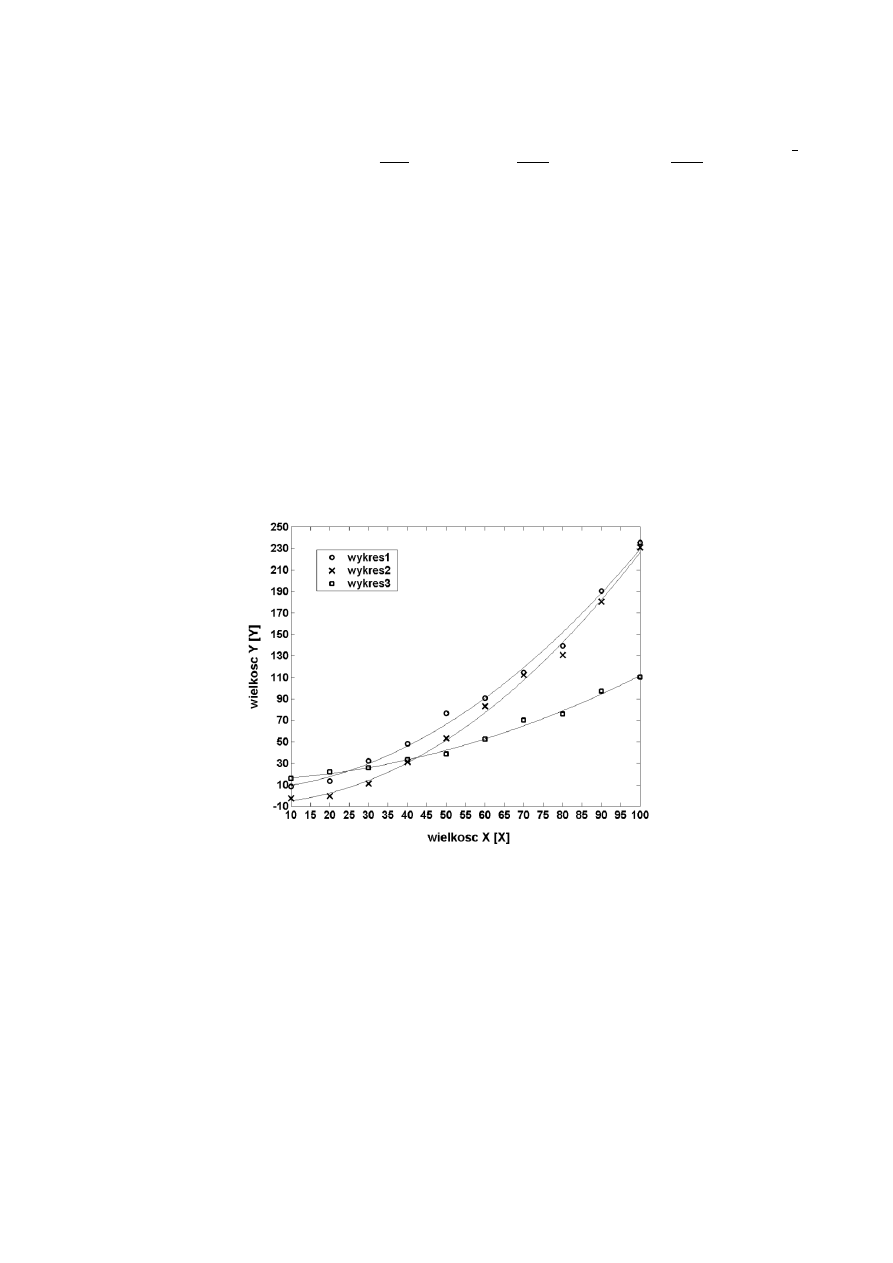
Ogólnie dostępny papier milimetrowy reprezentuje tzw. siatkę liniowo-liniową. Oprócz siatki li-

niowej, w celu uwypuklenia charakterystycznych zmian interesującej nas zależności, stosuje się
jeszcze siatki logarytmiczne: liniowo-logarytmiczną, logarytmiczno-liniową i logarytmiczno-
logarytmiczną – rys. 4.

Siatka liniowo-logarytmiczna znajduje zastosowanie gdy zakres liczbowy wartości osi rzęd-

nych (oś y) jest znaczny, tzn. poszczególne wartości y

i

różnią się między sobą o rzędy wielkości.

Pozwala ona ponadto na sprawdzenie istnienia między dwiema wielkościami zależności typu

y = Ae

ax

gdzie A, a – stałe, gdyż linearyzuje jej wykres.
Podobnie, gdy wartości osi odciętych x charakteryzują się dużym zakresem zmian, wykorzysty-

wana jest siatka logarytmiczno-liniowa. Dodatkowo pozwala na linearyzację zależności typu

y = A + alnx

gdzie A, a – stałe.

6

Siatkę logarytmiczno-logarytmiczną wykorzystuje się natomiast w sytuacji, gdy wartości na

obu osiach charakteryzują się użymi zakresami zmian oraz do sprawdzania zależności typu y = Ax

a

,

gdzie A, a – stałe.

Rys.4 Rodzaje siatek:

a) liniowa;

b) liniowo-logarytmiczna;

c) logarytmiczno-liniowa;

d) logarytmiczno-logarytmiczna.

Pewną odmianą skali logarytmicznej dla osi rzędnych jest skala decybelowa, służąca do wyra-

żania stosunku wartości interesującej nas wielkości np. U do pewnej wielkości odniesienia U

0

. War-

tość U/U

0

wyrażona w skali decybelowej wynosi:

0

0

lg

20

]

[

U

U

dB

U

U



gdzie lg jest oznaczeniem logarytm dziesiętnego. Wykorzystuje się ją do zobrazowania dużego za-
kresu zmian pewnych wielkości stosunkowych, np. wzmocnienia.

W przypadku braku dostępu do siatki logarytmicznej wykres można również wykonać na zwy-

kłym papierze milimetrowym stosując odpowiednie skalowanie.
Przykład.

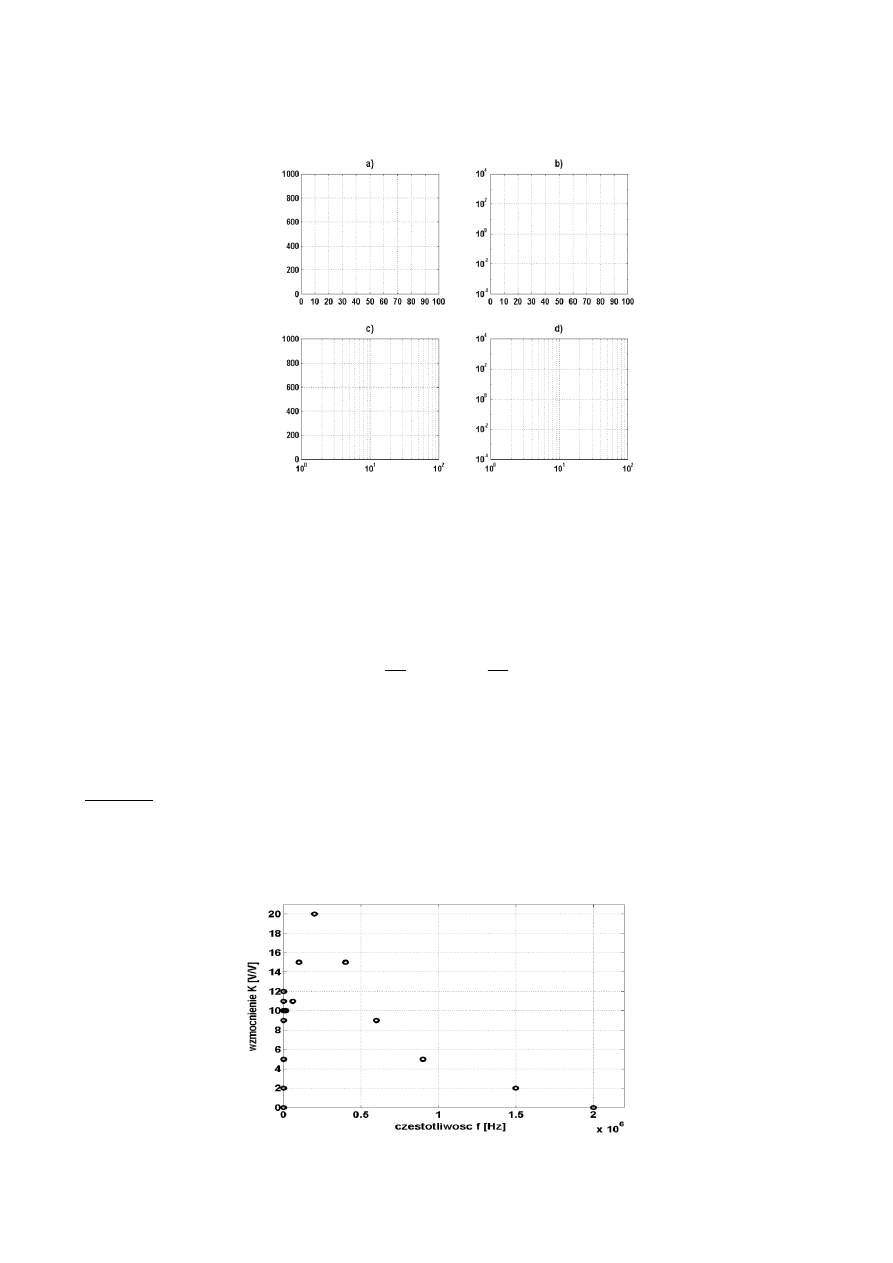
W tabeli 6 w wierszach 1-3 przedstawiono wyniki pomiaru przebiegu wzmocnienia pewnego

wzmacniacza w funkcji częstotliwości. Wykres sporządzony na podstawie wartości zawartych w
tabeli 6 i przedstawiony na rys. 5 w skali liniowej jest całkowicie nieczytelny dla małych częstotli-
wości.

Rys.5. Przykład źle dobranej skali dla osi częstotliwości

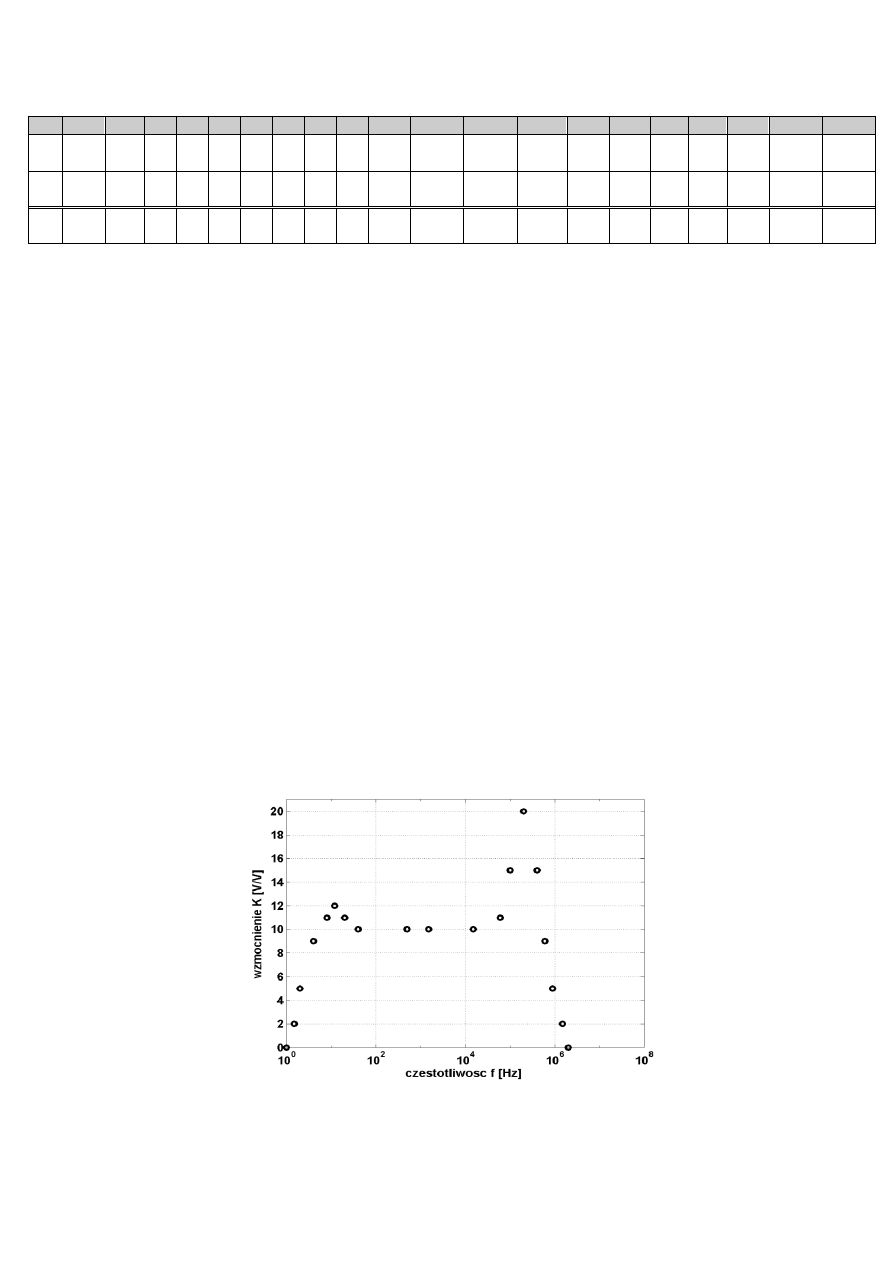
7

Warto zastanowić się chwilę nad wartościami f. Obejmują one zakres od 1 Hz do 2 MHz czyli

ponad 6 dekad. Dekadę tworzy przedział, którego górna granica jest 10 razy większa od dolnej.

Pierwsza dekada obejmuje więc zakres (0, 10) Hz,
druga (10, 100) Hz,
trzecia (100, 1000) Hz itd.

Długości tych przedziałów w skali liniowej rosną. Zastosowanie skali logarytmicznej (np. loga-

rytmu przy podstawie 10 z wartości częstotliwości) sprawia, że na rysunku będą one miały tę samą
długość. Przypuśćmy, że na wykonanie osi dla f mamy do dyspozycji 21 cm. Rezerwując na każdą
dekadę w skali logarytmicznej po 3 cm uzyskamy długość odcinka odpowiadającego wszystkim 6
dekadom równą 6



3 cm = 18 cm. Poszczególnym granicom przedziałów będą więc odpowiadały

następujące wartości w centymetrach:

10

0

Hz



0 cm

10

1

Hz



3 cm

10

2

Hz



6 cm

10

3

Hz



9 cm

itd.

Zależność przeskalowująca jest oczywista: wartościom częstotliwości wyrażonym w hercach należy
przypisać następujące odległości na osi wyrażone w centymetrach:

f’[cm] = {log

10

[f [Hz]]}



3 [cm].

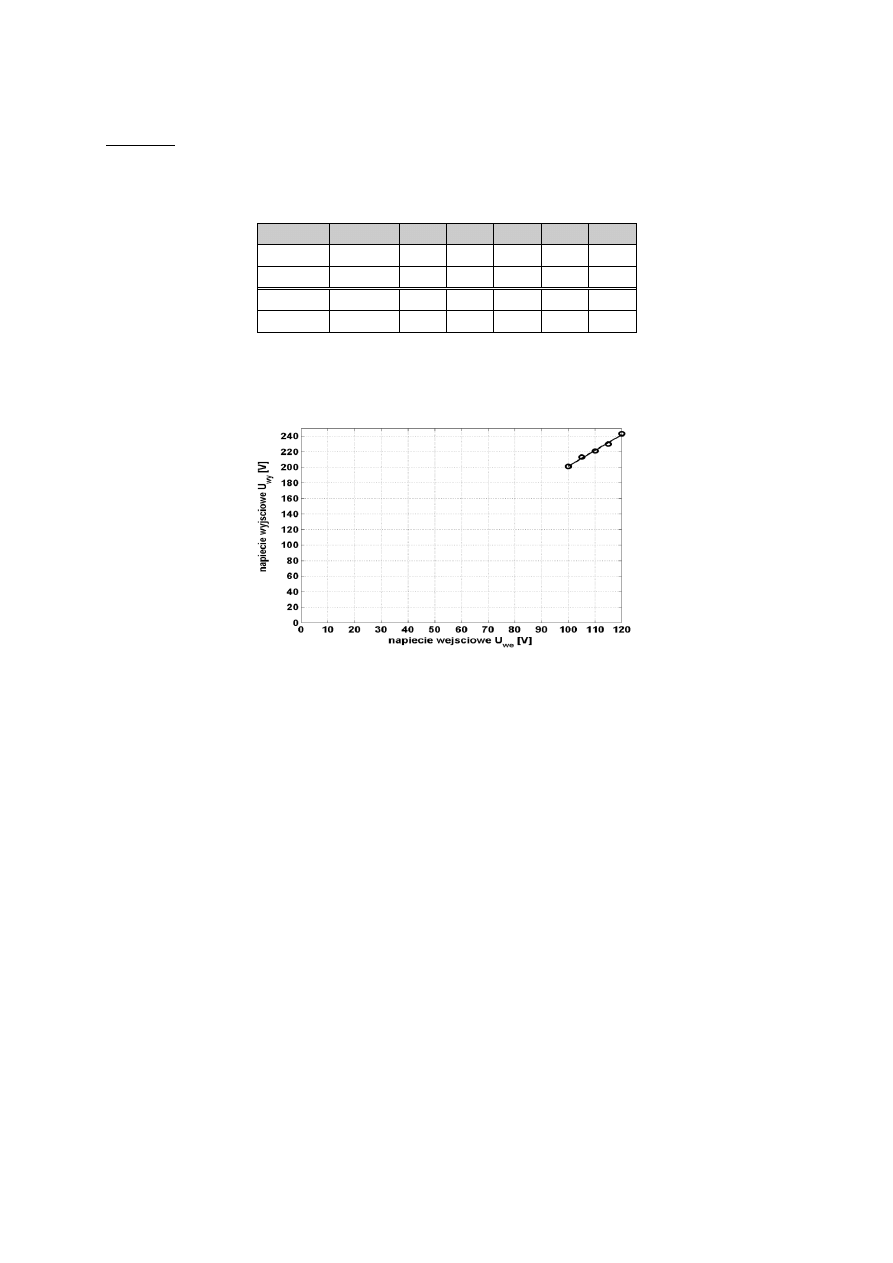
Wiersz 4 tabeli 6 zawiera obliczone wartości f’ [cm] a odpowiedni wykres w uzyskanej skali lo-

garytmiczno-liniowej przedstawia rys. 6. Można na nim zaobserwować pasmowy charakter
wzmocnienia wzmacniacza z dwoma podbiciami w zakresie niskich i wysokich częstotliwości.

Rys. 6. Przykład dobrze dobranej skali dla osi częstotliwości.

Tabela 6. Wyniki pomiarów wzmocnienia K pewnego wzmacniacza w funkcji częstotliwości f.

Lp

-

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

f

Hz

1

1.5

2

4

8

12 20 40

500 1.5



10

3

1.5



10

4

6



10

3

10

5

2



10

5

4



10

5

6



10

5

9



10

5

1.5



10

6

2



10

6

K

V/V

0

2

5

9

11 12 11 10

10

10

10

11

15

20

15

9

5

2

0

f’

cm

0

0,5 0,9 1,8 2,7 3,2 3,9 4,8

8,1

9,5

12,5

14,3

15,0 15,9 16,8 17,3 17,9

18,5

18,9

8

W celu wykorzystania pełnej powierzchni rysunku niejednokrotnie konieczne jest przesuwanie

początku układu współrzędnych.

Przykład.
W tabeli 7 w wierszach 1-3 przedstawiono wyniki charakterystyki przetwarzania pewnego

wzmacniacza.

Tabela 7. Przykładowa charakterystyka przetwarzania.

Lp.

-

1

2

3

4

5

U

we

mV

100 105 110 115 120

U

wy

mV

201 213 221 230 243

U’

we

mV

0

4

8

12

16

U’

wy

mV

0,5

6,5 10,5 15,0 21,5

Podobnie jak poprzednio, wykres sporządzony na ich podstawie – rysunek poniżej jest nieczy-

telny i wymaga przesunięcia początku układu współrzędnych.

Przypuśćmy, że mamy do dyspozycji 18 cm dla osi x i 25 cm dla osi y. Należy zastosować takie

zależności przeskalowujące, aby po pierwsze – wielokrotność działki podstawowej papieru milime-
trowego np. 1 cm, 2 cm, 3 cm itd. odpowiadała 1, 2, 5, 10, 20, 50 itd. jednostkom mierzonej wiel-
kości (należy to zapewnić zawsze, niezależnie od konieczności przesuwania początku układu
współrzędnych) i po drugie – aby w pełni wykorzystać powierzchnię wykresu. Rozważmy oś x.
Chcemy, aby długości ok. 18 cm odpowiadał przedział o szerokości

120 mV – 100 mV = 20 mV.

Przy skalach bazujących na jednostce papieru milimetrowego np. 1 cm/ 1mV i 1 cm/ 2mV uzysku-
jemy wartości

20 mV



(1 cm/ 1mV) = 20 cm

oraz 20 mV



(1 cm/2 mV) = 10 cm,

odpowiadające kolejno – przekroczeniu i znacznemu niewypełnieniu dostępnego zakresu 18 cm.
Przy zastosowaniu skali S

x

= 4 cm/ 5 mV bazującej na wielokrotności działki podstawowej papieru

milimetrowego uzyskujemy wartość

20 mV



(4 cm/5 mV) = 16 cm,

co już można uważać za rozsądne wypełnienie dostępnego zakresu. Zależność przeskalowująca
będzie więc miała postać:

U’

we

[cm] = (U

we

- U

wemin

)



S

x

= (U

we

– 100 mV)



(4 cm/ 5 mV).

Podobnie postępując można dla osi y wyprowadzić zależność:

U’

wy

[cm] = (U

wy

- U

wymin

)



S

y

,

W której S

y

najwygodniej wyznaczyć tak, aby zakresowi 25 cm odpowiadał przedział (200, 250)

mV, czyli przedział o szerokości 50 mV:

Rys. 7. Przykład złego rozplanowania powierzchni rysunku.

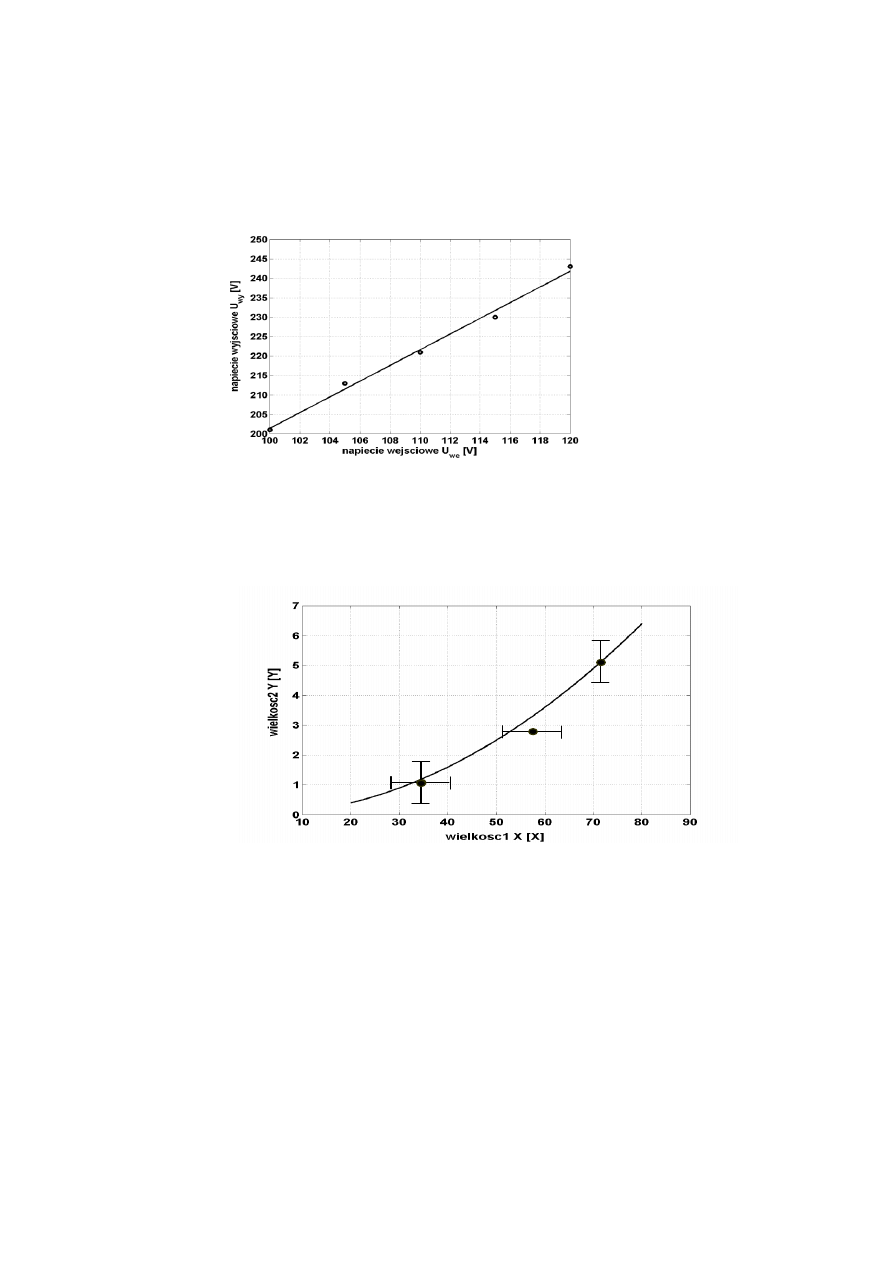
9

S

y

= 1 cm/ 2 mV,

gdyż 50 mV



S

y

= 25 cm. Ostatecznie więc:

U’

wy

[cm] = (U

wy

- 200 mV)



(1 cm/ 2 mV).

Wyznaczone wartości U’

we

[cm] i U’

wy

[cm] zawiera w wierszach 4-5 tabela 7, a sporządzony na ich

podstawie wykres przedstawia rys. 8.

Niekiedy należy na wykresie zaznaczyć stopień dokładności realizowanych pomiarów. Używa

się wówczas oznaczeń przedstawionych na rys. 9.

W większości przypadków należy również jako zasadę przyjąc fakt, iż poszczególnych punktów

wykresu nie należy łączyć krzywą łamaną. Można tak postapić jedynie wówczas, gdy
przedstawiane zależności mają znaczenie jedynie formalne. W przypadku wielkości fizycznych
należy dokonać przybliżenia dyskretnych wyników pomiarów wykonując tzw. aproksymację.

Zadaniem aproksymacji zależności między dwiema wielkościami X i Y jest szacowanie jej

przebiegu na podstawie przeprowadzonych pomiarów. Można tego dokonać w sposób graficzny za
pomocą krzywików i linijki, prowadząc krzywą aproksymującą tak, aby przechodziła ona przez jak
największą liczbę punktów określonych empirycznie lub blisko nich. Rozłożenie punktów
względem krzywej powinno być, według oceny “na oko”, symetryczne z zachowaniem, w miarę
możliwości, jednakowej liczby punktów po jej obu stronach.

Rys. 8. Przykład dobrego rozplanowania powierzchni rysunku.

Rys. 9. Przykłady oznaczania na wykresach dokładności pomiarów.

dokładność wielkości
Y

dokładność wielkości
X

dokładność wielkości X i Y

10

Znacznie dokładniejszą metodą aproksymacji jest metoda analityczna zwana metodą naj-

mniejszych kwadratów lub metodą regresji. W najbardziej elementarnym ujęciu jako funkcję
aproksymująca przyjmuje się wielomian n-tego rzędu:

n

n

X

a

X

a

X

a

a

X

f

Y













...

)

(

2

2

1

0

którego współczynniki a

0

, a

1

, ..., a

n

wyznacza się na podstawie wyników pomiarów. Stopień wie-

lomianu przyjmowany jest z reguły na podstawie pewnej wiedzy a priori o badanej zależności, tzn.
należy założyć, że jest ona liniowa (n = 1), kwadratowa (n = 2), sześcienna (n = 3) itd.

Przy braku tej wiedzy rząd wielomianu można dobierać eksperymentalnie, pamiętając jednak,

że jego wzrost prowadzi, co prawda, do zmniejszenia błędu dopasowania krzywej aproksymującej
do punktów empirycznych, ale kosztem pojawienia się między nimi niepożądanych oscylacji.

Zasada wyznaczania funkcji aproksymującej jest następująca.

Przypuśćmy, że chodzi o wyznaczenie często występującej w praktyce zależności liniowej dla N
punktów pomiarowych. Poszukujemy a

0

i a

1

w formule:

X

a

a

Y

1

0





Przy zakładanej liniowości danemu punktowi pomiarowemu x

i

powinna odpowiadać wartość

y’

i

= a

0

+ a

1

x

i

. Z pomiarów znamy jednak „błędne” y

i

, więc różnica



i

= y

i

- (a

0

+ a

1

x

i

) jest błędem

i-tego wyniku y

i

. Tworząc sumę kwadratów wszystkich błędów:

























N

i

i

i

N

i

i

x

a

a

y

1

2

1

0

1

2

możemy znaleźć takie a

0

i a

1

, dla których powyższa suma osiąga minimum (stąd uzasadnienie na-

zwy – metoda najmniejszych kwadratów). Badanie minimum jest zadaniem trywialnym i polega na
wyznaczeniu pochodnych względem a

0

i a

1

i przyrównaniu ich do zera. Z układu dwu równań wy-

znacza się wówczas wartości a

0

i a

1

:

  

 

,

1

0

2

2

1

N

x

a

N

y

a

x

x

N

y

x

y

x

N

a

i

i

i

i

i

i

i

i

























w których operacje sumowania odbywają się względem indeksu i. Otrzymane wartości dają najlep-
sze przybliżenie współczynników poszukiwanej prostej oparte na wynikach pomiarów w sensie
średniokwadratowym. Organizacja powyższych obliczeń powinna być w sprawozdaniu zobrazowa-
na tabelą zestawiającą kolejno wartości x

i

, y

i

, x

i

y

i

, x

i

2

potrzebne do końcowych wzorów.

Przedstawioną metodę łatwo uogólnić na przypadek wielomianu dowolnego stopnia lub dowolnej
funkcji y = f(x) zależnej od nieznanych parametrów a

0

, a

1

, ..., jednakże powstałe równania liniowe

mogą być wtedy trudne lub wręcz niemożliwe do rozwiązania.

Zagadnienia aproksymacji nie należy mylić z inną metodą znajdowania zależności funkcyjnej

między danymi uzyskanymi z pomiaru, zwaną interpolacją. Polega ona na wyznaczeniu krzywej,
która jest dopasowana z zerowym błędem do wyników pomiarów (przechodzi przez wszystkie
punkty empiryczne). W zagadnieniach interpolacji wykorzystuje się m. in. metody funkcji skleja-
nych (ang. splines).

P

RZYKŁADOWE PYTANIA KONTROLNE

1. Omów stosowany w metrologii sposób opisu błędów przypadkowych.
2. Przedstaw reguły przenoszenia błędów.

3. Omów pojęcia: skala liniowa, skala liniowo-logarytmiczna, skala logarytmiczno-liniowa, skala

decybelowa.

4. Wyjaśnij pojęcie aproksymacji.

5. Omów zagadnienie aproksymacji metodą najmniejszych kwadratów.

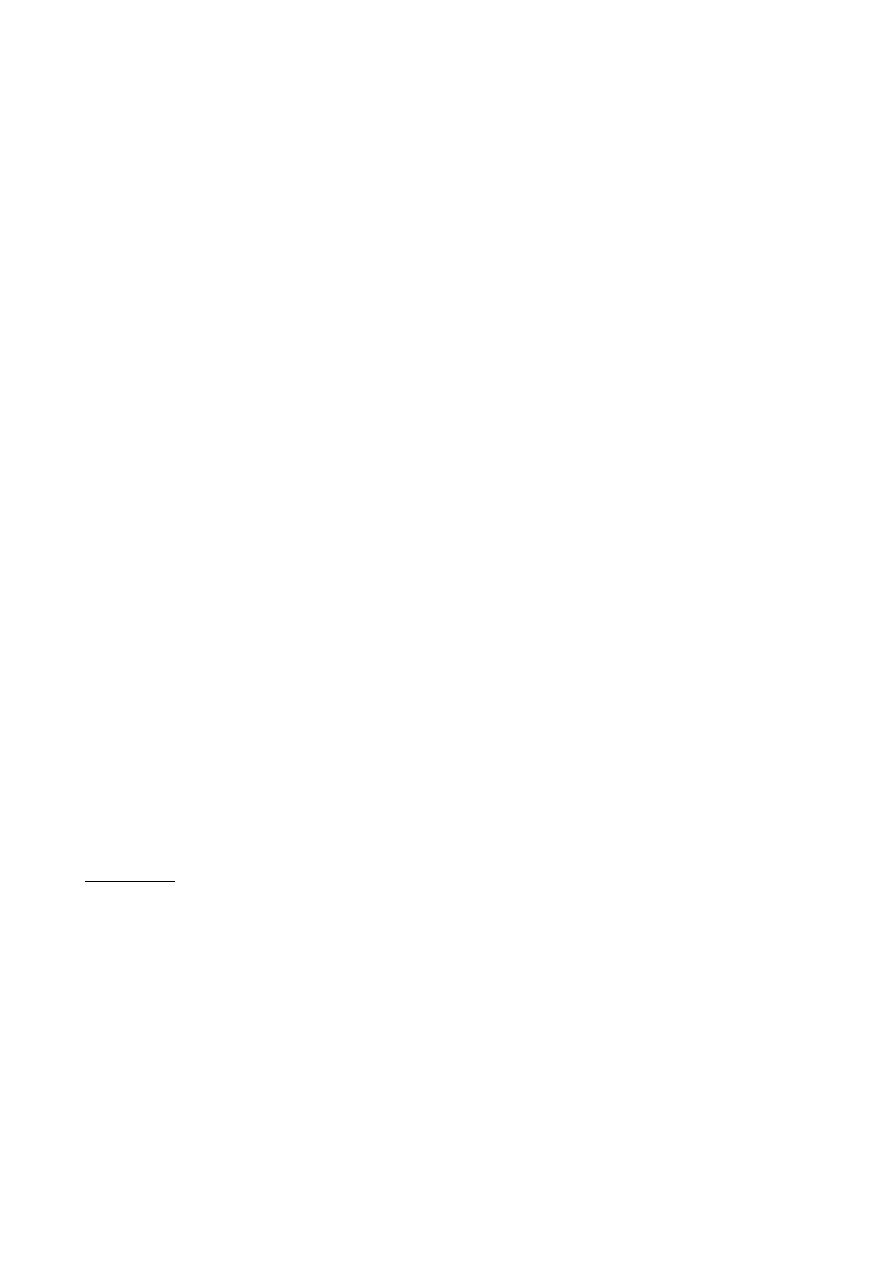
11

MULTIMETR ANALOGOWY HC - 5050E

NAPIĘCIE PRZEMIENNE:

Zakresy pomiarowe: 0…3-12-30-120-300 V napięcie skuteczne;

0…8,4-33-84-330-840 V napięcie międzyszczytowe (p-p);

skuteczne 1200 V (międzyszczytowe 3300 V).

Impedancja wejściowa: około 1 MΩ 80 pF, 2,5 MΩ na zakresie 3 V.

Dokładność: 30 Hz ÷ 1 MHz ± 3,5 % dla przebiegu sinusoidalnego na zakresie 3 V;

30 Hz ÷ 5 kHz ± 3,5 % dla przebiegu sinusoidalnego na zakresie 12 ÷ 300 V;

30 Hz ÷ 500 Hz ± 5 % dla przebiegu sinusoidalnego na zakresie 1200 V;

dB:

-10 dB ÷ + 63 dB na zakresach AC.

PRĄD PRZEMIENNY:

Zakresy pomiarowe: 0 – 12 A;

Dokładność:

± 3,5 % zakresu pomiarowego.

OSTRZEŻENIE

Podczas pomiarów instalacji wysokiego napięcia należy zachować szczególną ostrożność. Po-

mimo dobrej izolacji przyrządu i przewodów pomiarowych zaleca się, aby nie trzymać przyrządu w
chwili, gdy do mierzonego obwodu doprowadzane jest zasilanie.

Pomiary należy rozpoczynać zaczynając od wyższych zakresów pomiarowych, jeżeli nie jest

znana przewidywana wartość prądu lub napięcia. Pozycja przełącznika zakresu pomiarowego nie
powinna być zmieniana, gdy przyrząd znajduje się pod obciążeniem. Zaleca się, aby przewody po-
miarowe były odłączone od mierzonej instalacji podczas zmiany zakresów pomiarowych.

POMIAR SKUTECZNEGO NAPIĘCIA PRZEMIENNEGO 3 V ÷ 1200 V.

- Podłączyć czarny przewód pomiarowy do gniazda COM a czerwony przewód pomiarowy do

gniazda VΩA;

- Ustawić przełącznik zakresów pomiarowych na pozycję jednego z pięciu zakresów funkcji

pomiaru napięcia przemiennego (AC V). Pomiary należy rozpoczynać zaczynając od najwyż-
szych zakresów pomiarowych, jeżeli nie jest znana przewidywana wartość mierzonego napię-
cia.

- Włączyć zasilanie testowanego obwodu. Odczytać wartość napięcia na czerwonej skali podpi-

sanej jako ACV (rms) lub na czerwonej skali podpisanej jako ACV(P-P).

POMIAR PRĄDU NA ZAKRESIE 12A
Ostrzeżenie: Nie wolno podłączać przewodów pomiarowych do źródeł napięciowych przy pomia-
rach prądu. Spowoduje to uszkodzenie przyrządu.

- Podłączyć czarny przewód pomiarowy do gniazda COM a czerwony przewód pomiarowy do

gniazda 12A.

- Ustawić przełącznik zakresów pomiarowych na właściwą pozycję – dla AC pozycja AC12A,

dla DC pozycja 300mA.

- Przy wyłączonym zasilaniu mierzonego obwodu należy przerwać mierzony obwód w miejscu,

w którym ma być pomierzony prąd. Podłączyć przyrząd szeregowo w obwód zwracając uwa-
gę na właściwą polaryzację.

- Włączyć zasilanie mierzonego obwodu. Maksymalne odchylenie wskazówki w lewo oznacza,

że polaryzacja mierzonego obwodu jest odwrotna do przewidywanej. W takim wypadku nale-
ży wyłączyć zasilanie testowanego obwodu i zamienić przewody pomiarowe. Przełącznik
zmiany polaryzacji przy tym pomiarze musi być na pozycji „+”.

- Wartość prądu należy odczytywać na czerwonej skali opisanej jako AC12A