-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
1
2.3. Podstawy teorii przewodnictwa cieplnego
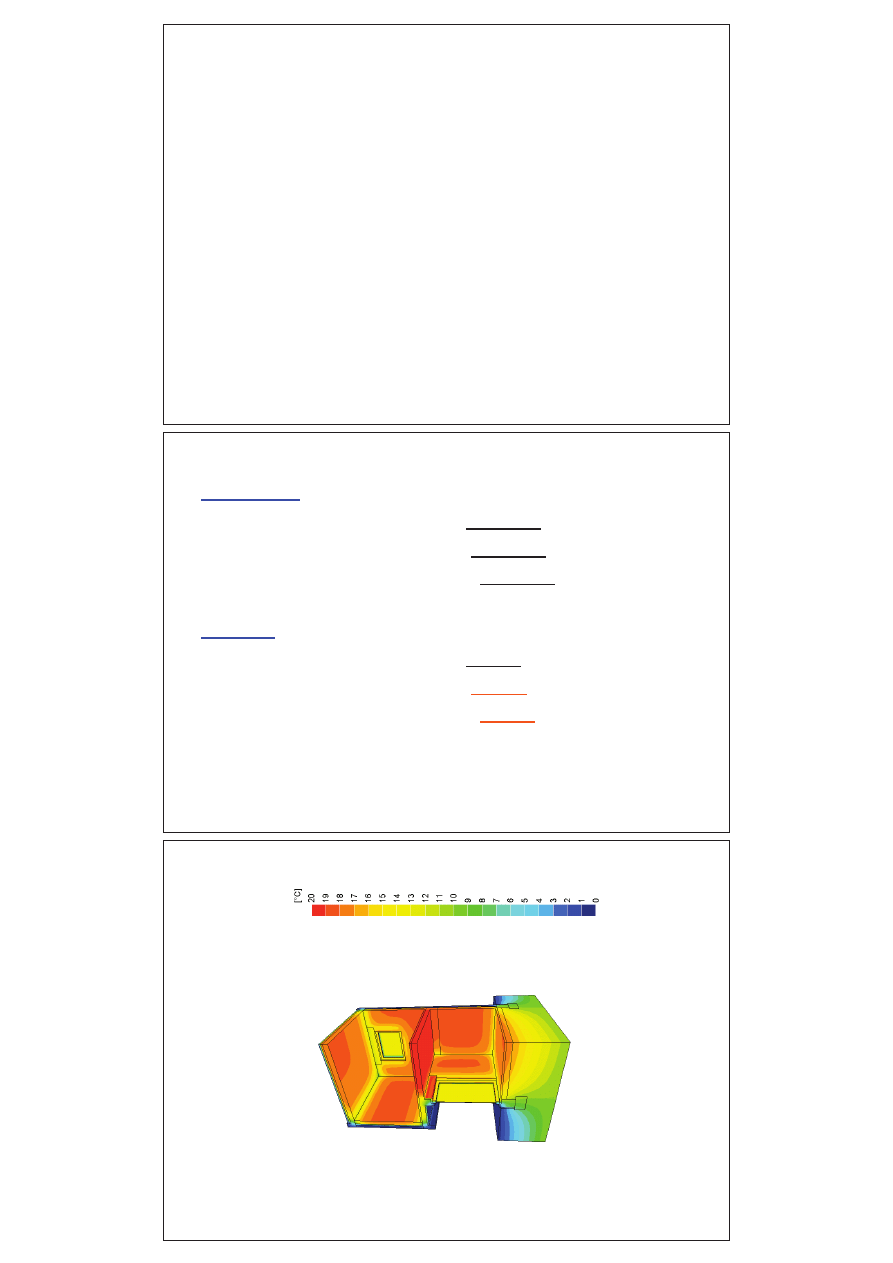
2.3.1. Pole temperatury
Polem temperatury
nazywany jest zbiór warto
ści temperatury
we wszystkich punktach rozpatrywanego ciała w danej chwili
tj. w funkcji czasu (zale
żność funkcyjna temperatury od
współrz
ędnych przestrzennych i czasu).
Pole temperatury mo
że być
nieustalone
(zale
żne od czasu)
i
ustalone
(niezale
żne od czasu)
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
2
Nieustalona wymiana ciepła przez przegrody budowlane
t = f (x, y, z,
τ
)
trójwymiarowe nieustalone pole temperatury
t = f (x, y,
τ
)
dwuwymiarowe nieustalone pole temperatury
t = f (x,
τ
)
jednowymiarowe nieustalone pole temperatury
Ustalona wymiana ciepła przez przegrody budowlane
t = f (x, y, z)
trójwymiarowe ustalone pole temperatury
t = f (x, y)
dwuwymiarowe ustalone pole temperatury
t = f (x)
jednowymiarowe ustalone pole temperatury
>>>(Obliczanie U)
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
-
W
y
k
ła
d
2
–
”
F
iz
y
k
a
B
u
d
o
w
li”
,
W
y
d
z
ia
ł
B
u
d
o
w
n
ic
tw
a
L
ą
d
o
w
e
g
o
i
W
o
d
n
e
g
o
P
o
lit
e
c
h
n
ik
i
W
ro
c
ła
w
s
k
ie
j
II
I
ro
k
,
ro
k
a
k
a
d
e
m
ic
k
i
2
0
1
1
/2
0
1
2
,
p
ro
w
a
d
z
ą
c
y
:
d
r
h
a
b
.
in
ż
.
H
e
n
ry
k
N
o
w
a
k
,
p
ro
f.
P
W
r
3
PO
L
E
T
EM
EP
ER
A
T
U
R
Y
P
RZ
Y
KŁ
A
D
O
W
Y
RO
Z
KŁ
A
D
T
E
M
P
E
R
A
T
U
R
Y
W
N
A
R
O
Ż
U
BUD
Y
NK
U
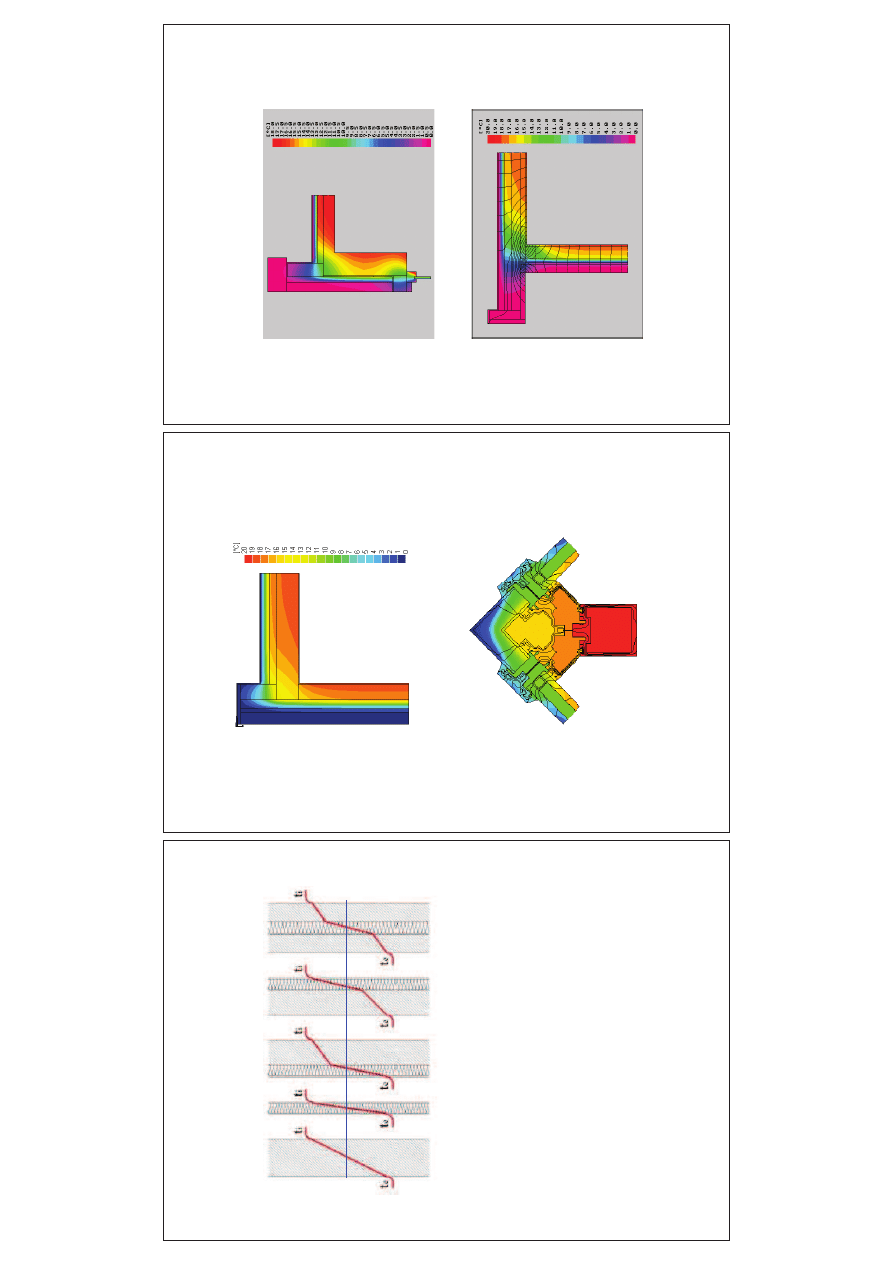
tró
jw
y
m
ia
ro
w
e
u
st
a
lo
n
e
p
o
le
te
m
p
era
tu
ry
t
=
f
(x
,y
,z
)
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
-
W
y
k
ła
d
2
–
”
F
iz
y
k
a
B
u
d
o
w
li”
,
W
y
d
z
ia
ł
B
u
d
o
w
n
ic
tw
a
L
ą
d
o
w
e
g
o
i
W
o
d
n
e
g
o
P
o
lit
e
c
h
n
ik
i
W
ro
c
ła
w
s
k
ie
j
II
I
ro
k
,
ro
k
a
k
a
d
e
m
ic
k
i
2
0
1
1
/2
0
1
2
,
p
ro
w
a
d
z
ą
c
y
:
d
r
h
a
b
.
in
ż
.
H
e
n
ry
k
N
o
w
a
k
,
p
ro
f.
P
W
r
4
d
w
u
w
y
m
ia
ro
w
e
u
st
a
lo
n
e
p
o
le
te
m
p
era
tu
ry
t
=
f
(x
,y
)
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
-
W
y
k
ła
d
2
–
”
F
iz
y
k
a
B
u
d
o
w
li”
,
W
y
d
z
ia
ł
B
u
d
o
w
n
ic
tw
a
L
ą
d
o
w
e
g
o
i
W
o
d
n
e
g
o
P
o
lit
e
c
h
n
ik
i
W
ro
c
ła
w
s
k
ie
j
II
I
ro
k
,
ro
k
a
k
a
d
e
m
ic
k
i
2
0
1
1
/2
0
1
2
,
p
ro
w
a
d
z
ą
c
y
:
d
r
h
a
b
.
in
ż
.
H
e
n
ry
k
N
o
w
a
k
,
p
ro
f.
P
W
r
5
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
--
-
W
y
k
ła
d
2
–
”
F
iz
y
k
a
B
u
d
o
w
li”
,
W
y
d
z
ia
ł
B
u
d
o
w
n
ic
tw
a
L
ą
d
o
w
e
g
o
i
W
o
d
n
e
g
o
P
o
lit
e
c
h
n
ik
i
W
ro
c
ła
w
s
k
ie
j
II
I
ro
k
,
ro
k
a
k
a
d
e
m
ic
k
i
2
0
1
1
/2
0
1
2
,
p
ro
w
a
d
z
ą
c
y
:
d
r
h
a
b
.
in
ż
.
H
e
n
ry
k
N
o
w
a
k
,
p
ro
f.
P
W
r
6
jed
n
o
w
y
m
ia
ro
w
e
u
st
a
lo
n
e
p
o
le
te
m
p
era
tu
ry
t
=
f
(x
)
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
7
2.3.2. Nieustalone przewodzenie ciepła w ciałach stałych
Model matematyczny przewodzenia ciepła w ciałach stałych obejmuje
matematyczne sformułowanie prawa przewodzenia ciepła, równania
różniczkowego bilansu energii oraz podanie warunków jednoznaczności
jego rozwiązania.
Przewodzenie ciepła w nieprzezroczystych ciałach stałych opisuje
prawo Fouriera, które brzmi -
gęstość przewodzonego strumienia ciepła jest
wprost proporcjonalna do gradientu temperatury mierzonego wzdłuż
kierunku przepływu ciepła i oblicza się ze wzoru:
dx
dT
gradT
q
λ
λ
−
=
−
=
w którym:
λ
λ
λ
λ
- współczynnik przewodzenia ciepła, [W/(m K)],
T
- temperatura, [K],
dT/dx - gradient temperatury [K/m] w kierunku prostopadłym do powierzchni izotermicznej
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
8
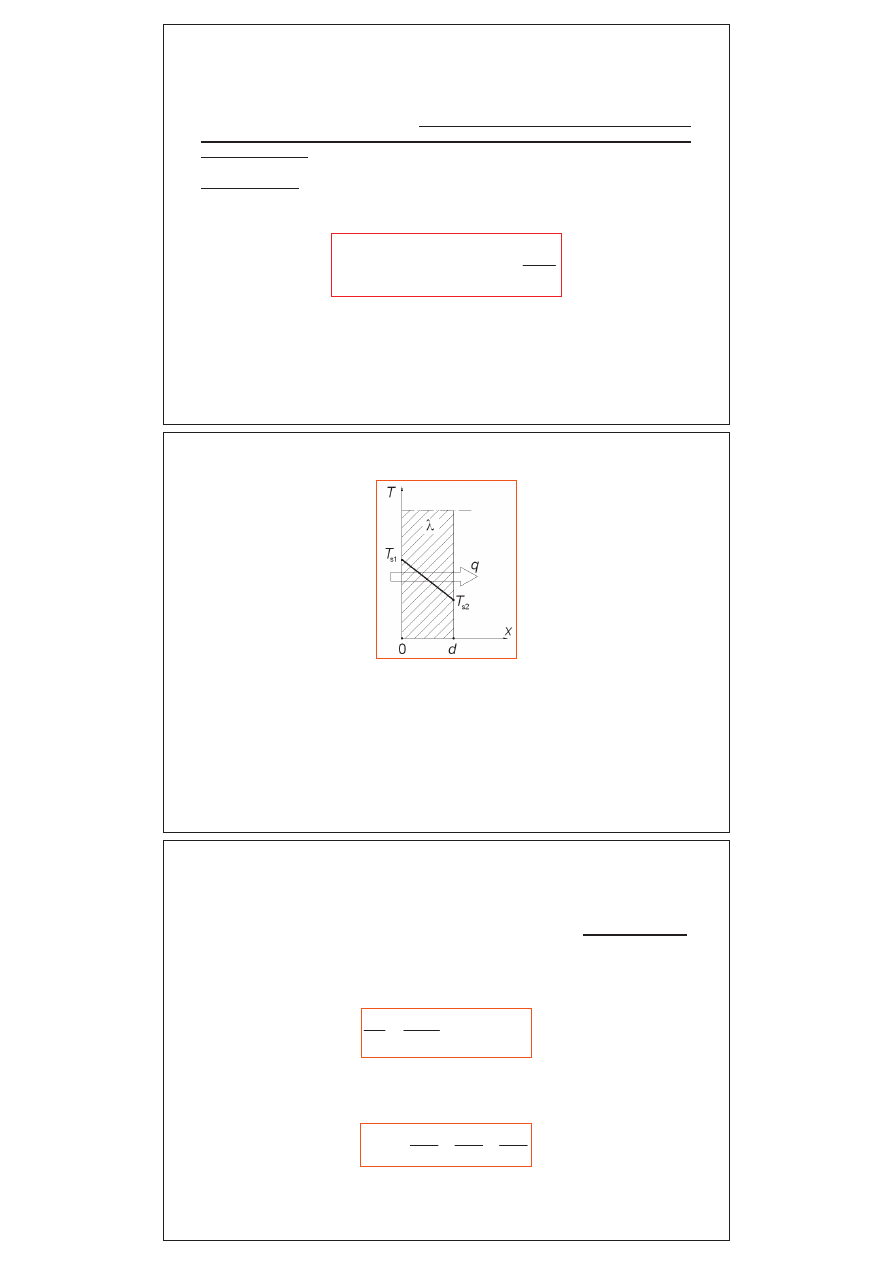
Przewodzenie ciepła w płaskiej przegrodzie jednowarstwowej
Znak minus we wzorach wynika z faktu, że ciepło płynie zgodnie ze
spadkiem temperatury i występuje ”ujemny przyrost” temperatury
(odcinkowi dx wzdłuż kierunku przepływu ciepła odpowiada ujemna
wartość przyrostu temperatury dT). Prawo Fouriera umożliwia obliczenie
gęstości strumienia ciepła i jest pomocne przy wyznaczaniu strumieni
cieplnych w stanie ustalonym (stacjonarnym).
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
9
Podstawą tworzenia modelu nieustalonej wymiany ciepła przegród
budowlanych z otaczającym środowiskiem jest równanie różniczkowe
nieustalonego przewodzenia ciepła w ciałach stałych, tj. równie Fouriera,
uzupełnione równaniami przejmowania ciepła przez konwekcję i przez
promieniowanie. Równanie Fouriera, przy założeniu stałej, tj. niezależnej od
temperatury, wartości współczynnika przewodzenia ciepła
λ
λ
λ
λ oraz braku
wewnętrznych źródeł ciepła, jest postaci:
T
a
T
c
T
p
o
2
2
∇
=
∇
=
∂
∂
ρ
λ
τ
gdzie a jest współczynnikiem wyrównywania temperatury (dyfuzyjność
cieplna), natomiast
∇
∇
∇
∇
2
T jest laplasjanem temperatury, który w układzie
współrzędnych prostokątnych ma postać:
2
2
2
2
2
2
2
z
T
y
T
x
T
T
∂
∂
+
∂
∂
+
∂
∂
=
∇
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
10
Równanie przewodnictwa (równanie Fouriera) mo
że być również zapisane we
współrz
ędnych walcowych i kulistych, z uwzględnieniem wydajności wewnętrznych
źródeł ciepła oraz dla zagadnień nieliniowych.
Rozwi
ązanie równania przewodnictwa cieplnego umożliwia określenie pola
temperatury w dowolnym punkcie rozpatrywanego obszaru nieprzezroczystego
(przegrody budowlanej). Zało
żenie o nieprzezroczystości analizowanego obszaru
jest bardzo istotne, poniewa
ż w przeciwnym razie ciepło byłoby przenoszone przez
promieniowanie, co zmieniłoby obraz pola temperatury.
Równanie Fouriera dla jednokierunkowego przewodzenia ciepła, np. przez
nieprzezroczyst
ą przegrodę budowlaną, jest postaci:
2
2
)
,
(
x
x
T
c
T
p
o
∂
∂
=
∂
∂
τ
ρ
λ
τ
gdzie:
τ
czas, [s],
x
współrzędna (w układzie kartezjańskim) normalna względem powierzchni przegrody,
okre
ślająca położenie punktu, [m],
T(x,
τ
) zależność funkcyjna temperatury od położenia punktu i czasu,
λ
λ
λ
λ, ρ, c
p
odpowiednio, współczynnik przewodzenia ciepła [W/(mK)], gęstość pozorna [kg/m
3
]
i ciepło właściwe [kJ/(kg C)].
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
11
Równanie różniczkowe nieustalonego przewodzenia ciepła w ciałach
stałych wyraża związek między temperaturą, czasem i współrzędnymi
przestrzeni
, który musi być spełniony dla każdego pola temperatury w ciele
stałym i w każdej chwili. Aby z dowolnie dużej liczby rozwiązań wybrać tylko
rozwiązanie odpowiadające rozpatrywanemu zjawisku, należy określić
warunki jednoznaczności rozwiązania tego równania. Do tych warunków
należą warunki początkowe i warunki brzegowe, zwane również warunkami
granicznymi.
Warunki brzegowe obowiązują zarówno w stanach nieustalonych jak
i ustalonych, przy czym w drugim przypadku zakłada się ich niezmienność
w czasie. Warunki brzegowe obowiązują zarówno przy nagrzewaniu jak
i przy stygnięciu ciała.
(animacje)
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
12
2.3.3. Dynamika cieplna przegród budowlanych - stateczność
cieplna przegród
Przepływ ciepła przez przegrody budowlane jest zawsze nieustalony
w czasie. Wynika to przede wszystkim ze zmienności elementów środowiska
zewnętrznego warunkujących przepływ ciepła (temperatura powietrza,
natężenie
promieniowania
słonecznego,
prędkość
wiatru,
itp.),
z nierównomierności pracy urządzeń grzewczych oraz ze zmiennych zysków
ciepła w pomieszczeniu. Proces nieustalonej wymiany ciepła jest ściśle
związany
z
dynamicznymi
cieplnymi
charakterystykami
przegrody
budowlanej, które zasadniczo wpływają na efekt akumulacji ciepła
i stateczność cieplną przegród.
W przypadku ogólnym dynamika rozpatrywanego procesu (w tym przypadku
procesu nieustalonego przepływu ciepła przez wielowarstwową przegrodę
budowlaną) związana jest z zachowaniem się tego procesu w czasie
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
13
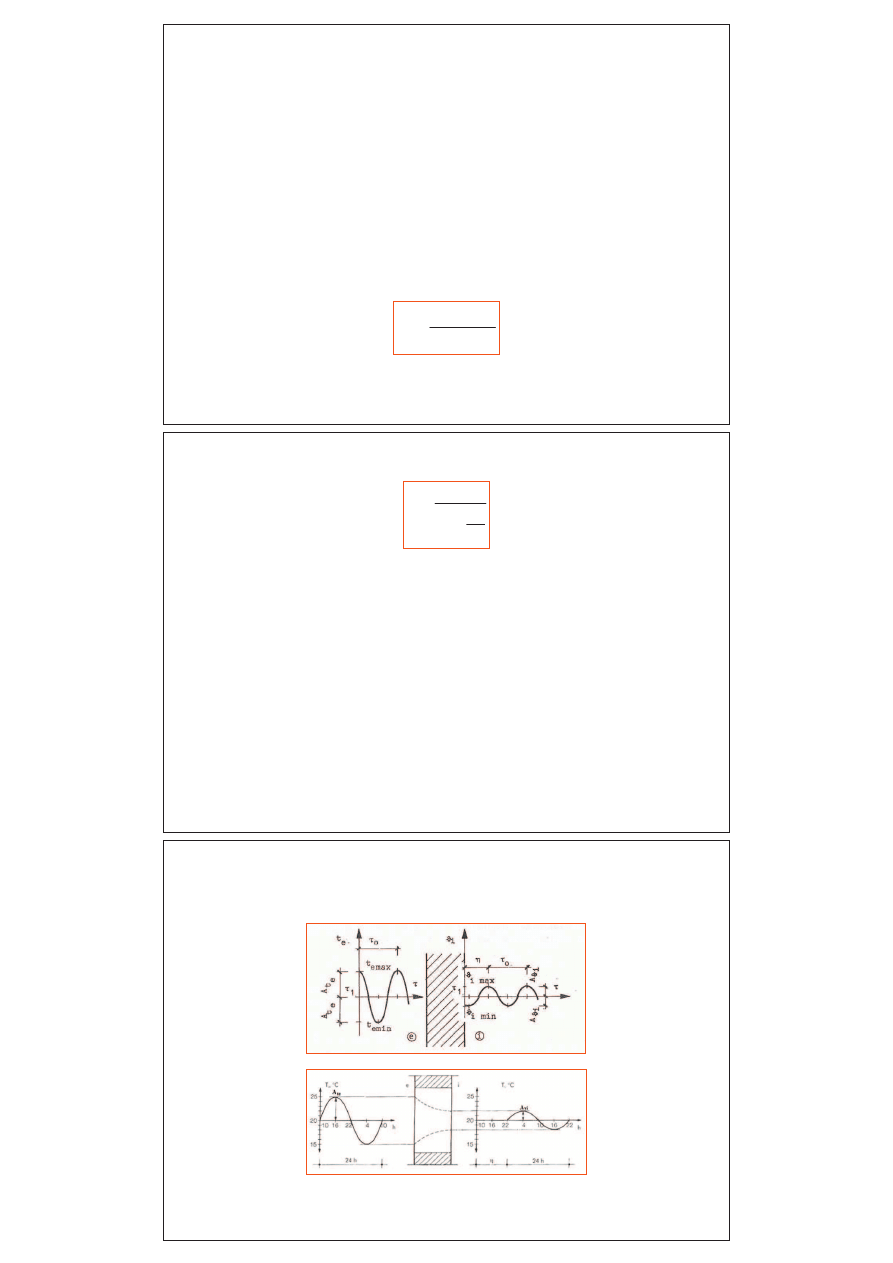
Stropodachy pełne
e
i
Ściany zewnętrzne
i
e
i
e
i e
część masywna przegrody izolacja termiczna
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
14
Dynamiczne cieplne właściwości przegrody budowlanej zależą od
struktury przegrody oraz od rozkładu oporów cieplnych i pojemności
cieplnej poszczególnych warstw.
Właściwości te zasadniczo
wpływają na efekt akumulacji ciepła przez przegrodę, na zdolność
tłumienia przepływającego przez nią strumienia ciepła oraz na tzw.
przesunięcie fazowe, które ma szczególne znaczenie w okresie lata.
Jest to ściśle związane z utrzymaniem właściwych parametrów
mikroklimatu pomieszczeń i warunków komfortu cieplnego.
W przypadku dobrze zaizolowanych termicznie, ale lekkich przegród
budowlanych (np. ściany szkieletowe wypełnione wełną mineralną w tzw.
domach kanadyjskich)
dynamiczne właściwości cieplne tych przegród
,
a właściwie ich brak,
znacząco wpływają na pracę urządzeń grzewczych i na
koszty ogrzewania budynku.
Zagadnienia te nabierają obecnie w Polsce
szczególnego znaczenia w związku z wprowadzaniem nowych technologii
wykonawstwa
przegród
budowlanych,
zwłaszcza
ścian budynków,
z tendencją do wykonywania coraz to lżejszych przegród.
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
15
Dynamiczne właściwości cieplne przegród budowlanych, ograniczających
ogrzewaną kubaturę budynku, mają istotny wpływ na:
•
chwilowe obciążenia instalacji grzewczych i klimatyzacyjnych,
•
na mikroklimat pomieszczeń i komfort cieplny ludzi oraz na
•
zużycie energii cieplnej w budynkach.
Znajomość tych właściwości przegród konieczna jest zwłaszcza wówczas,
gdy są stosowane układy regulacji automatycznej, których zadaniem jest
utrzymywanie założonych warunków cieplnych w pomieszczeniach,
niezależnie od zmiany warunków atmosferycznych lub też występowania
innych zakłóceń w postaci dodatkowych zysków lub start ciepła
w pomieszczeniach.
Przykładem
właściwego
wykorzystania
cieplnych
dynamicznych
właściwości przegród budowlanych
do poprawy bilansu cieplnego
pomieszczeń i warunków komfortu cieplnego w tych pomieszczeniach
jest
stosowanie tzw. stropodachów odwróconych,
z warstwą płukanego żwiru na
stropodachu, o frakcji ≥ 15 mm i grubości warstwy ok. 6-8 cm, czy też
stosowanie tzw. dachów zielonych.
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
16
Układ warstw w stropodachu odwróconym:
1. Płyty styropianowe
2. Strop
3. Izolacja przeciwwilgociowa
4. Warstwa wyrównawcza
5. Warstwa filtracyjna
6.
Żwir płukany (>15 mm)
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
17
Układ warstw ”zielonego dachu”:
1. Płyty styropianowe,
2. Strop,
3. Izolacja przeciwwilgociowa,
4. Warstwa wyrównawcza,
5. Warstwa filtracyjna,
6. Warstwa drenująca,
7. Warstwa wegetacyjna.
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
18
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
19
Stateczność cieplna przegrody budowlanej
– zdolność przegrody
do tłumienia przepływającego przez nią strumienia ciepła
inna definicja:
jest to zdolność przegrody do utrzymywania stałej bądź zmieniającej się
w dopuszczalnych granicach temperatury na powierzchni przegrody od
strony pomieszczenia
Stateczność cieplna przegrody w okresie zimowym
Stateczność cieplną w okresie zimowym charakteryzuje wskaźnik
stateczności Φ - stosunek różnicy temperatur obliczeniowych po obu
stronach przegrody do różnicy temperatury obliczeniowej powietrza
wewnątrz pomieszczenia i najniższej temperatury na powierzchni przegrody
od strony pomieszczenia.
Sens fizyczny
(rysunek)
:
min
i
i
e
i
t
t
t
υ
−
−
=
Φ
Przy obliczaniu wska
źnika stateczności cieplnej wykorzystuje się zależność:
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
20
i
i
T
U
m
R
R
+
=
Φ
gdzie:
Ф- wskaźnik stateczności cieplnej przegrody,
R
T
– całkowity opór przenikania ciepła przez przegrod
ę [m
2
K/W],
m - współczynnik nierównomierno
ści oddawania ciepła przez urządzenia
grzewcze,
U
i
- współczynnik przyswajania ciepła przez powierzchni
ę przegrody od strony
pomieszczenia [W/m
2
K].
UWAGA!!! U
i
- to nie jest współczynnik przenikania ciepła. Jest to współczynnik
przyswajania ciepła przez powierzchni
ę materiału od strony pomieszczenia
Przegroda musi spełnia
ć warunek:
Ф ≥ Ф
min
Przegroda budowlana jest tym lepsza pod względem stateczności cieplnej
im większy jest wskaźnik Ф.
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
21
Stateczność cieplna przegród w okresie letnim
-------------------------------------------------------------------------------------------------------------------------------------------
Wykład 2 – ”Fizyka Budowli”, Wydział Budownictwa Lądowego i Wodnego Politechniki Wrocławskiej
III rok, rok akademicki 2011/2012, prowadzący: dr hab. inż. Henryk Nowak, prof. PWr
22
Wielkości opisujące stateczność cieplną przegród w okresie letnim
Miarą skuteczności przegród w ochronie przed przegrzewaniem wnętrza jest:
•
wskaźnik tłumienia
-
tłumienie fali temperatury
ν
ν
ν
ν, jest to stosunek amplitudy
temperatury powietrza zewn
ętrznego do amplitudy temperatury na
powierzchni przegrody od strony pomieszczenia:
i
te
A
A
v
ϑ
=
[-]
Przegroda powinna spełniać warunek: v ≥ v
min
•
przesunięcie fazowe η
-
jest to czas mi
ędzy pojawieniem się maksymalnej
warto
ści temperatury powietrza zewnętrznego i maksymalnej wartości
temperatury na powierzchni przegrody od strony pomieszczenia.
Je
śli przegroda charakteryzuje się wysokim tłumieniem fali cieplnej (przegroda
masywna) to przesuni
ęcie fazowe ma już tylko niewielkie znaczenie.
Je
śli natomiast przegroda tłumi przepływ ciepła tylko w niewielkim stopniu
(przegroda lekka), to wymagane jest przesuni
ęcie fazowe rzędu 12 godzin.
(animacje)