DZIELENIE W SYSTEMIE U2 

(DZIELENIE NIEODTWARZAJĄCE)

Pierwszym krokiem w dzieleniu nieodtwarzającym jest ustawienie dzielnika do pierwszego odejmowania/dodawania. 
Dzielnik musi zostać przeskalowany tak, żeby być większym od dzielnej. Najłatwiej jest nam porównywać liczby 
dodatnie   więc   powinniśmy   zacząć   od   określenia   wartości   bezwzględnej   dzielnej   i   dzielnika   (wykorzystując 
uzupełnienie).

Gdy mamy już moduł z dzielnej i dzielnika ustawiamy dzielnik tak, żeby dzielna była od niego mniejsza (jeśli byśmy 
rozszerzyli  dzielną zerami  po prawej  stronie). W otrzymanym  wyniku musimy z  spowrotem przesunąć przecinek 
w o tyle miejsc, o ile przesunęliśmy dzielnik, ale w odwrotną stronę (najlepiej jest porównać pozycje przecinków 
dzielnej i dzielnika, i na tej podstawie od razu widać przesunięcie). Najbardziej optymalne jest ustawienie dzielnika 
najbardziej jak to możliwe na prawo (ale żeby warunek większości dzielnika od dzielnej był ciągle spełniony).

W poniższym przykładzie dzielnik został ustawiony właśnie w takim miejscu ponieważ
1011 0000 > 1011 1011. Wydaje się, że jest odwrotnie ale sprawa wyjaśnia się jeśli liczby zamienimy na ich wartości 
bezwzględne, wtedy od razu widać, że 0101 0000 > 0100 0101.

Gdy  dobrze   ustawimy  dzielnik,  cały  algorytm   sprowadza   się   jedynie  do  odejmowania  i   dodawania.  Na   początku 
musimy określić czy będziemy dodawać czy odejmować oraz jaką cyfrę otrzymaliśmy w wyniku po danej operacji.
ODEJMUJEMY zawsze gdy znak dzielnej i reszty jest ZGODNY, cyfrą wyniku jest wtedy  1,
DODAJEMY zawsze gdy znak dzielnej i reszty jest PRZECIWNE, cyfrą wyniku jest wtedy 0.
Za pierwszą resztę należy przyjąć po prostu dzielną ale cyfry wyniku zapisujemy dopiero po odczytaniu pierwszej 
reszty.
Uwaga: Jeśli otrzymana reszta (po rozszerzeniu) wynosi 0 to ZAWSZE kończymy dzielenie dopisując 1 jako 
cyfrę wyniku.

Oczywiście aby określić czy dane liczby mają ten sam czy przeciwny znak, wystarczy porównać ich najstarszy bit 
(pierwszy od lewej) ponieważ w kodzie U2 odpowiada on za znak danej liczby.

UWAGA:
Zamiast   odejmować   jakąś   liczbę   w   kodzie   U2,   możemy   dodać   jej   uzupełnienie.   Jeśli   masz   kłopoty 
z odejmowaniem w kodzie uzupełnieniowym zapisz sobie uzupełnienie dzielnej i dodawaj je zamiast odejmować 
dzielną.

PRZYKŁAD 1:

101110,11

U2

10,11

U2

=

10111011

U2

1011

U2

=

−1⋅01000101

2

−1⋅0101

2

=

69

10

5

10

= 13,8

10

= 1101,1100

2

= 01101,1100

U2

Pogrubione są kolejne cyfry z dzielnej, o które rozszerzamy reszty.

Otrzymaliśmy wynik 0,1101 ale ponieważ dzielną przestawiliśmy o 4 pozycje w lewo (lub inaczej, ponieważ pomiędzy 
przecinkiem dzielnej i dzielnika są 4 pozycje), powinniśmy przesunąć przecinek o 4 miejsca w prawo. Prawdziwym 
wynikiem jest wiec 01101.

Krzysztof Adamski  ::  http://mr-k.namyslow.eu.org

1

0

1

0

0

0 1, 0

1

0 1, 0

1 uzupełnienia

0, 1

1

0

1

WYNIK przesunięty o 4 bity

1

0

1

1

1 0, 1

1

:

1 0, 1

1 ZNAKI ZGODNE: odejmujemy

-

1

0, 1

1

0

0

0

0

1

ZNAKI PRZECIWNE: 0 i dodajemy

+ (1) 1 0, 1

1

(1) 1

1

0

0

0

ZNAKI ZGODNE: 1 i odejmujemy

- (1) 1

1 0, 1

1

(1) 1

1

1

0

1

1

ZNAKI ZGODNE: 1 i odejmujemy

- (1) 1

1

1 0, 1

1

(0) 0

0

0

0

0

0

1

ZNAKI PRZECIWNE: 0 i dodajemy

+ (1) 1

1

1

1 0, 1

1

(1) 1

1

1

1

1

0

0

ZNAKI ZGODNE: 1 i moglibyśmy dodawać

PRZYKŁAD 2:

101001,11

U2

0110,1

U2

=

10100111

U2

011010

U2

=

−1⋅01011001

2

011010

2

=−

89

10

26

10

= −3,423

10

= −1⋅11,0110

2

= 100,1010

U2

Dzielnik został tak ustawiony ponieważ  0110 1000 > 0101 1101 (uzupełnienie dzielnej).

Otrzymaliśmy wynik 1,001 ale jest on przesunięty o dwa bity więc prawdziwym wynikiem jest 100,1.

PRZYKŁAD 3:

1,0111

U2

0,1011

U2

=

10111

U2

01011

U2

=−

01001

U2

01011

U2

=−

9

10 

11

10

=−0,81

10 

=−0,11010001

U2

=1,00101111

U2

Krzysztof Adamski  ::  http://mr-k.namyslow.eu.org

2

0

1

0

1 1 1, 0

1

uzupełnienia

1, 0

0

1

WYNIK przesunięty o 2 bity

1

0

1

0 0 1, 1

1

:

0

1

1 0, 1 ZNAKI PRZECIWNE: dodajemy

+ 0

1

1 0, 1

(0) 0

0

0 1

1

ZNAKI ZGODNE: 1 i odejmujemy

- (0) 0

1

1 0

1

(1) 1

0

1 1

0

1

ZNAKI PRZECIWNE: 0 i dodajemy

+ (0) 0

0

1 1

0

1

(1) 1

1

1 0

1

0

1

ZNAKI PRZECIWNE: 0 i dodajemy

+ (0) 0

0

0 1

1

0

1

(0) 0

0

0 0

0

1

0

0

ZNAKI ZGODNE: 1 i moglibyśmy odejmować

0

1

0

0

1

uzupełnienie

1, 0

0

1

0

1

WYNIK przesunięty o 0 bitów bo 0,1011 > 0, 1001

1, 0

1

1

1

:

0, 1

0

1

1 ZNAKI PRZECIWNE: dodajemy

+ 0, 1

0

1

1

0

0

0

1

0

0

ZNAKI ZGODNE: 1 i odejmujemy

-

0

1

0

1

1

1

1

0

0

1

0

ZNAKI PRZECIWNE: 0 i dodajemy

+

0

1

0

1

1

1

1

1

0

1

0

ZNAKI PRZECIWNE: 0 i dodajemy

+

0

1

0

1

1

0

0

1

0

1

0

ZNAKI ZGODNE 1 i odejmujemy

-

0

1

0

1

1

1

1

1

1

1

0

ZNAKI PRZECIWNE: 0 i dodajemy

+

0, 1

0

1

1

0

1

0

0

1

0 ZNAKI ZGODNE: 1 

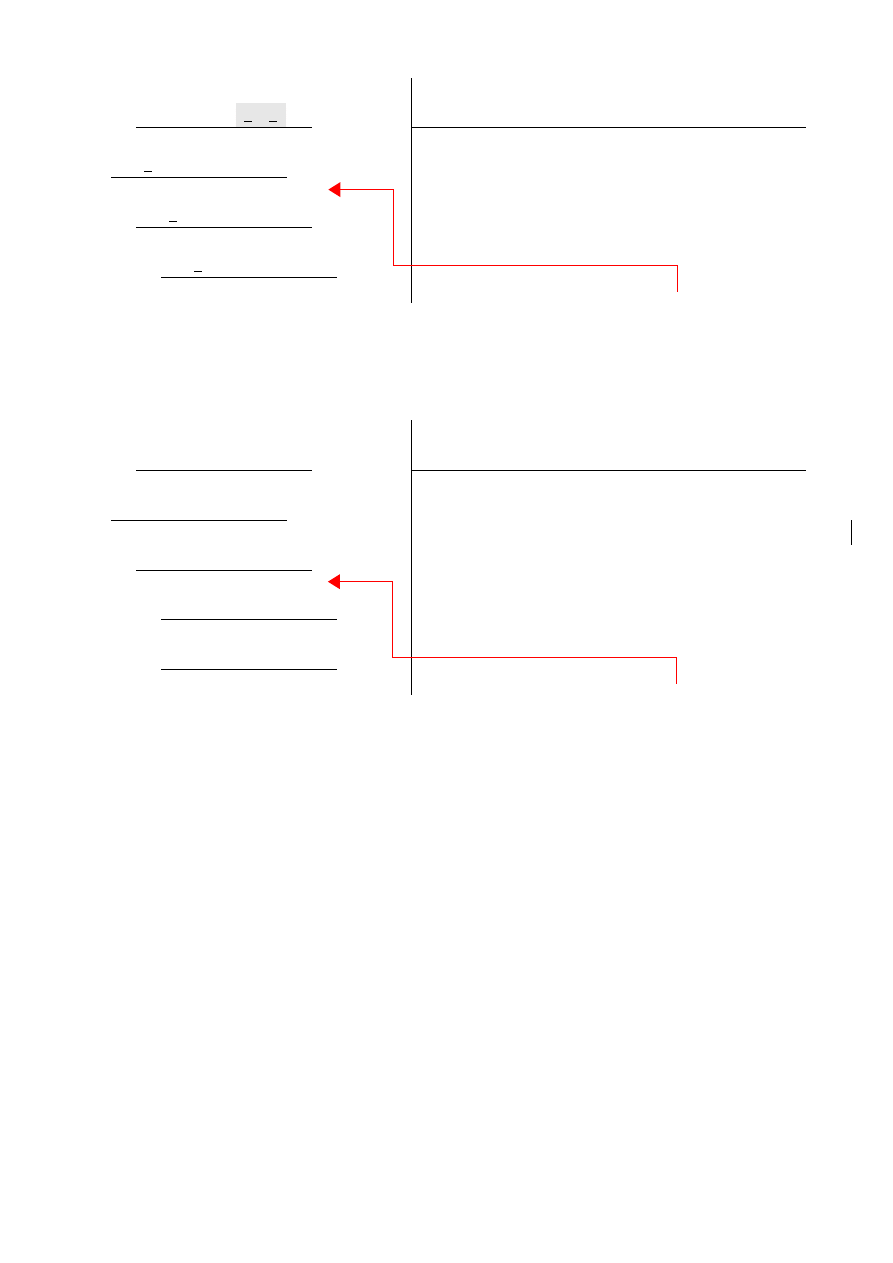
PRZYKŁAD 4a (ustawienie optymalne)

Otrzymaliśmy wynik 1,0(10) ale jest on przesunięty o 1 w prawo (przecinek dzielnika jest przesunięty o 1 w prawo 
w stosunku do przecinka dzielnej) więc prawdziwy wynik otrzymamy przesuwając przecinek o jeden w lewo: 1,(10).

PRZYKŁAD 4b (ustawienie nieoptymalne – o jeden w lewo)

Liczby są te same co w poprzednim przykładzie ale tym razem nie przeskalowaliśmy dzielnika w prawo. Skoro nie 
skalowaliśmy dzielnika to wynik jest rzeczywisty (nie skalujemy go). Jak widać wynik jest identyczny z poprzednim 
ale wykonaliśmy o jedną operację odejmowania więcej.

Proponuję policzyć również przypadek, w którym dzielnik przesunięto o jeden w LEWO. Wynik będzie przesunięty ale 
po   przeskalowaniu   równy  tym   otrzymanym   w  dwóch   ostatnich  przykładach.  Zwiększy   się   również   o   jeden   ilość 
wykonywanych odejmowań.

WNIOSEK:
Przesunięcie dzielnika za bardzo w prawo nie zmieni wyniku a jedynie zwiększy ilość wykonywanych operacji 
dodawania/odejmowania.

Krzysztof Adamski  ::  http://mr-k.namyslow.eu.org

3

0, 1

1

1

1 uzupełnienie

1

1 (1, 0) 1

WYNIK przesunięty o 1 bit w prawo

0, 0

1

0

1

:

1, 0

0

0

1 ZNAKI PRZECIWNE: dodajemy

+ 1 1, 0

0

0

1

1

1

0

1

1

0

ZNAKI ZGODNE: 1 i odejmujemy

-

1

1

0

0

0

1

0

0

1

0

1

0

ZNAKI PRZECIWNE: 0 i dodajemy

+ 1

1

0

0

0

1

1

1

0

1

1

0

i dostaliśmy okres (reszta taka sama jak ta    )

0, 1

1

1

1 uzupełnienie

1, (1 0)

WYNIK rzeczywisty, nie przesunięty

0, 0

1

0

1

:

1, 0

0

0

1 ZNAKI PRZECIWNE: dodajemy

+ 1, 0

0

0

1

1

0

1

1

0

0

ZNAKI ZGODNE: 1 i odejmujemy

-

1

0

0

0

1

1

1

0

1

1

0

ZNAKI ZGODNE: 1 i odejmujemy

-

1

0

0

0

1

0

0

1

0

1

0

ZNAKI PRZECIWNE: 0 i dodajemy

+

1

0

0

0

1

1

1

0

1

1

0

i dostaliśmy okres (reszta taka sama jak ta    )