Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–1

Dzielenie sekwencyjne

dzielenie całkowite

Iloraz Q (quotient) i reszta R (remainder) z dzielenia

dzielnej X (dividend) przez dzielnik D

≠

0 (divisor),

to liczby Q oraz R takie, e

X = Q

⋅

D + R, |R| < |D|

•

s 2 rozwi zania (Q

1

,R

1

) oraz (Q

2

,R

2

) takie, e X – R

i

= Q

i

⋅

D, przy tym

|R

1

–R

2

| = |D| , –|D|< R

1

, R

2

< |D| oraz |Q

1

–Q

2

| = 1

X

⋅

R > 0 – dzielenie znakowane (signed division) – znak reszty = znak dzielnej

R > 0 – dzielenie modularne (modulus division) – znak reszty dodatni

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–2

Przybli enia ilorazu (1)

dzielenie dowolne

Iloraz ułamkowy Q mo na obliczy z dowoln dokładno ci

ε













−

=

+

=

D

R

D

D

R

Q

D

X

,

m

i

n

,

ε

ε

W jednorodnym systemie stałobazowym o podstawie

β

i ze zbiorem cyfr D,

iloraz X/D mo na obliczy z dokładno ci nie gorsz ni

β

–r

jako:

D

∈

<

−

=

=

≅

−

−

=

−

+

−

−

∑

i

r

i

s

r

i

s

i

s

r

s

q

Q

D

X

q

q

q

q

Q

D

X

,

,

}

,

.

.

.

,

,

{

)

(

1

0

β

β

β

β

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–2a

Przybli enia ilorazu (2)

Pierwszym przybli eniem ilorazu jest

s

s

s

s

q

Q

q

β

β

=

=

1

,

}

0

,...,

0

,

{

takie, e

D

D

q

X

D

q

D

s

s

s

s

s

s

1

)

1

(

+

<

+

<

≤

≤

β

β

β

β

, gdy X D > 0

lub

D

D

q

X

D

q

D

s

s

s

s

s

s

1

)

1

(

+

>

+

>

≥

≥

β

β

β

β

, gdy X D < 0

czyli

D

D

q

X

s

s

s

β

β

<

−

,

sk d wynika numer s i warto wagi

β

s

najwy szej cyfry ilorazu oraz

D

D

q

X

R

s

s

s

β

β

<

−

=

1

Dokładniejsze przybli enie to

1

1

1

,

2

,

1

}

0

,...,

,

{

−

−

−

+

=

=

s

s

s

s

s

s

q

Q

Q

q

q

β

β

takie, e

D

D

q

R

R

s

s

s

1

1

1

1

2

−

−

−

<

−

=

β

β

,

Maj c wi c przybli enie z dokładno ci do

β

s–p

i bie

c reszt , mo na

obliczy przybli enie z dokładno ci do

β

s–p–1

D

D

q

R

R

p

s

p

s

p

s

p

p

−

−

−

+

<

−

=

β

β

)

(

)

1

(

,

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–2b

Przybli enia ilorazu (3)

Po skalowaniu reszt R

#

przez pot g podstawy odpowiadaj c indeksowi reszty

otrzymamy nierówno parametryczn

D

D

q

r

r

p

s

p

p

<

−

=

−

+

)

(

)

1

(

β

,

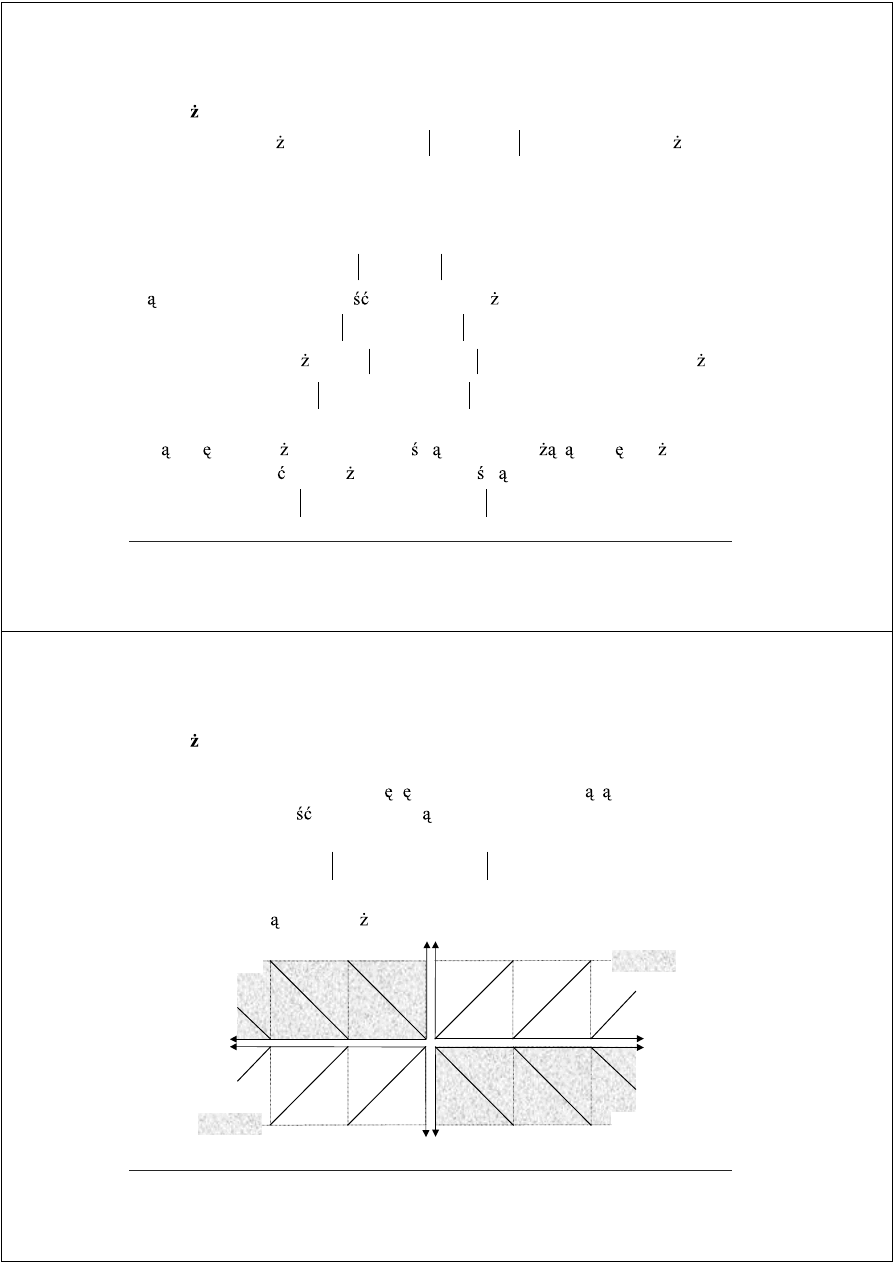
której odpowiadaj podane ni ej wykresy dzielenia

q

s–i

= 0

q

s–i

= 1

r

i+1

β

r

i

q

s–i

= 0

q

s–i

= 1

q

s–i

= 0

q

s–i

= 1

q

s–i

= 0

q

s–i

= 1

–r

i+1

–

β

r

i

r

#

≥

0, D>0

r

#

≥

0, D<0

r

#

<0, D>0

r

#

<0, D<0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–2c

Przybli enia ilorazu w systemie naturalnym (1)

Pierwszym przybli eniem ilorazu jest

s

s

s

s

q

Q

q

β

β

=

=

1

,

}

0

,...,

0

,

{

takie, e

D

D

q

X

D

q

D

s

s

s

s

s

s

1

)

1

(

+

<

+

<

≤

≤

β

β

β

β

,

sk d wynika numer s i warto wagi

β

s

najwy szej cyfry ilorazu oraz

D

D

q

X

R

s

s

s

β

β

<

−

=

≤

1

0

gdzie q

s

– liczba całkowita (dodatnia), q

s

∈

{0, 1, 2, … ,

β

– 1 }

Dokładniejsze przybli enie to

1

1

1

,

2

,

1

}

0

,...,

,

{

−

−

−

+

=

=

s

s

s

s

s

s

q

Q

Q

q

q

β

β

takie, e

D

q

D

Q

X

R

D

q

s

s

s

s

s

1

1

1

,

1

1

1

)

1

(

−

−

−

−

+

<

−

=

≤

β

β

,

D

D

q

R

R

s

s

s

1

1

1

1

2

0

−

−

−

<

−

=

≤

β

β

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–2d

Przybli enia ilorazu w systemie naturalnym (2)

Dokładniejsze przybli enie to

1

1

1

,

2

,

1

}

0

,...,

,

{

−

−

−

+

=

=

s

s

s

s

s

s

q

Q

Q

q

q

β

β

takie, e

D

q

D

Q

X

R

D

q

s

s

s

s

s

1

1

1

,

1

1

1

)

1

(

−

−

−

−

+

<

−

=

≤

β

β

,

D

D

q

R

R

s

s

s

1

1

1

1

2

0

−

−

−

<

−

=

≤

β

β

Kolejnymi przybli eniami ilorazu s zatem

i

s

i

s

i

s

i

s

q

Q

Q

−

−

+

+

=

β

,

1

,

takie, e

D

q

D

Q

X

R

D

q

i

s

i

s

i

s

i

i

s

i

s

−

−

−

−

+

<

−

=

≤

β

β

)

1

(

,

,

D

D

q

R

R

i

s

i

s

i

s

i

i

−

−

−

+

<

−

=

≤

β

β

1

0

co po skalowaniu (

1

−

−

=

s

i

i

i

R

r

β

) prowadzi do nierówno ci parametrycznej

D

D

q

r

r

i

s

i

i

<

−

=

≤

−

+

β

1

0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–3

Zbie no procedury dzielenia

Aby w standardowym systemie stałobazowym mo liwe było

obliczenie lepszego przybli enia ilorazu (kolejnej cyfry)
na podstawie przybli enia poprzedniego,
czyli aby istniało

1

1

1

,

2

,

−

−

+

=

s

s

s

s

q

Q

Q

β

takie, e

i

s

i

s

Q

D

X

Q

D

X

,

1

,

−

<

−

+

,

to kolejna reszta musi spełnia warunek

D

D

q

r

r

p

s

p

p

<

−

=

−

+

)

(

)

1

(

β

,

Je li obliczyliby my

D

r

p

≥

+

)

1

(

, to kolejna nierówno

D

D

q

r

r

p

s

p

p

<

−

=

+

−

+

+

)

1

(

)

1

(

)

2

(

β

,

nie ma rozwi zania w zbiorze dozwolonych warto ci cyfr (

β

<

#

q

).

Na przykład przy dodatnich r

#

oraz D, je li

δ

+

=

+

D

r

p

)

1

(

, to

D

D

D

q

D

q

D

r

p

s

p

s

p

>

+

≥

+

−

=

−

+

=

+

−

+

−

+

βδ

βδ

β

δ

β

)

(

)

(

)

1

(

)

1

(

)

2

(

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–4

Procedura dzielenia sekwencyjnego w systemie naturalnym

Parametryczne (X>0, D>0)

D

q

r

r

i

s

i

i

−

+

−

=

β

1

,

D

r

i

<

≤

0

,

X

r

s 1

0

−

−

=

β

Warunki zbie

ż

no

ś

ci procedury

•

D

D

q

r

q

D

r

i

s

i

i

s

i

<

−

≤

<

≤

∃

⇒

<

−

−

β

β

0

:

)

0

(

•

D

D

q

r

q

D

r

i

s

i

i

s

i

≥

−

<

≤

∀

⇒

≥

−

−

β

β

:

)

0

(

(3)

(3)

q

s–i

= 0

q

s–i

= 1

r

i+1

2r

i

2D

D

D

(0,0)

q

s–i

= 0

q

s–i

= 1

r

i+1

2r

i

2D

D

D

(0,0)

...(2)

...(2)

(2)

(2)

(1)

(1)

a)

b)

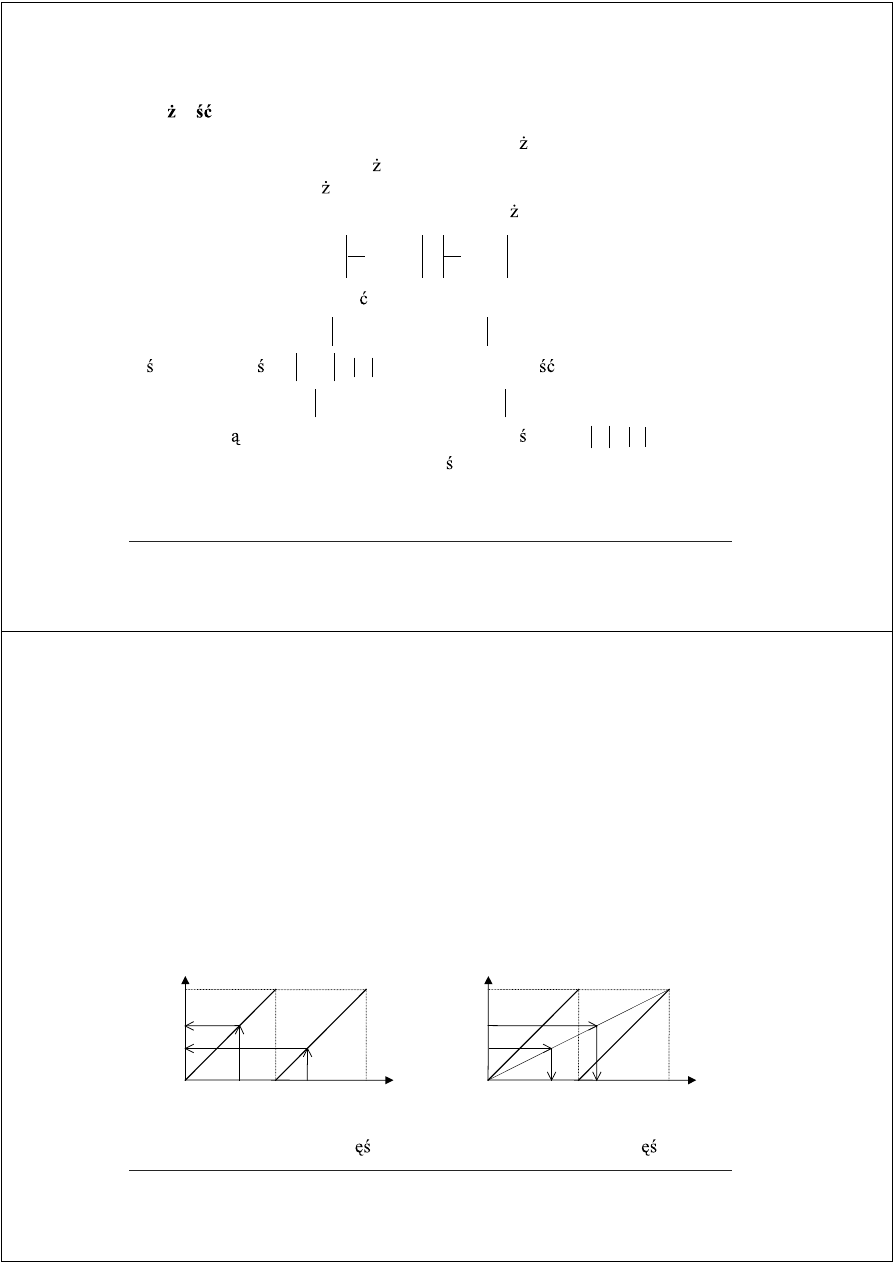
Wykres dzielenia sekwencyjnego w systemie dwójkowym a) wyznaczanie

cyfry ilorazu (1) i reszty cz ciowej (2), b) skalowanie reszty cz ciowej (3)

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–4a

Zbie no dzielenia w systemie naturalnym (1)

r

i+1

2r

i+1

2D

D

(0,0)

q

s–i

= 0

q

s–i

= 1

r

i+1

2r

i

2D

D

D

(0,0)

r

i

<

D

0

≤

q <

β

(zbie

ż

ne)

r

i

≥

D

? q=

β

–1

rozbie

ż

ne

q

s–i

= 0

q

s–i

= 1

r

i+2

β

= 2

r

i+2

> r

i+1

D

D

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–4b

Zbie no dzielenia w systemie naturalnym (2)

4r

i+1

4D

2D

(0,0)

q

s–i

= 0

q

s–i

= 3

r

i+1

4r

i

4D

2D

D

(0,0)

r

i

<

D

0

≤

q <

β

(zbie

ż

ne)

r

i

≥

D

? q=

β

–1

rozbie

ż

ne

q

s–i

= 0

q

s–i

= 3

r

i+2

β

= 4

r

i+2

> r

i+1

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–5

Dzielenie w systemach uzupełnieniowych

•

dzielna, dzielnik i iloraz mog by liczbami ujemnymi

•

liczba w systemie uzupełnieniowym – liczba w systemie stałobazowym
z niestandardowym zbiorem cyfr na wiod cej pozycji

∑

∑

−

−

=

−

−

−

−

=

−

−

−

+

=

+

−

=

2

1

1

2

1

1

1

]

)]

(

[

|

|

k

m

i

i

i

k

k

k

m

i

i

i

k

k

k

U

x

d

x

x

x

β

β

β

β

βϕ

β

X

,

gdzie

))

1

2

(

sgn

1

(

)

(

1

2

1

1

+

−

+

=

−

−

β

ϕ

k

k

x

x

– funkcja znaku liczby,

}

1

,...,

1

,

0

,

1

,...,

{

)

(

2

1

2

1

1

1

1

1

−

=

∈

−

=

−

−

−

−

β

β

βϕ

k

k

k

k

x

x

d

D

W

NIOSKI

:

•

je li X D < 0, to warto pierwszej cyfry ilorazu jest ujemna

•

wszystkie pozostałe cyfry ilorazu maj warto ci dodatnie

•

aby spełniony był warunek zbie no ci dzielenia |R|<|D|,

znak ka dej reszty musi by zgodny ze znakiem dzielnika (R D > 0)

•

pierwsza wielokrotno dzielnika musi by taka aby |R|<|D| oraz R D > 0

(je

ś

li byłoby R D < 0, odj

ę

cie ka

ż

dej dodatniej wielokrotno

ś

ci D

prowadziłoby, wskutek skalowania, do naruszenia warunku |R|<|D|)

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–6

Standaryzacja ilorazu w systemach uzupełnieniowych (1)

iloraz mo na łatwo skalowa do warto ci ułamkowej

m

F

m

F

Q

D

X

Q

D

X

Q

β

β

=

=

⇒

<

=

−

1

ułamek w systemie uzupełnieniowym ma zawsze posta (

1

→

”

β

−1

”):

0

0

,...}

,

,

,

1

{

,...}

,

,

,

0

{

3

2

1

3

2

1

<

>







=

−

−

−

−

−

−

F

F

F

Q

gdy

Q

gdy

q

q

q

q

q

q

Q

po standaryzacji ilorazu:

•

je li X D > 0, to q

0

= 0 oraz r

1

= X

β

−

m

−0⋅

D = X

β

−

m

•

je li X D < 0, to q

0

=

1

oraz r

1

= X

β

−

m

−(−1)⋅

D = X

β

−

m

+

D

•

warunkiem poprawno ci jest r

i

D

≥0

•

wszystkie kolejne cyfry ilorazu q

i

reprezentuj warto ci dodatnie,

a nast pn reszt jest r

i+1

=

β

r

i

−

q

i

D , r

i+1

D

≥0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–6a

Standaryzacja ilorazu w systemach uzupełnieniowych (2)

Je li X D < 0, to

1

<

=

−

D

X

Q

m

F

β

, ale tak e

1

1

0

<

+

=

+

<

−

−

D

D

X

D

X

m

m

β

β

wi c po dodaniu dzielnika do przeskalowanej dzielnej

znak pierwszej reszty jest taki sam jak znak dzielnika.

Zatem wszystkie kolejne cyfry ilorazu s dodatnie i spełniaj nierówno ci

|r

i+1

=

β

r

i

−

q

i

D | < | D | , r

i+1

D

≥0

Algorytm

1. Przeskaluj dzieln X, tak aby |r

0

=

β

−

m

X / D| < 1.

2. Je li X D > 0, to q

0

= 0 oraz r

1

= r

0

−

0

⋅

D = r

0

3. Je li X D < 0, to q

0

=

1

oraz r

1

= r

0

−

1

⋅

D = r

0

+ D

4. Obliczaj kolejno |r

i+1

=

β

r

i

−

q

i

D | < | D | , r

i+1

D

≥0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–6b

Standaryzacja ilorazu w dwójkowych systemach uzupełnieniowych

Je li X D < 0, to

1

2

<

=

−

D

X

Q

m

F

, ale tak e

1

2

1

2

0

<

+

=

+

<

−

−

D

D

X

D

X

m

m

wi c po dodaniu dzielnika do przeskalowanej dzielnej

znak pierwszej reszty jest taki sam jak znak dzielnika.

Wszystkie kolejne cyfry ilorazu s dodatnie, znak ka dej kolejnej reszty musi

by taki jak znak dzielnika (r

i+1

D

≥0)

, przy tym

je li |r

i+1

=

2

r

i

−

D | < | D | , t o q

i

= 1

je li |r

i+1

=

2

r

i

−

D | > | D | , t o q

i

= 0 oraz r

i+1

=

2

r

i

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–7

Dzielenie w systemie uzupełnieniowym (przykład – U10)

!! standaryzacja ilorazu – skalowanie dzielnej tak, aby |X

β

−

m

|

<|

D|

X = 7, 6 5 4

:

3 1, 2 = D

X = 7 6 5, 4

:

6, 8 8 = D

−

2, 3 6 6 :

+

3 1, 2

−

2 3 6, 6 :

−

3, 1 2

,

→

1

,

←

2

9, 2 4 8

X D < 0

0, 7 5 1

X D > 0

9 7 6. 5 4

: 3 1, 2

q

0

=−

1

9 7. 6 5 4

: 6, 8 8

q

0

=

0

+

0 3 1, 2

0

0 0 7 7 4

q

−

1

=

2

9 7 6 5 4

q

−

1

=

7

−

0 0 6 2 4

+

0 2 1 8 4 *

0 1 5 0 0

q

−

2

=

4

9 8 3 8 0

q

−

2

=

5

−

0 1 2 4 8

+

0 1 5 6 0 *

0 2 5 2 0

q

−

3

=

8

9 9 4 0 0

q

−

3

=

1

−

0 2 4 9 6

+

0 0 3 1 2

…

…

Q

=

9, 2 4 8 …

×

10

−

1

Q

=

0, 7 5 1 …

×

10

2

*

)

zamiast –qD mo

ż

na wykona

ć

q(–D)

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–8

Dzielenie odtwarzaj ce (restytucyjne)

standaryzacja ilorazu – skalowanie dzielnej, tak aby |X

⋅

2

−

m

|

<|

D|

1

0

0

0

gdy

gdy

2

2

0

0

0

=

⇒

=

⇒

<

>







+

=

−

−

q

q

D

X

D

X

D

X

X

r

m

m

D

q

r

r

i

i

i

−

=

−

1

2

,

0

|,

|

|

|

>

<

D

r

D

r

i

i

, i = 1,2,...







≥

<

=

−

−

.

|

|

|

2

|

|,

|

|

2

|

gdy

gdy

,

1

,

0

1

1

D

r

D

r

q

i

i

i

metody dzielenia restytucyjnego lub odtwarzaj

ą

cego (restoring division)

•

odj cie dzielnika D od tymczasowej reszty cz ciowej 2r

i

→

je li

0

)

2

(

1

<

−

−

D

D

r

i

– korekcja reszty przez dodanie dzielnika

•

porównanie tymczasowej reszty cz ciowej 2r

i

i dzielnika D

→

je li

0

)

2

(

1

≥

−

−

D

D

r

i

– odj cie dzielnika

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–9

Dzielenie nieodtwarzaj ce (nierestytucyjne)

W wyniku odj cia dzielnika od reszty r

i

=

2 r

i

−

1

−

D mo e powsta :

•

reszta r

i

poprawna, je eli r

i

⋅

D > 0

– odpowiada jej cyfra ilorazu o warto ci q

i

=

1

•

reszta r

i

niepoprawna, je eli r

i

⋅

D < 0

– odpowiada jej cyfra ilorazu o warto ci q

i

= 0

je li reszta r

i

jest niepoprawna, to

•

wła ciw kolejn reszt jest r

i

= 2 r

i

−

1

•

podstaw wyznaczenia warto ci kolejnej cyfry ilorazu jest

r

i

+

1

= 2 (2 r

i

−

1

)

−

D

•

t sam warto otrzymamy w wyniku opó nionej korekcji, dodaj c D

r

i

+

1

= 2 (2 r

i

−

1

−

D)

+

D

Je

ś

li X D < 0 to X

⋅

2

−

m

jest niepoprawn reszt , wi c

0

0

gdy

gdy

2

2

0

<

≥







+

−

=

−

−

D

X

D

X

D

X

D

X

r

m

m

,

0

0

gdy

gdy

1

0

0

0

0

>

<







=

D

r

D

r

q

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–10

Dzielenie nieodtwarzaj ce (nierestytucyjne)

Zale no kolejnej reszty od poprzedniej i wyznaczonej z niej q

•

0

0

2

1

=

⇒

<

−

=

−

i

i

i

q

D

r

r

oraz

D

r

D

D

r

r

i

i

i

+

=

+

−

=

−

+

2

)

2

(

2

1

1

•

1

0

2

1

=

⇒

≥

−

=

−

i

i

i

q

D

r

r

oraz

D

r

D

D

r

r

i

i

i

−

=

−

−

=

−

+

2

)

2

(

2

1

1

Algorytm dzielenia nieodtwarzaj cego w kodzie U2 (|X

⋅

2

−

m

|

<|

D|)

Krok 0.

0

0

gdy

gdy

2

2

0

<

≥







+

−

=

−

−

D

X

D

X

D

X

D

X

r

m

m

Krok 1. Je eli: a)

0

≥

D

r

i

podstaw

1

=

i

q

i oblicz

D

r

r

i

i

−

=

+

2

1

,

b)

0

<

D

r

i

podstaw

0

=

i

q

i oblicz

D

r

r

i

i

+

=

+

2

1

.

0

0

gdy

gdy

1

0

>

<







=

D

r

D

r

q

i

i

i

D

q

r

r

i

i

i

)

2

1

(

2

1

−

+

=

+

, i = 0, 1, 2, ...

Krok 2. Zwi ksz i. Je li i < p, wró do kroku 1.

Krok 3.

ulp

Q

Q

D

r

r

D

r

p

p

p

−

←

+

←

⇒

<

,

0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–11

Procedura dzielenia nieodtwarzaj cego

D

q

i

= 0

q

i

= 1

r

i+1

2r

i

−

D

(1)

(2)

(3)

−

D

D

−

2

D

2D

(0,0)

q

i+1

= 0

q

i+1

= 1

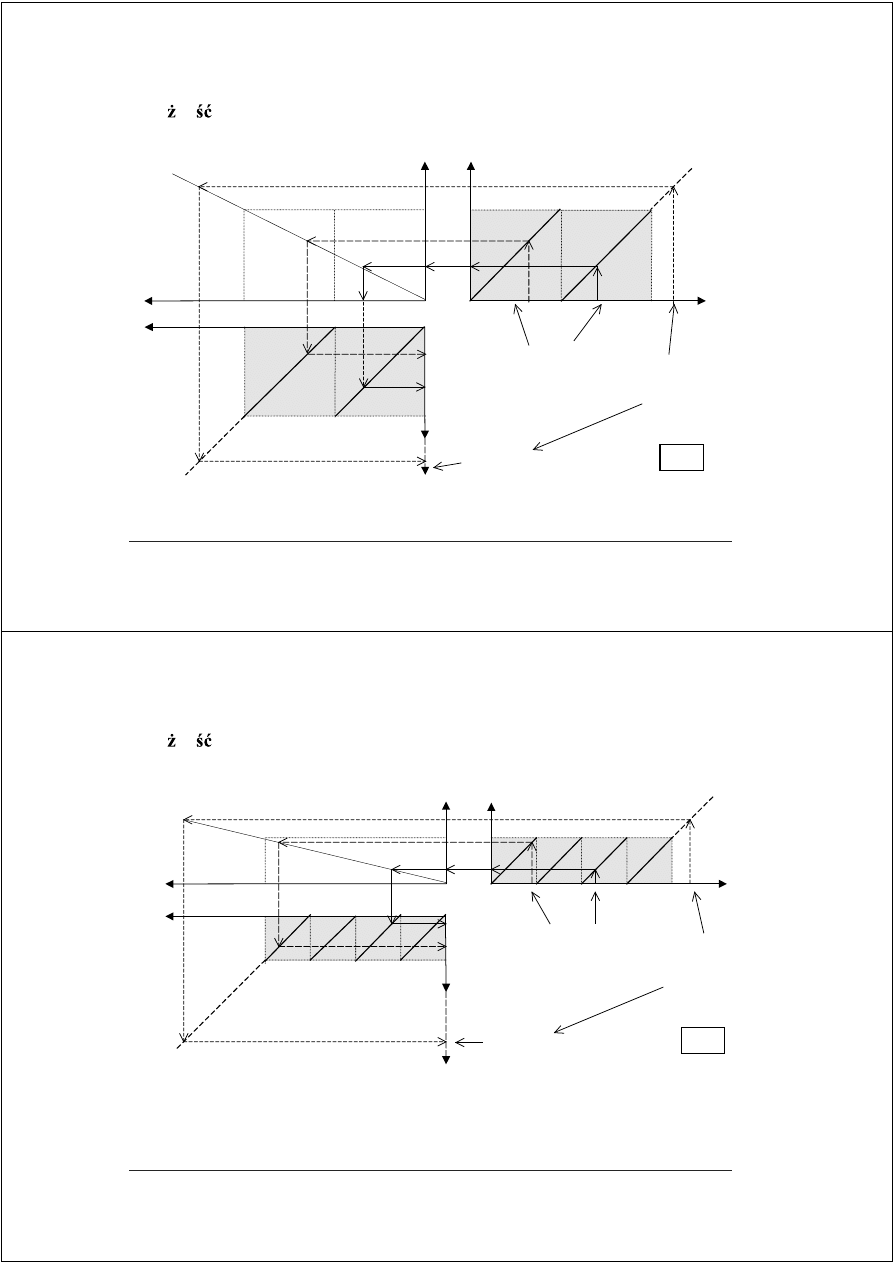
Wykres dzielenia nieodtwarzaj

ą

cego w kodzie U2 (D>0)

schemat wyznaczania cyfry ilorazu (1), reszty cz ciowej (2)

i przeskalowanej reszty cz ciowej (3)

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–12

Schemat dzielenia nieodtwarzaj cego

R

X/R

Q

D

Σ

C

ShL

0

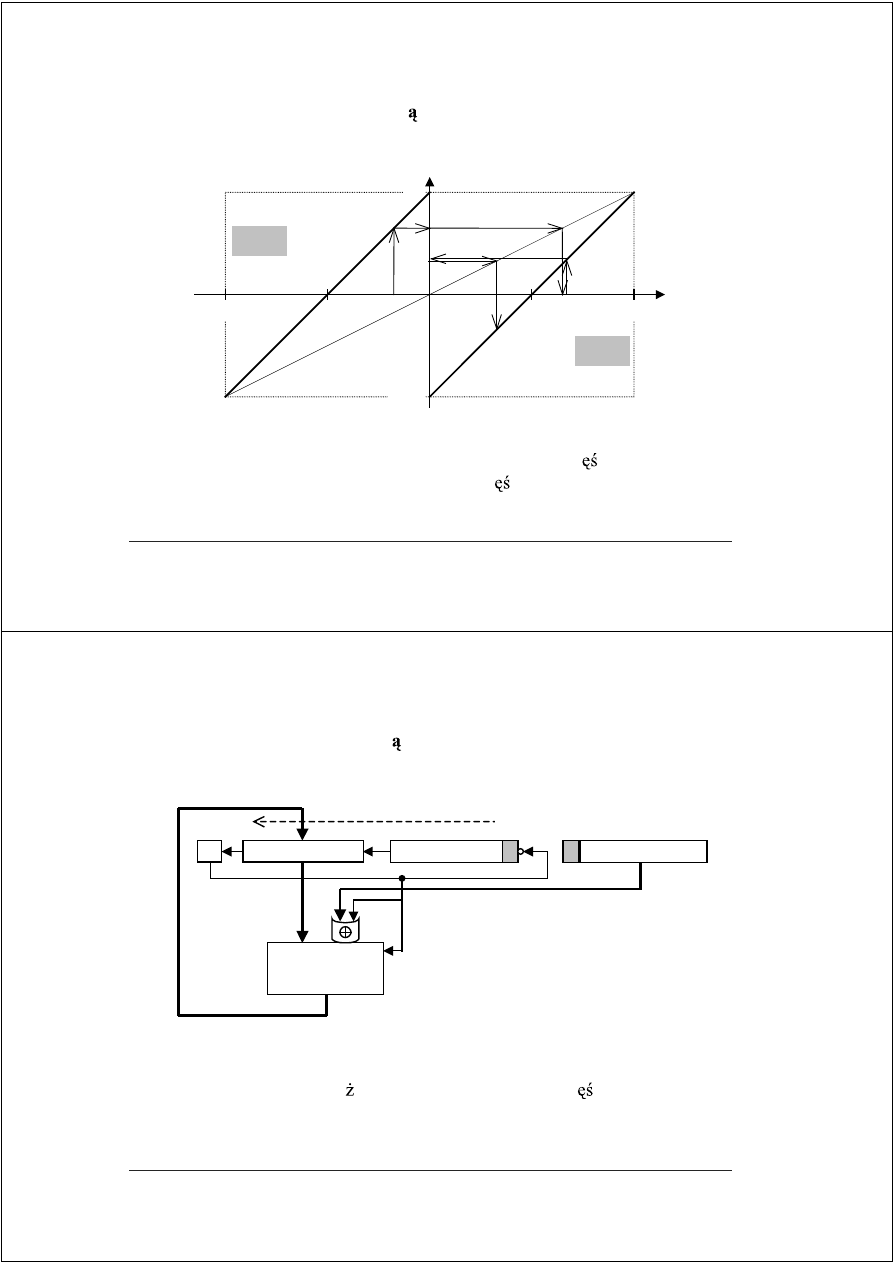
Schemat blokowy układu dziel

ą

cego liczby całkowite w kodzie U2:

C||X/R – przedłu ony rejestr dzielnej i reszt cz ciowych,

Q – rejestr ilorazu, D – rejestr dzielnika

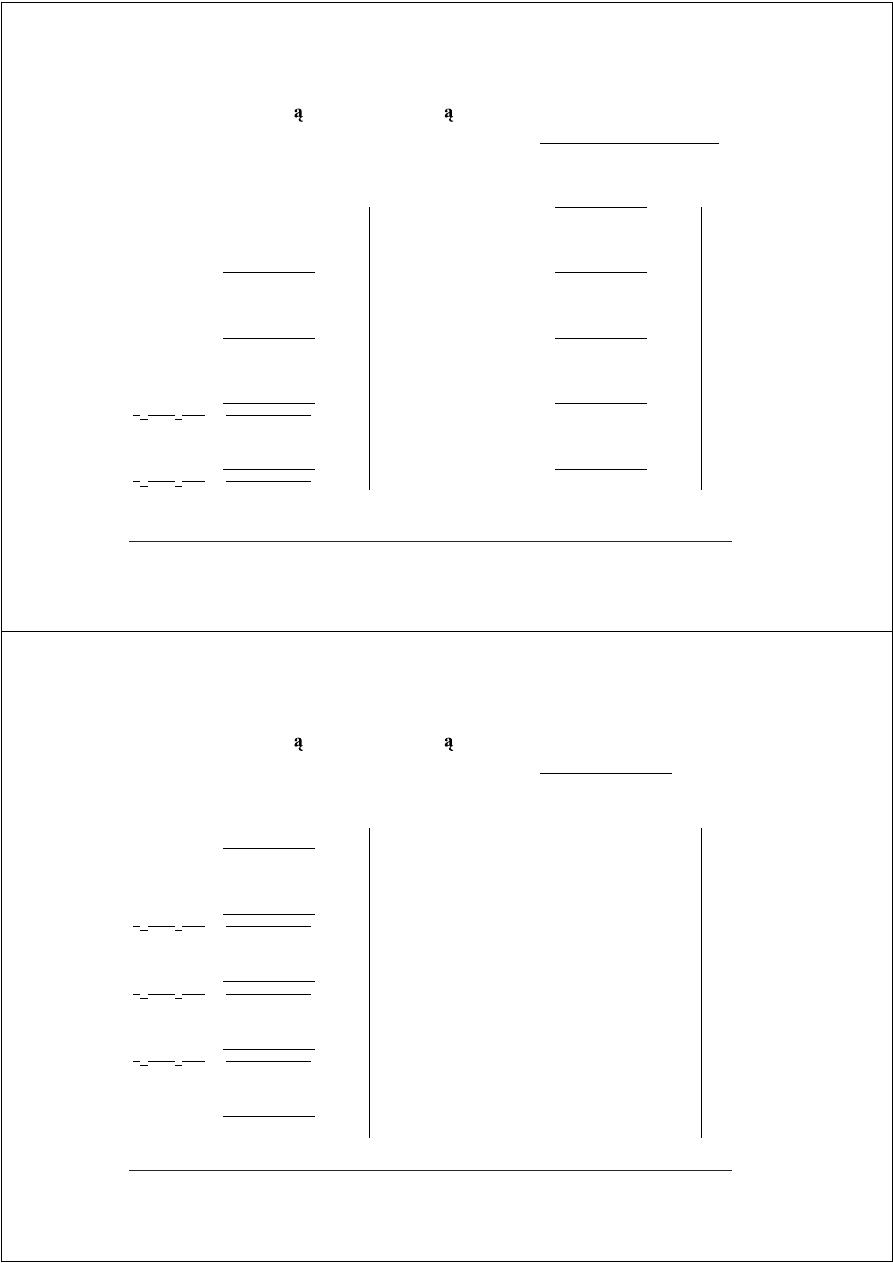
Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–13

Dzielenie odtwarzaj ce i nieodtwarzaj ce (U2) – maszynowe (przykład 1)

X

( 0 ) 0 , 1 0 1 1 (

11

/

16

)

X D > 0,

zb

ę

dne skalowanie, |X / D | < 1

D

( 0 ) 0 , 1 1 0 1 (

13

/

16

)

(nieodtwarzaj

ą

ce)

X

( 0 ) 0 , 1 0 1 1

(odtwarzaj

ą

ce)

– D

( 1 ) 1 , 0 0 1 1

r

0

= X

( 0 ) 0 , 1 0 1 1

q

0

= 0

r

0

= X– D

( 1 ) 1 , 1 1 1 0

rD

<

0

q

0

= 0

2r

0

= 2X

( 0 ) 1 , 0 1 1 0

2r

0

( 1 ) 1 , 1 1 0 0

– D

( 1 ) 1 , 0 0 1 1

+ D

( 0 ) 0 , 1 1 0 1

r

1

= 2r

0

– D ( 0 ) 0 , 1 0 0 1

rD

≥

0

q

1

= 1

r

1

= 2r

0

+ D ( 0 ) 0 , 1 0 0 1

rD

≥

0

q

1

= 1

2r

1

( 0 ) 1 , 0 0 1 0

2r

1

( 0 ) 1 , 0 0 1 0

– D

( 1 ) 1 , 0 0 1 1

– D

( 1 ) 1 , 0 0 1 1

r

2

= 2r

1

– D ( 0 ) 0 , 0 1 0 1

rD

≥

0

q

2

= 1

r

2

= 2r

1

– D ( 0 ) 0 , 0 1 0 1

rD

≥

0

q

2

= 1

2r

2

( 0 ) 0 , 0 1 0 1

2r

2

( 0 ) 0 , 0 1 0 1

– D

( 1 ) 1 , 0 0 1 1

– D

( 1 ) 1 , 0 0 1 1

r

3

= 2r

2

– D ( 1 ) 1 , 1 0 0 0

rD < 0

q

3

= 0

r

3

= 2r

2

– D ( 1 ) 1 , 1 0 0 0

rD < 0

q

3

= 0

2r

3

= 2

⋅

2r

2

( 0 ) 0 , 1 0 1 0

2r

3

( 1 ) 1 , 0 0 0 0

– D

( 1 ) 1 , 0 0 1 1

+ D

( 0 ) 0 , 1 1 0 1

r

4

= 2r

3

– D ( 1 ) 1 , 1 1 0 1

rD

<

0

q

4

= 0

r

4

= 2r

3

+ D ( 1 ) 1 , 1 1 0 1

rD < 0

q

4

= 0

Q = 0,1100…

U2

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

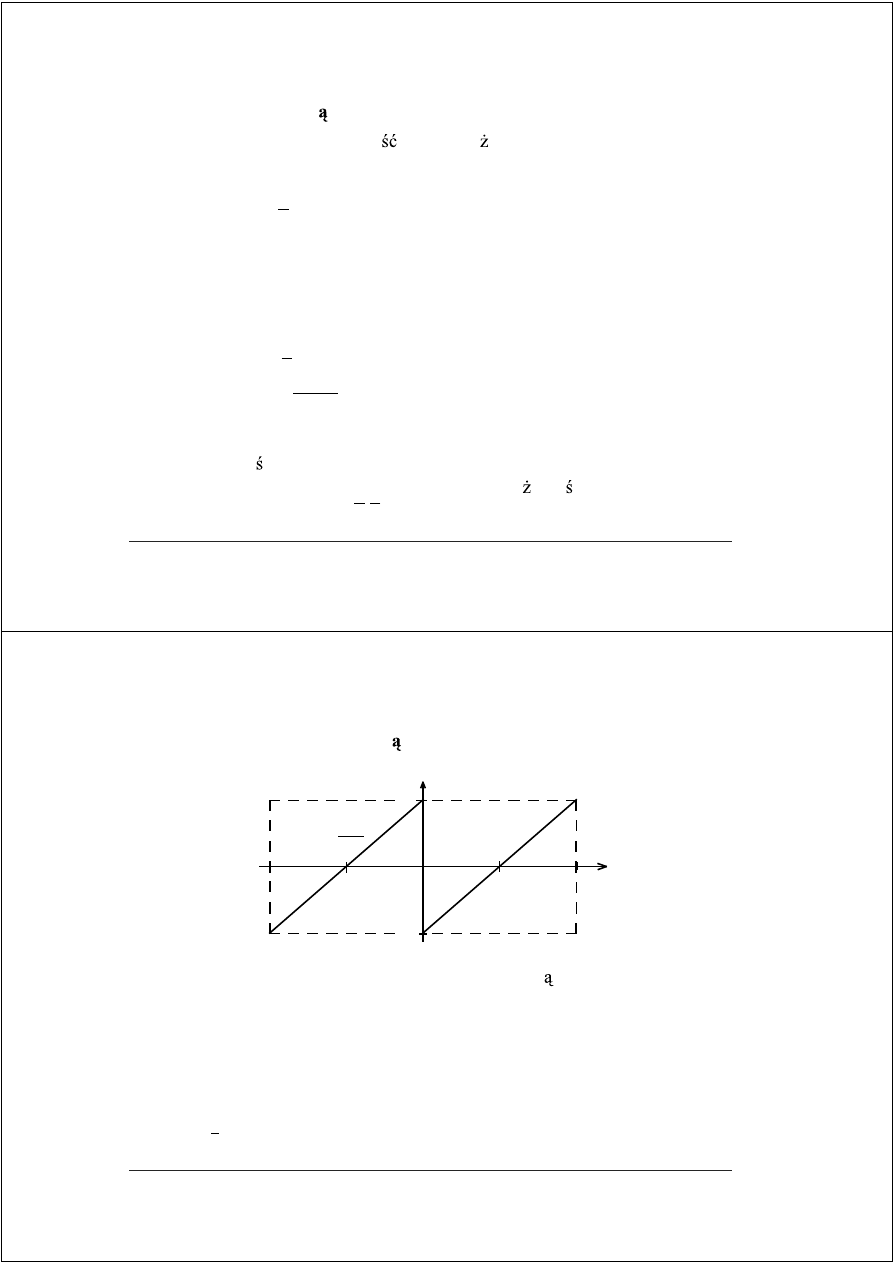
DIV–14

Dzielenie odtwarzaj ce i nieodtwarzaj ce (U2) – maszynowe (przykład 2)

X

0 1 0 , 1 0 0 1 (

41

/

16

)

X D < 0,

skalowanie, |X / D | > 1

D

1 , 0 1 0 1 (–

11

/

16

)

– D

( 0 ) 0 , 1 0 1 1 (

11

/

16

)

X’= X

×

2

–2

( 0 ) 0 , 1 0 1 0 0 1 0 …

X’= X

×

2

–2

( 0 ) 0 , 1 0 1 0 0 1 0 …

D

( 1 ) 1 , 0 1 0 1

D

( 1 ) 1 , 0 1 0 1

r

0

= X’+D

( 1 ) 1 , 1 1 1 1

q

0

= 1

r

0

= X’+ D ( 1 ) 1 , 1 1 1 1 rD

≥

0 q

0

= 1

2r

0

= 2X

( 1 ) 1 , 1 1 1 0

2r

0

( 1 ) 1 , 1 1 1 0

– D

( 0 ) 0 , 1 0 1 1

– D

( 0 ) 0 , 1 0 1 1

r

1

= 2r

0

– D ( 0 ) 0 , 1 0 0 1 rD

<

0 q

1

= 0

r

1

= 2r

0

– D ( 0 ) 0 , 1 0 0 1 rD

<

0 q

1

= 0

2r

1

= 2

⋅

2r

0

( 1 ) 1 , 1 1 0 1

2r

1

( 0 ) 1 , 0 0 1 1

– D

( 0 ) 0 , 1 0 1 1

+ D

( 1 ) 1 , 0 1 0 1

r

2

= 2r

1

– D ( 0 ) 0 , 1 0 0 0 rD

<

0 q

2

= 0

r

2

= 2r

1

+ D ( 0 ) 0 , 1 0 0 0 rD

<

0 q

2

= 0

2r

2

= 2

⋅

2r

1

( 1 ) 1 , 1 0 1 0

2r

2

( 0 ) 1 , 0 0 0 0

– D

( 0 ) 0 , 1 0 1 1

+ D

( 1 ) 1 , 0 1 0 1

r

3

= 2r

2

– D ( 0 ) 0 , 0 1 0 1 rD

<

0 q

3

= 0

r

3

= 2r

2

+ D ( 0 ) 0 , 0 1 0 1 rD

<

0 q

3

= 0

2r

3

= 2

⋅

2r

2

( 1 ) 1 , 0 1 0 0

2r

3

( 0 ) 0 , 1 0 1 0

– D

( 0 ) 0 , 1 0 1 1

+ D

( 1 ) 1 , 0 1 0 1

r

4

= 2r

3

– D ( 1 ) 1 , 1 1 1 1 rD

≥

0 q

4

= 1

r

4

= 2r

3

+ D ( 1 ) 1 , 1 1 1 1 rD

≥

0 q

4

= 1

Q = 1,0001…

U2

×

2

2

=100,01…

U2

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–15

Dzielenie nieodtwarzaj ce w kodzie dwójkowym SD oraz U2

•

iloraz w kodzie U2 – warto cyfry zale y od znaku dzielnika

•

iloraz w ograniczonej reprezentacji SD (bez zer)







<

≥

=

−

−

,

0

2

gdy

,

1

,

0

2

gdy

,

1

1

1

i

i

i

r

r

q

D

q

r

r

i

i

i

−

=

−

1

2

•

dzielna i dzielnik w kodzie U2, wynik w systemie SD

•

dzielna ujemna – znak ilorazu jest ustalany automatycznie

•

dzielnik ujemny – odwrotne przypisanie cyfr ilorazu, zatem

.

0

,

0

&

&

0

0

lub

lub

0

gdy

,

1

0

gdy

,

1

1

-

1

-

1

-

1

-

=

=

<

>







<

>

=

i

i

i

i

i

r

r

D

D

D

r

D

r

q

albo







≥

<

=

−

−

.

0

gdy

,

0

gdy

,

sgn

,

sgn

1

1

i

i

i

r

r

D

D

q

sgn D = |D|/D

•

korekcja je li XR < 0: (XD > 0 ⇒ R+D, Q–1), (XD < 0 ⇒ R–D, Q+1)

•

korekcja gdy

0

1

=

−

i

r

– w algorytmie brak mo liwo ci wytworzenia zera

iloraz

,...}

1

,

1

,

1

,

,...,

{

1

i

q

q

=

Q

zamiast

,...}

0

,

0

,

0

,

,...,

{

1

i

q

q

=

Q

. (!!|R| = |D|)

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–16

Schemat dzielenia nieodtwarzaj cego w kodzie SD oraz U2

•

iloraz w ograniczonej reprezentacji SD (bez zer)

r

|D|

–|D|

(0,0)

|D|

|D|

|D|

–|D|

r

–1

i

2

i

2

–2

q =

i

sgn

q =

i

sgn D

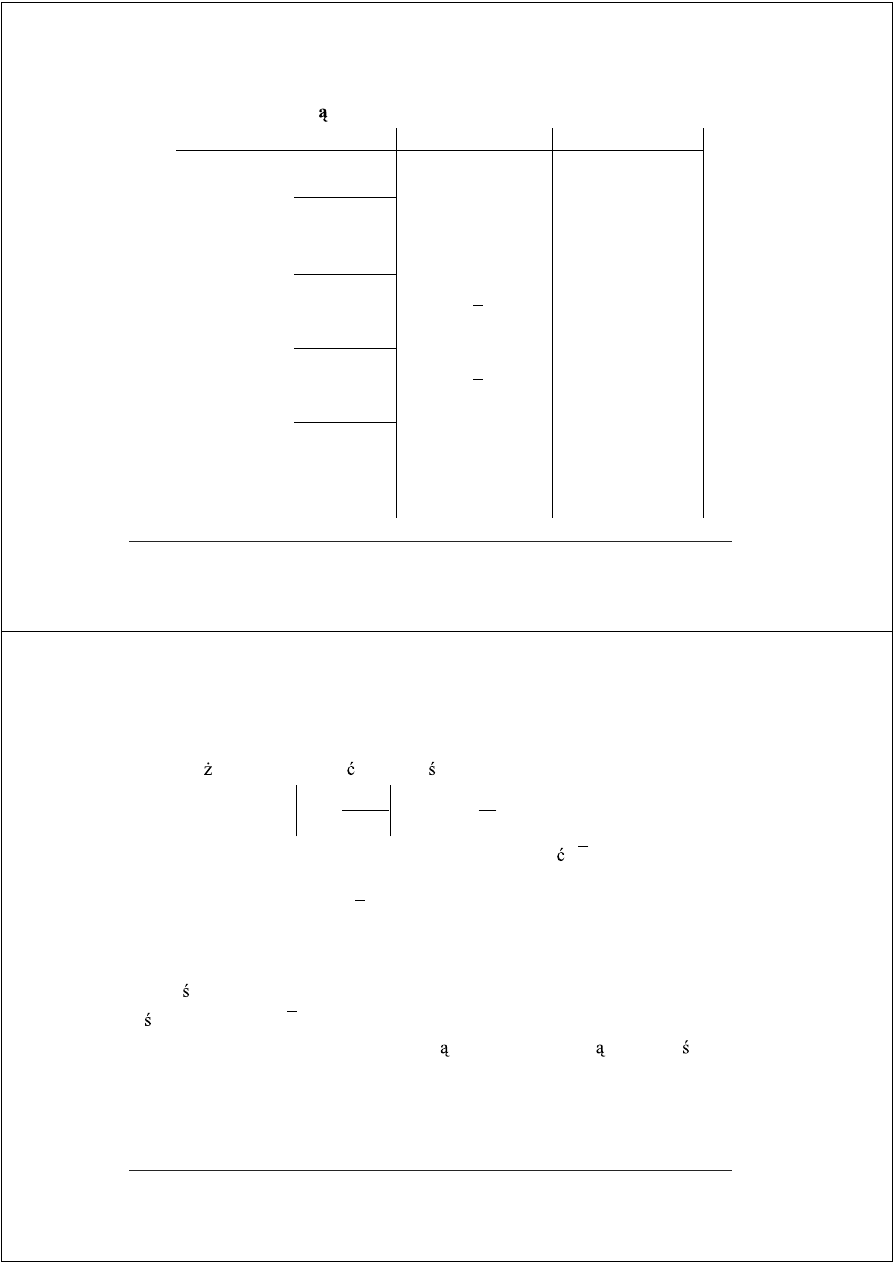
D

Parametryczny wykres dzielenia nieodtwarzaj cego w kodzie U2

iloraz Q

w kodzie SD

→

przekodowanie na kod U2: podstawienie

1

2

−

=

i

i

z

q

.

p

i

p

i

i

i

p

i

i

p

i

p

i

i

z

z

z

z

Q

−

−

−

=

+

+

−

=

−

−

=

+

+

−

−

=

+

−

−

=

−

=

∑

∑

∑

2

2

)

1

(

2

)

2

1

(

2

)

1

2

(

1

1

1

1

1

1

1

)

1

(

2

1

i

i

q

z

+

=

⇒

|

}

...,

,

,

,

0

{

|

|

}

1

,

...,

,

),

1

{(

|

3

2

1

2

3

2

1

SD

n

U

n

q

q

q

q

z

z

z

z

=

−

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–17

Dzielenie nieodtwarzaj ce (SD) – maszynowe (przykład)

D = 0,0110 X = 0,0011

U2–SD

NB

2r

0

= 2X

( 0 ) 0 , 0 1 1 0

≥

0 q

1

= 1

– D

( 1 ) 1 , 1 0 1 0

r

1

= 2r

0

– D ( 0 ) 0 , 0 0 0 0

≥

0 q

1

= 1

2r

1

( 0 ) 0 , 0 0 0 0

≥

0 q

2

= 1

– D

( 1 ) 1 , 1 0 1 0

r

2

= 2r

1

– D ( 1 ) 1 , 1 0 1 0

< 0 q

2

= 0

2r

2

( 1 ) 1 , 0 1 0 0 < 0 q

3

=

1

+ D

( 0 ) 0 , 0 1 1 0

q

2

q

3

= 01

r

3

= 2r

2

+ D ( 1 ) 1 , 1 0 1 0

< 0 q

3

= 0

2r

3

( 1 ) 1 , 0 1 0 0 < 0 q

4

=

1

+ D

( 0 ) 0 , 0 1 1 0

q

3

q

4

= 01

r

4

= 2r

3

+ D ( 1 ) 1 , 1 0 1 0 < 0

< 0 q

4

= 0

Q = 0,1001

korekcja

( 0 ) 0 , 0 1 1 0

q

4

= 0

Q = 0,1000

R = r

4

+ D

( 0 ) 0 , 0 0 0 0

Q = 0,1000

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

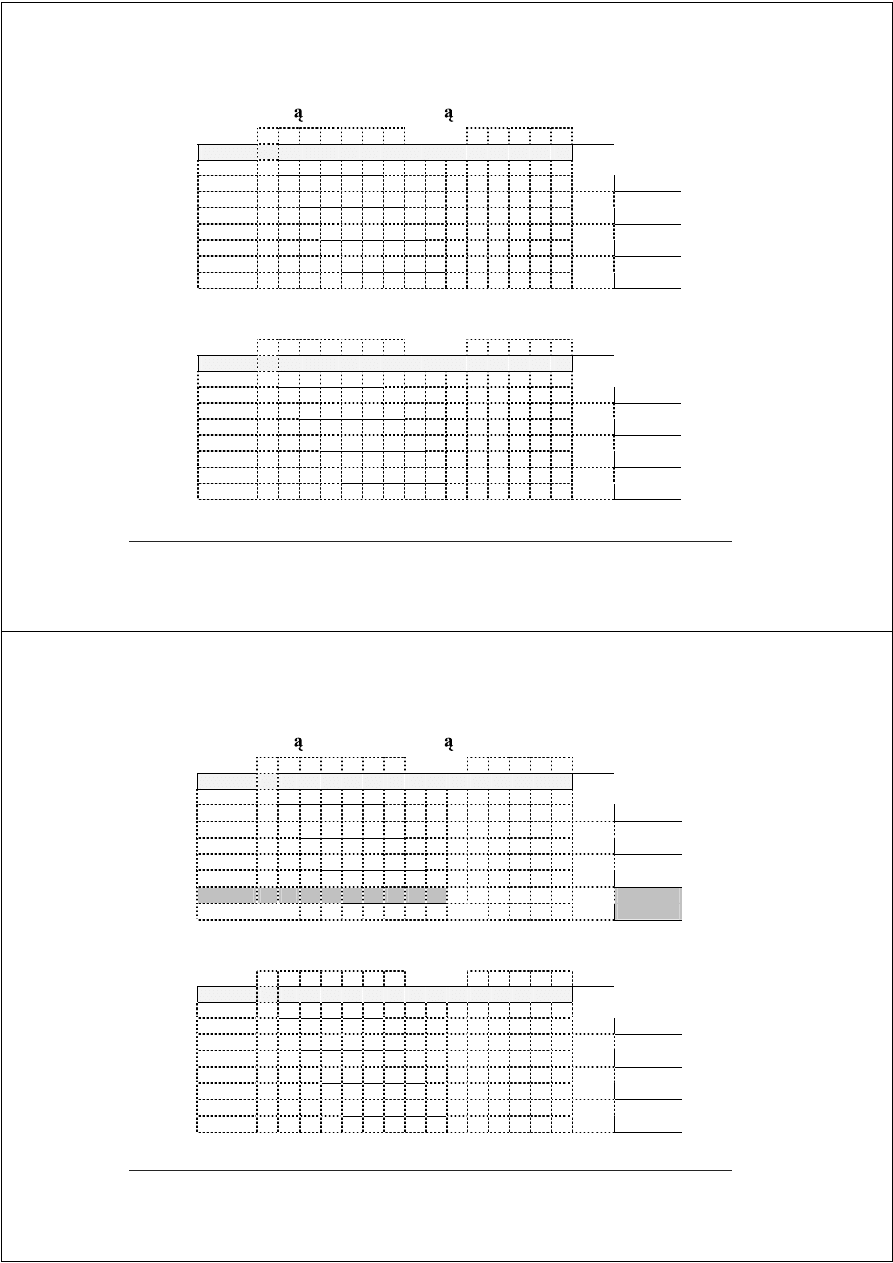
DIV–18

Dzielenie w dowolnym systemie SD

iloraz mo na łatwo skalowa do warto ci ułamkowej

m

F

m

F

Q

D

X

Q

D

X

Q

β

β

=

=

⇒

<

=

−

1

ułamek w systemie uzupełnieniowym ma zawsze posta (

1

→

”

β

−1

”):

0

0

,...}

,

,

,

1

{

,...}

,

,

,

0

{

3

2

1

3

2

1

<

>







=

−

−

−

−

−

−

F

F

F

Q

gdy

Q

gdy

q

q

q

q

q

q

Q

po standaryzacji ilorazu:

•

je li X D > 0, to q

0

= 0 oraz r

1

= X

β

−

m

−0⋅

D = X

β

−

m

je li X D < 0, to q

0

=

1

oraz r

1

= X

β

−

m

Zatem wszystkie kolejne cyfry ilorazu s dodatnie i spełniaj nierówno ci

|r

i+1

=

β

r

i

−

q

i

D | < | D | , r

i+1

D

≥0

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–12a

Dzielenie odtwarzaj ce i nieodtwarzaj ce (U2) – pisemne (1)

0, 1

0

1

1

====

−−−−

D

X =

0 1, 1

1 0

: 1, 0

1 0

1

====

++++

D

k=–2

++++

D

1, 0

1

0

1

1

1

1

0

0

0

q

0

= 1

–D

0

1

0

1

1

0

0

0

1

1

0

q

1

= 0

++++

D

1

0

1

0

1

1

1

0

1

1

0

q

2

= 1

–D

0

1

0

1

1

0

0

0

0

1

q

3

= 0

Iloraz jest równy Q =

.

1,010...

××××

2

2

= 101,0...

0

0

1

1

1

0

1

0

1

0

1

====

−−−−

D

X =

1, 1 0

0

1 0

:

0

1

0 1, 1

====

++++

D

k= 3

++++

D

0

1

0 1, 1

0

0

1

0

0

0

q

0

= 1

–D

1

0

1

0

1

1

1

1

0

1

0

q

1

= 0

++++

D

0

1

0

1

1

0

0

1

0

1

0

q

2

= 1

–D

1

0

1

0

1

1

1

1

1

1

q

3

= 0

Iloraz jest równy Q =

.

1,010...

××××

2

–3

= 1,111010...

Dzielenie

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

DIV–12b

Dzielenie odtwarzaj ce i nieodtwarzaj ce (U2) – pisemne (2)

0

1 0, 1

====

−−−−

D

X = (0) 0, 1 1 1 1

:

1 0 1, 1

====

++++

D

k=+1

++++

D

1

0 1, 1

1

1

1

0

1

rD

≥

0

q

0

= 1

−−−−

D

0

1

0

1

0

0

1

0

1

<0

q

1

= 0

++++

D

1

0

1

1

0

0

0

0

0

≥

0 (=0)

q

2

= 1, q

3+

= 0

−−−−

D

0

1 0

1

q

2

= 0

−−−−

2D

++++

D =

−−−−

D

0

1

0

1

0

( = – 2D)

<0

q

3+

= 111…

Iloraz jest równy Q = 1,01

U2

××××

2

–1

= 1,101

U2

lub Q = 1,00(1)

××××

2

–1

= 1,101

U2

0, 1

1

1

1

0, 0

1

1

====

−−−−

D

X = (1) (1) 1, 0 0 0 1

: 1, 1

0

1

====

++++

D

k= –1

−−−−

D

0 0, 1

1

(0) 0

0

1

0

rD <0

q

0

= 0

+D

1

1

0

1

(1) 1 1

1

0

≥

0

q

1

= 1

−−−−

D

0

0

1

1

0

0

0

1

1

<0

q

2

= 0

++++

D

1

1

0

1

0

0

0

0

0

≥

0 (=0)

q

3

= 1(0)

Iloraz jest równy Q =

.

1,010...

××××

2

–3

= 1,111010...

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–1a

Oszacowanie pierwiastka kwadratowego – algorytm intuicyjny

X

A

≅

z dokładno ci

ε

je li

2

2

)

(

ε

+

<

≤

A

X

A

•

jedyny uniwersalny algorytm – zgadywanie lub przegl

ą

d zupełny

suma kolejnych naturalnych liczb nieparzystych jest kwadratem ich liczby

(1=1

2

; 1+3=2

2

; 1+3+5=3

2

; 1+3+5+7=4

2

; 1+3+5+7+9=5

2

; …)

∑

=

=

−

⇒

−

=

−

−

n

i

n

i

n

n

n

1

2

2

2

)

1

2

(

1

2

)

1

(

•

n

X

≅

je li

2

2

)

1

(

+

<

≤

n

X

n

algorytm

0. i

=−1,

d

=−1,

S

=

X

1. i

=

i

+1,

d

=

d

+2

2. S

=

S

−

d

3. je li S<0 to

i

X

≅

, w przeciwnym razie id do 1

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–1b

Poprawa dokładno ci oszacowania w systemie pozycyjnym

Przybli eniem pierwiastka kwadratowego z liczby X

z dokładno ci do 1 cyfry znacz cej jest q

s

β

s

takie, e

2

2

2

2

2

2

)

(

)

)

1

(

(

)

(

+

≤

+

=

+

<

≤

≤

s

s

s

s

s

s

s

s

s

q

q

X

q

β

β

β

β

β

β

•

2s – najwy sza parzysta pot ga podstawy nie wi ksza od X

•

dokładno bezwzgl dna wynosi

β

s

•

2

2

2

)

1

(

+

<

≤

−

s

s

s

q

X

q

β

.

Dokładniejsze przybli enie

1

1

−

−

+

s

s

s

s

q

q

β

β

takie, e

2

1

1

2

1

1

)

)

1

(

(

)

(

−

−

−

−

+

+

<

≤

+

s

s

s

s

s

s

s

s

q

q

X

q

q

β

β

β

β

)

1

)

)

(

1

(

2

(

)

2

(

1

1

2

2

1

1

+

+

+

<

−

≤

+

−

−

−

−

−

s

s

s

s

s

s

s

s

q

q

q

q

X

q

q

q

β

β

β

Podobnie mo na obliczy dokładniejsze przybli enie pierwiastka Q

(r)

+q

r–1

β

r–1

na podstawie poprzedniego przybli enia Q

(r)

z dokładno ci

β

r

.

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–1

Przybli enia

Niech

β

,

.

.

.

}

0

,

.

.

.

,

,

,

{

2

1

)

(

p

s

s

s

p

q

q

q

Q

−

−

−

=

p

s

p

s

p

p

q

Q

Q

−

−

−

+

=

β

)

1

(

)

(

X

Q

p

≅

)

(

z dokładno ci

p

s

−

β

je li

2

)

(

2

)

(

)

(

)

(

p

s

p

p

Q

X

Q

−

+

<

≤

β

p

s

p

s

p

s

p

p

s

p

s

p

p

p

q

Q

X

q

Q

Q

Q

−

−

−

−

−

−

−

−

+

+

<

≤

+

=

≤

β

β

β

)

1

(

)

1

(

)

(

)

1

(

Jak znale

kolejn cyfr

q

s–p

rozwini cia i lepsze przybli enie

Q

(

p

)

pierwiastka

X

Q

Q

p

p

≅

≤

−

)

(

)

1

(

na podstawie wyznaczonego wcze niej przybli enia

Q

(

p

–

1

)

?

Mamy

2

)

1

(

2

)

1

(

)

)

1

(

(

)

(

p

s

p

s

p

p

s

p

s

p

q

Q

X

q

Q

−

−

−

−

−

−

+

+

<

≤

+

β

β

czyli

.

.

.

)

.

.

.

2

(

)

2

(

)

1

(

)

1

(

2

)

1

(

)

1

(

+

<

=

−

≤

+

−

−

−

−

−

−

−

−

p

p

p

p

s

p

s

p

s

p

s

p

Q

R

Q

X

q

q

Q

β

β

Wynika st d rekurencyjna zale no kolejnych reszt

]

2

[

]

[

]

[

)

1

(

2

)

(

2

)

1

(

)

1

(

)

(

p

s

p

s

p

p

s

p

s

p

p

p

p

q

Q

q

Q

Q

R

R

−

−

−

−

−

−

−

+

−

=

−

=

−

β

β

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–2

Algorytm odr czny

Kolejn p-t cyfr przybli enia pierwiastka jest najwi ksza taka

q

s–p

, e

)

1

(

)

1

(

)

2

(

−

−

−

−

−

−

≤

+

p

p

s

p

s

p

s

p

s

p

R

q

q

Q

β

β

gdzie

]

2

[

)

1

(

)

1

(

)

(

p

n

p

n

p

p

n

p

n

p

p

q

Q

q

R

R

−

−

−

−

−

−

+

−

=

β

β

Po skalowaniu

2

)

(

)

(

)

(

p

s

p

p

R

r

−

−

=

β

, kład c

)

(

)

(

p

p

s

p

Q

Q

−

−

=

β

, otrzymamy:

]

2

[

1

1

2

p

s

p

p

s

p

p

q

Q

q

r

r

−

−

−

−

+

−

=

β

β

gdzie

Q

p–

1

jest obliczonym poprzednim przybli eniem pierwiastka

skalowanym do warto ci całkowitej

algorytm

1.

s

X

r

2

0

−

=

β

2. przeskaluj poprzedni reszt cz ciow

r

p–

1

przez

β

2

3. podwój i przeskaluj przez

β

obliczone przybli enie pierwiastka

Q

p–

1

4. znajd najwi ksz

Q

s–p

, dla której kolejna reszta jest najmniejsza dodatnia

5. powtarzaj od 1. a do uzyskania wymaganej dokładno ci

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–3

Algorytm odr czny – przykład

8 4 3, 3 5 4 4

→

q

1

=2

843

10

= 29 29 +2

4 Q

1

=2

→

2

⋅

2

⋅

10

4 4 3 (40+q

0

)

×

q

0

≤

443

→

q

0

=9

4 4 1 Q

2

=29

→

2

⋅

29

⋅

10

2 3 5 (580+q

–1

)

×

q

–1

≤

235

→

q

–1

=0

2 3 5 4 4 Q

3

=290

→

2

⋅

290

⋅

10

2 3 2 1 6 (5800+q

–2

)

×

q

–2

≤

23544

→

q

–2

=4

1 1 0 1 0 0 1 0 1 1

→

q

4

=1

843

10

= 29

2

+2

1 Q

1

=1

1 0 0 1 (100+q

3

)

×

q

3

≤

1001

→

q

3

=1

1 0 1 Q

2

=11

1 0 0 0 0 (1100+q

2

)

×

q

2

≤

10000

→

q

2

=1

1 1 0 1 Q

3

=111

0 0 1 1 1 0 (11100+q

1

)

×

q

1

≤

1111

→

q

1

=0

0 0 0 0 0 Q

4

=1110

0 1 1 1 0 1 1 (111000+q

0

)

×

q

0

≤

111011

→

q

0

=1

1 1 1 0 0 1 Q

5

=11101

29

10

1 0 1 0 r

5

=10

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–4

Algorytm odr czny – sekwencyjne generowanie podwojenia

8 4 3, 3 5 4 4

→

q

1

=2

2

4 Q

1

=2

→

2

⋅

2

⋅

10

+2

4 4 3 (4q)

×

q

≤

443

→

q

0

=9

4 9

4 4 1 Q

2

=29

→

2

⋅

29

⋅

10

+9

2 3 5 (58q)

×

q

≤

235

→

q

–1

=0

5 8 0

2 3 5 4 4 Q

3

=290

→

2

⋅

290

⋅

10

=0

2 3 2 1 6 (580q)

×

q

≤

23544

→

q

–2

=4

5 8 0 4

1 1 0 1 0 0 1 0 1 1

→

q

4

=1

1

1 Q

1

=1

+1

1 0 0 1 (10q)

×

q

≤

1001

→

q

3

=1

1 0 1

1 0 1 Q

2

=11

1

1 0 0 0 0 (110q)

×

q

≤

10000

→

q

2

=1

1 1 0 1

1 1 0 1 Q

3

=111

+1

0 0 1 1 1 0 (1110q)

×

q

≤

1111

→

q

1

=0

1 1 1 0 0

0 0 0 0 0 Q

4

=1110

+0

0 1 1 1 0 1 1 (11100q)

×

q

≤

111011

→

q

0

=1

1 1 1 0 0 1

1 1 1 0 0 1 Q

5

=11101

+1

1 0 1 0 r

5

=10

1 1 1 0 1 0

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–5

Obliczanie pierwiastka kwadratowego w systemie NB

]

2

[

]

[

]

[

)

1

(

2

)

(

2

)

1

(

)

1

(

)

(

p

n

p

n

p

p

n

p

n

p

p

p

p

q

Q

q

Q

Q

R

R

−

−

−

−

−

−

−

+

−

=

−

=

−

β

β

,

Po skalowaniu

)

(

)

(

)

(

p

n

p

p

R

r

−

−

=

β

, otrzymamy wzór podobny jak w dzieleniu:

]

2

[

)

1

(

)

1

(

)

(

p

n

p

n

p

p

n

p

p

q

Q

q

r

r

−

−

−

−

−

+

−

=

β

β

analogia do dzielenia

→

obliczanie pierwiastka kwadratowego w układzie dziel cym

W systemie dwójkowym reguła upraszcza si bo

}

1

,

0

{

2

∈

=

i

i

q

q

.

Po normalizacji

n

X

X

2

0

−

=

β

i uproszczeniu indeksów (q

n–i

→

q

i

) otrzymamy

)

2

2

(

2

1

1

−

−

−

+

−

=

i

i

i

i

i

Q

q

r

r

, i = 1,2,..., p,

X

r

=

0

,







+

≥

+

<

=

−

−

−

−

−

−

).

2

2

(

2

gdy

,

1

),

2

2

(

2

gdy

,

0

1

1

1

1

i

i

i

i

i

i

i

Q

r

Q

r

q

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–6

Obliczanie pierwiastka kwadratowego w systemie NB –przykład

2

–i

+ 2Q

i – 1

q

i

r

0

= X

0 0 , 1 0 1 0 1 1 1 1

–

q

0

= 0 0,

2r

0

0 1 , 0 1 0 1 1 1 1 0

≥

00,1

q

1

= 1 0,1

– d

1

= – (2

–1

+ 2Q

0

)

1 1 , 1 0 0 0 0 0 0 0

r

1

= 2r

0

– d

1

0 0 , 1 1 0 1 1 1 1 0

2r

1

0 1 , 1 0 1 1 1 1 0 0

≥

01,01

q

2

= 1 0,11

– d

2

= – (2

–2

+ 2Q

1

)

1 0 , 1 1 0 0 0 0 0 0

r

2

= 2r

1

– d

2

0 0 , 0 1 1 1 1 1 0 0

2r

2

0 0 , 1 1 1 1 1 0 0 0 < 01,101

q

3

= 0 0,110

2r

3

= 2

⋅

2r

2

0 1 , 1 1 1 1 0 0 0 0

≥

01,1001

q

4

= 1 0,1101

– d

4

= – (2

–4

+ 2Q

3

)

1 0 , 0 1 1 1 0 0 0 0

r

4

= 2r

3

– d

4

0 0 , 0 1 1 0 0 0 0 0

2r

4

0 0 , 1 1 0 0 0 0 0 0 < 01,10101

q

5

= 0 0,11010

2r

5

= 2

⋅

2r

4

0 1 , 1 0 0 0 0 0 0 0 < 01,101001

q

6

= 0 0,110100

2r

6

= 2

⋅

2r

5

0 1 1 , 0 0 0 0 0 0 0 0

≥

01,1010001

q

7

= 1 0,1101001

– d

7

= – (2

–7

+ 2Q

6

)

1 1 0 , 0 1 0 1 1 1 1 0

r

7

= 2r

6

– d

7

0 0 1 , 0 1 0 1 1 1 1 0

2r

7

0 1 0 , 1 0 1 1 1 1 0 0

≥

01,10100101 q

8

= 1 0,11010011

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–7

Obliczanie pierwiastka kwadratowego – metoda nierestytucyjna

algorytm oparty na regule

)

2

2

(

2

1

1

−

−

−

+

−

=

i

i

i

i

i

Q

q

r

r

, i = 1,2,..., p,

X

r

=

0

mo na zrealizowa w wersji nieodtwarzaj cej reszty cz ciowe.

Bezpo rednie zastosowanie niemo liwe – kolejna cyfra jest wyznaczana po
okre leniu znaku nast pnej reszty. W pierwiastkowania warto tej reszty
zale ałaby od warto ci cyfry wyznaczanej na jej podstawie!

Problem znika, je li wynik wytwarzamy w kodzie SD

)

2

2

(

,

2

1

1

−

−

−

+

=

−

=

i

i

i

i

i

i

i

Q

q

d

d

r

r

,

X

r

=

0

, i = 1,2,...,p,







<

≥

=

−

−

,

0

2

gdy

,

1

,

0

2

gdy

,

1

1

1

i

i

i

r

r

q

! konieczna jest bie

ca korekcja po wyst pieniu cyfry ujemnej

Obliczanie

√√√√

—

© Janusz Biernat, Dzielenie'04, 19 listopada 2004

SQRT–8

Obliczanie pierwiastka kwadratowego – metoda nierestytucyjna

X =

49

/

256

2

–i

+ 2Q

i – 1

q

i

(SD) Q

i

r

0

= X

00,00110001

–

q

0

= 0

0,

2r

0

00,01100010

≥

0 00,1

q

1

= 1

– d

1

= – (2

–1

+ 2Q

0

)

11,10000000

0,1

r

1

= 2r

0

– d

1

11,11100010

2r

1

11,11000100

< 0 01,01

q

2

=

1

0,1

1

+ d

2

= + (2

–2

+ 2Q

1

) 00,11000000

00,11

0,01

r

2

= 2r

1

+ d

2

00,10000100

q

1

q

2

= 0 1

2r

2

01,00001000

≥

0 0,101

– d

3

= – (2

–3

+ 2Q

2

)

11,01100000

q

3

= 1

0,011

r

3

= 2r

2

– d

3

00,01101000

2r

3

00,11010000

≥

0 0,1101

– d

4

= – (2

–4

+ 2Q

3

)

11,00110000

q

4

= 1

0,0111

R = r

4

= 2r

3

– d

4

01,00000000

Pierwiastek ma sko czone rozwini cie Q = 0,0111 (

16

7

).

W drugim kroku dokonano zamiany przybli enia pierwiastka z kodu SD na U2