C

ZĄSTECZKI HETEROJĄDROWE

,

HYBRYDYZACJA

Opracował: mgr inż. Piotr Radomski
Gęstość elektronowa wokół jądra bardziej elektroujemnego jest większa niż wokół jądra
mniej elektroujemnego.
Różnice we właściwościach elektronowych pierwiastków decydują o rodzaju wiązania, jaki
mogą tworzyć ze sobą ich atomy. O ile bowiem w przypadku pierwiastków silnie różniących
się tymi właściwościami powstają wiązania jonowe, o tyle w przypadku niewielkich różnic –
wiązania kowalencyjne. Wspólna para elektronowa jest przyciągana przez oba atomy, choć
różnice w elektroujemności powodują, że orbital molekularny nie jest symetryczny (jak w
cząsteczkach homojądrowych).

W takich samych atomach poziomy o tej samej głównej i pobocznej liczbie kwantowej mają
taką samą energię. Dlatego w cząsteczce azotu orbitale 2s jednego z atomów mogą nakładać
się z orbitalami 2s drugiego atomu, ale nie z orbitalami 2px tego atomu, gdyż warunek
zbliżonej energii nie jest spełniony, nawet jeśli mają one taka samą symetrię względem osi
wiązania

b

a

b

a

c

c

c

c













2

1

2

1

*









w przypadku cząsteczek homojądrowych c

1

=c

2

dla hetero c

1

≠c

2

Jeżeli |c

1

| > |c

2

| wówczas gęstość elektronowa jest przy atomie B następuje wtedy polaryzacja

wiązań. Pojawiają się wówczas przesunięcia elektronu co skutkuje powstaniem ładunku
dodatniego i ujemnego w jednej cząsteczce.

DIPOL - cząsteczka w której można wyróżnić biegun dodatni (δ+) i ujemny (δ-).
Moment dipolowy jest miarą przesunięcia ładunku elektrycznego w cząsteczce dipolowej (μ)

μ = δ ∙ l [C∙m] lub D (debaj) 1D = 3,33564∙10

-30

[C∙m]

δ – bezwzględna wartość ładunku elektrycznego [C],
l – odległość od biegunów [m].

PRZYKŁADY CZĄSTECZEK HETEROJĄDROWYCH

LiH
Li: (1s

2

2s

1

)

H: (1s

1

)

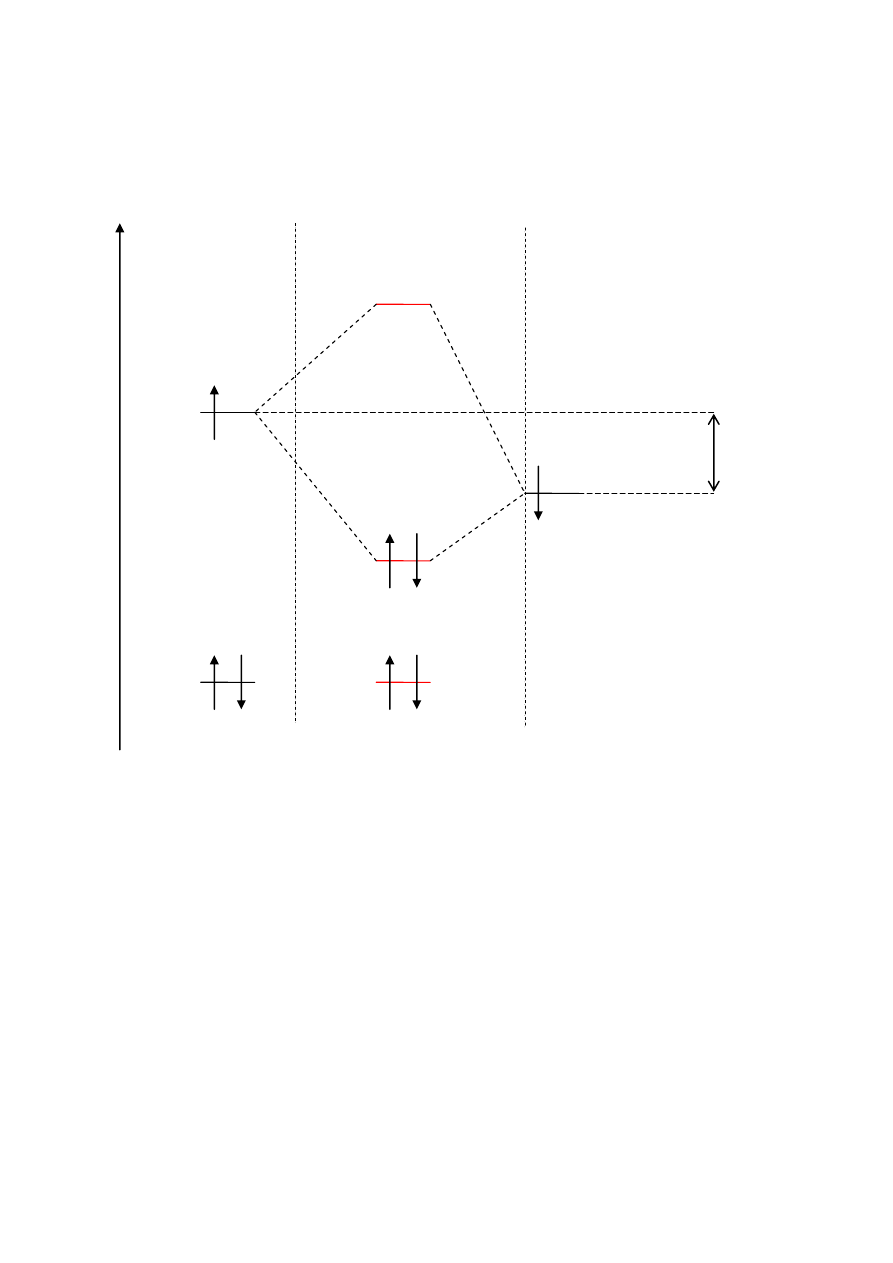
Atom wodoru jest bardziej elektroujemny niż atom litu dlatego energia jego orbitalu (1s)
biorącego udział w wiązaniu jest mniejsza niż energia obitalu (2s) pochodzącego od litu.
W cząsteczkach heteroatomowych tak jak i w przypadku cząsteczek homoatomowych
wiązanie powstaje poprzez uwspólnienie elektronów znajdujących się na ostatniej powłoce –
powłoce walencyjnej – pozostałem powłoki w wiązaniu udziału nie biorą.

σ*

E

σ

8,205 eV

2s

1

1s

2

1s

1

Li: (1s

2

2s

1

)

H: (1s

1

)

Orbitale cząsteczkowe LiH

LiH: (σ

s

)

2

HF
H: (1s

1

)

F: (1s

2

2s

2

2p

5

)

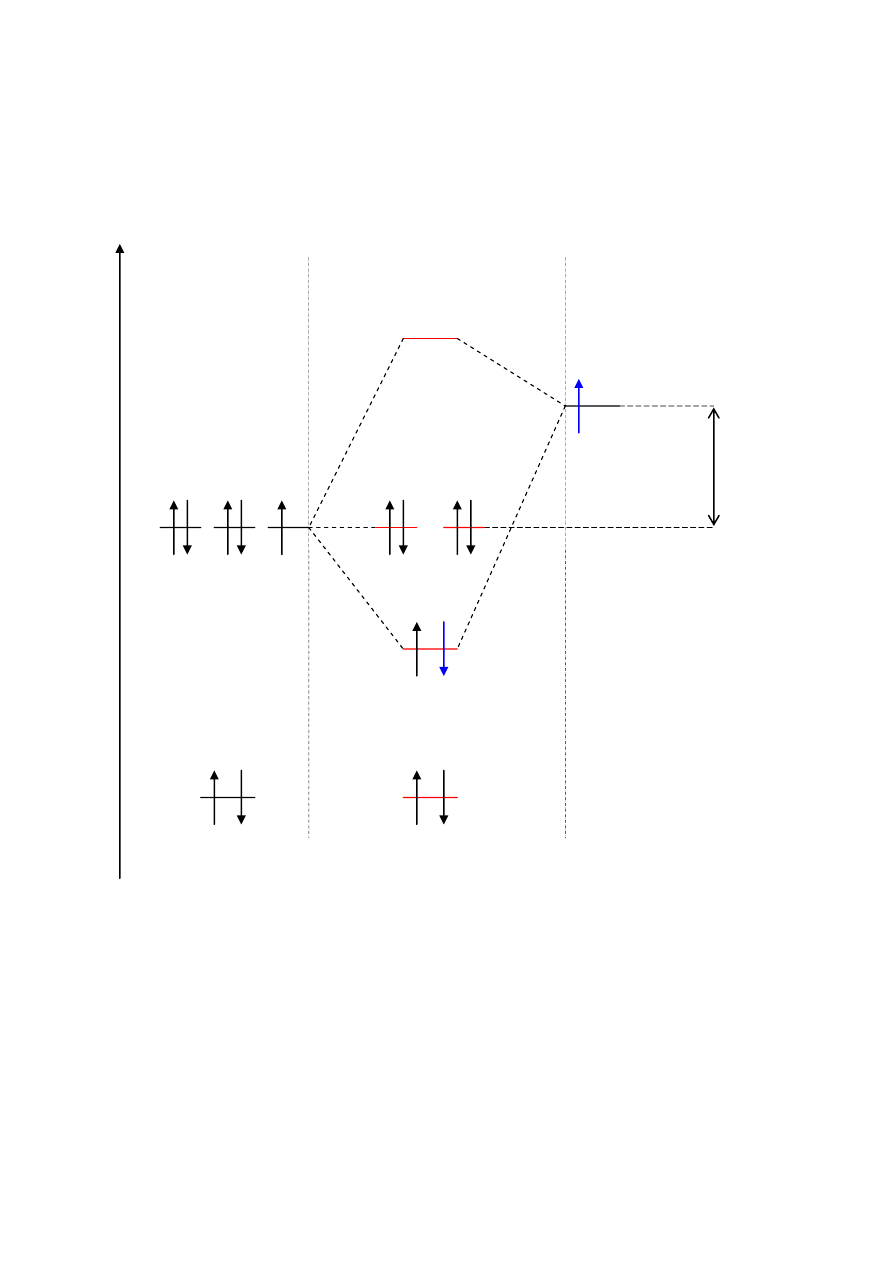
W cząsteczce HF poziomy energetyczne fluoru (konfiguracja w stanie podstawowym
1s

2

2s

2

2p

5

) różnią się znacznie od poziomu energetycznego wodoru (1s

2

). W atomie fluoru

najbardziej zbliżoną do elektronu atomu wodoru energie mają elektrony orbitali 2p (jest ona
tylko o 3,8 eV niższa niż energia orbitalu 1s wodoru). Dlatego w cząsteczce HF wspólną parą
elektronową będzie obsadzony przez 2 elektrony orbital wiążący utworzony z orbitali 1s
wodoru i 2p

x

fluoru. Ponieważ jednak orbital 2p

x

fluoru ma niższą energię, przeto w orbitalu

wiążącym σ będzie miał on większy udział. Skoro tak, to znaczy, że w orbitalu wiążącym
będzie miał on większy udział. Elektrony orbitalu wiążącego σ będą zatem częściej
przebywały w pobliżu jądra fluoru, a orbital cząsteczkowy nie będzie symetryczny. Elektrony
fluoru opisywane przez orbitale 2s, 2p

y

i 2p

z

nie tworzą żadnych orbitali molekularnych, gdyż

wodór nie ma żadnych orbitali atomowych o podobnych energiach i symetrii. które mogłyby
się z nimi nakładać. Dlatego mówimy, że przy atomie fluoru pozostają 3 pary elektronowe.
Skoro jednak ładunek wiązania został przesunięty w stronę fluoru, możemy mówić, że

σ*

HF

E

σ

HF

3,8 eV

2s

2

H: (1s

1

)

Orbitale cząsteczkowe HF

LiH: K(2s

F

)

2

(σ

HF

)

2

(2p

y

F

)

2

(2p

z

F

)

2

2p

y

2p

z

2p

x

2p

y

2p

z

1s

H

2s

F

F: 2s

2

2p

5

cząsteczka ta wykazuje charakter biegunowy, czyli polarny. Jeśli przesunięty został ładunek
efektywny δ, to „od strony fluoru” cząsteczka będzie posiadać ładunek – δ, a ”od strony
wodoru” ładunek +δ. Jeśli pomnożymy wielkość ładunku przez odległość „l” na jaką został
przesunięty, otrzymamy moment dipolowy cząsteczki: μ=δ∙l.

NO
N: (1s

2

2s

2

2p

3

)

O: (1s

2

2s

2

2p

4

)

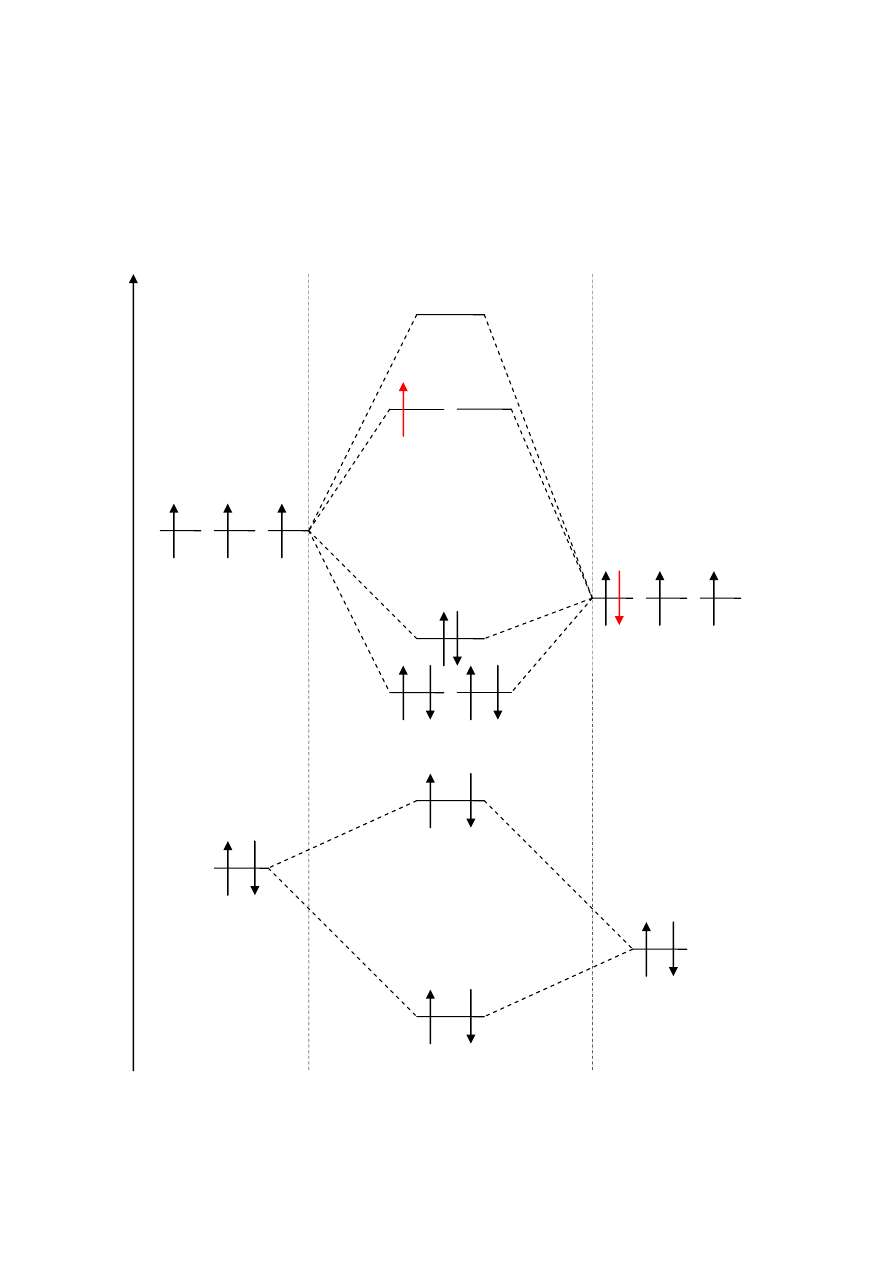
RW = 0,5 ∙ (6 – 1) = 2,5

σ*2s

σ 2s

N: 2s

2

O: 2s

2

E

N: 2p

3

O: 2p

4

2p

x

2p

y

2p

z

2p

y

2p

z

2p

x

π 2p

y

π 2p

z

σ 2p

x

π* 2p

z

π* 2p

y

σ *2p

x

NO: KK(σ 2s

NO

)

2

(σ *2s

NO

)

2

(π 2p

y NO

)

2

(π 2p

z NO

)

2

(σ 2p

x NO

)

2

(π* 2p

y NO

)

1

Orbitale cząsteczkowe NO

CN
N: (1s

2

2s

2

2p

3

)

C: (1s

2

2s

2

2p

2

)

Oba zapisy konfiguracji wiązania są poprawne (drugi jest wariantem

uproszczonym względem pierwszego)

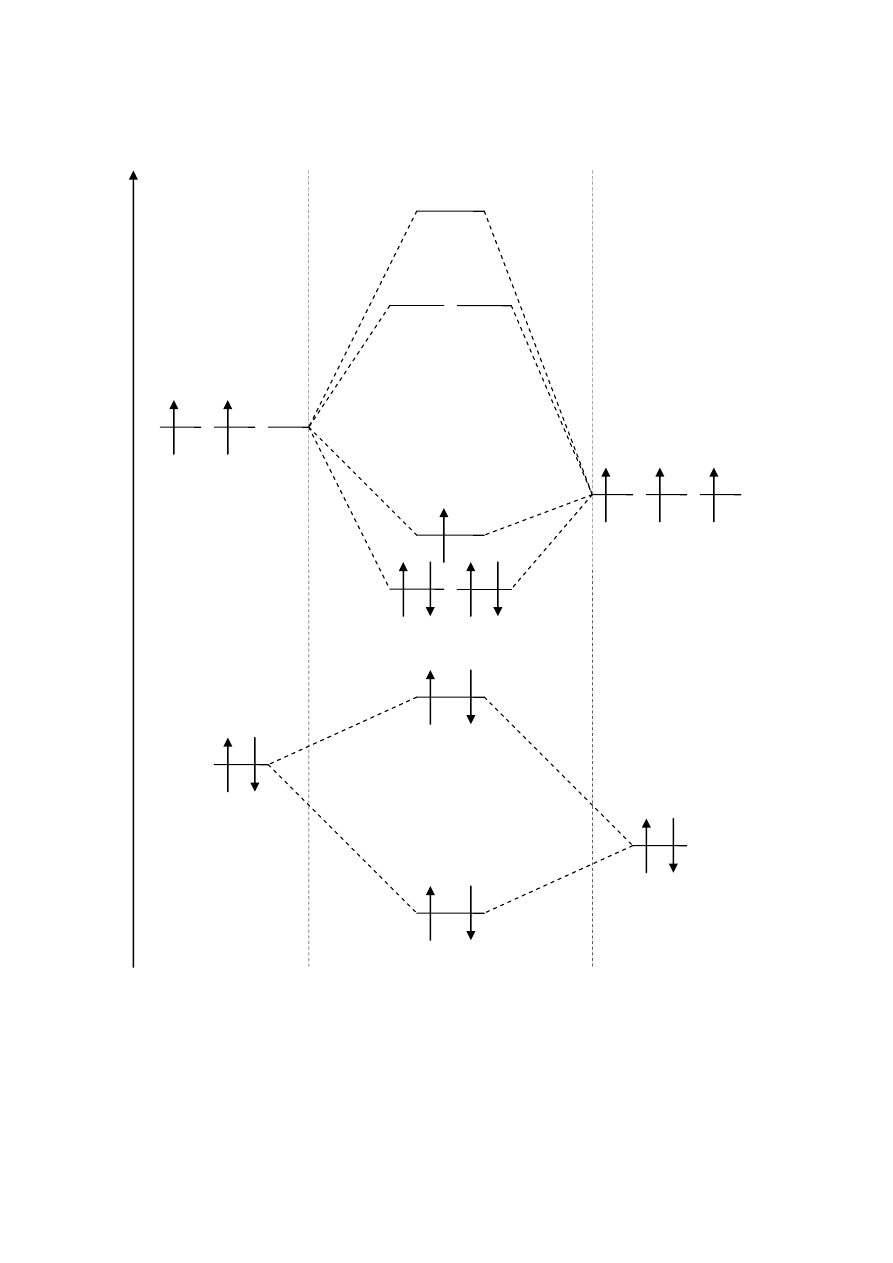
RW = 0,5 ∙ (5 – 0) = 2,5

σ*2s

σ 2s

C: 2s

2

N: 2s

2

E

C: 2p

2

N: 2p

3

2p

x

2p

y

2p

z

2p

y

2p

z

2p

x

π 2p

y

π 2p

z

σ 2p

x

π* 2p

z

π* 2p

y

σ *2p

x

CN: KK(σ 2s

CN

)

2

(σ *2s

CN

)

2

(π 2p

y CN

)

2

(π 2p

z CN

)

2

(σ 2p

x CN

)

1

CN: KK(σ 2s

CN

)

2

(σ *2s

CN

)

2

(π 2p

CN

)

4

(σ 2p

CN

)

1

Orbitale cząsteczkowe CN

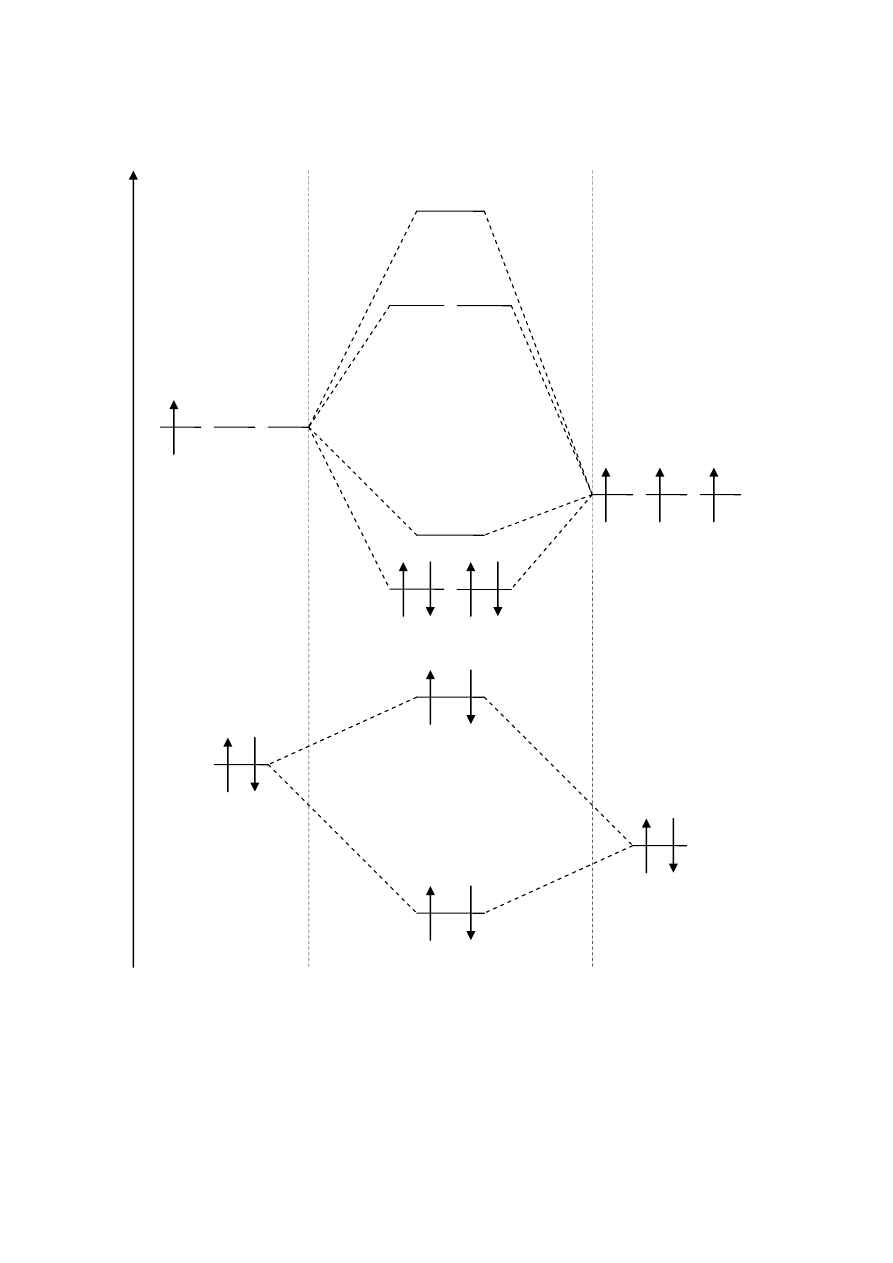
BN
N: (1s

2

2s

2

2p

3

)

B: (1s

2

2s

2

2p

1

)

RW = 0, 5 ∙ (4 – 0) = 2

σ*2s

σ 2s

B: 2s

2

N: 2s

2

E

B: 2p

1

N: 2p

3

2p

y

2p

z

2p

x

π 2p

y

π 2p

z

σ 2p

x

π* 2p

z

π* 2p

y

σ *2p

x

BN: KK(σ 2s

BN

)

2

(σ *2s

BN

)

2

(π 2p

y

BN

)

2

(π 2p

z BN

)

2

BN: KK(σ 2s

BN

)

2

(σ *2s

BN

)

2

(π 2p

BN

)

4

Orbitale cząsteczkowe BN

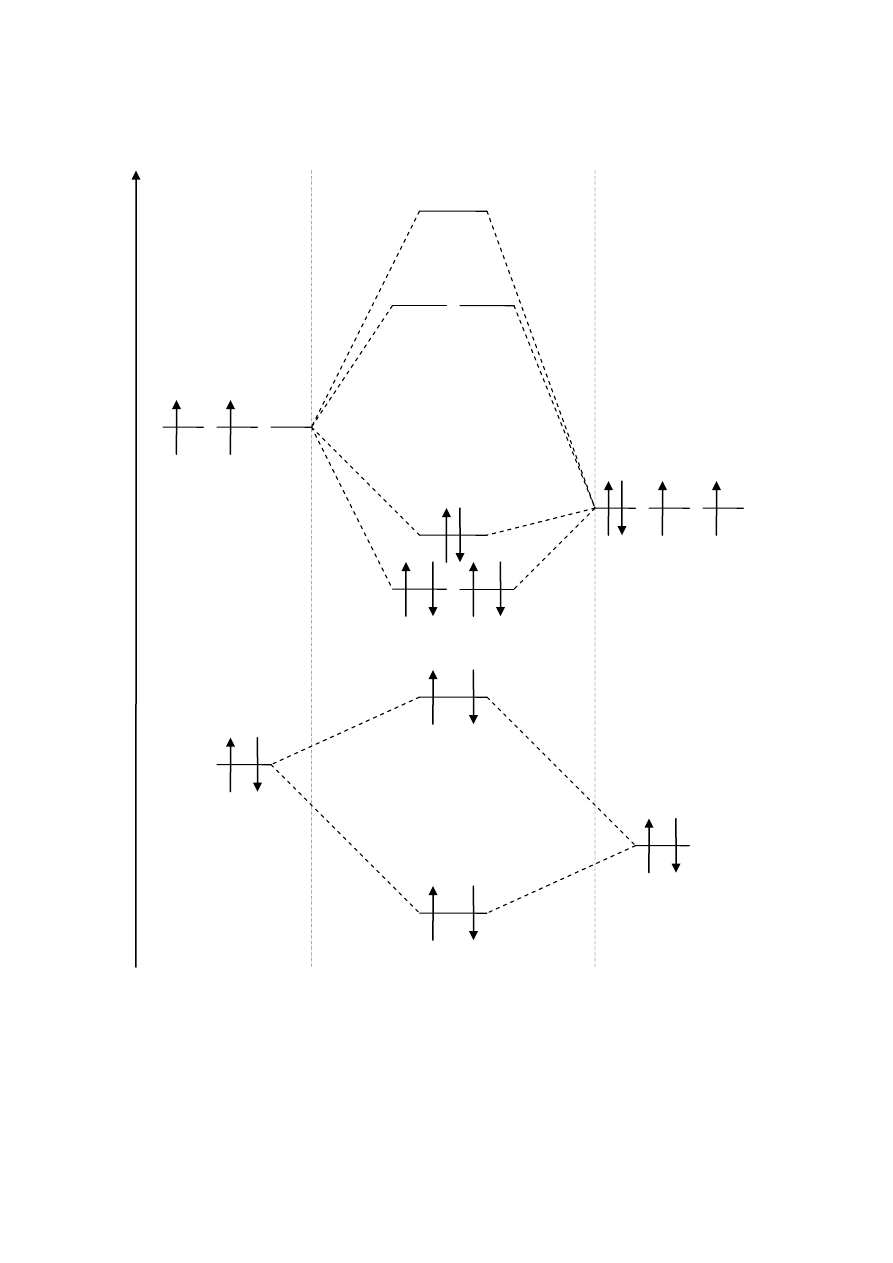
CO
C: (1s

2

2s

2

2p

2

)

O: (1s

2

2s

2

2p

4

)

RW = 0, 5 ∙ (6 – 0) = 3

σ*2s

σ 2s

C: 2s

2

O: 2s

2

E

C: 2p

1

O: 2p

3

π 2p

y

π 2p

z

σ 2p

x

π* 2p

z

π* 2p

y

σ *2p

x

CO: KK(σ 2s

CO

)

2

(σ *2s

CO

)

2

(π 2p

y CO

)

2

(π 2p

z CO

)

2

(σ 2p

x CO

)

2

CO: KK(σ 2s

CO

)

2

(σ *2s

CO

)

2

(π 2p

CO

)

4

(σ 2p

CO

)

2

Orbitale cząsteczkowe CO

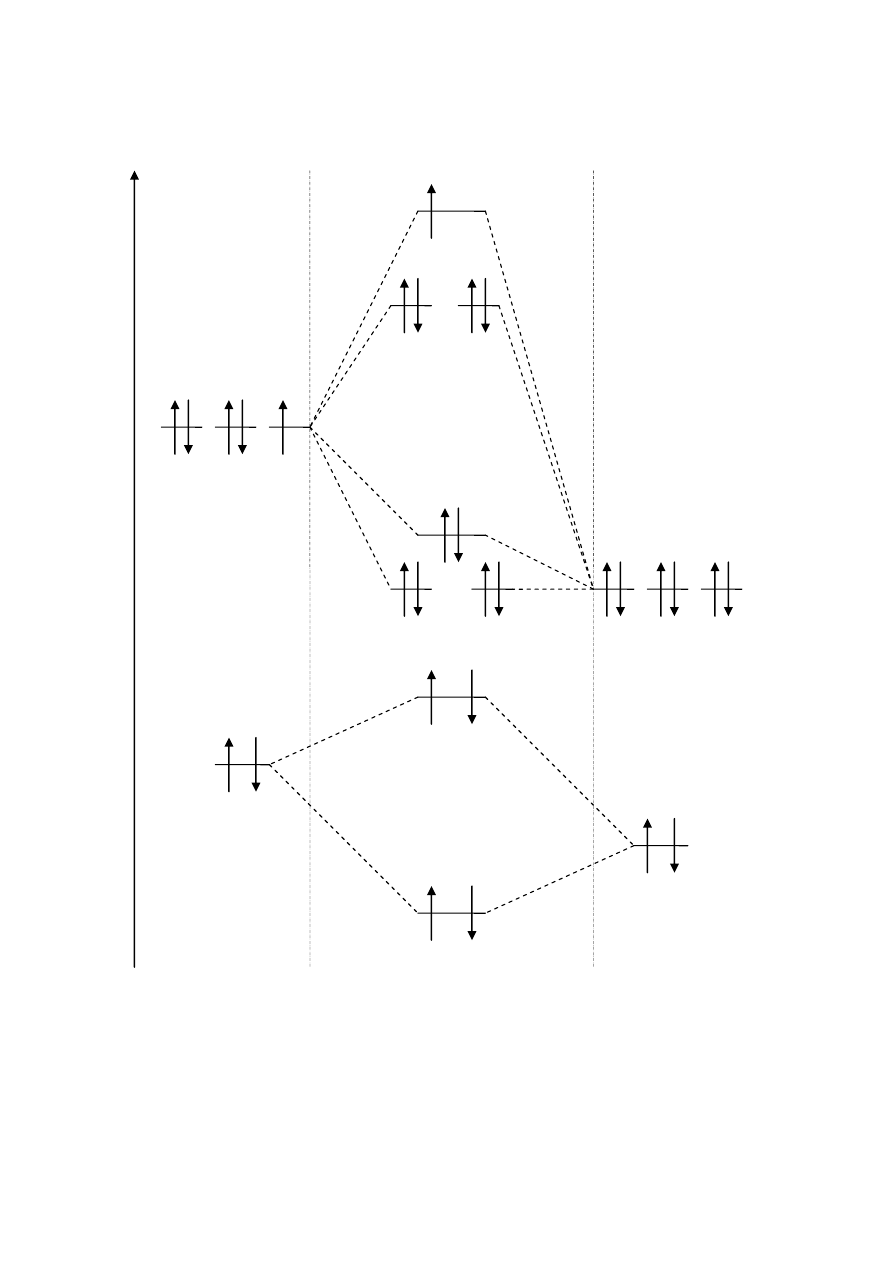
XeF
F: (1s

2

2s

2

2p

5

)

Xe: (1s

2

2s

2

2p

6

)

σ*2s

σ 2s

F: 2s

2

Xe: 2s

2

E

F: 2p

5

Xe: 2p

6

2p

x

2p

y

2p

z

2p

y

2p

z

2p

x

π 2p

y

π 2p

z

σ 2p

x

π* 2p

z

π* 2p

y

σ *2p

x

XeF: KK(σ 2s

XeF

)

2

(σ *2s

XeF

)

2

(π 2p

y XeF

)

2

(π 2p

z XeF

)

2

(σ 2p

x XeF

)

2

(π* 2p

y XeF

)

2

(π* 2p

z XeF

)

2

(σ * 2p

x XeF

)

1

XeF: KK(σ 2s

XeF

)

2

(σ *2s

XeF

)

2

(π 2

XeF

)

4

(σ 2p

XeF

)

2

(π* 2p

XeF

)

4

(σ * 2p

XeF

)

1

Orbitale cząsteczkowe XeF

HYBRYDYZACJA

Hybrydyzacja – przekształcenie funkcji orbitalnych polegające na „skrzyżowaniu” dwóch lub
więcej orbitali atomowych na skutek czego powstają orbitale hybrydyzowane posiadające
inny kształt i energię niż orbitale wyjściowe, zmienia się także orientacja w przestrzeni.
Orbitale wiązań chemicznych tworzy się nie ze „zwykłych orbitali atomowych” (tak jak przy
metodzie orbitali molekularnych) lecz z ich kombinacji liniowych – czyli hybryd.

Typy hybrydyzacji:

1. sp

3

– ujednolicenie jednego orbitalu s i trzech orbitali p:

np. CH

4

, CF

4

, NH

3

H

2

O

kształty czworościanu foremnego
2. sp

2

– ujednolicenie jednego orbitalu s i dwóch orbitali p:

np. BeF

2

, SO

2

, C

2

H

4

BCl

2

PbCl

2

kształt trójkąta foremnego
3. sp – ujednolicenie jednego orbitalu s I jednego orbialu p:
CO

2

, C

2

H

2

, BeH

2

, BeCl

2

kształt liniowy

Różnica w kątach dla hybrydyzacji sp

3

wynika z obecności pojedynczych niewiążących

powłok elektronowych które działają odpychająco na elektrony wiążące.

Nazwa
hybrydyzacji

Nazwa hybrydy

Liczba

orbitali

zhybrydyzowanych

Figura

geometryczna

określająca

położenie orbitali (kształt cząsteczki)

digonalna

sp

2

liniowa 180°

diagonalna

sp

2

3

trójkątna 120°

tetraedryczna

sp

3

4

tetraedr (czworościan)

bipiramidalna

d sp

3

5

bipiramida trygonalna

oktaedryczna

d

2

sp

3

6

bipiramida tetragonalna

bipiramidalna

d

3

sp

3

7

bipiramida pentagonalna

Orbitale zhybrydyzowane przyjmują takie same położenie w przestrzeni, aby układ osiągał
minimum energetyczne tj. kiedy chmury elektronowe orbitali zhybrydyzowanych są tak
rozmieszczone w przestrzeni, aby znajdowały się najdalej od siebie, dlatego różnym typom
hybrydyzacji przypisuję się odpowiednie kształty cząsteczek.

Orbitale zlokalizowane – dwucentowe wokół dwóch jąder dwóch atomów łączących się.
Orbitale zdelokalizowane – kombinacja liniowa orbitali atomowych kilku atomów.
Prawdopodobieństwo napotkania elektronów jest w sąsiedztwie kilku jąder (orbitale
wielocentowe).

Wolne pary elektronowe:
- dają możliwość przyłączania się lub czegoś,
- nadają moment dipolowy,
- zmieniają kąty w cząstce.

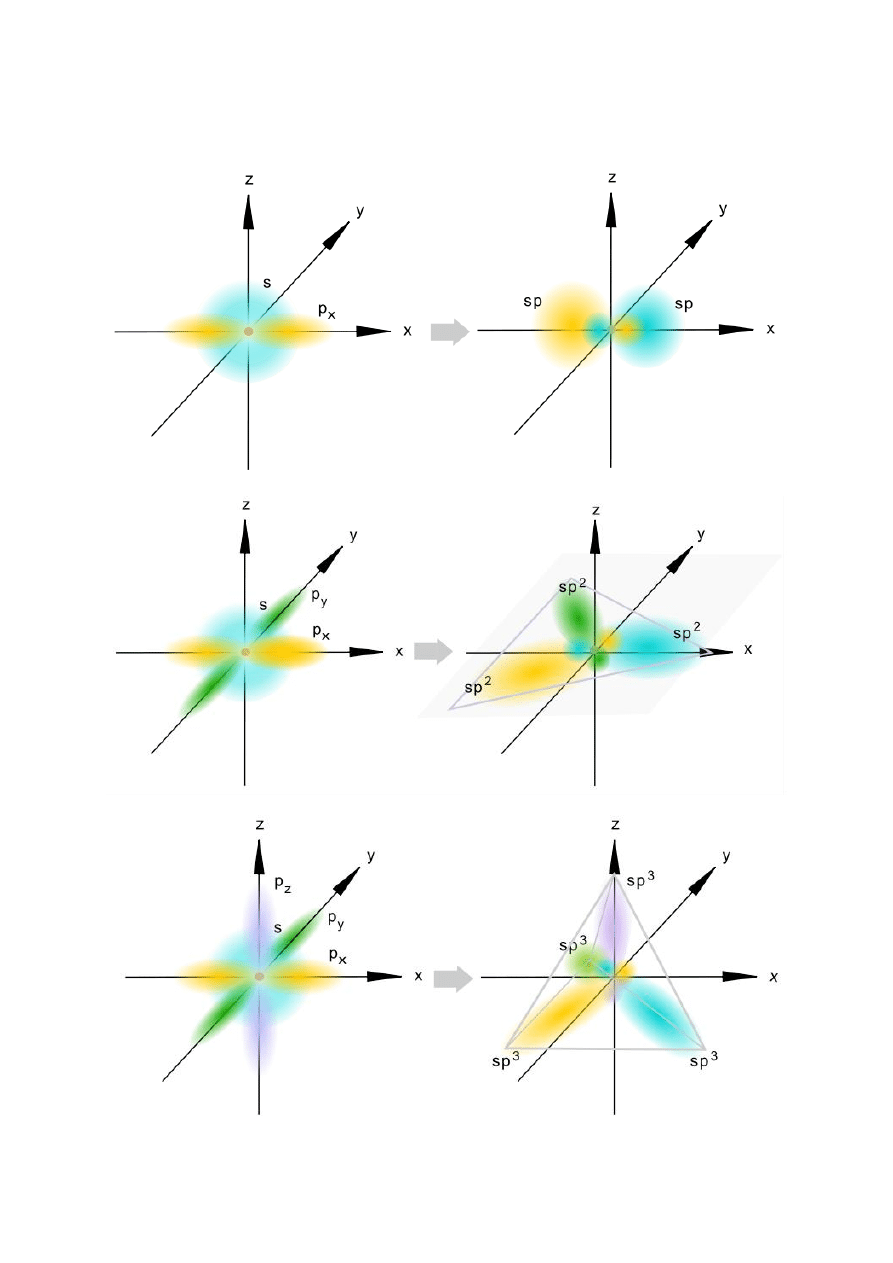
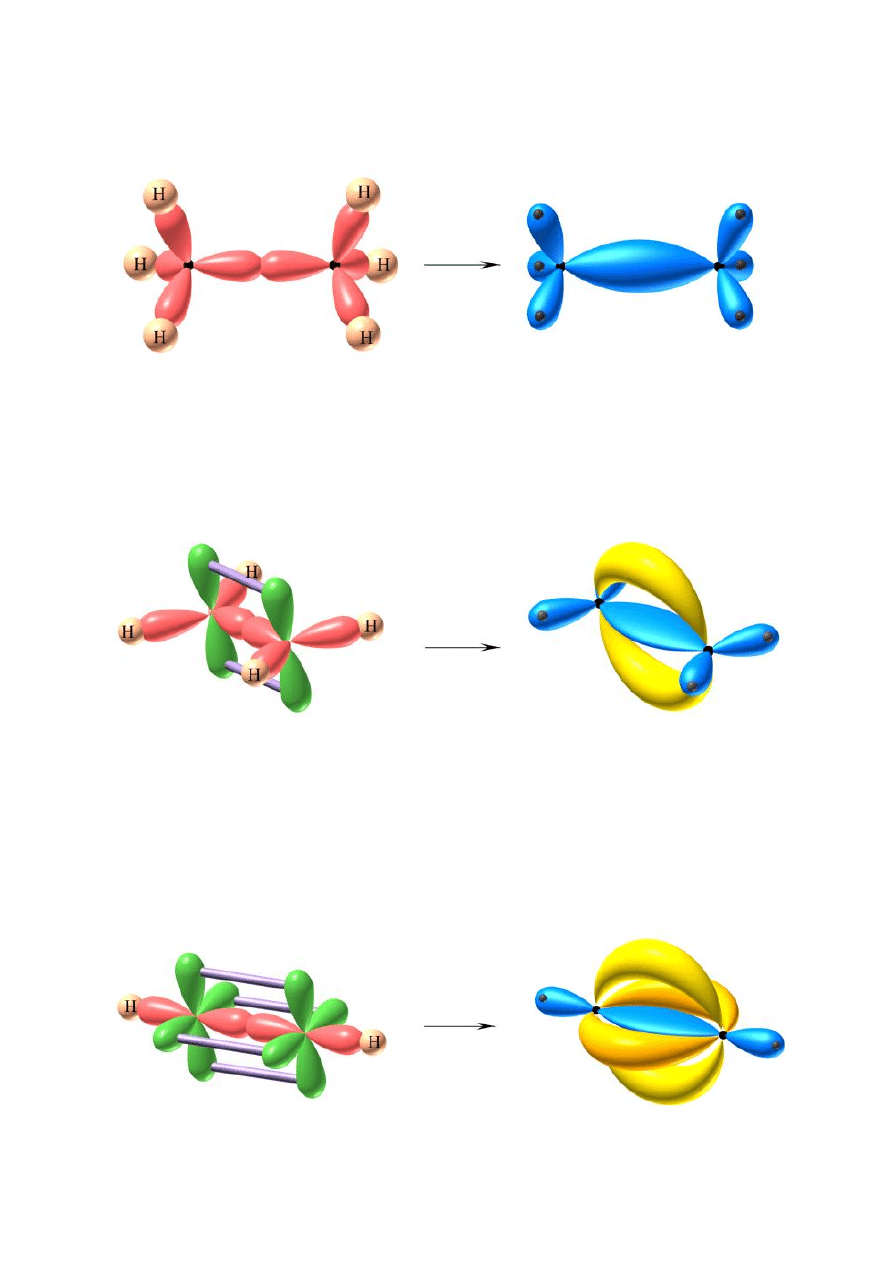
Powstawanie orbitali zhybrydyzowanych
1. Hybrydyzacja sp

2. Hybrydyzacja sp

2

3. Hybrydyzacja sp

3

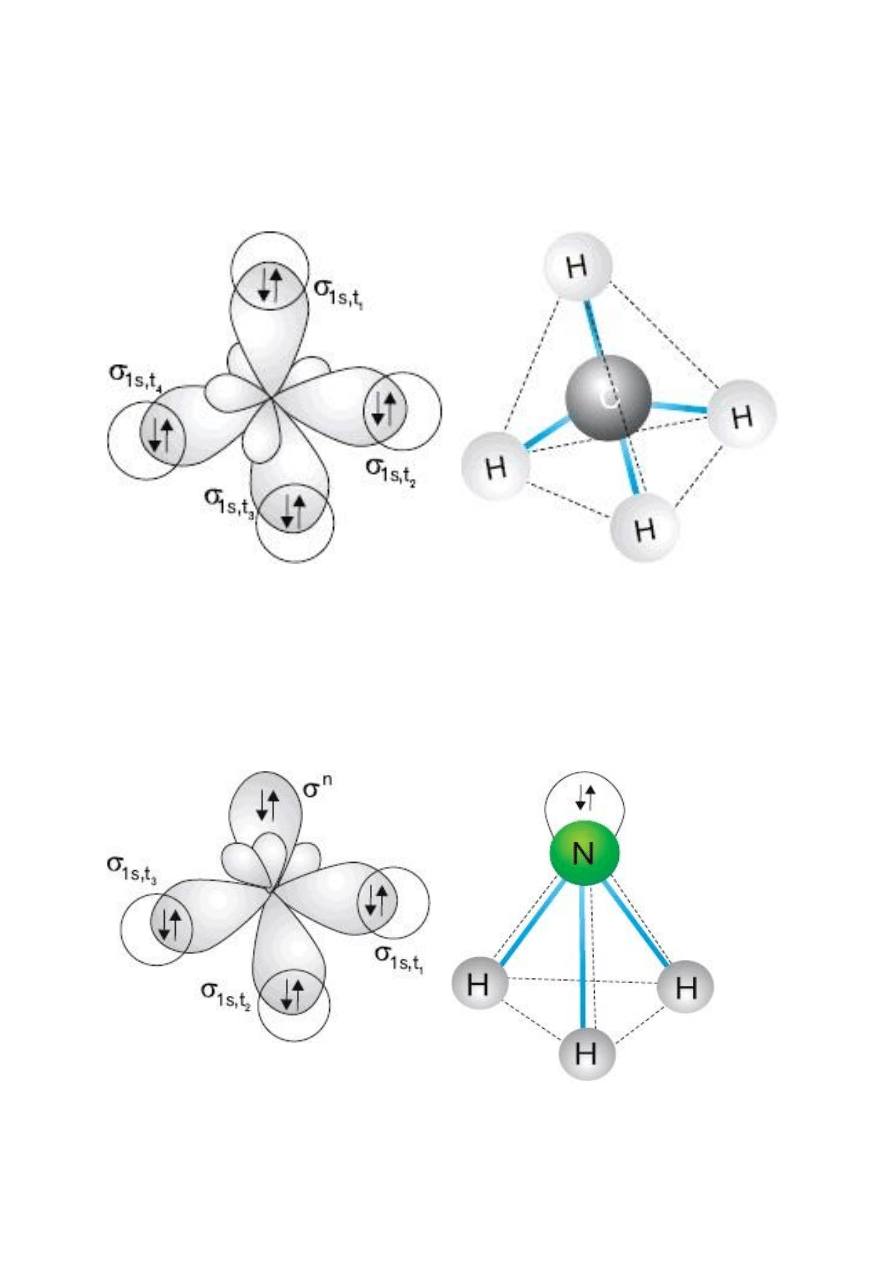
Przykłady cząsteczek – hybrydyzacja sp

3

CH

4

– metan

C: (1s

2

2s

2

2p

2

)

H: (1s

1

)

CH

4

: [He] (σ

s, t 1

)

2

(σ

s, t 2

)

2

(σ

s, t 3

)

2

(σ

s, t 4

)

2

NH

3

– amoniak

N: (1s

2

2s

2

2p

3

)

H: (1s

1

)

NH

3

: [He] (σ

s, t 1

)

2

(σ

s, t 2

)

2

(σ

s, t 3

)

2

(σ

t4

n

)

2

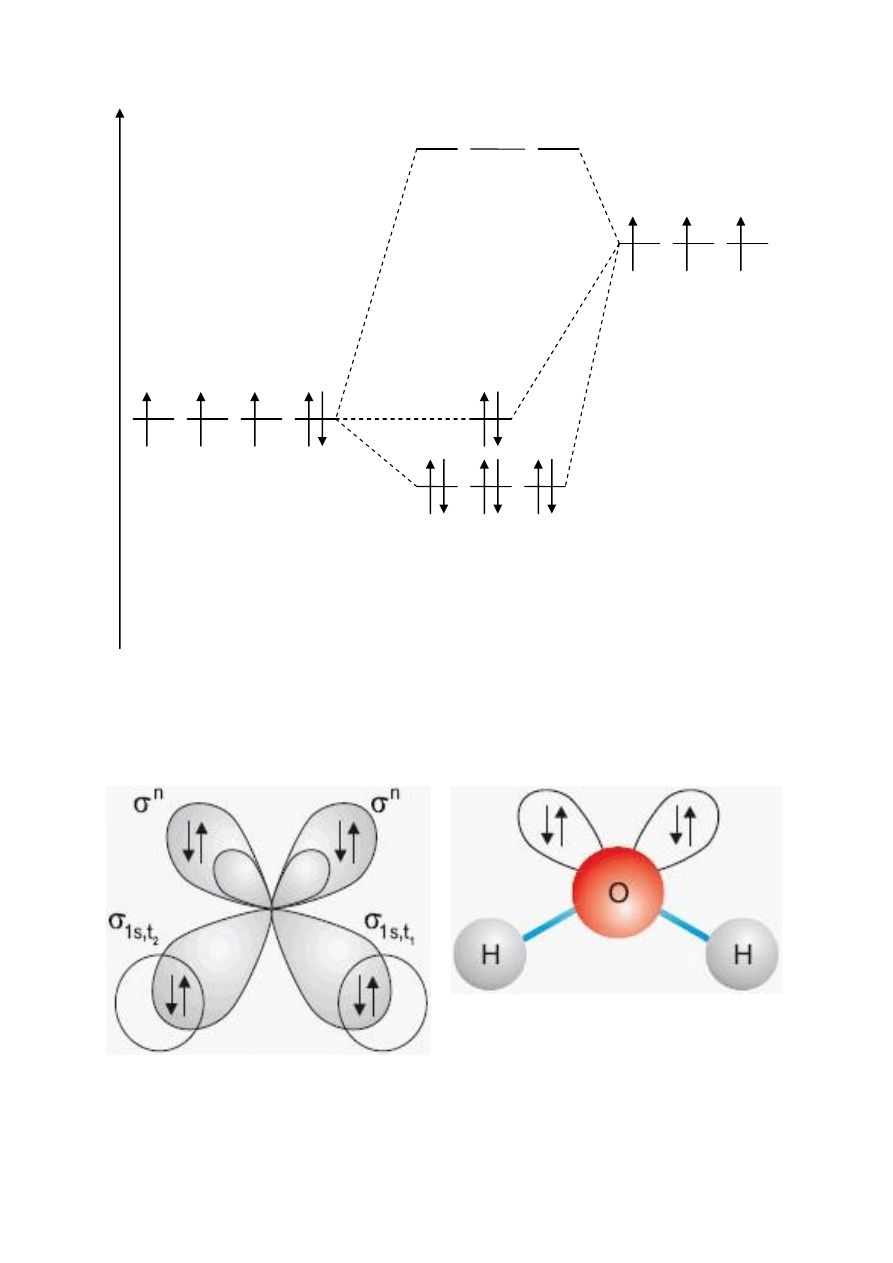
H

2

O – woda

O: (1s

2

2s

2

2p

4

)

H: (1s

1

)

H

2

O: [He] (σ

s, t 1

)

2

(σ

s, t 2

)

2

(σ

t3,4

n

)

4

σ*

s, t1,2,3

E

t

1

t

2

t

3

t

4

Zhybrydyzowany atom azotu

σ

s, t1,2,3

σ

s, t4

n

1s

1

1s

1

1s

1

Atomy wodoru

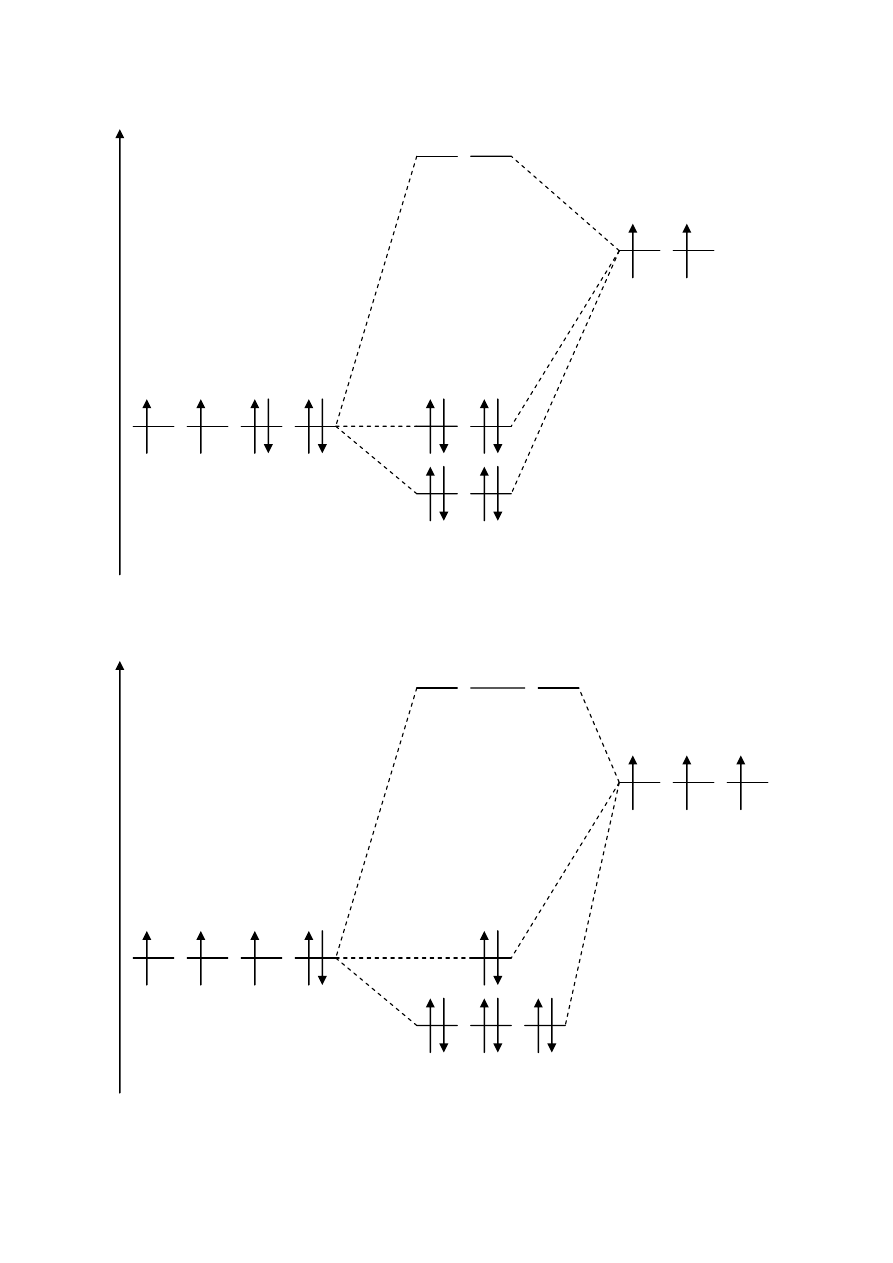
H

3

O

+

- Jon hydroniowy

O: (1s

2

2s

2

2p

3

)

H: (1s

1

)

H

3

O

+

: [He] (σ

s, t 1

)

2

(σ

s, t 2

)

2

(σ

s, t 3

)

2

(σ

t4

n

)

2

identyczna konfiguracja jak dla amoniaku –

cząsteczki izoelektryczne.

σ*

s, t1,2,3

E

t

1

t

2

t

3

t

4

Zhybrydyzowany jon tlenowy

σ

s, t1,2,3

σ

s, t4

n

1s

1

1s

1

1s

1

Atomy wodoru

σ*

s, t1,2,

E

t

1

t

2

t

3

t

4

Zhybrydyzowany atom tlenu

σ

s, t1,2,

σ

s, t 3,4

n

1s

1

1s

1

Atomy wodoru

C

2

H

6

– etan – hybrydyzacja sp

3

C: (1s

2

2s

2

2p

2

)

H: (1s

1

)

C

2

H

4

– eten – hybrydyzacja sp

2

C: (1s

2

2s

2

2p

2

)

H: (1s

1

)

C

2

H

2

– acetylen – hybrydyzacja sp

C: (1s

2

2s

2

2p

2

)

H: (1s

1

)

KONCEPCJA VSEPR

VSEPR (ang. Valence Shell Electron Pair Repulsion - pl. odpychanie par elektronowych
powłoki walencyjnej). Metoda ta została opracowana w 1940 roku przez Nevila Vincenta
Sidgwicka i H.M. Powella. Według niej o budowie przestrzennej cząsteczki decyduje łączna
liczba elektronów walencyjnych wokół atomu centralnego oraz orientacja przestrzenna
obszarów orbitalnych, w których mieszczą się te elektrony.

Teoria VSEPR zakłada, że pary elektronów są rozmieszczone wokół atomu centralnego tak,
aby siły wzajemnego odpychania były możliwie jak najmniejsze, przy czym w sumarycznym
efekcie wszystkich odpychań istotny jest udział wolnych (niewiążących) i wiążących par
elektronowych. Najsłabiej odpychają się pary wiążące, potem para wiążąca z wolną parą
elektronową, a najsilniej dwie wolne pary elektronowe. Inaczej mówiąc, jeżeli odległości par
decydujących o geometrii cząsteczki są maksymalne, to w zależności od liczby tych par
powstają pewne uprzywilejowane struktury o charakterystycznym rozmieszczeniu wolnych i
wiążących par elektronowych na wyróżnionych kierunkach wokół atomu centralnego.

Regularne kształty cząsteczek powstają tylko wtedy, gdy wszystkie pary elektronów
wiążących zostaną wykorzystane do związania takich samych atomów. Występowanie w
cząsteczce różnych ligandów wokół atomu centralnego i niewiążących par elektronowych
zaburza idealne struktury, np. wraz z rosnącą liczbą wolnych par elektronowych może
następować zmiana kąta wiązania.

W niektórych przypadkach metoda VSEPR nie nadaje się do przewidywania budowy
przestrzennej związków, gdyż nie prowadzi do prawidłowego opisu ich struktury, np. nie jest
wygodne zastosowanie jej do opisu budowy cząsteczek zawierających wiązania
zdelokalizowane.

Właściwości i geometrię cząsteczek typu AB

n

można opisać, przyjmując że:

A jest atomem centralnym i n atomów B (jednakowych bądź różnych), zwanych roboczo
ligandami, uczestniczy w tworzeniu orbitali molekularnych z atomem A:



cząsteczka zawiera pierwiastki grup głównych układu okresowego,



hybrydyzacji ulegają orbitale atomu centralnego A,



jeżeli cząsteczka zawiera więcej niż jeden atom centralny to hybrydyzacji ulegają
wszystkie atomy centralne (jak np. C w etenie CH

2

=CH

2

).

Wśród elektronów walencyjnych atomu centralnego wyróżnia się:



wolne pary elektronowe danego atomu (zlokalizowane w polu jednego jądra) -
stanowią pary niewiążące,



elektrony, które są wspólne dla dwóch sąsiadujących atomów - stanowią pary wiążące
(pary zlokalizowane w polu dwóch sąsiadujących jąder).

Wśród par wiążących wyróżnić można pary σ i pary π, które mogą tworzyć:
- wiązania typu σ (o symetrii względem osi łączącej jądra)
- wiązania typu π (o obszarze orbitalnym złożonym z dwóch fragmentów leżących poza osią
łączącą jądra).

Określonym wartościom liczby przestrzennej oznaczanej symbolem Lp, równej liczbie
orbitali zhybrydyzowanych (LH), odpowiada określona geometria cząsteczka. O kształcie
cząsteczki decyduje liczba wiążących par elektronowych (PW) i wolnych par elektronowych

(WPE). Ich suma wskazuje typ hybrydyzacji, a tym samym podstawowy wielościan
koordynacyjny, którego naroża zajmują atomy lub wolne pary elektronowe:

Lp = LH = σPW + WPE

gdzie:
σPW - liczba par elektronowych tworzących wiązanie a; wynosi ona tyle, ile atomów B jest
przyłączonych do atomu centralnego A. Przykład: dla PCl

5

σPW = 5, dla H

2

O σPW = 2, dla

COCl

2

σPW = 3,

WPE - liczba wolnych par elektronowych atomu centralnego; oblicza się ją odejmując od
liczby elektronów walencyjnych atomu centralnego A, taką liczbę elektronów, jaka jest
potrzebna do uzupełnienia konfiguracji wszystkich atomów B i dzieli przez 2, czyli WPE =
1/2 [liczby elektronów walencyjnych atomu A pomniejszona o liczbę elektronów potrzebną
do uzupełnienia oktetów (lub dubletów dla wodoru) dla n atomów B]. Dla jonów ujemnych
zwiększa się, a dla jonów dodatnich zmniejsza się liczbę elektronów walencyjnych o ładunek
jonu. Przykład: Dla H

2

O WPE = (6 − 2) / 2 = 2, dla SO

4

2-

WPE = (6 + 2 − 8) / 2 = 0

Wartość liczby przestrzennej możemy ustalić:
- ze wzoru elektronowego cząsteczki lub przez obliczenie:
- najpierw liczby wolnych par elektronowych atomu centralnego, a następnie liczby
przestrzennej,
- ostatni etap opisu budowy przestrzennej cząsteczki opiera się na fakcie, że do każdej
wartości Lp jest przyporządkowana charakterystyczna struktura przestrzenna. Można więc
powiedzieć, że przestrzenna budowa cząsteczki, a zatem kierunki, w jakich ustawiają się
ligandy i wolne pary elektronowe, są określone liczbą przestrzenną.

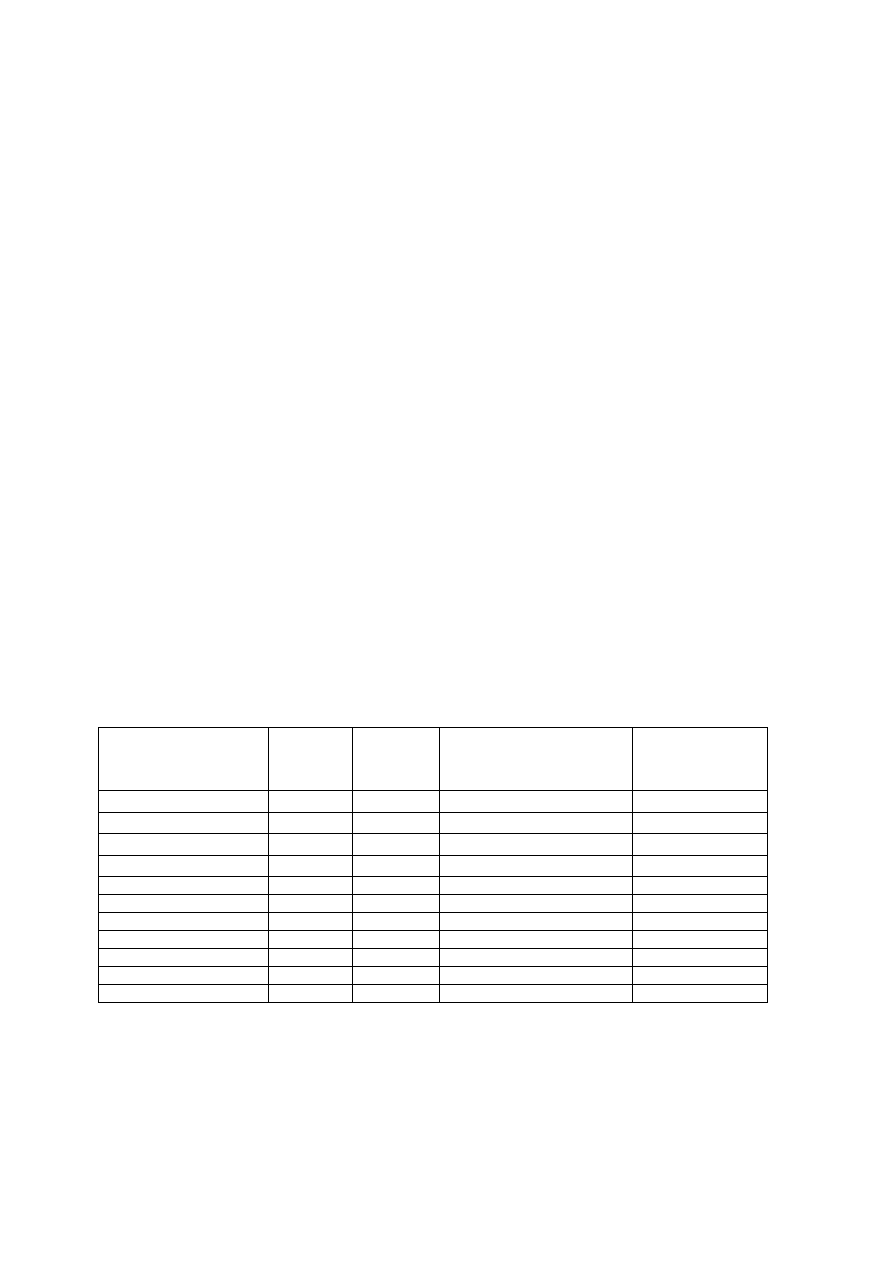
Zależność między liczbą wolnych i wiążących par elektronowych a kształtem cząsteczki
według modelu VSEPR:

Typ Cząsteczki:

A - atom centralny
X - ligandy
E - wolne pary elektronowe

Liczba

przestrzenna

Typ

hybrydyzacji

Kształt cząsteczki

Przykłady

AX

1

E

n

-

-

cząsteczka dwuatomowa

HF, O

2

AX

2

E

0

2

sp

linia

BeCl

2

, HgCl

2

, CO

2

AX

2

E

1

3

sp

2

kształt litery V

NO

2

−, SO

2

, O

3

AX

2

E

2

4

sp

3

kształt litery V

H

2

O, OF

2

AX

2

E

3

5

sp

3

d

nieregularny tetraedr

SF

4

AX

4

E

2

6

sp

3

d

2

kwadrat, płaski

XeF

4

AX

5

E

0

5

sp

3

d

bipiramida trygonalna

PCl

5

AX

5

E

1

6

sp

3

d

2

bipiramida kwadratowa

ClF

5

, BrF

5

AX

6

E

0

6

sp

3

d

2

oktaedr

SF

6

AX

6

E

1

7

sp

3

d

3

piramida pentagonalna

XeF

6

AX

7

E

0

7

sp

3

d

3

bipiramida pentagonalna

IF

7

CZĄSTECZKI O WIĄZANIU ZDELOKALIZOWANYM

Wiązania zdelokalizowane są to wiązania pośrednie miedzy pojedynczymi, a podwójnymi
lub miedzy podwójnymi, a potrójnymi.
Aby opisać ich właściwości, wprowadza się kombinacje liniową orbitali atomowych kilku
atomów.
Orbitale zdelokalizowae charakteryzują się tym, że prawdopodobieństwo napotkania na
elektron wiążący nie wypada w bezpośrednim sąsiedztwie dwóch lub, lecz kilku jąder
atomowych.
Kąty między orbitalami σ decydują o kształcie cząsteczki.

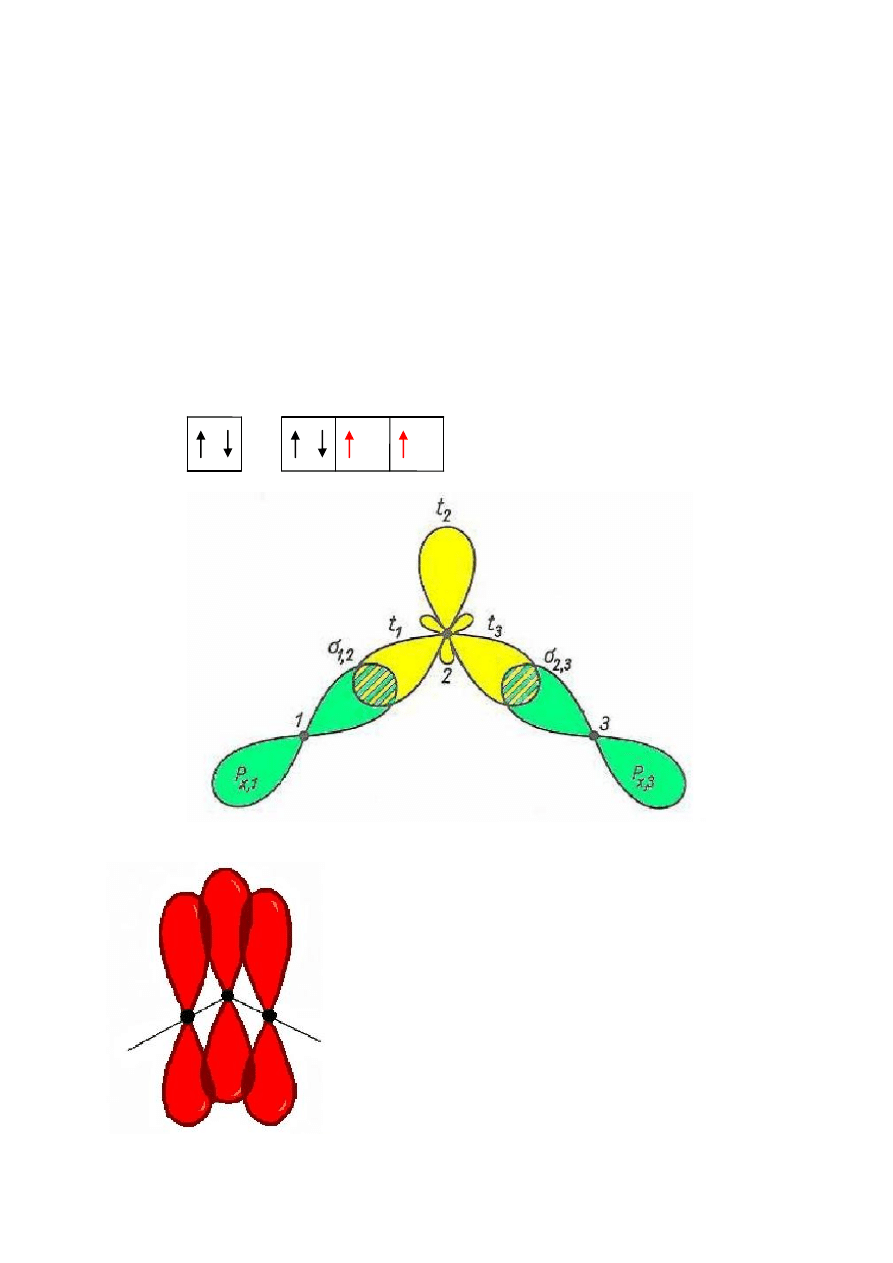
O

3

– ozon

O: (1s

2

2s

2

2p

4

)

[He] [He] [He] 2s

1

2

2s

3

2

t

2

2

σ

1,2

2

σ

3,2

2

Orbitale p

z

1, 2 , 3

p

x,1

+ t

1,2

= σ

1,2

pomiędzy atomami 2,3
p

x,3

+ t

2,3

= σ

3,2

Ich kombinacja liniowa daje 3 orbitale
molekularne:
- wiążący π

del

- niewiążący π

del

0

- antywiążący π

del

*

O

3

: [He] [He] [He] lub KKK (2s

1

)

2

(2s

3

)

2

(t

2

2

) (σ

1,2

)

2

(σ

3,2

)

2

(π

del

)

2

(π

del

0

)

2

(π

del

*

)

0

2s

2p

x

2p

y

2p

z

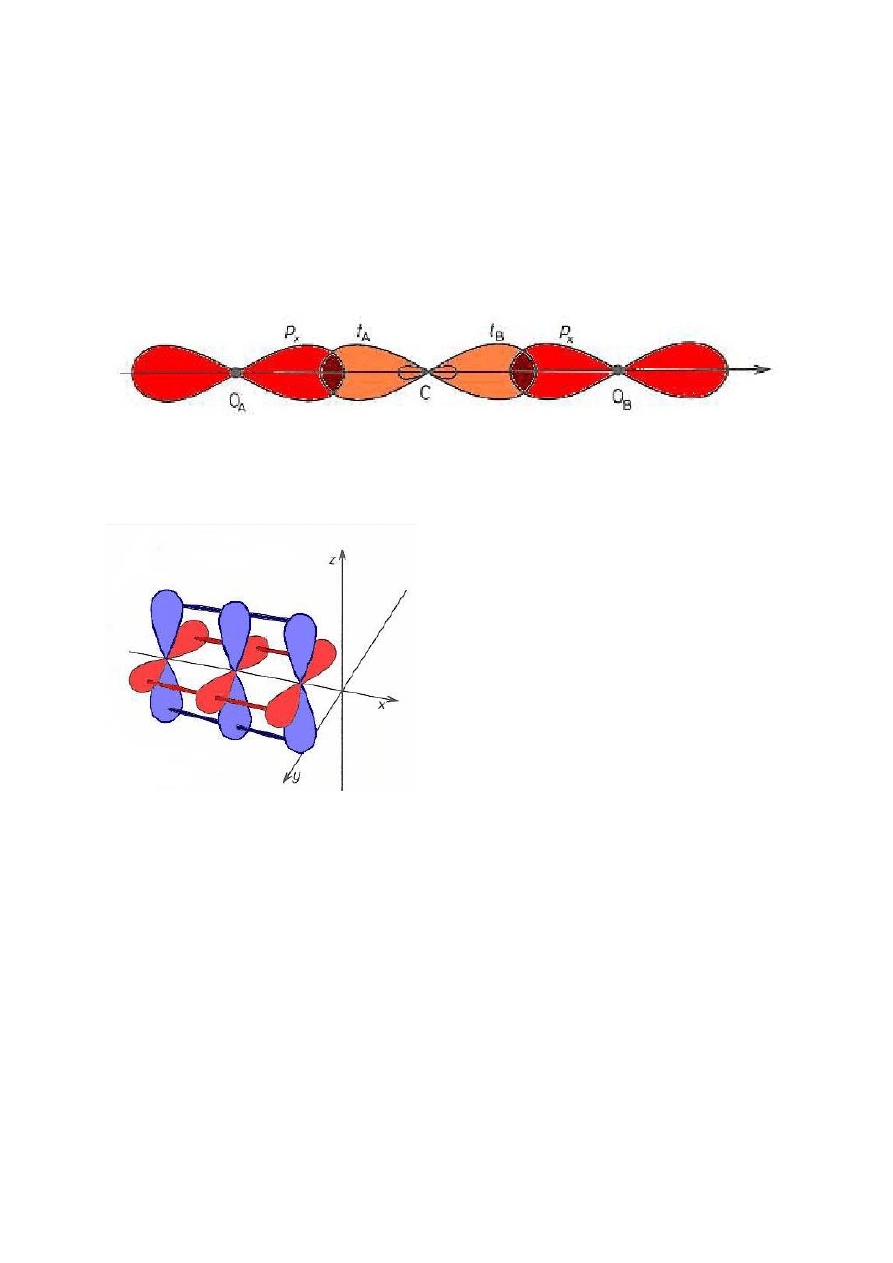
CO

2

– dwutlenek węgla

C: (1s

2

2s

2

2p

2

)

O: (1s

2

2s

2

2p

4

)

C*:(1s

2

2s

2

2t

1

1

2t

2

1

2p

y

1

2p

z

1

) – hybrydyzacja sp

Atom węgla jest atomem centralnym, a atomy tlenu znajdują się w równej odległości od
atomu węgla.
p

x,1

+ t

A

= σ

C-O (1)

p

x,2

+ t

B

= σ

C-O (2)

[He] [He] [He] 2s

1

2

2s

2

2

σ

CO (1)

2

σ

CO (2)

2

Zapełnienie orbitali wiążących σ

C-O (1)

i

σ

C-O (2)

powoduję iż zostaje jeszcze 6 elektronów.

Orbitale p

y

oraz p

z

atomów C, O (1) i (2)

nakładają się co prowadzi do powstania
dwóch grup orbitali zdelokalizowancyh
trójcentrowych.

Ich kombinacja liniowa daje 3 orbitale
molekularne:
- wiążący π

del

- niewiążący π

del

0

- antywiążący π

del

*

[(π

del

)

2

(π

del

0

)

2

(π

del

*

)

0

]

y

oraz [(π

del

)

2

(π

del

0

)

2

(π

del

*

)

0

]

z

zapis sumaryczny:

CO

2

: [He] [He] [He] lub KKK (2s

1

)

2

(2s

2

)

2

(σ

CO (1)

)

2

(σ

CO (2)

)

2

(π

del

)

4

(π

del

0

)

4

(π

del

*

)

0

ZWIĄZKI KOMPLEKSOWE

Związki kompleksowe (kompleksy, związki koordynacyjne) – związki chemiczne, w które w
swoim składzie chemicznym zawierają jeden lub więcej atomów centralnych, otoczonych
przez inne atomy lub grupy atomów zwane ligandami, przy czym przynajmniej jedno
wiązanie atomu centralnego z ligandem ma charakter wiązania koordynacyjnego.

Ze względu na całkowity ładunek elektryczny związków kompleksowych rozróżnia się:
kompleksy obojętne
kompleksy jonowe

Olbrzymia większość związków kompleksowych zawiera w centrum atom lub jon metalu.
Związki te nazywa się wspólnie kompleksami metalicznymi, lub kompleksami metali. Istnieją
jednak także związki kompleksowe, które nie zawierają metalu. Nazywa się je kompleksami
niemetalicznymi. Są to np.:
- kation hydroniowy H

3

O

+

- jon amonowy NH

4

+

- anion I

3

-

Ze względu na liczbę atomów (lub jonów) centralnych rozróżnia się:
- kompleksy jednocentrowe – z jednym atomem centralnym
- kompleksy wielocentrowe – z dwoma lub więcej atomami centralnymi
- klastery – w których występuje trzy lub więcej atomów metali, które są z sobą bezpośrednio
związane, tworząc centralną klatkę, do której są przyłączone ligandy w sposób podobny do
zwykłych kompleksów.

Ligandy mogą być grupami lub jonami nieorganicznymi (np. H

2

O, NH

3

, Cl

–

, CN

–

) lub

grupami wywodzącymi się od związków organicznych (np. aminy, alkohole, fenole, fosfiny,
etery). Kompleksy zawierające ligandy organiczne dzieli się na:
- związki metaloorganiczne – w których występuje choć jedno wiązanie metal-węgiel
- kompleksy organiczne – w których co prawda występują ligandy organiczne, ale nie łączą
się one wiązaniami węgiel-metal

Wg zaleceń IUPAC nazwy ligandów o ładunku ujemnym powinny kończyć się na "o",
natomiast nazwy ligandów obojętnych nie mają zmienianych końcówek. Przykłady:

cząsteczka H

2

O – akwa (dawn. akwo)

cząsteczka NH

3

– amina (dawn. ammino)

grupa CN

−

– cyjano

grupa SCN

−

- tiocyjaniano

grupa NO

2

-

– nitrito−N (dawn. nitro)

grupa ONO

–

– nitrito-O

grupa NO

3

– azotano

grupa NO – nitrozyl (dawn. nitrozylo)
grupa NS – tionitrozyl (dawn. tionitrozylo)
grupa CO – karbonyl (dawn. karbonylo)
grupa CS – tiokarbonyl (dawn. tiokarbonylo)
grupa OH

–

– hydrokso

grupa F

–

– fluoro

grupa Cl

–

– chloro

grupa SO

4

2-

– siarczano

grupa S

2

O

3

2-

– tiosiarczano

W nazwie jonu kompleksowego najpierw wymienia się ligandy, a na końcu nazwę atomu
centralnego, np. [Co(NH

3

)

6

]

3+

– jon heksaaminakobaltowy(III) (gdzie symbol "III" oznacza

wartościowość kobaltu). Liczbę ligandów określa przedrostek grecki mono-, di-, tri- itd. (wg
aktualnych zaleceń nomenklaturowych IUPAC; w nomenklaturze tradycyjnej jest to jedno-,

dwu-, trój- itd.). Przed grupą umieszczoną w nawiasach stosuje się liczebniki łacińskie bis-,
tris-, tetrakis- itd., np. jon dichlorobis(etylodiamina)chromowy(III).

W nazwach soli określany jest najpierw anion, np.

Na[Al(OH)

4

] – tetrahydroksoglinian sodu

Mg[Al(OH)

4

]

2

– bis(tetrahydroksoglinian) magnezu

[CoCl

2

(NH

3

)

4

]Cl – chlorek tetraaminadichlorokobaltu(III)

K

3

[Fe(CN)

6

] – heksacyjanożelazian(III) potasu

K

2

[Co(CN)(CO)

2

NO] – cyjanodikarbonylnitrozylkobaltan(II) potasu

[Pt(NH

3

)

6

]Cl

4

– chlorek heksaaminaplatyny(IV)

Literatura:

1. Adam Bielański „Podstawy chemii nieorganicznej” WNT Warszawa 2003
2. wikipedia
3. materiały do zajęć z chemii AGH, Kraków