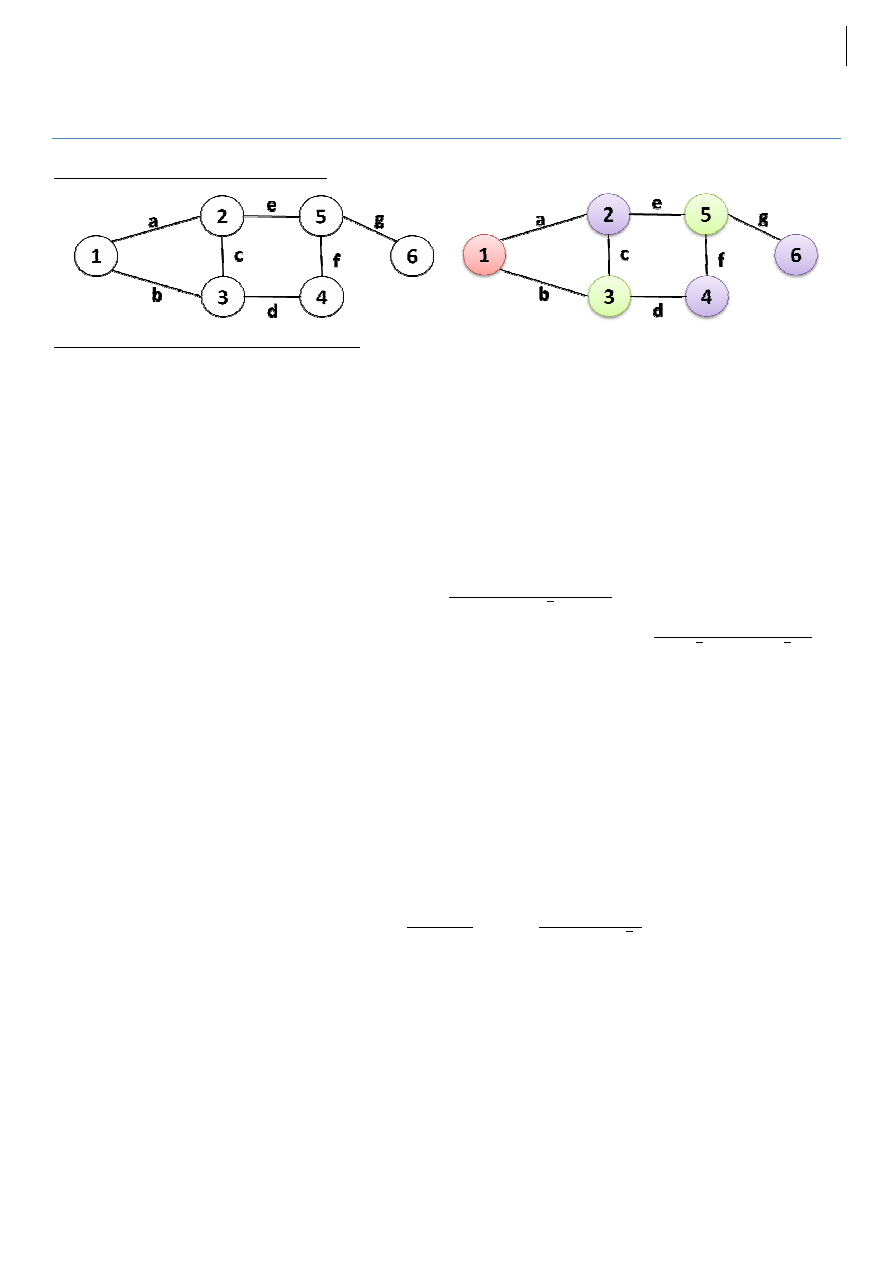
Kolorowanie wierzchołków – optymalne, przykład 1
Teoria grafów i sieci
1
Michał Kapałka
mkapalka@wat.edu.pl
Kolorowanie wierzchołków (o) – przykład 1
Pokoloruj graf przedstawiony na rysunku
Procedura pokolorowania wierzchołków grafu
1. Wyznaczenie wszystkich maksymalnych zbiorów wewnętrznie stabilnych (baz minimalnych)
( )
- wektor określający jednoznacznie zbiór wierzchołków,
( ) =
– binarna macierz incydencji
( )
=
→
łę
→
łę →
( )
ś
ę
( ) =
⎣
⎢
⎢
⎢
⎢
⎡
1
1
0
1
0
1
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
1⎦
⎥
⎥
⎥
⎥
⎤
(
) = (
+
) (
+
)(
+
)(
+
)
(
)
(
+
)(
+
)(
+
)
(
)
=
= (
+
)(
+
)(
+
) =
+
+
+
+
+
+
+
ą ę
Bazy minimalne:
= { , , }
= { , , }
= { , , , }
= { , , , }
= { , , , }
Maksymalne zbiory wewnętrznie stabilne:
= { , , }
= { , , }
= { , }
= { , }
= { , }
2. Wyznaczenie najmniej licznego pokrycia
( )
- wektor określający jednoznacznie zbiór wierzchołków,
- macierz „pokrycia” wierzchołków
( )
=
→
ł
→
ł ó →
( )
ś
=
⎣
⎢
⎢
⎢
⎢
⎡
0
1
0
1
0
0
1
0
0
1
0
1
1
0
1
0
1
0
0
0
1
0
0
1
0
0
1
0
1
0⎦
⎥
⎥
⎥
⎥
⎤
(
) = (
+
) (
+
)(
+
)(
+
)(
+
+
) =
= (
+
) (
+
) =
+
+
+
Wybieramy najmniej liczne pokrycie (wektor): np.
=
,
=
\
=
= { , , }
=
\
= { }
=
\(
∪
) = { , }
Wyszukiwarka
Podobne podstrony:
Optymalizacja przykł 1
Przykłady smiesznych kanapek kolorowe
11 MEYER Z i inni Optymalizacja warunków posadowienia dużej hali produkcyjnej na przykładzie budowy
Przykłady optymalizacji
Asembler ARM przyklady II
Sily przyklady
Przykłady roli biologicznej białek
Optymalizacja LP
style poznawcze jako przykład preferencji poznawczych
pytania przykladowe exam zaoczne(1)
przykładowa prezentacja przygotowana na zajęcia z dr inż R Siwiło oceniona
17 Metodologia dyscyplin praktycznych na przykładzie teorii wychowania fizycznego
Zasady ergonomii w optymalizacji czynności roboczych
optymalizacja fak
Organizacja stanowiska pracy przykładowa prezentacja słuchaczy
więcej podobnych podstron